Assignment of Calibration Information to Deeper Phylogenetic Nodes is More Effective in Obtaining Precise and Accurate Divergence Time Estimates

Abstract

Divergence time estimation has become an essential tool for understanding macroevolutionary events. Molecular dating aims to obtain reliable inferences, which, within a statistical framework, means jointly increasing the accuracy and precision of estimates. Bayesian dating methods exhibit the propriety of a linear relationship between uncertainty and estimated divergence dates. This relationship occurs even if the number of sites approaches infinity and places a limit on the maximum precision of node ages. However, how the placement of calibration information may affect the precision of divergence time estimates remains an open question. In this study, relying on simulated and empirical data, we investigated how the location of calibration within a phylogeny affects the accuracy and precision of time estimates. We found that calibration priors set at median and deep phylogenetic nodes were associated with higher precision values compared to analyses involving calibration at the shallowest node. The results were independent of the tree symmetry. An empirical mammalian dataset produced results that were consistent with those generated by the simulated sequences. Assigning time information to the deeper nodes of a tree is crucial to guarantee the accuracy and precision of divergence times. This finding highlights the importance of the appropriate choice of outgroups in molecular dating.

Introduction

Molecular dating has become an essential tool for understanding the historical scenarios associated with important evolutionary events.¹ Indeed, the inclusion of divergence time estimates in phylogenetic studies has become increasingly popular in the last decade, and the majority of works addressing macroevolutionary events incorporate time-dated trees.^2–4 The development of divergence time estimation methods based on Bayesian inference via Markov chain Monte Carlo has attracted widespread interest in the field mainly because they enable the incorporation of a priori knowledge about the divergence of lineages, such as fossil ages and geological events.^5,6

The purpose of divergence time inference is the estimation of node ages with an increasing accuracy and precision. To achieve this aim, numerous studies have explored different models of evolutionary rate variation along branches,^7,8 their robustness to taxonomic sampling,^9–11 the influence of distinct priors,^12–14 and the appropriate usage of calibration information.^15–18 For example, with respect to the influence of calibration information, Linder et al⁹ showed that the effects of calibration information on time estimation are greater on nodes close to where the calibration prior is placed, and Inoue et al.¹² added that priors on node ages have a major impact on posterior time estimation.

A greater uncertainty associated with deeper divergences has been described as being intrinsic to dating methods, which is evidenced by the linear relationship between the width of the CIs associated with such estimates and the mean of the posterior distribution of divergence times, even when the number of sites approaches infinity.^19,20 However, no study has yet explored the possibility of reducing the uncertainty associated with deeper nodes via the adoption of alternative calibration strategies. In fact, the effect of the arrangement of calibration information on the accuracy and precision of the obtained node ages remains an open question.

In this study, we investigated how the placement of calibration information at alternative nodes of a phylogeny affects the accuracy and precision of divergence time estimates. For this purpose, we relied on simulated and empirical data. The empirical data consisted of a dataset of mammalian genes in which the phylogenetic relationships were well resolved. Our findings suggest that the use of deeper calibration points significantly improves posterior time estimation.

Materials and Methods

Evaluation of the effect of calibration information on deeper nodes was conducted by analyzing simulated and empirical datasets. In the simulated datasets, rooted trees, with both symmetric and asymmetric shapes, were used to evolve gap-free alignments, which were then used to estimate divergence times under three different conditions representing distinct scenarios regarding calibration points. Empirical mammalian data were compiled to permit sampling of taxa resulting in symmetric and asymmetric topological shapes. In the analyses of simulated data, the performance of the molecular dating procedure was measured based on the accuracy and precision of the time estimates. In the empirical data analyses, only the precision, ie, the uncertainty, of the posterior distribution estimates was calculated. The details of the analyses are as follows.

Simulated datasets

When simulating nucleotide sequences, we relied on trees in which branch lengths were measured in terms of substitutions per site. Trees were obtained via the multiplication of branch lengths of ultrametric trees, in which the lengths of branches were measured in absolute times, by the evolutionary rates, that were independently drawn from a normal distribution.

Two tree topologies, with asymmetric and symmetric shapes, respectively, were employed to simulate DNA sequences (Fig. 1a and b). In both trees, all internal branches were set to have a time span of five million years. All of the model parameters and base frequency values used to generate the sequences were extracted from an alignment of 800 complete genes from 36 mammalian species downloaded from OrthoMaM.²¹ This was done in order to simulate alignments with mammal-like evolutionary features. Sequences consisting of 10,000 base pairs were simulated in the Seq-Gen program²² under the general time reversible model (GTR) and a gamma distribution of rate variation among sites with four categories. GTR relative rate parameters values were set at 0.67 (G→T), 1.0 (A→C), 3.33 (A→G), 0.6 (A→T), 0.73 (C→G), and 4.13 (C→T). The shape parameter of the gamma distribution that models rate heterogeneity across sites was set at 0.4, and the following base frequencies values were used: f_A = 0.255, f_C = 0.252, f_G = 0.251, and f_T = 0.222. We generated 100 replicate datasets for each studied topology (asymmetric and symmetric). Finally, the evolutionary rates at each branch were sampled from a normal distribution with mean equal to 2 × 10⁻⁹ substitutions/site/year (s/s/y) and the standard deviation (SD) of 4 × 10⁻¹⁰. The mean rate was obtained by dividing the sum of the lengths of the branches that connects the root of the mammalian tree, the Theriimorpha–Australosphenida node, to Homo by 176.1 million years. This is the average age of the early divergence between therians and monotremes.¹⁶ The lengths of the branches were obtained by parsing trees that contained Homo and platypus in the OrthoMaM database.

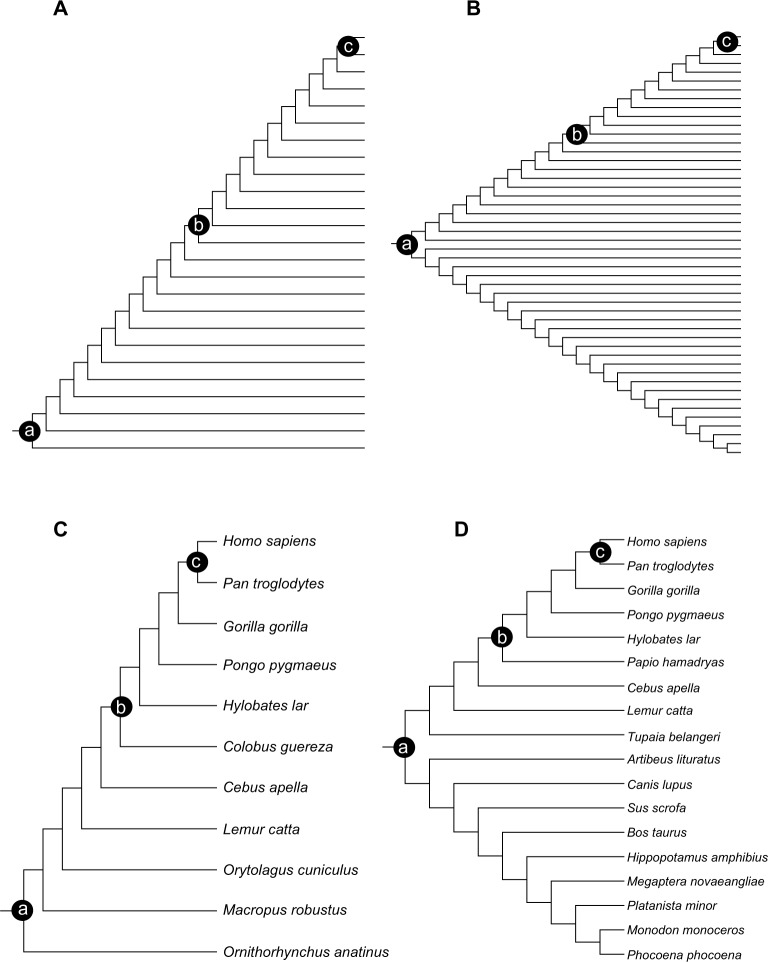
Figure 1.

Simulated (A, B) and empirical (C, D) tree topologies investigated in this study. Nodes at which calibration information was inserted are indicated with black circles. (a) Root calibration nodes, (b) median calibration nodes, and (c) shallow calibration nodes.

After the alignments were simulated, divergence times were estimated under three different conditions: calibration was assigned to (A) the root of the tree, at 120 Ma; (B) the median node, at 60 Ma; or (C) the shallowest node, at 5 Ma (Fig. 1). Under all calibration strategies, calibration priors were normally distributed around their true values (ie, the mean of the normal distribution was the true value of divergence – 120, 60, and 5 Ma). SDs were set allowing a ±1 Ma range of the 95% credibility interval. The same procedure was used to analyze the asymmetric and symmetric topologies. However, for the symmetric topologies, calibration information was placed solely at one of the daughter lineages of the root (Fig. 1b).

All divergence time inferences were conducted under a Bayesian framework implemented in BEAST 1.7.5²³ using the same model of evolution (GTR + G) applied to generate the sequences. An uncorrelated lognormal relaxed clock²⁴ was employed to model the evolution of evolutionary rates, and a Yule prior was employed to model the speciation process. Posterior distributions were obtained using the Markov chain Monte Carlo algorithm. In every analysis, Markov chains were sampled every 1,000th generation until 9,000 trees were obtained after an adjustable burn-in period. The tree topologies were fixed in BEAST, so we could evaluate the performance of the divergence time inferences alone. For the sake of comparison, we have also run the entire analyses with the MCMCTree program of the PAML package²⁵ and the results were unaltered. Therefore, we have only reported the estimates obtained with BEAST.

Empirical dataset

Two empirical datasets consisting of mammalian mitochondrial genes were chosen to construct a topology analogous to those used in the analysis of the simulated datasets. The first mammalian sample consisted of 11 species of mammals in which the phylogenetic relationships showed an asymmetric topology (Fig. 1a). The second mammalian sample consisted of 18 terminals in which the phylogenetic relationships presented a symmetric shape (Fig. 1b). The 13 mitochondrial genes that encode protein sequences were downloaded from GenBank (accession numbers are provided in Table 1 of the Supplementary Material) and were aligned separately in MUSCLE²⁶ based on their respective amino acid sequences. Then, single gene alignments were concatenated in SeaView²⁷ to obtain a supermatrix consisting of 11,478 and 11,649 base pairs, for the symmetrical and asymmetrical scenarios, respectively. These supermatrices were used in the subsequent molecular dating analysis.

Three distinct calibration scenarios were applied in which calibration priors were assigned to the shallowest, median, and root nodes of the asymmetric and symmetric topologies (Fig. 1c and d). The priors were specified based on normal distributions according to the ages and limits suggested by Benton and Donoghue.¹⁶ Therefore, for the asymmetric mammalian topology, the calibration priors were as follows: (A) Homo–platypus (mean = 176.08 Ma, SD = 9.0 Ma); (B) Homo–Colobus (mean = 28.45 Ma, SD = 3.3 Ma); and (C) Homo–Pan (mean = 8.25 Ma, SD = 1.0 Ma). For the symmetric topology, the following priors were employed: (A) Laurasiatheria–Euarchontoglires (mean = 104.15 Ma, SD = 5.6 Ma); (B) Homo–Macaca (mean = 28.45 Ma, SD = 3.3 Ma); and (C) Homo–Pan (mean = 8.25 Ma, SD = 1.0 Ma). Divergence time inference was also conducted in BEAST 1.7.5, with an uncorrelated lognormal relaxed clock, a Yule prior, and the GTR + G4 evolutionary model. In every analysis, Markov chains were sampled every 1,000th generation until the effective sample size (ESS) of divergence times was greater than 200, discarding the burn-in period. The ESSs of the inferred parameters were calculated in Tracer v. 1.5. The tree topologies were fixed during BEAST runs as well as in the analysis with simulated data.

Precision and accuracy of the divergence time estimates

To evaluate the uncertainty of the estimated posterior node ages in both the simulated and empirical data, we used the SD of the credibility intervals as a measure of precision. In the simulated dataset, 100 replicates were obtained for each experiment. Thus, in order to facilitate visualization and interpretation, all parametric values were averaged. To monitor the reduction of uncertainty from the root to the shallowest node, we conducted linear regressions between the ages of the nodes and their respective SDs. Second, in the analysis of simulated data, we also evaluated the accuracy of the node age estimates. To determine the accuracy of the estimates, we calculated the error of the estimates, ie, the difference between the mean of the posterior distribution and the true parametric value.

Results

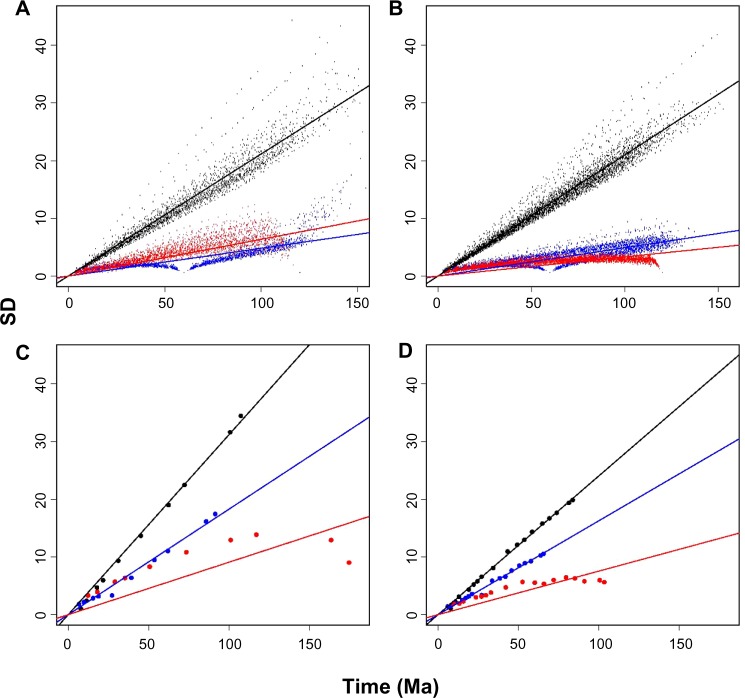
As theoretically predicted, the precision of the posterior distributions of the node ages associated with the three distinct calibration strategies increased from the deeper nodes to the shallowest nodes.^19,20 The effect of a lower precision in the node ages estimated for deeper nodes was, however, greatest under the scenario where the calibration point was set at the shallowest node (5 Ma). This effect is indicated by the slopes of the regressions of the mean divergence time estimates against their corresponding mean SD values, obtained from all MCMC replicates (Fig. 2a and b and Table 1). In general, when the calibration information was set to 5 Ma, the uncertainty of the time estimates along the nodes increased. These results were robust to tree symmetry, indicating that assigning calibration priors to shallow nodes is not the most appropriate strategy for ensuring higher levels of divergence time precision.

Figure 2.

Precision of the estimates, as measured by the SD of the posterior distribution of node ages, ordered from the leaves to the root. Each point indicates the SD values for each node along the replicates. The results for the shallow, median, and root calibrations are presented in black, blue, and red, respectively. The solid lines are the linear regressions of the respective values. In (A) and (B), the values were obtained using the simulated tree topologies (A) and (B) of Figure 1, respectively. In (C) and (D), the values were obtained via the empirical topologies (C) and (D) from Figure 1, respectively.

Table 1.

Linear regression parameters inferred. The intercept is the origin point in all cases. All P-values < 0.001.

DATASET	CALIBRATION POINT	SLOPE	R-SQUARED
Simulated asymmetrical	Shallow	0.212	1.0
	Median	0.048	0.88
	Deep	0.064	0.88
Simulated symmetrical	Shallow	0.208	1.0
	Median	0.049	0.95
	Deep	0.033	0.87
Empirical assymetrical	Shallow	0.312	0.99
	Median	0.183	0.99
	Deep	0.091	0.83
Empirical symmetrical	Shallow	0.240	0.99
	Median	0.163	0.99
	Deep	0.076	0.93

The analyses in which calibration information was placed at the median and root nodes (60 and 120 Ma, respectively) rendered lower SD values (ie, a higher precision) compared to the shallow-node calibration strategy. This finding indicates that adding a calibration point to either a median or root node improves the precision of the estimated divergence dates. The effect of tree symmetry on the median and root node strategies was also negligible. In the analysis of the asymmetric topology, employing the calibration prior at the 60 Ma node resulted in a slightly higher precision of the estimated node ages (lower SD). Conversely, in the analysis involving the symmetric topology, the opposite pattern was observed: setting the calibration prior at the root node (120 Ma) yielded slightly more precise estimates.

The results obtained from the empirical mammalian dataset were in agreement with the simulated sequences (Fig. 2c and d). In all cases, the estimated divergence dates were associated with the SD values, in other words, the mean of the posterior distribution of divergence times was positively correlated with the SD obtained for that distribution. As observed in the simulation analyses, the adoption of calibration priors at the shallowest nodes produced time estimates with higher SD values. In this case, however, independent of the tree topology, when the calibration was set at the root node, it unambiguously yielded estimates that were more precise than those obtained using the median node calibration. These results indicated that when calibration information was assigned to the root node, a greater gain of precision was observed.

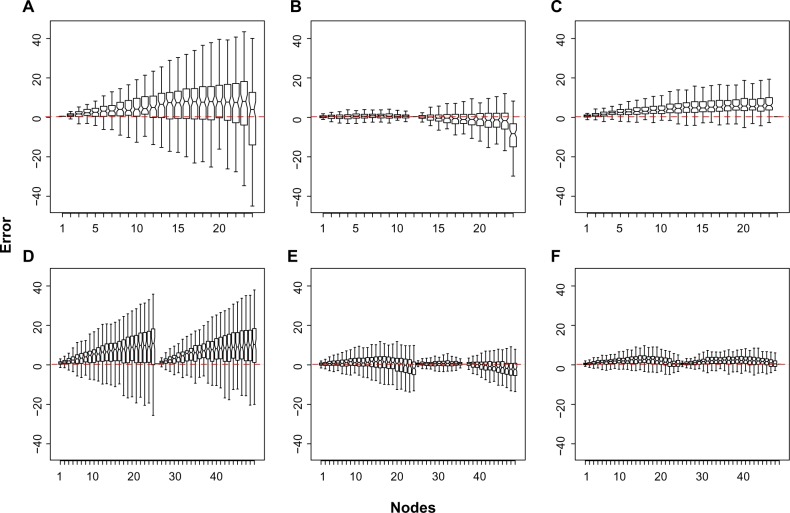
The boxplots of the accuracy of the estimates on each node, measured by the difference between the estimated value and the true parametric value, were generated for simulated dataset. Setting the calibration information at the shallowest node (5 Ma) yielded the least accurate estimates for both tree topologies, as shown in Figure 3. For the asymmetric tree topology, setting the calibration prior at either the median or root nodes resulted in time estimates with a similar accuracy. In this case, the divergence times clearly depicted a higher accuracy around the nodes close to the calibration information, resulting in a conspicuous increase in accuracy around the median nodes when the 60 Ma calibration was adopted (Fig. 3b). For the symmetric topology, the overall performance of the calibrations in informing the specular subtree topology was negatively impacted (Fig. 3d–f). Tree shape had a greater effect on the accuracy of the estimates than on their precision. However, this impact was higher when adopting the 5 Ma calibration. The median and root calibrations presented superior performances.

Figure 3.

Boxplots of the accuracy of the estimates on each node (x-axis), of the simulated tree topologies over the 100 replicates, as measured by the difference between the estimated value and the true parametric value. (A), (B), and (C) are asymmetric topology assigning the calibration at shallow, median, and root node, respectively; (D), (E), and (F) are symmetric topology assigning the calibration at shallow, median, and root node, respectively. Nodes were ordered from the leaves to the root. In (D–F), the tip node of the specular subtree is placed in the middle of the x-axis.

Discussion

The main purpose of this study was to determine the calibration strategy associated with the greatest gain in the accuracy and precision of divergence time estimations. To this end, we applied three distinct scenarios, with calibrations positioned on the shallowest, median, and root nodes of the tree and then compared the obtained time estimates based on both simulated and empirical data. We show that setting the calibration point at the root of the tree yielded the most precise time scale, whereas the median and root calibrations returned equally accurate estimates. Conversely, assigning calibration information to the shallowest phylogenetic nodes has proven to be an ineffective strategy for decreasing the uncertainty of estimated divergence times. Although the precision of the estimates was lower for deeper nodes under all of the analyzed calibration strategies,²⁰ this decrease in precision was steeper for those analyses in which calibrations were set at the shallowest nodes. Our findings in this regard were consistent, whatever the assumed tree topology (symmetric or asymmetric), and were observed in analyses based on both the simulated and empirical datasets, supporting the generality of the patterns reported here.

Similar patterns were observed in terms of accuracy, as the calibration strategies set at the root of the tree or at median nodes produced estimates with smaller errors. Calibration plays a crucial role in molecular dating,²⁸ and it is well accepted that relying on as many calibration points as possible is ideal to obtain accurate estimated divergence times, considering that such calibrations are reliable.^10,17,29 Indeed, because calibration information is pooled across nodes, a higher level of accuracy will be associated with adjacent divergence estimates.⁹ However, it is not always feasible to employ several different calibration points because the main source of calibration information, the fossil record, is often incomplete.³⁰ Nevertheless, we observed that when the calibration is set at a shallow node, it does not pool information efficiently for neighboring nodes. This observation therefore emphasizes the importance of relying upon the use of some calibration information at deeper nodes to ensure a greater accuracy of the obtained divergence time estimates.

It is important to consider one particular aspect of our results. Our estimates were based on nucleotide alignments of sequences consisting of 10,000 base pairs, each of which was generated from single parameters. Therefore, no partitioning scheme was applied. Although partitioning is biologically plausible, as distinct portions of the genome may evolve at different rates,^31,32 partitioning alignments into several subsets would substantially increase the number of variables required for estimation. However, our purpose in the present work was to elaborate the scenario with the smallest possible number of variables, specifically to evaluate our main question, ie, the uncertainty of the posterior density of node ages.

It has been previously shown that uncertainty in posterior time estimates is expected to increase as the estimated divergence time becomes older, either due to assuming a global clock¹⁹ or a variable-rate model.²⁰ However, the role of calibration in reducing these effects was previously unknown. Some recent studies have advised the use of time information at the root of a tree,^28,29 but none of them has formally performed statistical tests to evaluate the increase in the precision and accuracy associated with the calibration strategy. Our findings strongly suggest that the use of calibration information at deeper nodes improves posterior divergence time estimations. This result highlights the importance of the appropriate choice of outgroups in molecular dating, indicating that outgroup sampling should be based on the availability of calibration information. If reliable fossil records exist that are external to an ingroup, we propose that their extant relative taxa should be included to enable the use of calibration information at the root and/or deep nodes of a tree, which can only be achieved if molecular data are available.

Estimation of the age of splits between lineages enables us to better understand the historical scenario under which a lineage evolved. Therefore, the development of more efficient methods has been a constant focus of attention. Here, we examined the role of calibration in decreasing the uncertainty associated with posterior probabilities and found that assigning time information to the root of a tree is pivotal to ensure the accuracy and precision of timescales. Further studies considering larger and deeper phylogenies will be needed to determine the generality of our findings. Empirical data associated with such deep phylogenies may be used to evaluate the existence of the same possible pattern for these older divergences, such as divergences between phyla and ancient radiations.

Supplementary Material

Table S1. Accession numbers of the mammalian mitochondrial genomes used in this study.