An integrated computational model of the bone microenvironment in bone-metastatic prostate cancer

Abstract

Bone metastasis will impact most men with advanced prostate cancer. The vicious cycle of bone degradation and formation driven by metastatic prostate cells in bone yields factors that drive cancer growth. Mechanistic insights into this vicious cycle have suggested new therapeutic opportunities, but complex temporal and cellular interactions in the bone microenvironment make drug development challenging. We have integrated biological and computational approaches to generate a hybrid cellular automata (HCA) model of normal bone matrix homeostasis and the prostate cancer-bone microenvironment. The model accurately reproduces the basic multicellular unit (BMU) bone coupling process, such that introduction of a single prostate cancer cell yields a vicious cycle similar in cellular composition and pathophysiology to models of prostate-to-bone metastasis. Notably, the model revealed distinct phases of osteolytic and osteogenic activity; a critical role for mesenchymal stromal cells (MSCs) in osteogenesis; and temporal changes in cellular composition. To evaluate the robustness of the model is we assessed the effect of established bisphosphonate and anti-RANKL therapies on bone metastases. At ~100% efficacy, bisphosphonates inhibited cancer progression while, in contrast to clinical observations in humans, anti-RANKL therapy fully eradicated metastases. Reducing anti-RANKL yielded clinically similar results, suggesting that better targeting or dosing could improve patient survival. Our work establishes a computational model that can be tailored for rapid assessment of experimental therapies and delivery of precision medicine to prostate cancer patients with bone metastases.

Introduction

Prostate cancer frequently metastasizes to bone with approximately 90% of the men displaying evidence of skeletal lesions upon autopsy (1). Despite medical advances, prostate to bone metastases remain incurable with treatments being mainly palliative (2). Advances in our knowledge of the molecular mechanisms underlying the disease should provide therapeutic opportunities to improve overall survival rates but on a more microenvironmental scale, predicting how putative therapies will impact multiple cellular responses remains a challenge. However, integrating key biological findings with the power of computational modeling offers a unique opportunity to assess the impact of putative therapies on the progression of prostate cancer.

Understanding the normal BMU bone remodeling process is critical for the generation of a robust computational model (3). The initiation of the BMU by local or systemic signals results in the retraction of the osteoblasts from the bone surface and the formation of a canopy. Local MSCs generate RANKL-expressing osteoblasts precursors that subsequently facilitate osteoclast recruitment, maturation and bone resorption. Degradation of the bone results in the release of sequestered growth factors such as transforming growth factor beta (TGFβ) that in turn serve to control the extent of bone degradation and osteoblast expansion. After osteoclast apoptosis, osteoblasts rebuild the bone with a portion terminally differentiating into osteocytes and the remainder reconstituting the bone lining, ready for the next remodeling cycle.

In the metastatic prostate cancer-bone microenvironment, prostate cancer cells perturb the balance of the BMU to generate a “vicious cycle” via the expression of factors such as RANKL thereby inducing excessive bone resorption (4). The release of sequestered growth factors from the bone matrix such as TGFβ in turn stimulates the survival and growth of the metastatic prostate cancer cells. Of note, prostate to bone metastases are also characterized by areas of extensive bone formation/osteogenesis, a phenomenon that is mediated by factors such as, endothelins (ET) and bone morphogenetic proteins, BMP-2 and BMP-4 (5).

To date, the majority of our knowledge of the mechanisms driving prostate cancer progression has been garnered by focusing on the role of individual cancer/host derived molecules. However, this molecular reductionist approach often does not take into account the multiple cellular effects of molecular mechanisms being investigated. Mathematical and computational models are a powerful means with which to study complex in vivo interactions. Numerous advances using this approach have identified roles for tumor heterogeneity in cancer progression and evolution, accurately predicting glioma progression and response to disease and, describing the cellular dynamics of bone remodeling (6). To understand the simultaneous and multiple interactions occurring over time in the metastatic prostate cancer bone microenvironment we have generated a HCA based integrated computational model. Using this approach we tested the models response to therapies currently used in the clinic to treat prostate to bone metastases (7–9). We posit that computational models will be a powerful means with which to test the efficacy of available or putative therapies for the treatment of prostate to bone metastases.

Quick guide to assumptions and equations

For our HCA model we consider 6 different cell types, including 5 residents of the BMU: Osteoblasts (OBs), Osteoclasts (OCs), precursor Osteoblasts (pOBs), precursor Osteoclasts (pOCs), MSCs, as well as prostate tumor cells (PCa), capable of recruiting MSCs and producing TGFβ (Table 1). Next, we considered the interactions between the key cell types (Fig. 1A) and the microenvironmental factors that control those interactions which were defined as follows:

Table 1.

Parameter	Value	Normalized value	Reference
Osteoblast Diameter	15µm	1 px	(34)
Osteoclast Diameter	50–100µm	3–5px	(35)
Osteoclast migration speed	100µm/hr 5nm/s but can vary between 30 and 248 mm/h.	1px/ts	(36) (37) (38)
Osteoblast migration speed	10µm/hr 0.1470 +/− 0.02mm/day	1/6px/ts	(36) (39)
Cell cycle time	24h	240ts	Estimated
TGFβ diffusion rate	750 µm2/min 2×10−9 cm2/s DPP-10µm/2	0.01px/ts	(40) (8) (41)
TGFβ half-life	2 min 2–3 min. Presence of LAP can extend half life to 100 min in plasma.	0.5ts	(42) (43)
TGFβ Quantity released by OCL/day	0.00558ng per day	1 MaxTGFβ/ts	Estimated
TGFβ Quantity released by tumor cell/day	0.005pg per day	0.0001 MaxTGFβ/ts	Estimated
Rate of bone degradation	10µm/day 43µm3/hr-1225µm3/hr for ~2weeks	1/240px/ts	(44) (45)
Volume of a resorption pit	78539 um3 = 7.58× 10−14 m3	70px	Assumed from the diameter of an osteoclast and the amount of bone resorbed over a 24-hour period.
Bone formation	0.656 µm/day but up to .24mm/year 1 µm/day	1/850px/ts	(45) (46)
BMU size	2×0.5 mm2	200×50px	Estimated

Figure 1.

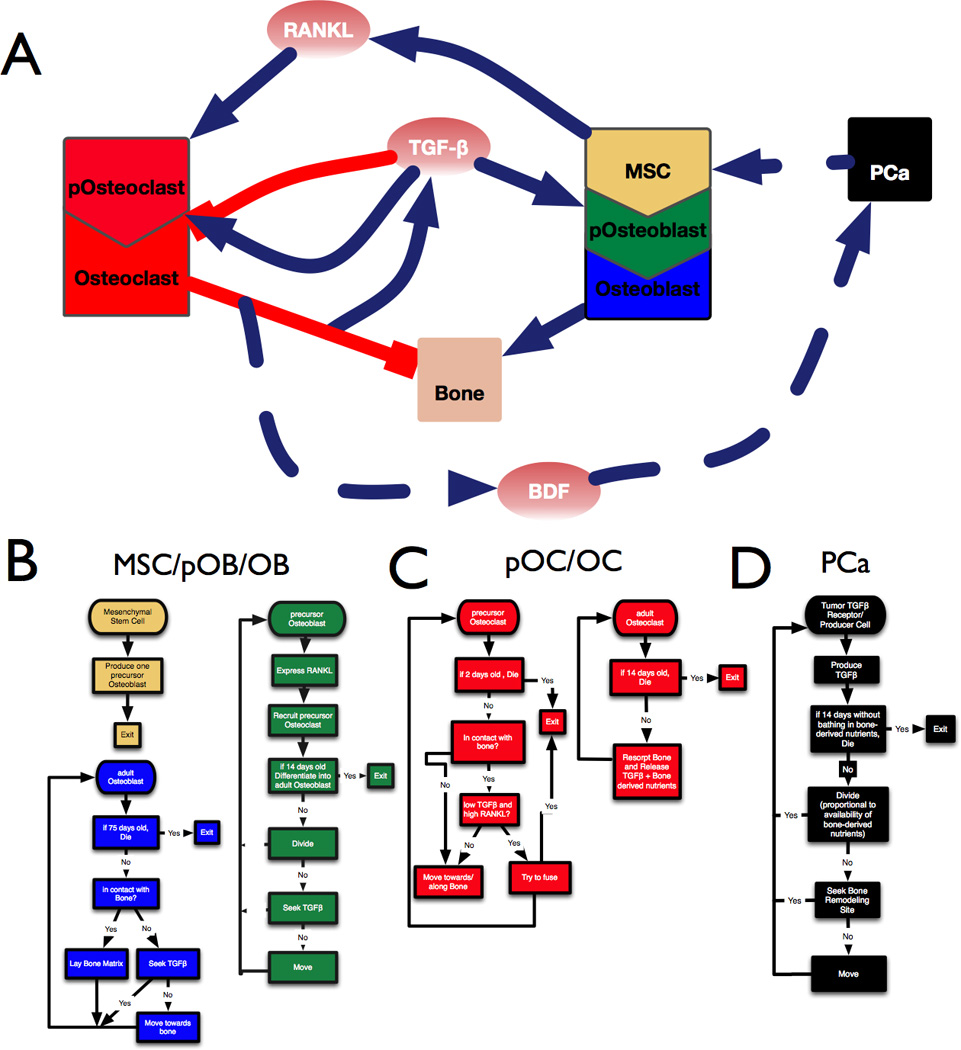
Developing a model of the prostate tumor bone microenvironment. A, Interaction diagram showing the positive (blue) and negative (red) interactions between cell types (boxes) and factors such as TGFβ, RANKL and BDFs. B-D, Flowchart describing the sequence of steps followed by osteogenic cells (B), osteolytic cells (C) and prostate cancer cells (D) in the mathematical model.

Bone

Bone is one of the richest reservoirs of TGFβ in the human body (700pg/mg of bone tissue) (10). We have modeled bone explicitly as static cells that, when resorbed, disappear from the domain and release bone derived factors (BDF) and TGFβ.

MSCs, pOBs and OBs

Bone generating osteoblasts (pOBs) are derived from MSCs (11). MSCs undergo asymmetrical division and pOBs proliferate in response to TGFβ, ultimately differentiating into bone matrix producing OBs, a process mediated by factors such as BMP-2 (12). In our model, pOBs express RANKL, migrate towards and expand clonally in response to TGFβ, and finally differentiate into OBs after 14 days. As adult OBs, the modeled cells seek TGFβ and bone. If in contact with bone, they lay down bone matrix with an active lifespan of 75 days (Fig. 1B).

pOCs and OCs

pOCs are derived from myeloid precursors and, in response to RANKL, undergo cellular fusion to generate mature OCs (13). OCs resorb the bone matrix leading to the release of BDFs and TGFβ (5, 14). We have explicitly modeled these processes. pOCs are recruited by RANKL from the vasculature, and have a lifespan of 2 days. Once on the bone surface, they will fuse together provided that the local levels of RANKL are high while those of TGFβ are low. A minimum of 3 pOCs (usually 5 or more) can fuse to form an OC. OCs have a lifespan of 14 days, in which their singular function is to resorb bone thereby releasing TGFβ and BDFs (Fig. 1C). Based on the amount of TGFβ present in bone, we have calculated that a single osteoclast measuring 100µm in diameter will resorb approx. 10µm³ of bone per day. Given the density of bone as 1500mg/Kg, we estimate that an osteoclast can resorb 1.17×10⁻³ mg/day. With the concentration of TGFβ in bone being 5ng/mg, we calculated that a mature osteoclast can generate up to 0.00558 ng of TGFβ per day.

PCa

Based on our empirical as well as published data, we engineered the PCa cells to express TGFβ ligands and receptors. Importantly, the level of PCa TGFβ (5×10⁻¹² pg/day) is approximately 1000 fold less than that generated by bone resorbing OCs (5×10⁻⁹ pg/day). This ensures the reliance of the prostate metastases on TGFβ released from the bone. In the computational model we have described the TGFβ producing PCa metastases as agents chemoattracted to the BMU, with an ability to recruit MSCs, based on our empirical studies (Fig. 2). PCa replication potential is proportional to the availability of bone-derived factors and, if not bathed with these essential factors, PCa cells will die within 14 days. The PCa metastases are the only ones that can destroy the canopy of the BMU as they grow (Fig.3B). We have considered that PCa promote OB differentiation, a phenomenon that is not noted in lytic lesions (14).

Figure 2.

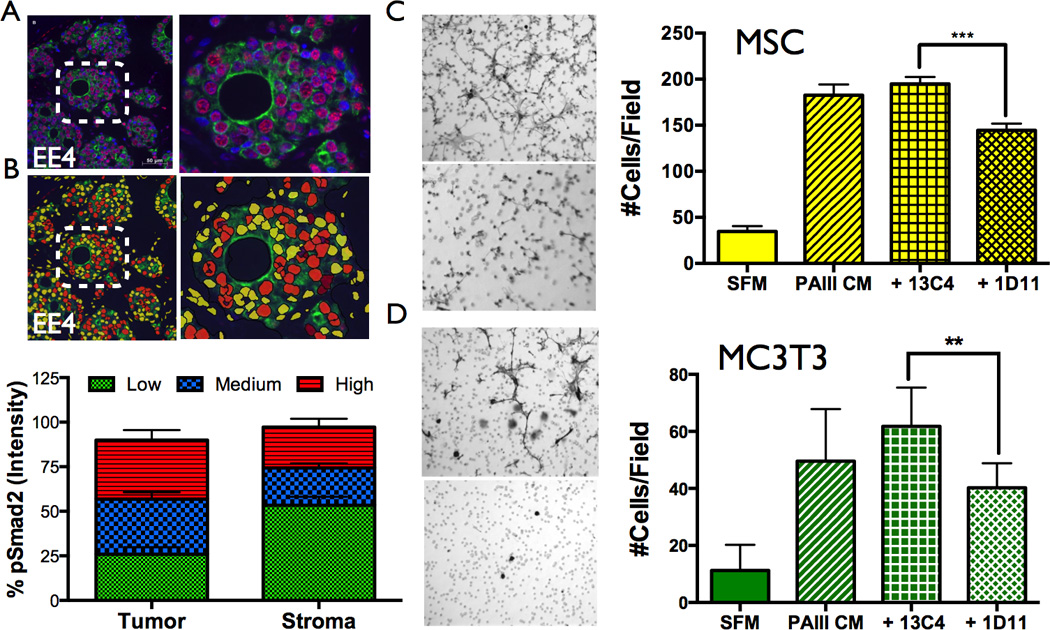
TGFβ expression in human prostate to bone metastases. A, Patient samples (N=9) were stained for pSMAD2 (red), pan-cytokeratin (green) with nuclear contrast (DAPI). Dashed inset is magnified in panel on right. B, The intensity of pSMAD2 staining in patient samples was assessed using Definiens Tissue Studio software. C–D, TGFβ significantly enhances the migration of MSCs and MC3T3 osteoblast precursors. Representative low power objective (20×) filters illustrating MSC (C) and MC3T3 (D) migration to prostate cancer conditioned media (PAIII CM) in the presence of a TGFβ blocking antibody (1D11) or IgG control (13C4). Serum-free media (SFM) was used as a baseline control for migration. Asterisk denotes statistical significance (p<0.05).

Figure 3.

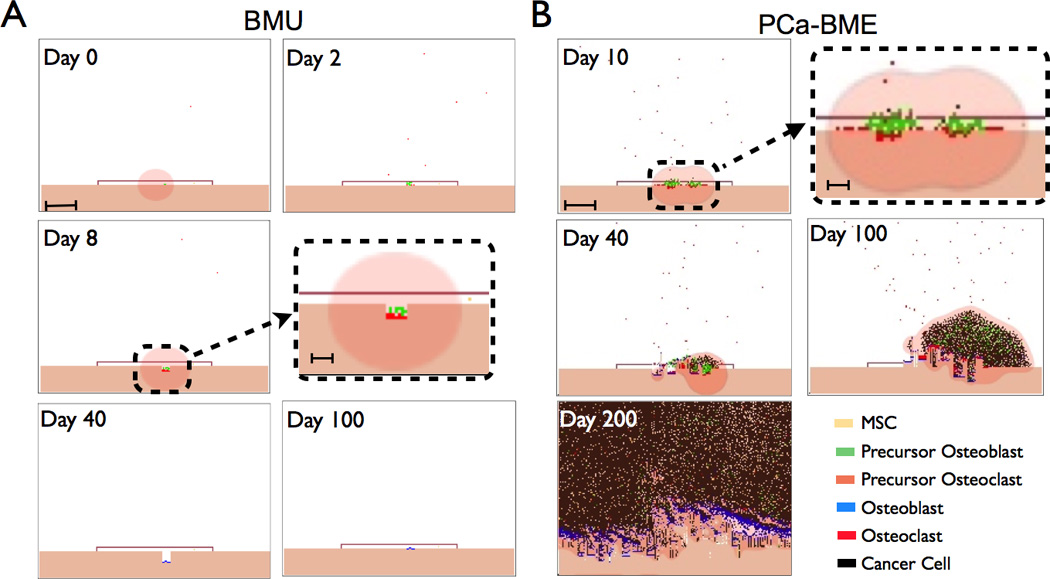
Simulation runs from the BMU model of the bone modeling unit (BMU) and the metastatic prostate cancer bone microenvironment (PCa-BME). A, Canopy formation in response to local/systemic stimuli (Day 0). Initial osteoid degradation by retracting osteoblasts can result in the release of TGFβ that stimulates pOB expansion subsequent to asymmetric division by MSCs. Scale bar represents 250 µm. pOBs recruit pOCs in a RANKL dependent manner (Day 2). As they fuse, the pOCs become fully differentiated OCs that start resorbing bone. Inset illustrates bone resorption in the BMU. Scale bar represents 100 µm. Upon osteoclast apoptosis, pOBs differentiate into adult osteoblasts (OBs) and begin the apposition phase (Day 40). OBs rebuild bone over the course of 3 months and undergo terminal differentiation into osteocytes during the process (Day 100). B, The introduction of a TGFβ ligand and receptor expressing metastatic PCa cell perturbs BMU homeostasis (Day 0). Inset highlights tumor-bone interaction. Scale bars are 250 µm. and 100 µm respectively. The BMU canopy is compromised at Day 40 and uncontrolled bone turnover results in the enhanced recruitment of MSCs and pOCs that establishes a vicious cycle (Day 100–200).

The microenvironment

TGFβ, RANKL and BDFs are generated by the behaviors and interactions amongst the cellular components; and are characterized by partial differential equations that are subsequently discretized and applied to a grid. TGFβ is produced by bone destruction (α_βB_i,j) and cancer cells (α_cC_i,j) in proportion to the local TGFβ concentration, with natural decay of the ligand (σ_βT_β); ensuring the density never exceeds a saturation level, m₀. TGFβ has pleiotropic effects on osteoblasts, osteoclasts and metastatic prostate cancer cells. Low concentrations of TGFβ stimulate osteoclastogenesis but high concentrations inhibit the process; illustrating the biphasic effects of this growth factor even on the same cell type (15, 16). Our group and others have shown that TGFβ supports tumor survival and growth by activating TGFβ receptors (TβR) on the tumor cell surface (17–19). TGFβ is governed by the following differential equation:

$$\frac{\partial T_{\beta }(x,y,t)}{\partial t}=\nabla (D_{\beta }(m_0-M)\nabla T_{\beta })+{\alpha }_{\beta }{B}_{i,j}+{\alpha }_c{C}_{i,j}-{\sigma }_{\beta }{T}_{\beta }$$

RANKL R_L is produced by precursor Osteoblasts, α_L0_i,j, in proportion to the local RANKL concentration, with natural decay of the ligand, σ_LR_L; ensuring the density never exceeds the saturation level n₀. The concentration of RANKL is determined by:

$$\frac{\partial R_L(x,y,t)}{\partial t}=\nabla (D_L(n_0-N)\nabla R_L)+{\alpha }_L{O}_{i,j}-{\sigma }_L{R}_L$$

Factors F_B are released by bone destruction, α_BB_i,j, in proportion to the local factor concentration, with natural decay of the factors, σ_BF_B; ensuring the density never exceeds the saturation level p₀. As such, the dynamics of the bone related factors are calculated through:

$$\frac{\partial F_B(x,y,t)}{\partial t}=\nabla (D_B(p_0-P)\nabla F_B)+{\alpha }_B{B}_{i,j}-{\sigma }_B{F}_B$$

Periodic boundary conditions were considered only for the left and right sides of the microenvironment, while no-flux boundaries were imposed on the top and bottom of the two dimensional grid.

Materials and Methods

Mathematical model

Parameters for the HCA model were derived from empirical and published data (Table 1) (9). The model is comprised of a grid (200×50 points) representing 2×0.5 mm² of the bone microenvironment. A major advantage of the HCA is in its intimate interconnection with experimental data, where the model and the experiments inform each other. This increases the accuracy of the model abstractions and connectivity of the basic elements, which yields reliable and biologically relevant emergent behaviors. To model the normal sequence of the BMU program, we have focused on understanding the role and behavior of the key regulators of the BMU dynamics. The principal cellular players: bone, MSCs, pOBs, OBs, pOCs and OCs, have been explicitly modelled as agents in a grid following specific rule sets in a physical microenvironment (see Quick guide to assumptions and equations). Collectively, these components find a natural homeostatic balance that recapitulate the dynamics of bone remodeling, a homeostasis that can be perturbed via the introduction of metastatic PCa cells.

Immunofluorescence and quantitation

Human prostate to bone metastases samples (5µm), provided by Dr. Robert Vessella (University of Washington), were rehydrated and blocked prior to the addition of phospho-specific anti-Smad2 (1:200 dilution; Millipore) and pan anti-Cytokeratin (1:200 dilution; Sigma) and appropriate IgG controls. Tissue sections were incubated overnight at 4°C. Subsequently, species-specific secondary AlexaFluor 568 and AlexaFluor 488-conjugated antibodies (1: 1000 dilution for one hour at room temperature; Invitrogen) were added for imaging by microscopy. For semi-quantitative analysis, regional images were segmented based on the intensity of staining using Definions Tissue Studio (TS)^©.

Migration

Osteoblast (MC3T3) and MSC migration was assessed using a modified Boyden Chamber assay. Cells (5×10⁵) were seeded in the upper chamber and their migration to TGFβ rich PAIII conditioned media in the presence of a TGFβ inhibitor (1D11; Genzyme) or isotype control (13C4) at a concentration of 5µg/mL was measured over a 5 hour period at 37°C. Migrated cells were stained with hematoxylin and air dried. The number of migrated cells was counted in 3 random 20× fields for each condition. All experiments were performed in triplicate.

Intratibial Prostate Model of osteogenesis, histology and TRAcP staining

All animal experiments were done with University of South Florida IACUC approval (CCL; #R3886). PAIII luciferase expressing cells were injected (1×10⁵ in 10 µl volume) into the tibia of anesthetized immunocompromised mice (recombinase activiating gene-2 null; RAG-2^−/−) (20). Tumor growth was imaged using bioluminescence imaging and quantitated with IVIS Living Image software. After two weeks, tumor bearing tibias were excised, soft tissue removed and processed for histology and histomorphometry as we have previously described (19, 21).

For cell culture and statistical methods, please see supplementary materials.

Results

Key for the generation of the BMU was the incorporation of major cellular players namely the PCa metastases, MSCs, pOBs, OBs, pOCs and OCs. Further, based on the literature, RANKL, TGFβ and bone derived factors were considered main mediators driving the cellular interactions (14). While RANKL has been well characterized in the context of prostate to bone metastases, few studies have explored the role of TGFβ signaling in this setting. Therefore, we initially examined the activity of TGFβ signaling in prostate to bone metastases in human specimens. Using phosphorylated SMAD2 (pSMAD2) as a readout for TGFβ receptor activity, our results indicated that TGFβ signaling is active in human prostate to bone metastases (Fig. 2A). Quantitative analysis revealed that in the human specimens, TGFβ signaling was highest in the prostate cancer cells but we also observed strong staining in stromal cells including osteoblasts (Fig. 2B). We also examined the effects of TGFβ on the proliferation and migration of the cellular components of the vicious cycle including prostate cancer cells, osteoclast precursors and osteoblast precursors, including MSCs. Of note, we observed that TGFβ significantly impacted the migration of MSCs and the osteoblast precursor cell line, MC3T3-E1 suggesting a role of the growth factor in the recruitment of cells that could impact prostate cancer induced osteogenesis (Fig. 2C–D).

Based on these empirical data and the literature, we parameterized a HCA computational model of the homeostatic BMU (Fig. 3A, supplemental Fig. 1 and Movie 1). Based on multiple simulations (N=25) of the computational model, we observed little variation in each populations cell number. In some instances (N=2), the BMU failed to initiate, in part, due to spatial and cytokine gradient differences between the different simulations (data not shown) but, we expect that persistent remodeling initiation stimuli would eventually lead to the formation of the BMU in vivo. We also observed that in a subset of BMU simulations (N=2) that simultaneous osteoclast fusion resulted in two sites of resorption. However, the generation of BDFs by the osteoclasts sufficiently increased osteoblast numbers and returned the BMU to baseline (data not shown). Importantly, the typical interactions between the different elements of the computational model result in a homeostatic BMU. It is important to note that each of the cells behave as autonomous agents and possesses the inherent ability to respond to the surrounding environment independently.

Next, we introduced a single metastatic PCa cell expressing TGFβ ligand and receptors into the BMU. Interestingly, we observed that in many of the simulations (N=18 of 25) the metastases failed to generate a lesion. We anticipate that the introduction of PCa emboli would significantly enhance the “take rate.” This “take rate” result emphasizes the stochastic nature of the model and reflects the in vivo reality where not every metastatic cancer cell that successfully invades a BMU would result in a viable lesion. In the simulations where lesions were initiated (N=7 of 25) we observed that after 10 days, the presence of the prostate cancer cells resulted in the integrity of the canopy being compromised and a resultant increase in osteoclast recruitment and maturation (Fig. 3B). Over time, the prostate cancer cells expanded resulting in MSC infiltration and osteoblast mediated bone formation ultimately recapitulating the “vicious cycle” paradigm (Fig. 3B, supplemental Fig. 2 and Movie 2).

Analysis of the computational prostate cancer-bone microenvironment at day 240 revealed striking histological similarities to an in vivo model of the osteogenic/osteolytic prostate to bone metastasis environment (Fig. 4A–B). We noted that the number of prostate cancer cells varied amongst simulations (8625 ±4580; N=5) but in general the growth rate predicted by the computational model was comparable to the growth rate of the prostate cancer cells in vivo (Supplemental Fig. 3). We also noted similar proportions of stromal cell populations at the computational and biological study endpoints (Fig4C–D). In the computational model, distinct phases of cell activity were observed. For example, the numbers of adult osteoblasts increased over time but notable plateaus prior to increases in cell number existed (Fig. 4C). These plateaus in adult osteoblasts corresponded with dips in the pOB and pOC precursor population. MSC numbers however, gradually increased over time and in general, paralleled increases in cancer cell number. In fact the model predicts that MSCs are crucial for the progression of the metastases since relaxing the probability of recruitment greatly impacts the growth of the metastases (Supplemental Fig. 4). Furthermore, we observed that osteoclasts were critical for cancer progression in the model with numbers changing over time from zero to 12 (Fig. 4E). While the in vivo model output has a similar number of osteoclasts per field (Fig. 4D and F) at the study endpoint, the phasic nature of osteoclast involvement is not apparent.

Figure 4.

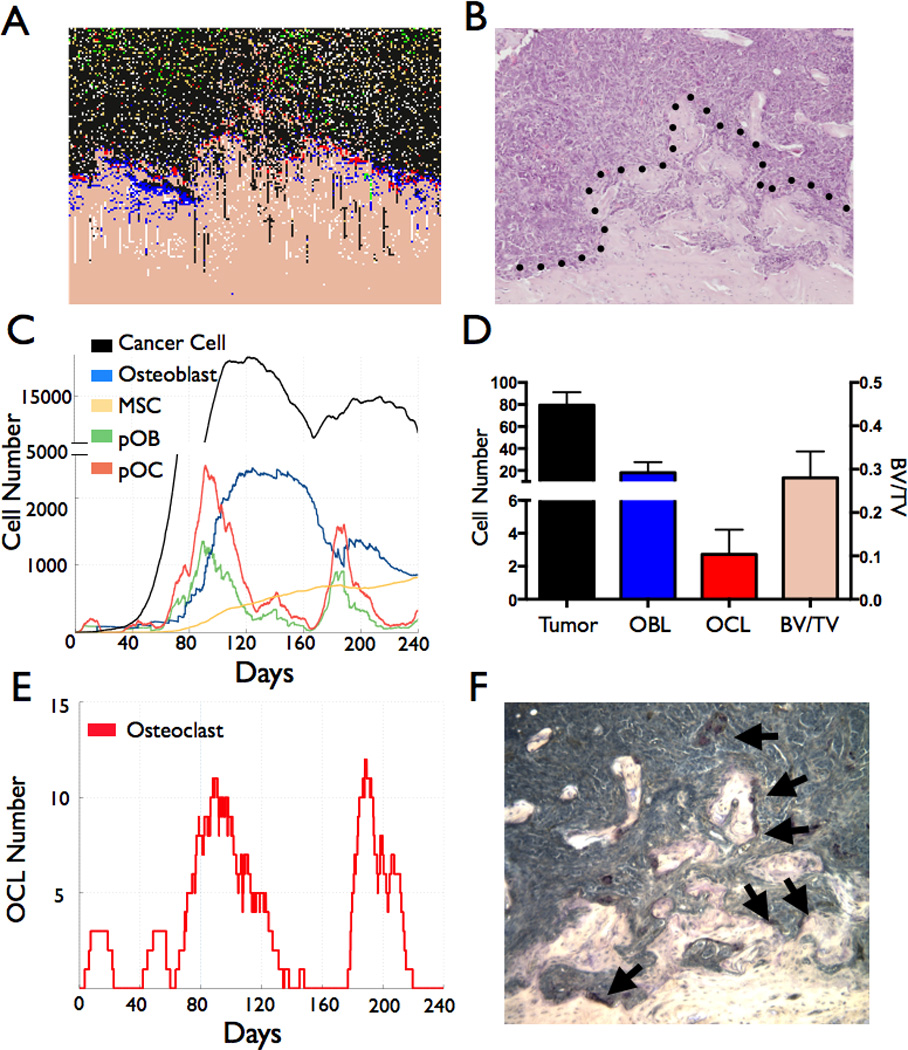
Computational and biological model output comparisons of the prostate cancer-bone microenvironment. A–B, The computational output (A) of the prostate cancer-bone microenvironment is similar to that of an in vivo prostate cancer to bone metastasis model (B). Dashed line in B represents the tumor-pathological bone interface. C, Temporal changes in cell population in the computational model. D, Analysis of cell populations (prostate cancer cells, bone rimming cuboidal osteoblasts and TRAcP positive osteoclasts) and bone volume in biological model endpoint. E–F, Computational model outputs reveal the fluctuation of osteoclast numbers over time (E), numbers that correlate with the numbers of TRAcP osteoclasts (arrows) in similar sized fields in vivo (F).

To test the applicability of the model in treating prostate to bone metastases we applied two standard of care treatments, namely, a bisphosphonate and an anti-RANKL inhibitor that induce osteoclast apoptosis during resorption and inhibit osteoclastogenesis respectively. To mimic the clinical scenario, we applied the bisphosphonate at a time where metastases had established (Day 80), although it should be noted that therapies could be applied at any juncture to the model (Fig. 5A–B and D; N=5 simulations per group). During bisphosphonate treatment, osteoclasts still formed but typically died within 24 hours of initiating bone resorption (Fig. 5B lower panel). However, residual bone resorption during bisphosphonate therapy was sufficient to sustain the metastases with the number of cancer cells on average at the final time point being 7138±2343 (n=5) compared to non-treated control of 8624±4580 (n=5; p>0.05). Interestingly, the application of an anti-RANKL inhibitor halted cancer growth with no cancer cells detectable after 20 days of administration (Fig 5C–D; p<0.05). These data suggest that treatment with anti-RANKL inhibitors should be curative in the clinical setting. However, in clinical trials with anti-RANKL inhibitors such as Xgeva, there is a slight but not significant increase in survival of patients on the therapy compared to bisphosphonates (2). In our simulations we found that reducing the efficacy of the anti-RANKL inhibitor from 100% to 40% resulted in an output of cancer cells (3157±3037; N=5)) that was comparable to that of the bisphosphonate treated group (7138±2343 cancer cells; N=5)(Fig. 5B and Supplemental Fig. 5). These data suggest that improved efficacy of anti-RANKL delivery into the prostate cancer bone microenvironment could be curative.

Figure 5.

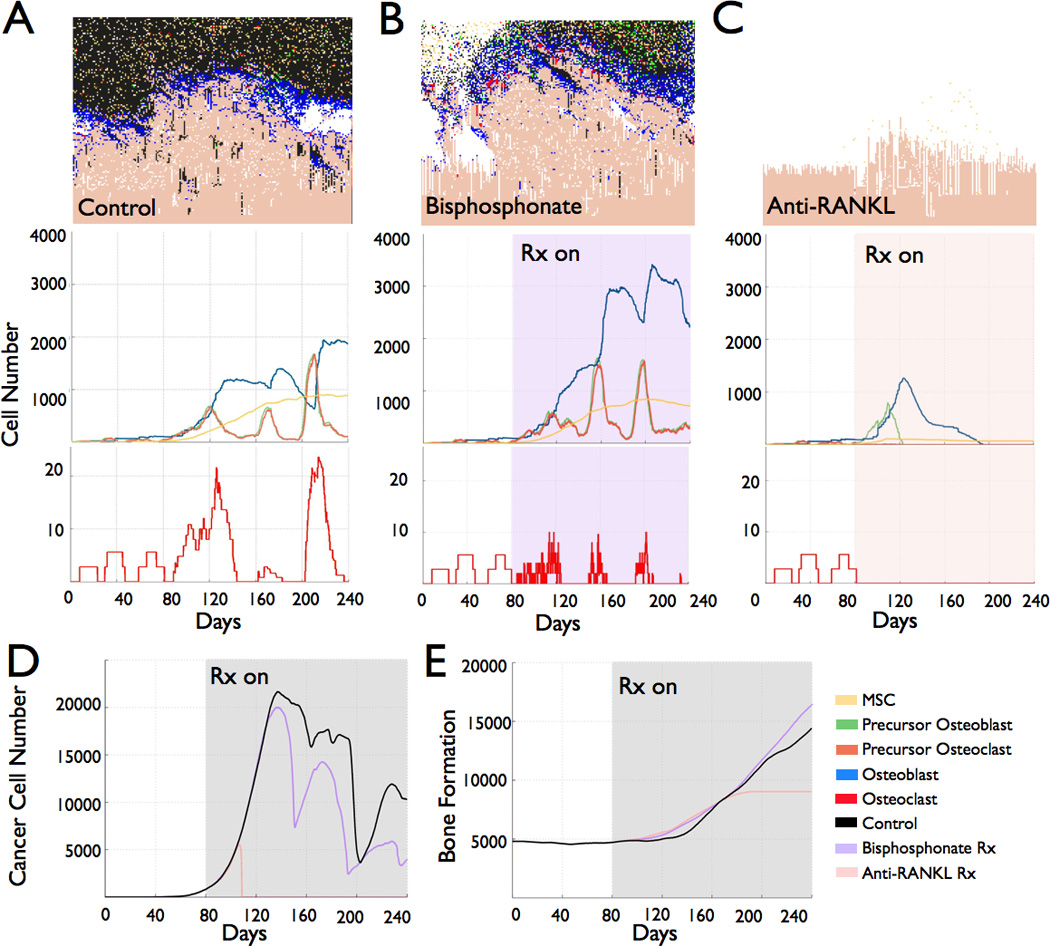
Application of therapies to the computational model of the metastatic prostate cancer bone microenvironment. A–C, The impact of standard of care therapies on the host microenvironment cell numbers in prostate to bone metastases was assessed in simulations where no therapy was applied (Control; A), Bisphosphonates at a dosing of 4mg/5ml intravenous (Bisphosphonate; B) or RANKL targeted therapy (Anti-RANKL; C) at a dose of 120mg/1.7ml intravenous were applied at approximately 80 days post metastasis (Rx On). D–E, The impact of placebo control and standard of care therapies on tumor volume (D) and bone volume (E) over time.

Discussion

In the current study we have generated a faithful computational model of the BMU. It is important to note that the homeostatic behavior is not hardcoded but emerges from the interactions between the different primary cell types of the bone in response to TGFβ, RANKL and BDFs. Further, informed by experimental evidence, the introduction of a simulated TGFβ ligand and receptor expressing PCa cell into the BMU resulted in a vicious cycle that yielded mixed osteogenic/osteolytic lesions over clinically relevant periods of time. Key findings arising from the computational model include: 1) the ability to assess temporal changes in cellular populations and dissect complex dynamics that are difficult to determine in vivo 2) the phasic osteolytic/osteogenic nature of the metastases, 3) the application of clinically used therapies such as bisphosphonates and anti-RANKL therapies illustrate the usefulness of the model in predicting the efficacy of targeted inhibitors and, 4) the impact of inhibitors at varying doses on the progression of prostate to bone metastases.

In our study, we selected the BMU as the primary target for metastatic PCa cells in which to establish and grow. This is logical since reports have shown that high rates of bone turnover correlate with poorer prognoses for prostate cancer patients and that the metastases can utilize many of the bioavailable factors present in the remodeling environment (22–24). Based on this rationale, we introduced a single metastatic prostate cancer cell into the BMU that over time recapitulated the vicious cycle paradigm. The “histological” output of the computational model at the endpoint was remarkably similar both in morphology and in cellular population proportion to an in vivo model used by our group to study mixed prostate to bone metastases. In contrast however, the computational model illustrates that the cellular population in the prostate cancer-bone microenvironment is dynamic and changes occur both exponentially (tumor growth) but also in phases (osteoclast, osteoblasts). For example, our model illustrates that osteoclast numbers rarely exceed a total of 20 out of approx. 2×10⁴ cells per computational field of view (Fig. 4C and E). Reports have shown that high levels of TGFβ can hinder osteoclastogenesis therefore, limiting the number of osteoclasts that can form in the tumor-bone microenvironment even in the presence of RANKL producing osteoblast precursors (25). In fact our results show that osteoclast mediated bone resorption is critical for the induction of the osteogenic metastases, an observation that is supports the use of anti-RANKL therapies in men with osteogenic prostate to bone metastases.

In a number of model iterations, we observed that the recruitment of MSCs to the prostate cancer-bone microenvironment was essential for the generation of osteoblast precursors and the development of osteogenic lesions. Our in vitro data also show that TGFβ contributes to MSCs and osteoblast precursor migration therefore, providing a means through which these cell types can be recruited to areas of prostate to bone metastases and contribute to their progression (Fig. 2). Although the role of MSCs in the prostate cancer-bone microenvironment has not been explicitly explored thus far, our model predicts an important role for this cell type in tumor growth. It is important to note that we did not consider the trans-differentiation of prostate cancer cells into osteoblasts but “osteomimicry” is a distinct possibility that could also be integrated into future iterations of the model (26).

The ability to dissect changes in cellular composition in the computational model provides key insights into how the cancer cells, MSCs, osteoblast precursors, osteoblasts, osteoclast precursors and osteoclasts are interacting with each other over a clinically relevant period of greater than 200 days. In vivo models are typically analyzed at end point or at predetermined time steps in order to assess cancer growth and changes in the microenvironment in control and test groups. For example, the MDA-MB-231 progression in bone is often measured at weekly time points (27). The computational model generated in this study clearly illustrates that a number of the host microenvironment components, notably the mature osteoclasts and osteoblasts, undergo phases of activity and rest (Figs. 3 & 4). This level of resolution is not available in biological models but demonstrates that the time-points or end-points chosen for in vivo models are a “snapshot” that may not be truly reflective of what has, or is about to happen in the tumor-bone microenvironment. Knowledge of the dynamic changes occurring over time in the computational cancer bone-microenvironment could lead to a better understanding of when to apply inhibitors or what happens to the cell populations over time once inhibitors have been applied.

Bisphosphonates and more recently anti-RANKL therapies are used as treatment strategies to protect patients with prostate to bone metastases from skeletal related events (SREs). Studies have shown that bisphosphonates can extend the average time to SRE for patients and anti-RANKL based therapies are significantly better than bisphosphonates in extending that time to first SRE (2, 28). However, neither treatment increases overall survival. We applied these inhibitors to our computational model. Assuming an efficacy of 100%, application of a bisphosphonate after a period in which the metastasis is actively growing (day 80) demonstrated an impact on osteoclast activity and on tumor growth. This time point was chosen based on the prostate metastases being established and actively growing but therapeutics could be applied at any juncture, a useful feature to study the response of multiple bone metastases at various stages of progression. Subsequent to the application of bisphosphonates to the model at day 80, we observed that osteoclasts still formed and that the residual production of TGFβ and bone derived factors was sufficient to sustain tumor growth, albeit to a lesser extent compared to the non-treatment control arm (Fig. 5). Significantly, we also assumed that the dosing of bisphosphonates was at 100% efficacy over the course of the therapy but in reality there are most likely changes in concentrations. Gradients in therapy concentration can be accounted for and pharmacokinetics can be explicitly simulated in the computational model and it will be interesting to determine the impact of dosing gradients on the behavior of the cell populations over time in the computational microenvironment.

Application of an anti-RANKL inhibitor, again at a presumed efficacy of 100%, significantly impacted the prostate tumor-bone microenvironment by preventing osteoclast formation, and subsequently, tumor growth. The model therefore, predicts that anti-RANKL inhibitors should be curative in the clinical setting. However, the clinical reality is that anti-RANKL inhibitors do not significantly extend overall survival in men with metastatic prostate cancer (2). Interestingly, reducing the efficiency of the anti-RANKL therapy to 40% closely mimics that of the bisphosphonate treatment and suggests that increasing doses or better targeting of the anti-RANKL inhibitors to the bone could enhance the efficacy of the drug provided that there are no or minimal increases in noted side effects such as osteonecrosis of the jaw (ONJ) or cataract formation (supplemental Fig. 3). Clinically, the dosage and frequency of administration of anti-RANKL therapy such as Xgeva is based on trials that demonstrated the optimal balance of efficacy, as determined by a greater than 70% decrease in urine N-terminal collagen fragments (NTX), and tolerability was 120mg sub-cutaneously delivered every four weeks (29). It is possible that higher doses may prove more efficient in significantly enhancing overall survival in patients with prostate to bone metastases as suggested by the computational model but this increase in dose may be outweighed by increased risks of side effects. A major advantage of the computational model is the application of combination or putative therapies to study cellular behavior in the prostate bone-microenvironment over time. For example, our results highlight the role of active TGFβ signaling in the cancer and host cells of human prostate to bone metastases and in the migration of MSCs and osteoblasts (Fig. 2). This observation is in keeping with other studies and underscores the key role TGFβ signaling plays in the bone microenvironment in regards to promoting the progression of prostate to bone metastases. The computational model could therefore easily test the efficacy of TGFβ inhibitors applied to the prostate cancer-bone microenvironment and predictions used to inform pre-clinical and ultimately clinical trials.

There are a number of caveats to the computational model described herein. Quantitative predictions from computational models are typically dependent on the information used to parameterize it. The key values used to parameterize the computational model presented in this paper are based on TGFβ and RANKL. The flexibility of the model ensures that ranges in the concentration and balance of other factors and cells that can impact the BMU in the normal and disease setting can be easily integrated. Enhancing these qualities will improve the accuracy of the generated predictions but our existing model is already quite robust to changes in the parameterization (Supplemental Fig. 4). While our model is relatively sophisticated, simpler less computationally intensive mathematical models have a number of advantages in that they are easier to understand and analyze. Furthermore, having fewer parameters they are amenable to the fitting of existing experimental data using techniques such as approximate Bayesian computation (ABC). Fitting extant experimental data to mathematical models has been used successfully to drive a model to closely represent a set of observations in cases such as imatinib response in leukemia patients (30). These approaches can also provide exact results when sufficient summaries are used (31). Simpler mathematical models are usually preferable, especially when values for biological parameters are largely unknown (32, 33). In this case, a more complex model was necessary to capture the bone homeostasis emerging from the interactions between MSCs, OCs, OBs, precursor OCs and precursor OBs. The existence of reliable empirical data made it possible to properly parameterize such model. This has allowed us to elucidate the mechanisms involved in the vicious cycle of prostate to bone metastases. One drawback of more complex computational models is that they are computationally intensive therefore, limiting the ability to perform large numbers of simulations that statistically can explore the robustness of each of the chosen parameters. However, in multiple simulations (N=25) we have ensured that the plausible plasticity of these parameters fall within the currently accepted biological empirical values. As such we have focused on investigating changes on the parameters that may vary experimentally; especially molecules such as RANKL and TGFB that are difficult to measure in vivo that have yielded interesting insights (Figure 5 & Supplemental Material). Follow-up experiments will use increased numbers of simulations to enhance statistical analysis and use new biological parameters being empirically determined in order to improve the accuracy of the model predictions.

In conclusion, using empirical and published data, we have generated a hybrid discreet model of the BMU and shown that the introduction of single active metastatic prostate cancer cell into the BMU is sufficient to generate osteogenic lesions that are similar in pathophysiology to those in an animal model of the disease. Further, the application of existing clinical therapies to the computational model underscores the value of this new approach for testing the impact of combining available therapies or putative targeted therapies for the treatment of prostate to bone metastases. Clinically, the versatility of the equations used to build the computational model ensure that it can be quickly individualized and be a powerful tool for the delivery of precision medicine to better treat and cure men with prostate to bone metastases.

Major Findings.

• The hybrid cellular automata model recapitulates the key aspects of the physiology of the BMU as well as the “vicious cycle” of prostate to bone metastases

• Progression of osteogenic prostate to bone metastases is critical on osteoclast activity and MSCs.

• The computational model also illustrates the temporal and phasic nature of the metastases.

• The application of clinically used bisphosphonates and anti-RANKL therapies to the computational model illustrates the power of the approach in predicting the efficacy of current and putative therapies.