Genomic-enabled prediction with classification algorithms

Abstract

Pearson's correlation coefficient (ρ) is the most commonly reported metric of the success of prediction in genomic selection (GS). However, in real breeding ρ may not be very useful for assessing the quality of the regression in the tails of the distribution, where individuals are chosen for selection. This research used 14 maize and 16 wheat data sets with different trait–environment combinations. Six different models were evaluated by means of a cross-validation scheme (50 random partitions each, with 90% of the individuals in the training set and 10% in the testing set). The predictive accuracy of these algorithms for selecting individuals belonging to the best α=10, 15, 20, 25, 30, 35, 40% of the distribution was estimated using Cohen's kappa coefficient (κ) and an ad hoc measure, which we call relative efficiency (RE), which indicates the expected genetic gain due to selection when individuals are selected based on GS exclusively. We put special emphasis on the analysis for α=15%, because it is a percentile commonly used in plant breeding programmes (for example, at CIMMYT). We also used ρ as a criterion for overall success. The algorithms used were: Bayesian LASSO (BL), Ridge Regression (RR), Reproducing Kernel Hilbert Spaces (RHKS), Random Forest Regression (RFR), and Support Vector Regression (SVR) with linear (lin) and Gaussian kernels (rbf). The performance of regression methods for selecting the best individuals was compared with that of three supervised classification algorithms: Random Forest Classification (RFC) and Support Vector Classification (SVC) with linear (lin) and Gaussian (rbf) kernels. Classification methods were evaluated using the same cross-validation scheme but with the response vector of the original training sets dichotomised using a given threshold. For α=15%, SVC-lin presented the highest κ coefficients in 13 of the 14 maize data sets, with best values ranging from 0.131 to 0.722 (statistically significant in 9 data sets) and the best RE in the same 13 data sets, with values ranging from 0.393 to 0.948 (statistically significant in 12 data sets). RR produced the best mean for both κ and RE in one data set (0.148 and 0.381, respectively). Regarding the wheat data sets, SVC-lin presented the best κ in 12 of the 16 data sets, with outcomes ranging from 0.280 to 0.580 (statistically significant in 4 data sets) and the best RE in 9 data sets ranging from 0.484 to 0.821 (statistically significant in 5 data sets). SVC-rbf (0.235), RR (0.265) and RHKS (0.422) gave the best κ in one data set each, while RHKS and BL tied for the last one (0.234). Finally, BL presented the best RE in two data sets (0.738 and 0.750), RFR (0.636) and SVC-rbf (0.617) in one and RHKS in the remaining three (0.502, 0.458 and 0.586). The difference between the performance of SVC-lin and that of the rest of the models was not so pronounced at higher percentiles of the distribution. The behaviour of regression and classification algorithms varied markedly when selection was done at different thresholds, that is, κ and RE for each algorithm depended strongly on the selection percentile. Based on the results, we propose classification method as a promising alternative for GS in plant breeding.

Introduction

Genomic selection (GS) is a novel strategy that aims to improve the prediction of complex agronomic traits using information from high-throughput genotyping platforms and phenotypic information of a training population (Meuwissen et al., 2001). Several methods for GS have been proposed and evaluated (Crossa et al., 2013; Gianola, 2013). The difference among them resides not only in their theoretical basis but also in their performance, which is variable and depends on the population and trait analysed (Heslot et al., 2012, Gianola, 2013).

Pearson's correlation coefficient (ρ) is the most reported metric of the prediction ability of the regression models; however, it may not be the most appropriate measure in real breeding situations, because it is a global measure that does not evaluate the quality of the regression at the tails of the distribution where the breeder decides whether or not to keep the lines for further breeding. González-Recio and Forni (2011) compared Bayes A and Bayesian LASSO (BL) with two machine learning models (Boosting and Random Forest) for predicting disease occurrence in simulated and real data sets. They found that the algorithm with the best correlation does not always have the best selection rate.

Classification methods are a successful branch of supervised machine learning; they are fully applied in several areas of research, for example, text mining and bioinformatics (Hastie et al., 2011). Despite this success, we found very few studies on its application in GS (Long et al., 2007; González-Recio and Forni, 2011).

Instead of building a regression curve that fits all the training data, classification algorithms construct a decision boundary that is optimised usually for separating two classes, that is, best (which can be located at the upper or lower tail of the distribution) and worst lines; thus we expect that they might be an alternative approach to regression methods.

The objective of this study was to compare the performance of six well-known GS methods with that of three classification methods, Random Forest Classification (RFC) and Support Vector Classification (SVC) (the latter with two different kernels), for selecting the best α% of individuals in 14 maize and 16 wheat data sets, α=(10, 15, 20, 25, 30, 35, 40%). We emphasised the analysis at α=15%, which is a common select proportion used by CIMMYT programmes.

Two of the regression methods are benchmarks for parametric GS: Ridge Regression (RR) and BL, while Reproducing Kernel Hilbert Spaces (RKHS) is a successful semi-parametric approach to GS, and Random Forest Regression (RFR) and Support Vector Regression (SVR) are state-of-the-art algorithms for non-parametric regression (Hastie et al., 2011).

Overall performance was evaluated by means of a cross-validation scheme (50 random partitions with 90% of individuals in the training set and 10% in the testing set) and using ρ as a criterion for measuring predictive ability. The metrics used to evaluate the performance of classification methods were Cohen's kappa coefficient (κ) and an ad hoc measure that we called relative efficiency (RE), which indicates the RE of selection when individuals are selected based on GS exclusively.

The α=15%, or other percentiles, can be positioned in the upper tail of the distribution if the trait considered is yield; in the lower tail, if the trait is disease resistance; or even in the middle of the distribution if the trait is, for example, the anthesis-silking interval (ASI), where the ideal situation is to have a value of the trait equal to zero.

The results of this study are promising. At a percentile value α=15%, SVC-lin achieved the best RE in 13 of the 14 maize data sets and in 9 of the 16 wheat data sets. We also compared the performance of regression and classification algorithms at other percentiles where differences between predictions were variable. As shown by González-Recio and Forni (2011), classification algorithms are a valuable alternative to traditional GS methods.

Materials and methods

Maize data sets

The maize data, including 14 trait–environment combinations measured on 300 tropical lines genotyped with 55 000 single-nucleotide polymorphisms, were previously used by González-Camacho et al. (2012). Six data sets cover information on grey leaf spot (GLS) resistance evaluated in six CIMMYT international trials (GLS-1 to GLS-6); another six data sets include information on female flowering time (FFL), male flowering time (MFL) and the MFL to FFL interval (ASI) evaluated under severe drought stress (SS) or in well-watered (WW) environments. The remaining data sets contain information on grain yield evaluated under severe drought stress (GY-SS) and well-watered (GY-WW) environments. The number of individuals and the type and number of markers are presented in Table 1. For further details, see González-Camacho et al. (2012).

Table 1. Information on the maize and wheat data sets used in this study.

Data set	Species	Trait–environment combination	Number of individuals	Number of markers
GY-WW	Maize	Yield—well watered	242	46 374 SNPs
GY-SS	Maize	Yield—drought stressed	242	46 374 SNPs
MLF-WW	Maize	Male flowering time—well watered	258	46 374 SNPs
MLF-SS	Maize	Male flowering time—drought stressed	258	46 374 SNPs
FLF-WW	Maize	Female flowering time—well watered	258	46 374 SNPs
FLF-SS	Maize	Female flowering time—drought stressed	258	46 374 SNPs
ASI-WW	Maize	Anthesis silking interval—well watered	258	46 374 SNPs
ASI-SS	Maize	Anthesis silking interval—drought stressed	258	46 374 SNPs
GLS-1	Maize	Grey leaf spot	272	46 374 SNPs
GLS-2	Maize	Grey leaf spot	280	46 374 SNPs
GLS-3	Maize	Grey leaf spot	278	46 374 SNPs
GLS-4	Maize	Grey leaf spot	261	46 374 SNPs
GLS-5	Maize	Grey leaf spot	279	46 374 SNPs
GLS-6	Maize	Grey leaf spot	281	46 374 SNPs
KBIRD-Srm	Wheat	Stem rust—main season	90	1355 DArT
KBIRD-Sro	Wheat	Stem rust—off season	90	1355 DArT
KNYANGUMI-Srm	Wheat	Stem rust—main season	176	1355 DArT
KNYANGUMI-Sro	Wheat	Stem rust—off season	191	1355 DArT
F6PAVON-Srm	Wheat	Stem rust—main season	176	1355 DArT
F6PAVON-Sro	Wheat	Stem rust—off season	180	1355 DArT
JUCHI-Ken	Wheat	Yellow rust—Kenya	176	1355 DArT
KBIRD-Ken	Wheat	Yellow rust—Kenya	191	1355 DArT
KBIRD-tol	Wheat	Yellow rust—Mexico	176	1355 DArT
KNYANGUMI-tol	Wheat	Yellow rust—Mexico	180	1355 DArT
F6PAVON-Ken	Wheat	Yellow rust—Kenya	147	1355 DArT
F6PAVON-tol	Wheat	Yellow rust—Mexico	180	1355 DArT
GY-1	Wheat	Yield-E1, low rainfall and irrigated	599	1279 DArT
GY-2	Wheat	Yield—high rainfall	599	1279 DArT
GY-3	Wheat	Yield—low rainfall and high temperature	599	1279 DArT
GY-4	Wheat	Yield—low humidity and hot	599	1279 DArT

Abbreviation: SNP, single-nucleotide polymorphism.

Wheat data sets

The wheat data included six stem rust resistance data sets, six yellow rust resistance data sets and four grain yield data sets genotyped with 1400 DArT markers. All rust data sets were previously presented in Ornella et al. (2012) and come from an experiment in which populations of recombinant inbred lines were evaluated for stem rust resistance in Kenya using two planting dates (the main season (Srm) and the off season (Sro)) and for yellow rust resistance under artificial inoculation in Mexico (Tol) or under natural infection in Njoro (Ken). The four grain yield data sets are included in the R package ‘BLR' (Pérez et al., 2010): 599 lines evaluated under different water and temperature conditions (Burgueño et al., 2012). Information regarding the number of individuals and the type and number of markers is presented in Table 1.

The response variables in the 30 data sets were centered at zero and standardised to unit variance (González-Camacho et al., 2012; Ornella et al., 2012). For classification, these response variables were divided into binary classes; the procedure is described in detail at the end of Material and methods section.

Regression methods

For performing GS regression, we chose the following methods.

RR and BL are linear parametric models. The phenotype of the i-th individual (y_i) can be represented by y_i=g_i+ɛ_i, where g_i indicates the genetic factor specific to the i-th individual and ɛ_i the residual comprising all other non-genetic factors ɛ_i∼N(0,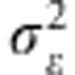). Meuwissen et al. (2001) proposed the linear model g_i=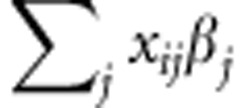, where x_ij are the marker covariates and β_j is the effect of the j-th marker (j=1,..., p). In matrix notation:

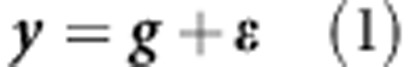where g=Xβ. The genomic-BLUP (for example, Endelman, 2011; de los Campos et al., 2012) is obtained assuming that g∼N(0,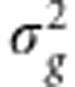G), where 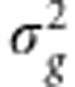is the genetic variance and the matrix G∝XX′. In a Bayesian framework (Pérez et al., 2012), the RR-BLUP is obtained assuming that the prior distribution for each marker effect is p(β_j|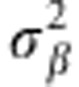)=N(β_j|0,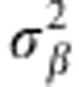). Marker effects are assumed independent and identically distributed a priori, whereas the distribution assigned to 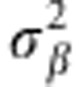(the prior variance of marker effects) and 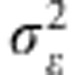(the prior of residual variance) is χ⁻²(df,s) (for example, de los Campos et al., 2012). The BL model assigns a double exponential (DE) distribution to all marker effects (conditionally on a regularisation parameter λ), centered at zero (Park and Casella, 2008), that is, p(β_j|λ,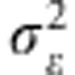)=DE(β_j|0,λ/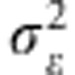). We used the R package ‘rrBLUP' (Endelman, 2011) to fit the RR-BLUP model, and the ‘BLR' package (Pérez et al., 2010) to fit the BL mode using the settings described in González-Camacho et al. (2012).

RKHS is a semi-parametric model in which the linear response takes the following form:

where x_i=(x_i1,…,x_ip) and x_i′=(x_i′1,…,x_i′p) are vectors of marker genotypes of the i and í-th lines, and K(x_i,x_i′)=exp(−γ||x_i−x_i′||²) is a Gaussian kernel (Gianola et al., 2006; Gianola and van Kaam, 2008) where ||x_i−x_i′|| is the Euclidean distance between pairs of marker genotypes and γ>0 is a bandwidth parameter. The prediction ability of RKHS method is sensitive with respect to the value of γ. We used a multi-kernel fitting strategy to estimate it as described in González-Camacho et al. (2012). We assigned a scaled inverse chi-squared distribution to the variance components. In the implementation, we set df=5 for all prior distributions. The prior expectation of the residual variance was set to one half of the phenotypic variance, in which case S_ɛ=0.5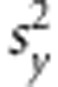(df−2). The prior expectation of the variance for each of the three kernels used in our implementation was set to 1/6 of the sample variance of the standardised phenotypes, S_k=0.5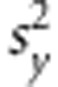(df−2)/3. This setting leads to weakly proper priors. The inferences in all models were based on 30 000 samples obtained after discarding 5000 that were taken as burn-in.

Finally, we selected RFR and SVR as representatives of non-parametric GS models. RFR is a combination of decision trees, each one generated from a subset of individuals selected by bootstrap (Breiman, 2001). Using stochastic perturbation (bootstrap) and averaging the outputs of the decision trees can avoid over-fitting (Hastie et al., 2011).

In this study, default choices of the R package ‘RandomForest' were used (Liaw and Wiener, 2002), which uses the decrease in mean squared error as a criterion for selecting the best split (Liaw, 2013). After a preliminary analysis for optimisation, we kept the default settings of the package, that is, number of variables tried at each split m_try=p/3, number of trees=500 and minimum node size=5.

SVR is based on the structural risk minimisation principle that aims to learn a function from finite training data. In this study, we used the ‘ɛ-insensitive' SVM regression or ɛ-SVR as implemented in Workbench WEKA (Hall et al., 2009). ɛ-SVR performs a robust linear regression by ignoring residuals smaller in absolute value than some constant (ɛ) and assigning a linear loss function for larger residuals. To learn non-linearly functions, data are implicitly mapped to a higher dimensional space by means of Mercer kernels that can be expressed as an inner product (Hastie et al., 2011).

We evaluate the performance of ɛ-SVR with a linear kernel, K(x_i,x_i′)=x_i·x_i′ and a Gaussian kernel, K(x_i,x_i′)=exp(−γ||x_i−x_i′||²), where γ>0 is the bandwidth parameter.

Optimisation of the C parameter (linear and Gaussian kernels) and γ (Gaussian kernel) was performed by a logarithmic grid search of base 2 over an extensive range of values. The constant C>0 determines the trade-off between the flatness of f and the amount up to which deviations larger than ɛ are tolerated. Each point on the grid was evaluated by internal five-fold cross-validation on the training set using ρ as a goodness-of-fit criterion. The ɛ parameter was used with the default values of WEKA (Ornella et al., 2012). For a more exhaustive presentation of ɛ-SVR, refer to SVR section Hastie et al. (2011).

Classification methods

Random Forest Classification

The concept behind RFC is the same as that in regression (Liaw and Wiener, 2002). Differences between them are: the splitting criteria, that is, the Gini Index instead of mean squared error, and the number of variables recommended for each split, (m_try=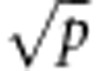); also, the class of an unseen example is predicted by majority vote, that is, the algorithm counts the number of votes (one vote per decision tree) and assigns the class with the highest number of votes (Liaw, 2013). A comprehensive explanation of RFC can be found in González-Recio and Forni (2011) or Hastie et al. (2011). As in regression, we evaluated different alternatives but finally kept the default settings of the package, that is, number of trees=500, node size=1 and m_try=215, 37 and 38 for all maize, rust and wheat-yield data sets, respectively.

Support Vector Classification

The goal of SVC is to calculate a maximal margin hyperplane separating the two classes; this hyperplane is fully specified by a subset of support vectors; classification was also performed using the Workbench WEKA (Hall et al., 2009). As in regression, optimisation of parameters was performed by a logarithmic grid search over an extensive range of values, that is, C=(2⁻¹⁵,…,2⁶) and γ=(2⁻²⁰,…,2¹⁵). Each point on the grid was evaluated by an internal fivefold cross-validation on the training set using κ as a criterion for success. For further reading, refer to Cortes and Vapnik (1995) or Hastie et al. (2011). For details about optimisation of SVR and SVC, refer to Witten and Frank (2005).

Improving the performance of classifiers by estimating the probability of the class

Classification in unbalanced data sets is a difficult problem from both the algorithmic and performance perspectives. Not choosing the right objective function while developing the classification model can introduce bias towards the majority, potentially uninteresting, class. Some algorithms circumvent this problem by using, for example, weighted loss functions or by giving different penalisations according to the misclassification group (Fernández et al., 2011). We explored the possibility of setting an appropriate threshold in order to balance the classes and select the α% best individuals according to the probability obtained by the classifiers, that is, lines with higher probability are ranked first. Classification methods can be divided into two main groups: soft and hard classifiers (Liu et al., 2011). Hard classifiers directly target the classification decision boundary without producing the probability estimation, whereas soft classifiers allow estimating class conditional probabilities and then performing classification based on the estimated probabilities. In Random Forest, this probability can be approximated by counting the number of votes of the decision trees (Liaw and Wiener, 2002), whereas in the support vector machine implementation of WEKA, this value is obtained by mapping the output of each SVM with a sigmoid function (Platt, 2000). This probability allows us to rank the candidates and select the best α% of individuals in the testing set at different percentiles.

In preliminary research, we explored the performance of both RFC and SVC for selecting the best 15% of individuals but with algorithms trained at different percentiles of the distribution, that is, setting the proportion of individuals in the best–worst classes in the training sets to 15–85, 20–80, 30–70, 40–60 or 50–50. Results presented here were obtained with algorithms trained with a best–worst line ratio of 40–60; this ratio showed the best performance among the different partitions evaluated. Results for the other percentiles were also obtained using this ratio in the training set.

Evaluating the methods (performance criteria)

Prediction assessment was performed by means of a cross-validation scheme. Fifty random partitions were generated using a predefined random binary matrix of order n × 50 (where n is the sample size); each partition was divided into a training set (90% of the lines) and a testing set (10% of the lines). Statistical evaluation was performed using the paired samples Wilcoxon test (Wilcoxon, 1945).

For prediction, regression models were evaluated using Pearson's correlation coefficient between observed and predicted values of the test sets, whereas for selecting the best individuals we used two measures: the κ coefficient and an ad hoc measure that we called RE.

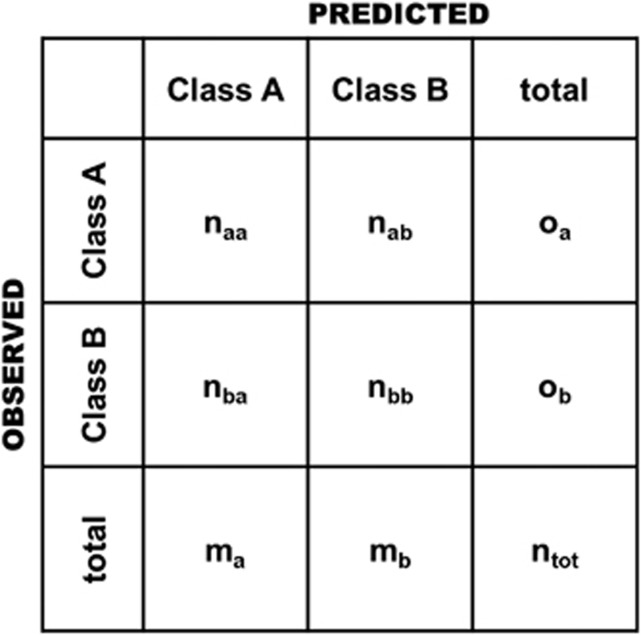
We used the κ coefficient because our data were unbalanced, that is, the classes were not approximately equally represented, and κ allows rectifying the fraction of cases correctly identified by the coincidence expected by chance (Fielding and Bell, 1997). The estimator can be calculated using the formula (Figure 1):

Figure 1.

Confusion matrix for a two-class problem. o_a and o_b are the number of observed cases for classes A and B, respectively; m_a=n_aa+n_ba and m_b=n_ab+n_bb are the number of predicted cases for classes A and B, respectively; n_aa and n_bb are the number of individuals correctly predicted for each class; n_ab is the number of individuals in class A predicted as B, whereas n_ba is the number of individuals in class B predicted as A. n_tot is the total number of cases in the experiment.

where P_o=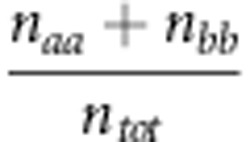 is the observed fraction of concordances between the observed and predicted values; P_e= 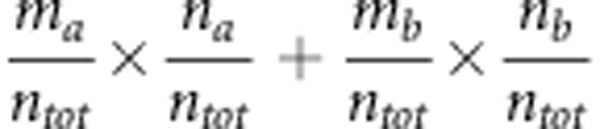is the expected concordance as determined by the marginal distributions (for example, 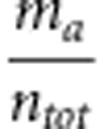) obtained from the confusion matrix (Figure 1); n_aa and n_bb are the number of cases correctly predicted for classes A and B, respectively; m_a and m_b are the observed cases for classes A and B, respectively; n_a and n_b are the number of predicted values for classes A and B, respectively; and n_tot=n_a+n_b=m_a+m_b is the total number of cases in the experiment.

The second measure, RE, was based on the expected genetic gain when individuals are selected only by GS given by:

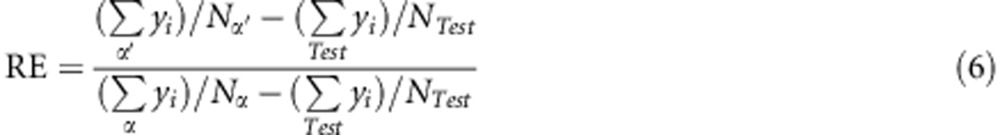where α and α′ are the groups of extreme individuals selected by the ranking of observed or predicted values, respectively; N_α=N_α′ are the numbers of individuals in each group; y_i is the observed value of each individual; and (∑_Test y_i)/N_Test represents the mean of the test group. In other words, the denominator is the differential selection of the individuals selected by traditional breeding (Falconer and Mackay, 1996), whereas the numerator is the differential selection of the individuals selected by GS.

Regarding the ASI phenotype, the best individuals are those whose phenotypic values are closer to zero. Therefore, equation (6) was modified as follows:

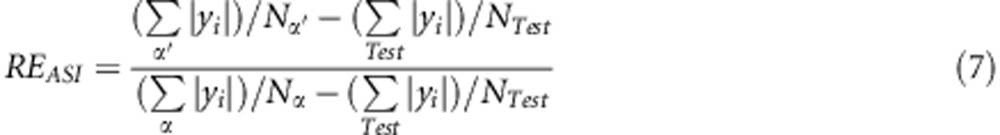where |·| is the absolute value.

To compute the values of these two estimators for GS methods, in each of the 50 random partitions we ranked the individuals in the test set according to their observed or predicted phenotypic values, high values first and lower values last. From both rankings, we selected the top α% of individuals (if the trait was yield), the bottom α% (flowering or disease resistance) or the α% located in the middle of the distribution (ASI). Coincidences between selected individuals in the two rankings were estimated by κ, while the efficacy of GS selection in terms of genetic gain was calculated by RE. This operation was performed for α=10, 15, 20, 25, 30, 35 and 40%.

Regarding GS classification, for each of the 50 test sets, we also prepared the first ranking using the phenotypic (observed) value and the second ranking using the probability of the desired class as estimated by the classifier (that is, the probability of a high yielding or resistant line).

Software

Scripts for evaluation were implemented in Java code using Eclipse platform v3.7 (Dexter, 2007) and R language (R Core Team, 2013). R was used to perform the statistical analyses. The Lattice package (Sarkar, 2008) was used to develop the Supplementary Figures.

Results

Evaluation of the overall performance of regression methods by Pearson's correlation coefficient

Before evaluating GS for selecting the extreme individuals, we performed a classic analysis of regression as reported elsewhere (for example, González-Camacho et al., 2012). Results are presented in Supplementary Tables S1 (maize) and S2 (wheat).

It can be seen in Supplementary Table S1 that RKHS nominally outperformed the other regression methods in four GLS data sets and three flowering data sets and tied with RR in one flowering data set. Wilcoxon's signed rank test showed that the superiority of RKHS was not statistically significant in any of these data sets. SVR-rbf performance succeeded in GLS-3, GLS-6 and MLF-SS data sets, although the difference was statistically significant only in MLF-SS. RR showed the best performance in the GY-WW data set, with a significance level of 0.05, whereas BL and RF outperformed the other models in ASI-WW and GY-SS, respectively (superiority of both was not statistically significant). As for the wheat data sets (Supplementary Table S2), RF achieved the best correlations in all six stem rust data sets, and the difference was statistically significant in five of them. In the yellow rust data sets, both KBIRD data sets and the KNYANGUMI-Tol data set, RF achieved the best results. The difference was statistically significant only in the last example. Finally, RKHS presented the best results in all yield data sets (GY-1 to GY-4), although this superiority was statistically significant only in GY-4.

Comparison of regression and classification for selecting the best 15% of individuals

We compared the performance of the six regression algorithms for selecting the best 15% of the individuals (using the same 50 random partitions). Table 2 shows κ coefficients for these algorithms plus two classification methods: RFC, SVC-lin, and SVC-rbf. Regarding κ, SVC-lin outperformed the rest of the algorithms in all data sets but one, GLS-6, where RR achieved the best performance. The superiority of SVC-lin was statistically significant in five GLS data sets and in four flowering data sets: MLF-WW, MLF-SS, FLF-WW, and ASI-SS.

Table 2. Cohen's kappa coefficient for 6 regression and 3 classification methods for genomic selection applied to 14 maize data sets and across trait–environment combinations when selecting the best 15% of individuals.

Data set	Regression						Classification
	RHKS	BL	RR	RFR	SVR rbf	SVR lin	RFC	SVC rbf	SVC lin
GLS-1	0.249	0.190	0.243	0.249	0.196	0.196	0.243	0.272	0.337**
GLS-2	0.329	0.329	0.318	0.323	0.364	0.376	0.329	0.318	0.545**
GLS-3	0.399	0.446	0.411	0.393	0.417	0.434	0.405	0.323	0.586**
GLS-4	0.368	0.338	0.356	0.344	0.380	0.338	0.315	0.250	0.480*
GLS-5	0.102	0.084	0.084	0.143	0.154	0.154	0.102	0.084	0.382**
GLS-6	0.178	0.154	0.183**	0.166	0.137	0.148	0.160	0.125	0.148
GY-SS	0.202	0.208	0.244	0.232	0.208	0.256	0.238	0.190	0.316NS
GY-WW	0.370	0.376	0.382	0.394	0.364	0.340	0.334	0.394	0.454NS
MLF-WW	0.580	0.592	0.586	0.557	0.580	0.586	0.575	0.468	0.699**
MLF-SS	0.580	0.586	0.610	0.545	0.580	0.610	0.569	0.510	0.722**
FLF-WW	0.557	0.586	0.580	0.539	0.580	0.586	0.610	0.445	0.693**
FLF-SS	0.569	0.610	0.616	0.504	0.610	0.598	0.480	0.421	0.669NS
ASI-WW	0.072	0.066	0.078	0.001	0.066	0.078	0.096	0.078	0.131NS
ASI-SS	0.049	0.090	0.073	0.007	0.060	0.107	0.120	0.155	0.303**

Abbreviations: BL, Bayesian LASSO; NS, not significant; RFR, Random Forest Regression; RHKS, Reproducing Kernel Hilbert Spaces; RR, Ridge Regression; SVR, Support Vector Regression with radial basis function (rbf) or linear (lin) kernels; RFC, Random Forest Classification; SVC, Support Vector Classification with radial basis function (rbf) or linear (lin) kernels.

Results presented are the average of 50 random partitions (the proportion of individuals in the training-testing data sets is 9:1).

For each data set the highest value is underlined.

*, ** Differences are significant at the 0.05 and 0.01 probability levels, respectively.

Table 3 shows the RE of the same models for selecting the best individuals at α=15%. SVC-lin also achieved the best performance in all the data sets except GLS-6, where RR had the best mean, although the difference was not statistically significant. The superiority of SVC-lin was statistically significant in all cases but GY-SS.

Table 3. Relative efficiency of 6 regression and 3 classification methods for genomic selection applied to 8 maize data sets and across trait–environment combinations when selecting the best 15% of individuals.

Data set	Regression						Classification
	RHKS	BL	RR	RFR	SVR rbf	SVR lin	RFC	SVC rbf	SVC Lin
GLS-1	0.358	0.300	0.341	0.354	0.278	0.296	0.331	0.336	0.487**
GLS-2	0.589	0.527	0.551	0.583	0.601	0.585	0.539	0.506	0.795*
GLS-3	0.702	0.730	0.706	0.700	0.707	0.721	0.693	0.600	0.841**
GLS-4	0.611	0.570	0.600	0.602	0.580	0.534	0.473	0.572	0.763**
GLS-5	0.283	0.287	0.260	0.325	0.331	0.354	0.264	0.237	0.664**
GLS-6	0.423	0.376	0.432NS	0.424	0.382	0.393	0.315	0.367	0.381
GY-SS	0.356	0.286	0.346	0.432	0.328	0.348	0.415	0.332	0.508NS
GY-WW	0.591	0.585	0.603	0.616	0.585	0.561	0.534	0.588	0.704*
MLF-WW	0.848	0.888	0.863	0.800	0.847	0.886	0.856	0.687	0.914**
MLF-SS	0.847	0.871	0.890	0.803	0.856	0.882	0.803	0.741	0.948**
FLF-WW	0.822	0.877	0.856	0.775	0.845	0.878	0.867	0.692	0.932**
FLF-SS	0.832	0.885	0.874	0.757	0.866	0.872	0.738	0.673	0.908**
ASI-WW	0.182	0.173	0.312	0.103	0.210	0.263	0.226	0.238	0.393*
ASI-SS	0.134	0.165	0.124	0.109	0.143	0.116	0.262	0.304	0.634**

Abbreviations: BL, Bayesian LASSO; NS, not significant; RFR, Random Forest Regression; RHKS, Reproducing Kernel Hilbert Spaces; RR, Ridge Regression; SVR, Support Vector Regression with radial basis function (rbf) or linear (lin) kernels; RFC, Random Forest Classification; SVC, Support Vector Classification with radial basis function (rbf) or linear (lin) kernels.

Results presented are the average of 50 random partitions (the proportion of individuals in the training-testing data sets is 9:1).

For each data set the highest value is underlined.

*, ** Differences are significant at the 0.05 and 0.01 probability levels, respectively.

Table 4 shows the κ values of the regression and classification models when selecting the best 15% of individuals in the 16 wheat data sets. SVC-lin produced the best results in all stem rust data sets, in five of the six yellow rust data sets and in one yield data set (GY-1). The differences were significant only in two SR data sets (F6PAVON-Srm and KNYANGUMI-Srm), one YR data set (F6PAVON-Ken) and one yield data set (GY-1). SVC-rbf gave rise to the best κ in one YR data set (KBIRD-Ken), but the difference was not statistically significant. Finally, RR achieved the best κ in GY-2, whereas RHKS tied with BL in GY-3 and showed the best value in GY-2. None of the differences were statistically significant.

Table 4. Cohen's kappa coefficient of 6 regression and 3 classification methods for genomic selection applied to 16 wheat data sets and across trait–environment combinations when selecting the best 15% of individuals.

Data set	Regression						Classification
	RHKS	BL	RR	RFR	SVR rbf	SVR lin	RFC	SVC rbf	SVC lin
KBIRD-Srm	0.100	0.303	0.280	0.145	0.258	0.213	0.145	0.235	0.438NS
KBIRD-Sro	0.322	0.392	0.344	0.425	0.344	0.322	0.235	0.168	0.528NS
KNYANGUMI-Srm	0.168	0.184	0.208	0.160	0.184	0.224	0.056	0.232	0.424**
KNYANGUMI-Sro	0.438	0.493NS	0.406	0.485	0.414	0.398	0.470	0.327	0.493NS
F6PAVON-Srm	0.256	0.264	0.248	0.296	0.240	0.176	0.360	0.360	0.464*
F6PAVON-Sro	0.288	0.384	0.352	0.320	0.400	0.312	0.320	0.264	0.464NS
JUCHI-Ken	0.258	0.258	0.258	0.078	0.168	0.213	0.145	0.235	0.280NS
KBIRD-Ken	0.033	0.078	0.033	0.078	0.033	0.010	0.078	0.235NS	0.213
KBIRD-tol	0.370	0.348	0.325	0.303	0.235	0.258	0.280	0.303	0.415NS
KNYANGUMI-tol	0.034	0.058	0.058	0.066	0.050	0.018	0.074	0.288	0.327NS
F6PAVON-Ken	0.158	0.158	0.112	0.146	0.181	0.054	0.181	0.287	0.354*
F6PAVON-tol	0.384	0.320	0.312	0.368	0.296	0.240	0.360	0.392	0.416NS
GY-1	0.229	0.142	0.135	0.234	0.210	0.119	0.231	0.271	0.401**
GY-2	0.250	0.239	0.265NS	0.205	0.239	0.142	0.137	0.244	0.179
GY-3	0.234	0.234NS	0.229	0.158	0.224	0.166	0.161	0.216	0.150
GY-4	0.422NS	0.346	0.344	0.401	0.383	0.208	0.286	0.346	0.297

Abbreviations: BL, Bayesian LASSO; NS, not significant; RFR, Random Forest Regression; RHKS, Reproducing Kernel Hilbert Spaces; RR, Ridge Regression; SVR, Support Vector Regression with radial basis function (rbf) or linear (lin) kernels; RFC, Random Forest Classification; SVC, Support Vector Classification with radial basis function (rbf) or linear (lin) kernels.

Results presented are the average of 50 random partitions (the proportion of individuals in the training-testing data sets is 9:1).

For each data set the highest value is underlined.

*, ** Differences are significant at the 0.05 and 0.01 probability levels, respectively.

Table 5 presents the RE of the different models for selecting the best 15% of individuals in the wheat data sets. SVC-lin produced the best results in four stem rust data sets (KBIRD, KNYANGUMI-Srm and F6PAVON-Srm). BL showed the best values in the other two data sets (KNYANGUMI-Sro and F6PAVON-Sro). As for the yellow rust data sets, SVC-lin gave the best results in all data sets but one, KBIRD-tol, where the best performance was obtained with RFR. RHKS achieved the best RE values in GY-2, GY-3 and GY-4, but they were significant only in GY-4. Finally, SVR-rbf presented the best mean in GY-1 (non-significant).

Table 5. Relative efficiency of 6 regression and 3 classification methods for genomic selection applied to 16 wheat data sets and across trait–environment combinations when selecting the best 15% of individuals.

Data set	Regression						Classification
	RHKS	BL	RR	RFR	SVR rbf	SVR lin	RFC	SVC rbf	SVC lin
KBIRD-Srm	0.284	0.600	0.549	0.558	0.517	0.544	0.326	0.118	0.707**
KBIRD-Sro	0.623	0.758	0.740	0.810	0.690	0.702	0.702	0.470	0.821NS
KNYANGUMI-Srm	0.506	0.596	0.588	0.667	0.601	0.640	0.305	0.504	0.811**
KNYANGUMI-Sro	0.654	0.738NS	0.632	0.676	0.652	0.614	0.672	0.483	0.732
F6PAVON-Srm	0.580	0.607	0.589	0.636	0.564	0.498	0.628	0.570	0.783**
F6PAVON-Sro	0.612	0.750NS	0.690	0.685	0.717	0.637	0.689	0.488	0.736
JUCHI-Ken	0.496	0.500	0.497	0.170	0.426	0.475	0.244	0.255	0.553NS
KBIRD-Ken	0.078	0.265	0.226	0.390	0.357	0.146	0.158	0.189	0.484NS
KBIRD-tol	0.463	0.515	0.483	0.636NS	0.440	0.483	0.507	0.443	0.619
KNYANGUMI-tol	0.086	0.204	0.204	0.315	0.230	0.119	0.157	0.343	0.551**
F6PAVON-Ken	0.317	0.209	0.177	0.267	0.285	0.175	0.304	0.264	0.565**
F6PAVON-tol	0.577	0.566	0.564	0.547	0.549	0.499	0.509	0.477	0.640NS
GY-1	0.530	0.380	0.377	0.519	0.491	0.215	0.533	0.617NS	0.479
GY-2	0.502NS	0.459	0.497	0.391	0.482	0.335	0.401	0.446	0.324
GY-3	0.458NS	0.449	0.441	0.366	0.448	0.266	0.367	0.226	0.338
GY-4	0.586*	0.480	0.472	0.558	0.540	0.354	0.451	0.471	0.363

Abbreviations: BL, Bayesian LASSO; NS, not significant; RFR, Random Forest Regression; RHKS, Reproducing Kernel Hilbert Spaces; RR, Ridge Regression; SVR, Support Vector Regression with radial basis function (rbf) or linear (lin) kernels; RFC, Random Forest Classification; SVC, Support Vector Classification with radial basis function (rbf) or linear (lin) kernels.

Results presented are the arithmetic means of 50 random partitions (the proportion of individuals in the training-testing data sets is 9:1).

For each data set the highest value is underlined.

*, ** Differences are significant at the 0.05 and 0.01 probability levels, respectively.

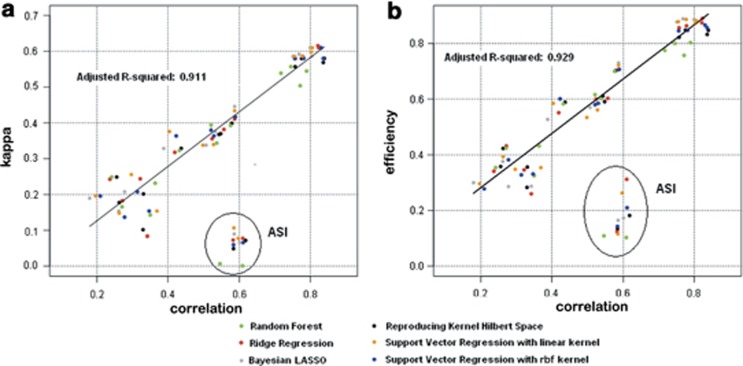
To test the widespread view that ρ is a good indicator of the performance of GS for selecting the best individuals, we made a scatter plot of ρ vs κ (Figure 2a) and ρ vs RE (Figure 2b) of selection at α=15% for the maize data sets. The figure shows these statistics are closely related. The exception is the ASI data, where the best individuals were selected from the middle of the distribution instead of the extremes. The other flowering traits and GLS resistance were selected from the lower tail of the distribution, whereas yield was selected from the upper tail.

Figure 2.

Scatter plot of Pearson's correlation coefficient vs Cohen's kappa coefficient (a) and Pearson's correlation vs RE (b) for the 6 regression methods evaluated on 14 maize data sets using a percentile value of 15%. ASI data sets were excluded from the regression analysis (ovals).

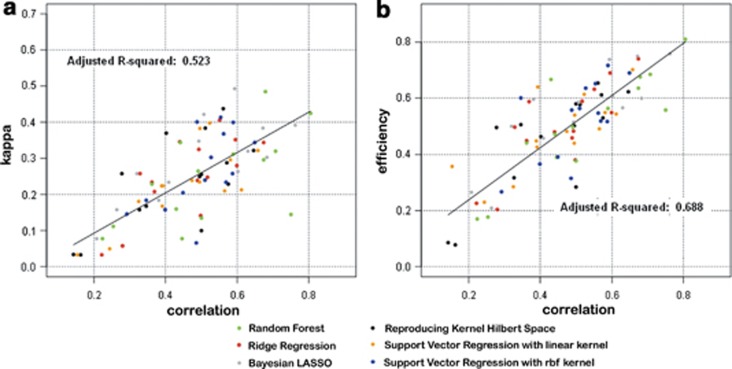
The same conclusions can be drawn from the wheat data set (Figures 3a and b), where individuals were selected from the lower tail (rust resistance) or the upper tail (yield) of the distribution.

Figure 3.

Scatter plot of Pearson's correlation coefficient vs Cohen's kappa coefficient (a) and Pearson's correlation coefficient vs RE (b) for the 6 regression methods evaluated on 16 wheat data sets using a percentile value of 15%.

Comparison of regression and classification for selecting the best individuals at different percentile values

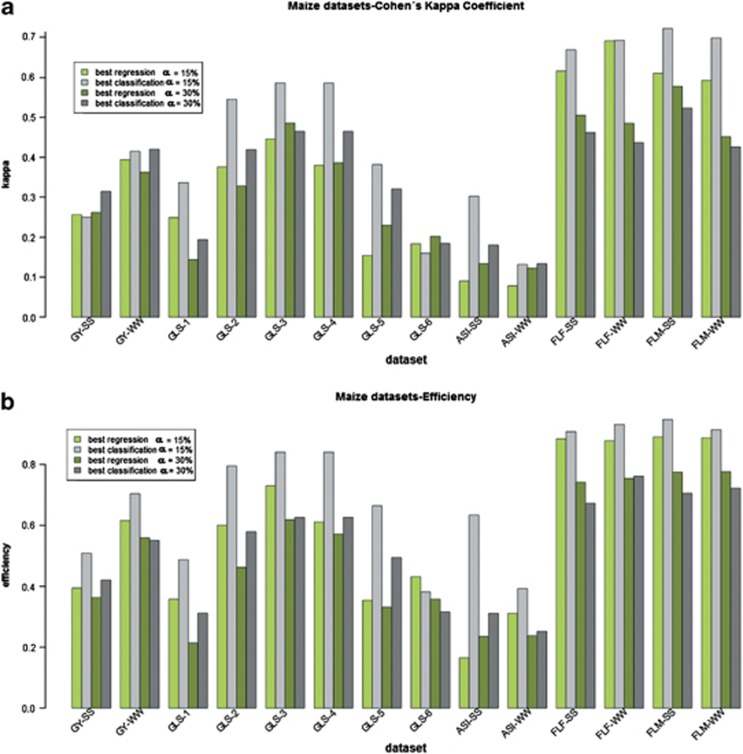
Although the percentile α=15% is a proportion commonly used in plant breeding, some breeders may require other values, that is, α=20 or 40%, depending on budget or programme demands. We therefore evaluated the success of regression and classification methods using the same criteria (κ and RE) at α=10, 15, 20, 25, 30, 35 and 40% of the distribution. For simplicity, the complete results of this evaluation are presented in Supplementary Figures S1–S5, which show that κ or RE of the different regression or classification algorithms is influenced by the data set or the percentile value. To summarise these different outputs, in Figures 4 and 5 we give bar plots comparing the performance of κ (A) and RE (B), for the best classification algorithm against the best regression algorithm for the maize and wheat data sets, respectively, at two percentiles: 15% and 30%. From our viewpoint (Supplementary Figures S1–S5), these two values summarise the behaviour of algorithms at low percentiles (<25%) or high percentiles (⩾25%), respectively. This behaviour is highly dependent on the trait and the crop evaluated. For example, when evaluating grain yield in wheat (Supplementary Figure S1), RE remained approximately constant, except for SVR-lin, which decreased in GY-4 as the percentile decreases. Something similar occurred in maize grain yield, except for SVC-lin, which increased as the percentile decreased (Supplementary Figure S1B). Regarding κ, it decreased in most algorithms, except SVC-lin in GY-1, where it was high and constant (Supplementary Figure S1A). Regarding yield, many methods showed a κ and RE response convex upwards, while in the flowering data sets (Supplementary Figure S2), for most methods, both κ and RE displayed straight horizontal lines or with a slight decrease at lower percentiles. RFC exhibited a particular behaviour in the RE of FLM or FLF data sets (Supplementary Figure S2B) or κ (Supplementary Figure S2A), where values dropped abruptly as α became lower than 0.2. GLS data sets (Supplementary Figure S3) showed similar behaviour to that detected in flowering, except that RFR showed the same performance as the remaining methods. With respect to the κ values observed in GLS analysis in the maize data sets (Supplementary Figure S3), all algorithms had approximately the same value (GLS-2, GLS-3 and GLS-4) as alpha decreased, except SVC with linear kernel, which exhibited continuous growth.

Figure 4.

Bar plot of Cohen's kappa coefficient (a) and RE (b) for the best regression method (green) and the best classification method (grey) evaluated on 14 maize data sets using a percentile α=15% (light colour) and 30% (dark colour).

Figure 5.

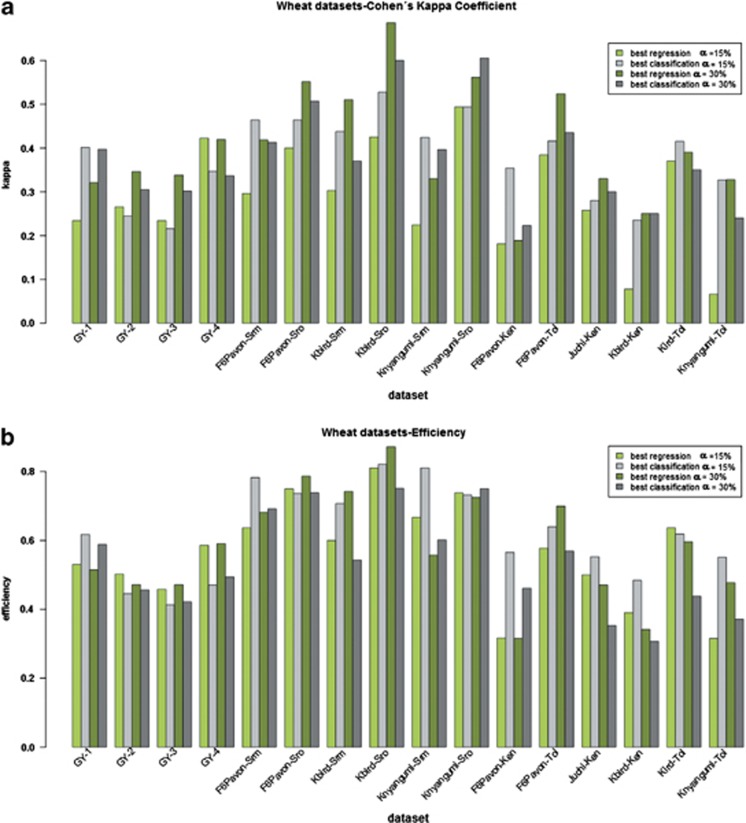
Bar plot of Cohen's kappa coefficient (a) and RE (b) for the best regression method (green) and the best classification method (grey) evaluated on 16 wheat data sets using a percentile α=15% (light colour) and 30% (dark colour).

Finally, in the analysis of yellow and stem rust, κ or RE variation proceeds in steps across the different percentiles, while in the other data sets these variables (κ or RE) showed a continuous variation. This may be due to the fact that the original phenotypes were recorded on a 1–6 scale (Ornella et al., 2012) and to an artifact generated by sampling a low number of individuals. GLS resistance was also recorded on a discrete scale but the number of individuals was higher (González-Camacho et al., 2012). These steps were more pronounced in KBIRD data sets (Supplementary Figure S4), where the population size was 90 individuals.

The summaries presented in Figures 4 and 5 show that the relative performance between regression and classification at the two percentiles is highly dependent on the trait analysed. In the FLF and FLM data sets, both regression and classification reduced κ and RE values when α=30%. In GLS, this reduction was less pronounced, and in most data sets, classification still outperformed regression. In the two ASI data sets, where individuals were selected from the middle of the distribution, RE of classification decreased in both cases, whereas RE of regression increased for ASI-SS and decreased for ASI-WW. The κ of regression increased for both ASI-SS and ASI-WW, whereas the κ of classification decreased for ASI-SS or remained roughly the same for ASI-WW. Finally, RE decreased for both classification and regression in GY-SS for the two yield data sets (Figure 4b), while κ was roughly the same for regression and increased for classification. For GY-WW, κ decreased for regression and remained in the same magnitude classification, while RE decreased for both classification and regression in GY-WW (Figure 4b).

For the wheat yield data, RE of regression and classification remained in the same order of magnitude (Figure 5b), whereas κ increased when α was set at 30% the exception was GY-4, where κ remained in approximately the same range (Figure 5a). Note that these observations are approximations used here to illustrate the tendency of the interaction between algorithms and traits. In all yellow rust data sets, the RE decreased markedly for classification, whereas for regression it increased or remained in the same order of magnitude. In stem rust, there is noticeable variation across data sets. When α=30%, RE of regression increased for all data sets, except those derived from the KNYANGUMI population, while RE of classification decreased or remained in the same order of magnitude. Lastly, κ of regression increased in all stem and yellow rust data sets, whereas κ of classification increased for data from off-season evaluation (-Sro) and decreased for data sets derived from main season evaluation (-Srm). Finally, κ decreased for three yellow rust data sets (KBIRD-Tol, KNYANGUMI-Tol and F6PAVON-Ken) and increased for the other three (KBIRD-Ken, JUCHI-ken and F6PAVON-Tol).

Discussion

Accuracy of GS algorithms for selecting the best individuals

GS aims to accurately predict breeding values with genome-wide marker data using a three-step process: (1) model training and validation, (2) predicting breeding values, and (3) selecting based on these predictions (Heffner et al., 2010).

Success of GS is mostly evaluated by Pearson's correlation coefficient between the observed and predicted values. However, ρ is a global measure that does not assess the goodness-of-fit of the regression in the critical zone, that is, the extreme values where the breeder decides whether or not to keep the lines for further breeding.

We evaluated the performance of 6 regression and 2 classification methods for selecting the best 15% of the individuals in 16 wheat data sets and 14 maize data sets (number of individuals ranging from 90 to 599) with variable marker coverage (Table 1) and variable population structure (González-Camacho et al., 2012; Crossa et al., 2013). However, as population size influences the decision on selection intensity, we also evaluated the behaviour of algorithms for α=10, 15, 20, 25, 30, 35 and 40% of the distribution.

We chose two measures to evaluate the performance of algorithms for selecting the best individuals. One is the kappa (κ) coefficient (Cohen, 1960), which estimates the number of individuals correctly selected adjusted by the proportion of the class. The second is RE (equations 6 and 7), which was proposed ad hoc upon the model of directional selection by truncation (Falconer and Mackay, 1996). Under this model, the genetic gain per generation is ΔG=ihσ_g (Falconer and Mackay, 1996), where i is the intensity of selection; h is the square root of heritability of the trait; and σ_g is the additive genotypic standard deviation of the initial generation. As RE is the ratio of selection intensity based on marker data to phenotypic selection intensity (assuming the same genetic variance), it also gives the expected ΔG when GS is used. Other statistics remain to be explored: the AUC (area under the curve) statistic, for example, which is interpreted as the probability that a given classifier assigns a higher score to a positive example than to a negative one, when the positive and negative examples are randomly picked (Vazquez et al., 2012). The choice of the proper statistic will depend on the experimental design.

Our results (Figures 2b and 3b) show that, except for the ASI data sets, ρ is a good indicator of the efficiency of GS in replacing phenotypic selection for α=15%. For both maize and wheat, the relation between ρ and κ or between ρ and RE is very similar. For example, if ρ=0.6, RE is approximately 0.7 for maize (Figure 2b) and 0.6 for wheat (Figure 3b). The difference between slopes may be influenced mainly by the number of markers as the number of lines overlaps. Concerning the trait, the best individuals in the data sets were not always located in the upper tail of the distribution, as in yield; they were also located in the extreme lower tails of the distribution, as in disease resistance or flowering traits. For MFL and FFL, we decided to evaluate the selection of lines located in the lower tail of the distribution, as our group is involved in a drought breeding programme and a short life cycle is one of the alternatives for drought escape.

When using classification instead of regression for GS, we observed that SVC-lin outperforms regression approaches in almost all data sets when the proportion of selected individuals is small, that is, at the tails of the distribution (see Supplementary Figures). This can be explained by the generalisation capabilities of SVC-lin in circumstances that may be similar to those presented in our work, that is, the Gaussian kernel may over-fit the training set data to yield an SVM model that is not robust (Jorissen and Gilson, 2005). Results of RFC were not so good, although other algorithmic alternatives remain to be explored (González-Recio and Forni, 2011).

The observed difference between classification and regression can sometimes exceed 50% (see, for example, GLS-5 results in Figure 4). When the percentile of the distribution is higher, that is, α⩾25%, either this difference is not so important or regression performs better. It should be noted that dissimilarities between performances of algorithms depend on the trait analysed (see Supplementary Figure S6). González-Recio and Forni (2011) obtained similar results when evaluating simulated and field data (disease resistance in pigs).

The superiority of binary classification over regression could be due to the skewness or asymmetry of the distribution per se (Supplementary Figure S1) or to the complexity of the relationship between genotypes and phenotypes. As discussed in Wang et al. (2012), it is still not clear how important epistasis in complex traits is in plant selection or what the effect of gene-by-environment interactions is. Machine learning algorithms, whether regression (SVR or RFR) or classification (SVC or RFC), can learn from finite training data sets taking into account the complexity of the hypothesis space without imposing any structure on the data (Hastie et al., 2011). Classification algorithms, in particular, optimise the function specifically to the region of selection; this may explain the differences observed at higher or lower percentiles.

Finally, there is a difference between the classification methods proposed by González-Recio and Forni (2011) and those used in this study. Whereas González-Recio and Forni (2011) chose hard classifiers, which directly target the classification decision boundary without producing probability estimation, we explored the behaviour of soft classifiers, which, besides emitting a probability of the class, allows using more balanced data sets as training.

Conclusions

In this study, we compared the performance of six regression and three classification algorithms for selecting the best individuals in maize and wheat data sets using high-throughput molecular marker information. Instead of fitting all the data, classification algorithms optimise the approximating function to separate the best and worst individuals. This competency is noticeable, especially at extreme values of the distribution where classification seems able to capture more efficiently the underlying relations connecting genotypes to phenotypes.

Data

The 30 data sets (14 maize trials and 16 wheat trials) and the R and Java scripts used in this work are deposited at http://repository.cimmyt.org/xmlui/handle/10883/2976.

The authors declare no conflict of interest.