Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2014 Feb 12;112(6):638–645. doi: 10.1038/hdy.2014.1

Bridging the gap between marker-assisted and genomic selection of heading time and plant height in hybrid wheat

Y Zhao 1,3, M F Mette 1,3, M Gowda 2,4, C F H Longin 2, J C Reif 1,*
PMCID: PMC4023446  PMID: 24518889

Abstract

Based on data from field trials with a large collection of 135 elite winter wheat inbred lines and 1604 F1 hybrids derived from them, we compared the accuracy of prediction of marker-assisted selection and current genomic selection approaches for the model traits heading time and plant height in a cross-validation approach. For heading time, the high accuracy seen with marker-assisted selection severely dropped with genomic selection approaches RR-BLUP (ridge regression best linear unbiased prediction) and BayesCπ, whereas for plant height, accuracy was low with marker-assisted selection as well as RR-BLUP and BayesCπ. Differences in the linkage disequilibrium structure of the functional and single-nucleotide polymorphism markers relevant for the two traits were identified in a simulation study as a likely explanation for the different trends in accuracies of prediction. A new genomic selection approach, weighted best linear unbiased prediction (W-BLUP), designed to treat the effects of known functional markers more appropriately, proved to increase the accuracy of prediction for both traits and thus closes the gap between marker-assisted and genomic selection.

Keywords: marker-assisted selection, genomic selection, heading time, plant height, hybrid wheat

Introduction

Functional markers linked to quantitative trait loci (QTLs) are routinely used to predict the performance of important traits in domestic animals (Goddard and Hayes, 2009) and crop plants (Bernardo, 2008). Nevertheless, marker-assisted selection has its limitations (Heffner et al., 2009), as it is efficient only if the trait under consideration is controlled by a limited number of QTLs with large contributions to phenotypic variation, but is inferior to traditional phenotypic selection in dealing with complex agronomic traits controlled by many QTLs with small effects (Bernardo, 2001). One major reason is that estimates of QTL effects for minor QTLs are often biased.

As a solution for the prediction of performance in complex traits, genomic selection has been suggested (Meuwissen et al., 2001). In genomic selection, large numbers of markers are included and their effects are estimated in populations that have been genotyped and phenotyped. The estimated marker effects are then applied to predict the breeding value of nonphenotyped individuals based on their molecular marker profiles. The great potential of genomic selection for complex traits has been demonstrated in several experimental studies in plant and animal breeding populations (Bernardo, 2008; Heffner et al., 2009; Heslot et al., 2012; Massman et al., 2013).

One crucial challenge in genomic selection is to choose the appropriate biometrical model (Heffner et al., 2009; Heslot et al., 2012). The relative performance of biometrical models is expected to depend on the genetic architecture of the traits under scrutiny. In a recent simulation study, Clark et al. (2011) observed substantial higher accuracies of prediction for BayesB in comparison with RR-BLUP (ridge regression best linear unbiased prediction) in a scenario assuming 100 QTLs underlying the trait under consideration. Whereas RR-BLUP is based on the infinitesimal model, BayesB implies that only a defined fraction of single-nucleotide polymorphisms (SNPs) contributes to the genotypic variation of the trait under consideration. The reported superiority of BayesB is challenged by a study based on experimental data in maize that described only marginal differences in accuracies between biometrical models and did not observe an association with genetic architecture (Riedelsheimer et al., 2013). One explanation for the deviation observed between prediction accuracies based on simulation versus experimental data could be the presence of linkage disequilibrium (LD) in experimental setups that would also enable infinitesimal model-based approaches to appropriately portray a genetic architecture with large effect QTLs. Besides the superiority of specific genomic selection models, comparison of the accuracy of marker-assisted versus genomic selection is of interest for those traits with QTLs exhibiting large effects on the genotypic variation. To the best of our knowledge, however, such a comparison based on experimental data sets for traits with known large effects is lacking.

Wheat is an important crop in which extensive studies of genetic architecture have been performed (Le Couviour et al., 2011; Würschum et al., 2013). Heading time and plant height are important traits for wheat production (Borlaug, 1983; Worland et al., 1998; Distelfeld et al., 2009) and key genes such as Ppd-D1, Rht-B1 and Rht-D1 controlling these traits have been characterized at the molecular level. Ppd-D1 encoding a pseudo-response regulator family member (Turner et al., 2005; Beales et al., 2007) is a major regulator of photoperiod response in wheat with also some effect on plant height (Worland et al., 1998), whereas Rht-B1 and Rht-D1 encoding gibberellin response modulators are major regulators of plant height (Peng et al., 1999). The photoperiod-insensitive allele Ppd-D1a promoting early flowering and short growth as well as the gibberellin-insensitive alleles Rht-B1b or Rht-D1b promoting semi-dwarf stature are well represented in wheat adapted to temperate zones (Guo et al., 2010; Le Couviour et al., 2011; Seki et al., 2011; Wilhelm et al., 2013a, 2013b). Nevertheless, there is room for additional QTLs, making heading time and in particular plant height interesting model traits for a comparative study of the predictability of combined known major and unknown minor effects.

Based on phenotypic data obtained in four environments (Longin et al., 2013) and genotypic data generated using a wheat 9k SNP array (Akhunov et al., 2009; Cavanagh et al., 2013) and functional markers at gene loci Ppd-D1, Rht-B1 and Rht-D1 (Ellis et al., 2002; Beales et al., 2007) for a large collection of 135 elite winter wheat inbred lines and 1604 F1 hybrids derived from them, we compared the accuracy of prediction of marker-assisted selection and current genomic selection approaches for the model traits heading time and plant height in a cross-validation approach. For heading time, accuracy was high for marker-assisted selection and low for genomic selection using RR-BLUP and BayesCπ, whereas for plant height, accuracy was low for marker-assisted selection as well as for RR-BLUP and BayesCπ. As a likely explanation for the different accuracies of prediction achieved for the two traits, differences in the LD structure of related functional and SNP markers were identified in a simulation study. We developed a weighted best linear unbiased prediction (W-BLUP) approach as a new genomic selection model with improved accuracy because of a more appropriate treatment of known functional markers. The W-BLUP approach efficiently bridges the gap between marker-assisted and genomic selection.

Materials and methods

Plant materials and field trials

Initially, we had sampled 68 potential male elite inbred lines with known good pollination characters and 275 potential female elite lines adapted to Central Europe and fingerprinted them with 24 simple sequence repeat (SSR) markers (Longin et al., 2013). Eliminating close relatives and maximizing the allelic diversity based on the simple sequence repeat marker profiles (while retaining >77% of simple sequence repeat alleles present in the starting set of 343 lines), 15 male and 120 female parental lines were selected for hybrid production in a 15 times 120 factorial mating design using chemical hybridization agents (Longin et al., 2013). Sufficient F1 hybrid seeds were obtained for 1604 out of the 1800 potential single-cross hybrid combinations (Zhao et al., 2013b). All lines and hybrids were evaluated in 4 environments in 2012 together with 10 commercial checks (Longin et al., 2013). The environments were Böhnshausen (latitude 51°51′N, longitude 10°57′E, 146 m above sea level (asl), sandy loam soil texture), Hadmersleben (latitude 51°59′N, longitude 11°18′E, 88 m asl, silt loam soil texture), Harzhof (latitude 54°24′N, longitude 9°51′E, 25 m asl, sandy loam soil texture) and Hohenheim (latitude 48°42′N, longitude 9°12′E, 390 m asl, sandy loam soil texture). The experimental designs were partially replicated α-designs (Williams et al., 2011), where all parents, checks as well as 29% of the hybrids were used in both replications (for details, see Longin et al., 2013). Sowing density ranged from 230 to 290 seeds per m2 and plot size ranged from 7.5 to 9.7 m2. The trials were treated with fertilizers, fungicides and herbicides according to standard agronomic practices for intensive wheat production. Heading time was recorded as the number of days from 1 January to the day when half of the heads had emerged from flag leaves; plant height was measured in cm at one time point after heading in each environment.

Phenotypic data analyses

Phenotypic data were analyzed in two steps. First, we estimated the adjusted entry means for each location (for details, see Zhao et al., 2013b). In a second step, adjusted entry means were used to estimate the genetic variance components of hybrids and parental lines as well as the variance of genotype × location interactions. We followed the suggestion of Möhring and Piepho (2009) and weighted each observation with one divided by the squared standard error. Significance of variance component estimates were tested by model comparison with likelihood ratio tests where the halved P-values were used as an approximation (Stram and Lee, 1994). In addition, we assumed fixed genetic effects and estimated the best linear unbiased estimates of the 1739 genotypes. The phenotypic data analyses were performed using the software ASReml-R 3.0 (Butler et al., 2009).

Genotypic data analysis

Genotyping was done with a 9k SNP array based on the Illumina Infinium assay (Cavanagh et al., 2013) (Illumina, San Diego, CA, USA). After excluding SNP markers with (1) a rate of missing values above 5%, (2) a rate of heterozygosity above 5% or (3) a minor allele frequency of <0.05 (Miedaner et al., 2012), in total 1280 SNP markers were retained (Supplementary Table S1). In addition, in genes Ppd-D1 (Beales et al., 2007), Rht-B1 and Rht-D1 (Ellis et al., 2002), one SNP each was analyzed as a functional marker using LGC Genomics KASP assays (LGC Genomics, Berlin, Germany). Missing genotypes were imputed following the approach suggested by Crossa et al. (2010).

Marker-assisted selection

The functional marker for Ppd-D1 (Beales et al., 2007) is used as a standard tool in European wheat breeding, explaining up to 30% of the genotypic variation of heading time. In addition, the functional markers for Ppd-D1 (Beales et al., 2007) as well as Rht-B1 and Rht-D1 (Ellis et al., 2002) are used routinely in wheat breeding in Europe, explaining up to 40% of the genotypic variation for plant height. We defined the design matrices for the additive and dominance effects of the three functional markers according to the F∞ metric of Falconer and Mackay (1996) and used a standard multiple regression approach to estimate their effects in the germplasm under consideration. A general term was fitted to groups of females, males and hybrids for plant height to take into account heterosis for this trait, whereas no such correction was needed for heading time in the absence of heterosis (Longin et al., 2013). Furthermore, we used a step-wise backward selection based on the Akaike information criterion to test for relevant two-way epistatic interactions using the step function (Venables and Ripley, 2002) implemented in the software package R (R Core Team, 2012).

Genomic selection

Based on the adjusted entry means of the 1739 genotypes, we applied three approaches for genomic selection considering additive and dominance effects: RR-BLUP (Whittaker et al., 2000), BayesCπ (Dekkers et al., 2009; Habier et al., 2011) and a newly developed modification of RR-BLUP using specific weights for the known functional markers denoted as W-BLUP. All statistical procedures for the genomic selection approaches were executed using R (R Core Team, 2012). Details of the implementation of the RR-BLUP and BayesCπ models have been described in Zhao et al. (2013a). Briefly, the general form of the three models is defined as the following:

graphic file with name hdy20141e1.jpg

where Y are the adjusted entry means of the 1739 genotypes across the four locations, 1n is a vector of ones and n is the number of genotypes; mu; refers to the overall mean across all four locations; a is the additive marker effect and d is the dominance marker effect. ZA and ZD are design matrices for the additive and dominance effects of the markers specified according to the F∞ metric of Falconer and Mackay (1996) and e is the residual.

RR-BLUP

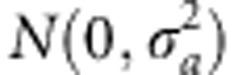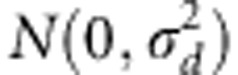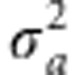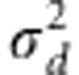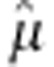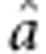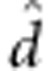For the RR-BLUP model, we assume that additive and dominance marker effects have normal distributions Inline graphic and Inline graphic with constant variances of additive effects Inline graphic and dominance effects Inline graphic. The estimates of mu;, a and d, which denote as Inline graphic, Inline graphic and Inline graphic, were obtained from the following mixed-model equation (Henderson, 1984):

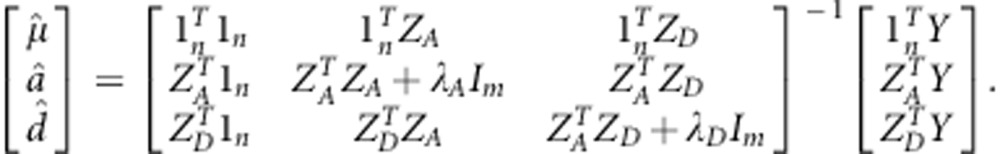graphic file with name hdy20141e9.jpg

Here, Im refers to an identity matrix with dimension of m, where m is the number of markers. The shrinkage parameters λA and λD are defined as the ratios between the variance of residuals and the variance of the marker effects (Meuwissen et al., 2001). Required variance components were estimated based on adjusted entry means of individual environments decomposing the variance of hybrids into variance due to general and variance due to specific combining ability effects (Hallauer and Miranda, 1988).

BayesCπ

Whereas in RR-BLUP it is assumed that all markers contribute to genetic variance, in BayesCπ only a fraction 1–πg (g denotes either a or d) of the used markers is considered to contribute to the genetic variance. Based on this assumption, the model for BayesCπ is:

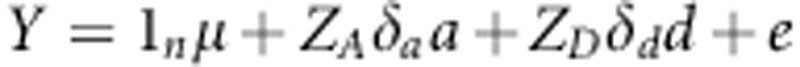graphic file with name hdy20141e10.jpg

The additional parameter δg has a prior distribution:

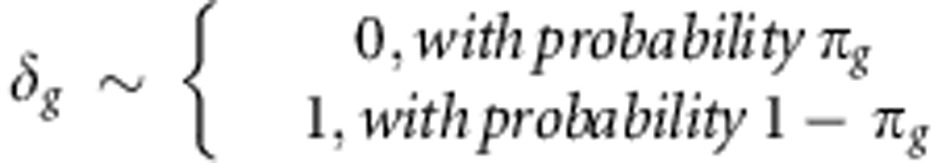graphic file with name hdy20141e11.jpg

In BayesCπ, a uniform (0, 1) prior was assumed for πg, resulting in a β-distribution for the full-conditional posterior (Habier et al., 2011). For BayesCπ, all above outlined parameters have to be sampled from their full-conditional posterior using a special Markov chain Monte Carlo method called Gibbs sampling.

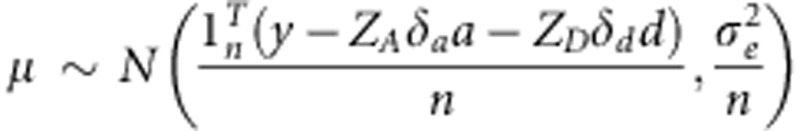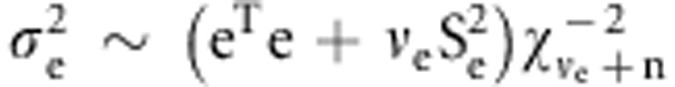The overall mean mu; is sampled from a normal distribution: Inline graphic The variance of residual and additive effects are sampled from the inverted χ2 distribution:

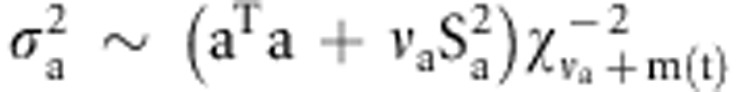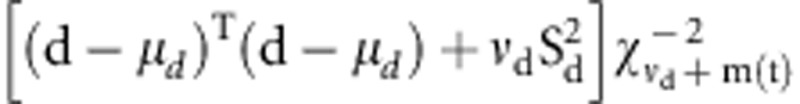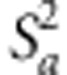Inline graphic, and Inline graphic. Here, m(t) refers to the number of non-zero additive effects in t-th Markov chain Monte Carlo iteration. The variance of dominance effects is sampled from the inverted χ2 square distribution: Inline graphic where mu;d is the expected mean for di, and m(t) refers to the number of non-zero dominance effects in t-th Markov chain Monte Carlo iteration. 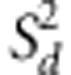In the above, the fixed parameters νe=νa=νd=4, whereas Inline graphic, Inline graphic and Inline graphic were calculated by the genetic variance approach we used in the above RR-BLUP model.

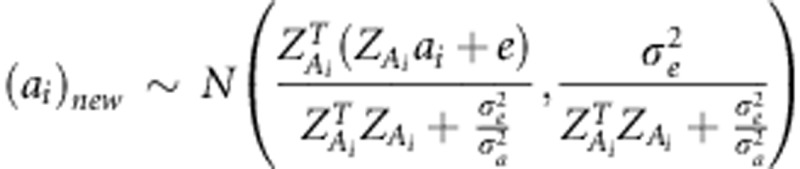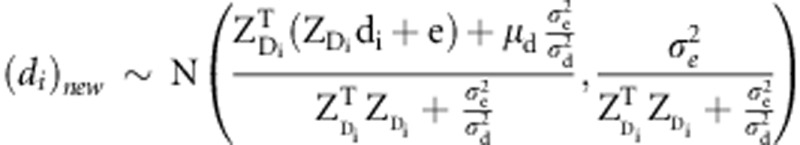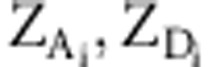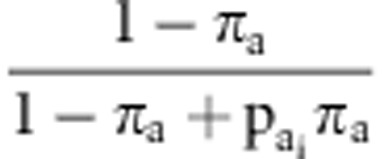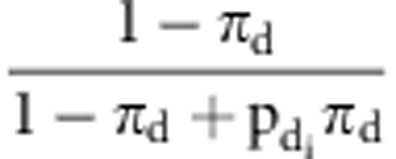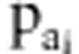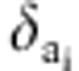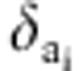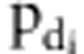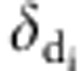For i-th marker effects ai and di, we sampled new ai and di from a full-conditional posterior Inline graphic, and Inline graphic, where Inline graphic refers to the i-th column of ZA and ZD. 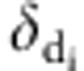Note that a new ai and di was only accepted with probability Inline graphic and Inline graphic, where Inline graphic was the ratio of likelihood with Inline graphic=0 and Inline graphic=1, and Inline graphic was the ratio of likelihood with Inline graphic=0 and Inline graphic=1.

After renewing all the parameters above, the πg(g=a or d) used for the next iteration was updated with a β-distribution 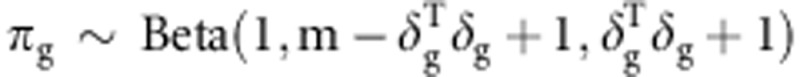Inline graphic.

The above Gibbs sampling was run for 10 000 times, and the first 1000 cycles were discarded as burn in.

W-BLUP

The model used in W-BLUP is similar to the BLUP model, but we added an additional effect for the functional markers:

Y=1nmu;+ZAa+FAaf+ZDd+FDdf+e, where af, df denote the additive and dominance effects of the functional markers, and FA and FD are the design matrices for them. Thus, the mixed model equation for this model will be:

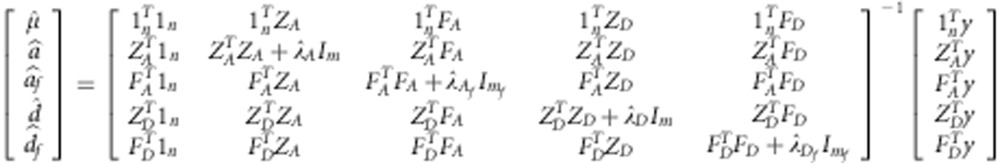graphic file with name hdy20141e31.jpg

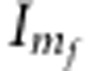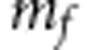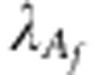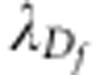Here, Inline graphicrefers to an identity matrix, whereas Inline graphicis the number of functional markers. The shrinkage parameters Inline graphic and Inline graphicare now defined as the ratio between the variance of residuals and the variance of the functional marker effects estimated by using marker-assisted selection in each training set. In this way, we give in particular a larger weight to the functional markers than to the general markers.

Hybrid performance was predicted based on the estimated additive and dominance effects (Zhao et al., 2013a). To study the influence of dominance effects on the prediction accuracy, we estimated the hybrid performance based solely on the additive or dominance effects.

Cross-validations

We evaluated the accuracy of prediction of heading time and plant height by genomic selection with the two established approaches RR-BLUP and BayesCπ as well as the newly developed W-BLUP using cross-validation. As population structure in factorial crosses strongly influences prediction accuracy, we used a cross-validation strategy in which training and validation were performed in sets that were not related via shared parental lines. We sampled 100 times 10 male and 80 female parental lines plus 610 hybrids derived from them as training set and estimated the additive and dominance effects. Only hybrids originating from the remaining 5 male and 40 female parental lines formed the validation set in which predictions derived from the training set were tested for their cross-validation accuracy. Prediction accuracy was estimated as Pearson's correlation coefficient between the observed and the predicted hybrid performance.

Evaluation of accuracy with computer simulations

We investigated the accuracy to predict the phenotypic performance by conducting computer simulations based on the marker data of our study. We followed the suggestion of Perez et al. (2010) and performed calculations based on the assumption that most markers have very small effects except for one marker that exhibits large additive and one marker that exhibits large dominance effects. We further assumed an average ratio of genetic variance explained by additive and dominance effects of 0.42 and a heritability of 0.77. Moreover, the influence of the LD pattern on the prediction accuracy was approached by comparing simulations. Data set LE-QTL, in which the selected marker of interest had no LD (r2 values <0.1) with all other markers involved, and data set LD-QTL, in which the selected marker was set to show strong linkage disequilibrium with r2 values >0.7 with at least 10 further markers, were designed based on representative SNPs from our study and employed in marker-assisted and genomic selection.

Results

Phenotyping revealed broad genotypic variation for heading time and plant height

A set of 135 elite winter wheat inbred lines and 1604 F1 hybrids derived from them, adding up to in total 1739 entries, was evaluated for heading time and plant height in the field under natural settings at four locations. This revealed substantial genetic variation within the experimental population, and comparably high estimates of heritability of above 0.82 for heading time and plant height (Table 1).

Table 1. Estimates of variance components (σ2) and heritability (H 2) on entry mean basis for heading time (in days after 1 January) and plant height (in cm) in 135 parental winter wheat inbred lines and their 1604 factorial crosses.

Source Heading time Plant height
Parents
 σ2 Genotype 3.58a 22.54b
 σ2 Genotype × environment 1.26a 6.58b
 H2 0.87 0.85
     
F 1 hybrids
 σ2 Genotype 2.04a 17.79b
 σ2 Genotype × environment 0.58a 5.39b
 σ2 Errorc 1.13 12.71
 H2 0.85 0.82
Open in a new tab
a

Significantly different from zero at the 0.001 level of probability.

b

Significantly different from zero at the 0.01 level of probability.

c

Assumed same error variance for parents and F1 hybrids.

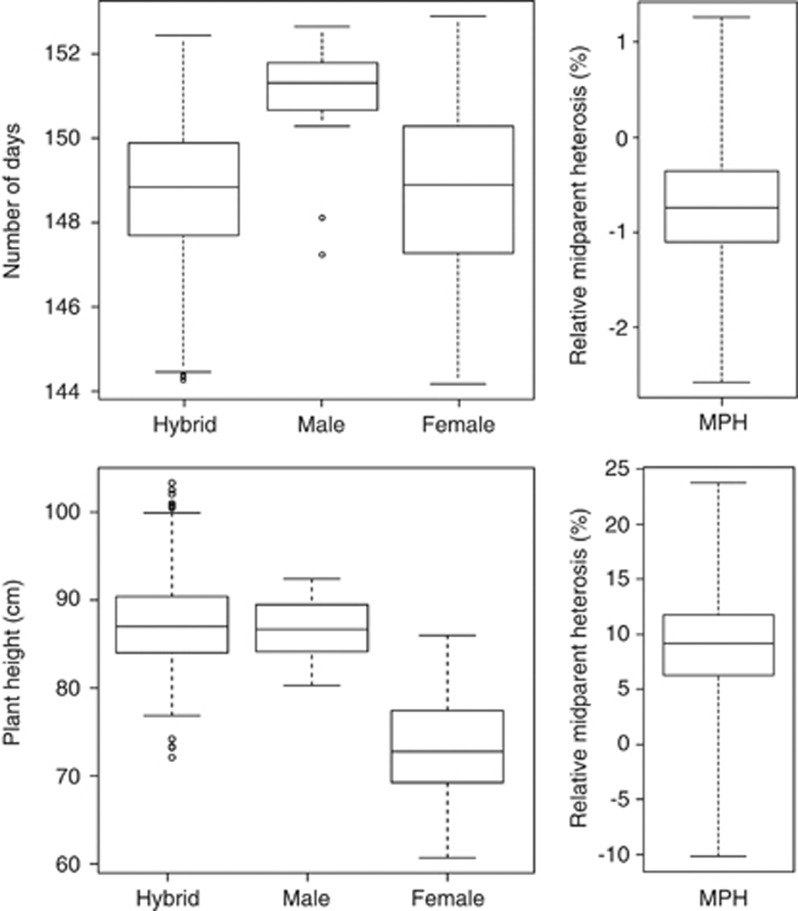
As a prerequisite for efficient hybrid seed production, the 135 inbred lines had to be split into a group of 15 later-heading, taller, open-pollinating types to be used as male and a group of 120 earlier, shorter types to be used as female parents. This grouping is well apparent in the distribution of genotypic values among the male and female inbred lines (Figure 1). Mean average heading time and plant height, respectively, were 151 days and 86.6 cm for male and 149 days and 73.6 cm for female parental lines, in comparison with 149 days and 75.0 cm for all inbred lines together.

Figure 1.

Figure 1

Open in a new tab

Box-and-whisker plots of the distribution of genotypic values for heading time and plant height for the 15 male and 120 female lines, and the resulting 1604 single-cross hybrids evaluated across four environments.

Alleles of major gene loci controlling heading time and plant height were distributed unevenly among male and female parental lines

The allele status of major gene loci controlling heading time and plant height was determined in parental inbred lines and hybrids. Locus Ppd-D1 is a major determinant of heading time in wheat, with the photoperiod-insensitive allele Ppd-D1a promoting early heading in temperate zones (Beales et al., 2007). All 15 late-heading inbred lines used as male parents were homozygous for the photoperiod-sensitive allele Ppd-D1b, whereas among the earlier female parents, lines homozygous for either Ppd-D1a or Ppd-D1b were present.

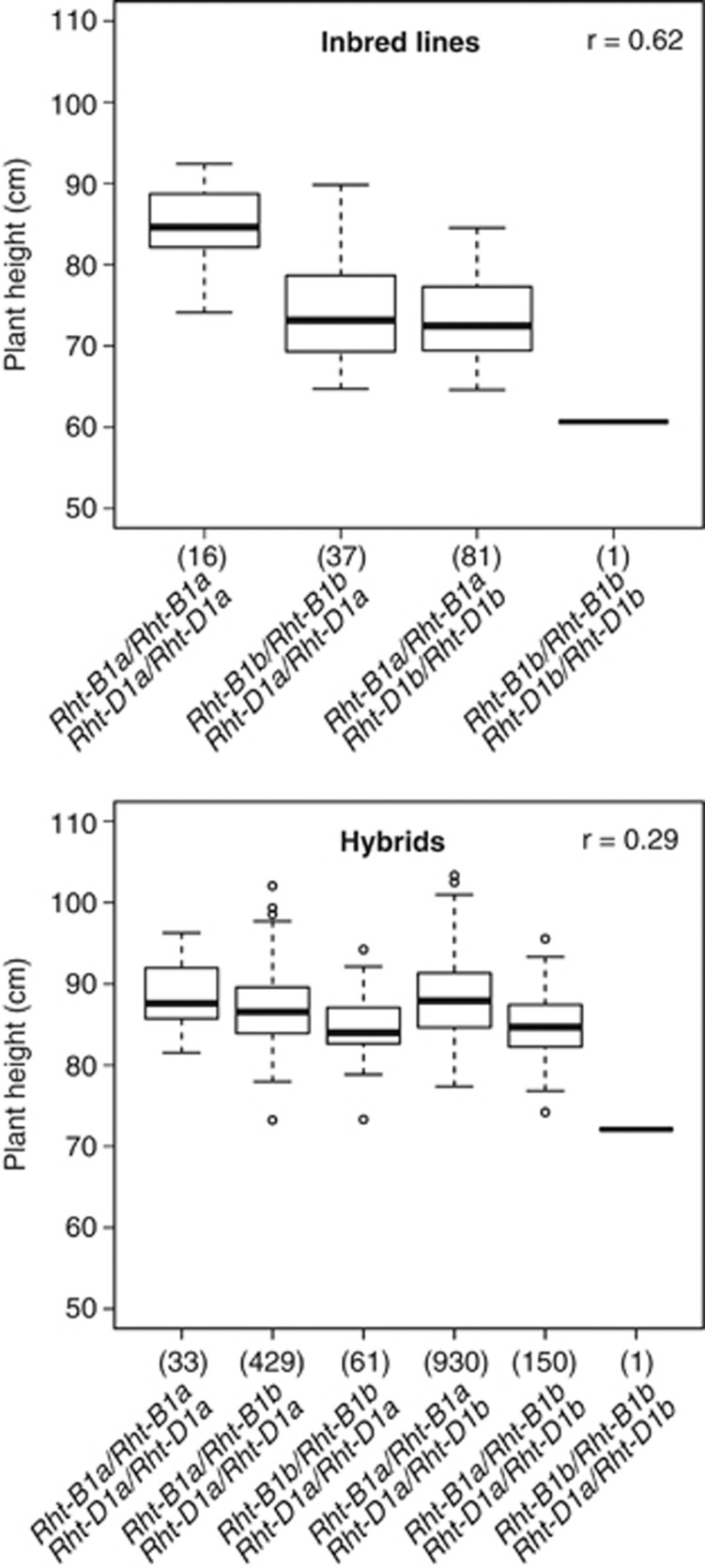
Plant height is mainly influenced by loci Rht-B1 and Rht-D1, with alleles Rht-B1a and Rht-D1a promoting tall plant stature and alleles Rht-B1b and Rht-D1b promoting dwarfing (Ellis et al., 2002). This is also reflected in our data (Figure 2). Inbred lines with allelic setup Rht-B1a/Rht-B1a;Rht-D1a/Rht-D1a were tallest with a median of average plant height of 84.6 cm, followed by Rht-B1b/Rht-B1b; Rht-D1a/Rht-D1a and Rht-B1a/Rht-B1a;Rht-D1b/Rht-D1b with 73.2 and 72.5 cm, respectively, and the only Rht-B1b/Rht-B1b; Rht-D1b/Rht-D1b line included, with an average plant height of 60.7 cm (Figure 2). Among the tall lines used as male parents in hybrid production, 13 were of type Rht-B1a/Rht-B1a;Rht-D1a/Rht-D1a and two were of type Rht-B1b/Rht-B1b;Rht-D1a/Rht-D1a, whereas among inbred lines used as female parents, all four possible homozygous Rht-B1;Rht-D1 allele combinations were present.

Figure 2.

Figure 2

Open in a new tab

Box-and-whisker plots of the distribution of the genotypic values for plant height for different Rht-B1 and Rht-D1 allele setups among the 135 parent lines and 1604 single-cross hybrids. Whereas alleles Rht-B1a and Rht-D1a promote tall plant stature, alleles Rht-B1b and RhtD1b promote dwarfing. Numbers in parentheses indicate numbers of inbred lines or hybrids with respective genotypes.

Hybrids displayed heterosis for plant height but not for heading time

We observed contrasting responses of the two traits of interest to hybridization (Figure 1). The median of average heading time of hybrids was more similar to that of the 120 earlier-heading inbred lines used as female parents, and average relative midparent heterosis of heading time was only 0.7%. This low average midparent heterosis observed in our study can be explained by small dominance effects and/or by a lack of genetic differentiation among the male and female lines. In contrast, average relative midparent heterosis was substantial for plant height, amounting to 9.2%. Thus, the median of average plant height of hybrids was more similar to that of the tall 15 inbred lines selected as male parents.

To further scrutinize the heterosis for plant height, hybrids were also grouped according to their allelic setup at gene loci Rht-B1 and Rht-D1 (Figure 2). As only two of the possible four homozygous Rht-B1;Rht-D1 allele combinations had been employed as male parents, only six of the possible nine Rht-B1;Rht-D1 allele combinations were present among the hybrids, including only two allowing direct comparison with parental inbred lines. For these two combinations, Rht-B1a/Rht-B1a;Rht-D1a/Rht-D1a and Rht-B1b/Rht-B1b;Rht-D1a/Rht-D1a, hybrids were taller than the respective inbred lines, with medians of average plant height of 87.6 cm (+4% compared with inbred lines) and 84.0 cm (+15%), respectively (Figure 2). Thus, heterosis of plant height manifested between inbred lines and hybrids carrying the same, homozygous Rht-B1;Rht-D1 allele setup.

As Ppd-D1 is also known to influence plant height (Worland et al., 1998; Beales et al., 2007), its allele status was checked in the compared plant groups. All Rht-B1a/Rht-B1a;Rht-D1a/Rht-D1a parental lines and hybrids that were included in our study were at the same time homozygous for the photoperiod-sensitive allele Ppd-D1b promoting a tall plant stature that excluded differences at this locus as an explanation for differences in plant height. Consistently, plant height heterosis between Rht-B1b/Rht-B1b;Rht-D1a/Rht-D1a inbred lines and hybrids persisted when subgroups containing only material homozygous for Ppd-D1b were compared.

Marker-assisted selection for heading time and plant height

The genotypic variation of heading time could be predicted by marker-assisted selection based on the functional marker for Ppd-D1 (Beales et al., 2007) with an accuracy of 0.45 for the parental inbred lines (data not shown) and with an accuracy of 0.53 for the hybrids (Table 2). In the pooled populations of parental inbred lines and hybrids, prediction accuracy of marker-assisted selection for heading time amounted to a rather high 0.54 based only on the functional marker for Ppd-D1. The degree of dominance was −0.72 in the direction of the early-flowering homozygous Ppd-D1a class.

Table 2. Average prediction accuracy of MAS and three different approaches of genomic selection for heading time and plant height.

Method Heading time
Plant height
  Accuracy s.d. Accuracy s.d.
MAS-NCVa 0.526 — 0.444 —
MASb 0.535 0.091 0.378 0.101
RR-BLUPc 0.404 0.112 0.395 0.135
BayesCπc 0.442 0.114 0.422 0.125
W-BLUPc 0.576 0.110 0.502 0.115
Open in a new tab

Abbreviations: MAS, marker-assisted selection; RR-BLUP, ridge regression best linear unbiased prediction; NCV, non-cross-validation; W-BLUP weighted best linear unbiased prediction; s.d., standard deviation.

a

MAS-NCV indicates MAS prediction accuracy without cross-validation based on functional marker Ppd-D1 for heading time and functional markers Ppd-D1, Rht-B1 and Rht-D1 for plant height. As only one value is available, s.d. could not be determined.

b

MAS prediction accuracy according to cross-validation.

c

Genomic selection accuracies according to cross-validation for RR-BLUP, BayesCπ and W-BLUP based on 1280 markers plus the functional markers.

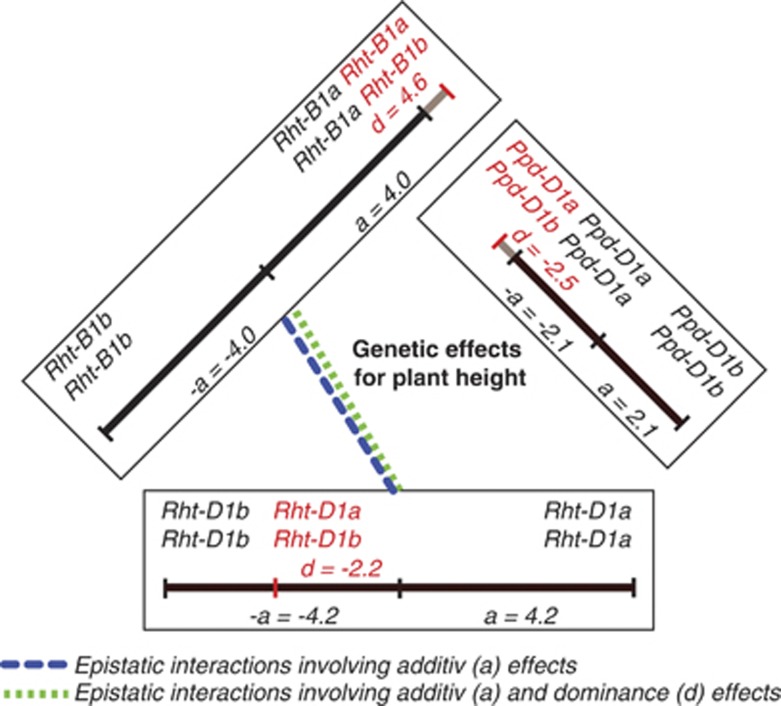
Prediction accuracy of marker-assisted selection for plant height based on the functional markers for Rht-B1 and Rht-D1 (Ellis et al., 2002) was much higher with 0.62 for the inbred lines as compared with 0.29 for the hybrids (Figure 2). Adding the functional marker information for Ppd-D1 (Beales et al., 2007) to the one for Rht-B1 and Rht-D1 led to an increased prediction accuracy of 0.44 in the population of the hybrids. In the pooled populations of inbred lines and hybrids, the prediction accuracy amounted to 0.69 based on all three functional markers for gene loci Ppd-D1, Rht-B1 and Rht-D1. The degrees of dominance of the three functional marker loci for plant height determined on the basis of combined inbred line and hybrid data with fitting general terms to groups of female parents, male parents and hybrids were 1.2 toward the tall allele Rht-B1a, and 0.5 and 1.2 toward the short alleles Rht-D1b and Ppd-D1a, respectively (Figure 3). The model selection revealed significant digenic epistatic interactions involving additive and dominance effects among gene loci Rht-B1 and Rht-D1.

Figure 3.

Figure 3

Open in a new tab

Genetic effects for plant height for Ppd-D1, Rht-B1 and Rht-D1 genotypes as determined in a population of 135 parent wheat lines and their 1604 single-cross hybrids.

Cross-validated accuracy of marker-assisted and genomic selection

The cross-validation of marker-assisted selection revealed no severe drop in prediction accuracies (Table 2) compared with the non-cross-validated accuracies (Figure 2) for both heading time and plant height. This is not surprising as we considered the accuracy of marker-assisted selection based on well-established functional markers for plant height and heading time. The marginally higher accuracy for cross-validated versus non-cross-validated values observed for heading time resulted from the fact that the accuracies of prediction were evaluated exclusively in the population of hybrids. For the non-cross-validated values, this applies to the estimation and the test set, as both are identical. In contrast, in the cross-validation study, we used parental inbred lines besides the hybrids to estimate the marker effects. Obviously, this contributed to the precision to estimate marker effects.

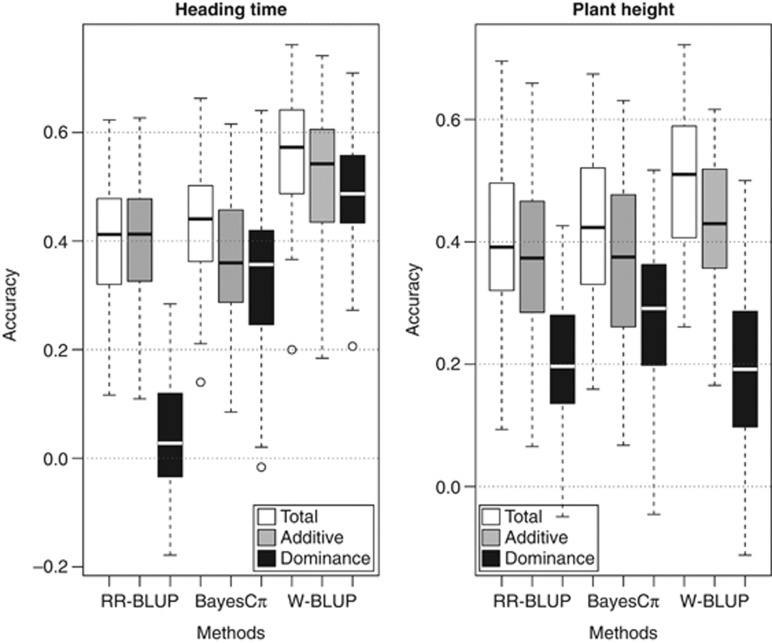
The genotypic variation of heading time and plant height was further predicted based on 1280 SNP markers in combination with functional markers by three different genomic selection approaches, including the well-established RR-BLUP and BayesCπ methods as well as the newly developed W-BLUP. Cross-validation studies of predicted values revealed that for most scenarios accuracies based on additive and dominance effects were higher than that based on additive or dominance effects alone for both traits (Figure 4). An interesting exception is made by the very low accuracies based on dominance effects observed for heading time and RR-BLUP that are in sharp contrast to the results from BayesCπ and W-BLUP. The differences in accuracies can be explained by the large contribution to the phenotypic variation of the dominance effect of Ppd-D1 that can only be properly handled by low shrinkage parameters for this marker. In the following, we will present only the prediction accuracies for combined additive and dominance effects.

Figure 4.

Figure 4

Open in a new tab

Box-and-whisker plots of accuracy to predict heading time and plant height for the three genomic selection methods RR-BLUP, BayesCπ and W-BLUP based on 1280 SNPs and trait-specific functional markers.

Accuracies of prediction from marker-assisted selection as well as accuracies of prediction from all three genomic selection approaches differed substantially between the two traits of interest (Table 2). For heading time, prediction accuracy decreased from 0.54 with marker-assisted selection to 0.40 with RR-BLUP (−25%), and 0.44 with BayesCπ (−17%), and only improved to 0.58 with W-BLUP (+7%). In contrast, for plant height, the low accuracy of 0.38 seen for marker-assisted selection gradually improved over 0.39 with RR-BLUP (+4%) and 0.42 with BayesCπ (+10%) to 0.50 with W-BLUP (+24%). However, even with W-BLUP, accuracy of prediction stayed lower for plant height compared with heading time.

Comparison of marker-assisted and genomic selection based on simulations

Although Ppd-D1 controlling heading date was found in LD (r2=0.15) with only one SNP marker, Rht-B1, Rht-D1 and Ppd-D1 relevant for plant height were found in total to be in LD with 16 SNP markers. In order to test this as an explanation for the different predictive powers of genomic selection based on combined genome-wide and functional marker information for different traits, we performed a simulation study contrasting a scenario in which functional SNPs of interest were in linkage equilibrium with the panel of markers (LE-QTL) with one in which functional SNPs were in LD with several markers (LD-QTL). This simulation scenario revealed that the pattern of LD between functional SNPs with a substantial contribution to the genotypic variance is crucial for the accuracy of genomic selection approaches (Table 3). Looking at prediction accuracies for combined additive and dominance effects, we observed for the LE-QTL scenario a decrease in prediction accuracy from 0.55 for marker-assisted selection to 0.46 for RR-BLUP (−16%), but an increased accuracy with 0.58 for BayesCπ (+5%) and 0.78 for W-BLUP (+42%). Using the preknowledge on important functional markers in the W-BLUP approach led to considerably improved prediction accuracy as compared with marker-assisted selection in this scenario. For the LD-QTL scenario, we also observed, although less pronounced, an increase in prediction accuracy when shifting from marker-assisted selection with 0.66 to genomic selection with close to 0.76 for all three approaches (+15%) irrespective of the method applied.

Table 3. Average prediction accuracies of MAS and three different approaches of genomic selection for simulated data sets.

Method LE-QTL
LD-QTL
  Total Additive Dominance Total Additive Dominance
MASa 0.55 0.46 0.31 0.66 0.61 0.35
RR-BLUPb 0.46 0.39 0.34 0.75 0.67 0.46
BayesCπb 0.58 0.47 0.36 0.76 0.66 0.43
W-BLUPb 0.74 0.63 0.45 0.77 0.69 0.43
Open in a new tab

Abbreviations: LD, linkage disequilibrium; LE, linkage equilibrium; MAS, marker-assisted selection; QTL, quantitative trait locus; RR-BLUP, ridge regression best linear unbiased prediction; W-BLUP weighted best linear unbiased prediction.

Based on representative single-nucleotide polymorphisms (SNPs) from our study, we assumed a scenario LE-QTL, in which a selected marker was in no LD with all other markers involved, and a scenario LD-QTL, in which a selected marker was in strong LD with at least 10 further markers.

a

MAS prediction accuracy according to cross-validation.

b

Genomic selection accuracies according to cross-validation for RR-BLUP, BayesCπ and W-BLUP.

Discussion

Development of hybrid breeding opens a new route to increase yield potential in wheat, but it is also connected with new challenges, the appropriate balancing of heading time and plant height being two of them (Longin et al., 2012). Heading time and plant height are traits important for performance of winter wheat and thus have received substantial attention in line breeding. Key gene loci controlling heading time (Ppd-D1) and plant height (Rht-B1, Rht-D1 and Ppd-D1) are well known, and favorable alleles have been pivotal in shaping current elite wheat (Worland et al., 1998; Peng et al., 1999; Beales et al., 2007). However, more QTLs with small to medium effects are to be expected to fine-tune these traits in both inbred lines and hybrids. Thus, we obtained heading time and plant height phenotypic data in field trials at four locations and generated genotyping data using a 9k wheat SNP array and functional marker tests for Ppd-D1, Rht-B1 and Rht-D1 for a population of 135 wheat inbred lines and 1604 hybrids derived from them.

Unexpectedly, marker-assisted selection as well as genomic selection approaches RR-BLUP and BayesCπ showed quite different accuracies of prediction for the two traits of interest in cross-validation tests. For heading time, prediction by marker-assisted selection based on Ppd-D1 alone was already highly accurate for inbred lines, hybrids and the combination of both. In contrast, for plant height, prediction by marker-assisted selection based on Rht-B1, Rht-D1 and Ppd-D1 was accurate only for inbred lines alone, but not for hybrids alone or the combination of inbred lines and hybrids. Cross-validation fully confirmed the high accuracy of prediction by marker-assisted selection for heading time, but indicated that the already lower accuracy of prediction for plant height was slightly overestimated. Genomic selection also showed different accuracies of prediction for the two traits in cross-validation. In comparison with marker-assisted selection, accuracy of prediction of heading time dwindled in genomic selection with RR-BLUP and was still low with BayesCπ for combined inbred lines and hybrids, whereas for plant height, it improved with RR-BLUP and even further with BayesCπ. Consequently, the advantage of marker-assisted versus genomic selection strongly depends on the trait of interest and the genetic architecture underlying it.

One further explanation for the differences in prediction accuracies of genomic selection for the two traits might be differences in the LD structure. Whereas Ppd-D1 controlling heading date is in LD with only one SNP marker, Rht-B1, Rht-D1 and Ppd-D1 relevant for plant height are all together in LD with a total of 16 SNP markers. Such an influence of LD was confirmed by our simulation studies. In a setup assuming a functional marker without SNP markers in LD, accuracies of prediction of marker-assisted selection, RR-BLUP and BayesCπ showed a drop with RR-BLUP similar to that seen for heading time, whereas in a setup assuming a functional marker in LD with several SNP markers, increasing accuracies similar to that seen for plant height were found.

Yet another reason for the differences in the accuracies of prediction between the two traits might reside in hybrid-related effects. For both heading time and plant height, additive as well as dominance effects contributed to the accuracies of genomic selection, but to different extents. Additive effects were found most important for heading time, in particular in context with RR-BLUP, whereas for plant height, additive and dominance effects contributed in a more balanced way. This is consistent with the very low midparent heterosis for heading time and the contrasting substantial midparent heterosis for plant height observed in our study.

With regard to the control of heading time and plant height, partial dominance of the Ppd-D1 allele promoting early heading (Ppd-D1a) and of the Rht-D1 allele promoting short plant stature (Rht-D1b) reported by Worland et al. (1998) and Beales et al. (2007) could be confirmed. In contrast, the apparent overdominance of alleles Ppd-D1a and Rht-B1a (the latter one even in the direction of tall plant stature) in context with plant height found in our study is inconsistent with these publications. However, there are previous reports of similar overdominance (Allan et al., 1968) and generally increased plant height (Allan et al., 1968; Fick and Qualset, 1973) in wheat F1 hybrids. Furthermore, because of the need to use late-heading tall inbred lines as male and early-heading shorter ones as female parents in wheat hybrid production, Ppd-D1, Rht-B1 and Rht-D1 alleles promoting early heading (Ppd-D1a) and short stature (Ppd-D1a, Rht-B1b and Rht-D1b) were distributed nonrandomly among the parental lines, and thus also among the hybrids.

The nonsatisfactory performance of RR-BLUP and also BayesCπ in the prediction of heading time and plant height is in part because of inappropriate weighting of functional marker versus SNP marker contributions. To resolve this limitation, we developed W-BLUP that balances the contributions from random and functional markers by including additional effect of the latter ones. Accordingly, W-BLUP performed better than both RR-BLUP and BayesCπ in prediction based on experimental as well as simulated data. Thus, W-BLUP provides a new robust tool to bridge the gap between marker-assisted and genomic selection.

Heading time and plant height also differed in their levels of heterosis, with heading time showing almost no response to hybridization, whereas plant height was increased by 4 to 15%. The difference in the response of the two traits to hybridization and the substantial heterosis in plant height toward tall plant stature had already shown up in the initial analysis of the data set (Longin et al., 2013). As a short, sturdy plant stature is favorable in wheat cultivation (Borlaug, 1983), a major challenge for future wheat hybrid breeding will be to counterbalance the heterosis in plant height and to mobilize the surplus in biomass into grain yield. In previous conventional wheat line breeding, plant height has been traded for yield gain by using dwarfing alleles Rht-B1b or Rht-D1b, usually either one or the other, but rarely both in combination, as homozygosity for both alleles leads to very small plants with diminished yield potential.

As the degree of heterosis in plant height seemed to be influenced by the Rht-B1 and Rht-D1 alleles present, with the already tall Rht-B1a; Rht-D1a homozygous setup allowing less heterosis than the shorter Rht-B1b;Rht-D1a setup, plant height heterosis in hybrids might actually be able to mend the drawbacks of even a Rht-B1b; Rht-D1b double-homozygous setup. A respective tendency toward increased plant height has been described for wheat hybrids obtained from crosses of semi-dwarf (likely Rht-B1b;Rht-D1b) lines previously (Allan et al., 1968). However, the single Rht-B1b; Rht-D1b double-homozygous inbred line included as a female parent in our study had the lowest grain yield of all inbred lines, ranking 135th among 135 lines, and it would be hard to produce Rht-B1b;Rht-D1b double-homozygous wheat hybrids on a large scale in practical terms, as the male parents need to be tall to be efficient as pollen donors. A practicable solution might be the generation of hybrids homozygous for Rht-B1b and heterozygous for Rht-D1b by crossing an Rht-B1b;Rht-D1a father and an Rht-B1b;Rht-D1b mother. In the one case available to us, the success of this approach was limited. Although the semi-dwarf Rht-B1b;Rht-D1b homozygous inbred line used as female parent had the lowest grain yield of all 135 lines in the study and the tall Rht-B1b; Rht-D1a homozygous inbred line used as male parent ranked 11th of all 135 lines with regard to grain yield, the resulting hybrid homozygous for Rht-B1b and heterozygous for Rht-D1b had a plant height within the appropriate range and ranked 1478th of 1604 hybrids with regard to grain yield, indicating a grain yield midparent heterosis of 12.3% (data not shown). Thus, although this one observation seems rather promising, the balancing of plant height heterosis in hybrid wheat is still providing a substantial challenge.

Data archiving

Original data are included as Supplementary Table S1 in form of a Microsoft Excel file and are available from the Dryad Digital Repository: doi:10.5061/dryad.461nc.

Acknowledgments

We thank Andreas Börner for critical comments on the manuscript. This research was conducted within the HYWHEAT project funded by BMBF (Grant ID: FKZ0315945D).

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Table S1
Click here for additional data file. (2.2MB, xls)
Supplementary Figure 1
Click here for additional data file. (2.1MB, tif)
Supplementary Figure 2
Click here for additional data file. (2.6MB, tif)
Supplementary Figure 3
Click here for additional data file. (2.4MB, tif)
Supplementary Figure 4
Click here for additional data file. (3MB, tif)

References

  1. Akhunov E, Nicolet C, Dvorak J. Single nucleotide polymorphism genotyping in polyploid wheat with the Illumina GoldenGate assay. Theor Appl Genet. 2009;119:507–517. doi: 10.1007/s00122-009-1059-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allan RE, Vogel OA, Peterson CJ. Inheritance and differentiation of semidwarf culm length of wheat. Crop Sci. 1968;8:701–704. [Google Scholar]
  3. Beales J, Turner A, Griffiths S, Snape JW, Laurie DA. A pseudo-response regulator is misexpressed in the photoperiod insensitive Ppd-D1a mutant of wheat (Triticum aestivum L.) Theor Appl Genet. 2007;115:721–733. doi: 10.1007/s00122-007-0603-4. [DOI] [PubMed] [Google Scholar]
  4. Bernardo R. What if we knew all the genes for a quantitative trait in hybrid crops. Crop Sci. 2001;41:1–4. [Google Scholar]
  5. Bernardo R. Molecular markers and selection for complex traits in plants: learning from the last 20 years. Crop Sci. 2008;48:1649–1664. [Google Scholar]
  6. Borlaug NE. Contributions of conventional plant breeding to food production. Science. 1983;219:689–693. doi: 10.1126/science.219.4585.689. [DOI] [PubMed] [Google Scholar]
  7. Butler D, Cullis BR, Gilmour AR, Gogel BJ.2009ASREML-R, Reference ManualVersion 3Queensland Department of Primary Industries and Fisheries: Brisbane [Google Scholar]
  8. Cavanagh CR, Chao S, Wang S, Huang BE, Stephen S, Kiani S, et al. Genome-wide comparative diversity uncovers multiple targets of selection for improvement in hexaploid wheat landraces and cultivars. Proc Natl Acad Sci USA. 2013;110:8057–8062. doi: 10.1073/pnas.1217133110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Clark SA, Hickey JM, van der Werf JHJ. Different models of genetic variation and their effect on genomic evaluation. Genet Sel Evol. 2011;43:18. doi: 10.1186/1297-9686-43-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Crossa J, de los Campos G, Perez P, Gianola D, Burgueno J, Araus JL, et al. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics. 2010;186:713–U406. doi: 10.1534/genetics.110.118521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dekkers J, Garrick D, Fernando R.2009Use of high-density SNP genotyping for genetic improvement of livestock A Short Course Organized by the Animal Breeding & Genetics Department of Animal Science Iowa State University: Ames; http://www.ans.iastate.edu/stud/courses/short/2009/ . [Google Scholar]
  12. Distelfeld A, Li C, Dubcovsky J. Regulation of flowering in temperate cereals. Curr Opin Plant Biol. 2009;12:178–184. doi: 10.1016/j.pbi.2008.12.010. [DOI] [PubMed] [Google Scholar]
  13. Ellis H, Spielmeyer W, Gale R, Rebetzke J, Richards A. ‘Perfect' markers for the Rht-B1b and Rht-D1b dwarfing genes in wheat. Theor Appl Genet. 2002;105:1038–1042. doi: 10.1007/s00122-002-1048-4. [DOI] [PubMed] [Google Scholar]
  14. Falconer DS, Mackay TF.1996Introduction to Quantitative Genetics4th ednLongman: Harlow [Google Scholar]
  15. Fick GN, Qualset CO. Genes for dwarfness in wheat, Triticum aestivum L. Genetics. 1973;75:531–539. doi: 10.1093/genetics/75.3.531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Goddard ME, Hayes BJ. Mapping genes for complex traits in domestic animals and their use in breeding programmes. Nat Rev Genet. 2009;10:381–391. doi: 10.1038/nrg2575. [DOI] [PubMed] [Google Scholar]
  17. Guo ZA, Song YX, Zhou RH, Ren ZL, Jia JZ. Discovery, evaluation and distribution of haplotypes of the wheat Ppd-D1 gene. New Phytol. 2010;185:841–851. doi: 10.1111/j.1469-8137.2009.03099.x. [DOI] [PubMed] [Google Scholar]
  18. Habier D, Fernando RL, Kizilkaya K, Garrick DJ. Extension of the bayesian alphabet for genomic selection. BMC Bioinformatics. 2011;12:186. doi: 10.1186/1471-2105-12-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hallauer AR, Miranda JB.1988Quantitative Genetics in Maize Breeding2nd edn.Iowa State University Press: Ames [Google Scholar]
  20. Heffner EL, Sorrells ME, Jannink JL. Genomic selection for crop improvement. Crop Sci. 2009;49:1–12. [Google Scholar]
  21. Henderson C. Application of Linear Models in Animal Breeding. University of Guelph: Ontario; 1984. [Google Scholar]
  22. Heslot N, Yang HP, Sorrells ME, Jannink JL. Genomic selection in plant breeding: a comparison of models. Crop Sci. 2012;52:146–160. [Google Scholar]
  23. Le Couviour F, Faure S, Poupard B, Flodrops Y, Dubreuil P, Praud S. Analysis of genetic structure in a panel of elite wheat varieties and relevance for association mapping. Theor Appl Genet. 2011;123:715–727. doi: 10.1007/s00122-011-1621-9. [DOI] [PubMed] [Google Scholar]
  24. Longin CF, Gowda M, Mühleisen J, Ebmeyer E, Kazman E, Schachschneider R, et al. Hybrid wheat: quantitative genetic parameters and consequences for the design of breeding programs. Theor Appl Genet. 2013;126:2791–2801. doi: 10.1007/s00122-013-2172-z. [DOI] [PubMed] [Google Scholar]
  25. Longin CF, Muhleisen J, Maurer HP, Zhang H, Gowda M, Reif JC. Hybrid breeding in autogamous cereals. Theor Appl Genet. 2012;125:1087–1096. doi: 10.1007/s00122-012-1967-7. [DOI] [PubMed] [Google Scholar]
  26. Massman JM, Jung HJG, Bernardo R. Genomewide selection versus marker-assisted recurrent selection to improve grain yield and stover-quality traits for cellulosic ethanol in maize. Crop Sci. 2013;53:58–66. [Google Scholar]
  27. Meuwissen TH, Hayes BJ, Goddard ME. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157:1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Miedaner T, Hubner M, Korzun V, Schmiedchen B, Bauer E, Haseneyer G, et al. Genetic architecture of complex agronomic traits examined in two testcross populations of rye (Secale cereale L.) BMC Genomics. 2012;13:706. doi: 10.1186/1471-2164-13-706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Möhring J, Piepho HP. Comparison of weighting methods in two-stage analysis of plant breeding trials. Crop Sci. 2009;49:1977–1988. [Google Scholar]
  30. Peng JR, Richards DE, Hartley NM, Murphy GP, Devos KM, Flintham JE, et al. ‘Green revolution' genes encode mutant gibberellin response modulators. Nature. 1999;400:256–261. doi: 10.1038/22307. [DOI] [PubMed] [Google Scholar]
  31. Perez P, de los Campos G, Crossa J, Gianola D. Genomic-enabled prediction based on molecular markers and pedigree using the Bayesian linear regression package in R. Plant Genome. 2010;3:106–116. doi: 10.3835/plantgenome2010.04.0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. R Core Team 2012R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing: Vienna; http://www.R-project.org/ . [Google Scholar]
  33. Riedelsheimer C, Endelman JB, Stange M, Sorrells ME, Jannink JL, Melchinger AE. Genomic predictability of interconnected biparental maize populations. Genetics. 2013;194:493–503. doi: 10.1534/genetics.113.150227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Seki M, Chono M, Matsunaka H, Fujita M, Oda S, Kubo K, et al. Distribution of photoperiod-insensitive alleles Ppd-B1a and Ppd-D1a and their effect on heading time in Japanese wheat cultivars. Breed Sci. 2011;61:405–412. doi: 10.1270/jsbbs.61.405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Stram DO, Lee JW. Variance-components testing in the longitudinal mixed effects model. Biometrics. 1994;50:1171–1177. [PubMed] [Google Scholar]
  36. Turner A, Beales J, Faure S, Dunford RP, Laurie DA. The pseudo-response regulator Ppd-H1 provides adaptation to photoperiod in barley. Science. 2005;310:1031–1034. doi: 10.1126/science.1117619. [DOI] [PubMed] [Google Scholar]
  37. Venables WN, Ripley BD.2002Modern Applied Statistics with S4th ednSpringer: New York [Google Scholar]
  38. Whittaker JC, Thompson R, Denham MC. Marker-assisted selection using ridge regression. Genet Res. 2000;75:249–252. doi: 10.1017/s0016672399004462. [DOI] [PubMed] [Google Scholar]
  39. Wilhelm EP, Boulton MI, Al-Kaff N, Balfourier F, Bordes J, Greenland AJ, et al. Rht-1 and Ppd-D1 associations with height, GA sensitivity, and days to heading in a worldwide bread wheat collection. Theor Appl Genet. 2013;126:2233–2243. doi: 10.1007/s00122-013-2130-9. [DOI] [PubMed] [Google Scholar]
  40. Wilhelm EP, Mackay IJ, Saville RJ, Korolev AV, Balfourier F, Greenland AJ, et al. Haplotype dictionary for the Rht-1 loci in wheat. Theor Appl Genet. 2013;126:1733–1747. doi: 10.1007/s00122-013-2088-7. [DOI] [PubMed] [Google Scholar]
  41. Williams E, Piepho HP, Whitaker D. Augmented p-rep designs. Biometrical J. 2011;53:19–27. doi: 10.1002/bimj.201000102. [DOI] [PubMed] [Google Scholar]
  42. Worland AJ, Börner A, Korzun V, Li WM, Petrovic S, Sayers EJ. The influence of photoperiod genes on the adaptability of European winter wheats (Reprinted from Wheat: Prospects for global improvement, 1998) Euphytica. 1998;100:385–394. [Google Scholar]
  43. Würschum T, Langer SM, Longin CF, Korzun V, Akhunov E, Ebmeyer E, et al. Population structure, genetic diversity and linkage disequilibrium in elite winter wheat assessed with SNP and SSR markers. Theor Appl Genet. 2013;126:1477–1486. doi: 10.1007/s00122-013-2065-1. [DOI] [PubMed] [Google Scholar]
  44. Zhao YS, Gowda M, Würschum T, Longin CF, Korzun V, Kollers S, et al. Genetic architecture of frost tolerance in wheat. J Exp Bot. 2013;64:4453–4460. doi: 10.1093/jxb/ert259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhao YS, Zeng J, Fernando R, Reif JC. Genomic prediction of hybrid wheat performance. Crop Sci. 2013;53:802–810. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (2.2MB, xls)
Supplementary Figure 1
Click here for additional data file. (2.1MB, tif)
Supplementary Figure 2
Click here for additional data file. (2.6MB, tif)
Supplementary Figure 3
Click here for additional data file. (2.4MB, tif)
Supplementary Figure 4
Click here for additional data file. (3MB, tif)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES