Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2014 Feb 19;112(6):666–674. doi: 10.1038/hdy.2014.4

Cuckoo search epistasis: a new method for exploring significant genetic interactions

M Aflakparast 1,2, H Salimi 3, A Gerami 4, M-P Dubé 5, S Visweswaran 6, A Masoudi-Nejad 1,*
PMCID: PMC4023449  PMID: 24549111

Abstract

The advent of high-throughput sequencing technology has resulted in the ability to measure millions of single-nucleotide polymorphisms (SNPs) from thousands of individuals. Although these high-dimensional data have paved the way for better understanding of the genetic architecture of common diseases, they have also given rise to challenges in developing computational methods for learning epistatic relationships among genetic markers. We propose a new method, named cuckoo search epistasis (CSE) for identifying significant epistatic interactions in population-based association studies with a case–control design. This method combines a computationally efficient Bayesian scoring function with an evolutionary-based heuristic search algorithm, and can be efficiently applied to high-dimensional genome-wide SNP data. The experimental results from synthetic data sets show that CSE outperforms existing methods including multifactorial dimensionality reduction and Bayesian epistasis association mapping. In addition, on a real genome-wide data set related to Alzheimer's disease, CSE identified SNPs that are consistent with previously reported results, and show the utility of CSE for application to genome-wide data.

Keywords: single-nucleotide polymorphism, epistatic interactions, dimensionality reduction, cuckoo search

Introduction

One source of complexity in biological systems is due to rich interactions among the components (Weng et al., 1999; Hlavacek and Faeder, 2009). The advent of high-throughput genotyping and sequencing technologies has enabled the measurement of millions of single-nucleotide polymorphisms (SNPs)—the commonest type of genetic variants—in an individual. This has paved the way for understanding the genetic architecture of common diseases, but has also given rise to challenges in developing efficient methods for identifying of interactions (epistasis) among genetic variants. Several methods have been developed for analyzing genetic data that focus on epistatic interactions and include frequentist and Bayesian statistical methods and computational methods (Ritchie et al., 2001; Zhang and Xu, 2005; Zhao and Xiong, 2006; Ferreira et al., 2007; Zhang and Liu 2007; Gayan et al., 2008; Li et al., 2008b; Park and Hastie, 2008; Jung et al., 2009; Miller et al., 2009; Wang, 2009; Wu et al., 2009). A key challenge is the large number of statistical tests that have to be performed in epistasis testing especially in genome-wide association (GWA) studies that measure a large number of SNPs (Bellman and Kalaba, 1959; Steen, 2011). Moreover, high-dimensionality arising from multi-locus combinations, the relatively small sample size and the resulting data sparsity lead to lack of power in data mining methods (Cordell, 2009; Steen, 2011). To address the challenge of high-dimensionality, several feature selection methods have been applied to GWA data as a first step in identifying informative SNPs (Dube et al., 2007, Saeys et al., 2007).

Feature selection methods can be broadly grouped into two categories that include filter and wrapper methods (Freitas, 2002). In addition, feature selection methods that leverage biological knowledge relevant to SNPs, such as INTERSNP and Biofilter, have been developed as alternatives to filter and wrapper methods that do not sue such knowledge (Bush et al., 2009; Herold et al., 2009). INTERSNP is a time-efficient approach to select combinations of SNPs for a further interaction analysis based on a priori information obtained from either statistical evidence of single-marker association or biologic/genetic relevance information sources (Herold et al., 2009). Similarly, Biofilter is a systematic knowledge-based approach to produce SNP models by integrating multiple genetic databases. This approach can be implemented with a variety of techniques such as logistic regression, classification and regression trees (Bush et al., 2009).

The filter methods, typically, assess the quality of each attribute (such as a SNP) using a selection criterion. These types of feature selection methods have the advantage of being fast, but are often criticized for their inability to select relevant attributes involved in a significant interaction effect on the susceptibility of a disease or trait but that would not show sufficient individual effects for selection. Wrapper approaches, on the other hand, attempt to evaluate subsets of attributes based on sample classification accuracy. In contrast to filter methods, wrapper methods allow for all attributes to be retained and use a selection probability (Moore et al., 2010). As a result, no attribute is eliminated from the analysis. There are different types of wrapper methods and among them evolutionary computing algorithms such as the genetic algorithm (GA) and the evolution strategy methods have attracted much attention for stochastic search of epistatic interactions (Li et al., 2001; Ooi and Tan, 2003; Moore et al., 2004; Shah and Kusiak, 2004; Jirapech-Umpai and Aitken, 2005). Recently, a GA-based hybrid algorithm called genetic ensemble (GE) was proposed by Yang et al. (2010); this method relies on a combination of an ensemble of classifiers and a multi-objective GA (Zhang and Yang 2008; Yang et al., 2010).

The GE algorithm was shown to outperform other GA-based methods (Zhang and Yang, 2008). However, ensemble methods such as GE require diverse and accurate classifiers to achieve better accuracy, and identifying an efficient set of classifiers can be difficult (Dietterich, 2000). Selecting appropriate classifiers for different data sets with different number of attributes and samples, and configuring parameters properly for each classifier is challenging. Moreover, ensemble methods are likely to be more computationally expensive than methods that use a single classifier. Finally, despite the superior performance of GAs in comparison with gradient-based optimization methods, they are sensitive to parameter settings, exhibiting varying performance for different configurations of parameters such as population size, crossover frequency and mutation rate (Kumar and Chakarverty, 2011).

Motivated by evolutionary algorithms, we develop and evaluate a fast stochastic search method named cuckoo search epistasis (CSE) for identifying significant epistatic interactions in GWA studies. CSE differs from wrapper feature selection methods in that CSE does not search for a subset of informative attributes that are further analyzed for epistasis, but performs stochastic search of epistasis with no classification or training/prediction scheme. CSE used a new and relatively fast evolutionary algorithm called cuckoo search (CS), which performs better than other evolutionary algorithms. In addition, CSE uses a computationally efficient Bayesian score to evaluate combinations of SNPs for association with the phenotype.

We compare CSE's ability to identify epistatic interactions to that of multifactorial dimensionality reduction (MDR) and Bayesian epistasis association mapping (BEAM) using synthetic data sets. We also apply CSE to an Alzheimer's disease GWA data set that contains over 300 000 SNPs.

Background

This section provides background information on Bayesian combinatorial method (BCM), which uses a Bayesian statistic for measuring genetic interactions. The CSE method uses the Bayesian statistic of BCM to evaluate combinations of SNPs. In addition, brief descriptions on MDR and BEAM are also provided.

Bayesian combinatorial method

BCM is a search algorithm that evaluates the association between a set of interacting genetic variants and phenotype with a Bayesian statistic. It exhaustively searches over all possible combinations of SNPs and identifies combinations with a high posterior probability (Visweswaran et al., 2009). BCM is one of several methods that have been developed to identify epistatic variants based on a statistical measure. BCM has several advantages including the ability to handle sparse and unbalanced data, ability to deal with nonlinear interactions, and is computationally efficient, nonparametric and model free.

BCM defines an interaction model M, as a set of probabilities denoted by P(Z|g=(g1, g2,··, gc)) for phenotype states Z, given combination of genotypes g. For a given g value, a multinomial distribution is assumed for Z (binomial, if Z has only two states). Assuming that the parameters of all multinomial distributions, that is, θc a priori follow a Dirichlet distribution, a posterior estimate for θc is obtained. The Bayes theorem is used to score the fitness of any given combinatorial model as the following:

graphic file with name hdy20144e1.jpg

where P(M) is the prior probability of model M, which is assumed to have a constant value for all models and P(Data|M) is the marginal likelihood, which is evaluated by the following equation:

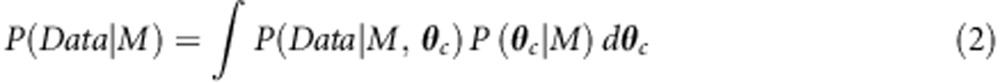graphic file with name hdy20144e2.jpg

where P(Data|M, θc) is the distribution of the data for a given genotype–phenotype table. Figure 1 presents an example of counts of genotypes for an interaction model with two SNPs (denoted SNP1 and SNP2) and a binary phenotype (for example, case and control).

Figure 1.

Figure 1

Open in a new tab

An example of genotype–phenotype table with two SNPs and a binary phenotype. This figure summarizes the genotype and phenotype data for a two-way interaction model with two SNPs. BCM assumes a binomial distribution for any combination of the SNP1 and SNP2 values, that is, each column of this table follows a binomial distribution. Thus, P(Data|M, θc) is obtained by multiplying nine independent binomial distributions.

A binomial distribution for each column (that is, the combination of genotypes for SNP1 and SNP 2) is assumed. Thus, P(Data|M, θc) is obtained by multiplying nine independent binomial distributions.

The closed form for P(Data|M) is given by the following equation and was originally derived by Cooper and Herskovits (1992):

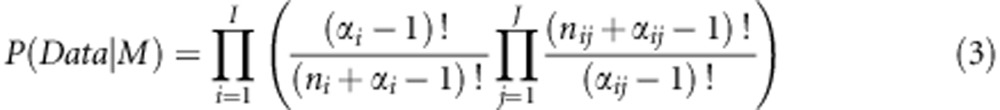graphic file with name hdy20144e3.jpg

where αij are the positive hyper-parameters of a Dirichlet distribution and Σαij=αi, I is the number of genotype combinations (for example, nine for a model with two SNPs with three states each), J is the number of phenotype states (for example, two for a case–control data set), ni is the number of samples for a given genotype combination in an epistatic model and nij is the number of samples for the jth phenotype and ith genotype combination.

Assuming that the prior distribution P(M) is uniform over all possible models and the Dirichlet hyperparameters are all set to 1, the following expression gives the score that is used by BCM for an interaction model:

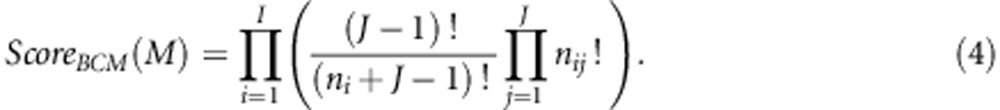graphic file with name hdy20144e4.jpg

A major limitation of BCM is that it searches exhaustively over all possible combinations of SNPs in a data set and hence it does not scale up to high-dimensional data sets. Our new algorithm overcomes this limitation such that BCM can be applied to explore the space of possible models in high-dimensional GWA data.

Multifactorial dimensionality reduction

MDR is a nonparametric data mining method for identifying SNP interactions (Ritchie et al., 2001). MDR is based on a dimensionality reduction strategy that projects the whole genotype space to one dimension with two values, that is, low-risk or high-risk genotypes. In addition, this method does not assume a model for the data and it has the advantage of flexibility to genetic model. Since MDR was first introduced, it has been widely used in association studies. Several modifications and extensions for MDR have also been proposed either by its original authors or others (Bush et al., 2007; Chung et al., 2007; Gui et al., 2007; Lee et al., 2007; Velez et al., 2007; Namkung et al., 2009), which have increased its applicability. However, MDR is an exhaustive method and is mostly applicable to candidate gene studies where the number of tested SNPs is <500. To address this limitation, filtering methods are typically used to alleviate the computational burden and to feasible analyze genome-wide data (Cordell, 2009). The MDR software is available from http://epistasis.org.

Bayesian epistasis association mapping

As an alternative to data mining methods, we compare CSE to a Bayesian statistical method called BEAM that has recently gained much popularity for epistasis detection. BEAM uses a model to partition markers into three categories. The first category contains markers assumed to have no impact on the disease, the second category contains markers assumed to have additive effects on the disease and the third category contains markers that are assumed to jointly influence the disease. In addition, a novel B statistic is proposed to exhaustively score interactions for candidate markers and is also used for further analyze of the resulting categories (Zhang and Liu, 2007). The BEAM software is available from http://www.fas.harv-ard.edu/Bjunliu/BEAM.

Materials and methods

This section provides details of the CSE method and then describes the experimental details including a description of the data sets. We first describe CS and a modification of CS and then describe CSE.

Cuckoo search

CS is a metaheuristic search algorithm developed by Yang and Deb (2009, 2010). The algorithm is motivated by the reproduction strategies used by cuckoos. Cuckoos lay their eggs in the nests of other host birds and sometimes the host bird may be of a different species. The host bird may discover that the eggs are alien and either destroy them or abandon the nest. To overcome this, cuckoo eggs have evolve to mimic the eggs of the host birds. This interesting reproductive strategy of the cuckoos has been encapsulated as an optimization strategy in the form of three idealized rules:

  • Each cuckoo lays one egg at a time and dumps it in a random nest. The eggs represent a set of epistatic models in our application.

  • A fraction of the nests containing the best eggs are carried over to the next generation. That is, in each step of the search procedure, a fraction of the epistatic models that represents the best interaction scores are carried over.

  • The number of nests is fixed and there is a probability that a host will discover an alien egg. When this happens, the host discards the nest and builds a new nest in a new location. That is, a model is discarded with probability P and a new model is created in its place. The probability P can also be interpreted as the fraction of models that is discarded.

CS uses the Lévy flight process for searching (Yang and Deb, 2009). The Lévy flight process is a random walk that consists of a series of jumps chosen from a probability density function that has a power law tail. When generating a new model in CS, a Lévy flight is performed starting at the position of a randomly selected model. If the new model is better than another randomly selected model then that model is replaced with the new model. The advantage of CS over other metaheuristic search algorithms like GA and particle swarm optimization is that there is only one parameter to adjust, namely, P the fraction of models that is discarded (Yang and Deb, 2009).

Modified CS

Although CS is guaranteed to find the optimal model, the rate of convergence is not guaranteed to be fast. Walton et al. (2011) modified CS so that the convergence rate is increased and thus allows CS to be applied to larger model spaces.

This modified CS consists of two modifications to the original CS (Walton et al., 2011). The first modification is the use of an adaptive step size in the Lévy flight. In CS, the step size is constant while in modified CS the step size decreases gradually as the algorithm progresses. This encourages more localized searching as the algorithm gets closer to the optimal model.

The second modification in modified CS is addition of information exchange among models to speed up convergence. In CS, each model is processed independently of other models while in modified CS a fraction of the best models is put into a group of top models. For each of the top models, a second model in the group is picked at random and a new model is then generated on the line connecting these two top models. Compared with CS, modified CS has two adjustable parameters: (i) the fraction of models that is discarded, and (ii) the fraction of models in the top group. Walton et al. (2011) determined empirically that setting the fraction of models that is discarded to 0.75 and the fraction of models that make up the top group to 0.25 yielded the best results. Figure 2 provides the pseudocode for the modified CS method.

Figure 2.

Figure 2

Open in a new tab

Pseudocode for modified CS.

CSE method

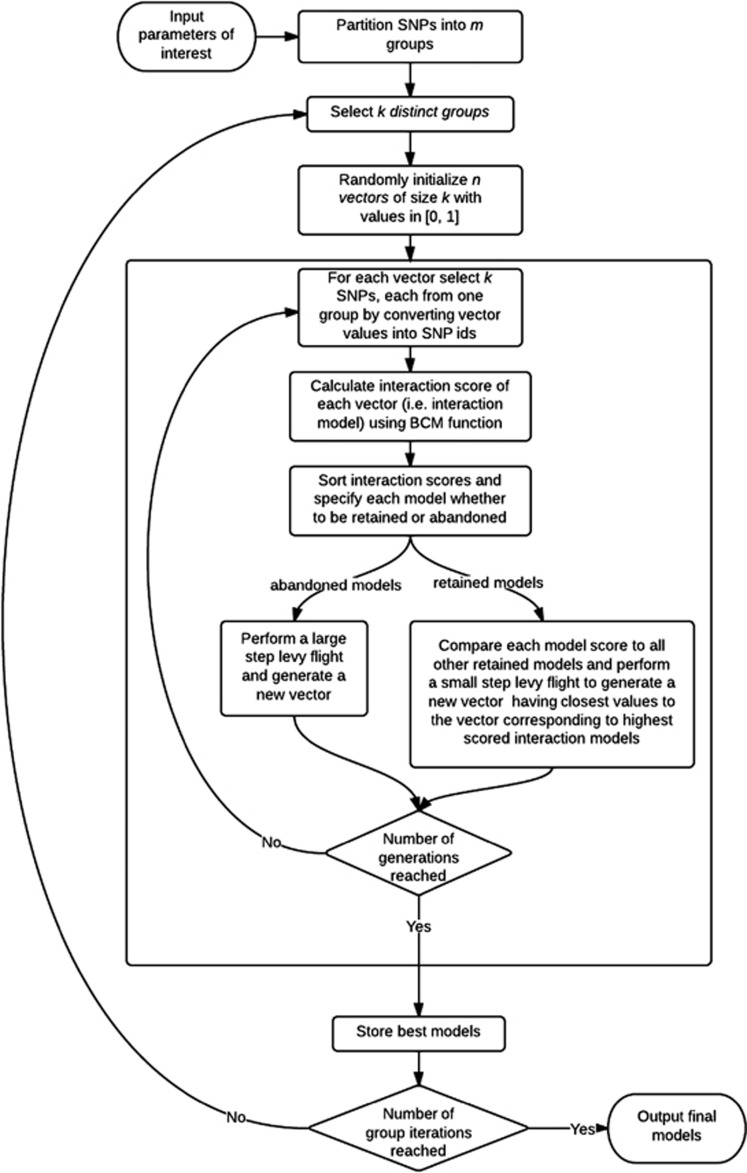
The CSE method combines modified CS search with the model score used in BCM, and enables searching for significant epistatic models in data, that is, on a genome-wide scale. CSE is substantially more efficient than GE for several reasons. First, modified CS is computationally faster than other evolutionary-based methods. Second, although GE uses several classification and voting techniques, CSE uses a single but efficient scoring function. Third, the scoring function in CSE does not use cross-validation that is computationally expensive and instead uses the entire data to compute the model score. Many computational methods focus on increasing classification accuracy, which does not necessarily result in models with the largest association with the phenotype; thus, we were motivated to use an efficiently computable scoring function instead of a classification technique. Figure 3 provides an overview of the main steps in CSE.

Figure 3.

Figure 3

Open in a new tab

Flowchart showing the main steps in CSE.

In CSE, each egg represents an interaction model, which is a combination of different SNP markers to be evaluated for their association with the disease of interest. Dependent on user-defined SNP interaction order, for example, a k-way interaction detection setting, to generate the initial set of models we assume each egg to represents a vector with k components. Then, CSE assigns a random value in [0, 1], based on random walks, for each component of the egg, which represents a SNP. It is guaranteed that each egg cannot contain the same SNP markers. Next, a model score is calculated for each egg using the BCM score. CSE tries to allocate continuous numbers to each component of the eggs in order to get nearer to the interaction model with a higher model score. This procedure can be repeated for detecting any-way SNP interaction model.

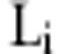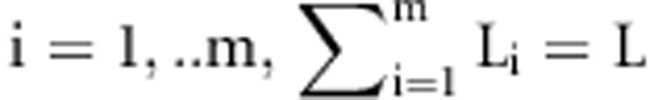In GWA data where an astronomical number of potential interaction models exist, the data redundancy and correlation structure between SNPs often produce inconsistent results. To address this problem, we considered several modifications to CSE so that it can be applied to GWA data. In the first stage, CSE partitions the SNPs into m groups with Inline graphic SNPs, Inline graphic. This partitioning of SNPs can be with respect to either their natural position in the genome or their associated gene. This is because there is considerable correlation among neighboring SNPs in the genome as measure by linkage disequilibrium (LD). Considering the k–SNP interaction detection problem, k groups are selected out of all m groups. Then, to construct each egg of the generation, a vector of k dimensions with continuous numbers in [0, 1] is assigned by the CSE algorithm as described earlier such that each component of the vector represents a SNP that is selected from one of the k selected groups. In the next steps of the algorithm, the top 100 highest scored interaction models with k SNPs for the selected groups are identified. The procedure continues by selecting other k groups either until a predefined number of iteration is reached or all possible k groups have been examined exhaustively. Finally, the best interaction models from the resulting models are reported. Figure 4 gives the pseudocode for CSE.

Figure 4.

Figure 4

Open in a new tab

Pseudocode for CSE method.

Grouping of SNPs

We partitioned GWA data into groups of SNPs in the first stage. Two partitioning schemes that are likely to be useful are:

  1. Group SNPs according to their natural genomic order such that adjacent SNPs are in the same group.

  2. Group SNPs according to their associated genes such that SNPS on a gene are in a single group.

There are other ways to partition SNPs in groups that may be useful. For instance, knowledge obtained from gene ontology or gene expression experiments may be used to partition SNPs in an association study. Determining which partitioning scheme is to be chosen depends on the goals of the analyses and the computational costs. If the goal is to detect gene–gene interactions as well as SNP–SNP interactions, then grouping SNPs based on genes is the preferred method. If the goal is to identify only SNP–SNP interactions, then partitioning SNPs according to their natural genomic order or based on their LD may be the preferred method. From the computational perspective, partitioning based on LD is more expensive than partitioning that is based on the genomic order or based on gene membership.

In addition, a partitioning scheme should balance the group size (that is, number of SNPs per group) and the number of groups. Considering dimension of data and computational facilities, the group size and number of groups can be defined by the user based on the importance of LD in the resulted interaction models. As a big group size induces less number of groups, which include SNPs with low LDs between two groups; the chance of deriving mixed results because of LD is expected to be minimized. However, as CSE, in a genome-wide scale, does not consider searching for interaction models inside a group; it is likely to ignore evaluating a possibly high-scored interaction model in the first place. As our main focus in this study was developing the main procedure of detecting interaction effects rather than proposing a specific procedure to partition SNPs, we have selected these parameters based on limited analyses of simulated data. However, in order to comprehensively consider the effect of these parameters, sensitivity analysis should be performed before implementation of the procedure.

Experimental methods

We evaluated the performance of CSE using several synthetic data sets. For comparison, we used two control methods including MDR and BEAM that represent two different schools of epistasis methods. We compared the performance of CSE, MDR and BEAM in terms of power and computational time.

Synthetic data

We used two different synthetic data sources that have been developed previously. Detection of two loci epistasis was assessed using the Velez data (Velez et al., 2007), and higher order SNP interactions detection was assessed using the Himmelstein data (Himmelstein et al., 2011).

The Velez data set includes 20 different non-linear genetic models (Velez et al., 2007). These data sets were developed with a case–control ratio of 1:1 and for penetrance functions with variable heritability levels (0.01 and 0.4) and varying minor allele frequencies (MAFs; 0.2 and 0.4). Genotype frequencies for epistasis models were consistent with Hardy–Weinberg proportions. The evaluations were performed on sample sizes of 400, 800 and 1600 with 1000 SNPs per individual. Each genetic model included 100 data sets in which two functional SNP markers were embedded within a set of 998 non-interacting SNP markers with a weak marginal effect. A total number of 2000 data sets were used for each sample size. These data sets are available online from http://discovery.dartmouth.edu/epistatic_data/.

We also used Himmelstein data sets with three to five functional SNPs, which had been generated with no predefined genetic models, to evaluate methods in identifying higher order interactions. For any interaction order, the data folders consisted of 100 data sets each having 1500 cases and 1500 controls for a SNP number as high as the considered interaction order. Assuming Hardy-Weinberg equilibrium proportions and MAF of 0.5, we randomly generated additional SNP data to embed with the Himmenstein data using a multinomial distribution. After embedding Himmelstein data with our generated data sets, the resulting data sets for any interaction order contained 1000 SNPs for 3000 samples. These data sets are available online from http://discovery.dartmouth.edu/model_free_data/.

GWA data

To evaluate the performance of the CSE method on a real GWA data set, we used a late-onset Alzheimer's disease (LOAD) GWA data set that was collected and analyzed previously (Reiman et al., 2007). Genotype data were obtained from 1411 samples including 861 cases diagnosed with LOAD and 550 controls. Of the 1411 samples, the case–control status was defined as neuropathological LOAD determined from brain tissue in 1047 samples and was determined based on clinical diagnosis for 364 samples. The genotype data consist of 502 627 SNPs that were measured using the 500K GeneChip (Affymetrix, Santa Clara, CA, USA) from which 312 316 SNPs remained after applying quality controls by the original investigators. In addition, the original investigators measured two apoplipoprotein E genotypes (rs429358 and rs7412) by either pyrosequencing or restriction fragment length polymorphism analysis because they are not measured on the Affymetrix chip. The apoplipoprotein E is the most reliably replicated genetic variant associated with LOAD (Corder et al., 1993; Pappassotiropoulos et al., 2006; Coon et al., 2007). On the basis of the two genotypes, the apoplipoprotein E gene has three common variants e2, e3 and e4 where e2 is the low-risk allele, and each copy of the e4 allele increases the risk.

Results

We first present results from the synthetic data sets and then present results from the LOAD GWA data set.

Application to synthetic data

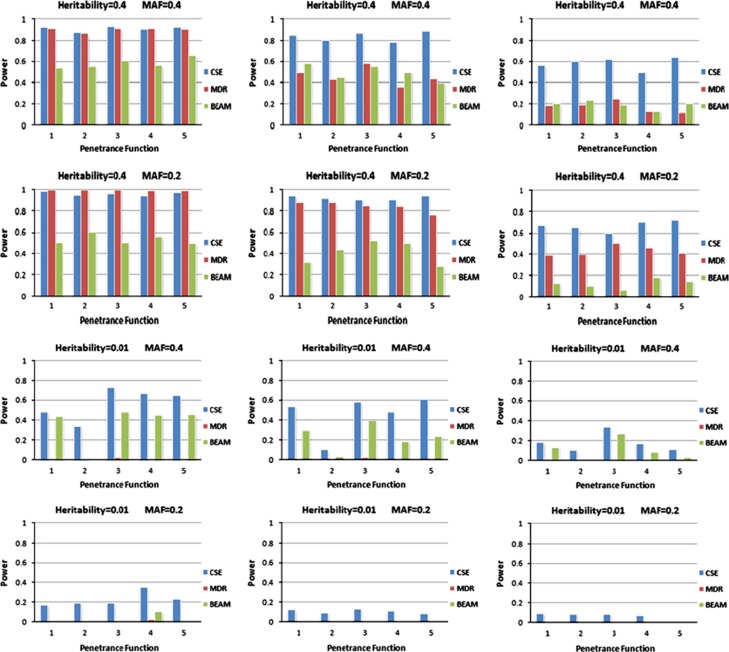
We have performed an extensive analysis of synthetic data to assess the performance of the CSE method and compare its performance with that of MDR and BEAM methods. We used the ReliefF filter method, which is implemented in the MDR software package, to filter the top 100 informative SNPs out of 1000 SNPs before testing for interaction detection. Thereafter, the MDR procedure was implemented to detect the best interaction models of different interaction orders. The analysis parameters such as number of chains/burn-ins and configurations of grouping priors for the BEAM algorithm were set according to recommended parameter settings by the authors (included in BEAM software package). We estimated the power as the proportion of the 100 replicate data sets for which the algorithm ranks the two functional SNPs as the top two SNPs.

Figure 5 presents the power comparison for the three methods for 20 different penetrance functions and for three sample sizes based on the Velez data set for two interacting loci. As can be seen in Figure 5, the performance of all methods is positively correlated with sample size. MDR had better performance than BEAM for genetic models with large values of MAF and heritability (models in the top two rows in Figure 5). However, for smaller values of MAF and heritability (models in the bottom two rows in Figure 5) BEAM performed better than MDR. On the Himmelstein data sets (see Table 1), BEAM does better than MDR in two out of three experiments. These results are supportive of BEAM having better performance than MDR in situations where interacting loci have modest main effects and interaction effects, and similar results were obtained in a comprehensive study that evaluated several epistasis detection methods (Chen et al., 2011).

Figure 5.

Figure 5

Open in a new tab

Powers obtained by three epistasis detection methods (CSE, MDR and BEAM) on synthetic data containing two interacting SNPs. The figure gives the power of the methods for three sample sizes of 1600, 800 and 400 with equal numbers of cases and controls. For each sample size, 20 penetrance functions with two MAFs and two heritability levels are examined. For each penetrance model, 100 data sets with 1000 SNPs are examined. The highest scoring interactions were evaluated using CSE, MDR and BEAM for each data set. Finally, the power was estimated as the number of correctly detected interacting SNPs divided by the number of SNPs in the data set.

Table 1. Powers obtained by three epistasis detection methods for three-way, four-way and five-way interactions.

Interaction order CSE MDR BEAM
Three-way 69 45 48
Four-way 47 40 35
Five-way 18 12 31
Open in a new tab

Abbreviations: BEAM, Bayesian epistasis association mapping; CSE, cuckoo search epistasis; MDR, multifactorial dimensionality reduction; SNP, single-nucleotide polymorphism.

Power is estimated as the proportion of the 100 replicate data sets for which the method ranks the functional SNPs as the top three, four or five SNPs.

CSE performed better than MDR and BEAM on both the Velez and Himmelstein data sets with marked increase in power for models with low heritability. The failure of the preprocessing filter procedure to retain the functional SNPs at the first step likely explains the weak performance of MDR.

We compared the computational time of the three methods using a desktop computer of 2.26 GHz CPU and 4 GB RAM. Table 2 summarizes the average computational time to run each data set. For a comprehensive comparison, we estimated the average running time for MDR when implemented exhaustively. As it is shown in Table 2, the running time of CSE is nearly eight times less than exhaustive MDR and two times less than BEAM.

Table 2. Running times for the three epistasis detection methods.

Sample size CSE MDR (exhaustive) MDR (filtered) BEAM
1600 69 s 480 s 16 s 134 s
800 54 s 390 s 12 s 102 s
400 40 s 190 s 7 s 75 s
Open in a new tab

Abbreviations: BEAM, Bayesian epistasis association mapping; CSE, cuckoo search epistasis; MDR, multifactorial dimensionality reduction; SNP, single-nucleotide polymorphism.

The running times were obtained from a data set with 1000 SNPs and different sample sizes of 400, 800 and 1600.

Application to GWA data

We imputed the missing genotypes in the GWA data using the IMPUTE software (Howie et al., 2009). A genotypic test using χ2 statistic with 2 df, was applied to each of the SNPs using the PLINK software (Purcell et al., 2007). Finally, 76 755 SNPs with P-value <0.2 were retained for further analysis for epistatic interactions.

In order to detect two-way interactions, we partitioned the SNPs into 295 groups each containing 260 SNPs considering a balance between group size and number of groups. Then, CSE was applied to explore every pairwise partition for epistatic interactions. We set CSE to identify the 100 top-ranked epistatic interactions for any experiment on a pair of partitions. Our experimental results with the LOAD data set identified the apoplipoprotein E SNP rs7412 to have the strongest association with LOAD. This is consistent with the knowledge that the SNP is the most representative disease involved in high-ranked interaction models with LOAD (Combarros et al., 2009).

Table 3 summarizes the 19 top-ranked SNP interactions in the LOAD data set detected by CSE. Of these SNPs, 16 have been initially identified as LOAD-associated SNPs in other GWA studies (Reiman et al., 2007; Li et al., 2008a; Shi et al., 2010).

Table 3. List of top-ranked SNPs that interact with the APOE SNP rs7412 that were identified by CSE.

Rank SNP identifier Chromosome number Associated gene Interaction score
1 rs7079348 10 C10ORF11 −833.573
2 rs934745* 18 MAPK4 −838.546
3 rs10499687* 7 VWC2 −840.237
4 rs2517509 6 MUC21 −841.314
5 rs2122339 2 STIM2 −841.828
6 rs7817227 8 C8orf80 −843.664
7 rs2779556* 9 GABBR2 −845.716
8 rs475093 1 LOC440585 −846.129
9 rs17126808 8 PSD3 −849.232
10 rs7585710 2 ATP6V1C2 −850.014
11 rs7097398 10 KIF20B −854.823
12 rs12162084 16 HS3ST4 −856.846
13 rs473367 8 POU5F1 −857.432
14 rs4394475 9 NXNL2 −857.973
15 rs17330779 7 NRCAM −857.989
16 rs17048904 4 NDST4 −858.782
17 rs17151710 5 CSNK1G3 −858.302
18 rs1763351 1 COL11A1 −859.012
19 rs10824310 1 PRKG1 −859.285
Open in a new tab

Abbreviations: APOE, apoplipoprotein E; CSE, cuckoo search epistasis; SNP, single-nucleotide polymorphism.

Of the 19 SNPs in the table, 16 SNPs have been initially identified in both Reiman et al. (2007) and Li et al. (2008a). Three of the 19 SNPs (indicated by a star) have not been documented in previous studies and are potential candidates for future studies. The interaction score is the natural logarithm of the Bayesian score given in Equation 4.

Discussion

The high dimensionality of SNP data sets poses a challenge to exhaustive search methods for the detection of genetic interaction in genome-wide data sets. Traditional filtering methods to reduce the number of SNPs rely on the selection of SNPs based on marginal effects and have limited ability to detect interactions in the absence of marginal effects. The newer multivariate filter methods such as ReliefF, which we used in conjunction with the MDR method, can detect interactions in the absence of marginal effects. However, they may suffer from lack of power. Our experimental results highlighted in particular the loss of power for genetic models with low heritability. Evolutionary computing methods, such as advanced wrapper methods, have gained more popularity in recent years as an alternative, however, they have classification limitations mostly because of the capacity of features, which does not necessarily identify epistatic interactions.

In this paper, we proposed CSE as a new method, which combines a computationally efficient Bayesian scoring function with an evolutionary-based heuristic search algorithm, for epistasis detection in genome-wide data. Although relying on an evolutionary computing strategy, CSE is much faster than other algorithms of its kind. A differentiating characteristic of CSE is that in contrast to computational methods such as wrapper methods, which rely on data classification, CSE uses an efficient function to score epistatic interactions. The epistatic scoring function gains in efficiency by eliminating the need to perform cross-validation. Furthermore, CSE can efficiently test for a variety of different multi-locus epistatic models, and because it does not eliminate SNP markers with filtering, it can conduct a heuristic search among all possible interaction models for all available SNPs in the data set.

The results obtained with synthetic data support the additional value of CSE over other epistasis methods for the detection of epistatic interaction. The results illustrate that preprocessing procedures may reduce the computational burden at the cost of power. The application of CSE to a real GWA data set of LOAD provided results that are consistent with previously reported findings, highlighting the value of CSE for the exploration of epistatic interactions in genome-wide data.

Software availability

The software package that implements CSE, the documentation and illustrative examples are available from the following website: http://lbb.ut.ac.ir/Download/LBBsoft/CSE.

Data archiving

There were no data to deposit.

Acknowledgments

We thank Jason H Moore, PhD and Peter C Andrews, AB for helpful discussions and assistance with the MDR algorithm and software. We also thank Zahra Narimani for her technical assistance.

Author contributions

MA, AM-N, AG and SV designed the study; MA and HS developed the algorithm; MA, HS and SV analyzed the data, and all authors wrote and edited the paper.

The authors declare no conflict of interest.

References

  1. Bellman R, Kalaba R. A mathematical theory of adaptive control processes. Proc Natl Acad Sci USA. 1959;45:1288–1290. doi: 10.1073/pnas.45.8.1288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bush WS, Dudek SM, Ritchie MD. Biofilter: a knowledge-integration system for the multi-locus analysis of genome-wide association studies. Pac Symp Biocomput. 2009. pp. 368–379. [PMC free article] [PubMed]
  3. Bush WS, Edwards TL, Dudek SM, McKinney BA, Ritchie MD. Alternative contingency table measuresimprove the power and detection of multifactor dimensionality reduction. BMC Bioinformatics. 2007;9:238. doi: 10.1186/1471-2105-9-238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen L, Yu G, Langefeld CD, Miller DJ, Guy RT, Raghuram J, et al. Comparative analysis of methods for detecting interacting loci. BMC Genomics. 2011;12:344. doi: 10.1186/1471-2164-12-344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chung Y, Lee SY, Elston RC, Park T. Odds ratio based multifactor-dimensionality reduction method for detecting gene-gene interactions. Bioinformatics. 2007;23:71–76. doi: 10.1093/bioinformatics/btl557. [DOI] [PubMed] [Google Scholar]
  6. Combarros O, Cortina-Borja M, Smith AD, Lehmann DJ. Epistasis in sporadic Alzheimer's disease. Neurobiol Aging. 2009;30:1333–1349. doi: 10.1016/j.neurobiolaging.2007.11.027. [DOI] [PubMed] [Google Scholar]
  7. Coon KD, Myers AJ, Craig DW, Webster JA, Pearson JV, Lince DH, et al. A high-density whole-genome association study reveals that APOE is the major susceptibility gene for sporadic late-onset Alzheimer;s disease. J Clin Psychiatry. 2007;68:613. doi: 10.4088/jcp.v68n0419. [DOI] [PubMed] [Google Scholar]
  8. Cooper G, Herskovits E. A Bayesian method for the induction of probabilistic networks from data. Mach Learn. 1992;9:309–347. [Google Scholar]
  9. Cordell HJ. Genome-wide association studies: detecting gene-gene interactions that underlie human diseases. Nat Rev Genet. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Corder EH, Saunders AM, Strittmatter WJ, Schmechel DE, Gaskell PC, Small GW, et al. Gene dose of apolipoprotein E type 4 allele and the risk of Alzheimer's disease in late onset families. Science. 1993;261:921. doi: 10.1126/science.8346443. [DOI] [PubMed] [Google Scholar]
  11. Dietterich, Thomas G. Multiple Classifier Systems. Springer: Berlin, Heidelberg pp1–15; 2000. Ensemble methods in machine learning. [Google Scholar]
  12. Dube MP, Schmidt S, Hauser E. Multistage designs in the genomic era: providing balance in complex disease studies. Genet Epidemiol. 2007;31 (Suppl 1:S1–S6. doi: 10.1002/gepi.20288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ferreira T, Donnelly P, Marchini J.2007Powerful Bayesian gene-gene interaction analysis Am J Hum Genet 81(Suppl3217564961 [Google Scholar]
  14. Freitas A. Data Mining and Knowledge Discovery with Evolutionary Algorithms. Springer: New York, NY; 2002. [Google Scholar]
  15. Gayan J, González-Pérez A, Bermudo F, Sáez ME, Royo JL, Quintas A, et al. A method for detecting epistasis in geneome-wide studies using casecontrol multi locus association analysis. BMC Genomics. 2008;9:360. doi: 10.1186/1471-2164-9-360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gui J, Andrew AS, Andrews P, Nelson HM, Kelsey KT, Karagas MR, et al. A robust multifactor dimensionality reduction method for detecting gene-gene interactions with application to the genetic analysis of bladder cancer susceptibility. Ann Hum Genet. 2007;23:71–76. doi: 10.1111/j.1469-1809.2010.00624.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Herold C, Steffens M, Brockschmidt FF, Baur MP, Becker T. INTERSNP: genome-wide interaction analysis guided by a priori information. Bioinformatics. 2009;25:3275–3281. doi: 10.1093/bioinformatics/btp596. [DOI] [PubMed] [Google Scholar]
  18. Himmelstein DS, Greene CS, Moore JH. Evolving hard problems: generating human genetics datasets with a complex etiology. Bio Data Mining. 2011;4:21. doi: 10.1186/1756-0381-4-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hlavacek W, Faeder J. The complexity of cell signaling and the need for a new mechanics. Sciences. 2009;2:pe46. doi: 10.1126/scisignal.281pe46. [DOI] [PubMed] [Google Scholar]
  20. Howie BN, Donnelly P, Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jirapech-Umpai T, Aitken S. Feature selection and classification for microarray data analysis: evolutionary methods for identifying predictive genes. BMC Bioinformatics. 2005;6:146. doi: 10.1186/1471-2105-6-148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jung J, Sun B, Kwon D, Koller DL, Foroud TM. Allelic-based gene-gene interaction associated with quantitative traits. Genet Epidemiol. 2009;33:332–343. doi: 10.1002/gepi.20385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kumar A, Chakarverty S.2011Design Optimization Using Genetic algorithm and Cuckoo Search. IEEE International Conference on Electro/Information Technology.
  24. Lee SY, Chung Y, Elston RC, Kim Y, Park T. Log-linear model-based multifactor dimensionality reduction method to detect gene-gene interactions. Bioinformatics. 2007;23 (19:2589–2595. doi: 10.1093/bioinformatics/btm396. [DOI] [PubMed] [Google Scholar]
  25. Li L, Weinberg C, Darden T, Pedersen L. Gene selection for sample classification based on gene expression data: study of sensitivity to choice of parameters of the GA/KNN method. Bioinformatics. 2001;17:1131–1142. doi: 10.1093/bioinformatics/17.12.1131. [DOI] [PubMed] [Google Scholar]
  26. Li H, Wetten S, Li L, St Jean PL, Upmanyu R, Surh L, et al. Candidate single nucleotide polymorphisms from a genome wide association study of Alzheimer disease. Arch Neurol. 2008;65:45–53. doi: 10.1001/archneurol.2007.3. [DOI] [PubMed] [Google Scholar]
  27. Li L, Yu M, Jason RD, Shen C, Azzouz F, McLeod HL, et al. Mixture model approach in gene × gene interaction for binary phenotype. J Biopharm Stat. 2008;18:1150–1177. doi: 10.1080/10543400802369038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Miller DJ, Zhang Y, Yu G, Liu Y, Chen L, Langefeld CD, et al. An algorithm for learning maximum entropy probability models of disease risk that efficiently searches and sparingly encodes multilocus genomic interactions. Bioinformatics. 2009;25:2478–2485. doi: 10.1093/bioinformatics/btp435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Moore JH, Asselbergs FW, Wiliams SM. Bioinformatics challenges for genome-wide association studies. Bioinformatics. 2010;26:445–455. doi: 10.1093/bioinformatics/btp713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Moore JH, Hahn LW, Ritchie MD, Thornton TA, White BC. Routine discovery of complex genetic models using genetic algorithms. Appl Soft Comput. 2004;4:79–86. doi: 10.1016/j.asoc.2003.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Namkung J, Elston R, Yang J, Park T. Identification of gene-gene interactions in the presence of missing data using the multifactor dimensionality reduction method. Genet Epidemiol. 2009;33:646–656. doi: 10.1002/gepi.20416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ooi C, Tan P. Genetic algorithms applied to multi-class prediction for the analysis of gene expressiondata. Bioinformatics. 2003;19:3744. doi: 10.1093/bioinformatics/19.1.37. [DOI] [PubMed] [Google Scholar]
  33. Papassotiropoulos A, Stephan DA, Huentelman MJ, Hoerndli FJ, Craig DW, Pearson JV, et al. Common KIBRA alleles are associated with human memory performance. Science. 2006;314:475–478. doi: 10.1126/science.1129837. [DOI] [PubMed] [Google Scholar]
  34. Park MY, Hastie T. Penalized logistic regression for detecting gene interactions. Biostatistics. 2008;9:30–50. doi: 10.1093/biostatistics/kxm010. [DOI] [PubMed] [Google Scholar]
  35. Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Reiman EM, Webster JA, Myers AJ, Hardy J, Dunckley T, Zismann VL, et al. GAB2 alleles modify Alzheimer's risk in APOE varepsilon4 carriers. Neuron. 2007;54:713–720. doi: 10.1016/j.neuron.2007.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet. 2001;69:138–147. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Saeys Y, Inza I, Larranaga P. A review of feature selection techniques in bioinformatics. Bioinformatics. 2007;23:2507–2517. doi: 10.1093/bioinformatics/btm344. [DOI] [PubMed] [Google Scholar]
  39. Shah SC, Kusiak A. Data mining and genetic algorithm based gene/SNP selection. Artif Intell Med. 2004;31:183–196. doi: 10.1016/j.artmed.2004.04.002. [DOI] [PubMed] [Google Scholar]
  40. Shi H, Medway C, Bullock J, Brown K, Kalsheker N, Morgan K. Analysis of genome-wide association study (GWAS) data looking for replicating signals in Alzheimer's disease (AD) Int J Mol Epidemiol Genet. 2010;1 (1:53–66. [PMC free article] [PubMed] [Google Scholar]
  41. Steen KV. Travelling the world of gene-gene interactions. Briefings Bioinform. 2011;10:1–19. doi: 10.1093/bib/bbr012. [DOI] [PubMed] [Google Scholar]
  42. Velez DR, White BC, Motsinger AA, Bush WS, Ritchie MD, Williams SM, et al. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet Epidemiol. 2007;31 (4:306–315. doi: 10.1002/gepi.20211. [DOI] [PubMed] [Google Scholar]
  43. Visweswaran S, Wong AL, Barmada MM. A Bayesian method for identifying genetic interactions. AMIA. 2009;2009:673–677. [PMC free article] [PubMed] [Google Scholar]
  44. Walton S, Hassan O, Morgan K, Brown MR. Modified cuckoo search: a new gradient free optimisation algorithm. Chaos Solitons Fractals. 2011;44 (9:710–718. [Google Scholar]
  45. Wang T. A partial least square approach for modeling gene-gene and gene-environment interactions when multiple markers are genotyped. Genet Epidemiol. 2009;33:644–651. doi: 10.1002/gepi.20351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Weng G, Bhalla U, Iyengar R. Complexity in biological signaling systems. Science. 1999;284:92–96. doi: 10.1126/science.284.5411.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wu TT., Chen YF, Hastie T, Sobel E, Lange K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics. 2009;25:714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Yang P, Ho JW, Zomaya A, Zhou BB. A genetic ensemble approach for gene-gene interaction identification. BMC Bioinformatics. 2010;11:524. doi: 10.1186/1471-2105-11-524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Yang X-S, Deb S.2009Cuckoo search via Levy flights Proceedings of World Congress on Nature & Biologically Inspired Computing (NaBIC 2009);December 2009, India. IEEE Publications: USA. pp210–214.
  50. Yang X-S, Deb S. Engineering optimisation by cuckoo search. PhD thesis. International Journal of Mathematical Modelling and Numerical Optimisation. 2010;1:330–343. [Google Scholar]
  51. Yang, Zhou BB, Zhang Z, Zomaya AY. A multi-filter enhanced genetic ensemble system for gene selection and sample classification of microarray data. BMC Bioinformatics. 2010;11 (Suppl 1:S5. doi: 10.1186/1471-2105-11-S1-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhang Y, Liu JS. Bayesian inference of epistatic interactions in case-control studies. Nat Genet. 2007;39:1167–1173. doi: 10.1038/ng2110. [DOI] [PubMed] [Google Scholar]
  53. Zhang YM, Xu S. A penalized maximum likelihood method for estimating epistatic effects of QTL. Heredity. 2005;95:96–104. doi: 10.1038/sj.hdy.6800702. [DOI] [PubMed] [Google Scholar]
  54. Zhang Z, Yang P. An ensemble of classifiers with genetic algorithm based feature selection. IEEE Intelligent Informatics Bulletin. 2008;9:18–24. [Google Scholar]
  55. Zhao J, Xiong M. Test for interaction between two unlinked loci. Am J Hum Genet. 2006;79:831–845. doi: 10.1086/508571. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES