Abstract.
The dual-wavelength diffuse correlation spectroscopy (DCS) flow-oximeter is an emerging technique enabling simultaneous measurements of blood flow and blood oxygenation changes in deep tissues. High signal-to-noise ratio (SNR) is crucial when applying DCS technologies in the study of human tissues where the detected signals are usually very weak. In this study, single-mode, few-mode, and multimode fibers are compared to explore the possibility of improving the SNR of DCS flow-oximeter measurements. Experiments on liquid phantom solutions and in vivo muscle tissues show only slight improvements in flow measurements when using the few-mode fiber compared with using the single-mode fiber. However, light intensities detected by the few-mode and multimode fibers are increased, leading to significant SNR improvements in detections of phantom optical property and tissue blood oxygenation. The outcomes from this study provide useful guidance for the selection of optical fibers to improve DCS flow-oximeter measurements.
Keywords: diffuse correlation spectroscopy, optical fiber mode, blood flow, blood oxygenation, signal-to-noise ratio
1. Introduction
Near-infrared (NIR) light has been recently employed to noninvasively measure relative change of blood flow (rBF) in deep tissues, which is referred to as NIR diffuse correlation spectroscopy (DCS)1–9 or diffusing wave spectroscopy (DWS).10–12 DCS blood flow measurement is accomplished by monitoring speckle fluctuations of photons resulting from moving scatterers in biological tissues. Moving red blood cells (RBCs) inside vessels are primarily responsible for these fluctuations. DCS provides several attractive new features for blood flow measurement in tissue microvasculature, including noninvasiveness, portability, high temporal resolution (up to several milliseconds), and relatively high penetration depth (up to several centimeters). DCS technology has been extensively validated in various tissues through comparisons with laser Doppler flowmetry,13,14 Doppler ultrasound,15,16 power Doppler ultrasound,17,18 Xenon-CT,19 fluorescent microsphere flow measurement,20 and arterial spin labeled magnetic resonance imaging (ASL-MRI).21,22
When using DCS to detect tissue blood flow, a pair of source and detector fibers is usually placed along the tissue surface with separation distance of a few millimeters to centimeters. NIR light generated by a continuous wave (CW) coherent laser emits into tissues through the source fiber and is detected by a single-photon-counting detector through the detector fiber. Photons travel inside tissue in a diffusive manner,8,13 and experience absorption by tissue absorbers (e.g., hemoglobin and water) and, more often, scattering by tissue scatterers (e.g., organelles and mitochondria). The probabilities of these events occurring within a unit distance are described by an absorption coefficient () and a reduced scattering coefficient (). The and are referred to as tissue intrinsic optical properties. The motions of moving scatterers cause temporal fluctuations in light intensity, leading to changes in the speckle pattern of interference.1–8,23,24 In most dynamic experiments the temporal statistics of light speckle fluctuations are monitored and the electric field temporal autocorrelation function or its Fourier transform is quantified. Using a correlation diffusion equation describing the propagation of electric field temporal autocorrelation function through tissues, the measured signal is then related to the motion of RBCs and, consequently, blood flow is determined.
Previous studies have used either single-mode3–5,9,25–31 or few-mode32–35 fibers separately for DCS flow detections. A single-mode fiber is an optical waveguide whose very small core radius is comparable with the wavelength of the transported light.32,36 Light intensity detected by the single-mode fiber, however, is low due to the fact that only the fundamental mode of light can be transported. By contrast, few-mode fibers allow a few higher-order modes of light to be guided through the fiber along with the fundamental mode. Enlarging the fiber diameter and numerical aperture () with few-mode fibers to cover multiple speckles increases the detected signal intensity, thus improving signal-to-noise ratio (SNR). Conversely, the multiple speckles detected by the few-mode fibers are uncorrelated and decrease the coherence factor () in a proportional fashion.32–35 As a result, the autocorrelation function curve becomes flatter, which may reduce the sensitivity of DCS flow measurements.37,38 The detected light intensity can be further increased using multimode fibers with a large core diameter (e.g., 1 mm), although the autocorrelation function may not be detectable due to very low value of (i.e., the autocorrelation function curve becomes a straight line).36,39 There have been no studies that concurrently use different types of fibers to experimentally compare/improve the SNRs of DCS flow measurements.
Recently, our laboratory developed a portable dual-wavelength DCS flow-oximeter that can simultaneously measure blood flow and oxygenation variations.5,9,14,23,24,26 The oxygenation information is extracted by recording the detected light-intensity changes at two wavelengths. DCS flow-oximeter can generate multiple hemodynamic variables including rBF and changes in oxy-hemoglobin concentration () and deoxy-hemoglobin concentration (). As mentioned earlier, few-mode and multimode fibers collect more photons than single-mode fibers, which leads to the following hypothesis. Increased light intensities measured at two wavelengths by few-mode or multimode fibers should improve the SNRs in measurements of light intensity as well as tissue blood oxygenation. High SNR is particularly crucial when applying DCS technologies in the study of human tissues where the detected signals are usually very low due to the need of large source-detector (S-D) separation for deeper light penetration.3–7,14,23–26,40
The purpose of this study was to experimentally explore the use of different mode fibers for photon collection to improve the SNR of DCS flow-oximeter measurements. Three fibers with different modes (i.e., single-mode, few-mode, or multimode) were examined in tissue-like liquid phantoms with varied optical properties and in human forearm muscles during arterial cuff occlusion. The SNRs of the measured variables were calculated and compared to aid in the selection of fiber(s) for the improvement of DCS flow-oximeter measurements.
2. Materials and Methods
2.1. DCS Flow-Oximeter
2.1.1. Flow measurement
DCS flow indices were quantified by a dual-wavelength DCS flow-oximeter with two CW coherent laser sources at 785 and 853 nm (100 mw, Crystalaser Inc., Nevada).14 The coherence length for both lasers was longer than 5 m. The two DCS sources emitted NIR light alternately into the tissue via two multimode optical fibers with a core diameter of 200 μm (WF200/220/245, Ceramoptec, Massachusetts) bundled at the same location on the phantom/tissue surface. Three detector fibers, including a single-mode fiber with a core diameter of 4.3 μm (SM600, Fibercore, California), a 6-mode fiber with a core diameter of 4.5 μm (SM980, Fibercore, California) and a multimode fiber with a core diameter of 1 mm, were confined by a foam pad at an equal distance of 2.5 cm from the two source fiber bundle (Fig. 1). These detector fibers were connected, respectively to three single-photon-counting avalanche photodiodes (APDs) (PerkinElmer Inc., Canada) inside the DCS device. The outputs of APDs were sent to a four-channel autocorrelator board (Correlator.com, New Jersey) yielding normalized light intensity temporal autocorrelation functions:1,2,8
| (1) |
Fig. 1.
A fiber-optic probe consisting of two source fibers ( and ) and three detector fibers ( to ). Multimode fiber (1 mm) locates in , single-mode fiber (SM600) locates in , and few-mode fiber (SM980) locates in . The separations between the sources and detector fibers are equal (i.e., ). The separations between detector fibers are , , and , respectively.
Here, is the light intensity detected at position and time , is the correlation delay time, denotes a time average.
The normalized electric field temporal autocorrelation function can be derived from the measured using the Siegert relation:41
| (2) |
Here, is a coherence factor depending mainly on the laser coherence and detection optics, and is inversely proportional to the number of guided modes/speckles ().8,32 satisfies the correlation diffusion equation in highly scattering media, and the homogeneous CW solution to this equation under semi-infinite geometry is8
| (3) |
Here, is the S-D separation, is source light intensity, is the speed of light in the medium, is the wavenumber of light in the medium, () is the photon diffusion coefficient, , , , , , and (for both tissue and phantom). The term accounts for the mismatch between the medium and the air indices of refraction with being the ratio between them.
From Eq. (3), is a function of and as well as the mean-square displacement of moving scatterers. For the case of diffuse motion, , where is an effective diffusion coefficient of the moving scatterers. An term (ranging from 0 to 1) is added to account for the fact that not all scatterers in biological tissues are dynamic, and is defined as the ratio of moving (dynamic) scatterers to total (dynamic and static) scatterers. The combined term, , is referred to as the blood flow index in tissues and is commonly used to calculate the rBF compared with the baseline flow index before physiological changes. In contrast to tissue samples, all scatterers in liquid phantom solutions (see Sec. 2.3) are considered dynamic with , and the flow index is thus reported as simply . The flow index (or ) and coherence factor are determined simultaneously by fitting derived from DCS measurements to its analytical expression based on Eqs. (1) to (3).42
2.1.2. Optical property measurement
DCS for flow measurement needs only one wavelength of light source, as previous studies have shown insensitivity of DCS flow measurements to wavelengths.14 Adding a second laser to the DCS device allows for simultaneous measurements of both blood flow and blood oxygenation. Photons emitted by lasers are scattered and/or absorbed when they travel through the tissue from the source to detector, leading to light intensity reductions in detected wavelengths. The relative change in the tissue absorption coefficient () can be derived from the light intensity changes measured at the two wavelengths.43 Variations of oxy- and deoxyhemoglobin concentrations ( and ) relative to their baseline values (determined before physiological changes) can be resolved from the measured at two wavelengths using the modified Beer-Lambert Law.44
2.2. Optical Fiber Modes
For an optical fiber the number of guided modes depends on the core radius (), relative refractive-index difference, and operating wavelength (). The relation between the properties of a given dielectric optical waveguide (fiber) and guided waves (number of modes) can be described by introducing a normalized frequency :36
| (4) |
Here and are the refractive indices of fiber core and cladding, respectively. The square root of () is defined as numerical aperture . When is smaller than the critical cutoff frequency (e.g., 2.405 for a step-index fiber whose refractive index is constant within the fiber core), only the fundamental mode can be guided through the fiber. Notice that a single-mode fiber can transmit two independent orthogonally polarized waves; the fiber is actually “bimodal.”36 The operating wavelength corresponding to is called the cutoff wavelength (). When the value of is larger than , the fiber can guide a few higher-order modes along with the fundamental mode; it becomes a few-mode fiber. The propagating vector modes [i.e., the transverse electric mode (TE), transverse magnetic mode (TM), or hybrid mode] can be determined by the following three steps: (1) calculating the value based on the fiber property using Eq. (4); (2) using the value to obtain transported linear polarized (LP) modes corresponding from literature values45 where the LP modes are the eigenmodes of guided conventional modes (i.e., TE, TM, hybrid mode) and each of them has designation of conventional modes (wave modes);39 (3) determining the guided wave modes according to the compositions of different LP modes.
We used three detector fibers for photon collection in our experiments. According to the method described above, the single-mode fiber (SM600) has a of , between 0.1 and 0.14, and fiber core diameter of which guides only two orthogonal polarization modes of light at the two operating wavelengths of 785 and 853 nm.36 The few-mode fiber (SM980) has a of , between 0.17 and 0.19, and fiber core diameter of which guides six modes of light operating at both 785 and 853 nm wavelengths. In Sec. 3.1, we experimentally checked and confirmed these calculated numbers of guided modes using measured values of . The third fiber used is a regular multimode fiber with a diameter of 1 mm.
2.3. Phantom Experiment
Distilled water, India ink (Black India 44201, Higgins, Massachusetts), and Intralipid (30%, Fresenius Kabi, Uppsala, Sweden) were utilized in constructing liquid phantoms, which provided a homogeneous tissue model.5,24,25 India ink was used to manipulate (). The () values at both 785 and 853 nm wavelengths were calculated based on the concentration of India ink. Intralipid was used to control () via changing its concentration and provided particle Brownian motion ().
An optical probe shown in Fig. 1 was placed on the surface of the liquid phantom solution contained inside a glass aquarium. A custom-made probe holder attached to a lab stand held the probe at the center of solution to simulate a semi-infinite geometry. Room light was turned off during experiments. In order to test the SNR at different levels of light intensity, a titration protocol of gradually varying was applied. The optical property of liquid phantom was set initially at and at 853 nm. The corresponding and for the second wavelength (785 nm) at each titration step were calculated according to the volumes of water, India ink, and Intralipid in the phantom solution.24 The (853 nm) was then gradually increased up to at a step size of by adding ink to the liquid phantom while was kept constant (without changing the concentration of Intralipid). Optical measurements were taken by the DCS flow-oximeter for 10 min at each titration step and 260 curves were collected for each wavelength. The measurement duration for each autocorrelation function at each wavelength was 1 s. Only 150 data points measured at each wavelength and each step were used for data analysis, as the noisy data collected during the periods of adding, stirring and dissolving ink were excluded. At the final step of the titration (), the light intensity collected by the single-mode fiber (SM600) reached a minimal value of counts per second (kcps) that could barely be detected by DCS.
For flow data analysis theoretical and from the phantom at each titration step were used as inputs when fitting flow index .24 Relative changes in were calculated by normalizing/dividing the time-course data to the mean values of the first titration data. For the analysis of phantom absorption coefficient, at the first titration step was assigned to be the theoretical value of the phantom [e.g., ] and values at other titration steps were then calculated by adding the corresponding () values measured by the DCS flow-oximeter. Standard deviations of the measured variables were calculated and displayed as error bars along with the mean values.
2.4. In Vivo Tissue Measurement
The single-mode, few-mode, and multimode fibers were further used to investigate the SNRs in DCS flow-oximeter measurements on human tissues. The in vivo experiments were approved by the University of Kentucky Institutional Review Board. Seven healthy subjects signed consent forms and participated in this study. Each subject was asked to lay supine on a bed and extend his/her forearm. Prior to the DCS flow-oximeter measurement a commercial frequency-domain NIRS tissue-oximeter (Imagent, ISS Inc., Ilinois) with a handheld probe was used to obtain absolute baseline values of , , [Hb] and [] in the participant’s forearm flexor carpiradialis muscle.46 The handheld probe was removed and the fiber-optic probe developed for this study (Fig. 1) was taped on the same location in forearm muscle to continuously monitor rBF, and during 5-min arterial cuff occlusion. An optical attenuator was attached to the multimode detector fiber to avoid saturating the highly sensitive APD. The forearm muscle went through three different physiological stages during the cuff occlusion on upper arm: 5-min resting baseline, 5-min cuff inflation (230 mmHg), and 5-min recovery following cuff deflation.
Similar to the phantom data analysis the baseline and measured by the Imagent were used as inputs when fitting flow index . Relative changes in were calculated by normalizing/dividing the time-course data to the mean values of the 5-min resting baselines. The [Hb] and [] were calculated by adding their baseline values measured by the commercial Imagent and the corresponding and measured by the DCS flow-oximeter. To be consistent with the phantom data analysis 150 data points at each stage were used to calculate the corresponding SNRs. Standard errors were calculated over the seven subjects and plotted as error bars along with the mean values in the figures.
2.5. SNR Calculation
The variables measured by or derived from the DCS flow-oximeter include , , light intensity , , , and . SNR calculations for most of these variables except follow the conventional definition:47
| (5) |
Here, “STD” represents standard deviation, “mean” represents mean value, “signal” is the measured raw data, and “noise” is the high-frequency component of the measured raw data. The high-frequency noises originate from electronics, optics, positioning of the source and detectors, and physiological variations (only applicable to in vivo measurements).48 The electronic noises include shot noise, thermal noise, and the noise induced by the dark current of APD. The optic noises arise mainly from the fiber modal noise and the loss/variation of higher order modes due to the fiber bending/vibration. The physiological variations come from the respiration, heartbeat, and subject’s movement.
The “noise” in Eq. (5) for each set of measured raw data (150 data points) was obtained using a first order Butterworth high-pass filter with a corner frequency of 0.05 Hz.42 This corner frequency was determined by analyzing the power spectral densities (PSDs) of the measured hemodynamic signals from forearm muscles, and was selected to be higher than the highest frequency (0.05 Hz) of the valid signals (i.e., slow hemodynamic changes during cuff occlusion) but lower than the DCS sampling rate () and the highest frequency of noises. The MEAN (signal) may be equal to 0 for some variables (e.g., during cuff occlusion), resulting in zero SNR. In this case the STD (noise) was used to evaluate measurement variability.
Unlike those variables (described above) depending only on time (), is a function of delay time at each measurement time point (). To calculate the SNR of at multiple , a previously established method is followed:37,42
| (6) |
The calculation was carried out among the 150 datasets of []. The mean and STD of the 150 [] curves at each delay time were used to estimate SNR () according to Eq. (6).
Differences among the three fibers in mean values of SNR or STD averaged over seven subjects were tested using the statistical analysis system (SAS) Version 9.3 software package and assessed by wavelength (only applicable to rBF) and during baseline, cuff occlusion, and recovery stages. Normality of the mean differences over seven subjects was assessed using Shapiro-Wilks test.49 Any -value less than 0.10 was considered to result in a departure from normality of the mean difference and a Wilcoxon Signed-Rank test50 was used to assess whether the mean difference was significant in this case. Where there was no departure from normality the paired -test was used to assess significance of the mean differences. A -value of 0.05 was considered significant for the mean differences examined in SNR or STD of rBF between the single-mode and few-mode fibers. A Bonferroni-corrected -value of 0.017 () was considered significant for the mean differences examined in SNRs or STDs of [Hb] and [] between any two groups of single-mode, few-mode, and multimode fibers.
3. Results
3.1. Phantom Experimental Results
3.1.1. Flow measurement
During the phantom titration experiments (853 nm) was varied from 0.050 to with a step size of while was kept constant () throughout all steps. Figure 2(a) shows typical data (dots) and fitting curves (solid lines) recorded at 785 nm and collected by the single-mode (SM600) and few-mode (SM980) fibers. The data presented in Fig. 2(a) were randomly selected from curves over each titration step. As mentioned in Sec. 2.1, and can be simultaneously derived by fitting the measured . In addition, can also be estimated based on the Siegert relation using the measured data at earliest and letting the normalized autocorrelation function , i.e., . For example, the values for the single-mode and few-mode fibers can be estimated by the intercept values of fitted curves, noted as A and B in Fig. 2(a). For the first titration (Step 1), the values calculated over 150 measurements were and for the single-mode (SM600) and few-mode (SM980) fibers, respectively. Correspondingly, values were approximately equal to the numbers of guided modes of light (): for the single-mode (SM600) fiber and for the few-mode (SM980) fiber. These numbers agreed with the theoretical values calculated based on fiber properties in Sec. 2.2. As increased the curves became noisier for both single-mode and few-mode fibers. However, the curves collected by the few-mode fiber were always smoother than those recorded by the single-mode fiber over the titration steps [Fig. 2(a)]. To further quantify the performance of the two fibers we calculated the SNRs over 150 curves at each delay time for all titration steps using the method described in Sec. 2.5. Results shown in Fig. 2(b) indicated that the SNRs of detected by the few-mode fiber were slightly higher than the single-mode fiber, which appeared more obvious at the early decay time . Similar results were found at the wavelength of 853 nm (data are not shown).
Fig. 2.
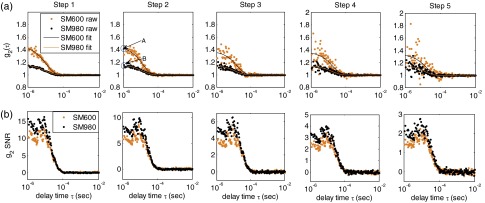
(a) Typical data (dots) and fitting curves (solid lines) recorded at 785 nm and collected by the single-mode (SM600) and few-mode (SM980) fibers at five titration steps. The curves are randomly selected at a single measurement time point over five steps. The intercepts (e.g., A and B at Step 2) can be used to estimate values (i.e., ), which are the inverse of guided mode numbers ( for SM600 and for SM980); (b) corresponding SNRs calculated from the 150 curves at each titration step.
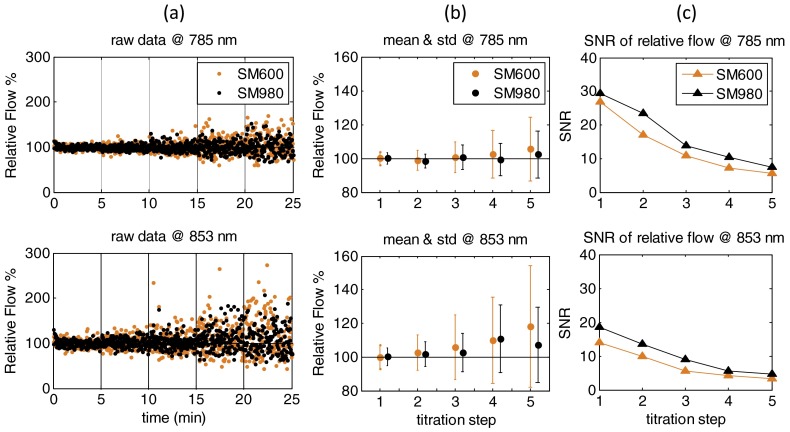
The relative flow data (normalized ) at five titration steps are shown in Fig. 3(a). Vertical lines separate different titration steps. Since multiple uncorrelated speckle fluctuations were collected by the multimode fiber (1 mm), the measured autocorrelation function curve became completely flat (a straight line), which cannot be fit using the algorithm described in Sec. 2.1. Therefore, only flow data (150 data points) collected by the single-mode and few-mode fibers were reported. As increased relative flow data recorded at two wavelengths became noisier for both single-mode and few-mode fibers, but the signal fluctuation observed when using the few-mode fiber was less than using the single-mode fiber. The difference in flow variations between the two fibers can be seen more clearly from Fig. 3(b) where the STDs of noises are illustrated as error bars. Notice that flow increased slightly with the progress of titration, which was likely due to the fitting errors at the titration steps with higher values associated with higher noises.42 Figure 3(c) shows the SNRs of relative flow at five titration steps calculated using Eq. (5). The SNRs for both single-mode and few-mode fibers decreased as increased, and the few-mode fiber achieved slightly higher SNRs than the single-mode fiber. These results are consistent with the findings shown in Fig. 3(a) and 3(b).
Fig. 3.
(a) Measured relative flow (normalized ) during the phantom titration experiment detected by the single-mode (SM600) and few-mode (SM980) fibers at the two wavelengths (785 and 853 nm); (b) mean values of relative flow and standard deviations of noise (error bars); and (c) corresponding SNRs of relative flow at the two wavelengths and five titration steps.
3.1.2. Optical property measurement
Figure 4(a) displays the light intensities at two wavelengths collected by the three fibers during titrations. As expected, higher mode fibers collected more photons. Figure 4(b) shows the mean values of light intensities and STDs of noises (error bars) at five titration steps. In order to clearly show the error bars they were multiplied by a factor of 100. It can be observed from Fig. 4(b) that with the increase of light intensity both mean (signal) and STD (noise) increased. The noise level increased because the higher light intensity increased shot noises from the photon detectors and random noises generated by photons transporting through the medium. Nevertheless, the increase of mean (signal) was larger than the increase of STD (noise). As a result, the SNR increased with the increase of light intensity [Fig. 4(c)]. The SNRs tended to decrease with the increase of , although such decreases were not remarkable at the early titration steps where the light intensities and SNRs were relatively high.
Fig. 4.

(a) Measured light intensities at the two wavelengths (785 and 853 nm) collected by the single-mode (SM600), few-mode (SM980), and multimode (1 mm) fibers during the phantom titration experiment. The light intensity unit of “kcps” stands for kilo counts per second; (b) averaged light intensities and standard deviations of noise (error bars) at the two wavelengths. The standard deviations of noise are multiplied by a factor of 100 to clearly display the error bars; and (c) corresponding SNRs of light intensities at the two wavelengths and five titration steps.
The retrieved values at five titration steps and two wavelengths using the three fibers with different modes are displayed in Fig. 5(a). The value at the first titration step was assigned to be the theoretical value of the phantom (i.e., at the wavelength of 853 nm). Figure 5(b) shows the mean values of and STDs of noises at five steps and two wavelengths. Again, in order to clearly show the error bars they were multiplied by a factor of 100. Horizontal dashed lines displayed in Fig. 5(a) and 5(b) indicate the theoretical values of the phantom at each step. All three fibers were able to extract with relatively small errors. The measurement error in was estimated by the percentage difference between the measured and theoretical values. The maximum measurement errors from the few-mode (1.6% at 785 nm and 1.3% at 853 nm) and multimode (4.3% at 785 nm and 4.8% at 853 nm) fibers were much smaller than those from the single-mode fiber (6.3% at 785 nm and 11% at 853 nm). Although differences in measurement error existed between the few-mode () and multimode () fibers, the measurement errors () from both fibers were comparable with previous NIRS results () using multimode fibers.24,46The STDs of measurement noises (error bars) increased with the increase of and the decrease of fiber mode number. The SNRs of at the five steps and two wavelengths are displayed in Fig. 5(c). It is clear that higher SNRs for can be achieved by increasing the number of optical fiber modes.
Fig. 5.
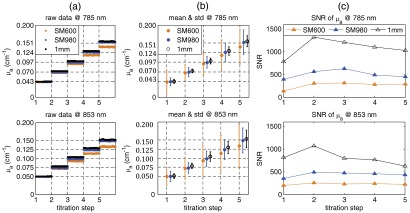
(a) Measured values at the two wavelengths (785 and 853 nm) collected by the single-mode (SM600), few-mode (SM980), and multimode (1 mm) fibers during the phantom titration experiment. The horizontal dashed lines indicate theoretical values of the phantom at each step; (b) averaged values and standard deviations of noise (error bars) at the two wavelengths. The standard deviations of noise are multiplied by a factor of 100 to clearly display the error bars; and (c) corresponding SNRs of values at the two wavelengths and five titration steps.
3.2. In Vivo Tissue Measurement Results
3.2.1. rBF measurement
Figure 6(a) shows typical rBF data at 785 and 853 nm collected by the single-mode and few-mode fibers during 5-min arterial cuff occlusion from one subject. Similar to phantom measurements the measured curve collected by the multimode fiber (1 mm) was a straight line (data are not shown), which cannot be used to extract blood flow information. The raw rBF data (150 data points at each stage) were processed by the high-pass filter with a corner frequency of 0.05 Hz to extract the noises [Fig. 6(b)]. Vertical lines in Fig. 6(a) and 6(b) separate different stages of occlusion (i.e., baseline, occlusion, recovery). The mean SNRs and standard errors (error bars) over seven subjects at the baseline and recovery stages are displayed in Fig. 6(c). The SNRs of rBF at the occlusion stage were equal to zero and thus not reported. Instead, the STDs of rBF noises and their variations (standard errors shown as error bars) over seven subjects at all three stages are shown in Fig. 6(d). Assessed by SAS software (see Sec. 2.5), the -values from the paired -tests/Wilcoxon Signed-Rank tests were larger than 0.222 indicating that the mean differences in SNR/STD of rBF over seven subjects between the single-mode and few-mode fibers were not significant at all three stages of cuff occlusion.
Fig. 6.
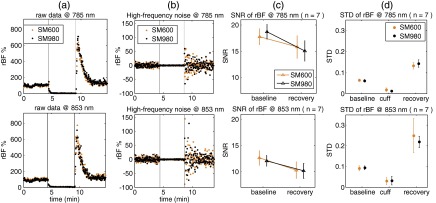
(a) Typical forearm muscle rBF responses during 5-min arterial cuff occlusion collected from one subject using the single-mode (SM600) and few-mode (SM980) fibers; (b) rBF noise processed by the high-pass filter with a corner frequency of 0.05 Hz; (c) averaged SNRs of rBF and corresponding standard errors (error bars) of noise at baseline and recovery stages over seven subjects; and (d) averaged standard deviations of high-frequency noises and corresponding standard errors (error bars) at baseline, cuff occlusion, and recovery stages over seven subjects.
3.2.2. Oxygenation measurement
Figure 7(a) displays the [Hb] and [] data during 5-min arterial occlusion measured by the three fibers with different modes from the same subject shown in Fig. 6. Apparently, [Hb] and [] curves became smoother [Fig. 7(a)] and noises were less [Fig. 7(b)] when using higher mode fibers. Figure 7(c) displays the mean SNRs and their standard errors (error bars) over seven subjects. Assessed by SAS software (see Sec. 2.5), the -values from the paired -tests/Wilcoxon Signed-Rank tests were smaller than 0.016 when evaluating the significance between the few-mode and single-mode fibers and between the multimode and single-mode fibers. As noted in Sec. 2.5, a Bonferroni-corrected -value of was considered significant. This result indicated that the mean SNRs of both [Hb] and [] using the few-mode and multimode fibers were significantly higher than those using the single-mode fiber.
Fig. 7.
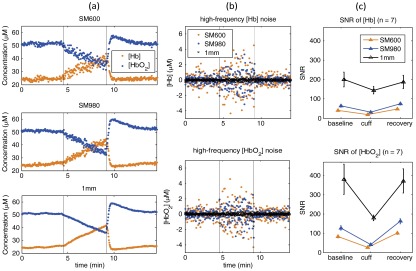
(a) Typical [Hb] and [] responses during 5-min arterial cuff occlusion collected from the same subject shown in Fig. 6 using the single- (SM600), few- (SM980), and multimode (1 mm) fibers; (b) [Hb] and [] noises processed by the high-pass filter with a corner frequency of 0.05 Hz; (c) averaged SNRs of [Hb] and [] and corresponding standard errors (error bars) of noises at baseline, cuff occlusion, and recovery stages over seven subjects.
4. Discussion and Conclusions
Traditional NIRS can measure tissue optical properties including , , [Hb] and [] while the emerging DCS can measure rBF in deep tissues. By combining these two technologies to form a hybrid instrument, rBF, [Hb], and [] can be obtained simultaneously.51,52 Consequently, relative changes in tissue oxygen metabolism can be derived using simple models.52–54 While the hybrid instruments () can be used to measure multiple hemodynamic/metabolic parameters providing deeper insights about tissue physiological status than one parameter alone, they are relatively large, complex, and expensive. The dual-wavelength DCS flow-oximeter is an emerging technique enabling simultaneous measurements of tissue blood flow and oxygenation changes.5,9,14,23,24,26 Being noninvasive, fast, relatively inexpensive and truly portable (dimensions: in.), DCS flow-oximeter is suitable for bedside monitoring in the clinics. Furthermore, the new probe designed for the DCS flow-oximeter shares source and detector fibers for both flow and oxygenation measurements (see Fig. 1). Therefore, it covers exactly the same tissue volume and avoids any discrepancies between the blood flow and oxygenation measurements owing to the tissue heterogeneity.
For clinical measurements large light penetration is needed to probe optical properties in deep tissues (e.g., adult brain and muscle). According to photon diffusion theory a given source-detector (S-D) pair is mostly sensitive to the area at a depth of to of the S-D separation.8,13,24,55 However, the larger the S-D separation the weaker the signal detected. Improving SNR is especially crucial when the detected signal is extremely low, which is not unusual for DCS measurements in human tissues.3–7,23,31
According to Eq. (5), SNR can be improved by increasing the light intensity injected into the tissue, which is, however, not unlimited and has to be controlled to meet American National Standards Institute standards for laser safety usage. An alternative method is to use a low-pass filter to reduce the high-frequency noises, but this may not be possible when the bandwidths of signal and noise are overlapped. This study was designed to investigate the possibility of using the few-mode or multimode detection fibers instead of the single-mode fiber to increase the light intensity detected and thus improve SNRs of DCS flow-oximeter measurements. The rationale behind this hypothesis is that few-mode or multimode fibers allow higher-order modes of light to be guided through along with the fundamental single mode which would increase the light intensity detected.36
To test the hypothesis the single-mode (SM600), few-mode (SM980), and multimode (1 mm) fibers were examined in tissue-like liquid phantoms with varied optical properties and in forearm muscles during arterial cuff occlusion. The liquid phantom provided a homogeneous tissue model without the interference of physiological variations that exist in biological tissues,5,24,25 while the use of human muscles allowed for the evaluation of fiber performance in real tissues.4,6,22,26,40
The results obtained from the phantom titration experiments indicated that the few-mode fiber slightly improved the SNRs of relative flow measurements compared to the single-mode fiber used [see Fig. 3(c)]. Although the slight SNR improvement in flow measurements was somewhat disappointing, it was not surprising because the few-mode fiber with larger diameter and numerical aperture increased the detected signal intensity [see Fig. 4(a) and 4(b)] but decreased the coherence factor in a proportional fashion [see Fig. 2(a)]. A smaller corresponded with a flatter autocorrelation function curve leading to a lower sensitivity of DCS flow measurements.37,38 Therefore, the SNR of autocorrelation function, depending on both light intensity detected and coherence factor ,37 may not be highly improved [see Fig. 2(b)]. Although the detected light intensity can be further increased by using the multimode fiber with a large diameter of 1 mm [see Fig. 4(a) and 4(b)], the autocorrelation function was not detectable in this case due to the very low value of . Furthermore, the SNR improvements were not obvious during in vivo rBF measurements in forearm muscles [see Fig. 6(c) and 6(d)]. Unlike phantom experiments, in vivo measurements could be influenced by many factors such as physiological variations, motion artifacts, fiber-tissue coupling coefficient, and tissue heterogeneity, which could have an impact on the measurements differently on different fibers.7,9,22,40 Such in vivo “noises” may bury the slight SNR improvements of flow measurements observed in phantom experiments.
In contrast with flow measurements, significant SNR improvements were achieved when using the few-mode or multimode fiber (versus single-mode fiber) in both phantom measurements of light intensity [see Fig. 4(c)] and [see Fig. 5(c)] and in in vivo measurements of [Hb] and [] [see Fig. 7(c)]. The significant SNR improvements for these variables were expected, as they all depended on the light intensities detected which were highly different among the three fibers [see Fig. 4(a) and 4(b)]. The larger the number of optical fiber modes, the higher the detected light intensity.
The level of the detected light intensity also greatly impacted SNRs of the measured variables at different titration steps and different physiological stages. For example, with the increase of during the phantom titration, the detected light intensity decreased step by step leading to a continual decrease in SNRs for all three fibers and two wavelengths (see Figs. 3 and 4). One exception is the derived value of during phantom experiments where the SNRs of at the first titration step for both wavelengths were lower than those at other steps [see Fig. 5(c)], although the light intensities detected at the first step were higher [see Fig. 4(a) and 4(b)]. Since the values at the first titration step were much smaller than those at other steps (e.g., times smaller than the second step), but the STDs of at all steps did not vary much; it was not surprising that the SNRs of at the first titration step for both wavelengths were smaller than those at other steps according to Eq. (5). Furthermore, the SNRs of [Hb] and [] during the cuff occlusion stage were lower than those at baseline and recovery stages for all three fibers [see Fig. 7(c)], which was again due to the lower light intensities detected during occlusion compared with other two stages. In addition, the light intensity detected from the wavelength of 853 nm was times lower than the 785 nm wavelength [see Fig. 4(a) and 4(b)], resulting in lower SNRs for the 853 nm wavelength at most titration steps and physiological stages (see Figs. 3 to 6), although laser stability could also impact the SNRs.
Besides the SNR improvements the few-mode and multimode fibers measured the optical property more accurately than the single-mode fiber [see Fig. 5(a) and 5(b)]. Smaller measurement error represented higher measurement accuracy. The measurement errors in from the few-mode and multimode fibers were for both wavelengths [Fig. 5(a)] which were comparable with those () observed in previous studies using NIRS with multimode fibers.24,46 The maximum errors from the single-mode fiber () were much larger than those from the other two fibers () [Fig. 5(a)] and those reported in literature (), which was again due to less light intensities collected (associated with higher noises) by the single-mode fiber.
In conclusion, the experiments in this study demonstrated the advantages of using the few-mode fiber for DCS flow-oximeter measurements of both blood flow and oxygenation compared with using the single-mode fiber. The few-mode fiber enabled collection of more photons from the phantoms/tissues resulting in higher SNRs in both flow and oxygenation measurements, although the SNR improvements with the few-mode fiber were found to be significant only in oxygenation measurements. The multimode fiber can further increase the detected light intensities and SNRs for tissue oxygenation measurements, but the autocorrelation functions for extracting flow information cannot be detected due to the very low value of .
Based on these results, selection of fibers with certain modes will depend on the particular application. For the measurements of blood flow only either single-mode fiber or few-mode fiber can be used, although the few-mode fiber will generate slightly higher SNRs of flow data. For simultaneous measurements of tissue blood flow and oxygenation using the dual-wavelength DCS flow-oximeter, a few-mode fiber (instead of single-mode fiber) should be used to obtain significantly higher SNRs of tissue oxygenation measurements. An alternative way is to use a detection fiber bundle consisting of one single-mode (or few-mode) fiber and one multimode fiber. The single-mode or few-mode fiber can measure autocorrelation functions to extract flow information while the multimode fiber can detect light intensities at the two wavelengths with significantly higher SNRs (than both single-mode and few-mode fibers) to extract oxygenation information. However, the latter option requires two detectors connected to the fiber bundle which would increase the instrumentation costs.
This pilot study was limited to comparing the SNRs of DCS flow-oximeter measurements among three types of fibers (i.e., single-mode, few-mode, multimode). The selection of these specific three fibers was mainly based on fiber availability. The optimization of fiber modes used for achieving optimum SNRs in tissue hemodynamic measurements will be the subject of future study.
Acknowledgments
This study was supported partially by the grants R01 CA149274, R21 AR062356, and UL1RR033173 from National Institutes of Health (NIH). The content is solely the responsibility of the authors and does not necessarily represent the official views of NIH.
References
- 1.Boas D. A., Campbell L. E., Yodh A. G., “Scattering and imaging with diffusing temporal field correlations,” Phys. Rev. Lett. 75(9), 1855–1858 (1995). 10.1103/PhysRevLett.75.1855 [DOI] [PubMed] [Google Scholar]
- 2.Boas D. A., Yodh A. G., “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A-Opt Image Sci. Vis. 14(1), 192–215 (1997). 10.1364/JOSAA.14.000192 [DOI] [Google Scholar]
- 3.Cheng R., et al. , “Noninvasive optical evaluation of spontaneous low frequency oscillations in cerebral hemodynamics,” Neuroimage 62(3), 1445–1454 (2012). 10.1016/j.neuroimage.2012.05.069 [DOI] [PubMed] [Google Scholar]
- 4.Gurley K., Shang Y., Yu G., “Noninvasive optical quantification of absolute blood flow, blood oxygenation, and oxygen consumption rate in exercising skeletal muscle,” J. Biomed. Opt. 17(7), 075010 (2012). 10.1117/1.JBO.17.7.075010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dong L., et al. , “Noninvasive diffuse optical monitoring of head and neck tumor blood flow and oxygenation during radiation delivery,” Biomed. Opt. Express 3(2), 259–272 (2012). 10.1364/BOE.3.000259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Munk N., et al. , “Noninvasively measuring the hemodynamic effects of massage on skeletal muscle: a novel hybrid near-infrared diffuse optical instrument,” J. Bodywork Mov. Ther. 16(1), 22–28 (2012). 10.1016/j.jbmt.2011.01.018 [DOI] [PubMed] [Google Scholar]
- 7.Yu G., “Near-infrared diffuse correlation spectroscopy in cancer diagnosis and therapy monitoring,” J. Biomed. Opt. 17(1), 010901 (2012). 10.1117/1.JBO.17.1.010901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boas D. A., “Diffuse Photon Probes of Structural and Dynamical Properties of Turbid Media: Theory and Biomedical Applications,” University of Pennsylvania, Philadelphia, PA: (1996). [Google Scholar]
- 9.Shang Y., et al. , “Diffuse optical monitoring of repeated cerebral ischemia in mice,” Opt. Express 19(21), 20301–20315 (2011). 10.1364/OE.19.020301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maret G., Wolf P. E., “Multiple light scattering from disordered media. The effect of brownian motion of scatterers,” Z. Phys. B 65(4), 409–413 (1987). 10.1007/BF01303762 [DOI] [Google Scholar]
- 11.Pine D. J., et al. , “Diffusing-wave spectroscopy,” Phys. Rev. Lett. 60(12), 1134–1137 (1988). 10.1103/PhysRevLett.60.1134 [DOI] [PubMed] [Google Scholar]
- 12.Stephen M. J., “Temporal fluctuations in wave propagation in random media,” Phys. Rev. B 37(1), 5 (1988). 10.1103/PhysRevB.37.1 [DOI] [PubMed] [Google Scholar]
- 13.Durduran T., Non-Invasive Measurements of Tissue Hemodynamics with Hybrid Diffuse Optical Methods, University of Pennsylvania, Philadelphia, PA: (2004). [Google Scholar]
- 14.Shang Y., et al. , “Portable optical tissue flow oximeter based on diffuse correlation spectroscopy,” Opt. Lett. 34(22), 3556–3558 (2009). 10.1364/OL.34.003556 [DOI] [PubMed] [Google Scholar]
- 15.Buckley E. M., et al. , “Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound,” Opt. Express 17(15), 12571–12581 (2009). 10.1364/OE.17.012571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roche-Labarbe N., et al. , “Noninvasive optical measures of CBV, StO(2), CBF index, and rCMRO(2) in human premature neonates’ brains in the first six weeks of life,” Hum. Brain Mapp. 31(3), 341–352 (2010). 10.1002/hbm.v31:3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Menon C., et al. , “An integrated approach to measuring tumor oxygen status using human melanoma xenografts as a model,” Cancer Res. 63(21), 7232–7240 (2003). [PubMed] [Google Scholar]
- 18.Yu G., et al. , “Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy,” Clin. Cancer Res. 11(9), 3543–3552 (2005). 10.1158/1078-0432.CCR-04-2582 [DOI] [PubMed] [Google Scholar]
- 19.Kim M. N., et al. , “Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,” Neurocrit. Care 12(2), 173–180 (2010). 10.1007/s12028-009-9305-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhou C., et al. , “Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,” J. Biomed. Opt. 14(3), 034015 (2009). 10.1117/1.3146814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Durduran T., et al. , “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett. 29(15), 1766–1768 (2004). 10.1364/OL.29.001766 [DOI] [PubMed] [Google Scholar]
- 22.Yu G., et al. , “Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,” Opt. Express 15(3), 1064–1075 (2007). 10.1364/OE.15.001064 [DOI] [PubMed] [Google Scholar]
- 23.Shang Y., et al. , “Cerebral monitoring during carotid endarterectomy using near-infrared diffuse optical spectroscopies and electroencephalogram,” Phys. Med. Biol. 56(10), 3015–3032 (2011). 10.1088/0031-9155/56/10/008 [DOI] [PubMed] [Google Scholar]
- 24.Irwin D., et al. , “Influences of tissue absorption and scattering on diffuse correlation spectroscopy blood flow measurements,” Biomed. Opt. Express 2(7), 1969–1985 (2011). 10.1364/BOE.2.001969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lin Y., et al. , “Noncontact diffuse correlation spectroscopy for noninvasive deep tissue blood flow measurement,” J. Biomed. Opt. 17(1), 010502 (2012). 10.1117/1.JBO.17.1.010502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yu G., et al. , “Intraoperative evaluation of revascularization effect on ischemic muscle hemodynamics using near-infrared diffuse optical spectroscopies,” J. Biomed. Opt. 16(2), 027004 (2011). 10.1117/1.3533320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yu G., et al. , “Real-time in situ monitoring of human prostate photodynamic therapy with diffuse light,” J. Photochem. Photobiol. 82(5), 1279–1284 (2006). 10.1562/2005-10-19-RA-721 [DOI] [PubMed] [Google Scholar]
- 28.Zhou C., et al. , “Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy,” J. Biomed. Opt. 12(5), 051903 (2007). 10.1117/1.2798595 [DOI] [PubMed] [Google Scholar]
- 29.Zhou C., et al. , “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt. Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 30.Sunar U., et al. , “Noninvasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study,” J. Biomed. Opt. 11(6), 064021 (2006). 10.1117/1.2397548 [DOI] [PubMed] [Google Scholar]
- 31.Mesquita R. C., et al. , “Direct measurement of tissue blood flow and metabolism with diffuse optics,” Phil. Trans. R. Soc. A 369(1955), 4390–4406 (2011). 10.1098/rsta.2011.0232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gisler T., et al. , “Mode-selective dynamic light scattering: theory versus experimental realization,” Appl. Opt. 34(18), 3546–3553 (1995). 10.1364/AO.34.003546 [DOI] [PubMed] [Google Scholar]
- 33.Dietsche G., et al. , “Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue,” Appl. Opt. 46(35), 8506–8514 (2007). 10.1364/AO.46.008506 [DOI] [PubMed] [Google Scholar]
- 34.Li J., et al. , “Transient functional blood flow change in the human brain measured noninvasively by diffusing-wave spectroscopy,” Opt. Lett. 33(19), 2233–2235 (2008). 10.1364/OL.33.002233 [DOI] [PubMed] [Google Scholar]
- 35.Li J., et al. , “Noninvasive detection of functional brain activity with near-infrared diffusing-wave spectroscopy,” J. Biomed. Opt. 10(4), 44002 (2005). 10.1117/1.2007987 [DOI] [PubMed] [Google Scholar]
- 36.Neumann E. G., Single-Mode Fibers: Fundamentals, pp. 66–82, Springer-Verlag, Berlin: (1988). [Google Scholar]
- 37.Zhou C., In-vivo Optical Imaging and Spectroscopy of Cerebral Hemodynamics, University of Pennsylvania, Philadelphia, PA: (2007). [Google Scholar]
- 38.Zhou C., et al. , “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 39.Yeh C., Shimabukuro F., The Essence of Dielectric Waveguides, p. 267, Springer, New York: (2008). [Google Scholar]
- 40.Shang Y., et al. , “Effects of muscle fiber motion on diffuse correlation spectroscopy blood flow measurements during exercise,” Biomed. Opt. Express 1(2), 500–511 (2010). 10.1364/BOE.1.000500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rice S. O., “Mathematical analysis of random noise,” in Noise and Stochastic Processes, Wax N., Ed., p. 133, Dover, New York: (1954). [Google Scholar]
- 42.Dong L., et al. , “Simultaneously extracting multiple parameters via fitting one single autocorrelation function curve in diffuse correlation spectroscopy,” IEEE Trans. Biomed. Eng. 60(2), 361–368 (2013). 10.1109/TBME.2012.2226885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fantini S., et al. , “Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy,” Phys. Med. Biol. 44, 1543–1563 (1999). 10.1088/0031-9155/44/6/308 [DOI] [PubMed] [Google Scholar]
- 44.Strangman G., Franceschini M. A., Boas D. A., “Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters,” Neuroimage 18(4), 865–879 (2003). 10.1016/S1053-8119(03)00021-1 [DOI] [PubMed] [Google Scholar]
- 45.Ghatak A. K., Optics, p. 29.4, Tata McGraw-Hill, New Delhi: (2009). [Google Scholar]
- 46.Fantini S., Franceschini M. A., Gratton E., “Semi-infinite-geometry boundary-problem for light migration in highly scattering media—a frequency-domain study in the diffusion-approximation,” J. Opt. Soc. Am. B-Opt. Phys. 11(10), 2128–2138 (1994). 10.1364/JOSAB.11.002128 [DOI] [Google Scholar]
- 47.Lyons R. G., Understanding Digital Signal Processing, pp. 1–984, Prentice Hall, New Jersey: (2010). [Google Scholar]
- 48.Choe R., Diffuse Optical Tomography and Spectroscopy of Breast Cancer and Fetal Brain, University of Pennsylvania, Philadelphia, PA: (2005). [Google Scholar]
- 49.Zar J. H., Biostatistical Analysis, Prentice-Hall, NJ, pp. 88–89 (1999). [Google Scholar]
- 50.Zar J. H., Biostatistical Analysis, Prentice-Hall, NJ, p. 110 (1999). [Google Scholar]
- 51.Cheung C., et al. , “In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,” Phys. Med. Biol. 46(8), 2053–2065 (2001). 10.1088/0031-9155/46/8/302 [DOI] [PubMed] [Google Scholar]
- 52.Yu G., et al. , “Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies,” J. Biomed. Opt. 10(2), 024027 (2005). 10.1117/1.1884603 [DOI] [PubMed] [Google Scholar]
- 53.Culver J. P., et al. , “Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia,” J. Cerebr. Blood F Met. 23(8), 911–924 (2003). 10.1097/01.WCB.0000076703.71231.BB [DOI] [PubMed] [Google Scholar]
- 54.Durduran T., et al. , “Diffuse optical measurement of blood flow in breast tumors,” Opt. Lett. 30(21), 2915–2917 (2005). 10.1364/OL.30.002915 [DOI] [PubMed] [Google Scholar]
- 55.Irwin D., Influence of Tissue Absorption and Scattering on Diffuse Correlation Spectroscopy Blood Flow Measurements, University of Kentucky, Lexington, KY: (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]