Cerebrospinal Fluid Flow Impedance is Elevated in Type I Chiari Malformation

Short abstract

Diagnosis of Type I Chiari malformation (CMI) is difficult because the most commonly used diagnostic criterion, cerebellar tonsillar herniation (CTH) greater than 3–5 mm past the foramen magnum, has been found to have little correlation with patient symptom severity. Thus, there is a need to identify new objective measurement(s) to help quantify CMI severity. This study investigated longitudinal impedance (LI) as a parameter to assess CMI in terms of impedance to cerebrospinal fluid motion near the craniovertebral junction. LI was assessed in CMI patients (N = 15) and age-matched healthy controls (N = 8) using computational fluid dynamics based on subject-specific magnetic resonance imaging (MRI) measurements of the cervical spinal subarachnoid space. In addition, CTH was measured for each subject. Mean LI in the CMI group (551 ± 66 dyn/cm⁵) was significantly higher than in controls (220 ± 17 dyn/cm⁵, p < 0.001). Mean CTH in the CMI group was 9.0 ± 1.1 mm compared to −0.4 ± 0.5 mm in controls. Regression analysis of LI versus CTH found a weak relationship (R²= 0.46, p < 0.001), demonstrating that CTH was not a good indicator of the impedance to CSF motion caused by cerebellar herniation. These results showed that CSF flow impedance was elevated in CMI patients and that LI provides different information than a standard CTH measurement. Further research is necessary to determine if LI can be useful in CMI patient diagnosis.

1. Introduction

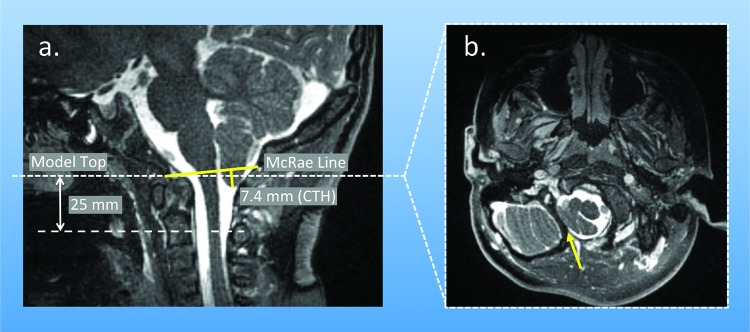
Type I Chiari malformation (CMI) is a complex disorder of the craniospinal system that has historically been radiologically defined by cerebellar tonsillar herniation (CTH) greater than 3–5 mm below the foramen magnum (FM) into the spinal subarachnoid space (SSS) (Fig. 1 ) [1–3]. Patients with CMI can have a variety of neurological symptoms and pain ranging from mild to severe [1]. It is thought that these symptoms result from abnormal pressure acting on the spinal cord, brain stem, and/or cerebellum due to crowding of the tissue in the posterior cranial fossa and craniovertebral junction (CVJ) [4–6]. However, large retrospective clinical studies have shown that CMI symptom severity does not always correlate with CTH depth [7]. Patients with large CTH may present with mild neurological symptoms and vice versa [6].

Fig. 1.

(a) Midsagittal MRI image of the cervical spine of a CMI patient showing the McRae line, CTH measurement (approximately 7.4 mm for this case), and planes where pressure drop was calculated; (b) transverse MRI image from the plane used to demarcate the model top, highlighting the separation between the cerebellar tonsils and body of the cerebellum. Note: patient tonsils for this case are asymmetric with greater CTH on the left side.

As such, clinicians have sought additional objective measurements to assist in the diagnostic process. In clinical practice, the diagnostic process can vary widely; clinicians have differing views on the importance of CTH alongside many factors such as symptom history, neurologic deficit, degree of craniocervical “crowding” bony landmark positions, and cisterna magna volume. CTH greater than 3–5 mm as a marker for CMI has been established as a ‘rule of thumb’ over time. This is problematic, as incidental observation of CTH has become more common with increases in the use of magnetic resonance imaging (MRI) for head and neck injury examinations. Recent research has shown that as much as 3% of the pediatric population, 2% of the adult female population, and 1% of the adult male population have greater than 5 mm CTH [8,9] and CTH varies throughout life (Fig. 2).

Fig. 2.

CTH as a function of age (in decade range, e.g., first decade 0–10 y) and sex for healthy subjects showing a parabolic trend with females having greater CTH values throughout life. Positive CTH values are in the caudal direction to the FM (data based on Smith et al. [8]). CMI patients, not shown, would have positive CTH values greater than 3 mm.

In hydrodynamic terms, CTH creates a stenosis near the CVJ that partially blocks the pulsatile motion of cerebrospinal fluid (CSF) between the cranial and spinal subarachnoid spaces. Although the pulsatile CSF stroke volume is only ∼1 cc with each cardiac cycle [10,11], the partial stenosis near the CVJ causes elevated CSF pressure gradients [12,13] that can result in severe neurologic consequences. At present, MRI techniques are being developed to measure CSF pressure gradients noninvasively [14], but these methods are not in standard use and have not been validated. In principle, changes in CSF pressure gradients are related to alterations in impedance to CSF motion, CSF velocities [15–22], neural tissue motion [23–25], and craniospinal compliance [26–28]. We suspect that alterations in each of these biomechanical parameters could prove useful to quantify the biomechanical environment near the CVJ in CMI.

Of interest in this study is longitudinal impedance (LI), or the impedance to the pulsatile component of CSF motion, in the cervical SSS near the CVJ [29]. While CTH is typically indicative of a blockage, it only accounts for one linear dimension, depth, and does not consider the three-dimensionality of the stenosis (e.g., the girth of the blockage) at the CVJ (Fig. 1) or the dynamic changes to the biomechanical environment caused by the stenosis. In contrast, LI is a pressure-based parameter (ratio of pressure drop to volume flow) that is dependent on the complex conduit geometry. By quantifying the severity of the stenosis in terms of LI, rather than by a single geometric dimension such as CTH, LI may provide a better parameter to assess the pathoanatomy of CMI. Martin et al. [29] demonstrated the utility of LI to quantify CMI blockage in a pilot study with one healthy subject and two CMI patients before and after surgery. LI was found to be elevated in patients compared to a healthy subject and to decrease after surgery, but the limited number of subjects analyzed did not permit statistical analysis. The aim of the present study was to utilize the methods of Martin et al. [29] to analyze LI in a larger patient and control group to determine statistical differences, if any, and understand the relation of LI and CTH. Our hypothesis was that LI would be higher in CMI patients than in healthy volunteers due to the stenosed CVJ and would increase with CTH.

Materials and Methods

Ethics Statement.

MRI data acquisition was performed at the University of Wisconsin (UW), the Cleveland Clinic Foundation (CCF), and Emory University (EU). The study was approved by the institutional review board of each institution. Prior to scanning, written informed consent was obtained for all subjects. All MRI data were anonymized before being transferred for analysis.

Study Population.

Fifteen adult CMI patients (age 17 or older) volunteered to participate in the study (six at UW, nine at CCF). Consistent with the conventional definition of CMI, the inclusion criterion was CTH greater than 3–5 mm below the FM. Among these 15 patients were ten symptomatic CMI patients and five “asymptomatic” CMI patients. Patients were classified as symptomatic based on the presence of sufficiently severe neurological symptoms to warrant corrective craniocervical decompression surgery. Patients were classified as asymptomatic that had only mild symptoms or symptoms that were not attributable to CTH and were not recommended for corrective surgery. Although patients in this group can have symptoms, neurosurgeons commonly refer to this group as asymptomatic. Patients were excluded that had secondary causes of CTH, such as hydrocephalus, had undergone previous decompression surgery or had implanted CSF shunts. A group of eight healthy volunteers with no history of neurological disorder or spinal trauma volunteered for the control group (two at UW, five at CCF, one at EU).

MRI.

The cervical spine of each subject was imaged using a 3D balanced steady-state free precession (SSFP) gradient echo sequence on a 3T scanner (GE Medical Systems, Milwaukee, WI or Siemens Healthcare, Malvern, PA). The result of each scan was a set of axial T₂-weighted images of the lower cranial and upper cervical SSS. The sequence was optimized to provide high contrast between the CSF and surrounding tissues. Additional image parameters were as follows: slice thickness = 0.8–1.0 mm with no interslice spacing, frame of view (FOV) = 260 × 260 mm or 210 × 280 mm, and matrix size = 320 × 320 or 240 × 320.

Phase-contrast MRI (pcMR) images were obtained for only 15 of the subjects at sites were the sequence was available. Images were acquired in a transverse plane at the caudal end of the C2 vertebra using a retrospective peripheral pulse-gated sequence with a velocity encoding of 10 cm/s. Each pcMR scan yielded a set of 20 images over the cardiac cycle. Additional image parameters were as follows: repetition time (TR) = 49.3 ms, flip angle (FA) = 15 deg, FOV = 240-180 mm, matrix size = 256 × 192, and slice thickness = 6 mm.

CTH Measurement.

Measurement of CTH was performed independently by two neurosurgeons using the high-resolution T₂-weighted anatomy images. The procedure for measurement of CTH was as follows: (1) select the sagittal slice with greatest tonsillar descent, (2) identify the basion and opisthion within the selected slice, (3) draw the McRae line between the basion and opisthion, and (4) measure the length of a second line that is perpendicular to the McRae line and ends at the tip of the cerebellar tonsils. Interoperator variability was assessed by computing the intraclass correlation coefficient (ICC) between measurement sets.

Anatomy Modeling and Meshing.

3D geometric models of the SSS were reconstructed for each subject over the first 40–50 mm caudal to the FM by a single operator. The boundary of the SSS was segmented using the level-set edge detection feature of the freely available Segment software (Medviso, Sweden). The top (cranial end) of each model was positioned in-line with the z-plane of the MRI image set at the most cranial location where the SSS could still be considered an annular conduit. That location was found by identifying the first image where the body of the cerebellum was only visible in a separate cavity from the SSS (Fig. 1(b)). This was generally in close proximity to the McRae line at the FM. The bottom of each model was chosen to be 40–50 mm caudal to the top.

Each of the 3D segmentations was converted to an STL surface and smoothed to remove pixilation artifacts using Geomagic (Geomagic Inc, Morrisville, NC). The inlet and outlet faces of each model were extruded 2–5 hydraulic diameters normal to the plane of each face to create entry and exit lengths and minimize the influence of boundary effects in the anatomical section of the geometry. Models were then converted to nonuniform rational Bezier spline (NURBS) surfaces for better compatibility with the meshing software. All models were meshed for computational fluid dynamics (CFD) analysis using ICEM CFD (Ansys Inc., Canonsburg, PA). The meshing process comprised the following steps: applying an unstructured tetrahedral mesh to the entire volume using the Octree algorithm, smoothing the mesh using the Delaunay algorithm, splitting the mesh near the model wall to create a layer of prismatic boundary layer cells, splitting the prismatic layer to create five smaller prismatic layers of linearly increasing aspect ratio, and resmoothing the tetrahedral core using the Delaunay algorithm. Depending on the size of the original SSS model and length of the model extensions, this procedure yielded meshes of 1–2 × 10⁶ cells.

Flow Waveforms.

For those subjects who were imaged at a site where pcMR was available, subject-specific CSF waveforms were obtained from pcMR measurements at the caudal end of the C2 vertebra (15 of 23 cases). A custom matlab graphical user interface was developed to allow manual masking of pixels within the SSS that had cardiaclike pulsatile velocity profiles. Volume flow waveforms were then computed from the sum of pixel velocity multiplied by pixel area for each pixel in the mask in each phase image. Flow waveforms were scaled by area of the top face of each anatomy model to create an average velocity waveform, which was used as the inlet boundary condition for CFD modeling.

CFD Model Setup.

Walls of the SSS were modeled as rigid with the model top specified as a velocity inlet and the model bottom specified as a zero-pressure outlet. CSF was modeled as water at 37 °C (ρ = 1.0 gm/cm³, μ = 0.01 P) [30]. The distribution of instantaneous Reynolds number at peak systole for each model was calculated using the relation Re_SYS = (4*Q _SYS)/(P _{WET *}ν), where Q _SYS was volume flow rate at peak systole, P _WET was the wetted perimeter at each slice in the segmented image stack, and ν was the kinematic viscosity of the fluid. For all models, the maximum instantaneous Reynolds number in each distribution was 300 or less. Hence, flow was assumed to be laminar in all models. The commercial finite volume solver Fluent (Ansys Inc., Canonsburg, PA) was used to carry out fluid flow simulations. The Navier–Stokes equations were discretized using a second-order upwind scheme in space and a second-order implicit scheme in time. SIMPLE was chosen as the pressure-velocity coupling algorithm. PRESTO was chosen as the pressure interpolation scheme.

Longitudinal Impedance.

In each simulation, the unsteady pressure drop near the CVJ was computed as the difference in area-weighted average pressure in cross-sectional planes located at the FM $P_{\mathit{FM}}(t)$ and at a plane located 25 mm caudal to the FM, $P_{2.5}(t)$, such that $\Delta P\left(t\right)=P_{2.5}\left(t\right)-P_{\mathit{FM}}(t)$. A distance of 25 mm was chosen as clinical studies have reported that CTH >25 mm has rarely been observed [1]. Hence, it was assumed that 25 mm in the longitudinal direction would encompass the entire region of the SSS where the geometry could be affected by CTH. Impedance modulus, $Z_L$, was calculated by computing the ratio of Fourier coefficients of the pressure drop $\mathfrak{F}\left(\Delta P\left(t\right)\right)$ and flow waveforms $\mathfrak{F}(Q(t))$ at each harmonic, where $Z_L=|\mathfrak{F}(\Delta P(t))/\mathfrak{F}(Q(t))|$. The resulting $Z_L$ (dyn-s/cm⁵) values for each harmonic were integrated from 1–8 Hz to obtain integrated longitudinal impedance (LI) for each subject [29]. The range of 1–8 Hz was chosen because 90–100% of the signal power for all the flow waveforms used as inlet boundary conditions was contained between those frequencies. Thus, LI in this study was the impedance to the frequency components that displaced most or all of the fluid in a particular waveform (i.e., the dominant carrier frequencies).

Mesh Independence.

To ensure mesh-independent solutions, a global mesh-sizing scheme was developed by simulating flow in an SSS model with moderate CTH (6.9 mm). Using an SSS model with a constricted inlet region allowed testing of mesh independence in the presence of high pressure gradients. The working assumption for this approach was that a sizing scheme that yielded a mesh-independent solution for an SSS model with large pressure gradients should also yield a mesh-independent solution for an SSS model with smaller gradients. For the test model, a coarse mesh and a fine mesh with cell counts of 896,172 and 2,298,224, respectively, were generated using maximum element edge sizes of 0.5 and 0.25 mm. Each model was tested with time steps of T/100 and T/1000 and simulated for three periods of the inlet waveform to assess time step and period independence. Solution independence was determined by comparing LI values obtained from each simulation.

The maximum relative change in LI obtained by refining the time step was 2.5%. The maximum relative change obtained by refining grid size was less than 1%. The relative change in LI between periods of the inlet waveform was a maximum of 1% between the second and third cycles of each simulation in all cases. Hence, the remaining CFD simulations were run using the 0.5 mm maximum element edge length sizing scheme with a time step of T/100 for two periods of the waveform.

Sensitivity to Inlet Boundary Conditions.

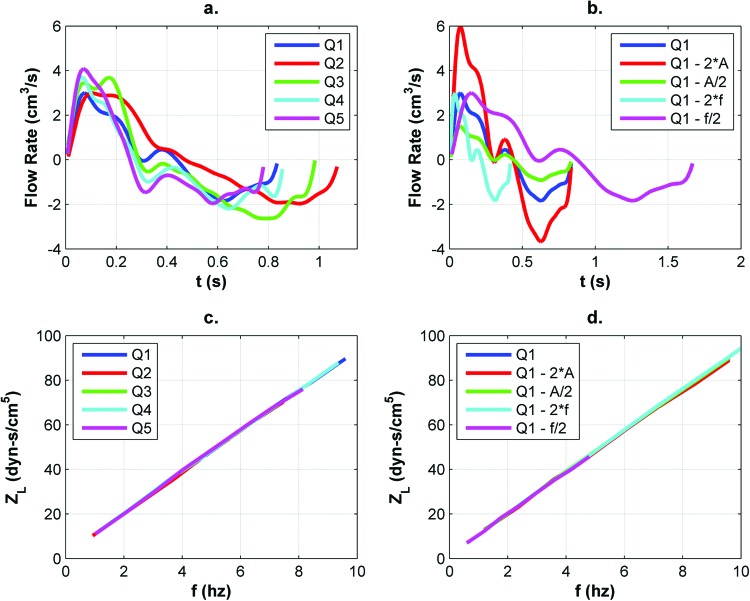
Subject-specific volume flow waveforms were only available for 15 of the 23 cases in this study. To test whether it was feasible to use nonsubject-specific flow waveforms for the remaining eight cases, a preliminary study was conducted to assess the dependence of the LI calculation on the shape of the inlet boundary condition waveform. This was accomplished by varying the waveform in each of nine CFD simulations conducted on the same SSS model. The nine different boundary conditions were as follows: five subject-specific CSF flow waveforms (Q1–Q5 in Fig. 3(a)); four variants of the Q1 waveform altered by doubling (2 × A) and halving (A/2) the waveform amplitude and doubling (2 × f) and halving (f/2) the waveform fundamental frequency. Sensitivity to the shape of the inlet boundary condition waveform was assessed by computing and comparing LI for each of the nine simulations.

Fig. 3.

(a) CSF flow waveforms (Q#) from five different subjects and (b) example waveform with modified properties used to demonstrate that LI values (c and d), integrated from the sum of Z_L values on the y-axis, were independent of flow waveform shape over the range of frequencies analyzed (A and f represent waveform amplitude and frequency, respectively)

For the nine waveform independence simulations, Z_L values for each harmonic between 1 and 8 Hz were in agreement (Fig. 3). Relative standard deviation for the nine values of LI was 0.3%, which demonstrated that that LI was only weakly dependent on the shape, amplitude, and fundamental frequency of the CSF input waveform. Hence, it was assumed that a nonsubject-specific CSF flow waveform could be used to analyze impedance in the 15 SSS models for which subject-specific waveforms were unavailable.

Modeling Repeatability Assessment.

Repeatability of the SSS modeling methodology was assessed by obtaining MRI measurements on the same healthy subject at all three MRI measurement sites. This was important as cerebellar tonsil position may vary with neck orientation. Also, the anatomy imaging parameters were slightly different at each imaging site (e.g., different slice spacing and in-plane resolution) based on the spatial resolution capabilities of each MR system. For the healthy subject, SSS models were reconstructed from the images acquired at each site and CFD simulations were performed. Intersite variability was assessed by comparing LI for the three models. Values of LI obtained from the three simulations were 246, 251, and 286 dyn/cm [5] for SSS models from sites 1, 2, and 3, respectively. This showed that LI computed by the methods of this study may be as much as 16% different if a particular subject were imaged at a different site or on a different day.

Statistical Analysis.

Distributions of LI in each group were verified for normality and unequal variances. A one-tailed two-sample t-test was then used to test the null hypothesis that mean LI was equal in the CMI patient and healthy volunteer groups. Assuming a significance level of 0.05 and minimum group size of eight, the power of the statistical comparison was estimated to be approximately 0.9. Measured CTH values for each subject were compared in a similar manner. Outliers in each group were defined as values outside the range (Q1-1.5*IQR, Q3 + < 1.5*IQR), where Q1 and Q3 were the data points at the 25th and 75th percentiles of the distribution of each parameter, respectively, and IQR, the interquartile range, was Q3–Q1. Finally, linear regression analysis was used to assess the relationship between LI and CTH.

Results

Study Population.

Mean ages in years for the CMI patient and healthy volunteer groups were 38 with a range of 17–58 and 29–47 years, respectively. The gender divisions (female/male) were 15/0 and 3/5 for the CMI patient and healthy volunteer groups, respectively. Due to limited subject availability, only female CMI patients were available to participate in the study; thus, gender was not controlled for.

Longitudinal Impedance.

Mean values of LI in dyn/cm⁵ were 551 ± 66 and 220 ± 17 for the CMI patient and healthy volunteer model groups, respectively. Statistical analysis showed that mean LI in the CMI patient model group was significantly higher than in the healthy volunteer model group (p< 0.001). However, there was a large range of values (216–1122 dyn/cm⁵) in the LI distribution for the CMI patient models (Fig. 4(a)) and no clear stratification of symptomatic and asymptomatic CMI models. The two lowest values in the LI distribution for CMI patients fell within the range of values (157–303 dyn/cm⁵) for the healthy volunteer group. These data points were from one symptomatic CMI model (290 dyn/cm [5]) and one asymptomatic CMI model (216 dyn/cm⁵).

Fig. 4.

(a) Distribution and (b) data spread of LI compared with (c) distribution and (d) data spread of CTH for the healthy volunteers (HV) and CMI patients (CMI). Note, + indicates a statistical outlier in (a) and (c); the order of data points in (b) and (d) is identical.

Cerebellar Tonsil Herniation.

Mean values of CTH in mm were 9.0 ± 1.1 and −0.4 ± 0.5 in the CMI patient and healthy volunteer groups, respectively. Statistical analysis showed that mean CTH in the CMI patient group was significantly higher than in the healthy volunteer group (p < 0.001). Similar to LI there was a large range of CTH values (3.7–20.8 mm) in the CMI patient group distribution and no clear stratification of symptomatic and asymptomatic CMI patients. One statistical outlier was identified in each of the CMI patient and healthy volunteer groups. Recomputing the statistical test with the outliers excluded did not affect the results. The ICC for the two sets of CTH measurements was 0.9, indicating good inter-operator agreement.

Relationship Between LI and CTH.

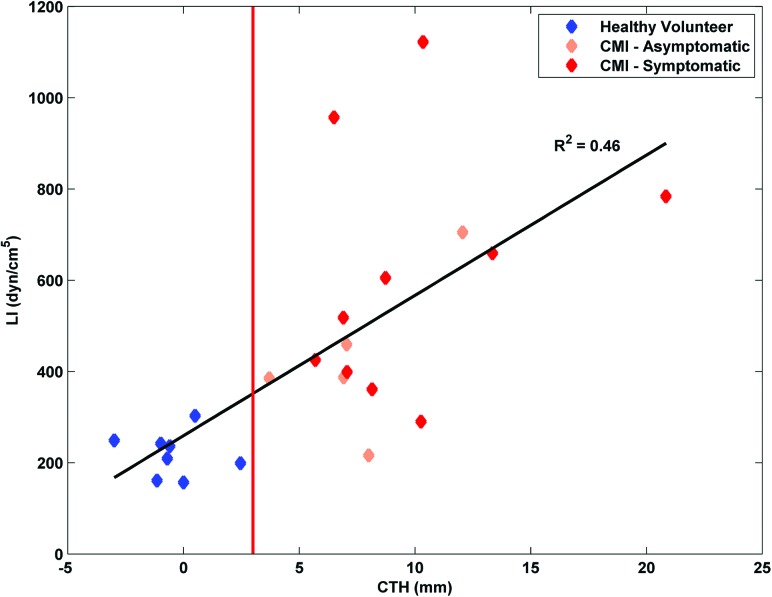
Linear regression analysis revealed that the relationship between LI and CTH was weakly correlated (R ²= 0.46, p<0.001). In general, LI was higher in cases with larger CTH as expected (Fig. 5), but there was also greater dispersion in LI among cases with larger CTH.

Fig. 5.

Relationship between CTH and LI is shown to be weakly correlated. The red line denotes the 3 mm minimum cutoff above which a subject would typically be considered anatomically positive for CMI.

Discussion

This study presents, for the first time, LI as a metric for comparing the biomechanical environment in the SSS of symptomatic and asymptomatic CMI patients and healthy volunteers. Our approach was to use CFD methods to assess severity of the partial blockage to CSF motion in terms of the magnitude of the impedance to pulsatile CSF motion and to compare those values with the commonly used clinical morphometric parameter, CTH. The results showed that mean LI was significantly higher in CMI patients compared to controls. Likewise, mean CTH was significantly larger for CMI patients. Thus, CMI patients stratified from healthy volunteers by both parameters. However, the relationship between LI and CTH in both groups was weakly correlated, suggesting that CTH and LI give different information about the pathoanatomy in CMI.

Importance of Dynamic Parameters to Assess CMI.

From the regression analysis, it was shown that CTH was a poor predictor of the impedance to the pulsatile component of CSF motion resulting from the stenosis at the CVJ caused by CTH. Thus, it may be that static morphometrics oversimplify the complex partial blockage to CSF motion present in CMI. Because of this, parameters that are based on dynamic analysis, such as LI, may be useful to quantify biomechanical differences between CMI states. Further, utilization of novel parameters that capture the dynamic aspects of the CVJ in CMI could lead to more complete characterization of CMI pathoanatomy and pathophysiology and potentially lead to new treatment options.

Considering CMI from a hydrodynamics perspective, CSF pressure gradients [4], also termed pressure “dissociation” by the medical community [12,13], are the driving force from which tissue damage and CMI symptomatology precipitate. Pressure gradients are not easily measured in vivo, but in principle are related to (a) impedance to CSF motion, (b) CSF velocities, (c) neural tissue motion, and (d) craniospinal compliance. Further, CMI has a variety of underlying causes (e.g., secondary to hydrocephalus, tethered spinal cord, spina bifida, etc.). Thus, we do not expect better characterization of CMI from a single “silver bullet” parameter but rather from a combination of biomechanical factors.

CTH Measurement Variability.

Though an ICC of 0.9 suggested good interoperator agreement for the CTH measurements, the maximum interoperator differences in the CTH measurements were 4.6, 6.7, and 4.8 mm for the symptomatic, asymptomatic, and healthy volunteer groups, respectively. Hence, the same CMI patient could be considered a relatively mild herniation or much more severe depending on the operator. This difference was likely due to the complexity in making CTH measurements, as described earlier. Each step involved in CTH measurement can introduce error. Thus, it was not surprising that some large disagreements between data points were observed. A study is currently underway by our group to examine CTH measurement accuracy and repeatability.

Symptomatic versus Asymptomatic CMI.

From a clinical perspective, the difference between a symptomatic and an asymptomatic CMI patient is not always distinct. Our group is interested in identifying a biomechanical parameter or set of parameters that could stratify symptomatic from asymptomatic CMI patients in cases that have moderate CTH or CMI that could be considered anatomically “borderline.” For the CMI patients in this study with CTH in the range 3–9 mm there was a great deal of overlap in LI (Fig. 5). Mean LI for the symptomatic (n = 10) and asymptomatic (n = 5) CMI subgroups was 612 ± 86 and 430 ± 79 dyn/cm⁵, respectively. Using the same statistical test as the general groups, the difference was not statistically significant (p = 0.073) despite a notable difference in the means. However, the power of this post hoc test was only 0.3 and the difference between the subgroup means may have been incidental.

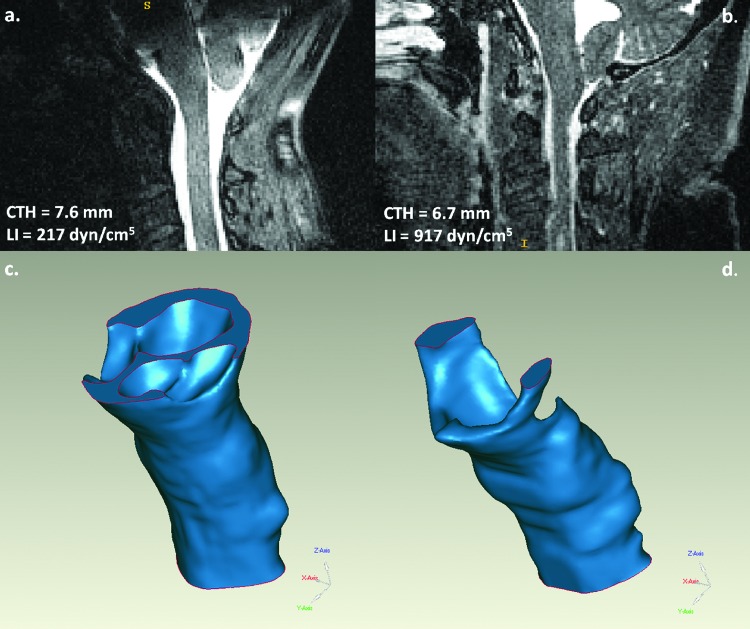
Most cases followed the general trend of the regression line in Fig. 5. However, four CMI cases highlight differences between LI with similar values of CTH. Two cases that could be considered anatomically borderline (CTH = 6.7 versus 7.6 mm) are shown in Fig. 6. From both the midsagittal MRI images (Figs. 6(a) and 6(b)) and the reconstructed SSS models (Figs. 6(c) and 6(d)), it was apparent that the SSS was more constricted in the symptomatic CMI case in which LI was 4.2 times higher (216 versus 917 dyn/cm⁵). Similarly, two symptomatic CMI cases were measured to have similar CTH (10.3 versus 10.4 mm), but LI was 3.9 times higher in the second patient (290 versus 1122 dyn/cm⁵). In both instances, LI captured a feature of the pathoanatomy that was not obvious from the static morphometric measurement alone.

Fig. 6.

(a) Midsagittal MRI image for an (a) asymptomatic CMI patient and (b) symptomatic CMI patient and (c and d) 3D models for each, respectively. CTH was similar for the two cases. However, LI in the symptomatic patient was 4.2 times greater than the asymptomatic patient.

It should be noted that classification of patients as symptomatic or asymptomatic in neurosurgical evaluation was difficult; the reporting of symptom severity by the patients can be highly subjective (e.g., patients have different pain thresholds). Thus, asymptomatic patients may have similar biomechanics to symptomatic patients and could progress to become symptomatic. In future work, it would be helpful to consider the natural history of LI in CMI patients to determine what level of measurement variability exists and if LI may have predictive value for progression to a symptomatic CMI state. In addition, biomechanics is likely not the only factor involved in symptoms.

Limitations.

The gender disparity in the CMI patient group may have introduced some bias into both the LI and CTH results. CTH is typically greater in females (Fig. 2) that in turn may have resulted in higher mean LI in the symptomatic group. Considering the importance of age and gender on average CTH values, it would be prudent to use stricter gender matching in future work to reduce the effect of any confounding factors, though the feasibility of such restrictions must be considered in the context of the limited patient availability. Likewise, we were unable to control for additional factors that could influence CVJ anatomy, such as height, weight, or body mass index.

Geometric reconstructions of the SSS were performed by a single operator and only one case was analyzed for LI repeatability. Ideally, repeatability of the geometric reconstruction methodology would be assessed for multiple operators and repeatability of the end-to-end model reconstruction and impedance analysis for image sets from different sites would be assessed on multiple pilot subjects to quantify the impact of small differences in the SSS models. Also, the tops of the SSS models could not be perfectly aligned to the McRae line and, thus, neck angulation could not be accounted for. However, all patients were imaged using a head coil, so any neck angulation in the SSS models was consistent.

LI was computed using pressure drop over the first 25 mm of the SSS models and integrated from the 1–8 Hz to have a consistent metric by which to compare models. While the pressure drop length was justifiable in the context of a clinical “worst case scenario,” it is not known whether 25 mm was the optimal distance over which to analyze LI. That is, some finer details of the spatial distribution of pressure drop may have been missed by only considering the pressures at the two endpoints of the region of interest. Similarly, the frequency range was justifiable as it accounts for most of the signal power in the flow waveforms that drive CSF motion, but it was not parametrically optimized. Though it is outside the scope of this study, both the pressure drop distance and frequency range used to compute LI could be parametrically optimized. For example, pressure drop distance could be optimized by analyzing the spatial distribution of LI near the CVJ or by using a relative length based on CTH, though the latter would be difficult to normalize.

CFD simulations were performed using the assumption that the inner and outer walls of the SSS (i.e., the spinal cord and dura) were rigid. It has been shown that CFD may underestimate the velocity field in rigid-wall SSS models compared to velocities observed in vivo in the SSS using 4D pcMRI [10]. Thus, pressure gradients and, consequently, LI may have been underestimated by this particular CFD methodology. Further, bulk neural tissue displacement in the spinal cord and cerebellar tonsils throughout the cardiac cycle in the rostrocaudal direction ranging from 0 to 0.6 mm has been documented for CMI patients and healthy subjects [10, 24–26, 29]. This data suggest that elastic elements could be added to the boundary conditions that in turn may impact the pressure and velocity fields. With regard to impedance, the methodology described in this study was concerned with impedance to the main carrier frequencies (1–8 Hz) of the inlet boundary condition waveforms. It is unclear how analyzing impedance in this frequency range would impact the rigid wall assumption. Thus, the assumption of a rigid-walled SSS should be examined in more detail in future studies.

The ICC of 0.9 between the two measurement sets indicated good intraoperator agreement. However, only two sets of measurements were used and repeatability could suffer from the addition of more operators with varying levels of experience in making CTH measurements. For example, different operators may measure CTH on different images from the set, depending on which they perceive to capture the lowest tonsil descent.

Conclusion

Diagnosis and treatment of CMI patients may benefit from an assessment of their subject-specific biomechanical environment. This work investigates the use of LI as a biomechanical parameter to assess the extent of CVJ stenosis in CMI patients. LI was found to be significantly higher in CMI patients compared to controls. LI and CTH were found to have a weakly linear relationship, suggesting that different morphometric measurements and/or biomechanical parameters may be necessary to characterize the pathoanatomy of CMI. Future work in a larger and age/sex matched study population is planned to fully understand the potential, if any, of LI as a clinical diagnostic tool for CMI.