Short abstract
This study introduces a framework for co-simulating neuromuscular dynamics and knee joint mechanics during gait. A knee model was developed that included 17 ligament bundles and a representation of the distributed contact between a femoral component and tibial insert surface. The knee was incorporated into a forward dynamics musculoskeletal model of the lower extremity. A computed muscle control algorithm was then used to modulate the muscle excitations to drive the model to closely track measured hip, knee, and ankle angle trajectories of a subject walking overground with an instrumented knee replacement. The resulting simulations predicted the muscle forces, ligament forces, secondary knee kinematics, and tibiofemoral contact loads. Model-predicted tibiofemoral contact forces were of comparable magnitudes to experimental measurements, with peak medial (1.95 body weight (BW)) and total (2.76 BW) contact forces within 4–17% of measured values. Average root-mean-square errors over a gait cycle were 0.26, 0.42, and 0.51 BW for the medial, lateral, and total contact forces, respectively. The model was subsequently used to predict variations in joint contact pressure that could arise by altering the frontal plane joint alignment. Small variations (±2 deg) in the alignment of the femoral component and tibial insert did not substantially affect the location of contact pressure, but did alter the medio-lateral distribution of load and internal tibia rotation in swing. Thus, the computational framework can be used to virtually assess the coupled influence of both physiological and design factors on in vivo joint mechanics and performance.
Keywords: forward dynamics, computational biomechanics, knee contact forces, validation, muscle forces
Introduction
The magnitude and location of joint contact forces are important to consider when assessing the causes and treatment of knee pathologies [1]. Since internal loads cannot normally be measured in vivo, computational models are needed to estimate the joint contact forces that can arise during functional tasks such as walking. The traditional modeling approach involves two steps. A multibody neuromuscular dynamics model is used in the first step to estimate the muscle and net joint forces associated with a task performance [2,3]. These forces are subsequently applied as boundary conditions to a knee mechanics model to estimate ligament forces and the distribution of joint contact loads [4-6]. However, this serial simulation approach may not capture two-way interactions that can exist between musculoskeletal dynamics and internal joint mechanics. In particular, musculoskeletal models used to simulate movement typically use a simplified knee model with pre-assumed constraints on secondary knee motions [7-9]. This approach assumes that contact forces do not induce moments about the primary joint axis and that muscle forces are not important contributors to secondary motion constraints [10]. However, the validity of such assumptions was questioned in a recent study that showed that muscle force estimates are sensitive to the constraints included in the knee model [10]. Hence, it would seem preferable to co-simulate neuromuscular dynamics and knee joint mechanics, such that the muscle, contact, and ligament loads are considered within the context of whole body movement dynamics.
The co-simulation of movement and localized tissue mechanics represents a computationally demanding problem that has only recently been explored in the biomechanics literature [11,12]. A major challenge involves the computation of appropriate muscle controls that drive a model to emulate coordinated movement. Prior studies have pre-assumed the muscle excitation patterns [13] or used dynamic optimization to compute muscle excitations that achieve a desired performance criterion [11]. While dynamic optimization is an attractive approach, obtaining a global optimum can be very challenging and require many iterations to converge [14].
We previously introduced a computed muscle control (CMC) algorithm which uses feedforward and feedback control to modulate muscle excitations to track measured joint angle trajectories [15,16]. The CMC algorithm was originally formulated to work on models in which all joints have constrained translational degrees of freedom (e.g., a gimbal joint). Translational constraints allow for instantaneous force transmission across the joint and, hence, a quantitative assessment of a muscle’s capacity to induce movement throughout the body. However, in a dynamic multibody model with 6 degree-of-freedom (d.o.f.) joints, time is required to deform the soft tissues and thereby transmit forces across a joint. Hence, the first objective of this study was to extend the CMC algorithm to co-simulate musculoskeletal dynamics and joint mechanics when using models that include 6 d.o.f. joints spanned by soft tissues. Second, we sought to assess the veracity of the co-simulation framework by comparing the model predictions of knee contact forces to in vivo measures obtained with an instrumented total knee joint replacement during walking [17]. Finally, we demonstrate the capacity of the framework to assess the sensitivity of contact loading patterns to variations in frontal plane knee alignment, which is an important consideration in joint replacement procedures.
Methods
Experimental Data.
The experimental data used in this study were collected as part of the 4th grand challenge competition for predicting in vivo knee loads [17]. We simulated the gait of a male subject (age 88 yr, mass = 68 kg, and height = 1.66 m) who received an instrumented total knee replacement on the right side for primary osteoarthritis. The data downloaded from the competition website2 included the knee replacement geometry, post-operative CT scans, electromyographic data, whole body kinematics, ground reactions, and tibiofemoral contact forces during overgound walking. Medial and lateral tibiofemoral contact forces were delineated using four uniaxial force transducers embedded in the tibial tray [18].
Knee Mechanics Model.
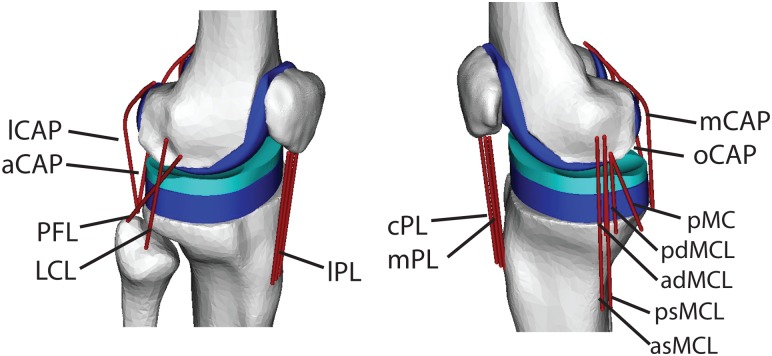
We created a 3-body model of knee mechanics that included a 1 d.o.f. patellofemoral joint and a 6 d.o.f. tibiofemoral joint [4,19]. Superior patella translation was the independent degree of freedom for the patellofemoral joint. The patellofemoral angles and anterior and lateral patella translation were defined as constrained functions of superior translation, such that the patella could translate and rotate within a constrained path relative to the femur [9]. Seventeen knee ligament bundles were included in the model (see Fig. 1): the patellar ligament (medial, mid, and lateral bundles), medial collateral ligament ((MCL), 5 bundles), lateral collateral ligament (LCL), popliteofibular ligament (PFL), posterior cruciate ligament (anterior and posterior bundles), posterior capsule (4 bundles), and the illiotibial band (ITB). The anterior cruciate ligament (ACL) was not included since it was resected in the subject whose gait was simulated [17]. Ligament geometry data was not available for the test subject, thus ligament origins and insertions were based on nominal descriptions in the literature [20-25]. Wrapping objects were affixed to the femur to represent the collateral ligaments wrapping about the condyles. The nonlinear relationship between the ligament force and strain was represented by
Fig. 1.
The three body knee mechanics model included 17 ligament bundles acting about the tibiofemoral and patellofemoral joints. Contact pressure between the femoral component and tibial insert was computed via an elastic foundation model. Ligament abbreviations are given in Table 1.
| (1) |
where (=0.03) is the transition strain and k is the ligament stiffness expressed in units of force per unit strain. At any time point, the ligament bundle strain was computed from the current length () and slack length () of the ligament. The slack length of each bundle was computed by scaling the ligament length in a reference configuration with its assumed reference strain
| (2) |
The ligament stiffness and reference strains were adapted from representative values used in comparable knee models in the literature [4,19] (see Table 1).
Table 1.
Ligament stiffness and reference strains used in the knee mechanics model. A negative reference strain assumes that the ligament is slack in the reference posture
| Ligament a | Stiffness (N) b | Reference strain c |
|---|---|---|
| aPCL | 3000 | −0.10 |
| pPCL | 1500 | −0.05 |
| asMCL | 1500 | 0.02 |
| psMCL | 1500 | 0.02 |
| adMCL | 1000 | 0.02 |
| pdMCL | 1000 | 0.02 |
| pMC | 2000 | 0.02 |
| LCL | 4000 | 0.02 |
| PFL | 2000 | −0.05 |
| aCAP | 1500 | 0.02 |
| lCAP | 2000 | 0.02 |
| oCAP | 1500 | 0.02 |
| mCAP | 2000 | 0.02 |
| mPL | 4000 | 0.00 |
| cPL | 4000 | 0.00 |
| lPL | 4000 | 0.00 |
| ITB | 5000 | 0.00 |
Notation: aPCL/pPCL, anterior and posterior cruciate ligament; asMCL and ps MCL, anterior and posterior superior medial collateral ligament; adMCL and pdMCL, anterior and posterior deep medial collateral ligament; pMC, posteromedial capsule; LCL, lateral collateral ligament; PFL, popliteofibular ligament; aCAP, lCAP, oCAP, and mCAP, arcuate, politeal lateral, medial, and oblique politeal bundles of posterior capsule; mPL, cPL, and lPL, medial, central, and lateral patellar ligament; ITB, ilitotibial band.
Stiffness is expressed in units of force per unit strain.
Reference strains are used to compute the ligament lengths in the upright reference configuration.
The geometry of the implanted femoral component and tibial insert were represented by triangulated polygon meshes of the subject’s joint replacement. The tibiofemoral contact loads were computed using an elastic foundation model in which pressure was assumed to be a function of the depth of penetration of intersecting bodies [27]. Intersecting regions between the femoral and tibia surface geometry were detected using ray casting in conjunction with hierarchical bounding volumes. To do this, the femoral surface was first subdivided into a tree of geometrically coherent subsections and tight-fitting oriented bounding boxes (OBB) were fit over each subdivision [26]. A normal ray was then cast for each triangle of the tibia and a ray-OBB intersection test was performed with the largest OBB. If intersected, the ray-OBB tests continued to subhierarchical levels, ultimately identifying the leaf node (single triangle) of the femoral surface intersected by the ray [26,28-30]. The penetration depth d was defined as the distance from the center of a tibia triangle to the point at which a normal ray intersected the corresponding femoral leaf node. The contact pressure p on the tibia surface triangle was then calculated using a linearized version of an elastic foundation model [27]
| (3) |
where h is the insert thickness, ν is Poisson’s ratio (=0.46) and E is Young’s modulus (=463 MPa) for a ultrahigh molecular weight polyethylene tibial insert [31]. The force acting on the tibia surface triangle was obtained by multiplying the pressure by the triangle cross-sectional area and applying the force normal to the triangle. Equal and opposite forces were applied at the same point in the femoral surface.
Lower Extremity Musculoskeletal Model.
We started with a generic lower extremity musculoskeletal model [7] that included the pelvis, right femur, tibia, patella, and foot segments. The hip was represented by a 3 d.o.f. ball-and-socket joint and the ankle as a 1 d.o.f. joint that allowed for dorsi- and plantarflexion. We replaced the 1 d.o.f. knee in the generic model with the 3-body knee model described earlier. The femoral component surface geometry was positioned such that it closely aligned with the condyles of the generic model’s femur. The tibia insert surface geometry was then positioned in the tibia reference frame so that it closely aligned with the femoral component when the model was in an upright standing posture. The lower extremity model was scaled to represent the subject. Each body segment was scaled such that anatomical landmarks were optimally aligned with anatomical marker positions recorded with the subject standing upright. During scaling, the frontal plane knee angle was fixed at 4 deg valgus, as was measured from the post-operative CT scans of the subject.
The model included 44 Hill-type musculotendon units acting across the hip, knee, and ankle joints [7]. The input to each muscle was an excitation that could vary between 0 and 1. Excitation-to-activation dynamics were represented by a bilinear differential equation with activation and deactivation time constants of 15 and 40 ms, respectively. The contraction dynamics was represented by a nonlinear differential equation describing the interaction of tendon compliance and the force-length-velocity properties of muscle [33]. The lower extremity model was implemented in SIMM [34], with the Dynamics Pipeline (Musculographics Inc., Santa Rosa, CA) and SD/Fast (Parametric Technology Corp., Needham, MA) used to generate code describing the multibody equations of motion.
Computed Muscle Control Algorithm.
With the muscles and knee model included, the multibody dynamic equations of motion are of the form
| (4) |
where is the mass matrix, is a vector of forces arising from gravity, are forces arising from the Coriolis and centripetal accelerations, and represents the generalized forces arising from external loads or prescribed accelerations. The force vectors arising from muscle (), ligament (), and articular contact () are scaled by the moment arm matrices , , and , respectively. The generalized coordinates include the 6 d.o.f. pelvis motion (translation and orientation) relative to ground, three hip rotation angles, three tibiofemoral angles, three tibifemoral translations, superior patella translation, and ankle dorsiflexion. The pelvis, hip, and tibiofemoral angles are expressed as a Cardan rotation sequence consisting of flexion, adduction, and then rotation about the long axis of the distal segment [35].
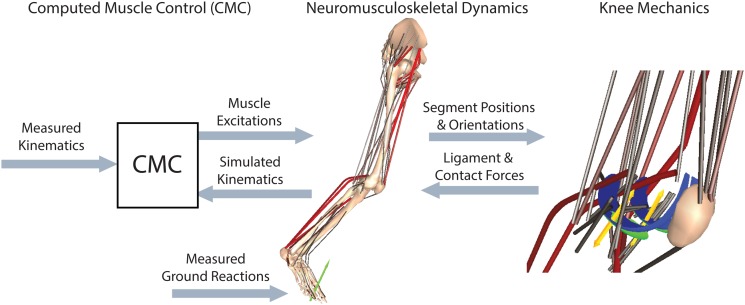
A computed muscle control (CMC) algorithm was used to determine the muscle excitations needed to drive the model to closely track the measured hip flexion, hip adduction, knee flexion, and ankle dorsiflexion trajectories (see Fig. 2). The CMC is a feedforward-feedback controller that uses the experimentally measured accelerations () together with current errors in generalized speeds () and coordinates () to compute a set of desired generalized accelerations in the degrees of freedom being tracked
Fig. 2.
A computed muscle control (CMC) algorithm was used to modulate the lower limb muscle excitations such that the simulation closely tracked the measured hip, knee, and ankle angles. At every time step, the tibia, patella, and femur positions were used to ascertain the tibiofemoral contact and ligament forces. These forces were then applied within the forward dynamic simulation of the neuromusculoskeletal model.
| (5) |
where and are the velocity and position feedback gains, respectively.
The original formulation of the CMC was implemented for multibody models in which all joints had constrained translational degrees of freedom, allowing for instantaneous load transfer across the joint to occur. Such a formulation allows for a muscle’s potential to induce motion, defined as the generalized accelerations generated per unit muscle force [36], to be directly computed from the whole body equations of motion. Computationally, muscle potential is determined by applying a unit muscle force and then solving the equations of motion (see Eq. (4)) for the resulting accelerations (). However, in the case of a 6 d.o.f. tibiofemoral joint, it is not feasible for a muscle proximal to the knee to instantaneously generate segment accelerations distal to the knee. Time is needed for ligament and contact surface deformations to occur, such that force is transmitted across the joint. To handle this challenge, we adapted CMC to compute a muscle’s potential to induce joint accelerations assuming the knee translational accelerations are instantaneously zero. This assumption was used since contact and ligament forces restrict the knee translations to relatively small magnitudes. A zero translational acceleration constraint therefore allowed for instantaneous force transmission across the knee and, thus, provided an estimate of the effect of ligament and contact forces on joint rotational accelerations. To implement the constraint, we first defined a vector as the subset of generalized coordinates associated with the tibiofemoral (, , ) and patellofemoral () translational degrees of freedom
| (6) |
We used a finite difference technique to estimate a sensitivity matrix describing the dependency of generalized accelerations to variations in the knee translational degrees of freedom
| (7) |
These sensitivities were then used to determine virtual perturbations to the translation knee coordinates that, in conjunction with a unit muscle force, would negate translational knee accelerations. This assumption was applied for each muscle i by solving the following linear equations
| (8) |
| (9) |
for and . The vector is an estimate of the potential of muscle i to induce accelerations throughout the limb per unit muscle force.
The muscle potential acceleration information was used to update muscle controls every T = 0.01 s within a simulation. When updating controls, we first determined muscle force increments that, when added to the current muscle forces, would induce desired accelerations in the tracked degrees of freedom
| (10) |
In Eq. (10), n is the number of muscles and represent the generalized accelerations resulting from current muscle forces, ligament forces, contact forces, external force and gravity acting on the system. Muscle redundancy was resolved by simultaneously minimizing a cost function J which, in this study, was taken as the sum of muscle-volume (V) weighted squared activations (a) [37]
| (11) |
where muscle activations are determined based on the force-length-activation properties of muscle [15]. Excitations were then determined from the activations by inverting activation dynamics. After computing the controls, the skeletal equations of motion, muscle activation dynamics, and contraction dynamics were integrated forward using a forward-backwards implicit numerical integration routine [32]. The control process was then repeated every T = 0.01 s throughout a gait simulation.
Simulations of Knee Mechanics During Gait.
We generated simulations of five overground walking trials with an average gait speed of 1.25 (±0.02) m/s. For each gait trial, a global optimization inverse kinematics routine was first used to determine the pelvis translations, pelvis rotation, hip angles, knee flexion, and ankle dorsiflexion that best agreed with the measured pelvis and lower extremity marker trajectories. At this stage, the knee abduction angle was maintained at 4° while the tibiofemoral internal rotation and translations were assumed to be constrained functions of knee flexion as defined in the generic lower extremity model of Arnold et al. [7].
We then used the CMC algorithm to compute muscle excitations that drove the dynamic multibody model to track the measured hip flexion, hip adduction, knee flexion, and ankle dorsiflexion trajectories over a gait cycle. Measured ground reactions were applied directly on the feet [15], while pelvis generalized coordinates were prescribed to track measured values. The tibiofemoral translations, patellofemoral translation, tibiofemoral internal rotation, and tibiofemoral adduction were unconstrained in the dynamic simulations and, thus, evolved naturally as a function of the external and internal loads acting on the system. We compared the timing of the muscle excitations to temporal patterns of electromyographic data that were recorded from the subject during the simulated walking trials. Model predictions of tibiofemoral contact forces acting in the medial and lateral compartments were quantitatively compared to in vivo measures using Pearson’s correlation, the coefficient of determination, the average difference in the force predictions (bias), the standard deviation of the force prediction errors (precision), and the root-mean-squared (RMS) error. We also evaluated the agreement between the medial, lateral, and total contact forces at the time of the two peak contact forces that arise in the stance phase of normal gait.
Sensitivity of Model Predictions to Frontal Plane Alignment.
We performed a sensitivity study analyzing the dependence of tibiofemoral loading patterns to variations in frontal plane alignment between the femoral component and tibia insert. To do this, we first re-ran the inverse kinematics routine with fixed knee valgus angles 2 deg greater and less than that measured (4 deg valgus) on the CT scans. For each case, we re-oriented the femoral component and tibia insert by counter-rotating each surface by 1 deg in the coronal plane, such that they were aligned and just contacting with the model in the upright standing configuration. We then used the CMC to regenerate dynamic simulations using the re-aligned models to track the gait kinematics. Note that tibiofemoral adduction and rotation were not fixed in these forward dynamic simulations, but evolved as a result of tibiofemoral contact and internal soft tissue loadings. The effect of alignment on loading was quantitatively evaluated by comparing the tibiofemoral contact force and pressure patterns at heel strike and the time of the first and second peak of the tibiofemoral contact force.
Results
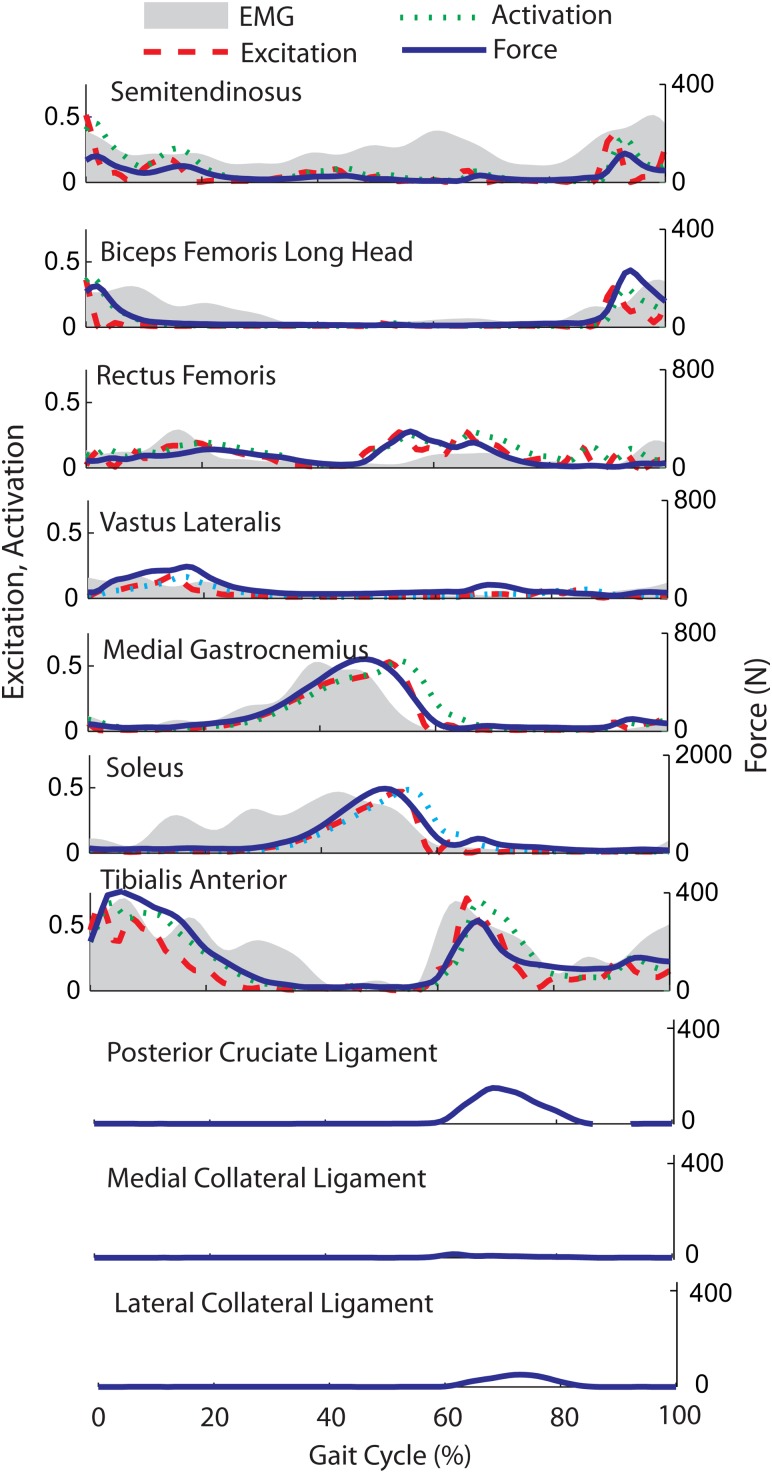
The modified CMC algorithm modulated muscle excitation patterns (see Fig. 3) to successfully track the measured hip flexion, hip adduction, knee flexion, and ankle angle trajectories with average root-mean-square errors of 0.4 deg, 0.3 deg, 0.9 deg, and 1.0 deg respectively. Simulated posterior cruciate and collateral ligament forces were relatively small (generally <100 N), with peak magnitudes arising during swing phase (see Fig. 3).
Fig. 3.
Comparison of average electromyographic (EMG) data with simulated muscle excitations, activations, and forces over a gait cycle. Reasonably good temporal agreement is seen for the vastus lateralis, medial gastrocnemius, soleus, and tibialis anterior. Normal bursts of hamstring activity (semitendinosus, biceps femoris long) in late swing and early stance are also predicted, though the subject exhibited greater medial hamstring EMG activity throughout the gait cycle. Rectus femoris EMG activity near toe-off is slightly lower than that used in the model to initiate swing limb motion between 50% and 60% of the gait cycle. Simulated posterior cruciate and collateral ligament forces were greatest in mid-swing.
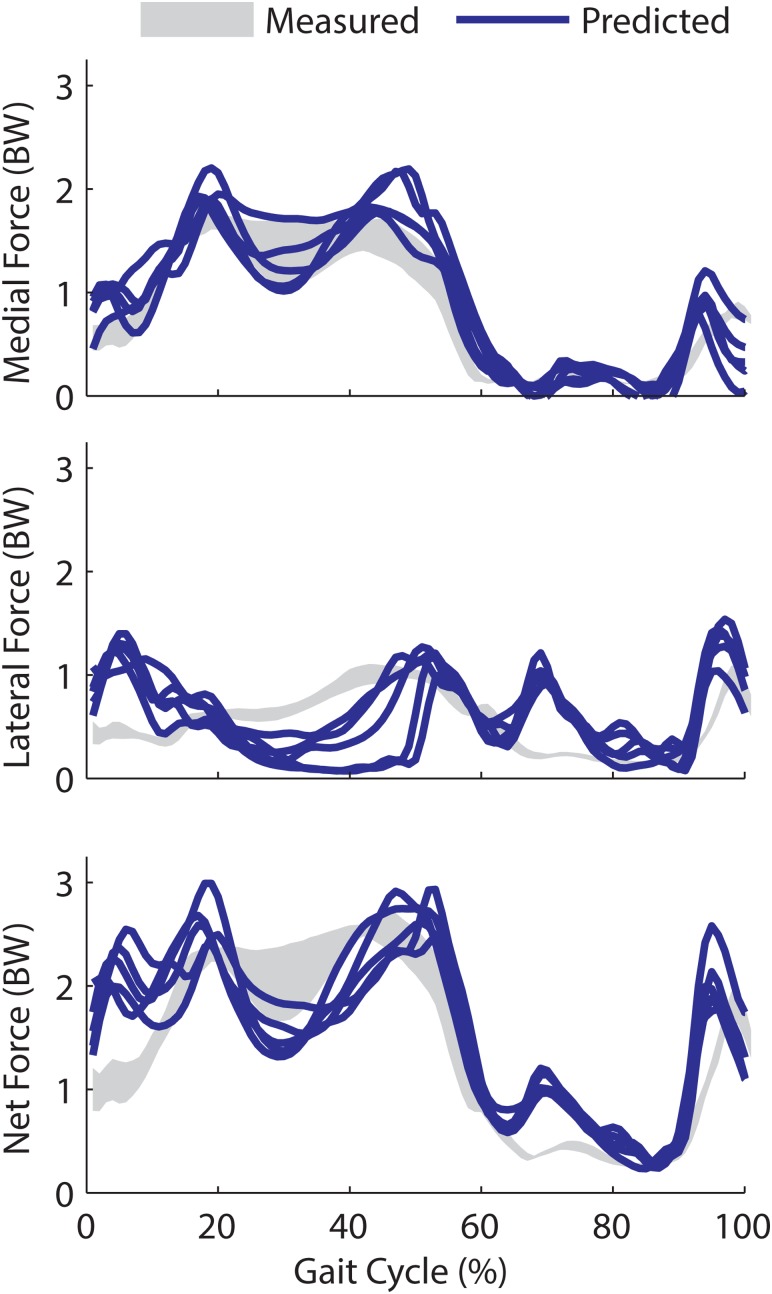
The model predictions of the tibiofemoral contact forces exhibited the characteristic double peak in stance, with a greater load borne on the medial side (see Fig. 3). The temporal patterns of medial and total tibiofemoroal contact forces agreed well with the measurements, with an average Pearson R 2 of 0.87 and 0.68, respectively. Temporal patterns of lateral forces were not as well predicted (R 2 = 0.07), with the model overestimating lateral contact forces in early stance and mid-swing. The magnitude of medial contact forces estimates agreed well with measurements, with an average root-mean-squared (RMS) error of 0.26 body weight (BW) and a slight bias (+0.09 BW) to overpredicting the loads (Table 2). Errors in lateral force estimates were slightly larger, with average RMS errors of 0.42 BW (see Fig. 4). The first peak in the estimated medial load averaged 1.95 BW, which was 13% greater than the experimental measures. The second medial peak estimate was 1.6 BW, which was 4% above the average measurements. The first and second total peak forces of 2.76 and 2.71 BW were 17% and 5% greater than the corresponding peak force measurements.
Table 2.
Agreement (mean ±1 s.d.) between measured and model-predicted tibiofemoral joint contact forces over five trials of normal walking
| Medial | Lateral | Total | |||||
|---|---|---|---|---|---|---|---|
| R 2, Pearson's | 0.87 | (0.03) | 0.07 | (0.08) | 0.68 | (0.08) | |
| R 2, Coefficient of determination | 0.81 | (0.05) | −1.29 | (0.92) | 0.60 | (0.09) | |
| Bias (BW) | 0.09 | (0.02) | 0.06 | (0.08) | 0.15 | (0.09) | |
| Precision (BW) | 0.24 | (0.03) | 0.42 | (0.08) | 0.48 | (0.08) | |
| RMS error (BW) | 0.26 | (0.03) | 0.42 | (0.08) | 0.51 | (0.07) | |
| Peak 1 (BW) | Predicted | 1.95 | (0.08) | 0.81 | (0.31) | 2.76 | (0.32) |
| Measured | 1.73 | (0.09) | 0.65 | (0.06) | 2.37 | (0.12) | |
| Error | 0.22 | (0.10) | 0.17 | (0.34) | 0.39 | (0.34) | |
| Peak 2 (BW) | Predicted | 1.60 | (0.17) | 1.11 | (0.13) | 2.71 | (0.17) |
| Measured | 1.56 | (0.14) | 1.05 | (0.06) | 2.60 | (0.10 | |
| Error | 0.04 | (0.23) | 0.06 | (0.14) | 0.11 | (0.20) | |
Fig. 4.
Model-predicted medial, lateral, and total tibofemoral contact forces (expressed in units of body weight (BW)) over five experimental walking cycles. Experimentally measured contact forces represent the mean (+/-1 s.d.) over the same five repeat walking cycles. Peak lateral contact forces are of comparable magnitude to experimental forces in late stance, but the model predicts greater lateral contact forces in early stance (0–10%) and the first half of swing (60–80%) than was measured.
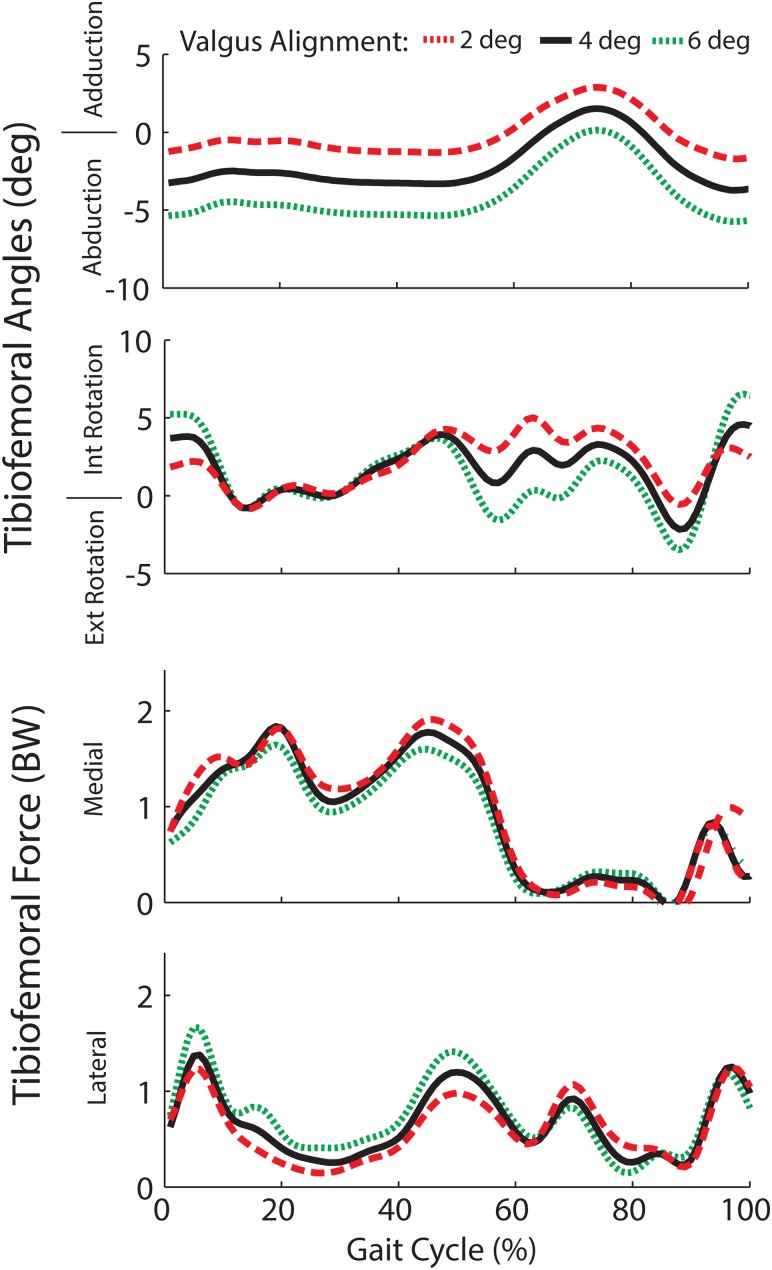
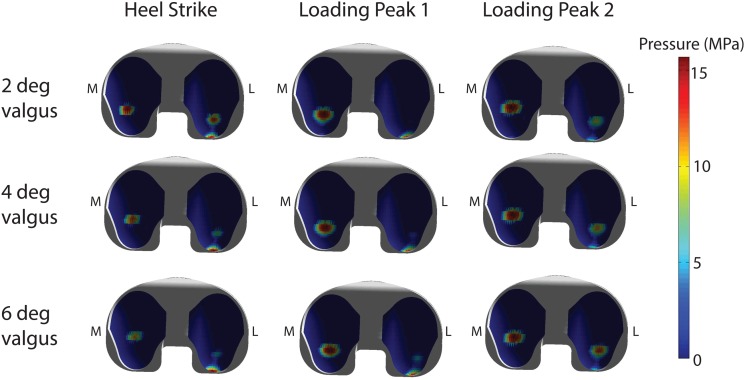
The frontal plane alignment of the joint replacement had a substantial influence on the secondary tibiofemoral kinematics and joint loading patterns. A 2° shift toward greater valgus alignment increased external rotation in swing and internal rotation in early stance (see Fig. 5). A more varus alignment had the opposite effect on tibia rotation. The change in frontal plane knee alignment affected the predicted load distribution across the medial and lateral compartments. At the time of the first peak in tibiofemoral loading, the percentage of load borne on the medial component was 87%, 78%, and 66% of the total load for 2°, 4°, and 6° valgus alignments. A more equal distribution of load was observed at the time of the second peak with 66%, 59%, and 52% of the total load on the medial aspect of the tibial insert. These effects carried over to the contact pressure estimates, with lower peak pressures on the medial side and greater peak pressures on the lateral side with more valgus alignment (see Fig. 6). The coronal alignment affected the location of pressure at heel strike, but did not substantially alter the location of peak pressure regions when the limb was loaded in mid-stance.
Fig. 5.
Frontal plane alignment of the joint replacement substantially altered tibia rotation in swing and early stance, but had little effect on rotation when the limb was loaded in mid- and terminal stance. A more valgus joint replacement alignment induced greater knee abduction, lower medial contact forces, and higher lateral contact forces throughout stance.
Fig. 6.
Predicted contact pressures on the tibial insert at the time of heel strike and the first and second peaks of the tibiofemoral contact loading. Greater valgus alignment of the joint replacement resulted in a more posteriorly loaded lateral compartment at heel strike. During stance, the location of the peak pressures did not vary with alignment, but more even pressure distribution across the medial and lateral compartments is predicted in the valgus alignment.
Discussion
We have introduced a framework for simulating the interaction of muscle, ligament, and joint contact forces within the context of dynamic multijoint movement. We first showed that the framework can be used to predict knee contact force patterns that compare well with those measured directly using an instrumented knee implant [18]. We then demonstrated that the co-simulation framework can be used to predict the sensitivity of knee contact loading patterns to variations in implant alignment. Such an approach allows one to virtually assess the coupled influence of physiological, surgical, and design factors on in vivo musculoskeletal loads.
Biomechanical models have long been used to estimate the tibiofemoral loading patterns during gait. Early inverse modeling approaches tended to overpredict the tibiofemoral joint reaction forces, with estimates nearly 7 times body weight [37]. More recent studies using dynamic gait analysis and knee mechanics models have produced substantially lower knee contact force estimates (2–3 times body weight) that are closer to experimentally measured values (as reviewed in Ref. [17]). However, a primary limitation of prior studies is that a simplified knee model is often used when estimating muscle forces that arise in gait [6]. A common approach uses a constrained 1 d.o.f. knee joint in which muscles only actuate flexion-extension. It has recently been shown that releasing these constraints can alter both muscle and joint contact force estimates [10]. However, this prior study only considered knee mechanics in isolation, which does not account for the action of multijoint muscles.
This study represents the first attempt to use the computed muscle control algorithm [15] on a model with 6 d.o.f. joints. Most musculoskeletal models utilize joints in which inter-segmental translations are fixed or are constrained functions of joint angles [38-40]. Such joints allow for instantaneous transfer of forces, which means one can use multibody equations of motion to directly assess the potential of a muscle to generate whole body accelerations [35]. Such is not the case in a 6 d.o.f. joint restrained by soft tissues and articular contact, in which time is required to deform elastic tissues and transmit forces. In this study, we numerically assessed the translational stiffness arising from ligament stretch and cartilage elasticity at a point in time (see Eq. (7)). Using this information, we were able to approximate the translational d.o.f.’s as fixed when estimating the capacity of a muscle to induce whole body accelerations. This information could then be used within the controller to track joint angular motions about the primary degrees of freedom, as originally formulated in the CMC algorithm [15,42]. A major advantage of using 6 d.o.f. joints is that secondary kinematics (e.g., tibiofemoral translations and nonsagittal rotations) evolve naturally from the muscle, ligament, contact, and external forces acting on the system and, thus, are fully consistent with whole body dynamics. Such a framework would be well suited to investigate how muscles can be used to stabilize joints that may be compromised by injury-induced changes in ligamentous properties [43,44].
The co-simulation framework was solvable in reasonable time periods, with approximately 100 min of computation time on a desktop computer needed to generate a single cycle of gait. The greatest computational burden was in detecting contact between the femoral component and tibial insert surface geometries. We were able to accelerate contact detection by using hierarchical oriented bounding boxes to quickly identify the closest triangles of adjacent polygonal surfaces [28-31]. It is possible that further computational gains are achievable by using surrogate modeling approaches to infer contact pressures directly from tibiofemoral orientation and positions [11,43]. Contact pressures were computed using an elastic foundation model in which it was assumed that pressure is a simple function of the depth of penetration. The ability of the elastic foundation model to ascertain contact stress patterns in joint replacements has previously been demonstrated [44].
We demonstrated the predictive capacity of the computational framework by varying the alignment of the knee joint replacement and assessing how the secondary motions and contact change in response. The importance of frontal alignment on the performance of knee joint replacements is well-recognized [45]. For example, a recent large scale study showed that excessive valgus and varus alignments are associated with substantially higher rates of failure [46]. Our sensitivity analysis suggests that internal tibia rotation is highly dependent on joint alignment when the limb is unloaded in swing and early stance. However, internal tibia rotation was relatively independent of loading during stance, with the greatest effect of alignment being on the mediolateral distribution of load across the tibiofemoral joint. A more equal distribution and lower pressure on the medial insert in the knee occurred with greater valgus alignment (see Fig. 6). These results are similar to experimental observations made when simulating gait on cadaveric specimens with varus and valgus alignments of the tibial insert [47]. We did predict a peak contact pressure on the posterior edge of the lateral insert at heel strike (see Fig. 6), though this effect may have arisen in part from the overprediction of lateral compartment loading in early stance (see Fig. 4).
There are a number of limitations to consider in our knee model. We represented the ligaments as spring elements, rather than deformable 3D representations that account for spatial variations in strain. A 1 d.o.f. patellofemoral joint allowed for patella glide to occur as a result of patellar tendon stretch, but did not allow for mediolateral translation and tilt. These choices were made for computational reasons since the simplified ligament and patellofemoral model could be more efficiently solved within the context of whole body movement. Increased knee model complexity can be easily incorporated into the framework and is certainly warranted as improvements are made in the computational speed at which more complex soft tissue and contact models can be solved. We directly applied measured ground reaction forces within the gait simulation. Future studies will investigate the potential to use the elastic foundation framework to simulate foot-floor interactions within the context of whole body gait simulations. Finally, our framework relies on a static objective function to resolve muscle redundancy at every time step within the gait simulation. We used a popular objective function (the sum of squared activations) that has been shown to reasonably predict muscle coordination in normal gait [48,49]. Our formulation overpredicted the lateral compartment loading in early stance, which, in part, results from excess hamstring activity being recruited upon heel strike (see Fig. 3). Future studies may be able to better replicate experimental muscle recruitment patterns by incorporating objective functions that maximize agreement with electromyographic (EMG) activities.
It is worth noting that generic musculoskeletal and ligament geometries were scaled to the subject and then used to simulate subject-specific gait dynamics. This scaling approach is often used in biomechanical simulation software [50] and avoids the time consuming task of creating subject-specific musculoskeletal models from medical images. It is reassuring that this approach generated plausible estimates of tibiofemoral contact forces, supporting the use of model scaling until more efficient approaches emerge for creating truly subject-specific musculoskeletal models. Posterior cruciate and collateral ligament forces were relatively low throughout the gait cycle, although stretching of these structures during swing did contribute to the overprediction of the lateral and total tibiofemoral forces (see Fig. 6). Ligament stretch with knee flexion is highly dependent on the assumed ligament geometry, such that further work is needed to accurately characterize ligament origins, insertions, and wrapping about anatomical structures.
This study demonstrates the potential for co-simulating ligament, muscle, and joint contact mechanics within the context of coordinated multijoint movement. When applied to gait, model predictions of medial and total knee contact forces closely emulated experimental measures and exhibited a dependency on tibiofemoral alignment. We conclude that the new framework provides a powerful approach for virtually investigating how coupled physiological, surgical, and design factors could affect joint mechanics and performance during functional tasks.
Acknowledgment
The authors thank the knee load grand challenge team, led by B. J. Fregly, Ph.D. and Darryl D’Lima, M.D., Ph.D. (https://simtk.org/home/kneeloads), for providing the images, biomechanical measures, and in vivo knee contact forces used in this study. The authors gratefully acknowledge the support of the NSF (Grant No. 0966535) and the NIH (Grant No. EB 151410), and the contributions of Dan Negrut, Ph.D., to the contact detection formulation.
Footnotes
See https://simtk.org/home/kneeloads for the competition data.
Contributor Information
Darryl G. Thelen, Department of Mechanical Engineering, University of Wisconsin-Madison, Madison, WI 53706;; Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI 53706; Department of Orthopedics and Rehabilitation, University of Wisconsin-Madison, Madison, WI 53706, e-mail: thelen@engr.wisc.edu
Kwang Won Choi, Department of Mechanical Engineering, University of Wisconsin-Madison, Madison, WI 53706.
Anne M. Schmitz, Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI 53706
References
- [1]. Andriacchi, T. P. , Mundermann, A. , Smith, R. L. , Alexander, E. J. , Dyrby, C. O. , and Koo, S. , 2004, “A Framework for the in vivo Pathomechanics of Osteoarthritis at the Knee,” Ann. Biomed. Eng., 32(3), pp. 447–457. 10.1023/B:ABME.0000017541.82498.37 [DOI] [PubMed] [Google Scholar]
- [2]. Anderson, F. C. and Pandy, M. G. , 2001, “Dynamic Optimization of Human Walking,” ASME J. Biomech. Eng., 123(5), pp. 381–390. 10.1115/1.1392310 [DOI] [PubMed] [Google Scholar]
- [3]. Taylor, W. R. , Heller, M. O. , Bergmann, G. , and Duda, G. N. , “Tibio-Femoral Loading During Human Gait and Stair Climbing J. Orthop. Res.,22(3), pp. 625–632. 10.1016/j.orthres.2003.09.003 [DOI] [PubMed] [Google Scholar]
- [4]. Shelburne, K. B. , Torry, M. R. , and Pandy, M. G. , 2006, “Contributions of Muscles, Ligaments, and the Ground Reaction Force to Tibiofemoral Joint Loading During Normal Gait,” J. Orthop. Res., 24(10), pp. 1983–1990. 10.1002/jor.20255 [DOI] [PubMed] [Google Scholar]
- [5]. Shelburne, K. B. , Torry, M. R. , and Pandy, M. G. , 2005, “Muscle, Ligament, and Joint-Contact Forces at the Knee During Walking,” Med. Sci. Sports Exercise, 37(11), pp. 1948–1956. 10.1249/01.mss.0000180404.86078.ff [DOI] [PubMed] [Google Scholar]
- [6]. Kim, H. J. , Fernandez, J. W. , Akbarshahi, M. , Walter, J. P. , Fregly, B. J. , and Pandy, M. G. , 2009, “Evaluation of Predicted Knee-Joint Muscle Forces During Gait Using an Instrumented Knee Implant,” J. Orthop. Res., 27(10), pp. 1326–1331. 10.1002/jor.20876 [DOI] [PubMed] [Google Scholar]
- [7]. Arnold, E. M. , Ward, S. R. , Lieber, R. L. , and Delp, S. L. , 2010, “A Model of the Lower Limb for Analysis of Human Movement,” Ann. Biomed. Eng., 38(2), pp. 269–279. 10.1007/s10439-009-9852-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Wilson, D. R. , Feikes, J. D. , and O’Connor, J. J. , 1998, “Ligaments And Articular Contact Guide Passive Knee Flexion,” J. Biomech., 31(12), pp. 1127–1136. 10.1016/S0021-9290(98)00119-5 [DOI] [PubMed] [Google Scholar]
- [9].Delp, S. L., Loan, J. P., Hoy, M. G., Zajac, F. E., Topp, E. L., and Rosen, J. M., 1990, “An Interactive Graphics-Based Model of the Lower Extremity to Study Orthopaedic Surgical Procedures,” IEEE Trans. Biomed. Eng., 37(8), pp. 757–767. 10.1109/10.102791 [DOI] [PubMed] [Google Scholar]
- [10]. Lin, Y. C. , Walter, J. P. , Banks, S. A. , Pandy, M. G. , and Fregly, B. J. , 2010, “Simultaneous Prediction of Muscle and Contact Forces in the Knee During Gait,” J. Biomech., 43(5), pp. 945–952. 10.1016/j.jbiomech.2009.10.048 [DOI] [PubMed] [Google Scholar]
- [11]. Halloran, J. P. , Ackermann, M. , Erdemir, A. , and van den Bogert, A. J. , 2010, “Concurrent Musculoskeletal Dynamics and Finite Element Analysis Predicts Altered Gait Patterns to Reduce Foot Tissue Loading,” J. Biomech., 43(14), pp. 2810–2815. 10.1016/j.jbiomech.2010.05.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Halloran, J. P. , Ackermann, M., Erdemir, A. , and van den Bogert, A. J. , 2009, “Adaptive Surrogate Modeling for Efficient Coupling of Musculoskeletal Control and Tissue Deformation Models,” ASME J. Biomech. Eng., 131(1), p. 011014. 10.1115/1.3005333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Piazza, S. J. and Delp, S. L. , 2001, “Three-Dimensional Dynamic Simulation of Total Knee Replacement Motion During a Step-Up Task,” ASME J. Biomech. En., 123(6), pp. 599–606. 10.1115/1.1406950 [DOI] [PubMed] [Google Scholar]
- [14]. Neptune, R. , 1999, “Optimization Algorithm Performance in Determining Optimal Controls in Human Movement Analyses,” ASME J. Biomech. Eng., 121(2), pp. 249–252. 10.1115/1.2835111 [DOI] [PubMed] [Google Scholar]
- [15]. Thelen, D. G. and Anderson, F. C. , 2006, “Using Computed Muscle Control to Generate Forward Dynamic Simulations of Human Walking From Experimental Data,” J. Biomech., 39(6), pp. 1107–1115. 10.1016/j.jbiomech.2005.02.010 [DOI] [PubMed] [Google Scholar]
- [16]. Thelen, D. G. , Anderson, F. C. , and Delp, S. L. , 2003, “Generating Dynamic Simulations of Movement Using Computed Muscle Control,” J. Biomech., 36(3), pp. 321–328. 10.1016/S0021-9290(02)00432-3 [DOI] [PubMed] [Google Scholar]
- [17]. Fregly, B. J. , Besier, T. F. , Lloyd, D. G. , Delp, S. L. , Banks, S. A. , Pandy, M. G. , and D'Lima, D. D. , 2012, “Grand Challenge Competition to Predict in vivo Knee Loads,” J. Orthop. Res., 30(4), pp. 503–513. 10.1002/jor.22023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. D'Lima, D. D. , Townsend, C. P. , Arms, S. W. , Morris, B. A. , Colwell, C. W. Jr. , 2005, “An Implantable Telemetry Device to Measure Intra-Articular Tibial Forces,” J. Biomech., 38(2), pp. 299–304. 10.1016/j.jbiomech.2004.02.011 [DOI] [PubMed] [Google Scholar]
- [19]. Shin, C. S. , Chaudhari, A. M. , and Andriacchi, T. P. , 2007, “The Influence of Deceleration Forces on ACL Strain During Single-Leg Landing: A Simulation Study,” J. Biomech., 40(5), pp. 1145–1152. 10.1016/j.jbiomech.2006.05.004 [DOI] [PubMed] [Google Scholar]
- [20]. Davies, H. , Unwin, A. , and Aichroth, P. , 2004, “The Posterolateral Corner of the Knee: Anatomy, Biomechanics and Management of Injuries,” Injury, 35(1), pp. 68–75. 10.1016/S0020-1383(03)00094-9 [DOI] [PubMed] [Google Scholar]
- [21]. Edwards, A. , Bull, A. M. , and Amis, A. A. , 2007, “The Attachments of the Fiber Bundles of the Posterior Cruciate Ligament: An Anatomic Study,” Arthroscopy, 23(3), pp. 284–290. 10.1016/j.arthro.2006.11.005 [DOI] [PubMed] [Google Scholar]
- [22]. Petersen, W. M. D. , and Zantop, T. M. D. , 2007, “Anatomy of the Anterior Cruciate Ligament with Regard to Its Two Bundles,” Clin. Orthop. Relat. Res., 454, pp. 35–47. [DOI] [PubMed] [Google Scholar]
- [23]. Sugita, T. , and Amis, A. A. , 2001, “Anatomic and Biomechanical Study of the Lateral Collateral and Popliteofibular Ligaments,” Am. J. Sports Med., 29(4), pp. 466–472. [DOI] [PubMed] [Google Scholar]
- [24].Liu, F., Yue, B., Gadikota, H. R., Kozanek, M., Liu, W., Gill, T. J., Rubash, H. E., and Li, G., 2010, “Morphology of the Medial Collateral Ligament of the Knee,” J. Orthop. Surg. Res., 5, p. 69. 10.1186/1749-799X-5-69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].LaPrade, R. F., Ly, T. V., Wentorf, F. A., and Engebretsen, L., 2003, “The Posterolateral Attachments of the Knee: A Qualitative and Quantitative Morphologic Analysis of the Fibular Collateral Ligament, Popliteus Tendon, Popliteofibular Ligament, and Lateral Gastrocnemius Tendon,” Am. J. Sports Med., 31(6), p. 854–860. [DOI] [PubMed] [Google Scholar]
- [26].van den Bergen, G., 2003, Collision Detection in Interactive 3D Environments, Morgan Kaufmann Publishers, an Imprint of Elsevier, San Francisco, CA, pp. 192–209. [Google Scholar]
- [27]. Bei, Y. and Fregly, B. J. , 2004, “Multibody Dynamic Simulation of Knee Contact Mechanics,’ Med. Eng. Phys., 26(9), p. 777–789. 10.1016/j.medengphy.2004.07.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Gottschalk, S. , Lin, M. C., and Manocha, D., 1996, “OBBTree: A Hierarchical Structure for Rapid Interference Detection,” SIGGRAPH '96 Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pp. 171–180. [Google Scholar]
- [29].Schmidl, H., Walker, N., Lin, M., 2004, “CAB: Fast Update of OBB Trees for Collision Detection Between Articulated Bodies,” J. Graph. Tool, 9, pp. 1–9. 10.1080/10867651.2004.10504891 [DOI] [Google Scholar]
- [30].Kurt, S. M., Jewett, C. W., Bergstrom, J. S., Foulds, J. R., and Edidin, A. A., 2002, “Miniature Specimen Shear Punch Test for UHMWPE Used in Total Joint Replacements,” Biomaterials, 23(9), pp. 1907–1919. 10.1016/S0142-9612(01)00316-7 [DOI] [PubMed] [Google Scholar]
- [31].Hindmarsh, A. C., Brown, P. N., Grant, K. E., Lee, S. L., Serban, R., Shumaker, D. E., and Woodward, C. S., 2005, “SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers,” ACM Trans. Math. Softw., 31(3), pp. 363–396. 10.1145/1089014.1089020 [DOI] [Google Scholar]
- [32]. Thelen, D. G. , 2003, “Adjustment of Muscle Mechanics Model Parameters to Simulate Dynamic Contractions in Older Adults,” ASME J. Biomech. Eng., 125(1), pp. 70–77. 10.1115/1.1531112 [DOI] [PubMed] [Google Scholar]
- [33]. Delp, S. L. and Loan, J. P. , 1995, “A Graphics-Based Software System to Develop and Analyze Models of Musculoskeletal Structures,” Comput. Biol. Med., 25(1), pp. 21–34. 10.1016/0010-4825(95)98882-E [DOI] [PubMed] [Google Scholar]
- [34]. Grood, E. S. and Suntay, W. J. , 1983, “A Joint Coordinate System for the Clinical Description of Three-Dimensional Motions: Application to the Knee,” ASME J. Biomech. Eng., 105(2), pp. 136–144. 10.1115/1.3138397 [DOI] [PubMed] [Google Scholar]
- [35].Arnold, A. S., Anderson, F. C., Pandy, M. G., and Delp, S. L., 2005, “Muscular Contributions to Hip and Knee Extension During the Single Limb Stance Phase of Normal Gait: A Framework for Investigating the Causes of Crouch Gait,” J. Biomech., 38(11), pp. 2181–2189. 10.1016/j.jbiomech.2004.09.036 [DOI] [PubMed] [Google Scholar]
- [36]. Happee, R. , 1994, “Inverse Dynamic Optimization Including Muscular Dynamics, a New Simulation Method Applied to Goal Directed Movements,” J. Biomech., 27(7), p. 953–960. 10.1016/0021-9290(94)90267-4 [DOI] [PubMed] [Google Scholar]
- [37]. Seireg, A. , and Arvikar, R. J., 1975, “The Prediction of Muscular Lad Sharing and Joint Forces in the Lower Extremities During Walking,” J. Biomech., 8(2), pp. 89–102. 10.1016/0021-9290(75)90089-5 [DOI] [PubMed] [Google Scholar]
- [38]. Wilson, D. , and O’Connor, J. , 1997, “A Three-Dimensional Geometric Model of the Knee for the Study of Joint Forces in Gait,” Gait and Posture, 5(2), pp. 108–115. [Google Scholar]
- [39]. Yamaguchi, G. T. and Zajac, F. E. , 1989, “A Planar Model of the Knee Joint to Characterize the Knee Extensor Mechanism,” J. Biomech., 22, p. 1–10. 10.1016/0021-9290(89)90179-6 [DOI] [PubMed] [Google Scholar]
- [40]. Thelen, D. G. , Anderson, F. C. , and Delp, S. L. , 2003, “Generating Dynamic Simulations of Movement Using Computed Muscle Control,” J. Biomech., 36(3), p. 321–328. 10.1016/S0021-9290(02)00432-3 [DOI] [PubMed] [Google Scholar]
- [41]. Shelburne, K. B. , Torry, M. R. , and Pandy, M. G. , 2005, “Effect of Muscle Compensation on Knee Instability During ACL-Deficient Gait,” Med. Sci. Sports Exercise, 37(4), pp. 642–648. 10.1249/01.MSS.0000158187.79100.48 [DOI] [PubMed] [Google Scholar]
- [42].Shao, Q., MacLeod, T. D., Manal, K., and Buchanan, T. S., 2011, “Estimation of Ligament Loading and Anterior Tibial Translation in Healthy and ACL-Deficient Knees During Gait and the Influence of Increasing Tibial Slope Using EMG-Driven Approach,” Ann. Biomed. Eng., 39(1), pp. 110–121. 10.1007/s10439-010-0131-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lin, Y. C., Farr, J., Carter, K., and Fregly, B. J., 2006, “Response Surface Optimization for Joint Contact Model Evaluation,” J. Appl. Biomech., 22(2), pp. 120–130. [DOI] [PubMed] [Google Scholar]
- [44]. Halloran, J. P. , Petrella, A. J., Rullkoetter, P. J., Easley, S. K., Anthony J. Petrella, Paul J. Rullkoetter and Sarah K. Easley, 2005, “Comparison of Deformable and Elastic Foundation Finite Element Simulations for Predicting Knee Replacement Mechanics,” ASME J. Biomech. Eng., 127(5), pp. 813–818. 10.1115/1.1992522 [DOI] [PubMed] [Google Scholar]
- [45]. Jeffery, R. S. , Morris, R. W. , and Denham, R. A. , 1991, “Coronal Alignment After Total Knee Replacement,” J. Bone Jt. Surg., Br. Vol., 73(5), pp. 709–714. [DOI] [PubMed] [Google Scholar]
- [46]. Fang, D. M. , Ritter, M. A. , and Davis, K. W. , 2009, “Coronal Alignment in Total Knee Arthroplasty: Just How Important is It?,” J. Arthroplasty, 24(6), pp. 39–43. 10.1016/j.arth.2009.04.034 [DOI] [PubMed] [Google Scholar]
- [47].Werner, F. W., Ayers, D. C., Maletsky, L. P., and Rullkoetter, P. J., 2005, “The Effect of Valgus/Varus Malalignment on Load Distribution in Total Knee Replacements,” J. Biomech., 38(2), pp. 349–355. 10.1016/j.jbiomech.2004.02.024 [DOI] [PubMed] [Google Scholar]
- [48]. Crowninshield, R. D. and Brand, R. A. , 1981, “A Physiologically Based Criterion of Muscle Force Prediction in Locomotion,” J. Biomech., 14(11), pp. 793–801. 10.1016/0021-9290(81)90035-X [DOI] [PubMed] [Google Scholar]
- [49]. Anderson, F. C. and Pandy, M. G. , 2001, “Static and Dynamic Optimization Solutions for Gait are Practically Equivalent,” J. Biomech., 34(2), pp. 153–161. 10.1016/S0021-9290(00)00155-X [DOI] [PubMed] [Google Scholar]
- [50].Delp, S. L., Anderson, F. C., Arnold, A.S., Loan, P., Habib, A., John, C. T., Guendelman, E., Thelen, D. G., 2007, “OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement,” IEEE Trans. Biomed. Eng., 54(11), pp. 1940–1950. [DOI] [PubMed] [Google Scholar]