Spectral Characterization of Hierarchical Modularity in Product Architectures

Short abstract

Despite the importance of the architectural modularity of products and systems, existing modularity metrics or algorithms do not account for overlapping and hierarchically embedded modules. This paper presents a graph theoretic spectral approach to characterize the degree of modular hierarchical-overlapping organization in the architecture of products and complex engineered systems. It is shown that the eigenvalues of the adjacency matrix of a product architecture graph can reveal layers of hidden modular or hierarchical modular organization that are not immediately visible in the predefined architectural description. We use the approach to analyze and discuss several design, management, and system resilience implications for complex engineered systems.

1. Product Architectures and Their Modularity

One important architectural property of products and complex engineered systems is their modularity. A module is a component or subsystem in a larger system that performs specific function(s) and emerges as a tightly coupled cluster with elements sharing dense intramodule interactions and sparse intermodule interactions. Modular products carry some advantages over their integrated counterparts [1,2] including ease of redesign and redevelopment, component re-use in other products [3], adaptability over the product life-cycle [4], and lowered production and related costs [5]. Modules within products can form the basis for the platform for a family of products [6–8] and the organizational structure of the design team [9]. As such, there is a general preference for modular products in industry [10]. Understanding the structural modularity of products and complex engineered systems is important because it helps us to understand the sets of functions performed specifically by each module and the functions that can only be performed by interactions between modules. This knowledge can inform several optimization criteria relevant to the design of these systems and subsystems, such as decisions on architecture or energy, material, or information flows in the system.

2. Research Gaps in Modularity Identification

In this paper, we focus on identifying the hierarchical-overlapping organization of modularity in products and systems, and its related implications for mechanical design. While research exists on developing modularity metrics for product architectures [1,11–16] and characterizing the topological characteristics of modular organization in networks [17,18], the issue of identifying hierarchical and overlapping organization of modules in product architecture is yet to be resolved. We discuss three limitations in current approaches to identify modularity in product architectures specifically, and networks more generally.

2.1. Naturally Existing Hierarchy in Product Architecture.

First, it is well-known that product architectures contain hierarchies at multiple scales of hierarchical organization, often characterized and predefined at the subsystem and component levels. For example, the systems architecture of a spaceship or aircraft contains entire subsystems that are systems in their own right. Hierarchical modularity, at least for some product families, has been shown to be a manifestation of a power-law functional relationship between the clustering coefficients of individual nodes and the centrality of respective nodes [17,18]. Yet, existing modularity identification techniques assume predefined hierarchies, as is the case in hierarchically based design optimization formulations such as Analytical Target Cascading [19], and/or they then operate recursively to each defined hierarchical level. As we demonstrate through this paper, an explicit predefined assumption of hierarchical levels and modular boundaries (and design components, inputs, outputs, and variables at that level) may hide other naturally occurring or possibly emergent and unintended embedded hierarchies resulting from interactions between subsystems, components, or parts [20]. Therefore, a modularity finding technique must have the capacity to reveal naturally existing scales of hierarchical organization in the product architecture without any a priori knowledge or assumptions about the levels of organization.

2.2. Naturally Existing Modular Overlaps in Product Architecture.

Second, most modularity identification techniques make an essential a priori assumption about the characteristics of the modules [1,11,15,16]: modules do not overlap—they are strictly partitioned. Hence, these techniques cannot account for overlapping modules. If a system has naturally overlapping modules (such as one component that performs multiple functions, interdisciplinary design teams with shared experts, etc.), then a technique that defines and detects modules as disjoint sets will never discover overlapping structure. The degree to which modules or components within modules are allowed to interface with each other can affect the degree to which a final designed product architecture is integral or modular or whether a component can be included into one subsystem and another. In most circumstances, the component and module interfaces are important design decisions, and the degree to which modules share interfaces (or modular overlap) can have wide ranging effects on performance, production, and design [21]. This requirement for strict partitioning is similar to the engineer having to make an explicit choice as to which subsystem a component belongs [22] and obfuscates the situation when a component has multiple significant spatial or functional dependencies such that it should be attributed to multiple subsystems.

2.3. False Positives for Modularity of Product Architectures.

Lastly, even without the consideration of hierarchical and overlapping modularity, research in quantitative metrics of modularity in product architectures have produced conflicting and inconclusive results. Hölttä and de Weck proposed the Singular Modularity Index (SMI) as a metric for assessing modularity from a functional perspective [12], but a later paper compared the SMI to other metrics [13] and concluded that Whitney Index and Change Cost were more useful metrics. Alternatively, Wang and Antonsson [14] proposed an information-theoretic measure of modularity. Part of the lack of agreement among these metrics stems from the difference between defining modularity from the component level [e.g., Ref. [15]] versus the module level and the connectivity of components within the module [e.g., Ref. [12]]. At a component level, Sosa recommended centrality as a measure of component modularity [15]. At a subsystem level though, the same authors developed a metric of modularity based on cross-boundary interfaces [16].

Beyond the lack of agreement on a single metric, one weakness of these metrics is their graph-theoretic validity: the above modularity metrics would ascribe nonzero modularity to a system even if there were no modularity in the system, such as in a random graph, which is neither an integral system nor a modular system. The SMI for a random graph implies a modular network because the SMI is nonzero. For example, for a random graph with 64 nodes and a probability of connection between nodes of 0.1, the SMI is 0.43. Conversely, Wang and Antonsson's [14] information theoretic measure can not be calculated, since it assumes the existence of modularity, whereas there is none other than by chance in a random graph.

3. Research Question and Paper Summary

An open question thus revolves around an appropriate metric to provide integrated insights into the natural modularity of a given system (system modularity) or of a set of components (component modularity) at any desired level of abstraction (instead of predefined levels) and the associated method for finding modules, since these two problems go hand-in-hand. The manner in which modularity is defined and the associated metric directly affects the modules within the system that can be identified [1]. The lack of a uniform metric for modularity can result in methods for identifying modules in product architecture yielding divergent results [23].

In this paper, we use findings from the study of complex networks to develop such a metric and method. It has been long known that product architectures can be represented as graphs or equivalent component-based design structure matrices. In parallel, the field of complex networks in physics in the last decade has produced concentrated research on the identification of naturally existing modularity (including hierarchical-overlapping modularity) in artificial and biological complex systems. For an exhaustive review of algorithms, see Ref. [24]. It is also known that modular networks exhibit particular topological properties, such as having a high clustering coefficient [17,18]. Principal to the work reported in this article is finding modularity given no predefined subsystems or component modules a priori. The main contribution of this paper is a new spectral technique to detect modules in the system. In our recent work, we have extended some classical results on the identification of modularity and hierarchical modularity in complex networks [25,26]. Specifically, we have derived two principal findings by using and extending classical spectral approaches to modularity identification [24] and graph classification [27] that are relevant to the problem being addressed in this paper. First, we have developed an algorithm for detecting naturally existing hierarchical and overlapping modules in complex networks [25]. Second, we have shown that modular and hierarchical modular graphs can be clearly distinguished from other graphs having no modularity using spectral fingerprints of their graph adjacency matrix [26]. Thus, the spectra of a graph can itself be a powerful metric for measuring modularity. We briefly state these results in this paper, apply, demonstrate, and verify the results on synthetically produced modular and hierarchical modular networks, and then apply and discuss the findings for studying the hierarchical modularity of a Pratt and Whitney aircraft engine [16].

In summary, using idealized graph models, we show that their eigenvalue spectra can formally identify the absence, presence, and type of modularity. Then, we examine the spectrum of a Pratt-Whitney aircraft engine [16] and explain its hierarchical-overlapping modular organization with reference to idealized models. Finally, through the aircraft engine example, we discuss new design insights into hierarchical modularity in product architectures and the role of highly connected “overlap” or hub components that can critically affect system redesign, resilience and safety, and maintenance.

4. Method and Approach

We define an idealized system as a graph model with predefined properties that characterize the limits within which real world systems lie. Real world engineering systems are neither perfectly hierarchical nor perfectly modular. Neither are they completely regular nor completely random. However, randomness, regularity, and degrees of modularity and hierarchy are organizing properties that all systems contain to varying degrees. Using ideal models to characterize the degree of randomness, modularity, or hierarchical modularity can therefore establish a generalized and objective way of characterizing modularity in a real world system. Our method is based on comparing the eigenvalue spectra of a graph or matrix representation of real world systems to idealized models [26–28]. The role of using singular value decomposition, and in general graph spectra, to characterize modularity has received significant attention in research [12,24–26,29,30], and this work extends concepts on the relation between the spectral properties of graphs and their topological configuration.

We discuss four idealized graph models and synthesize networks using the models: random, regular, modular, and hierarchical modular. We will show that these idealized models can be distinctly classified or “finger-printed” according to their eigenvalue spectra, the set of eigenvalues of the graph. The spectra will then become the basis for a metric to classify the modularity of a real–world system.

We note here that singular values have been previously used in to define a modularity index [12], which we diverge from in three ways. First, our approach does not require an approximation or error computation with reference to an idealized exponential function, as used by Hölttä and de Weck [12]. Second, in our method, product modularity can be classified according to a spectral signature with reference to random, regular, modular and hierarchical modular graph models. Thus, the modularity signature rests on assessment of multiple parameters (randomness, modularity, and hierarchy), instead of a single numeric parameter which can only measure a single attribute. Third, spectra serve as the basis for optimally decomposing networks into modules, including identification of module overlaps and hierarchy. The work by Hölttä and de Weck did not take hierarchy and overlaps into account and cannot be used to optimally decompose a system in the form as presented.

We examine the spectrum of each idealized graph model and present an accompanying algorithm based on the work in Ref. [25] that provides a computationally fast and efficient way to identify the hierarchical-overlapping modules in a system.

4.1. Product Architecture as a Graph and Its Adjacency Matrix.

We define a system as a graph S = (C, E), where $C=\{c_1,c_2,\dots ,c_n\}$ is a set of components in the system, and E is a set of edges that describe any design relationship between two components; i.e., edges can represent spatial proximity, energy, material, or information interactions between components. We do not differentiate between component, module, and subsystem definitions in this representation. The level of granularity for a description of a system can be made arbitrarily large or small, depending on the product architecture and design task. The main idea behind this is that a modularity metric and modularity detection algorithm must be able to identify the modularity characteristics for any arbitrary system, even if hierarchical levels and module boundaries are not specified explicitly. In many design phases, this is exactly what the design decision is: where should an engineer place the module boundaries?

The graph S can be represented in matrix form, such as a Design Structure Matrix (DSM). S can also be represented equivalently as an adjacency matrix that can be binary or weighted. In a binary adjacency matrix, A_ij = 1 if an edge (design relationship) exists between nodes i and j, and A_ij = 0 otherwise. The weighted adjacency matrix takes the form A_ij = w_ij if an edge exists between nodes i and j, where w_ij is a numerical weight assigned to the edge, and 0 otherwise. If the edges are undirected, then A is symmetric. A symmetric matrix (undirected graph) will have eigenvalues that are all real. We study the eigenvalue decomposition of A, and the analysis presented in the paper is primarily for binary (unweighted) undirected representations. Although the analysis, in principle, can be extended to weighted counterparts, in this paper, we work with undirected binary graphs because: (a) they are the most commonly used class in modeling complex networks; (b) the aeroengine product architecture example we study was represented in binary form by the original authors [16]; and, (c) including weighted versions would considerably extend the analysis and demonstration of our approach and constitutes an altogether separate study.

4.2. Idealized Graph Models and Spectra.

We examine four idealized graph models and show that the pattern of eigengaps, i.e., the gaps between successive eigenvalues in their spectra, can uniquely fingerprint their modularity characteristics.

4.2.1. Non-Modular Graph Models and Spectra: Random and Regular Ring Lattice Graphs.

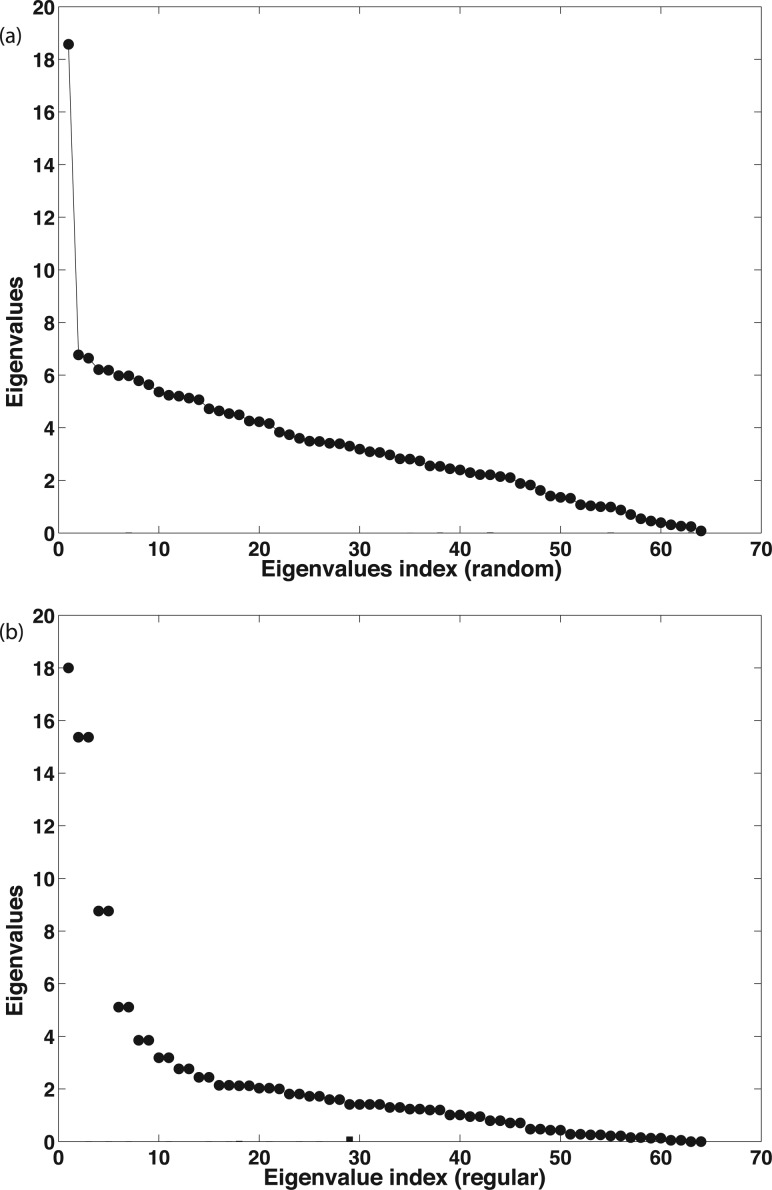
An Erdös-Rényi uncorrelated random graph is a graph of N nodes where the probability for any two pairs of vertices in the graph being connected is the same, p, and these probabilities are independent variables [24]. Thus, the random graph is defined in terms of a binary adjacency matrix, where each matrix entry is 1 (edge) with probability p and 0 (no edge) with probability 1 − p. The entries in the adjacency matrix of the graph have a common expectation (mean) value of p with a variance of σ². The main classically known results about the spectrum of an uncorrelated random graph that are of relevance in the present work relate to the distribution of its eigenvalues [27]. First, as the number of nodes N grows, the principal eigenvalue (the largest eigenvalue λ₁) grows much faster than the second eigenvalue with ${lim}_{N\to \infty }({\lambda }_1/N)=p$ with probability 1, whereas for every $\varepsilon$ > 1/2, ${lim}_{N\to \infty }({\lambda }_2/N^{\mathrm{\varepsilon }})=0$. The same relationship holds for the smallest eigenvalue λ_N. For every $\varepsilon$ > 1/2, ${lim}_{N\to \infty }({\lambda }_N/N^{\mathrm{\varepsilon }})=0$. Thus, the largest eigenvalue λ₁ scales as pN and the other eigenvalues ${\lambda }_2,\dots ,{\lambda }_N$ scale as $\sigma \sqrt{N}$. Simply described, the spectrum of a random graph typically shows one large eigenvalue, followed by other eigenvalues after a large gap. Random graphs form one extreme graph model, which, by definition, do not have a modular structure except by chance. No modular structure, except for what occurs through chance, should be revealed using any module detection algorithm. It would be incorrect to ascribe any positive modularity to this graph using any metric. Fig. 1(a) shows the binary adjacency matrix for a 64 node random graph. As expected, no modular structure is visible. The typical eigenspectrum for a random graph is illustrated in Fig. 2(a): there is one large eigenvalue separated from the bulk distribution of eigenvalues.

Fig. 1.

Network models: (a) 64 node random graph with p = 0.29 and average degree = 18; (b) 64 node regular graph with degree = 18; (c) typical 128 node Newman-Girvan modular network [24]; (d) finding the 4 modules in the network in (c); (e) typical hierarchical modular graph from Ref, [26] with 3 hierarchical levels

Fig. 2.

Spectra of random and regular models: eigenvalues arranged in descending order for (a) the random graph in Figs 1(a) and 1(b) the regular graph in Fig. 1(b)

A regular graph G _reg = (N, d) is defined with N nodes, with each node having a degree d [24]. A ring lattice also has no modular structure, because each node symmetrically has the same number of neighbors. In a ring lattice, each node is connected to exactly d/2 nodes before and after it. Figure 1(b) shows the regular graph matrix with a thick spine filled along the diagonal and two triangular portions at two ends.

We note here a point of difference with [12], wherein the authors propose this structure to be perfectly modular. However, we note that this regular graph structure shows that components in the system are locally connected to their immediate neighbors, and that there are no system-level distant connections or preferential, dense, localized connections. This organizing principle, of itself, will not produce a modular structure. To prove this more formally, we note that any cut in the graph at any point, i.e., deleting edges between two nodes, will simply produce a long chain like structure instead of a ring structure. In contrast, a single cut in a modular graph (discussed below) will produce at least two distinct modules. A regular ring lattice graph has a typical stepped spectrum (for the detailed formulae for spectra of regular graphs, refer to Ref. [31]): pairs of equal eigenvalues, then a large eigengap, followed by a pair of equal eigenvalues again, and so on (Fig. 2(b)). The number of degenerate eigenpairs varies as the size of the graph and the node degree is varied, decreasing with increasing node degree.

4.2.2. Modular Graph Models and Spectra.

As opposed to random and regular graphs, which have no modular structure, a graph with modules will have a characteristic property: the number of intramodule edges will be much higher than the number of intermodule edges. The widely accepted definition of a module [24] is that the actual number of edges existing within a module should be much higher than the expected number of edges derived from an equivalent random graph model with the same number of vertices and similar degree distribution but with no modular structure.

To relate modular and hierarchical modular graphs with the nonmodular graph models, a typical stochastic block model is used to generate modular and hierarchical modular networks, as presented in Ref. [26]. We briefly review the model construction steps here. We start with an unperturbed modular network G(N,m) with N nodes and m equally sized disconnected modules that are random networks (as defined in Sec. 4.2.1) of size s and nodes connected with probability p using the random network model described in the previous section. The adjacency matrix A for this network has m random blocks on the diagonal, with 1 s signifying the presence of an edge and 0 s signifying the absence of an edge.

Now, this ideal modular network is perturbed with block matrices of size s, each of which represents a random network of s nodes and probability of connection pq, where q is a numeric parameter that sets a level of decrease in probability of an edge between two nodes. That is, the entries of the perturbation matrices are 1 (edge) with probability pq, and 0 (no edge) with probability 1 − p. These perturbation matrices P are placed in the off-diagonal positions of the perturbed adjacency matrix A, with $\mathbf{A}\text{'}=\mathbf{A}+\mathbf{P}$, where $\mathbf{A}\text{'}$ has the block form

$$\mathbf{A}\text{'}=\left[\begin{array}{cccc}\multicolumn{1}{c}{\mathbf{A}}& \hfill \mathbf{P}\hfill & \hfill \dots \hfill & \hfill \mathbf{P}\hfill \\ \multicolumn{1}{c}{\mathbf{P}}& \hfill \mathbf{A}\hfill & \hfill \dots \hfill & \hfill \mathbf{P}\hfill \\ \multicolumn{1}{c}{\dots }& \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \multicolumn{1}{c}{\mathbf{P}}& \hfill \dots \hfill & \hfill \mathbf{A}\hfill & \hfill \mathbf{P}\hfill \\ \multicolumn{1}{c}{\mathbf{P}}& \hfill \mathbf{P}\hfill & \hfill \dots \hfill & \hfill \mathbf{A}\hfill \end{array}\right]$$ (1)

As we have proven in Ref. [26] by using and extending classical results from random matrix theory [27,32], the mean values of the eigenvalue spectrum of the perturbed modular network $\mathbf{A}\text{'}$ is

$$S_{\mathbf{A}\text{'}}=\left[\begin{array}{ccc}\multicolumn{1}{c}{\mathit{sp}+(m-1)\mathit{spq}}& \hfill \mathit{sp}-\mathit{spq}\hfill & \hfill O(\sigma \sqrt{N})\hfill \\ \multicolumn{1}{c}{1}& \hfill m-1\hfill & \hfill N-m\hfill \end{array}\right]$$ (2)

The largest eigenvalue of the perturbed matrix has a mean expected value of sp + (m − 1)spq and the next m − 1 largest eigenvalues have a mean expected value of sp − spq. All the other eigenvalues are bounded by a radius of $\sigma \sqrt{N}$ with a mean value of 0, where σ is the standard deviation of the entries in $\mathbf{A}\text{'}$. Thus, exactly m eigenvalues are well separated from the bulk distribution of eigenvalues around the origin.

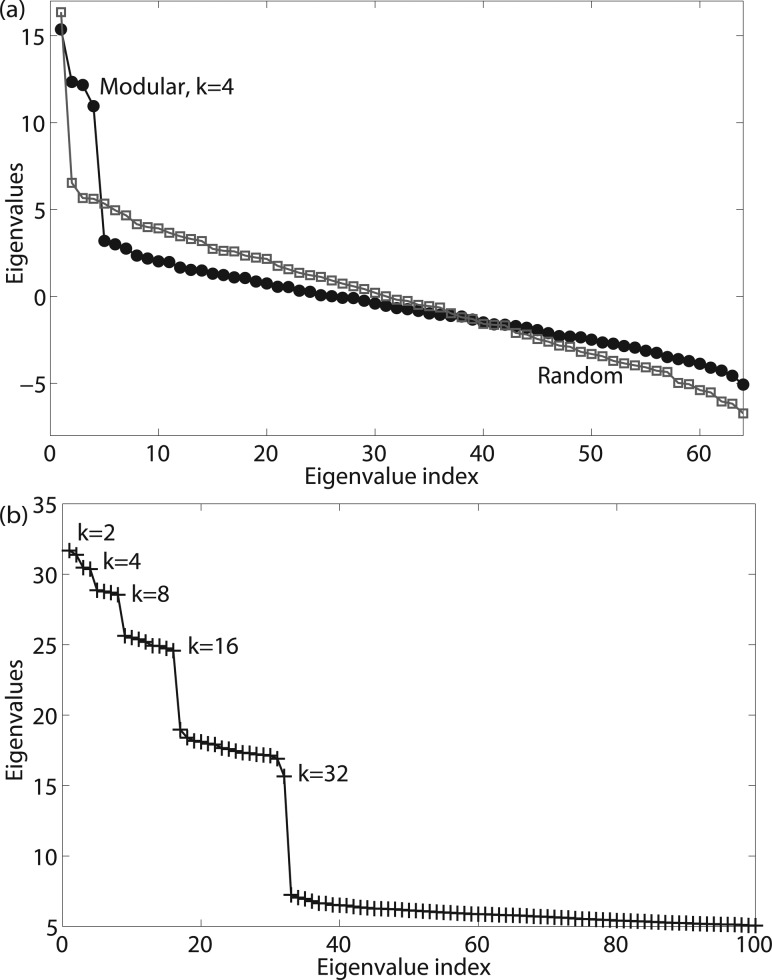
Figure 3(a) shows the spectrum of a 64 node modular graph with 4 modules. Note the 4 large eigenvalues, showing that the optimal number of modules in the system is 4, which is the correct solution. Fig. 1(c) shows the modular network's original adjacency matrix, and Fig. 1(d) shows the 4 modules as detected using the eigenspectrum in Fig. 3(a) and the module detection algorithm presented later in this paper. In contrast, a random network of the same size and degree distribution shows only 1 large eigenvalue.

Fig. 3.

Spectra of modular and hierarchical modular networks: (a) A 64 node modular network with 4 modules (black) compared to 64 node random network, p = 0.1 (grey). (b) A 1024 node network with nested modules at 5 hierarchical levels with only the first 100 eigenvalues shown. Lines are for visual presentation only.

4.2.3. Hierarchical Modular Graph Models.

In hierarchical modular graphs, the underlying structural theme is a “modules nested inside modules” approach. The probability of there being an edge inside the lowest level (smallest) module is the highest, and progressively decreases as the level of hierarchy increases.

We follow the typical stochastic block model form for constructing a hierarchical network, similar to the method described above for modular networks and as presented in Ref. [26]. A hierarchical modular network is constructed by recursively placing random matrix blocks with decreasing levels of connectivity between nodes in hierarchical levels in a block diagonal form. We consider, as before in Sec. 4.2.2, the matrix

$$\mathbf{A}\text{'}=\left[\begin{array}{cc}\multicolumn{1}{c}{\mathbf{A}}& \hfill \mathbf{P}\hfill \\ \multicolumn{1}{c}{\mathbf{P}}& \hfill \mathbf{A}\hfill \end{array}\right]$$ (3)

where A is a binary random network of size s and edge probability p, and P is a random network of size s and edge probability pq. Here, the parameter q sets the level of decrease in connectivity between the various levels of hierarchy.

That is, q is a numeric parameter that is varied to define the connectivity of the first level hierarchy of off-diagonal networks or embedded modules represented by P. For example, if q = 0.5, then the connectivity in P is 50% of the connectivity in A. If q = 1, the network will no longer be hierarchical, but will simply be a random network of size 2 s with connection probability p (since, in this case, p = pq). It is clear from the formulation that the lower the value of q, the stronger the hierarchical modular structure, and higher the value of q (to 1), the weaker the hierarchical modular structure.

We now define the second level of perturbation $\mathbf{A}\text{'}\text{'}$ as

$$\mathbf{A}\text{'}\text{'}=\left[\begin{array}{cc}\multicolumn{1}{c}{\mathbf{A}\text{'}}& \hfill \mathbf{P}\hfill \\ \multicolumn{1}{c}{\mathbf{P}}& \hfill \mathbf{A}\text{'}\hfill \end{array}\right]$$ (4)

where $\mathbf{A}\text{'}$ is the matrix defined in Eq. (3) and P is a random network or matrix of size 2 s and edge probability pq ². Note here the second hierarchical level: $\mathbf{A}\text{'}$ already has the first level of hierarchy built in as described previously, with the first level off-diagonal blocks having connectivity pq and the diagonal blocks having connectivity p, with pq < p. Now, the second level off-diagonal blocks, represented by matrix P, have connectivity pq ² with pq ²< pq < p. In general, the matrix P defines each successive level L of perturbations of increasing size (s, 2 s, 4 s,…,N/2) and decreasing probability of connection ($\mathit{pq},{\mathit{pq}}^2,\dots ,{\mathit{pq}}^{L-1}$), producing an extra level of hierarchical modular structure with each perturbation level. Figure 1(e) shows an example hierarchical network adjacency matrix with 3 hierarchical levels.

We have proven in Ref. [26], using results from random matrix theory [27,32], that in general, for L hierarchical levels, the expected values of the largest eigenvalues (those separated from the bulk of the eigenvalues) of a hierarchical network ${\mathbf{A}}_L$, along with their algebraic multiples, are

$$\mathit{Sp}({\mathbf{E}}_L)=\left[\begin{array}{cc}\multicolumn{1}{c}{s[p+\mathit{pq}\sum _{i=0}^{L-1}{(2q)}^i]}& \hfill 1\hfill \\ \multicolumn{1}{c}{s[p+\mathit{pq}\{\left[\sum _{i=0}^{L-2}{(2q)}^i\right]-{(2q)}^{L-1}\}]}& \hfill 1\hfill \\ \multicolumn{1}{c}{\dots }& \hfill \dots \hfill \\ \multicolumn{1}{c}{s[p+\mathit{pq}(1-2q)]}& \hfill 2^{L-2}\hfill \\ \multicolumn{1}{c}{s[p-\mathit{pq}]}& \hfill 2^{L-1}\hfill \end{array}\right]$$ (5)

In general, for all hierarchical networks, the spectrum in Eq. (5) has a clustered, stepped form, with eigenvalues clustered in groups and successive large gaps between these groups. These gaps reveal the hierarchical organization of the network.

Figure 3(b) shows the spectrum of a 1024 node hierarchical modular graph. As is clearly seen, there are clusters of eigenvalues organized on a number of levels. Note the large eigengaps in Fig. 3(b) corresponding to the hierarchical levels, showing 2 modules at the highest level, followed by 4, 8, 16, and 32 modules at subsequent, lower-hierarchy levels. This corresponds exactly with the actual hierarchy in the idealized network. The capability of the eigenvalue spectrum to reveal hierarchical modularity can help to resolve the problem the granularity of system decomposition and the influence of this modeling choice on the degree of modularity detected [33]. Modules associated with low-level decompositions would appear as modules associated with higher-level decompositions assuming that the modeler includes the relations between the higher levels of decomposition (major subsystems/modules) and the lower level counterparts.

Thus, we have shown that the eigenvalue spectrum of modular and hierarchical modular networks uniquely shows the optimal number of modules in these idealized systems.

4.2.4. Spectra of Hierarchical and Modular Networks With Unequal Sized Modules.

In the idealized models presented above, the module sizes were all equal. In this section, we show that the results are valid even if the module sizes are dissimilar, as it is almost certain that real world networks have a distribution of module sizes rather than a single module size. We generated modular and hierarchical modular networks of various sizes with dissimilar module sizes and found that the spectra can successfully capture the same information as discussed above about the size and the number of modules, as long as the probability parameters chosen for the random blocks ensure a sufficiently strong modularity structure [26]. We present some detailed demonstrations below.

We first show the results for the simplest idealized case: a graph with fully connected modules on the diagonal (i.e., each node is connected to all the other nodes in its own module). For an idealized model having m modules of sizes $s_1,s_2,\dots ,s_m$ and respective multiplicities $m_1,m_2,\dots ,m_m$, the spectrum is

$$S_M=\left[\begin{array}{ccccc}\multicolumn{1}{c}{s_1}& \hfill s_2\hfill & \hfill \dots \hfill & \hfill s_m\hfill & \hfill -1\hfill \\ \multicolumn{1}{c}{m_1}& \hfill m_2\hfill & \hfill \dots \hfill & \hfill m_m\hfill & \hfill n-(m_1+\dots +m_m)\hfill \end{array}\right]$$ (6)

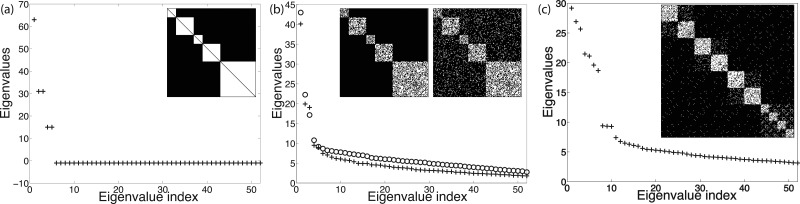
For example, the spectrum for a perfectly modular 160 node network with m = 5 modules and the following module size distribution: M = {16, 32, 16, 32, 64}, as shown in Fig. 4(a), is

Fig. 4.

Spectra of networks with unequal modules: (a) Inset: Perfect modular network with 5 modules of sizes 16, 32, 16, 32, 64; Spectrum shows 1 eigenvalue of 64, 2 eigenvalues of 32, and 2 eigenvalues of 16. (b) Left inset: Unperturbed random block modular network, 5 modules with connection probability p = 0.6, and sizes 16, 32, 16, 32, 64; Spectrum (crosses) shows the same eigenvalue pattern with 1 large eigevalue, followed by 2 large eigenvalues, followed by 2 large eigenvalues, but the eigenvalues scale as pN; Right inset: Perturbed random block modular network, with intermodule connectivity pq = 0.1 and same module sizes as left inset; Spectrum (circles) continues to echo the same pattern, though as the intermodule connectivity increases, the eigenvalues move away from the means, showing larger randomness in structure; (c) Inset: Hierarchical modular network of 3 levels, with unequal module sizes: at the coarsest level is a 256 node network, at the next level three 64 node subnetworks further divide into 32 node finest level networks, and a 64 node subnetwork divides into four 16 node finest level subnetworks; There are 3 hierarchical levels, and the finest level shows 10 modules; Spectrum fingerprints this hierarchical modular organization: there are 10 large eigenvalues, and 3 gaps signifying 3 hierarchical levels.

$$S_M=\left[\begin{array}{cccc}\multicolumn{1}{c}{64}& \hfill 32\hfill & \hfill 16\hfill & \hfill -1\hfill \\ \multicolumn{1}{c}{1}& \hfill 2\hfill & \hfill 2\hfill & \hfill 155\hfill \end{array}\right]$$ (7)

which is simply the union of the 5 distinct spectra of the individual modules. Thus, there are five eigenvalues that are separated from the rest. Their respective values show the module sizes and their respective multiplicities correspond with how many modules of that size are present in the network.

In the next step, we produce an unperturbed modular network using the stochastic block model/random matrix approach introduced previously. The results are shown in Fig. 4(b), with the network having five modules with connection probability p = 0.6 and sizes 16, 32, 16, 32, 64. The spectrum, marked in crosses, shows the same eigenvalue pattern, but the eigenvalues scale as pN (mean values around which the eigenvalues fluctuate: 1 large mean eigenvalue at 64 × 0.6 = 38.4, 2 large mean eigenvalues at 32 × 0.6 = 19.2, and 2 large mean eigenvalues at 16 × 0.6 = 9.6). Further, we now introduce perturbation or intermodule connection probability of 0.1. The spectrum, marked in circles, continues to echo the same pattern, though as the intermodule connectivity increases, the eigenvalues move away from the means, showing larger randomness in structure.

Finally, as shown in Fig. 4(c), we generate a hierarchical network with three hierarchical levels, and unequal module sizes. At the coarsest level is a 256 node network, at the next level three 64 node sub-networks further divide into 32 node finest level networks, and a 64 node subnetwork divides into four 16 node finest level subnetworks. There are three hierarchical levels: the coarsest level has 4 modules, the second level has seven modules, and the finest level has ten modules. The spectrum fingerprints this: there are ten large eigenvalues, and three gaps signifying three hierarchical levels.

Next, we show that this finding can be used in an algorithm to reveal the hierarchical-overlapping modularity of a system. Specifically, we demonstrate the algorithm using the unequal modules hierarchical network example just discussed, Fig. 4(c).

4.3. Module Identification.

The module identification method is based on a generalization of a technique that we developed to reformulate design optimization problems into feasible and tractable subproblems [29] and further refined to address the problem of modularity detection in complex networks [25,26]. We briefly review it here. It is similar to the family of spectral graph partitioning problems in complex networks [24], but we do not impose the strict partitioning assumption. Instead, we allow nodes to be part of multiple modules.

The method contains three aspects. First, the Eigen Value Decomposition (EVD) of the adjacency matrix is computed as $\mathbf{A}={\mathbf{VDV}}^T$. If A has N nodes, then V is the N × N orthonormal matrix of its eigenvectors and D is an N × N diagonal matrix of its eigenvalues, with the eigenvalues arranged in a decreasing order. Now, the connectivity of each node with other nodes is expressed as a vector in space as a linear combination of an eigenvector component times the corresponding eigenvalue as

$${\mathbf{a}}_i=[v_{i1}{\lambda }_0,v_{i2}{\lambda }_1,\dots v_{\mathit{iN}}{\lambda }_{N-1}]$$ (8)

as in Ref. [25]. Thus, connectivity is now expressed as a function of position in space.

Second, we perform a dimensionality reduction on the original adjacency matrix by preserving the k largest eigenvectors and eigenvalues to produce a reduced approximation of the node vectors as

$${\mathbf{a}}_i^{(k)}=[v_{i1}{\lambda }_0,v_{i2}{\lambda }_1,\dots v_{\mathit{ik}}{\lambda }_k]$$ (9)

Using the results presented in Sec. 4.2, k is chosen as follows:

• (1)Plot the indexed spectrum of the system's adjacency matrix A by arranging its eigenvalues in decreasing order.
• (2)Compare the plot to the spectrum of a random graph of the same size and average node degree; if the two correspond, there is only one principal eigenvalue sharply separated from the rest, and there is no modularity.
• (3)For a system with modularity, there will be a large gap between the kth and kth + 1 eigenvalues. Retain this k (or k + 1) as the number of values and vectors to compute an optimal approximation of the system; this k value is also the number of modules in the system.
• (4)For a system with hierarchical modularity, eigenvalues will be clustered in groups, with large gaps between these groups. Identify these indices k where large gaps occur between successive values. Each k value corresponds to the number of modules at a specific hierarchical level in the system.

Preserving the k largest vectors implies we are searching for k modules. A real world engineering system will not have a spectra that is as clear as the idealized models. As we will show in Sec. 5, the Pratt and Whitney aeroengine model spectra shows aspects of randomness and hierarchical modularity present together. Thus, the above procedure can provide a heuristic to select the number of modules (actual number of subsystems) during system decomposition, a parameter that is left for the user to choose a priori by many system decomposition algorithms.

The dimensionality reduction step is essential to identify redundancy in the adjacency matrix. In an adjacency matrix, each of the N nodes is a separate dimension. However, all N dimensions are not needed to calculate modularity as the number of modules will always be lower than N. In a module, two nodes with many common neighbors or the same set of neighbors are likely to fall in the same module, while two nodes that do not share common neighbors are likely to fall in separate modules. If two nodes have exactly the same set of neighbors, then there are dependent rows and columns in the matrix. If they share many common neighbors, then their vertex vector representations will share high dot products. In either case, this redundancy in the matrix means that there is a lower number of dimensions that can be used to represent the modular organization of the system. This redundancy in the graph matrix is used to compute a linear least squares, optimal, lower dimensional approximation of the original matrix by retaining the k largest eigen (singular) vectors and eigen (singular) values. These, when arranged in decreasing order, capture the relative information content that each orthogonal dimension contains about modular organization.

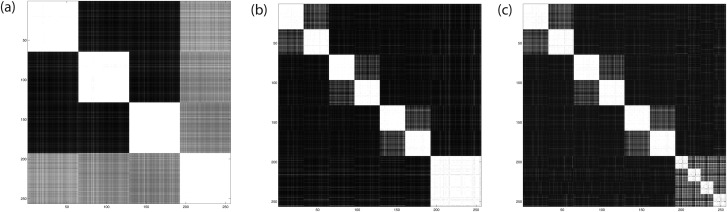
Finally, to find the modules, dot products are computed between all the k reduced vector representations of nodes, resulting in a dot product or cosine matrix. The higher the cosine between two node vectors, the higher the probability that they belong to the same module. The lower the cosine, the higher the probability that they belong to different modules. With the cosine matrix suitably reordered to reveal the highly connected groups of nodes along the block diagonal (We provide an algorithm for reordering in Ref. [25]), we can identify the modular hierarchical-overlapping organization in the network. Fig. 5 shows the reordered cosine matrices after performing the modularity identification using k = 4, 7, 10, respectively, for the hierarchical network shown in Fig. 4(c). Note that when k = 4, the coarsest hierarchical arrangement is visible, when k = 7, the second hierarchical level is visible, and when k = 10 the finest hierarchical level is visible.

Fig. 5.

Performing module identification for hierarchical networks using the spectral algorithm. Reordered cosine matrices shown for hierarchical network of Fig. 4(c), with (a) k = 4, (b) k = 7, and (c) k = 10. k values correspond to the largest gaps in the spectrum, and at each k value the hierarchical organization of nodes at the three hierarchical levels is shown.

5. Results: Aeroengine System Analysis

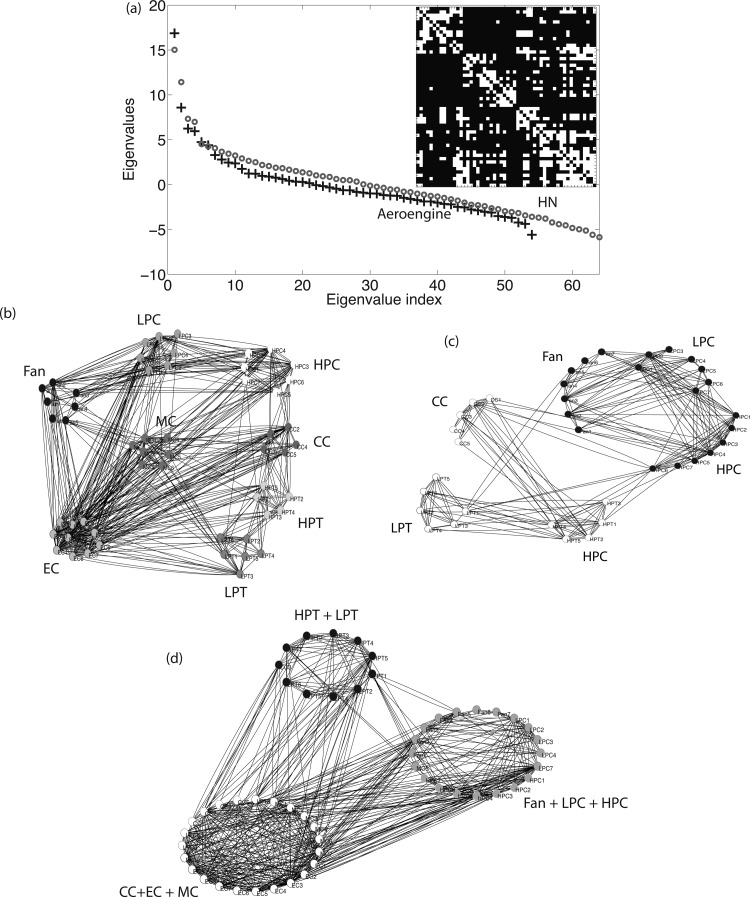
In this section, we present detailed results on applying the method to study the hierarchical modularity properties of a Pratt and Whitney aircraft engine [16]. Prior knowledge of the existing system modules allows us to verify the validity of our approach. The engine has 54 components forming 8 subsystems: Fan System (FS), Low Pressure Compressor (LPC), High Pressure Compressor (HPC), Combustion Chamber (CC), High Pressure Turbine (HPT), Low Pressure Turbine (LPT), Mechanical Components (MC), and Externals and Controls (EC). We create a binary, unweighted design dependency adjacency matrix based on the DSM used in Ref. [16]. We think of each component as a node in a graph, with an edge existing between nodes i and j if, by reading across rows of the equivalent adjacency matrix, node i depends on node j for functionality. Equivalently, node j needs to feed into node i for functionality. The purpose is to identify the modular and integrative subsystems, based on the design dependency data, and also to study the presence or absence of hierarchy in the subsystem interactions. Figure 6(b) shows the unweighted symmetric adjacency matrix for the engine. The average node degree for the aeroengine model is 10.5.

Fig. 6.

Pratt Whitney Aircraft Engine: (a) Spectrum of eigenvalues of aeroengine model compared with spectrum of a 3-level hierarchical network. Inset shows the original adjacency matrix. (b) Original definition of clusters, with 8 predefined subsystems; note that distinct clusters share high density of links and this fails to bring out the latent natural clustering. (c) clusters plotted using 2D reduced vector representation showing 2 main clusters identified by algorithm at highest hierarchical level, using Eq. (9) and k = 2; data plotted without EC and MC systems that are known to be integrative. (d) 3D reduced vector representation showing 3 main clusters at next hierarchical level, using Eq. (9), and k = 3; data plotted with the EC and MC systems that are densely linked to both the Fan-LPC-HPC cluster and the CC-LPT-HPT cluster.

For the study, we compare this system to other idealized systems of similar size and varying complexity. We generated five model networks: (a) a random network of 54 components with average node degree 10; (b) a regular network of 54 components with node degree 10; (c) a perfectly modular network of 54 components, with module sizes corresponding to the real engine, but the nodes fully connected to each other within a module and sharing no dependencies with any other module; (d) a modular network of 56 nodes, with average node degree 10, and with 8 modules of 7 nodes each, using our modular network generation model; and (e) a hierarchical modular network with 64 nodes at the highest level, 2 modules of 32 nodes at the mid level, and 4 modules of 16 nodes at the lowest level, using our hierarchical modular network generation model. We fingerprint the aeroengine network topology by superimposing the spectra of the model networks with the spectrum of the aeroengine, similar to Ref. [34], as the model networks are generated using the same average node degree and number of nodes as the aeroengine. Since the largest eigenvalue and the distribution of eigenvalues is classically known to be bounded and characterized by the node degree characteristics, these comparisons are structural and not merely visual.

The analysis of the modularity fingerprint of the aeroengine spectrum revealed previously unidentified levels of organization in the system. The comparison of the spectra of these model networks with the spectrum of the aeroengine network showed that the aeroengine spectrum was closest to the hierarchical network [model (e) above]. The first few largest eigenvalues appear in clusters with large eigengaps, shown in Fig. 6(a), but a large gap between the first and the second eigenvalue shows a high degree of randomness [model (b) above]. Thus, overall, the aeroengine architecture shows the presence of hierarchical modularity, accompanied by a high degree of intermodular interaction that takes the system towards a random architecture.

Although the accepted and known modular structure of the aeroengine contains 8 modules, the spectrum shows large gaps after the 2nd, 4th, and 6th eigenvalues, suggesting 2 modules at the first hierarchical level, 3-4 modules at the next, and 5-6 modules at a third level of hierarchy. We varied the k value from 2 to 8 and performed modularity analysis of the aeroengine using the algorithm described in Sec. 4.3.

Our first main finding was that at k = 8, both the original dot product matrix and the reordered cosine matrix show that the predefined 8 subsystems do not emerge as clearly separated modules. Instead, there are high amounts of overlaps between subsystems. Figure 6(b) plots the network of 54 subsystems with the 8 predefined systems plotted as 8 modules. As is evident, even visually, there is a high density of interaction between them, and the modules are not at all obvious.

To understand the hierarchical organization in detail, Figs. 6(c) and 6(d) show the network plots resulting from the application of the algorithm defined in Sec. 4.3 using k = 2 and k = 3, respectively. The results clearly show that due to high interaction between two or more modules, the actual number of modules in the system is lower than the 8 known modules [16]. At the highest hierarchical level, k = 2, the FS, LPC and HPC systems emerge as a large integrated module, and the other systems emerge as another integrated module, Fig. 6(c). Note now the sparse interaction between the CC-LPT-HPT systems and the tightly coupled FS-LPC-HPC systems.

At the next hierarchical level, k = 3, the FS, LPC, and HPC systems continue to emerge as a large integrated module (module 1), while the LPT and HPT emerge as another module (module 2), and the CC, EC and MC systems emerge as a third module (module 3), Fig. 6(e). This shows that the larger integrated module of the previous hierarchical level breaks into two at this level. Additionally, many of the individual components from these systems show clear overlaps [for further details, see discussion on hubs, and Fig. 7(b)]. For example, specific components from the LPC, HPC, FS, and CC systems appear in overlaps between modules, and components from the EC and MC systems appear in all three modules, establishing them as strongly integrative. As the k value is further increased to k = 8, these 3 large subsystems break into smaller subsystems. However, at k = 8, the 8 predefined subsystems are not retrieved. The 8 modules that emerge are finer granularity distinctions of these three large modules. This clearly shows that the predefined subsystems and their interactions may lead to unidentified and emergent levels of organization in the system.

Fig. 7.

Eigenvector and degree centrality of aeroengine components

5.1. Design, Management, and System Safety Implications.

5.1.1. Hierarchical Organization Affects the Engineering Design Team Structure.

Instead of simply classifying a certain system as modular or integrative, our results show that subsystems can be hierarchically organized and have overlaps with other subsystems. Defying a coarse decomposition, some modular subsystems share nodes (components) with other modular subsystems. This arrangement, revealed by our module finding method, can be used to organize and better manage and plan design team organization and interaction. For example, the data and the analysis clearly show that the FS, LPC, and HPC subsystem design teams need to be tightly integrated even though they are purportedly modular subsystems, and the LPT design team needs to be tightly coupled to both the CC and the HPT design teams, even though all three subsystems are purportedly separate subsystems.

It is worth noting here that when Sosa et al. [15] analyzed the superposition of the design interface matrix of the aeroengine (physically meaningful interfaces) with the design team interaction matrix (team interactions based on the product architecture), they found a large number of anomalies where (a) existing design interfaces were not supported by team interactions, and (b) there were team interactions planned with no design interfaces between two components. On analyzing the distribution of these, we identified that out of the total 220 (100%) entries in the matrix where an existing design interface was unsupported by a team interaction, 65 (about 30%) of these entries occur between the Fan-LPC-HPC subsystems, and 26 (about 12%) of these entries occur between the CC-LPT-HPT subsystems, with 47 entries occurring between MC and all other subsystems, and 92 entries between the EC and all other subsystems. These analyses clearly show that the missing entries, i.e., team interactions that should have existed as per the physical product architecture, are not distributed evenly across the entire system. Forty two percentage of these are concentrated within two larger level subsystems: the FS-LPC-HPC and CC-LPT-HPT. Similar findings have been reported by other, very recent studies on product architecture modularity and distributedness in other related contexts [35,36].

This finding has important management implications. For any complex engineering system, if there are unidentified emergent hierarchical levels of organization, then identifying and making such organization explicit can guide the manner in which team interactions are planned. For example, in the aeroengine example, it is clear that the larger level hierarchical FS-HPC-LPC cluster and the CC-LPT-HPT cluster can be better managed by having members of both design teams solely support the interfaces. The existence of product design team “hubs” would also reduce errors and defects in complex product design and development projects while increasing the capacity of the product development process to recover from changes to individual tasks [18].

5.2. Hub Components as Modular Overlaps Affect System Design, Safety and Resilience.

Hubs are defined as high degree centrality components that play critical integrative and coordinating roles in the system. Hubs have been classified to be of two types [37]: provincial and connector. Provincial hubs are high degree nodes within a single module that share most connections with other nodes from the same module. Obviously, they do not fall in an overlap between multiple modules. Connector hubs are high degree nodes that are connected to nodes from multiple modules; i.e., they fall in overlaps between modules. Thus, connector hubs are responsible for making the system more integrative, and less modular.

The detection of hubs is related to the issues of system safety and resilience or tolerance to ‘attacks' on the hub nodes [18,38]. There may also be a trade–off between system quality [39] and tolerance to attack. Clearly, if a provincial hub fails, there is high chance of a module failure in the system, but if a connector hub fails, there is a high chance of systemic failure. The basic idea is that if a component is highly connected to many other components, and sits in an overlap between multiple modules, then this component needs special attention during the design stage due to the integrative and coordinating roles it plays in the system. Further, as a critical component, its failure can have a serious effect on the functioning of the entire system. For example, it has been shown the in the context of scale free networks that a planned attack on these hub nodes can quickly result in a systemic failure [38]. While we do not examine in- and out-degree of nodes and their relation to system resilience, other research shows “asymmetry” and “skeweness” of node degree are also closely related to the robustness and sensitivity of large-scale networks to modifications in the nodes [18].

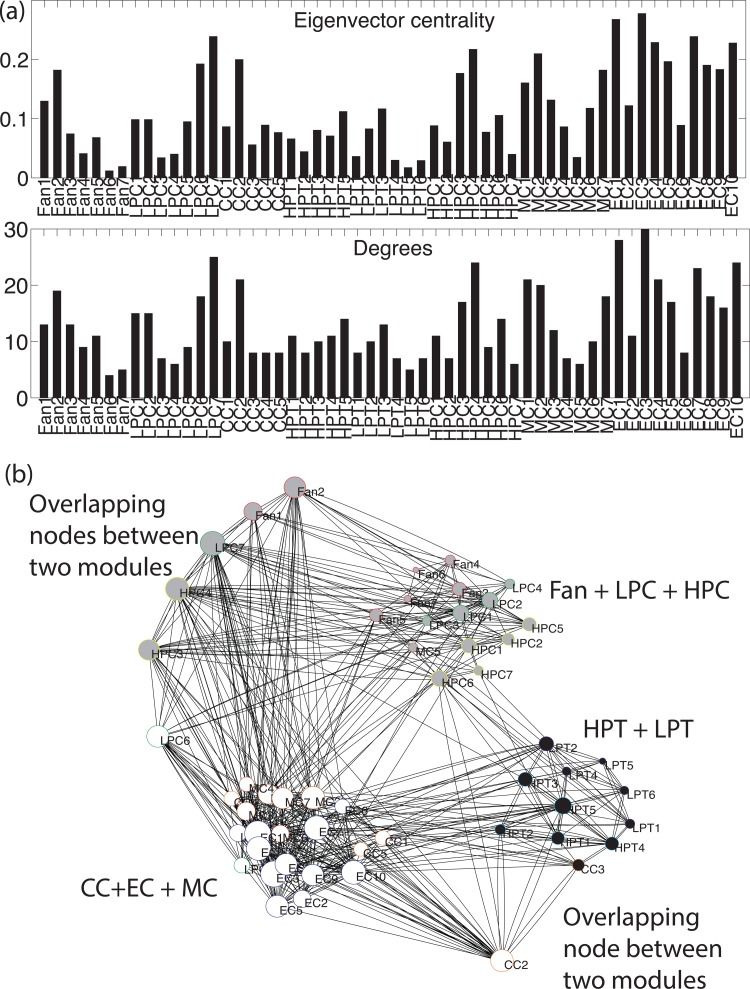
To relate the modularity analysis to identification of hub nodes, we compute the centrality of each node in the system as $x_i=\frac{1}{\lambda }\sum _{j=1}^n{A}_{\mathit{ij}}{x}_j$, where x_i is the centrality of node i which is made proportional to the average of the centralities of i's neighbors in the system, and 1/λ is a constant of proportionality. In other words, the centrality of each node measures the degree of its overall influence in the system, i.e., a connection to a highly connected component should matter more and have more influence than a connection to a not so well connected component. This is the well known eigenvector centrality [24], which when written in matrix form becomes λx = Ax. In other words, the vector of centralities x is an eigenvector of matrix of A with eigenvalue λ. For obtaining non-negative centralities, it can be shown by the Perron-Frobenius theorem, the centrality vector corresponds to the first (all positive) eigenvector with the largest eigenvalue. Relating this to our analysis of modularity presented in previous section, this is simply the eigenvector corresponding to the largest eigenvalue in the EVD/Singular Value Decomposition (SVD) of A.

In the algorithm described in Sec. 4.3, a cosine matrix captures the pairwise dot products between vectors representing node connectivity. If a node falls in an overlap between two modules, it will share high dot products with nodes from both modules. When the cosine matrix is reordered to make it as block diagonal as possible to reveal the modules, these high degree connector nodes, which fall in overlaps between modules, will be revealed as off-diagonal high cosine rows or columns, Fig. 7(b)).

Combining the eigenvector centrality score and the results of our algorithm, which identify the connector nodes, we see that the nodes that fall in an overlap between multiple modules, and also have a high eigenvector centrality score, are connector hubs that push the system towards an integrative structure. This correlation has also been observed in product development networks [40].

The results of our analysis show that certain specific components from specific subsystems appear as connector hubs, i.e., they show high coupling with other subsystems, despite the fact that the subsystem they belong to is itself modular. That is, these components are part of more than one module. For example, as shown in Fig. 7(b) [sizes of nodes correspond to eigenvector centralities of nodes], specific components of the FS (for example, exit guide vanes and cases), LPC (for example, bleed BOM and intermediate case), HPC (for example, blades, inner shrouds and seals, variable vanes), and CC (for example, diffuser) subsystems show very tight coupling with the full system, even though the FS, LPC, and CC are purportedly modular subsystems. These components are responsible for “pushing” the entire system towards an integrative architecture, while the HPT, and LPT are clearly much more modular (not considering the MC and EC systems, which are fully integrative). During the design stage, these hub components sitting inside modular subsystems will need extra focus because they are responsible for increasing the complexity of the system and bringing down architectural modularity. These components increase design complexity not just because they have many dependent components within their own modules; they are complex because they have many connections outside their modules [41] and may provide subordinate functions to other components and subsystems.

Perhaps most importantly, because they participate in multiple functions across (intended) modular systems, they are critical components. Malfunctions to these components would have serious flow-on effects beyond their specific subsystems, and a targeted or specific attack on these components and their failure can lead to systemic failure. In the design stage, therefore, an important analysis is to first identify if there are any such emergent hub components that bring down architectural modularity, push up the integrative architecture, and play multiple functional roles. The related important design decisions then become whether it is possible to redesign some of the interfaces so as to reduce the vulnerability of the system via these components, or increasing the reliability of these components if their “hubness” cannot be significantly reduced.

6. Discussion and Conclusions

The field of complex networks, which uses graph theory to study complex systems, shows that all complex systems, natural or artificial, show the presence of hierarchical-overlapping modularity. Such a structural configuration has deep relationships with the functional configurations of these systems. Product architectures are no exception. We have exploited this connection to identify a new way to characterize the modularity of an engineered product or system. We have shown how our methodology correctly identifies the existence or lack of existence of modules in random, regular, modular, and hierarchically modular graph models. We further showed that ideal graph models and eigenvalue spectra can be used to correctly identify the modularity characteristics of a known complex product, an aeroengine. More important, we showed that modularity is a characteristic governed by multiple properties, one that is not easily captured by a single metric. Conscious efforts at redesign can be initiated to make the system more modular, where the number of modules and hierarchical modules are determined by the eigenvalue spectra as described in the mathematical proof and empirical results of Sec. 4.2. However, if despite redesign efforts, the signature does not change significantly, then this shows that despite desiring high levels of modularity, there can be theoretical or empirical limits on how much modularity can be achieved. Our method will make this choice explicit to the engineer.

Further, our analysis of the aeroengine shows distinctly identifiable levels of hierarchical modularity, which was not originally revealed, and were in fact masked, in the initial component-module-system description [16]. These multiple levels of organization show us which subsystems are modular and which ones are integrative, along with specific components belonging to otherwise modular subsystems that are responsible for making the entire system function. Revealing this can aid design development, concentrating on specific systems for the possibility of testing whether they can be redesigned to be made more modular. Finally, the results show that the strict partitioning requirement of modularity identification algorithms can produce inappropriate results from an engineering design perspective, such as not revealing emergent hub nodes. By not permitting nodes to overlap into multiple modules, algorithms that assume strict partitioning may characterize systems as having higher degree of modularity (and therefore reliability) than is actually warranted.

We believe that our work points in the direction of a single modularity metric, but highlights that such a metric would be an aggregate that must attend to multiple criteria affecting modularity, such as degrees of randomness, modularity, hierarchy and overlap, rather than being based on single or isolated measurements of a system property that describe modularity. For example, the well known Newman modularity metric Q measures modularity of a complex system by comparing it to another random system with the same node degree distribution, number of nodes/edges, and other such properties: the idea is to define the degree of modularity of a system by comparing it to a random system with exactly the same properties but no modularity [24]. However, this still leaves the problem of characterizing hierarchy and overlaps open. Since the spectra of matrices and graphs contain information on these multiple properties, the method described in this paper uses the spectra of graphs and networks to characterize modularity of product architecture, thereby capturing the multiple organizational properties that complex systems are typically characterized by.