Subject-Specific Finite Element Modeling of the Tibiofemoral Joint Based on CT, Magnetic Resonance Imaging and Dynamic Stereo-Radiography Data in Vivo

Short abstract

In this paper, we present a new methodology for subject-specific finite element modeling of the tibiofemoral joint based on in vivo computed tomography (CT), magnetic resonance imaging (MRI), and dynamic stereo-radiography (DSX) data. We implemented and compared two techniques to incorporate in vivo skeletal kinematics as boundary conditions: one used MRI-measured tibiofemoral kinematics in a nonweight-bearing supine position and allowed five degrees of freedom (excluding flexion-extension) at the joint in response to an axially applied force; the other used DSX-measured tibiofemoral kinematics in a weight-bearing standing position and permitted only axial translation in response to the same force. Verification and comparison of the model predictions employed data from a meniscus transplantation study subject with a meniscectomized and an intact knee. The model-predicted cartilage-cartilage contact areas were examined against “benchmarks” from a novel in situ contact area analysis (ISCAA) in which the intersection volume between nondeformed femoral and tibial cartilage was characterized to determine the contact. The results showed that the DSX-based model predicted contact areas in close alignment with the benchmarks, and outperformed the MRI-based model: the contact centroid predicted by the former was on average 85% closer to the benchmark location. The DSX-based FE model predictions also indicated that the (lateral) meniscectomy increased the contact area in the lateral compartment and increased the maximum contact pressure and maximum compressive stress in both compartments. We discuss the importance of accurate, task-specific skeletal kinematics in subject-specific FE modeling, along with the effects of simplifying assumptions and limitations.

1. Introduction

Finite element (FE) modeling is a powerful tool for studying joint and tissue mechanics, as it enables manipulation of variables and simulation of situations that may be challenging or infeasible to evaluate clinically or experimentally. The accuracy of FE model solutions depends on well-defined anatomical geometry, material properties and boundary conditions [1]. Given the considerable inter-subject variability in tissue structure morphology, personalized analyses and insights would require subject-specific FE modeling [2]. In vivo FE modeling efforts have been limited by difficulties in acquiring and analyzing multimodality data for model construction and validation, including proper co-registration and integration of all necessary data. Recent advances in the fields of medical imaging and image reconstruction have increased the potential to incorporate accurate tissue morphology and boundary conditions into in vivo subject-specific models [3].

Nevertheless, the veracity of FE model predictions hinges upon at least two challenging aspects: accurate representation of joint kinematics during functional tasks, and validation or verification of the model with experimentally measurable parameters obtained in vivo. Previous in vivo tibiofemoral (TF) FE modeling efforts have created models without sufficiently considering the functional joint kinematics involved in the joint loading process [4,5]. Studies have incorporated skeletal kinematics from either nonsubject-specific data [6–8] or skin surface marker measurements [9,10]—the latter are prone to soft-tissue artifacts [11] due to marker movement [12,13] and inaccurate marker positioning on the skin relative to the bone [14,15]. Two FEM studies have employed advanced imaging techniques to acquire skeletal kinematics: Beillas et al. [7,8] used X-ray imaging that required surgical implantation of radio-opaque markers into the bone; Yao et al. [16] utilized a loading device to exert a force on the knee as it was undergoing magnetic resonance imaging (MRI) in a supine position. While these studies were successful attempts to incorporate task-specific [7,8] or load-specific [16] kinematics, quantitative verification of their FE model predictions was not conducted. Validation or verification is a crucial step before making interpretations based on model predictions or using the model for clinical applications [17,18]. Conventional measures for FE model validation, such as contact pressure [3], cannot be reliably acquired without invasive procedures and are not applicable to in vivo subject-specific models. However, it is possible to estimate the contact area and centroid in vivo without invasive procedures with a technique we present here.

This study was motivated by the need for a validated subject-specific FE modeling methodology to study joint mechanics and functions in response to various musculoskeletal injuries and their treatments. While the methodology can be generalized to other articulating joint structures, this study focused on the TF joint, meniscus injury and meniscectomy. The meniscus is an integral component of the knee, playing a vital role in stability, proprioception, lubrication and load distribution [19–22]. It has been shown that meniscectomy, a common treatment for meniscal injuries and one of the most frequently performed orthopaedic procedures, can lead to degenerative changes of the articular cartilage in the knee [17,20,23–26]. In order to better understand the relationship between meniscectomy and the onset as well as progression of articular cartilage damage, it is important to first assess the joint and tissue mechanical changes involved—a problem well suited for investigation based on FE modeling.

Specifically, we aimed to explore subject-specific FE modeling of the TF joint based on in vivo measurements of tissue morphology from high-resolution MRI and three-dimensional (3D) skeletal kinematics from dynamic stereo-radiography (DSX). This latter technology provides an ability to measure skeletal kinematics during functional tasks with sub-millimeter accuracy [27]. We proposed a novel in situ contact area analysis (ISCAA) technique, allowing the use of a subject's own data to validate the subject-specific FE model.

2. Materials and Methods

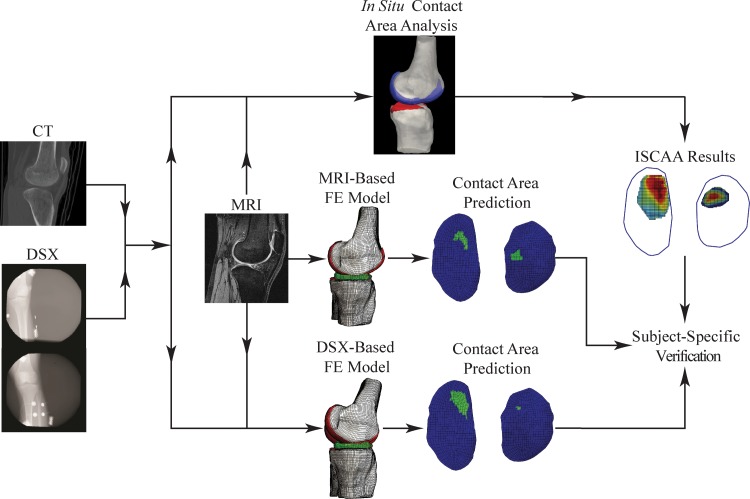
The knee morphological and kinematic data for FE modeling were from an IRB-approved meniscus allograft transplantation experimental study. We used the data of one subject (female, age 19) who had previously undergone a left knee lateral meniscectomy. Data for both the meniscectomized left knee and intact right knee, collected prior to the transplantation surgery, were used. An overview of how multimodality data (DSX, CT, and MRI) were acquired and integrated for model creation and verification is presented in Fig. 1. The individual procedures from data acquisition to model verification are described as follows.

Fig. 1.

A flow chart of the FE model development and verification process incorporating multimodality data

2.1. Data Acquisition.

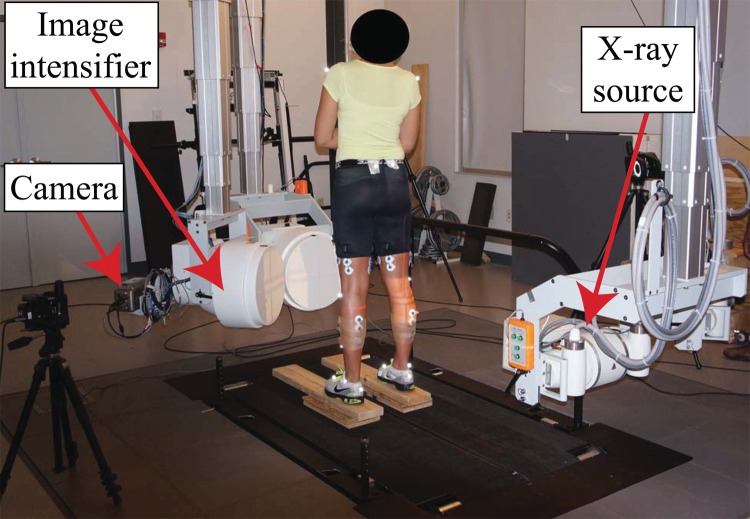
A DSX system was used to acquire 3D TF skeletal kinematics data (Fig. 2), with a precision of 0.2 mm in translation and 0.2 deg in rotation [27]. The particular static standing trial data used in this study were collected while the subject held a static, natural, upright posture.

Fig. 2.

Experimental setup for measuring 3D TF skeletal kinematics using a dynamic stereo-radiography system

A bilateral computed tomography (CT) scan (GE Medical Systems Lightspeed Pro 16, Waukesha, WI) of the subject's knees was obtained with the following specifications: pixel size = 0.586 × 0.586 mm², slice thickness = 1.25 mm, pixel resolution = 512 × 512 pixels, field of view (FOV) = 30.0 cm, number of slices = 123, excitation voltage = 120 kV, current-time = 402.8 mAs. The CT data were imported into Mimics 14.0 (Materialise, Ann Arbor, MI, USA) and segmented slice-by-slice to create a 3D bone model for both the femur and tibia. A custom model-based tracking software program was used to create a virtual testing configuration replicating that of the actual physical DSX system. The 3D bone models produced from CT were placed within the virtual environment to, through a ray-tracing algorithm, create digitally reconstructed radiographs (DRRs). A volumetric image-matching algorithm was then employed in a co-registration process between the DRRs and DSX images, optimizing the 3D position of the DRRs relative to the corresponding bone in the DSX images for each frame. Additional details on this model-based tracking technique can be found in a previous publication [28].

An MRI scan (Siemens Trio 3.0 T, Washington, DC) of each knee joint was acquired while the subject was in a nonweight-bearing, supine position using a sagittal 3D dual echo steady state water excitation (DESS-WE) sequence. The MRI scan specifications were: pixel size = 0.365 × 0.365 mm², slice thickness = 0.7 mm, pixel resolution = 384 × 384 pixels, FOV = 14.0 cm, number of slices = 160.

2.2. Model Geometry.

The MRI data were imported into Mimics 14.0 for creation of 3D models of the femur, tibia, femoral cartilage, tibial cartilage, and menisci. Once the 3D models were created, they were imported into TrueGrid (XYZ Scientific, CA, USA) for manual linear hexahedral meshing. Each component was meshed separately and then imported into ABAQUS CAE 6.9 (Simulia, RI, USA), where they were combined into a single FE model for an implicit static analysis. Figure 3 shows an example of the FE model geometry development process. The numbers of elements in the FE models of individual components in each knee are listed in Table 1.

Fig. 3.

FE model geometry development sequence for the tibia

Table 1.

Numbers of linear hexahedral elements in individual model components

	Meniscectomized Knee	Healthy Knee
Femur	41,984	76,308
Tibia	61,440	87,852
Femoral Cartilage	5,632	3,648
Tibial Cartilage	11,264	2,816
Lateral Meniscus	16,896	2,352
Medial Meniscus	16,896	2,112
Total	154,112	175,088

2.3. Material Properties.

Tissue material properties were taken from literature. The femur and tibia were modeled as rigid structures, which greatly reduced the computational time and has been shown to have minimal effect on the model predictions [1,4,6,9,23,29–39]. Articular cartilage is known to be an anisotropic, biphasic material with a time constant approaching 1500 s [40,41]. The compressive loading in this study was quasi-static. It has been shown that under this condition, the biphasic response of cartilage can be negligible and the single-phase linear isotropic constitutive law be applicable [40,41]. Therefore, cartilage was modeled as a homogeneous, elastic, linearly isotropic material [1,2,4–7,9,16,23,25,30,32,33,35–39, 42–46] with a modulus of 15 MPa [4,9,25,30,35,45] and a Poisson's ratio of 0.46 [31–33,47,48].

For the menisci, a transversely isotropic constitutive law was used in order to emphasize the dominant role played by the circumferential fibers in load distribution and function [19,21,49–51]. The menisci were therefore modeled as linearly elastic, transversely isotropic materials [1,2,4,9,10,16,25,30,34–36,39,43–45, 52], where the modulus and Poisson's ratio were 20 MPa and 0.2, respectively, in the radial and axial directions, and 140 MPa and 0.3, respectively, in the circumferential direction [4,30,45,52]. Time dependent effects of the cartilage and menisci properties were not considered due to the quasi-static nature of the models [4,7,8,23,30,32,35,40–42,48,53,54]. The anterior and posterior meniscal roots for each meniscus were modeled as linear springs with spring constants of 2000 N/mm [9,23,25,30,35,36,45,52].

2.4. Kinematics and Loading Conditions.

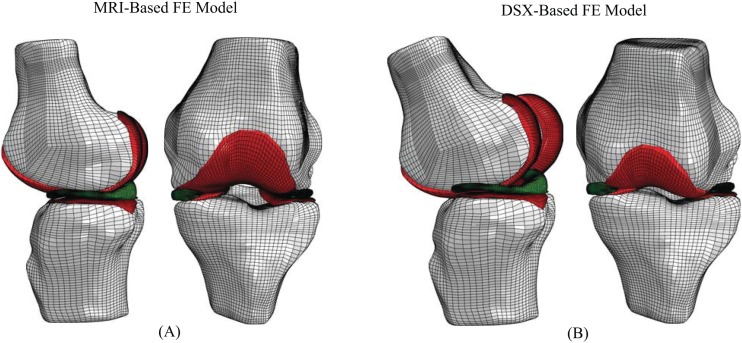
Two FE models were created for each knee, one incorporating MRI-based supine kinematics and the other DSX-based standing kinematics (Fig. 4). The first FE model developed for each knee was based on the MRI data using the procedure described above, resulting in a model in the supine MRI position. In order to incorporate the standing, DSX-based kinematics, the DSX-acquired kinematics had to be transformed into the MRI-based coordinate system. For both the femur and tibia, the CT-based 3D model was co-registered to the MRI-based 3D model using Geomagic Studio 10 (Geomagic, North Carolina, USA). A manual n-point registration was completed by choosing three landmark points on the surface of the CT 3D bone model and then choosing the same three points on the surface of the MRI 3D bone model. This was done to create a close initial estimate for an automatic global registration process. The automatic global registration process was then executed, minimizing the co-registration error between the two 3D models. The average ( ±SD) error in the co-registration process for the bones was 0.472 (±0.305) mm. This procedure output a transformation matrix from the CT coordinate system to the MRI coordinate system (CT-MRI). One output of the model-based tracking process was a transformation matrix from the laboratory coordinate system to the CT coordinate system (lab-CT). The lab-CT and CT-MRI transformation matrices for each respective bone were combined to yield a transformation matrix from the laboratory coordinate system to the MRI coordinate system (lab-MRI). These transformations were then applied to each knee's MRI-based supine position FE model to create a model in the DSX-based standing position. The tibial side lab-MRI transformation was applied to the tibia, tibial cartilage and menisci, while the femoral side lab-MRI transformation was applied to the femur and femoral cartilage.

Fig. 4.

Lateral and anterior views of FE models of the meniscectomized knee in (a) MRI-based and (b) DSX-based positions

For both the MRI-based and DSX-based models, the tibia was held in a fixed position while the femur was allowed to move in response to an axial force of half the subject's body weight (275 N) applied to the proximal end of the femur towards the tibia. This force, along with contact pairs and prescribed boundary conditions, determined the “final position” of each model. For the model in the MRI-based supine position, five degrees of freedom (DOF) were allowed for the femur while the flexion-extension was fixed. For the model in the DSX-based standing position, since the prescribed position of the femur relative to tibia is a final, known position from the experimental data, the only DOF permitted was an axial translation, allowing the femur to settle into its final position in response to the force applied. The femoral and tibial cartilage components were tied to the femur and tibia surfaces, respectively, while hard, frictionless contact was assumed for cartilage-cartilage and cartilage-meniscus interfaces [1,4,16,23,30,32–35,37–39,42,43,45,46,48,55]. In all models, a large-strain formulation was used [38,46] to account for potentially substantial strains in the soft tissue components. The contact area between the femoral and tibial cartilage from the resulting FE analysis was used as the measure for verification. The contact centroid was determined on the tibial cartilage for each compartment based on a transverse view of the superior cartilage surface.

2.5. Verification.

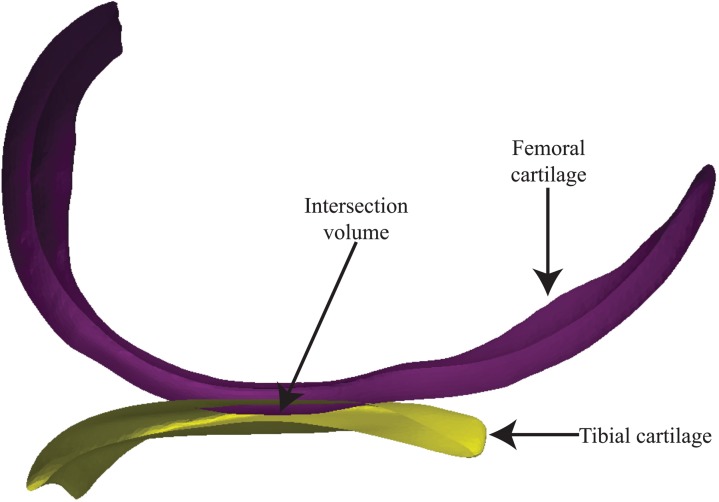
An in situ contact area analysis (ISCAA) method was developed in order to verify the predictions of the FE models using cartilage-cartilage contact as the measure. The femoral and tibial cartilage in the DSX-based standing position was utilized. The cartilage surfaces in the MRI-based supine position were imported into MATLAB 2012a (MathWorks, Massachusetts, USA). Cartilage was transformed into the DSX-based standing position by applying the lab-MRI transformation. The overlapped area between nondeformed femoral and tibial cartilage (Fig. 5) was calculated and projected onto a single transverse plane determined as the least-squares-fit plane of the tibial cartilage, which provided a common reference for comparing the FE model-predicted and ISCAA-assessed contact centroids. The depth of overlap can be used as a surrogate measure of total cartilage strain [56]. The contact centroid for the ISCAA (C_ISCAA) result was calculated and compared to the contact centroids obtained from the MRI-based supine position model (C_MRI) and the DSX-based standing position model (C_DSX).

Fig. 5.

In situ contact area analysis (ISCAA) to determine the contact area, defined as the intersection between femoral and tibial cartilage, by co-registering the MRI-acquired cartilage models with DSX-acquired bone models

For the FE models, the contact centroid (C_MRI or C_DSX) was found by projecting the tibial cartilage on the aforementioned least-squares-fit plane and determining the geometric center in two dimensions (2D). For the ISCAA, the C_ISCAA was found by discretizing the contact area into grid sections (size: 0.368 mm²) and then identifying the section with the smallest weighted-average Euclidean distance to all other sections. Numerically, C_ISCAA was located by the grid section ID (i) resulting from the following optimization procedure:

$$\underset{i}{\mathrm{argmin}}\sqrt{\sum _{j=1}^N\frac{s_{\mathit{ij}}^2}{d_i^2}}$$ (1)

where s is the distance from one grid section i to another grid section j; d is the localized cartilage depression (i.e., the depth of overlap) at a grid section, and N is the total number of grid sections. Note that when cartilage depression d is uniform across the entire contact area, the solution from Eq. (1) would be the geometric center as in the case for C_MRI and C_DSX.

A sensitivity analysis was performed to assess how sensitive C_MRI and C_DSX predictions would be to changes in assumed material properties of the articular cartilage, menisci, and meniscal roots. Seven material property values (elastic modulus and Poisson's ratio of articular cartilage, elastic modulus and Poisson's ratio of meniscus in the circumferential direction, elastic modulus and Poisson's ratio of meniscus in the axial and radial directions, spring stiffness of the meniscal roots) were each varied by ±5% and ±10%, resulting in a total of 28 model variants.

3. Results

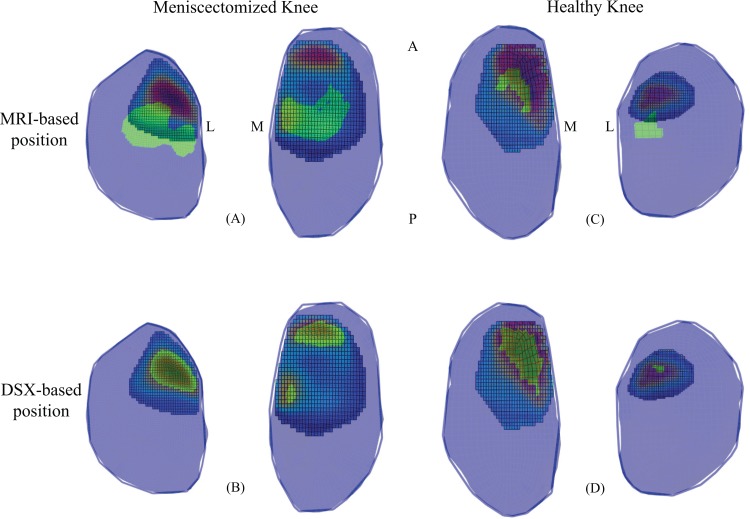
When overlaying the FE model predictions for contact centroid with the ISCAA results, the DSX-based position models were in better agreement with the ISCAA results compared to MRI-based position models, as evidenced in Fig. 6 by the alignment of the FE contact area prediction with the areas of greater contact depth in the ISCAA.

Fig. 6.

Left: meniscectomized knee ISCAA results overlapped with (a) MRI-based position and (b) DSX-based position FE model predictions. Right: healthy knee ISCAA results overlapped with (c) MRI-based position and (d) DSX-based position FE model predictions. The green area represents the FE model contact area predictions, while the other colors are the color coded ISCAA estimate. Penetration depth increases from blue to red. M = Medial, L = Lateral, A = Anterior, P = Posterior.

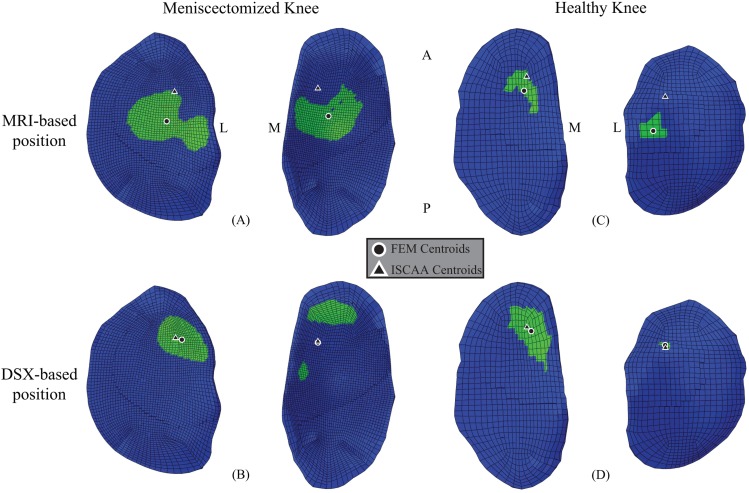
With C_ISCAA as the benchmark estimate for the contact centroid, C_DSX predicted the contact centroid more accurately than C_MRI (Fig. 7). The mean absolute distance from C_FE to C_ISCAA was 6.395 mm (SD: 2.296 mm, range: from 3.242 mm to 8.234 mm) for the MRI-based FE models, and 0.747 mm (SD: 0.457 mm, range: from 0.205 mm to 1.307 mm) for the DSX-based FE models. C_DSX estimate was closer to C_ISCAA by 85% (±17%), on average, than C_MRI (See Table 2).

Fig. 7.

Left: contact centroid of ISCAA estimation and (a) MRI-based and (b) DSX-based FE model predictions for left, meniscectomized knee plotted on FE tibial cartilage. Right: contact centroid of ISCAA estimation and (c) MRI-based position and (d) DSX-based position FE model predictions for right, healthy knee plotted on FE tibial cartilage. M = Medial, L = Lateral, A = Anterior, P = Posterior.

Table 2.

Distances (mm) between FEM-predicted and ISCAA-estimated contact centroids

	Meniscectomized Knee		Healthy Knee
	Lateral Compartment	Medial Compartment	Lateral Compartment	Medial Compartment
MRI-based FE model	7.95	6.15	8.23	3.24
DSX-based FE model	0.84	0.21	0.64	1.31

Once the model in the DSX-based position was verified, contact area between the femoral and tibial cartilage (reported as a percentage of the superior surface area of the tibial cartilage), maximum compressive stress and maximum contact pressure were extracted from the FE results and compared between the meniscectomized and healthy knees (Table 3). All three variables, in both the lateral and medial compartments, were greater for the meniscectomized knee compared to the healthy knee. It was also noted that the differences in these three variables between healthy and meniscectomized states were much greater in the lateral compartment than in the medial compartment.

Table 3.

DSX-based FE model predictions of contact area, maximum contact and compressive stresses in meniscectomized and healthy knees

		Meniscectomized Knee	Healthy Knee
Contact Area (%)	Medial	8.3	8.2
Lateral	5.8	0.4
Maximum Contact Pressure (MPa)	Medial	2.95	2.69
Lateral	4.32	0.70
Maximum Compressive Stress (MPa)	Medial	2.86	2.27
Lateral	3.96	0.56

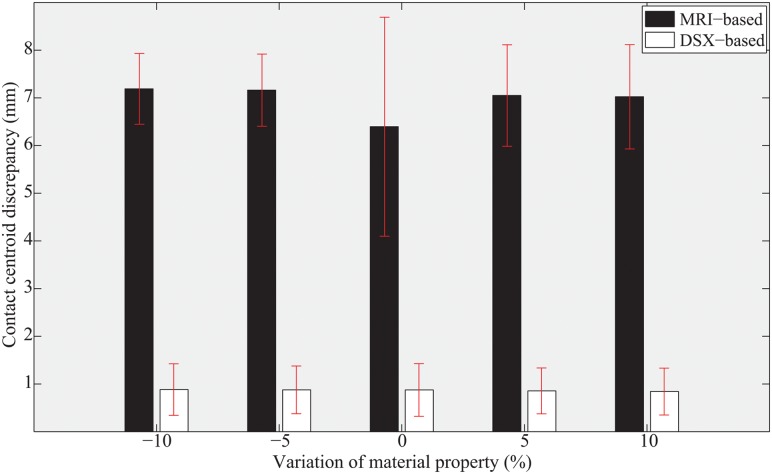
The sensitivity analysis showed that variations of material properties by ±5% and ±10% had no marked effect on the average model-predicted contact centroid locations (Fig. 8). The conclusion that the DSX-based model outperformed the MRI-based model and provided accurate predictions holds for the range of material property variations considered.

Fig. 8.

Average distances between FEM-predicted and ISCAA-estimated contact centroids at different levels of material property variation for both MRI-based and DSX-based models

4. Discussion

The current study presents a novel approach to creating subject-specific FE models of the tibiofemoral joint. This approach distinguishes itself from past efforts in two ways: (a) physiologically realistic weight-bearing states are modeled with high morphological and kinematic fidelity, and (b) the model is verified, in vivo, with a unique technique using the subject's own data.

The FE model of the subject in a standing posture, developed by integrating CT, MR and DSX images, was compared to an MRI-based FE model incorporating supine kinematics—a technique applied in past FE studies investigating tibiofemoral mechanics [4,5]. The contact centroid was used as a benchmark variable to discern the differences between the two FE models. The contact centroid was selected as a variable for verification/comparison since contact pressure and stress are currently infeasible to measure in vivo without surgically invasive procedures (which would also inevitably alter the characteristics of the contact itself). Further, accurate material properties, which are difficult to determine in vivo for the various components in the TF joint, are necessary for prediction of contact pressure and stress. On the other hand, the contact centroid remains largely unaffected by the choice of material properties.

Application of highly accurate task-specific kinematics is critical for achieving accurate FE model predictions, as demonstrated by results from the current study. Creating a model in a weight-bearing state using nonweight-bearing kinematics [4,5] incurs an artifact of joint congruity change, as evidenced by the differences in predicted contact area as well as the contact centroid. This could compromise the accuracy of predictions of the TF mechanical response and potentially obscure the true effects of structural alteration due to an injury or treatment. Customized loading devices have been used to emulate weight-bearing conditions during the MRI scan [16,57] but these alternatives are much less flexible in accommodating a variety of functional kinematics as compared to the dynamic X-ray imaging we used.

Experimental studies by Bingham et al. [58], Li et al. [59], and Van de Velde et al. [60] using biplane X-ray images of subjects in a full-extension weight-bearing position have showed that the contact centroids lie anterior to the anterior-posterior (AP) midline of the cartilage for both the lateral and medial compartments. Contact centroid estimation by the DSX-based model in the current study was consistent with those previous findings. However, studies using a supine position from MR imaging have provided different and often inconsistent estimates. For example, Perie et al. estimated the contact location to be anterior in the medial compartment, but toward the center in the lateral compartment, based on estimates of hydrostatic stress distribution from a supine MRI-based FE model of a healthy knee [5]. The discrepancy in the location of contact in the lateral compartment is similar to the prediction from the MRI-based FE model of the healthy knee in the current study. On the other hand, experimental investigations by Shefelbine et al. [57] and Von Eisenhart-Rothe et al. [61] predicted the contact centroid to be posterior in the medial compartment and anterior on the lateral side with respect to the AP midline of the cartilage. A collective look at these studies conclusively establishes the potential for erroneous predictions when FE models rely on nontask-specific kinematics. Small changes in the positioning of the bones can cause substantial inaccuracies in FE model predictions, as shown by a previous sensitivity analysis [16].

The demonstration of a viable approach to verifying FE model predictions using subject-specific data is another unique contribution of this study. To our knowledge, there has not been any tibiofemoral joint FE model employing a subject's own in vivo data to verify the model predictions. Peña et al. [31–33] developed several 3D FE models that considered in vivo functional kinematics using weight-bearing MRI, but all of these models lacked validation or verification against data from the same subjects. Instead, verification was done by comparing the model results with literature data, some of which were based on in vitro cadaveric data. Considering the morphometric variations across individuals [13] and the discrepancies between in vitro and in vivo modalities in relation to sometimes subtle effects or differences, conventional verification can serve at best as a qualitative “reality check.” With access to or the ability to acquire in vivo data, validating a subject-specific FE model by the subject's own data obviates errors arising from inter-individual morphological variations. As in vivo measurements of joint pressure and stress continue to be a formidable challenge, we believe the in situ contact area analysis proposed in the current study offers a viable alternative for quantitative verification of subject-specific FE models based on in vivo data.

Once the validity has been established, the model can be used with confidence to analyze the contact pressure and stress distribution in the joint complex. The subject modeled in this work had previously undergone a meniscectomy of the lateral meniscus on the left knee. The predicted contact area, maximum contact pressure and maximum compressive stress in both the lateral and medial compartments were all greater in the meniscectomized knee than in the right, healthy knee during the static, standing trial. The difference was most evident in contact area in the lateral compartment. The trends found in this study—increased cartilage-to-cartilage contact area, increased maximum contract pressure and increased maximum compressive stress in the meniscectomized versus healthy knee—were consistent with prior reports based on FE analysis [23,33–35].

While the contact centroid locations predicted by the FE model in DSX-based bone positions were in close agreement with those from the ISCAA, the actual contact area resulting from the ISCAA was noticeably greater than the area predicted by the corresponding DSX-based FE model. This discrepancy may be attributable to two simplifying assumptions. First, in the ISCAA, the intersection between nondeformed cartilage volumes was assumed to represent the total volume in contact (i.e., experiencing stress). Had the deformation been taken into account, which is not yet achievable in vivo, the total volume or area in contact would likely be smaller, considering there would be deformed but noncontacting cartilage areas. Second, material properties used in the FE models were taken from literature on the subject of TF FE modeling, which may have contributed to the inaccuracy in prediction of contact area. in vivo subject-specific material properties remains the “holy grail” in biomechanics and having such property values for model development as well as validation would greatly reduce the putative error caused by use of generic “one-size-fits-all” data. It must be pointed out that for a “within-model” comparative evaluation as done in the current study, the use of generic but consistent property values would be much less consequential, as confirmed by the sensitivity analysis conducted.

The cruciate ligaments (ACL, PCL) and collateral ligaments (MCL, LCL) were not included in the models in this study. It is understood that the ligaments play a central role in maintaining joint stability and therefore can affect the kinematics [62]. Inclusion of these ligaments in the DSX-based models would not have any effect on the kinematics, which was prescribed from experimental data. Inclusion of the ligaments in the MRI-based models might have an effect on the contact centroid predictions as the model permitted a large number of DOFs. Given that the MRI-based models saw only small femoral movement relative to the tibia (displacement <1 mm) in response to the quasi-static loading, and that the standing position is considered the most “neutral” position in terms of ligament tensions and effect, we believe the effect would be minimal. However, caution must be exercised when the proposed methodology is applied to modeling a joint in more dynamic acts and/or deviate positions. Another limitation of this study was the assumption of the loading condition applied to the TF joint. One-half of the body weight was administered only in the axial direction. Although we elected to use a simple loading scenario in order to minimize possible interaction effects on predicted joint mechanical responses and loading “bias” in model comparison, the actual loading would be more complex than a uniformly applied axial load. Our ongoing work involves the use of a musculoskeletal dynamic modeling tool OpenSim [63] to determine a more realistic ensemble force input for the FE model.