Novel Method to Evaluate Angular Stiffness of Prosthetic Feet From Linear Compression Tests

Short abstract

Lower limb amputee gait during stance phase is related to the angular stiffness of the prosthetic foot, which describes the dependence of ankle torque on angular progression of the shank. However, there is little data on angular stiffness of prosthetic feet, and no method to directly measure it has been described. The objective of this study was to derive and evaluate a method to estimate the angular stiffness of prosthetic feet using a simple linear compression test. Linear vertical compression tests were performed on nine configurations of an experimental multicomponent foot (with known component stiffness properties and geometry), which allowed for parametric adjustment of hindfoot and forefoot stiffness properties and geometries. Each configuration was loaded under displacement control at distinct pylon test angles. Angular stiffness was calculated as a function of the pylon angle, normal force, and center of pressure (COP) rate of change with respect to linear displacement. Population root mean square error (RMSE) between the measured and predicted angular stiffness values for each configuration of the multicomponent foot was calculated to be 4.1 N-m/deg, dominated by a bias of the estimated values above the predicted values of 3.8 ± 1.6 N-m/deg. The best-fit line to estimated values was approximately parallel to the prediction, with R²= 0.95. This method should be accessible for a variety of laboratories to estimate angular stiffness of experimental and commercially available prosthetic feet with minimal equipment.

Introduction

Prosthetic foot stiffness has been recognized as an important factor influencing the walking performance of amputees [1–3]. Commercial feet are available in a range of stiffness categories and geometries. The stiffness of linear displacements of the hindfoot and forefoot for several commercially available feet have been reported to be within a range of 27–90 N/mm [4,5] and 5–76 N/mm [5,6], respectively, but these values are relevant only to the earliest and latest portions of stance phase, when linear compression or rebound naturally occur. In contrast, midstance kinetics are more related to the angular stiffness of the foot, which describes the relationship between ankle torque and the angular progression of the lower limb over the foot during this phase. The variety of commercially available foot designs makes a direct prediction of effective angular stiffness from foot design challenging, because of geometric changes under different loading conditions, intricate deformation mechanics of the structural components, and mechanical interaction between hindfoot and forefoot components. Mechanical testing could, in principle, measure stiffness directly, but it is nontrivial to produce pure rotations for comparison against measured moments and to control for the variations in induced external force. The most common approximation is to estimate ankle “quasistiffness” from ankle torque versus moment plots measured with gait analysis [7,8]. However, this technique does not isolate the properties of a foot prosthesis, because the ankle moment measurements include confounding effects due to fluctuating ground reaction forces and the unique gait behaviors of different subjects. Furthermore, it requires a gait laboratory for analysis, which is expensive and not always available to clinicians. A technique is thus needed that will provide estimation of angular stiffness in a variety of prosthetic feet, using a minimal set of equipment, so that researchers and clinicians can begin to utilize this important property. Therefore, the objective of this study was to derive and evaluate a method to estimate angular stiffness from measurements easily obtained from linear displacement tests. We performed linear compression tests using several configurations of an experimental multicomponent foot, in which angular stiffness properties were predicted from measured component properties and design geometry, to evaluate the derived method.

Methods

Experimental Multicomponent Foot.

The experimental multicomponent foot (Figs. 1 and 2) consists of a reconfigurable custom mounting block (aluminum 7075 T6), independent hindfoot and forefoot structural keels (G10/FR4 woven glass-epoxy composite), and angular adjustment mounting blocks (aluminum 7075 T6) for each keel. The main mounting block allows the anterior-posterior position of the keels and the pylon to be adjusted in 10-mm and 14-mm increments, respectively. The angular adjustment blocks allow both keel orientations to adjust in 5 deg increments with respect to the mounting block. Several interchangeable hindfoot and forefoot keels were machined to have linear stiffness ranges of 22–69 N/mm [4] and 14–90 N/mm [6], respectively, spanning the ranges similar to prior literature [4–6]. Linear stiffness was adjusted by tapering the thickness of the composite, leaving the mounted end at stock thickness (6–13 mm) and increasing the angle of the taper to increase compliance in increments of roughly 15 N/mm. The outline shape of all hindfoot keels was constant, with length 130 mm from mounting block to tip. Forefoot keels were made in two versions, generally similar but with lengths of 140 mm or 175 mm. The linear stiffness of each forefoot and hindfoot component was measured in a compression test similar to that described under evaluation (below) but using only single-keel contact.

Fig. 1.

Two-phase loading demonstrates superposition of linear and angular terms in determining the force and deflection of the hindfoot and forefoot. (a) Pure vertical compression results in equal deflections of the forefoot and hindfoot, each with a force proportional to its linear component stiffness. The resultant equals the applied force (F _z), acting at a COP that remains constant as load increases (Eq. (2)). The moment supported by the ankle constraint is $M=y_{\mathrm{COP}-\mathrm{compression}}{F}_{\mathrm{z}}$. (b) The angle constraint can be replaced by its equivalent moment. Adding a differential moment (dM) shifts the load, moving the COP and changing the forefoot and hindfoot forces by ±dF. The accompanying deflection changes in each component result in an angular rotation dα. The overall angular stiffness relates this angle to the moment: $\mathit{dM}=K_{\mathrm{angular}}d\alpha$. The final state is equivalent to rotating first and then compressing, as in the proposed test method. This equivalence is used to derive an expression for angular stiffness based on measured changes in F _z and y _COP (Eq. (6)).

Fig. 2.

Test setup for vertical compression tests. The test foot is rigidly mounted to the ground such that the pylon is normal to surface of the force plate while the foot is in a foot-flat orientation. The force plate, which is mounted to a 6-DOF parallel robot, is rotated to test angle, α, and displaced along the axis of the pylon. Force, COP, and displacement data are recorded while the foot is compressed at 5 mm/s.

Mechanical Model of the Experimental Prosthesis.

During midstance, with the foot flat on the ground, the experimental foot prosthesis transmits load through compliant keels that contact at distinct hindfoot and forefoot contact points. We model this system as a rigid beam supported by two vertical springs acting in parallel: one at each end. We develop the model through a two-stage loading pattern: pure vertical compression up to a defined force (similar to the defined force of body weight that acts in situ) followed by the addition of a pure moment to cause rotation under constant total force. In pure compression, the characteristics of the two springs determine how the applied load is shared, revealing the useful property that the center of pressure (COP) underfoot is independent of vertical force. The added moment increases load on one spring and decreases load on the other and results in angular displacement. The relationship between applied moment and angular deflection defines the angular stiffness of the whole foot.

Angular Stiffness Prediction From Component Linear Stiffness.

The hindfoot and forefoot components each exhibit a characteristic force (F) versus deflection (z) curve F(z), which we assume to be linear to define the component's linear stiffness, K _hind or K _fore (F = K_z). If the foot is aligned in a foot-flat position, fixed against rotation, and then displaced vertically toward the ground, these component stiffnesses determine the whole-foot behavior (Fig. 1). The vertical stiffness of the whole foot (K _z), describing the change in force resulting from a pure vertical deflection (i.e., equal deflection at hindfoot and forefoot), is a simple sum,

$$K_z=K_{\mathrm{hind}}+K_{\mathrm{fore}}=\frac{\mathit{dF}\mathrm{z}}{\mathit{dz}}$$ (1)

The center of pressure (y _COP) under the foot is determined by the forces ($F_{\mathrm{hind}}=K_{\mathrm{hind}}z$ and $F_{\mathrm{fore}}=K_{\mathrm{fore}}z$), weighted by their locations (y _hind and y _fore),

$$y_{\mathrm{COP}}=\frac{y_{\mathrm{hind}}{K}_{\mathrm{hind}}z+y_{\mathrm{fore}}{K}_{\mathrm{fore}}z}{K_{\mathrm{hind}}z+K_{\mathrm{fore}}z}=\frac{y_{\mathrm{hind}}{K}_{\mathrm{hind}}+y_{\mathrm{fore}}{K}_{\mathrm{fore}}}{K_{\mathrm{hind}}+K_{\mathrm{fore}}}$$ (2)

Note that the actual value of vertical displacement cancels out, implying that the value of y _COP does not depend on displacement.

From this compressed configuration, the constraint preventing rotation can be replaced by its equivalent ankle moment, $M=y_{\mathrm{COP}}{F}_z$. Adding a further differential moment, dM, while maintaining a constant externally applied force, F_z, changes the hindfoot and forefoot forces by equal and opposite increments, balancing the added moment. The magnitude of the force increments depends on the distance between the contact points, $l=y_{\mathrm{fore}}-y_{\mathrm{hind}}$ (Fig. 1),

$${\mathit{dF}}_{\mathrm{fore}}=-{\mathit{dF}}_{\mathrm{hind}}=\frac{\mathit{dM}}{l}$$ (3)

With the sign shown in Fig. 1, the force increment is positive on the forefoot and negative at the hindfoot. Each force increment is associated with a change in deflection, ${\mathit{dz}}_{\mathrm{fore}}={\mathit{dF}}_{\mathrm{fore}}/K_{\mathrm{fore}}$ or ${\mathit{dz}}_{\mathrm{hind}}={\mathit{dF}}_{\mathrm{hind}}/K_{\mathrm{hind}}$. These linear deflection changes are equivalent to an angular rotation dα of the whole foot, $\sin d\alpha =({\mathit{dz}}_{\mathrm{fore}}-{\mathit{dz}}_{\mathrm{hind}})/l$. Substituting Eq. (3), applying a small angle approximation, and solving for $\mathit{dM}/d\alpha$, we obtain the angular stiffness as a function of hindfoot and forefoot stiffnesses,

$$K_{\mathrm{angular}}=\frac{\mathit{dM}}{d\alpha }=\frac{l^2{K}_{\mathrm{hind}}{K}_{\mathrm{fore}}}{K_{\mathrm{hind}}+K_{\mathrm{fore}}}$$ (4)

This expression forms a theoretical prediction of angular stiffness in the experimental multicomponent foot, which we compare against estimates derived from a simple vertical-compression test below.

The derivations presented are developed using linear spring characteristics for simplicity, but this simplification is not strictly necessary. The COP is constant in compression (Eq. (2)) in any case where the force versus deflection curves of the hindfoot and forefoot are proportional ($F_{\mathrm{hind}}(z)={\mathit{cF}}_{\mathrm{fore}}(z)$). If even this assumption is violated, the behavior degrades only gradually, according to the deviation from proportionality divided by the total applied force. The formula for angular stiffness (Eq. (4)) makes no assumption about the force-deflection characteristics, so it takes the same form for all cases, using locally linearized K _hind and K _fore to produce a locally valid angular stiffness.

Angular Stiffness Estimation From Vertical Compression Test.

We derived an expression to estimate the sagittal angular stiffness of any foot prosthesis from a simple, linear vertical compression test. A direct method of estimating angular stiffness would be to compress the foot vertically and then rotate the shank through some known angle (while keeping force constant) and measure the change in ankle moment. The same final state can be obtained via an alternative loading pattern, in which the foot is rotated first and then vertically compressed. We use these equivalent loading patterns to estimate angular stiffness using a test modeled on the second pattern and an analysis modeled on the first.

The mechanics used to derive this estimate are similar to Fig. 1. Total ankle moment (M) in any state is the cross product of the moment arm from the ankle to the COP (y _COP), with the total measured force ($F=F_{\mathrm{hind}}+F_{\mathrm{fore}}$). Because we load the foot in a near-normal direction, force is roughly normal to the surface and the expression simplifies to scalar form, $M=y_{\mathrm{COP}}{F}_{\mathrm{z}}$. By equivalence, this loading state can be obtained from a two-phase loading pattern: pure vertical compression plus pure rotation. From Eq. (2), we assume there exists a center of pressure ($y_{\mathrm{COP}-\mathrm{compression}}$) that is constant for any load under pure vertical compression. The moment due to pure vertical compression is therefore $y_{\mathrm{COP}-\mathrm{compression}}{F}_{\mathrm{z}}$. The added moment due to pure rotation is $K_{\mathrm{angular}}\alpha$. The summation of the two-phase loading pattern is equivalent to the total ankle moment,

$$y_{\mathrm{COP}}{F}_{\mathrm{z}}=M=y_{\mathrm{COP}-\mathrm{compression}}{F}_{\mathrm{z}}+K_{\mathrm{angular}}\alpha$$ (5)

Equation (5) could be used to estimate angular stiffness ($K_{\mathrm{angular}}$) directly, but this is often impractical, because it requires knowledge of the COP location with respect to the ankle (y _COP) as well as knowledge of the vertical-compression COP ($y_{\mathrm{COP}-\mathrm{compression}}$). Determining such spatial relationships typically requires a motion capture laboratory. Instead, we divide through by F _z and then differentiate with respect to normal displacement z, causing the constant term $y_{\mathrm{COP}-\mathrm{compression}}$ to drop out. After simplification, the expression becomes

$$K_{\mathrm{angular}}=\frac{-F_{\mathrm{z}}^2}{\alpha }\frac{\frac{{\mathit{dy}}_{\mathrm{COP}}}{\mathit{dz}}}{\frac{\mathit{dFz}}{\mathit{dz}}}$$ (6)

In this differential form, the need for spatial registration between the COP measurement and the foot is eliminated: the result only requires the measured change in y _COP, which is identical in the foot reference frame and the world (force-platform) reference frame for z-direction compression. Thus, Eq. (6) estimates angular stiffness using only current and differential measurements of z, F _z, and y _COP, with a single parameter of foot mounting angle, α.

Evaluation.

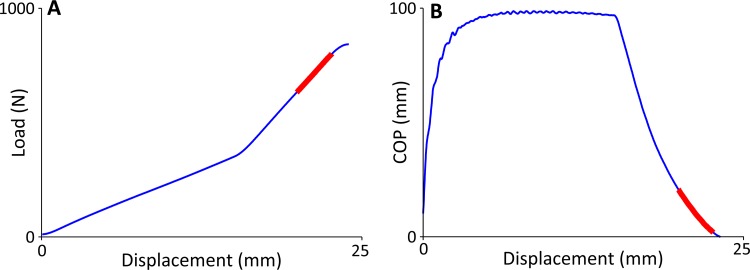
Force, displacement, and center of pressure (COP) measurements of 9-different foot configurations were tested on a force plate (Kistler Instrument Corp., Amherst, NY) that was mounted to a 6-degree of freedom (DOF) parallel robot (Mikrolar Inc., Hampton, NH) [9]. The test foot was aligned with the force plate such that the pylon was normal to the surface and the foot was at 0 deg of internal-external rotation with respect to the force plate coordinate system when the robot was in its home position (Fig. 2). For each test, the robot was rotated to a desired sagittal angle α and the foot was displaced by moving the force plate along the axis of the pylon at 5 mm/s until at least 800 N were applied or 40 mm of displacement occurred, whichever came first (Fig. 2). This implementation differs slightly from the derivation (displacement was assumed to be along ground/force plate normal), but the small angles used (–4 to + 6 deg) make any discrepancy negligible. Force and center of pressure data (Fig. 3) were collected at 250 Hz, and displacement was calculated from the programmed movement speed. Angular stiffness was determined at orientations in which a single-component loading phase was followed by a double-component loading phase within the prescribed loading criteria stated above. These typically occurred at sagittal plane pylon angles within 10 deg of zero; the value varied depending on the stiffness of each keel. Configurations were established by altering hindfoot and forefoot keel stiffness and mounting position as well as forefoot keel length. Orientations of both keels remained at 15 deg declination with respect to the ankle block for all configurations tested. Angular stiffness was calculated as the average of two double-component contact test angles (α) for each configuration: one each with hindfoot-first and forefoot-first ground contact. The average error (bias), standard deviation of error (precision), root mean square error (RMSE), and R ² value were calculated between the measured angular stiffness (Eq. (6)) in comparison to the predicted angular stiffness (Eq. (4)) over all nine configurations.

Fig. 3.

Example data plots from one compression test (–4 deg angle, heel-first contact): (a) normal force versus displacement and (b) center of pressure (COP) versus displacement. The sections shown in bold represent the data used to calculate the inputs for Eq. (4): F _z, $\mathit{dF}\mathrm{z}/\mathit{dz}$, and ${\mathit{dy}}_{\mathrm{COP}}/\mathit{dz}$.

Results

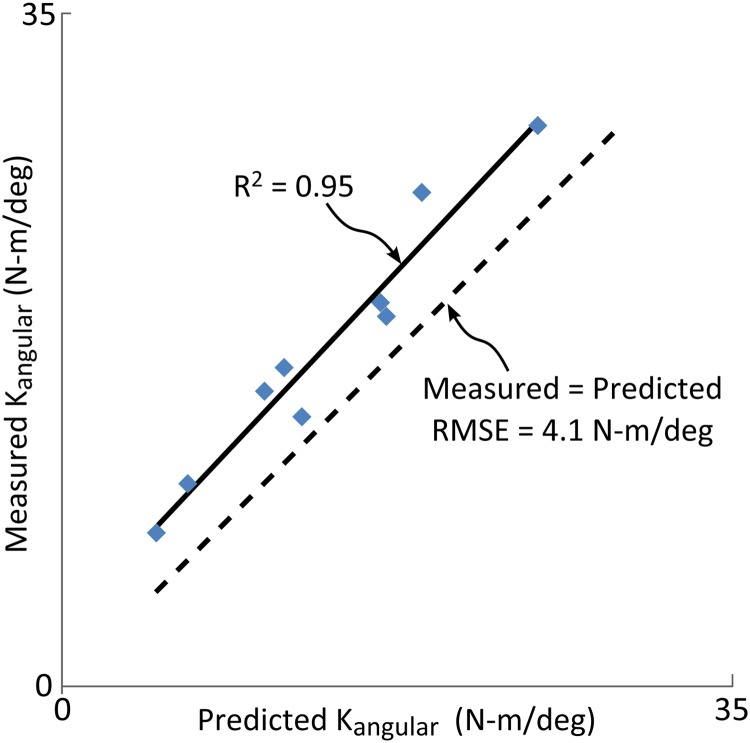
Angular stiffness was predicted to range from 4.9 to 24.8 N-m/deg, whereas the measured values ranged from 7.9 to 29.1 N-m/deg. The measured angular stiffness slightly overestimated the predicted angular stiffness by 3.8 ± 1.6 N-m/deg, with RMSE of 4.1 N-m/deg. The best-fit line of measured versus predicted stiffnesses had slope 1.06, roughly parallel to the equality line, and R ²= 0.95. Figure 4 shows the correlation of the measured angular stiffness with respect to the predicted angular stiffness from different combinations of components.

Fig. 4.

Measured (Eq. (6)) versus predicted (Eq. (4)) angular stiffness. The best fit line (solid) between the predicted and measured values has R²= 0.95. The dashed line represents the identity, to visualize prediction errors. Measured values exceeded predicted values by an average of 3.8 ± 1.6 N-m/deg, with RMSE (from predicted) of 4.1 N-m/deg.

Discussion

Few data are available describing the angular stiffness of prosthetic feet, despite the clear connection to midstance kinetics when the tibia is progressing over the ankle. The lack of mechanical data available in the literature may be due to challenges intrinsic to traditional angular stiffness estimation techniques when applied to prosthetic feet. Thus, the objective of this study was to derive and evaluate a method to measure angular stiffness of prosthetic feet using basic linear displacement test methods. A simplified differential expression (Eq. (6)) allowed estimation of the angular stiffness of a prosthetic foot within 4.1 N-m/deg (RMSE).

The RMSE between the measured and predicted angular stiffness was mainly attributed to a measurement bias of 3.8 N-m/deg. However, the error analysis revealed high precision and near parallel slopes between the best-fit and equality lines, which suggests that this method will precisely measure the relative change in angular stiffness between a set of prostheses. Therefore, while the method proposed here may not achieve perfect absolute accuracy, it is an effective tool for studies in which a comparison of different angular stiffnesses is the critical component.

The utility of this method for estimating angular stiffness of foot prostheses is clearest in contrast to other, more direct methods. One direct method is to have a human subject walk with the prosthesis in a gait laboratory—the ankle moment versus shank angle plot can be used to compute an angular quasistiffness. However, this method is confounded by fluctuations in the applied force, such that the estimate includes effects from the true angular stiffness as well as from the coupling of force to moment through the moment arm of the COP. These fluctuations depend on the individual subject, so the estimate will reflect human behavior alongside mechanical properties. Furthermore, it requires a gait laboratory, personnel, and extensive analysis, at significant cost. Another method is to artificially load the foot (e.g., with weights) and rock the foot forward and back [10] while recording motion and COP data. This method is straightforward and largely experimenter-independent but still requires specialized laboratory equipment, including motion capture and a force plate with proper spatial registration. In addition, postprocessing similar to inverse dynamics is required. The method proposed requires only a vertical slider with position measurements, a force measurement system that reports vertical force and COP, and rigid mounting of a foot prosthesis to the slider.

Despite the difficulty of obtaining an equivalent measure of angular stiffness from other methods, it is useful to compare an approximate range against the closest available approximations. Ankle quasistiffness data from normal walking has been estimated as roughly 3.5–17.3 N-m/deg [7] or 3.5–24.4 N-m/deg [8] during different phases of gait. The angular stiffness values estimated here (7.9–29.1 N-m/deg) span a similar range. Alternatively, we can use Eq. (4) to convert linear stiffness properties from the heel and toe of commercially available prostheses to estimates of angular stiffness based on foot geometry. The range of linearized stiffness values reported in the literature is roughly 27–90 N/mm [4,5] for the heel and 5–76 N/mm [5,6] for the forefoot, measured mostly from size 27-cm prostheses. Assuming that the hindfoot-to-forefoot distance l is between 0.16 and 0.23 m, the angular stiffness estimated using Eq. (4) could range from about 4 to 24 N-m/deg. Thus, it appears that the experimental prosthesis tested here covers a biomechanically relevant range of angular stiffness.

It is important to note that changes in the precision of the input measures to Eq. (6) will alter the overall error of the proposed method. Because the derivative of the COP with respect to normal displacement will cause an amplification of noise in COP measurements, the overall error of Eq. (6) is more sensitive to changes in the precision of the COP measurement than the rest of the measurement variables (F _z, z, and α). The error measurements reported here were evaluated using high-precision test equipment. In application, if a simpler system has sufficient COP resolution, the outcome of these estimates should yield good results.

The linear stiffness characteristics of the experimental multicomponent foot made it such that the selection of data ranges analyzed for the total linear stiffness, normal force, and change in COP was irrelevant. However, most commercially available prosthetic feet likely have nonlinear compressive stiffness characteristics. In walking, the angular stiffness felt by the user may be impacted by hysteresis effects that contribute to this nonlinearity, changing the relationship between force and incremental deflection or relaxation. While it may be assumed the derivations of the present study are valid for some nonlinear cases, the stiffness values estimated will be local to the loading condition tested. In application of this technique, the ranges used should be selected carefully to represent the clinically significant loading range for a given prosthetic foot.

For the derivation of Eq. (6), an important assumption is that the COP under pure vertical compression ($y_{\mathrm{COP}-\mathrm{compression}}$) is constant across increasing load. Equation (2) shows why this assumption is likely to be satisfied, yet the design features of particular prostheses may violate it, confounding the measurement. We examined this assumption for one commercially available prosthesis and found that, during pure vertical compression, $y_{\mathrm{COP}-\mathrm{compression}}$ changed by less than 5% between 300 N and 800 N of applied force. This change is small compared to changes in y _COP of 50% or more that we observed during double-component contact periods when the same foot was mounted at ±2 deg. Therefore, we believe that this assumption is reasonable, though each individual foot should be tested to ensure validity. If the assumption is not satisfied, it may be possible to rederive Eq. (6) without this assumption and instead characterize the changes in y _COP with deflection for use in the formula.

The general accessibility of the angular stiffness estimation technique presented here makes this method a valuable tool for the biomechanics and prosthetics research community. More specifically, it may be useful for laboratories or clinics with limited access to motion analysis equipment.