Simulating the Dynamics of an Aortic Valve Prosthesis in a Pulse Duplicator: Numerical Methods and Initial Experience

Each year, approximately 250,000 surgical procedures are performed to repair or to replace cardiac valves [1], and of these, approximately 50,000 are aortic valve replacement operations. Despite decades of development, many of the limitations of cardiac valve prostheses remain consequences of the fluid dynamics generated by the replacement valve [1]. To enable cross-validation studies that allow for detailed comparisons of experimental and computational results, we are developing fluid-structure interaction (FSI) models of the dynamics of aortic valve prostheses mounted in a ViVitro Systems, Inc. pulse duplicator apparatus. Such an experimentally validated computational model promises both to facilitate the design of novel valve prostheses, and also to assist in the regulatory process, by providing access to detailed spatially- and temporally-resolved flow data that are challenging to obtain via experimental approaches.

Our numerical approach to FSI is based on the immersed boundary (IB) method [2]. The structural dynamics are described in Lagrangian form using a material coordinate system, whereas the momentum of the fluid-solid system and the viscosity and incompressibility of the fluid are described in Eulerian form using fixed Cartesian physical coordinates. Lagrangian and Eulerian variables are coupled by integral transforms with Dirac delta function kernels. When the equations are discretized, the singular delta function is replaced by a regularized version of the delta function. See Peskin [2] for details.

To treat rigid body dynamics within the framework of the IB method, we adopt an approach similar to that recently developed by Kim and Peskin [3], in which the continuous equations are:

$$\rho (\frac{\partial \mathit{u}}{\partial t}(\mathit{x},t)+\mathit{u}(\mathit{x},t)·\nabla \mathit{u}(\mathit{x},t))\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}=-\nabla p(\mathit{x},t)+\mu {\nabla }^2\mathit{u}(\mathit{x},t)+\mathit{f}(\mathit{x},t)$$ (1)

$$\nabla ·\mathit{u}(\mathit{x},t)=0$$ (2)

$$\mathit{f}(\mathit{x},t)={\int }_U\mathit{F}(\mathit{s},t)\delta (\mathit{x}-\mathit{X}(\mathit{s},t))\mathrm{d}\mathit{s}$$ (3)

$$\frac{\partial \mathit{X}}{\partial t}(\mathit{s},t)={\int }_{\Omega }\mathit{u}(\mathit{x},t)\delta (\mathit{x}-\mathit{X}(\mathit{s},t))\mathrm{d}\mathit{x}$$ (4)

$$\frac{\partial \mathit{Y}}{\partial t}(\mathit{s},t)=\mathit{V}(t)+\mathit{W}(t)\times \mathit{R}(\mathit{s},t)$$ (5)

$$\mathit{F}(\mathit{s},t)=\kappa (\mathit{Y}(\mathit{s},t)-\mathit{X}(\mathit{s},t))$$ (6)

in which $\mathit{x}\in \Omega$ are physical coordinates, $\mathit{s}\in U$ are material coordinates, $\mathit{X}(\mathit{s},t)$ and $\mathit{Y}(\mathit{s},t)$ are time-dependent mappings from material coordinates to current coordinates, $\mathit{u}(\mathit{x},t)$ is the Eulerian velocity field, $p(\mathit{x},t)$ is the Eulerian pressure field, $\mathit{f}(\mathit{x},t)$ and $\mathit{F}(\mathit{s},t)$ are equivalent Eulerian and Lagrangian force densities, $\rho$ is the fluid density, $\mu$ is the fluid viscosity, and $\delta (\mathit{x})=\delta (x)\delta (y)\delta (z)$ is the three-dimensional Dirac delta function. The force field $\mathit{F}(\mathit{s},t)$ acts to impose the rigidity constraint

$$\frac{\partial \mathit{X}}{\partial t}(\mathit{s},t)=\mathit{U}(\mathit{s},t)=\mathit{V}(t)+\mathit{W}(t)\times \mathit{R}(\mathit{s},t)$$

in which $\mathit{V}(t)$ and $\mathit{W}(t)$ are respectively the linear and angular velocity of the structure and $\mathit{R}(\mathit{s},t)$ is the radius vector. In the limit $\kappa \to \infty$, the constraint is imposed exactly; for finite $\kappa >0$, the constraint is only approximately satisfied. The dynamics of $\mathit{V}(t)$ and $\mathit{W}(t)$ are determined from the requirement that the time rate of change of the “excess” linear and angular momentum (i.e., in excess of the momentum accounted for by the momentum equation (1)) be proportional to the net force ${\int }_{\Omega }-\mathit{F}(\mathit{s},t)\mathrm{d}\mathit{s}$ and net torque ${\int }_{\Omega }-\mathit{F}(\mathit{s},t)\times \mathit{R}(\mathit{s},t)\mathrm{d}\mathit{s}$ acting on the body.

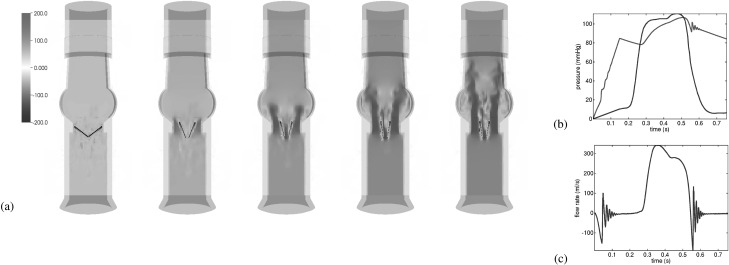
Geometrical models of the aortic section of the ViVitro pulse duplicator and of a St. Jude Regent valve were created using SolidWorks (Dassault Systèmes SolidWorks Corp., Waltham, MA). These geometrical models were meshed using CUBIT (Sandia National Laboratory, Albuquerque, NM). To drive flow through the valve, we impose a physiological left ventricular pressure waveform, and characteristic downstream compliance and resistance to mimic the response of the systemic circulation. Simulations used the IBAMR software [4]. Initial simulation results are shown in Fig. 1, demonstrating that realistic flow rates can be obtained using this model under realistic driving and loading conditions. We are presently fine tuning this model in preparation for validation studies.

Fig. 1.

(a) Opening dynamics, (b) imposed driving pressure and computed loading pressure, and (c) computed flow rate