Abstract
The present work is devoted to study the numerical simulation for unsteady MHD flow and heat transfer of a couple stress fluid over a rotating disk. A similarity transformation is employed to reduce the time dependent system of nonlinear partial differential equations (PDEs) to ordinary differential equations (ODEs). The Runge-Kutta method and shooting technique are employed for finding the numerical solution of the governing system. The influences of governing parameters viz. unsteadiness parameter, couple stress and various physical parameters on velocity, temperature and pressure profiles are analyzed graphically and discussed in detail.
Introduction
The flow problems of non-Newtonian fluids are attracted the interest of many researchers because of its significance in modern technology and industries. The natural and industrial applications of such fluids are volcanic lava, extrusion of polymer fluids, drilling mud, suspension solutions, cosmetic and food products, solidification of liquid crystals, cooling of metallic plates in a bath, exotic lubricants, colloidal and many others. In recent times, among various non-Newtonian fluid models, the couple stress fluid model has got the special status because of the spin field in the fluid which sets up an anti-symmetric stresses, known as couple stresses. The basic theory and constitutive equations for couple stress fluid initially developed by Stokes [1], is one amongst the polar fluid theories which consider couple stresses in addition to the classical Cauchy stresses. This type of fluid encloses inflexible and random-oriented particles in a viscous medium. Examples of couple stress fluids are liquid crystals, colloidal fluids, liquids containing long-chain molecules such as polymer suspensions, blood, lubrications and additive electro-rheological fluids etc. These fluids are considered by many investigators because of the simplest model of couple stress fluid amongst others. (See recent attempts [2]–[4]).
Magnetohydrodynamics (MHD) occurs when a conducting fluid flows in the presence of an electromagnetic field, such that the induced electromagnetic force affects the motion of the fluid. Some significant technological applications of MHD are, in experiments of controlled thermonuclear fusion where a strong magnetic field is used to confine rings or columns of hot plasma, to generate electricity where liquid metals are driven through a magnetic field, etc. Moreover, MHD principles are used in plasma accelerators for ion thrusters, for spacecraft propulsion and for light-ion-beam powered inertial confinement. Some remarkable attempts have been made to study the influence of MHD on various flow situations. The influences of MHD stagnation point flow was analyzed by Hayat et al. [5], MHD flow in a circular magnetic field was considered by Kumar et al. [6], viscous dissipation and Joule heating on unsteady mixed convection MHD flow was discussed by Osalusi et al. [7]. Investigation of fractional MHD Oldroyd-B fluid over an oscillating plate was the subject of Jamil et al. [8], and the influence of MHD in the porous medium and heat transfer analysis of couple stress fluid between two parallel plates with variable viscosity was investigated by Sreenadh et al. [9]. Numerical methods to obtain the solutions of some complicated MHD flow problems were presented in [10]–[12].
Rotating-disk flow of non-Newtonian fluids is intriguingly growing interest, as it is momentous in the study of engineering flows on rotating machineries, spin-coating, centrifugal pumps, rotational viscometers, computer storage devices and some aerodynamic related problems in fluid mechanics. Taking into account both industrial and technological applications, there have been a number of studies presented in literature on steady flow of various types of fluid over a rotating disks and sphere with and without considering magnetic effect [13]–[25]. It is worth mentioning that the real world applications encounter the unsteadiness in the flow and temperature fields of almost all processes. Osalusi et al. [26] presented the effects of Ohmic heating and viscous dissipation on unsteady MHD and slip flow over a porous rotating disk. The series solutions for unsteady laminar MHD flow near forward stagnation point of an impulsively rotating and translating sphere in presence of buoyancy forces are found by Dinarvand et al. [27]. Chamkha et al. [28] studied the unsteady MHD flow of mixed convection fluid with heat and mass transfer. Ram et al. [29] analyzed the influence of phase difference between highly oscillating magnetic field and magnetization on the unsteady ferro fluid flow due to a rotating disk. Nadeem et al. [30] worked out on the analytical treatment of unsteady mixed convection MHD flow on a rotating cone in a rotating frame.
Takhar et al. [31] examined the unsteady MHD flow of an ambient fluid with heat transfer over a rotating disk, present study aims at extending aforesaid work to incorporate the couple stress effects with magnetic field and heat transfer analysis is also taken into account. However, to the best of our knowledge, no attempt is available in the literature regarding unsteady MHD flow of couple stress fluid over a rotating disk. In this note, an investigation has been carried out to analyze the unsteady flow and heat transfer of couple stress fluid with the effect of transverse magnetic field on an infinite rotating disk along  -axis. The governing time dependent momentum and energy partial differential equations are transformed into a system of ordinary differential equations by using suitable similarity transformations. These ODEs are then solved numerically by employing a Runge-Kutta technique coupled with shooting method. The variations in the flow field, heat transfer and pressure of the fluid due to pertinent parameters are obtained through graphs and discussed thoroughly.
-axis. The governing time dependent momentum and energy partial differential equations are transformed into a system of ordinary differential equations by using suitable similarity transformations. These ODEs are then solved numerically by employing a Runge-Kutta technique coupled with shooting method. The variations in the flow field, heat transfer and pressure of the fluid due to pertinent parameters are obtained through graphs and discussed thoroughly.
Problem Formulation
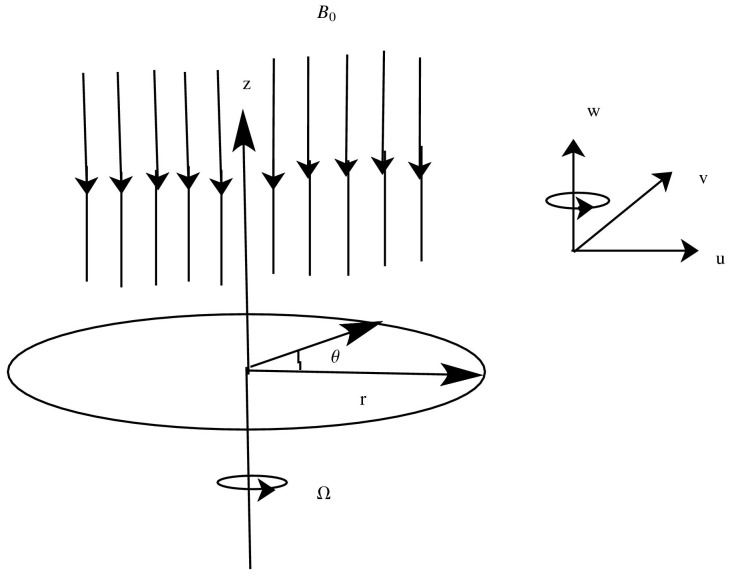
Consider the three dimensional, unsteady, laminar, incompressible, MHD flow and heat transfer of couple stress fluid over a rotating disk which rotates about the  -axis with angular velocity
-axis with angular velocity  in a cylindrical polar coordinate system
in a cylindrical polar coordinate system  ,
,  and
and  . The
. The  -axis is in the direction of radius of disk, and the applied uniform magnetic field
-axis is in the direction of radius of disk, and the applied uniform magnetic field 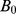 is in the direction of
is in the direction of  -axis, normal to the surface of disk. As the flow is axisymmetric therefore radial, tangential and axial components of velocity
-axis, normal to the surface of disk. As the flow is axisymmetric therefore radial, tangential and axial components of velocity  ,
,  ,
, 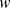 , temperature
, temperature 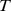 and pressure
and pressure 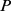 are independent of
are independent of  . The induced magnetic field can be neglected in comparison with the applied magnetic field by considering the magnetic Reynolds number
. The induced magnetic field can be neglected in comparison with the applied magnetic field by considering the magnetic Reynolds number 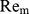 much less than 1. Fig. 1 represents the flow description and geometrical configuration of the physical model.
much less than 1. Fig. 1 represents the flow description and geometrical configuration of the physical model.
Figure 1. Coordinates system and flow configuration.
The governing partial differential equations are
| (1) |
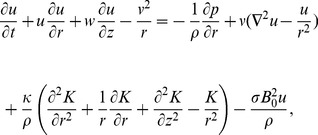 |
(2) |
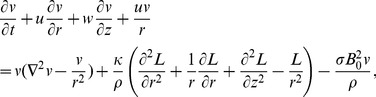 |
(3) |
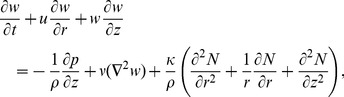 |
(4) |
| (5) |
where 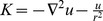 ,
, 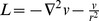 ,
, 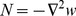 ,
, 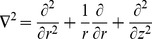 .
.
The boundary conditions are
| (6) |
| (7) |
Here,  ,
,  and
and 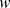 are the components of velocity along the
are the components of velocity along the  ,
,  and
and  directions respectively,
directions respectively, 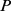 and
and 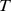 are the pressure and temperature, respectively.
are the pressure and temperature, respectively. 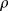 ,
,  and
and  are density, viscosity and thermal diffusivity, respectively.
are density, viscosity and thermal diffusivity, respectively. 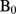 is the applied magnetic field,
is the applied magnetic field,  is the fixed time and
is the fixed time and  is the couple stress parameter respectively.
is the couple stress parameter respectively.
Using similarity transformations
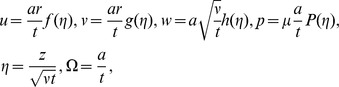 |
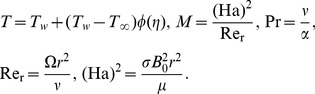 |
(8) |
The equation of continuity yields the relation
| (9) |
And Eqs.  , after using Eqs. (
, after using Eqs. ( reduce to
reduce to
| (10) |
| (11) |
| (12) |
| (13) |
with boundary conditions
| (14) |
Here  ,
, 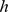 and
and 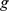 are the radial, axial and tangential components of the dimensionless velocity,
are the radial, axial and tangential components of the dimensionless velocity, 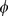 and
and 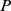 are the dimensionless temperature and pressure of the flow,
are the dimensionless temperature and pressure of the flow,  is the dimensionless unsteadiness parameter which measures the decrease or increase in the angular velocity
is the dimensionless unsteadiness parameter which measures the decrease or increase in the angular velocity  ,
, 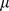 is the coefficient of viscosity,
is the coefficient of viscosity, 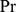 is the Prandtl number,
is the Prandtl number, 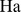 is the Hartmann number,
is the Hartmann number, 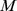 is the magnetic parameter,
is the magnetic parameter, 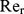 is the Reynolds number with respect to radius respectively. The dimensionless couple stress parameter
is the Reynolds number with respect to radius respectively. The dimensionless couple stress parameter  depends on time
depends on time  , the Eqs.
, the Eqs. are not pure similarity equations, to avoid ambiguity,
are not pure similarity equations, to avoid ambiguity,  has been fixed which led the above equation to approximate similarity. Therefore
has been fixed which led the above equation to approximate similarity. Therefore 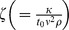 is valid approximation. And the solutions obtained here are approximations to solutions of the original nonlinear PDEs.
is valid approximation. And the solutions obtained here are approximations to solutions of the original nonlinear PDEs.
The shear stress of the fluid in the radial and axial directions can be found as
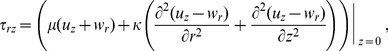 |
(15) |
and
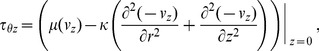 |
(16) |
Hence the local skin friction coefficients are given by
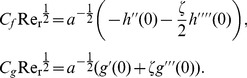 |
(17) |
The heat transfer coefficient in terms of the Nusselt  number can be expressed as
number can be expressed as
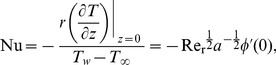 |
(18) |
We use the result  with a radial strip integration to find the total torque required to turn a disk of radius
with a radial strip integration to find the total torque required to turn a disk of radius 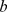 .
.
| (19) |
The dimensionless moment coefficient for a disk of radius 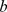 can be defined as
can be defined as
| (20) |
The system of Eqs.  have been modeled the unsteady flow of a couple stress fluid over a rotating disk. The case when there is no body couples or rotation in the fluid, we set the couple stress parameter
have been modeled the unsteady flow of a couple stress fluid over a rotating disk. The case when there is no body couples or rotation in the fluid, we set the couple stress parameter  equal to zero in the governing system, which results in the following form
equal to zero in the governing system, which results in the following form
| (21) |
| (22) |
| (23) |
It can be noticed that the Eqs.  represents the model of unsteady flow of an electrically conducting viscous fluid which was considered and studied by Takhar et. al. [31].
represents the model of unsteady flow of an electrically conducting viscous fluid which was considered and studied by Takhar et. al. [31].
Numerical Procedure
The resulting highly nonlinear system of ODEs  with boundary conditions
with boundary conditions 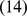 are solved numerically using fourth-order Runge-Kutta integration scheme with shooting technique for fixed time
are solved numerically using fourth-order Runge-Kutta integration scheme with shooting technique for fixed time 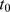 . In shooting method, the resulting system of nonlinear ordinary differential equations is transformed to a set of simultaneous first order differential equations. A systematic guessing of initial conditions and numerical integration as an initial value problem has been done until the desired degree of accuracy has obtained. We have relied on the computational software MATHEMATICA package to solve the considered problem. Influences of all relevant parameters are presented graphically.
. In shooting method, the resulting system of nonlinear ordinary differential equations is transformed to a set of simultaneous first order differential equations. A systematic guessing of initial conditions and numerical integration as an initial value problem has been done until the desired degree of accuracy has obtained. We have relied on the computational software MATHEMATICA package to solve the considered problem. Influences of all relevant parameters are presented graphically.
Results and Discussion
The numerical solution of the problem has been computed via fourth order Runge-Kutta method based on shooting technique. The effect of various physical parameters namely the unsteadiness parameters  , magnetic parameter
, magnetic parameter 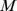 , couple stress parameter
, couple stress parameter  and Prandtl number
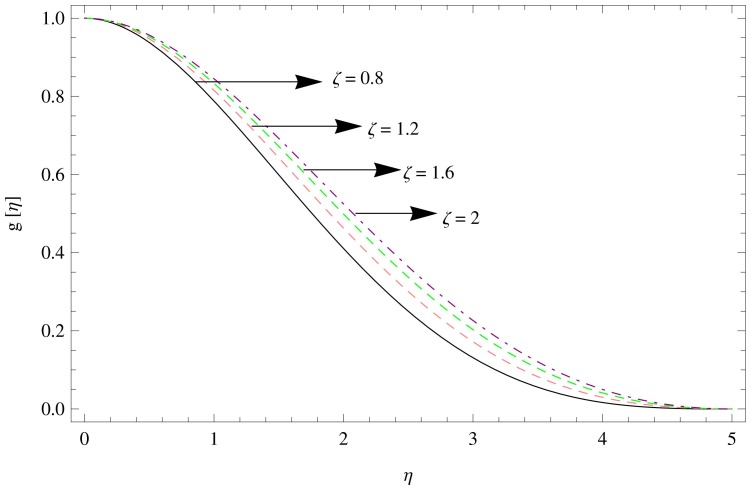
and Prandtl number 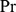 have been examined to measure the variations in the angular velocity, in the velocity field, in the temperature gradient and in the pressure distribution of the fluid (see Figs. 2–15). The changes in radial velocity
have been examined to measure the variations in the angular velocity, in the velocity field, in the temperature gradient and in the pressure distribution of the fluid (see Figs. 2–15). The changes in radial velocity 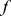 for the variations in the parameters
for the variations in the parameters  ,
, 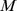 and
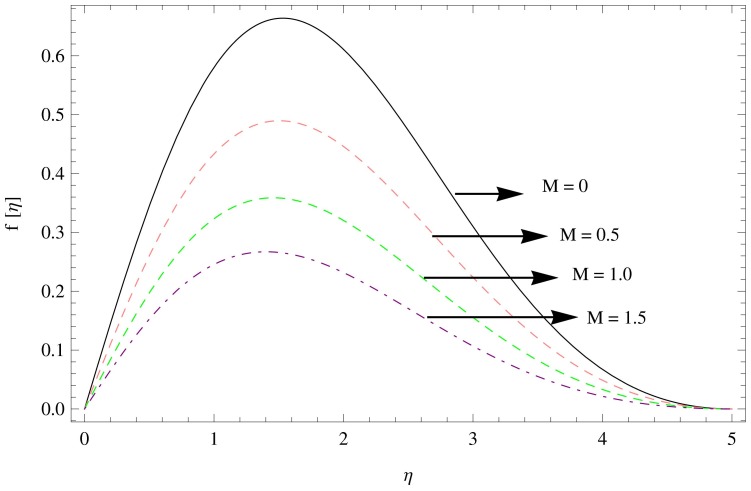
and  are displayed in Figs. 2–4. It can be seen from Fig. 2 that the unsteadiness parameter
are displayed in Figs. 2–4. It can be seen from Fig. 2 that the unsteadiness parameter  decreases the radial velocity
decreases the radial velocity 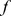 , the stress due to the micro rotation particles in the fluid also weakens the motion of the couple stress fluid as increase in the couple stress parameter
, the stress due to the micro rotation particles in the fluid also weakens the motion of the couple stress fluid as increase in the couple stress parameter  decreases the radial velocity (see Fig. 3), whereas Fig. 4 shows that the increase in magnetic parameter
decreases the radial velocity (see Fig. 3), whereas Fig. 4 shows that the increase in magnetic parameter 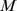 results in the decline of velocity function in radial direction which indicates that the inhibiting Lorentz forces opposes the flow in this direction.
results in the decline of velocity function in radial direction which indicates that the inhibiting Lorentz forces opposes the flow in this direction.
Figure 2. The radial velocity field for 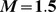 ,
, 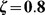 .
.
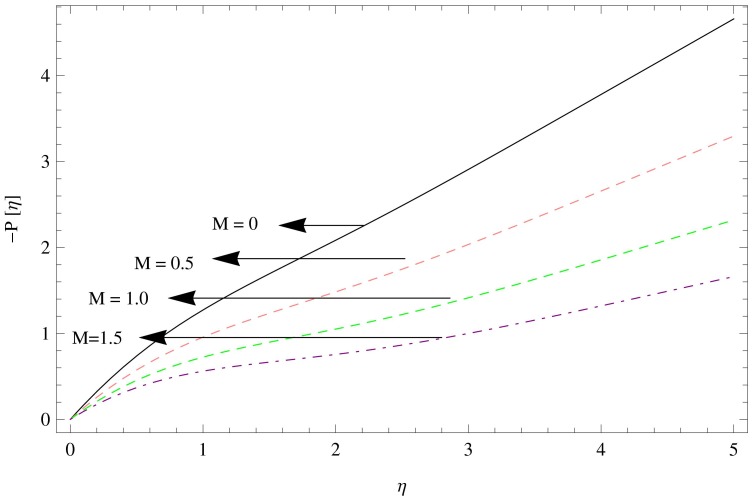
Figure 15. The pressure gradient for 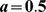 ,
, 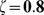 .
.
Figure 4. The radial velocity field for 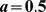 ,
, 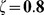 .
.
Figure 3. The radial velocity field for 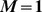 ,
, 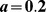 .
.
Figure 14. The pressure gradient for 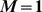 ,
, 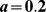 .
.
The effects of tangential velocity 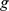 as a function of
as a function of 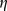 for
for  ,
, 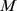 and
and  are shown in Figs. 5–7. The decline in the tangential velocity component can be observed with the increase in unsteadiness parameter
are shown in Figs. 5–7. The decline in the tangential velocity component can be observed with the increase in unsteadiness parameter  as shown in Fig. 5. An increase in the tangential flow over the disk is observed with the increment in the couple stress parameter
as shown in Fig. 5. An increase in the tangential flow over the disk is observed with the increment in the couple stress parameter  increasing the boundary wall thickness (see Fig. 6). Since the magnetic force is in the direction normal to the disk, it opposes the tangential flow velocity, therefore the tangential velocity is lowered everywhere. Thus the effect of the Lorentz forces leads to decelerate the azimuthal velocity with increase in
increasing the boundary wall thickness (see Fig. 6). Since the magnetic force is in the direction normal to the disk, it opposes the tangential flow velocity, therefore the tangential velocity is lowered everywhere. Thus the effect of the Lorentz forces leads to decelerate the azimuthal velocity with increase in 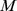 . (see Fig. 7).
. (see Fig. 7).
Figure 5. The azimuthal velocity field for 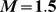 ,
, 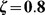 .
.
Figure 7. The azimuthal velocity field for 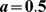 ,
, 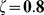 .
.
Figure 6. The azimuthal velocity field for 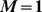 ,
, 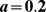 .
.
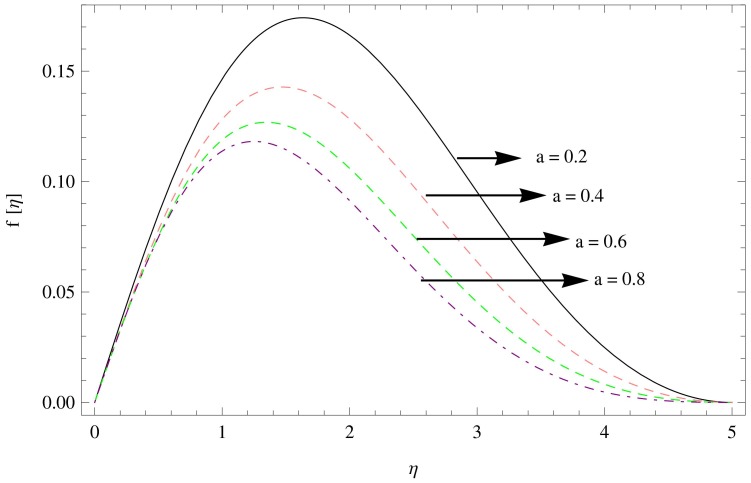
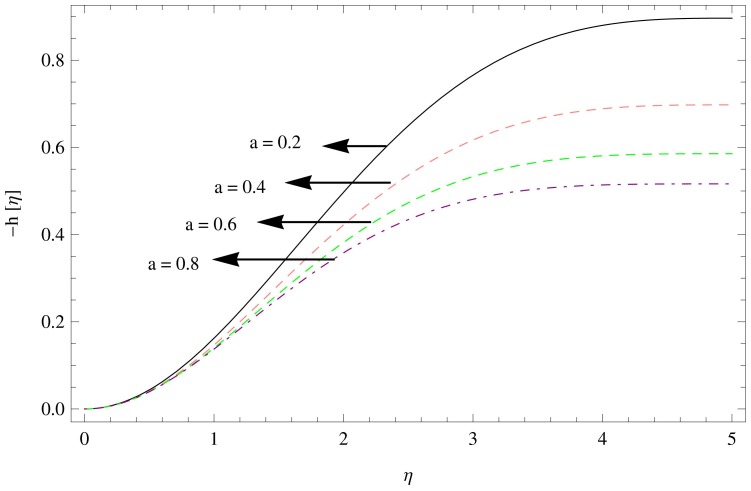
Figs. 8–10 shows the effect of aforesaid parameters on axial velocity 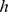 as a function of
as a function of 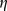 . The axial velocity field behaves in a similar way to the radial velocity field. Flow field is reduced in the axial direction with the enhancement in the unsteadiness parameter
. The axial velocity field behaves in a similar way to the radial velocity field. Flow field is reduced in the axial direction with the enhancement in the unsteadiness parameter  (as shown in Fig. 8), Fig. 9 shows the effects of increasing couple stress parameter which brings unfavorable change in the axial velocity component. The effect of magnetic parameter can be observed in Fig. 10 which displays the fall in the axial velocity component of couple stress fluid flow with the increase in magnetic parameter
(as shown in Fig. 8), Fig. 9 shows the effects of increasing couple stress parameter which brings unfavorable change in the axial velocity component. The effect of magnetic parameter can be observed in Fig. 10 which displays the fall in the axial velocity component of couple stress fluid flow with the increase in magnetic parameter 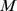 .
.
Figure 8. The axial velocity field for 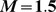 ,
, 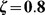 .
.
Figure 10. The axial velocity field for 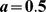 ,
, 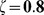 .
.
Figure 9. The axial velocity field for 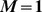 ,
, 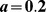 .
.
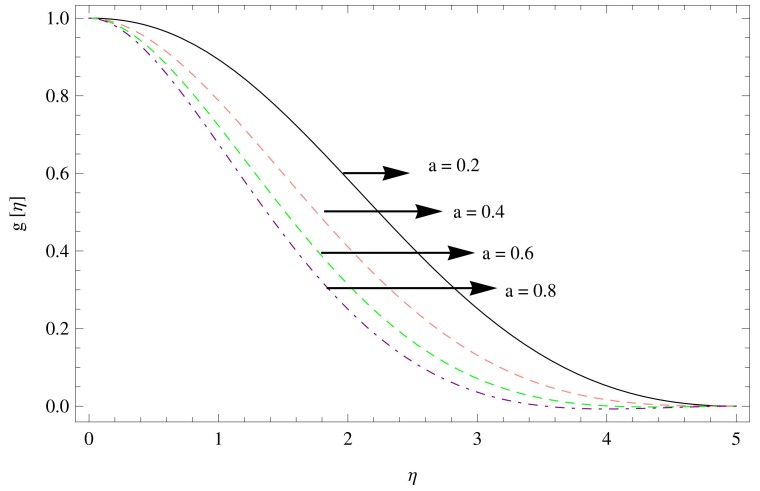
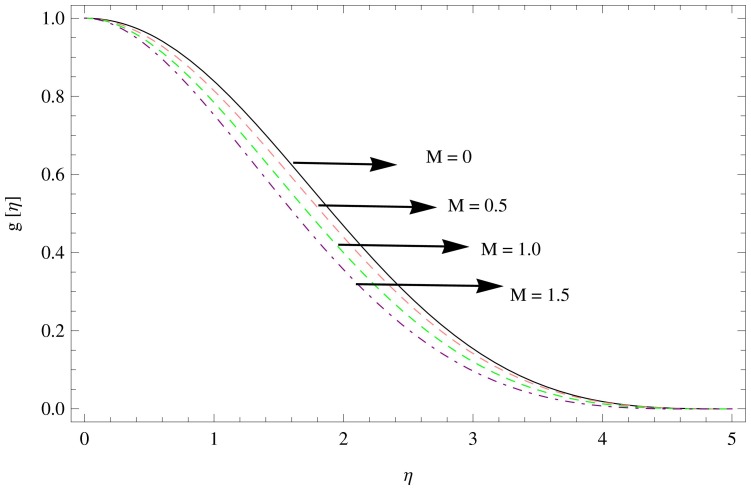
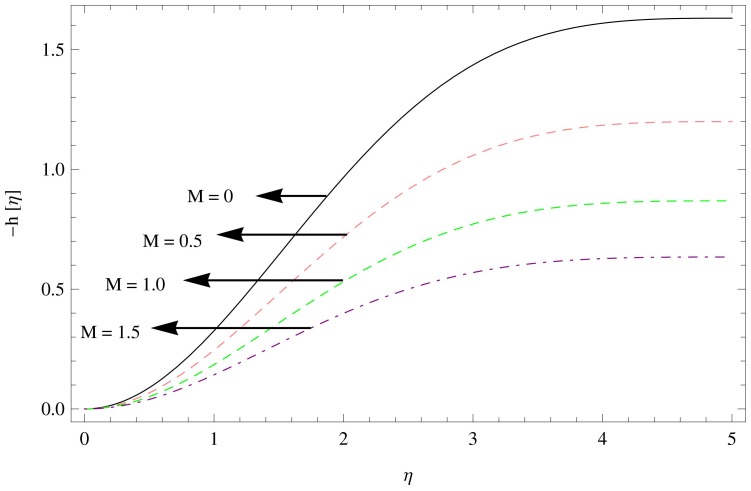
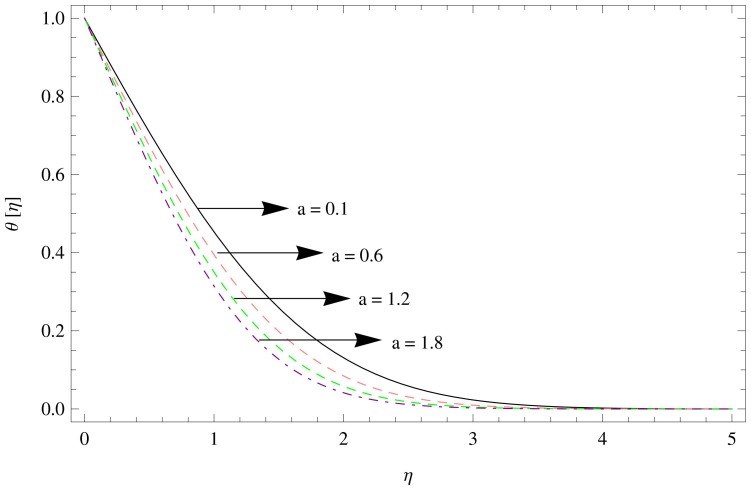
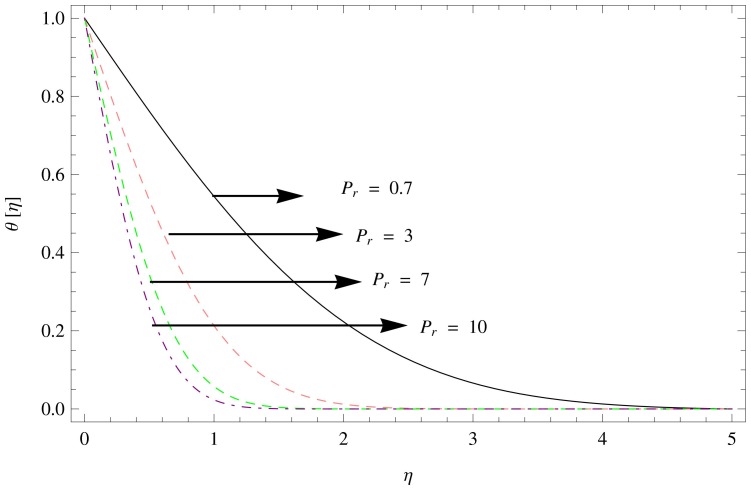
In Figs. 11–12, the effect of temperature gradient 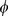 as a function of
as a function of 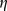 on the different values of
on the different values of 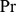 and
and  are observed. Increasing
are observed. Increasing  results in decline in the temperature gradient (Fig. 11), while the similar behavior is observed with increasing
results in decline in the temperature gradient (Fig. 11), while the similar behavior is observed with increasing 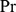 (Fig. 12).
(Fig. 12).
Figure 11. The temperature gradient for 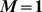 ,
, 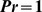 ,
, 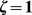 .
.
Figure 12. The temperature gradient for 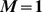 ,
, 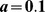 ,
, 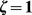 .
.
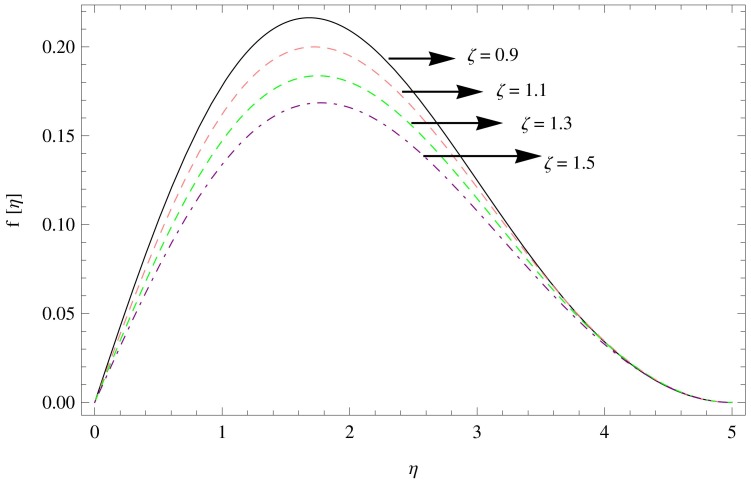
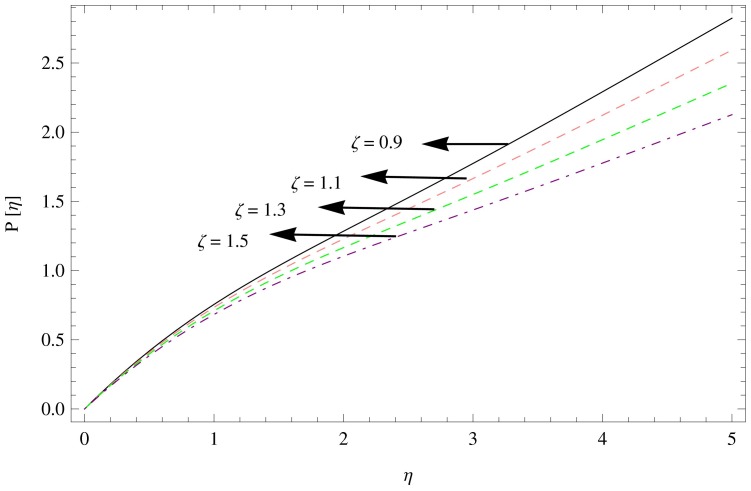
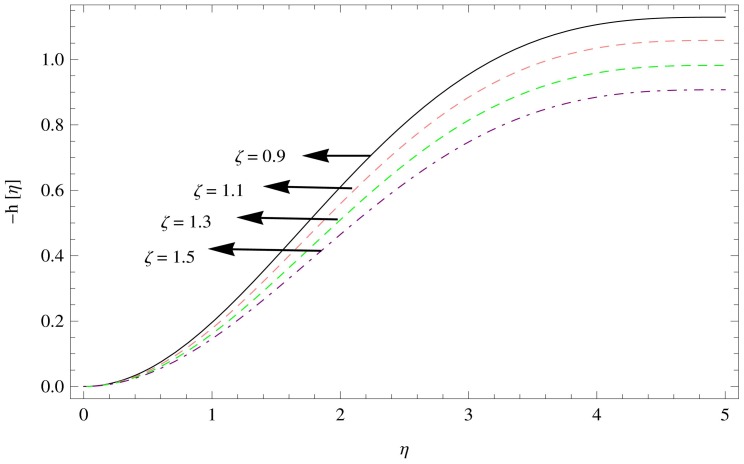
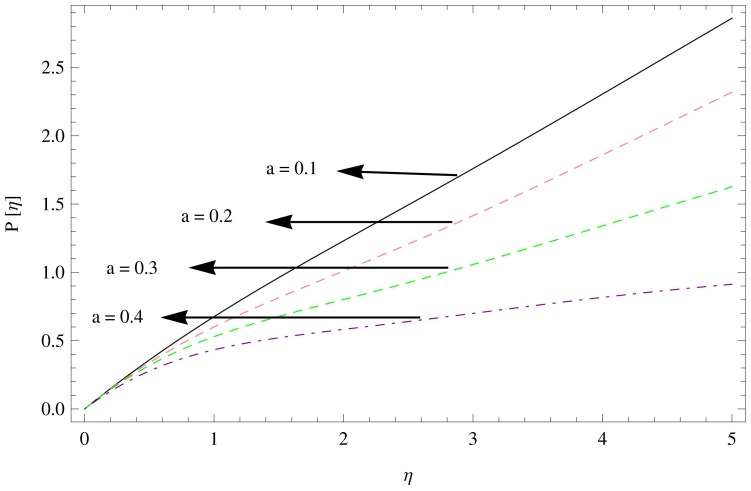
Figs. 13–15 describes the outcome of the pressure distribution against  ,
, 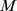 and
and  . These figures depicts the inverse relation between pressure distribution and the unsteadiness parameter, magnetic parameter and couple stress parameter, indicating an increase in above mentioned parameters led the decreasing behavior of the pressure distribution.
. These figures depicts the inverse relation between pressure distribution and the unsteadiness parameter, magnetic parameter and couple stress parameter, indicating an increase in above mentioned parameters led the decreasing behavior of the pressure distribution.
Figure 13. The pressure gradient for 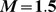 ,
, 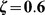 .
.
Limitations of the Study and Future Recommendations
It is imperative to enlighten diverse limitations of this research. This discussion aims at assisting readers to comprehend this study, which ultimately, provide an opportunity to extend the current research. The following assumptions and limitations are considered.
Flow is unsteady, incompressible and laminar.
Flow is three dimensional and rotating over a disk about the
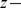 axis.
axis.A uniform magnetic field is applied in the direction normal to the surface of the disk which is assumed unchanging with a small magnetic Reynolds number
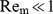 .
.It is assumed that the effect of dissipation in the energy equation is negligible.
In this study we attempt to solve governing equations numerically for a fixed value of 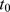 (i.e., at a fixed time ) since
(i.e., at a fixed time ) since 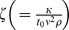 . It is interesting to note that for large time the higher derivatives in equations
. It is interesting to note that for large time the higher derivatives in equations  are vanished as
are vanished as  tends to zero. This leads the case of degenerate limit and difficult to solve with the presented technique, so a different approach should be sought such as singular perturbation theory to solve the problem for the large-time limit. It is worth observing that, on considering the aforesaid limitations for future research, it will turn out to be a demanding task for the researchers regardless of their particular interests in this area. For the model like couple stress fluid, an extensive range of problems can be defined for both theoretical and experimental aspects, i.e. flow over an off centered disk, between two coaxial disk, due to rotating sphere, over an inclined disk etc. So, fascinated by the diverse applications of non-Newtonian fluids, the present work can be extended to other non-Newtonian fluids model by employing a variety of numerical methods.
tends to zero. This leads the case of degenerate limit and difficult to solve with the presented technique, so a different approach should be sought such as singular perturbation theory to solve the problem for the large-time limit. It is worth observing that, on considering the aforesaid limitations for future research, it will turn out to be a demanding task for the researchers regardless of their particular interests in this area. For the model like couple stress fluid, an extensive range of problems can be defined for both theoretical and experimental aspects, i.e. flow over an off centered disk, between two coaxial disk, due to rotating sphere, over an inclined disk etc. So, fascinated by the diverse applications of non-Newtonian fluids, the present work can be extended to other non-Newtonian fluids model by employing a variety of numerical methods.
Conclusions
In this paper, the response of unsteady MHD flow of couple stress fluid over a rotating disk is discussed. The nonlinear differential equations have been solved numerically using Runge-Kutta method and shooting technique. The numerical formulas for radial and tangential shear stress, heat transfer coefficient in term of Nusselt number and dimensionless moment coefficient are presented. The influence of various physical parameters and couple stress parameter on the velocity field, temperature and pressure distributions are all examined numerically and discussed graphically. The following results can be drawn:
The unsteadiness parameter decelerates the flow and temperature field over the rotating disk.
The presence of couple stresses in the fluid enhances the fluid motion in tangential direction and weakens in radial and axial directions.
The magnetic field opposes the fluid velocity in all directions i.e. radial, tangential and axial.
There is a significant reduction in the temperature field due to an increase in Prandtl number and unsteadiness parameter.
Pressure gradient decline while unsteadiness parameter, magnetic parameter and couple stress parameter increases.
Acknowledgments
We would like to express our gratitude to the anonymous referees for their careful assessment and very constructive comments.
Funding Statement
The authors have no external support or funding to report.
References
- 1. Stokes VK (1966) Couple stresses in fluids. Phy Fluids 9: 1710–1715. [Google Scholar]
- 2. Khan NA, Mahmood A, Ara A (2013) Approximate solution of couple stress fluid with expanding or contracting porous channel. Eng Comput 30: 399–408. [Google Scholar]
- 3. Farooq M, Islam S, Haroon T (2011) Heat transfer analysis of the couple stress fluid between two parallel plates. Heat Trans Res 42: 737–780. [Google Scholar]
- 4. Ramzan M, Farooq M, Alsaedi A, Hayat T (2013) MHD three-dimensional flow of couple stress fluid with Newtonian heating. Europe Phy J 128: 1–15. [Google Scholar]
- 5. Hayat T, Abbas Z, Sajid M (2009) MHD stagnation point flow of an upper convected Maxwell fluid over a stretching sheet. Chaos Solitons and Fractals 39: 840–848. [Google Scholar]
- 6.Kumar SK, Thacker WI, Watson LT (1987) Rotating magnetohydrodynamic flow in a circular magnetic field. Dept. of computer Science, Winthrop College, Rock Hill, S.C. Tech. Rept. 321.
- 7. Osalusi E, Side J, Harris R, Clark P (2008) The effect of combined viscous dissipation and Joule heating on unsteady mixed convection MHD flow on a rotating cone in a rotating fluid. Int Commun Heat Mass Transf 35: 413–429. [Google Scholar]
- 8. Jamil M, Khan NA, Shahid N (2013) Fractional MHD Oldroyd-B fluid over an oscillating plate. Therm Sc 17: 997–1011. [Google Scholar]
- 9. Sreenadh S, Kishore SN, Srinivas ANS, Hemadri R (2011) The influence of MHD on the couple stress fluid in the porous medium. Adv Appl Sc 2: 215–222. [Google Scholar]
- 10.Lorrain P, Lorrain F, Houle S (2006) Magneto-fluid dynamics: fundamentals and case studies of natural phenomena. Springer, New York.
- 11. Dehghan M, Mirzaei D (2009) Meshless local Petrov-Galerkin (MLPG) method for the unsteady magnetohydrodynamicow through pipe with arbitrary wall conductivity. Appl Numer Math 59: 1043–1058. [Google Scholar]
- 12. Dehghan M, Mirzaei D (2009) Meshless local boundary integral equation (LBIE) method for the unsteady magnetohydrodynamic flow in rectangular and circular pipes. Comput Phys Commun 180: 1458–1466. [Google Scholar]
- 13. Maleque AK, Sattar AM (2005) Steady laminar convective flow with variable properties due to a porous rotating disk. J Heat Transf 127: 1406–1409. [Google Scholar]
- 14. Wiesche SAD (2007) Heat transfer from a rotating disk in a parallel air cross-flow. Int J Therm Sc 46: 745–754. [Google Scholar]
- 15. Ariel PD (2001) On computation of MHD flow near a rotating-disk. Z Angew Math Mech 82: 235–246. [Google Scholar]
- 16. Fang T (2007) Flow over a stretchable disk. Phy Fluids 19: 128105. [Google Scholar]
- 17. Rashidi MM, Dinarvand S (2009) Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by homotopy analysis method. Nonlinear Anal RWA 10: 2346–2356. [Google Scholar]
- 18. Khan I, Fakhar K, Sharidan S (2012) Magnetohydrodynamic rotating flow of a generalized Burgers’ fluid in a porous medium with hall current. Transport in Porous Media 91: 49–58. [Google Scholar]
- 19. Rashidi MM, Mohimanian SAP, Hayat T, Obaidat S (2012) Analytic approximate solutions for steady flow over a rotating disk in porous medium with heat transfer by homotopy analysis method. Comp and Fluids 54: 1–9. [Google Scholar]
- 20. Khan I, Fakhar K, Anwar MI (2012) Hydromagnetic rotating flows of an Oldroyd-B fluid in a porous medium. Special Topics and Review in Porous Media 3: 89–95. [Google Scholar]
- 21. Ming C, Zheng L, Zhang X (2011) Steady flow and heat transfer of the power-law fluid over a rotating disk. Int Commun Heat and Mass Transf 38: 280–284. [Google Scholar]
- 22. Turkyilmazoglu M (2012) MHD fluid flow and heat transfer with varying Prandtl number due to a rotating disk subject to a uniform radial electric field. Appl Therm Eng 35: 127–133. [Google Scholar]
- 23.Rashidi MM, Mehr NF (2012) Series solutions for the flow in the vicinity of the equator of an MHD boundary-layer over a porous rotating sphere with heat transfer. Therm Sc DOI:10.2298/TSCI120301155R.
- 24. Turkyilmazoglu M (2012) Three dimensional MHD stagnation flow due to a stretchable rotating disk. Int J Heat Mass Transf 55: 6959–65. [Google Scholar]
- 25. Bellout H, Vajravelu K, Van Gorder RA (2013) Existence results for coupled nonlinear systems approximating the rotating MHD flow over a rotating sphere near the equator. Z Angew Math Phy 64: 83–100. [Google Scholar]
- 26. Osalusi E, Side J, Harris R (2007) The effects of Ohmic heating and viscous dissipation on unsteady MHD and slip flow over a porous rotating disk. Int Comm Heat Mass Transf 34: 1017–1029. [Google Scholar]
- 27. Dinarvand S, Doosthoseini A, Doosthoseini E, Rashidi MM (2010) Series solutions for unsteady laminar MHD flow near forward stagnation point of an impulsively rotating and translating sphere in presence of buoyancy forces. Nonlinear Anal, RWA 11: 1159–1169. [Google Scholar]
- 28. Chamkha AJ, Ahmed SE (2012) Unsteady MHD heat and mass transfer by mixed convection flow in the forward stagnation region of a rotating sphere at different wall conditions. Chem Eng Comm 199: 122–141. [Google Scholar]
- 29. Ram P, Bhandari A (2013) Effect of phase difference between highly oscillating magnetic field and magnetization on the unsteady ferrofluid flow due to a rotating disk. Results in Phy 3: 55–60. [Google Scholar]
- 30. Nadeem S, Saleem S (2013) Analytical treatment of unsteady mixed convection MHD flow on a rotating cone in a rotating frame. J Taiwan Int Chem Eng 44: 596–604. [Google Scholar]
- 31. Takhar HS, Singh AK, Nath G (2002) Unsteady MHD flow and heat transfer on a rotating disk in an ambient fluid. Int J Therm Sc 41: 147–155. [Google Scholar]