Assessing host extinction risk following exposure to Batrachochytrium dendrobatidis

Abstract

Wildlife diseases are increasingly recognized as a major threat to biodiversity. Chytridiomycosis is an emerging infectious disease of amphibians caused by the fungus Batrachochytrium dendrobatidis (Bd). Using a mathematical model and simulations, we study its effects on a generic riparian host population with a tadpole and adult life stage. An analytical expression for the basic reproduction quotient, Q_o, of the pathogen is derived. By sampling the entire relevant parameter space, we perform a statistical assessment of the importance of all considered parameters in determining the risk of host extinction, upon exposure to Bd. We find that Q_o not only gives a condition for the initial invasion of the fungus, but is in fact the best predictor for host extinction. We also show that the role of tadpoles, which in some species tolerate infections, is ambivalent. While tolerant tadpoles may provide a reservoir for the fungus, thus facilitating its persistence or even amplifying its outbreaks, they can also act as a rescue buffer for a stressed host population. Our results have important implications for amphibian conservation efforts.

1. Introduction

Infectious wildlife diseases are linked to many recent animal population declines and are considered a major threat to biodiversity [1,2]. Understanding the dynamics of diseases and the factors that determine their long-term effects on host populations is an important step for conservation measures. Chytridiomycosis, an emerging infectious disease of amphibians [3], is caused by the fungus Batrachochytrium dendrobatidis (Bd) [4]. Bd has a wide host range and is now found on all continents where amphibians occur [5]. Its invasion can have devastating effects on host populations [6], and chytridiomycosis is currently linked to the decline or local extinction of over 200 amphibian species [7]. Nevertheless, many amphibian populations currently seem to be in a long-term endemic state with the fungus [8–10], often with a substantial reduction in survival [11].

The life cycle of Bd is a succession of a motile, waterborne, infectious zoospore and a substrate-bound thallus, the zoosporangium [12]. The zoospore encysts in a keratinized epidermal cell of its host [13] and transforms into a zoosporangium within a few days [14]. In the zoosporangium, new zoospores form, which are released towards the skin surface and into the external environment [15]. The exact pathophysiology of Bd is not fully understood, but disturbance of epidermal intercellular junctions seems to be involved in pathogenesis [16].

The prevalence of Bd and its effects on host populations have been statistically linked to abiotic conditions, such as temperature [17] and precipitation [18]. However, a complete mechanistic understanding of the interactions of demographic, immunological and environmental factors and their influence on the epizootic dynamics of Bd is lacking. Simple deterministic epizootic models with density-dependent transmission predict an eventual fade out of diseases, once the host population falls below a certain threshold. Recent findings, however, highlight the role of tadpoles, which are less affected by infection than adults [19,20], as a potential reservoir facilitating the persistence of Bd [21], or even promoting host extinction [22]. Moreover, recent reports, suggesting the presence of Bd on aquatic birds [23] and crayfish [24], signify the risks of possible environmental reservoirs. It has also been theorized that a potentially long-lived free zoospore stage might contribute to local host extinctions [22,25,26].

Previous theoretical work on Bd by Mitchell et al. [22] and Briggs et al. [21] has succeeded in showing that all three scenarios, Bd clearance, Bd–host coexistence and host extinction, are possible epizootic outcomes even for the same host species. Mitchell et al. [22], however, neglect infected adults, do not consider within-host disease dynamics and ignore any possible variation in individual zoospore load. Keeping track of zoospore loads is important because (i) the progression of infection depends on reinfection events [12,17] and can vary greatly between individuals [27], (ii) zoospore load strongly influences pathogenesis [15,28] and (iii) the release of zoospores increases with fungal load [14]. Briggs et al. [21], on the other hand, assume that tadpoles are resistant to chytridiomycosis, a trait that may not be present in all frog species [20,29]. In addition, none of these models considers the possibility of seasonal variation of Bd transmission [30] and a possible regulation of on-host fungal growth (although its potential importance has been pointed out by Briggs et al.).

We propose a generic, continuous-time dynamical model for the interaction between Bd and an amphibian host population in an aquatic environment that addresses the above shortcomings of previous models. The host population includes two life stages, tadpoles and adults, and infections occur in both life stages through contact with zoospores in the water. Using analytical tools and numerical simulations, we investigate the short- and long-term consequences of an exposure of the host population to Bd. By systematically sampling the entire relevant parameter space, we assess the risk of host extinction as a function of the model parameters. We quantify the relative importance of model parameters using a dimensionless measure which we call risk effect. Finally, we investigate the role of the tadpoles in the epizootic and show that the host extinction risk need not necessarily increase when tadpoles tolerate infection (e.g. do not develop chytridiomycosis).

2. Material and methods

(a). Model description

In this section, we outline the epizootic model. A detailed description and justification of the model are provided in the electronic supplementary material, §1. We consider a single, closed, well-mixed amphibian population in a single aquatic habitat, interacting with a single Bd strain. The population is structured into two life stages, tadpoles and adults. Adults lay eggs at a constant or seasonally varying rate. Eggs quickly hatch as tadpoles and tadpoles metamorphose into adults at a constant rate. All newly recruited individuals are healthy. In the absence of Bd, the population is density regulated through competition, with adult and tadpole carrying capacities K_A and K_T, respectively.

The model keeps track of the distribution of the zoospore load, or degree of infection (DOI), across individuals. We denote by P_A(t, n) and P_T(t, n) the number of adults and tadpoles, respectively, that at time t are infected with n ∈ 0, 1, … zoospores, i.e. have DOI n. Because fungal load is usually estimated through the zoospore concentration on the host's skin [31], a zoospore-focused model allows for comparison with observations, as opposed to, say, a sporangium-focused model. We denote by 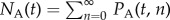the total number of adults and by

the average DOI among all adults. N_T(t) and S_T(t) are defined in a similar way for tadpoles. The subscript s used hereafter for model parameters and variables, shall stand for either A (adults) or T (tadpoles).

New infections occur through contact with free zoospores released into the water by infected individuals [14]. This corresponds to findings suggesting that infested waters and sand might be the primary source of infection [21,28,32]. Infections might also change due to within-host disease dynamics, modelled through transition probability rates between DOIs. These transition rates depend on the exponential, within-host, disease growth or decay rates soon after exposure (λ_s), as well as the natural within-host zoospore loss rates (μ_S,s).

The negative effects of Bd on the population are modelled by (i) an increased mortality rate of individuals, (ii) a decreased adult fecundity and (iii) a higher failure rate of metamorphoses [19,33]. The severity of all three effects increases with the DOI. For example, the yearly host survivorship is halved at a certain DOI tolerance level, 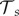and the adult breeding rate is halved at a certain DOI, . Individuals die immediately if their DOI reaches a lethal threshold [28,32,34]. We also explicitly considered the case where tadpoles completely tolerate their infections, e.g. do not develop chytridiomycosis [19,20]. In that case, the tadpoles’ DOI is nevertheless limited to a maximum possible value.

The model gives the temporal dynamics for the DOI distributions P_A(t, n), P_T(t, n) and the total number of free, active zoospores present in the water, the zoospore pool Z(t). For the DOI distribution of adults, we have

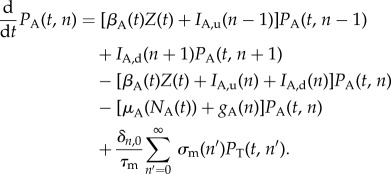2.1

The first three rows in (2.1) correspond to transitions between different DOIs. Here, β_A(t) is the pool-to-adult transmission rate. It can be constant or annually oscillating, allowing us to investigate possible effects of seasonal variation. In our investigations, we varied its average value 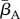, its relative oscillation amplitude (b) and its phase lag (φ) with respect to the breeding season. The terms I_A,u, I_A,d (up and down) represent transition rates between DOIs due to within-host dynamics. The fourth row corresponds to disease-independent and -dependent host mortality, the former increasing linearly with density. The last row describes the continuous metamorphosis of tadpoles into adults, at a rate 1/τ_m and with a DOI-dependent probability of success 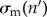. The Kronecker delta δ_n,0 is 1 if n = 0 and 0 otherwise, ensuring that new recruits are healthy. Similarly, for the tadpoles

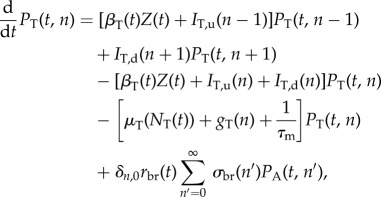2.2

with the difference being the additional loss term 1/τ_m, which accounts for failed or successful metamorphoses. The breeding rate r_br(t) can be constant or have an annual peak at the breeding season. We varied both the width of that peak (breeding period), as well as the overall scale of r_br, quantified by the cumulative yearly fecundity, 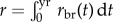. The breeding rate is modulated by 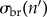, which mediates a possible DOI-dependent reduction in fecundity. See figure 1 for a schematic illustration of the dynamics (2.1) and (2.2). The dynamics of the zoospore pool are

Here, μ_Z is the free zoospore loss rate and η_s are the rates at which zoospores on hosts release new zoospores into the water. Z_o is the equilibrium size of a possible external zoospore pool in the absence of infected amphibians, referred to as environmental reservoir.

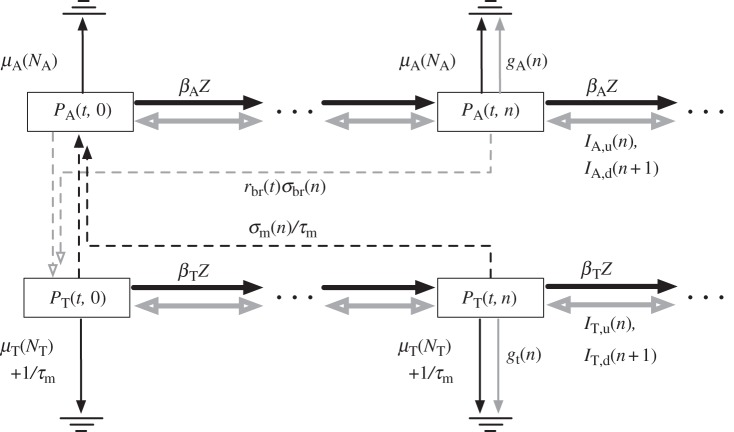
Figure 1.

Schematic of the dynamics for the DOI distributions of adults (2.1) and tadpoles (2.2). Dashed arrows correspond to adult and tadpole recruitment, thin full arrows to disease-independent and disease-induced deaths, thick black arrows to new infections and thick grey arrows to within-host disease dynamics.

We note that one can derive mean field approximations of the dynamics (2.1) and (2.2), which are similar in structure to, but more general than the ones considered by May et al. [35, eqns (19,20)] (see the electronic supplementary material, §2.1). If the characteristic time scales of the zoospore pool are short compared with the epizootic dynamics [36, §6], we obtain a host-to-host transmission model similar to the one derived by Anderson et al. [37, eqn. (8)] (see the electronic supplementary material, §2.2). Important generalizations of our model, compared with [35,37], are the involvement of two host life stages and a seasonal variation of recruitment.

(b). Numerical simulations

The considered model parameter ranges for all simulations are given in table 1. Whenever possible, these ranges were chosen to roughly represent the values reported in the literature, or otherwise taken within plausible limits. Simulations typically ran for 10 years, and started with a healthy host population that was exposed to the pathogen during the second year.

Table 1.

Parameter ranges used in simulations. Exact parameter definitions are given in the electronic supplementary material, §1. Chosen values are justified in the electronic supplementary material, §5.1. All rates are in d⁻¹. Subscripts A and T refer to adults and tadpoles, respectively; the subscript s to either one. The case 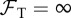corresponds to tadpoles tolerating their infection.

description	symbol	values
environmental reservoir	Zo	0, 10–1015
free zoospore loss rate	μZ	10−3–1
on-host zoospore loss rate	μS,A	10−3–1
on-host zoospore loss rate	μS,T	10−3–1
early infection growth rate	λA	(−1)–1
early infection growth rate	λT	(−1)–1
mean adult transmission rate		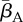10−10–10−3
mean tadpole transmission rate		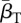10−10–10−3
phase lag of transmission rates βs(t)	φ	0–1 year
relative oscillation amplitude of βs(t)	b	0–1
zoospore release rate	ηA	1–10
zoospore release rate	ηT	1–10
adult lethal DOI threshold		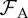104
tadpole lethal DOI threshold		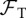104, ∞
adult DOI tolerance		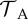10–FA
tadpole DOI tolerance		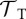10–FT
metamorphose DOI tolerance		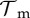10–106
breeding DOI tolerance		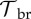10–106
yearly adult fecundity	r	10–103
tadpole lifetime	τm	10 days to 4 years
breeding period	τbr	1 day to 0.5 year
maximum adult survivorship	σA	0.1–0.9
maximum tadpole survivorship	σT	0.01–0.2
adult carrying capacity	KA	10–103
tadpole carrying capacity	KT	10–103

We categorized each simulation outcome into one of the following three scenarios: (i) frog extinction, (ii) clearance of the fungus from the population and (iii) Bd persistence, i.e. the coexistence of the host and fungus in an endemic state by the end of the simulation. Using Monte Carlo simulations [38], we estimated the probability of any of the above scenarios, for varying values of each individual parameter, when all other parameters are randomly chosen from their entire range. We evaluated the effects of the different parameters on the probability of a disease-driven host extinction. We quantified the relative importance of each parameter by its so-called risk effect, which measures the change in the probability of host extinction, when the parameter is varied from its minimum to its maximum value. Risk effects were estimated through linear regression of the probability of extinction obtained from 10⁴ trials (see the electronic supplementary material, §5.2).

We differentiated between cases where Z_o = 0 (no environmental reservoir) or Z_o > 0, and between cases where tadpoles suffer from infection or completely tolerate it. We also examined the effects of stochastic host demographics, by replacing the deterministic, disease-independent mortality in our simulations with random fatal events occurring at a constant Poissonian rate. This stochastic model is otherwise identical to the deterministic model described earlier. We refer to the electronic supplementary material, §5 for technical details.

3. Results and discussion

(a). Early invasion dynamics

Using a mean field approximation and standard linear stability theory [39], we analytically calculated the basic reproduction quotient Q_o of the fungus [40,41], introduced by Roberts et al. [36] for macroparasite models. Q_o (termed basic reproduction ratio, R_o, in Roberts et al.'s original formulation) has been defined as the number of adult parasites arising in the next generation from a single adult parasite, in a completely susceptible host population. It is comparable to the basic reproduction ratio in microparasite models [42]. Here, it gives the expected number of zoospores released into the water, originating from a single free zoospore, at the early stage of invasion in a newly exposed habitat. The condition Q_o > 1 is therefore a deterministic predictor for the successful invasion of Bd. We assumed that Bd-induced mortalities only become significant at a relatively high DOI and do not affect the early growth of the epizootic [3,34]. We refer to the electronic supplementary material, §2.3 for the derivation.

We find that the early epizootic dynamics strongly depend on (i) the exponential rate λ_s at which early infections decay (λ_s < 0) or grow (λ_s > 0) within hosts, when excluding external reinfections and (ii) the time-averaged per capita recruitment (or turnover) rate 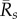of each life stage s in the population prior to exposure. In particular, whenever 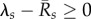for at least one life stage s, the fungus will successfully invade upon exposure (in fact, in this case Q_o is formally infinite). But invasion is still possible, even if all 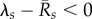. Then Q_o takes the form

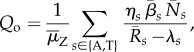3.1

where 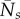are the time-averaged population sizes in the uninfected community, 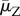is the time-averaged zoospore loss rate and 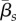are the time-averaged transmission rates. The derivation of (3.1) assumes that the initial exposure is so weak and the resulting early Bd dynamics so slow that linear stability theory applies beyond the time scales over which the averaged variables change. In the alternative limit of rapid Bd growth, all time averages should be replaced by their instantaneous values.

In fact, the above results, and in particular equation (3.1), hold for communities of multiple host species with multiple life stages and arbitrary recruitment flows and mortalities. The index s then runs through all species and life stages (see the electronic supplementary material, §2). Equation (3.1) highlights the increased risk of invasion associated with larger host population sizes. It also shows that the susceptibility of a single host species or life stage (i.e. for which 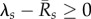) can jeopardize the entire community of a riparian habitat.

(b). Post-invasion dynamics

Simulations of the single-species model reproduce all three possible scenarios: (i) host extinction, (ii) clearance of the fungus from the population (or failure to invade) and (iii) long-term persistence of the fungus. All of these scenarios occur for a substantial parameter range, although by definition, clearance is only possible in the absence of an environmental reservoir (Z_o = 0).

Fungal persistence is typically accompanied by a permanent reduction of the host population to a fraction of its initial carrying capacity, as observed in numerous host–pathogen interactions and predicted by standard theory [43]. This reduction tends to be more severe as Bd transmission rates β_s or the reservoir Z_o increase. Figures 2a–d and 3a illustrate typical simulations resulting in long-term Bd persistence. Host population sizes increase during breeding periods (figure 3a), but can also vary due to epizootic cycles (figure 2a) or even due to stochastic mortalities. In fact, in many cases this stochasticity induces coherent cycles around an otherwise stable endemic state, a phenomenon known as quasi-cycles [44]. Furthermore, using cross-correlation analysis [45, §14.2], we found that Bd prevalence positively correlates with recent host population sizes, usually with a delay that depends on the characteristic time scales of the epizootic (up to several months).

Figure 2.

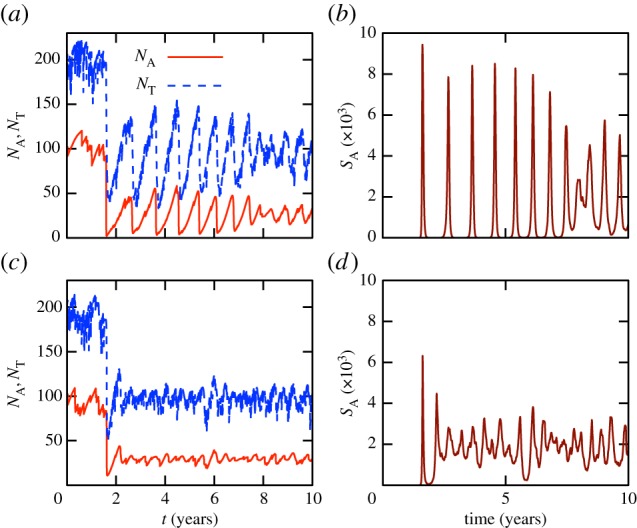
Simulations of the stochastic model (one per row), leading to endemic states. Panels (a,c) show population sizes, panels (b,d) show the mean adult DOI. The breeding rate r_br and transmission rates 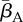, 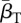are time-independent. Populations are exposed to Bd during the second year. (a,b) Tadpoles do not suffer from infection and have a long life time (τ_m = 1 year). The observed cycles are purely due to host-demographic delays, as Bd-intrinsic time scales are very short (μ_Z = 1 d⁻¹, 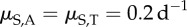). (c,d) Tadpoles strongly suffer from infection, but with otherwise identical parameters as in (a,b). Model parameters are given in the electronic supplementary material, table S1. (Online version in colour.)

Figure 3.

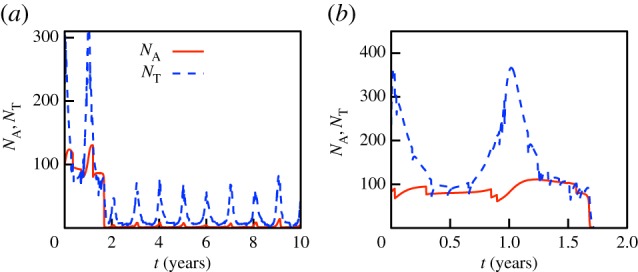
Adult population sizes during two similar simulations of the stochastic model. Annual peaks coincide with breeding seasons. The host population is exposed to the fungus during the second year. (a) Tadpoles do not suffer from infection and enable host survival, albeit at a reduced population size. (b) Tadpoles suffer from infection; all other parameters are identical to (a). Upon exposure to the fungus, the population quickly goes extinct. Model parameters are given in the electronic supplementary material, table S1. (Online version in colour.)

When host population sizes are low due to high Bd pressure, stochastic fluctuations can eventually cause host extinction [46]. But host extinction is also possible in the deterministic case, provided that Bd proliferation and host vulnerability are sufficiently high. Simple deterministic models of density-dependent disease transmission predict an eventual fade out of the pathogen, once the host population falls below a certain threshold [46]. However, if zoospores remain viable for a long time in lake water or sediments [25,26], then feedback delays in the density regulation of Bd proliferation can result in host extinction. Similar delays can appear if host recovery time scales exceed those of population crashes.

(c). Risk effects

The risk effects of the model parameters and Q_o are given in table 2. We note that even though Q_o is not an independent model parameter, its risk effect can still be defined and estimated (see the electronic supplementary material, §5.2).

Table 2.

Risk effects of model parameters and Q_o. Risk effects measure the direction and magnitude of change in the probability of host extinction, when a parameter is varied from its minimum to its maximum value. Only risk effects over 0.1 are shown; dash (—) represents lower values. Data columns 1 and 3: tadpoles suffer from infection. Data columns 2 and 4: tadpoles tolerate infection. Data columns 1 and 2: Z_o sampled from 10 to 10¹⁵. Data columns 3 and 4: Z_o = 0. All model parameters were sampled in their entire range, given in table 1. Similar results were obtained for the stochastic model.

parameter	Zo > 0		Zo = 0
	suffer	tolerate	suffer	tolerate
Qo	+0.66	+0.83	+0.81	+0.71
Zo	+0.66	+0.78	n.a.	n.a.
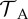	−0.38	−0.47	−0.17	−0.28
μZ	−0.11	−0.20	−0.44	−0.46
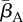	+0.32	+0.34	+0.38	+0.39
KT	—	—	−0.27	−0.35
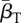	+0.17	+0.27	+0.24	+0.18
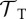	−0.24	n.a.	—	n.a.
KA	—	—	−0.22	−0.12
λA	+0.17	+0.19	+0.18	+0.12
μS,A	—	—	−0.14	−0.11
ηA	—	—	+0.13	—
μS,T	—	—	—	−0.12
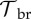	—	—	—	−0.10

Our results indicate that environmental reservoirs can have detrimental effects on host populations, and extinction becomes almost certain as their size (Z_o) exceeds a certain threshold. In the absence of environmental reservoirs (Z_o = 0), the two most important model parameters are the average transmission rate 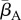and free zoospore loss rate μ_Z, in accordance with previous work [21,22]. Figure 4a–d shows the probabilities of host extinction, Bd prevalence and Bd clearance as functions of the tuple 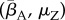. When Z_o = 0, all three parameter regions seem to be strongly determined by 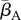and μ_Z, with the endemic regime separating regions favouring extinction (low μ_Z, high 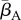) from those favouring Bd clearance (high μ_Z, low 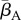). The negative risk effect of μ_Z underlines the risks associated with a potentially long-lived infectious zoospore, the existence of which still remains controversial [25,26,30]. We did not find significant risk effects for many of the other model parameters. For some of them, such as the zoospore release rates η_s, this was due to their relatively narrow ranges.

Figure 4.

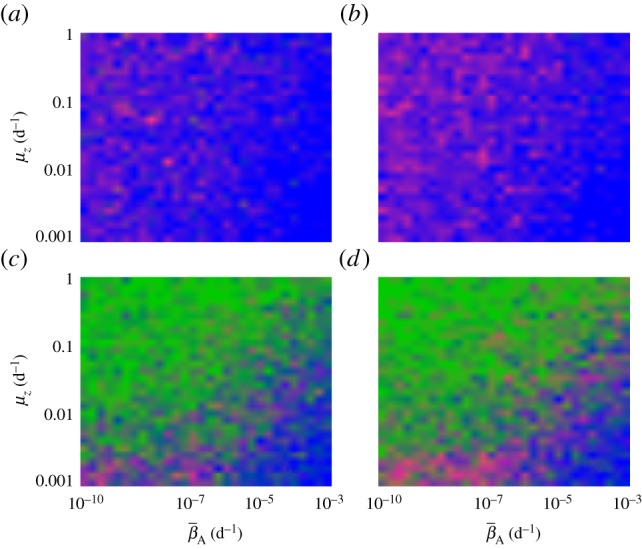
Estimated probabilities of Bd persistence, Bd clearance and host extinction, as functions of 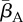and μ_Z in the deterministic model, shown as colour codes. Pure colours green, magenta and blue correspond to 100% Bd clearance, Bd persistence and host extinction, respectively. Mixed probabilities appear as compound colours. (a,b) Z_o > 0. (c,d) Z_o = 0. (a,c) Tadpoles suffer from infection. (b,d) Tadpoles tolerate Bd. All other model parameters were sampled within their entire range, as described in the electronic supplementary material, §5.2. Similar results were obtained for the stochastic model.

Interestingly, we found that the basic reproduction quotient Q_o shows the greatest predictive power for the extinction risk. The risk reaches 100% when Q_o exceeds a certain threshold, as seen in figure 5a–d. For Z_o = 0, Bd persistence becomes most likely at intermediate values Q_o ≈ 1. Strictly speaking, Q_o only characterizes the early growth of the epizootic. Our results suggest that the efficiency of the fungus in proliferating at a site shortly after exposure strongly determines its long-term effect on host demographics. We point out that Q_o, as given by (3.1), is only valid if 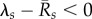for all host types. In the alternative case, Q_o is formally infinite and even though the fungus is expected to invade, our numerical results on its role in host extinction should not be extrapolated to these cases.

Figure 5.

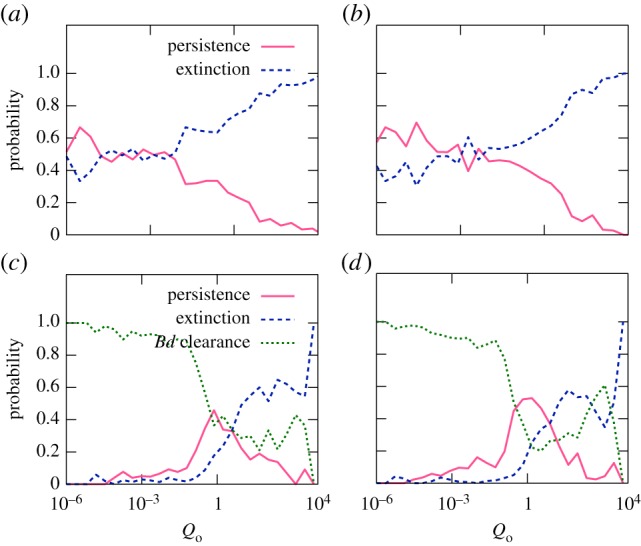
Estimated probabilities of Bd persistence, Bd clearance and host extinction in the deterministic model, as functions of the basic reproduction quotient, Q_o. (a,b) The environmental reservoir Z_o ranges from 10 to 10¹⁵ zoospores. (c,d) No reservoir (Z_o = 0). (a,c) Tadpoles suffer from infection. (b,d) Tadpoles tolerate infection. All other model parameters were sampled within their entire range. Similar results were obtained for the stochastic model. (Online version in colour.)

We emphasize that the risk effects calculated for the considered parameters, and therefore their order of importance, depend on their chosen ranges (table 1), more precisely on their true (unknown) probability distribution within those ranges. The resulting assessment should therefore be appreciated qualitatively. In special cases, the effect of certain parameters on the extinction risk might be stronger or even opposite to the predictions given here, as the latter are merely statistical and taken over a large parameter space. For example, in some cases we found that larger host carrying capacities actually increase the risk of extinction despite their negative risk effect, as they facilitate stronger epizootic outbreaks.

(d). The role of tadpoles

As adult densities decrease, tadpoles can act as a temporary reservoir for Bd, if they can tolerate infection and remain in the tadpole stage for long times. This effect can lead to strong Bd outbreaks and host population declines, even when zoospore death and within-host clearance rates are high (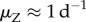, 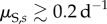). Shorter tadpole stages dampen these outbreaks, but Bd prevalence is still generally higher and adult densities lower when tadpoles tolerate Bd, compared with when they do not. These observations are exemplified by simulations shown in figure 2a–d. In figure 2a,b, a long tadpole stage and Bd tolerance lead to strong outbreaks and fluctuations in host densities. An increased Bd-induced tadpole mortality dampens these outbreaks, as demonstrated by the simulations in figure 2c,d. Adult population sizes are greatest when tadpoles suffer from Bd and the tadpole stage is short. These findings are supported by observations linking longer tadpole stages and decreased tadpole vulnerability to increased Bd prevalence [19,47].

In the presence of environmental reservoirs (Z_o > 0), or for long zoospore life expectancies within and outside of hosts 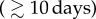, the significance of tadpoles as a reservoir diminishes. The fungus then persists even when tadpoles suffer from infection and the overall host mortality becomes important. The negative risk effect of the tadpole carrying capacity K_T (table 2), which is particularly strong when tadpoles completely tolerate infection, suggests that tolerant tadpoles act as a rescue buffer during strong outbreaks. Figure 3a,b exemplifies this idea. It shows two similar simulations in which tadpoles either tolerate infection (a) or suffer from it (b), with extinction only occurring in the latter case. When sampling over the entire parameter space (with Z_o = 0), we observed a slightly increased fraction of host extinctions (25%) when tadpoles suffer from infection, compared with cases where tadpoles tolerate Bd (only 21% extinctions).

Our findings underline the complex role of the tadpole–adult life cycle in the epizootic [19]. We tested the robustness of these results against a variation in the way this life cycle is modelled. We investigated an alternative model, in which tadpoles attempt metamorphosis once they reach a certain age τ_m, but not before. Such a delayed metamorphosis is in contrast to our original model, in which tadpoles metamorphose at a constant rate right from the start of their life as tadpole. All other aspects of our original model are kept identical, allowing a cross-comparison of the two schemes. We refer to the electronic supplementary material, §3 for details. Simulations generally showed behaviour that was qualitatively similar to our original model. However, the parameter space for which the host population persists for longer times (even in the absence of disease) is somewhat smaller. This is because the prolonged tadpole stage exposes tadpoles to a higher cumulative risk of death and tends to destabilize dynamics. Nevertheless, this alternative model reproduces the reported ambivalent role of tadpoles, depending on their susceptibility and life time as well as the zoospore loss rate.

4. Conclusion

We have investigated the short- and long-term demographic effects of Bd on an exposed host population, using a generic, mechanistic mathematical model that includes various possible host–pathogen interactions. Our statistical assessment provides a rank of importance for several epizootic, immunological and demographic parameters with respect to their influence on the risk of extinction. Our approach can be seen as an alternative to conventional elasticity analysis [48] as well as regression methods used in sensitivity analysis [49,50]. Both theories aim at estimating the importance of demographic parameters for population growth and extinction risk. A novelty of our approach is the systematic evaluation of the entire 25-dimensional parameter space, which was able to reveal relationships between focal parameters and the epizootic dynamics, independently of a particular choice of the other parameters. Moreover, the population viability analysis given here [51] can easily be adapted to virtually any wildlife disease model that includes host demographics [36].

The transmission rates 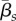, zoospore loss rates μ_Z, μ_S,s and immunological parameters such as λ_s and 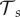, are strongly linked to abiotic factors like temperature and pH [4,14,30]. A better understanding of these links will provide a connection between our parametrization and site-specific abiotic factors. This will enable a possible translation of our results, or at least methodology, to an explicit risk assessment for the numerous amphibian species threatened by the fungus. However, for accurate site- and species-specific predictions, further details are required on Bd physiology and the interaction with its hosts, in order to narrow down the parameter ranges to be considered. In table 2, we have provided a suggested priority list of parameters expected to be of particular importance.

The strong predictive power of 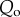for host extinction, as found by our simulations, suggests that the efficiency of the fungus in proliferating at a site shortly after exposure strongly determines its long-term effects on host demographics. Rapid epizootic growth during the invasion phase should therefore be seen as a strong warning signal for a possible imminent local extinction. Thus, estimating Q_o for individual sites holds great potential for prioritizing future conservation efforts.

We showed that the effect of tolerant tadpoles on host extinction risk is ambivalent, and depends on the loss rate of zoospores within and outside of hosts. Our results complement prevailing, but simplistic views of tolerant tadpoles contributing to stronger outbreaks and facilitating Bd persistence [19–21].

We emphasize that if more than one host species are involved, the epizootic dynamics are likely to be more complicated [52]. In fact, in that case a tolerant species acting as a reservoir could induce the extinction of another more susceptible coexisting species [19,53]. Our derivation of the basic reproduction quotient, Q_o, in multi-species communities (§3.1) is a small step towards the theoretical understanding of the expected dynamics.

Funding statement

This work was supported by the PIMS IGTC for Mathematical Biology and NSERC (Canada).