Is discrimination enhanced at the boundaries of perceptual categories? A negative case

Abstract

The human visual system imposes discrete perceptual categories on the continuous input space that is represented by the ratios of excitations of the cones in the retina. Is discrimination enhanced at the boundaries between perceptual hues, in the way that discrimination may be enhanced at the boundaries between speech sounds in hearing? In the chromaticity diagram, the locus of unique green separates colours that appear yellowish from those that appear bluish. Using a two-alternative spatial forced choice and an adapting field equivalent to the Daylight Illuminant D65, we measured chromatic discrimination along lines orthogonal to the locus of unique green. In experimental runs interleaved with these performance measurements, we obtained estimates of the phenomenological boundary from the same observers. No enhancement of objectively measured discrimination was observed at the category boundary between yellowish and bluish hues. Instead, thresholds were minimal at chromaticities where the ratio of long-wave to middle-wave cone excitation was the same as that for the background adapting field.

1. Introduction

Human perceptual systems often impose discrete subjective categories that are not present in the input [1]. At the input level, for example, all colours can be represented in a two-dimensional space that has as its axes the ratios of excitation of the long-wave (L), middle-wave (M) and short-wave (S) types of retinal cone. An example of such a representation is the widely used chromaticity diagram of MacLeod & Boynton [2], shown in figure 1. Although the two axes of the diagram are both continuous variables, human perception imposes discrete categories on to the input space. If the eye is adapted to daylight, then a line running obliquely in the diagram (from approx. 475 to 575 nm) divides chromaticities into reddish and greenish hues; and a second, superposed division into yellowish and bluish hues is made by a line that runs from approximately 520 nm to the white point and then nearly horizontally [4–8]. Chromaticities lying along the first of these boundaries comprise ‘unique blues’, ‘unique yellows’ and white (i.e. hues that are neither reddish nor greenish and that appear phenomenologically unmixed). Chromaticities lying along the second boundary comprise ‘unique greens’, ‘unique reds’ and white (i.e. hues that are neither yellowish nor bluish).

Figure 1.

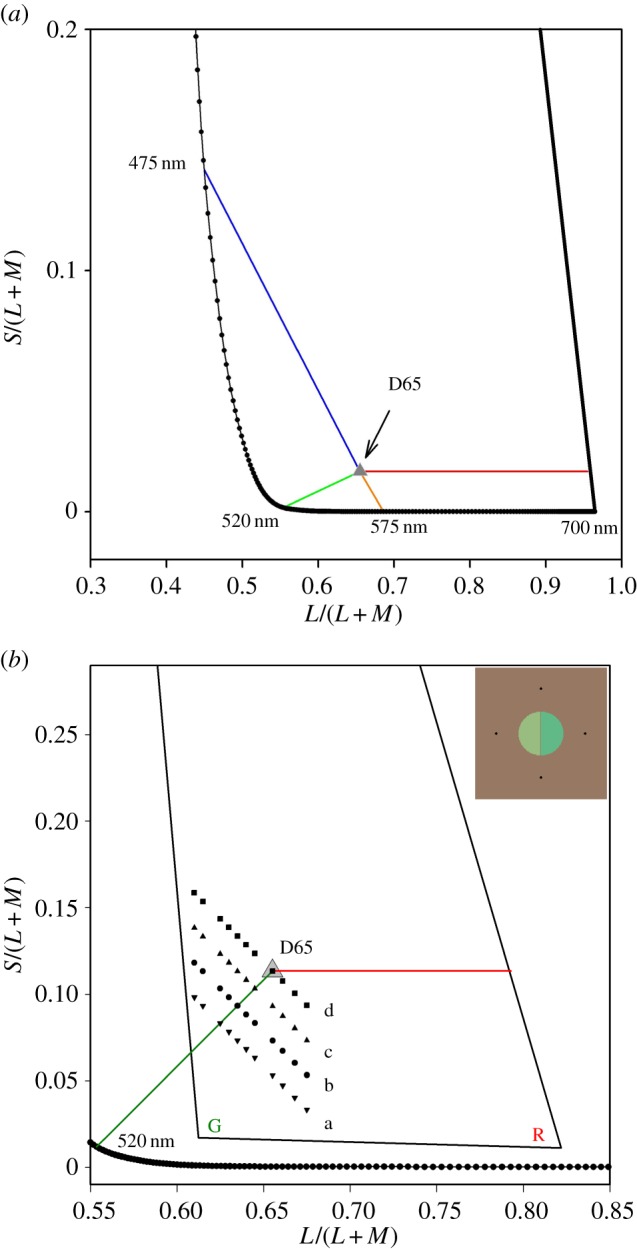
(a) Part of the MacLeod–Boynton chromaticity diagram, constructed using the cone sensitivities tabulated by DeMarco et al. [3]. The axes of the diagram are the ratios S/(L + M) and L/(L + M), where L, M and S are the excitations of the long-, middle- and short-wave cones respectively. The dotted line shows part of the spectrum locus of monochromatic lights. ‘D65’ indicates the chromaticity of the standard Daylight Illuminant D65, the chromaticity used as the background field in our experiments. Although the two axes of the diagram represent continuous variables, human perception imposes discontinuous hue categories on the input: when the eye is adapted to D65, the diagram is divided into reddish and greenish hues by a line that runs from approximately 475 to 575 nm; and it is divided into yellowish and bluish hues by a line that runs from approximately 520 nm to D65 and then nearly horizontally. (b) A magnified section of the MacLeod–Boynton diagram showing the four sets of referent stimuli (a, b, c, d) used in the present experiment. R and G indicate the measured chromaticities of the phosphors of the monitor. (Online version in colour.)

(a). Discrimination at category boundaries

Do subjective categories have an objective effect on human performance? Is discrimination enhanced at the boundaries between perceptual categories? In the case of speech perception, Liberman et al. [9,10] classically showed that discrimination is enhanced at the boundaries between phonemes, such as the boundaries between the voiced stops b, d and g or the boundary between the voiced and unvoiced stops d and t. Does an analogous enhancement of discrimination occur at the boundaries between phenomenological colour categories?

A number of studies have reported that the speed of discrimination is accelerated for colours that lie on either side of a category boundary. For example, Witzel et al. [11], equating stimuli for discriminability in a threshold task, found that reaction times were shorter for colours that lay either side of the blue–green boundary than for colours that fell within one category. Moreover, there is evidence that linguistic categories may influence the speed of discrimination. The Russian language has no general term for ‘blue’, but subdivides this part of chromaticity space with two terms, goluboy and siniy, which identify two ranges of blue that differ in hue and saturation. Using a series of blue stimuli, Winawer et al. [12] showed that native Russian speakers responded more rapidly when the target and distractor colours fell on opposite sides of the goluboy/siniy boundary, whereas native speakers of English did not exhibit a comparable advantage at the boundary between ‘light blue’ and ‘dark blue’. Roberson et al. [13] reported a similar difference between English and Korean speakers at the boundary that Korean marks between yellow–green and green.

Differences in reaction time, however, could arise at a late stage of the participant's response. Is there evidence that the actual fineness of the observer's discrimination—his or her sensory threshold—is enhanced at the boundaries of colour categories? In our own recent work, we have studied chromatic discrimination at the boundary between reddish and greenish hues under conditions of adaptation to a neutral field [14–16]. Measurements were made along lines in chromaticity space orthogonal to the hue boundary. In interleaved experimental runs, the subjective red–green boundary was established for the same observers. Optimal discrimination was consistently found near the category boundary (i.e. at chromaticities that were judged unique blue, unique yellow or white). This was true for both the fovea and the parafovea. Making measurements around the hue circle, Witzel & Gegenfurtner [17] found no enhancement of discrimination near unique yellow and unique blue, but their experiment differed from ours in two critical ways. First, the direction of modulation in colour space was necessarily different for each position on the hue circle, and thresholds were expressed in terms of hue angle, whereas our measurements were for a single direction of modulation and were expressed in terms of the ratios of cone excitations. Second, Witzel & Gegenfurtner's [17] measurements were made at relatively high saturations, where we have ourselves have found little enhancement at the category boundary [14, p. 7]. For similar reasons, it is difficult directly to compare our results with those of Bachy et al. [18], who measured thresholds around an elliptical locus in the CIE (1931) diagram and found threshold minima offset in a red direction from unique yellow and unique blue.

(b). What is the appropriate metric to use in judging whether discrimination is enhanced at category boundaries?

In asking whether discrimination is enhanced at the boundaries of mental categories, it is necessary to select the metric in which the stimuli, and the difference limens, are specified. This choice of metric is of critical interest for any research on perceptual categories.

In the present case of colour categories, several alternatives offer themselves. One possibility would be to follow the example of Liberman's experiments on phoneme boundaries, where thresholds were expressed in terms of a physical variable, such as voice onset time. However, there are two reasons why it may be inappropriate to use a physical metric such as wavelength or wavenumber (frequency) when examining discrimination at chromatic boundaries. First, colour discrimination is necessarily limited by the rate of change of the cone absorptions (L, M, S), or their ratios, as wavelength changes [19,20]. The change of the cone absorption ratios with wavelength depends on the shapes of the absorption curves of the individual photopigments and on the relative positions of the three curves in the spectrum. As wavelength changes, the ratios M/L and S/(L + M) change at different rates in different parts of the spectrum (see e.g. fig. 5 of Nunn et al. [21] or fig. 5b of Mollon & Estévez [22]). These large variations with wavelength, arising from basic properties of the photopigments, impose inescapable limitations on wavelength discrimination that would obscure any additional, more central effects of perceptual category boundaries. But a second and important reason why it is inappropriate to use the physical variable of wavelength is that monochromatic lights are rare in nature, and the human visual system is instead designed to discriminate between the broadband spectral power distributions that dominate in natural scenes. Such spectral power distributions cannot be specified in terms of a single wavelength.

An alternative possibility would be to express discrimination thresholds in terms of a perceptually uniform colour space such as the Munsell system, or the CIELAB or CIELUV spaces. In such systems, the spacing of colours has already been adjusted on the basis of empirical measurements (either of discrimination or of suprathreshold judgements of perceptual distance), so as to approximate to a space in which equal distances correspond to equal discriminability. Such a metric was adopted in the classic paper by Kay & Kempton [23], who asked speakers of either English or Tarahumara to judge suprathreshold differences among Munsell chips in the blue–green region of the hue circle. At first sight, it may seem inappropriate for Kay and Kempton to have used Munsell stimuli: if discrimination is enhanced at category boundaries, then this enhancement should already have influenced the topography of the space. However, Kay and Kempton were explicitly testing the Sapir–Whorf hypothesis that lexical categories alter perception. They were seeking a lexical effect additional to any sensory factors that determine perceived chromatic differences. Tarahumara does not make the basic lexical distinction between green and blue that is made in English; and under conditions where experimental conditions encouraged a naming strategy, only the English speakers showed an expansion of perceptual distances near the blue/green boundary. In a second experiment, where Kay and Kempton introduced an experimental arrangement that precluded a name strategy, the difference between English and Tarahumara speakers disappeared.

If, however, the experimenter is not explicitly concerned with lexical influences but wishes to ask more generally whether discrimination is enhanced at the boundaries of colour categories, then it seems inappropriate to express thresholds in terms of a uniform colour space in which equal distances are designed to correspond to equal discriminability.

These considerations lead to the conclusion that the most appropriate metrics may be intermediate ones that represent stimuli in terms of the actual excitations that the physical stimulus produces in the three types of retinal cone, since those excitations are the inputs to the neural systems that analyse colour. By working in a metric of this kind, we remove the more distal effect of changes of cone absorptions with wavelength, and we reduce to three variables the multidimensional space of spectral power distributions. In our own recent work on category boundaries [14–16], we have worked in the metric of the MacLeod–Boynton chromaticity diagram (figure 1) and have expressed discrimination thresholds in terms of changes in the ratios of excitation of the cones.

(c). The neural basis for enhancement

Improved discrimination at a boundary between colour categories would be readily explained if the boundary corresponded to the equilibrium state of a neural channel, because sensory channels typically have a compressive, negatively accelerated response function, and thus exhibit optimal discrimination for departures from the equilibrium state [24].

The primary difficulty for an explanation of this kind is that the category boundaries for hue are not related in any simple way to the two chromatic signals traditionally thought to be present at early stages of the primate visual system. One of these neural signals represents the difference, or ratio, of the L- and M-cone excitations, and it is carried by the midget ganglion cells of the retina and by parvocellular units of the lateral geniculate nucleus [25–27]. The other opponent signal represents the ratio S/(L + M) and is carried by the small bistratified ganglion cells and by units in koniocellular laminae 3 and 4 of the lateral geniculate [28]. The signals of these two neural channels correspond respectively to the horizontal and the vertical axes of the MacLeod–Boynton diagram (figure 1a), but the sets of chromaticities that place one or other channel in equilibrium (vertical or horizontal lines through white in the diagram) do not correspond to hue boundaries (except possibly in the case of unique red) [6,8].

To explain our earlier finding that thresholds were minimal close to the boundary between reddish and greenish hues, we considered the possibility of a chromatic channel in which long-wave and short-wave signals were synergistic and opposed to a middle-wave signal [15]. This hypothetical channel would be in equilibrium at unique blue and unique yellow. It might correspond to a class of ganglion cells that extracted an M/(L + S) signal or it might correspond to a channel formed more centrally by rearrangement of the traditional lateral geniculate channels, as for example in the models of De Valois & De Valois [29] or of Stockman and Brainard [30].

In the present experiment, we examine discrimination at the boundary between yellowish and bluish hues—the boundary that is the locus of unique green. In terms of cone excitations, unique green would represent the equilibrium state of a neural channel that opposed the L-cone signal to a weighted combination of M- and S-cone signals [8]. We might expect to find optimal discrimination at the locus of unique green. In fact, our results exhibit no such enhancement.

(d). Stimulus duration as a critical variable

In many classical experiments on chromatic discrimination, the target stimuli were of long duration or were continuously present [31,32]. Even if a neutral surround field is present, then the observer is likely to become adapted to the stimuli that he or she is discriminating; in other words, the equilibrium states of the underlying chromatic channels will shift to coincide with the average of the currently offered stimuli. Such a shift was demonstrated directly in single units of the lateral geniculate nucleus of the macaque by De Valois et al. [33]. For our present purpose, such adaptive shifts would blur any attempt to show enhanced discrimination at a particular locus in chromaticity space. We therefore follow Krauskopf & Gegenfurtner [34] in holding adaptation steady with a neutral adapting field and probing discrimination with brief test flashes at relevant locations in chromaticities space. However, because chromatic adaptation occurs quickly, we use an even shorter flash duration (150 ms) than did Krauskopf and Gegenfurtner.

2. Material and methods

(a). Apparatus and stimuli

Measurements were made in Cambridge (UK) and in St Petersburg (Russia). In both laboratories, the stimuli were presented on calibrated Mitsubishi colour monitors (Diamond Pro 2070), which were controlled by Cambridge Research Systems (CRS) graphics systems (VSG 2/3 in Cambridge, Visage in St Petersburg). The VSG system allowed outputs to be specified with a precision of 15 bits per gun, and the Visage allowed 14 bits. In Cambridge, the monitor was set to a refresh rate of 100 Hz and a resolution of 1024 × 768 pixels, and in St Petersburg these values were 92 Hz and 1280 × 980 pixels. The experimental programs and the calibration procedures were the same in the two laboratories. The spectral power distributions of the monitor's guns were measured with a JETI spectroradiometer, and the screens were linearized using a photodiode device (CRS ‘ColorCal’ in Cambridge; ‘OptiCal’ in St Petersburg).

The measurements were made in the central fovea. When discrimination was being measured, the stimuli to be discriminated (the discriminanda) formed the left and right halves of a circular test field that had a diameter of two degrees of visual angle (see inset in figure 1b) and a duration of 150 ms. When the chromaticity of unique green was being estimated, the test field was a uniform two-degree field with properties otherwise as for the discrimination measurements. Test fields were presented on a steady white background that had a luminance of 10 Cd m⁻² and had the chromaticity of CIE Illuminant D65 [35]. The display was viewed binocularly from a distance of 570 mm. Fixation was guided by a diamond array of dark dots centred on the area in which the test field was presented.

Chromaticities were specified in a MacLeod–Boynton diagram (figure 1) constructed from the cone sensitivities of DeMarco et al. [3]. The diagram represents a plane of equal luminance for the Judd₁₉₅₁ Observer, where luminance is equal to the sum of the L- and M-cone signals [36]. The scale of the vertical ordinate of a MacLeod–Boynton diagram is arbitrary: for the present experiment, we scaled the diagram, so that a line running through 520 nm and the chromaticity of Illuminant D65 lay at +45°. This is a line that encompasses stimuli that are approximately unique green (i.e. lights that are neither yellowish nor bluish). We refer to this line as the provisional unique green line.

The test field had an average luminance that was 30% greater than that of the background when expressed in the L + M units of our space; but to ensure that the observers could not discriminate the test fields on the basis of differences in sensation luminance, we jittered independently the L + M value of each hemifield by ±5% (in steps of 1%).

(b). Procedure

Measurements were made along four lines orthogonal to the provisional unique green line (figure 1b). In separate, but interleaved, experimental runs, we made two types of measurements: performance measurements of chromatic discrimination and phenomenological measurements of the chromaticities that were unique green (i.e. neither yellowish nor bluish). At the beginning of all experimental runs, observers adapted to the neutral background field for 1 min before measurements started.

For the discrimination experiments, observers were asked to make a spatial forced choice, indicating by pushbuttons which half-field of the target had the higher L/(L + M) coordinate. Sometimes this was a matter of judging which was ‘yellower’, sometimes which was ‘less blue’, but auditory feedback was given after each response, and observers were instructed to be guided always by this feedback. In any one experimental run, discrimination was measured along one of the four lines of figure 1b. Within one experimental run, thresholds were measured at 11 referent chromaticities (shown as solid points in figure 1b). Referents were tested in random order. These reference chromaticities were never themselves presented, but the discriminanda lay on the same line, straddling the reference point. The stimulus of higher L/(L + M) value was presented randomly on the left or the right. The chromatic separation of the discriminanda was increased or decreased symmetrically around the reference chromaticity according to the observer's accuracy. The staircase procedure tracked 79.4% correct [37], and the separation between each of the discriminanda and the referent was adjusted in logarithmically equal steps. The reference and test chromaticities were expressed in terms of the abscissa of the MacLeod–Boynton diagram (i.e. the L/(L + M), or l, coordinates). At any one point on the staircase, one of the discriminanda had an l coordinate l_t1, and the other had an l coordinate l_t2, where l_t1 was equivalent to the reference coordinate l_r multiplied by a factor a and l_t2 was equivalent to l_r divided by a, where a is always more than 1.0. After three correct responses, the value (a − 1) was reduced by 10%, and after each incorrect response, it was increased by 10%. The staircase terminated after 15 reversals, the last 10 reversal points being averaged to give the threshold. There were six sets of experimental runs, the first set being treated as practice and not included in the analysis. Thus, any given threshold for a given subject is based on five independent repetitions.

Interleaved with the discrimination measurements, there were also six independent experimental sessions in which we estimated the subjective yellow–blue transition point, the first of these sessions being treated as practice. In individual blocks of trials within one experimental session, the chromaticity of the uniform test disc was varied along one of the −45° lines of figure 1b, and the observer was asked to indicate by pushbuttons whether it appeared yellowish or bluish. To avoid sequential effects in these phenomenological measurements, four randomly interleaved staircases were used to estimate the transition point between reddish and greenish hues, two staircases starting on each side of the expected match [38]. Each staircase terminated after 15 reversals. The last 10 reversals of each of the four staircases were pooled to give an estimate of the unique hue for a given line. In any one experimental session, the perceptual transition points were estimated for all four of the −45° lines of figure 2, in a different random order in different sessions.

Figure 2.

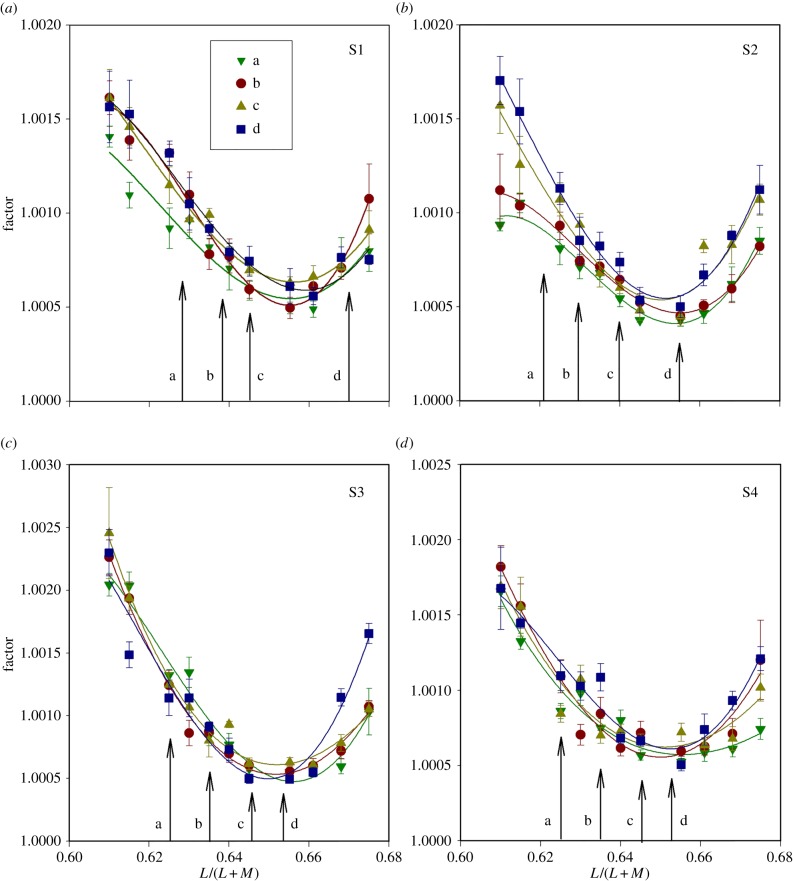
Discrimination thresholds for individual observers (S1–S4). The abscissa of each plot shows the L/(L + M) coordinate at which the measurement was made (figure 1b) and the ordinate shows the factor by which each of the discriminanda must differ from the referent stimulus to sustain a performance level of 79.4% correct (see Material and methods). In each panel, the four sets of data (a, b, c, d) correspond to the four lines plotted in figure 1b. The solid lines fitted to the data are inverse third-order polynomials: they have no theoretical significance but allow a consistent means of estimating the minimal thresholds. The minimal thresholds in every case fall near to the L/(L + M) value (0.6552) of the adapting field. They do not coincide with the coordinates of unique green, which are shown for each observer and for each line by vertical arrows. (Online version in colour.)

(c). Observers

There were four observers (S1–S4). S1 and S2 were the authors J.D.M. and M.V.D., respectively. The other observers were highly practised, but were naive as to the purpose of the measurements. Observers S2 and S3 are female. All observers had normal colour vision as tested by the Cambridge colour test [39,40]. All observers except M.V.D. were tested in Cambridge.

3. Results and discussion

Figure 2 shows for each observer the discrimination thresholds for the four sets of referent stimuli, a, b, c and d (figure 1b). In each case, the threshold is plotted against the L/(L + M) coordinate at which the measurement was made, and thresholds are expressed in terms of the factor by which each of the discriminanda needed to differ from the referent chromaticity in order to give a performance level of 79.4% correct. The patterns of data are very similar for different observers and the minimal thresholds occur at similar positions for each of the lines a–d. Each dataset has been fitted with an inverse third-order polynomial. These functions have no theoretical significance, but offer a consistent way of estimating the L/(L + M) coordinate of the minimal thresholds. Note that the minimal thresholds do not systematically coincide with the settings of unique green, which are indicated for each observer by vertical lines in the diagram.

An analysis of variance (ANOVA) was performed on the data of figure 2 with factors set (a, b, c, d) and referent (1–11). There was a significant effect of set (F₃ = 4.6, p = 0.004) and a highly significant effect of referent (F₁₀ = 55.5, p < 0.001). There was no significant interaction between the two factors.

Figure 3a shows the mean data for all observers, using the same ordinates as for figure 2. For each of the lines a–d, the minimal thresholds occur near the L/(L + M) value of the adapting field (indicated by the vertical arrow in the figure) and they vary little between lines (reflecting the absence of a significant interaction in the ANOVA). The coincidence of the minimal thresholds with the L/(L + M) coordinate of the adapting field suggests that for all four lines (a–d) the discrimination is based on a neural channel that is in equilibrium—and thus at its most sensitive (see Introduction)—when the excitations of the long- and middle-wave cones are in a constant ratio. Traditionally, such a channel would be taken to correspond to the midget ganglion cells and the parvocellular units to which they project in the lateral geniculate nucleus [25,41]. Previous studies of discrimination along the L/M axis of colour space (the horizontal dimension of the MacLeod–Boynton diagram) have shown that discrimination is optimal at the chromaticity of the adapting field [42].

Figure 3.

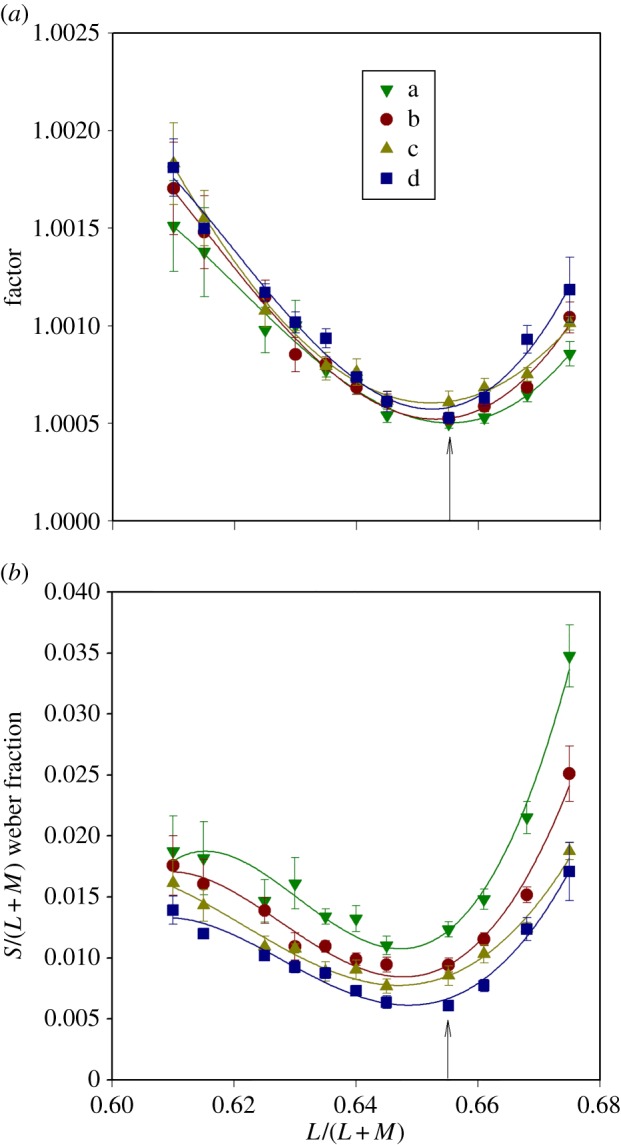
Mean discrimination thresholds for all observers. (a) The axes of the plot are the same as for figure 2. Each dataset has been fitted with an inverse third-order polynomial in order to estimate the L/(L + M) coordinate at which discrimination is optimal. The vertical arrow shows the L/(L + M) value of the adapting field and it is clear that the minimal thresholds for all four testing lines (a–d) fall close to the L/(L + M) coordinate of the adapting field—rather than the coordinate of unique green for each line. (b) S-cone Weber fractions plotted against the L/(L + M) coordinate of the referent. Weber fractions are calculated as ΔS/S_R, where ΔS is the difference in the S/(L + M) coordinate at threshold and S_R is the S/(L + M) coordinate of the referent. The datasets are fitted with inverse third-order polynomials as in (a) and the vertical arrow again indicates the L/(L + M) coordinate of Illuminant D65. The minimal Weber fractions all lie at a similar value of the L/(L + M) coordinate. (Online version in colour.)

Explicitly, we find no evidence that the minimal thresholds occur at the L/(L + M) coordinates of unique green, which are necessarily different for each of the lines a–d. We obtained our own estimates of the locus of unique green for the observers and the adaptation conditions of the present experiment (see §2b). The mean coordinates of unique green for our observers fall on a locus in the MacLeod–Boynton diagram that is similar to the locus expected from the literature [6,8]. These values are plotted as solid triangles in figure 4, which shows a magnified section of the MacLeod–Boynton diagram. Shown as solid circles in figure 4 are the coordinates of the minimal thresholds obtained by fitting curves to each of the datasets in figure 3a. They fall on a locus that is close to vertical and quite distinct from the locus of unique green.

Figure 4.

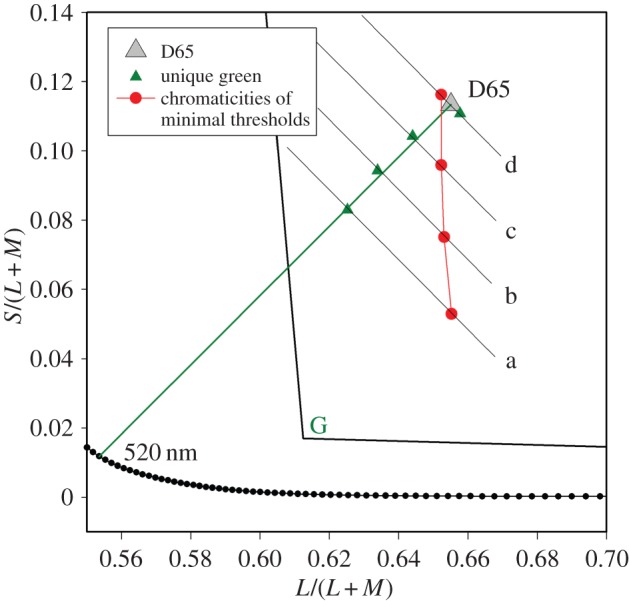
A magnified section of the MacLeod–Boynton diagram showing the average settings of unique green (solid triangles) and the loci of the minimal thresholds (solid circles). (Online version in colour.)

The metric used to express thresholds in figures 2 and 3a is only one of several potential ways of expressing thresholds in terms of cone signals. If we expressed thresholds in terms of the Euclidean distance between the discriminanda at threshold, the pattern of results would be unchanged, because the S/(L + M) and L/(L + M) coordinates are multiplied concomitantly by the same factor as the experimental program moves the test coordinates towards or away from one of the referents on lines a–d. However, for a given factor, the S-cone contrast will vary with the absolute level of S excitation. Therefore, in figure 3b, we plot S-cone Weber fractions against the L/(L + M) coordinate of the referent. The Weber fraction has been calculated as ΔS/S_R, where ΔS is the difference between the discriminanda in the S/(L + M) coordinate at threshold and S_R is the S/(L + M) coordinate of the referent stimulus. The fitted minima all lie at very similar values of L/(L + M). They lie at slightly higher values of L/(L + M) than do the minima of figure 3a and this reflects the fact that the denominator of the S-cone Weber fraction becomes smaller as one moves downwards along one of the lines a–d. What is clear is that minimal thresholds expressed in terms of the S-cone signal also do not fall on the locus of unique green.

Figure 5 shows explicitly that the minimal thresholds do not correspond with a particular value of S-cone excitation (such as the level of S excitation of the background). For each of the lines a–d, we plot the average S-cone contrast at threshold (expressed as a Weber fraction) against the S-cone level of each referent. Each dataset has been fitted with an inverted third-order polynomial. The minima of the different datasets are not brought into coincidence by being plotted in this way, in contrast to the coincidence introduced by the plots of figure 3.

Figure 5.

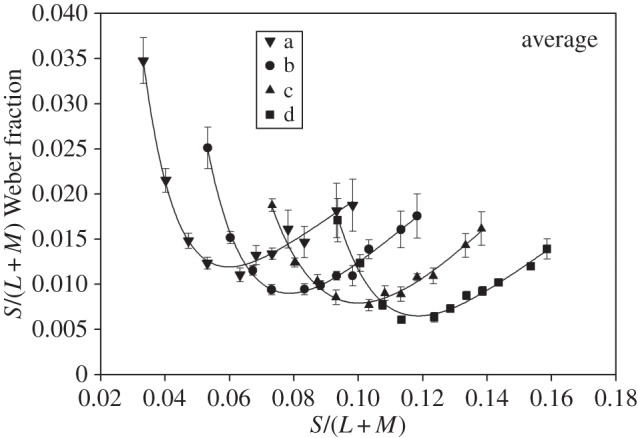
Average values for the S-cone contrast at threshold plotted against the S/(L + M) value of the referent. Each of the datasets corresponds to one of the four lines a–d shown in figure 1b. The fitted functions are inverse third-order polynomials. Note that the minima of the functions do not coincide, as would be expected if discrimination depended on a chromatic channel that extracted the ratio S/(L + M).

Although the minimal thresholds, however expressed, always lie close to the L/(L + M) value of the background and thus on the same tritan line in the chromaticity diagram, is it nevertheless possible that there are secondary minima of thresholds that coincide with unique green? To construct figure 6, we proceeded as follows. For each average threshold for each observer, we recorded the residual error relative to the third-order polynomials fitted to the individual datasets in figure 2. The set of residuals for each line (a–d) for each observer were then plotted not against the absolute L/(L + M) value at which they were measured but at this value relative to the observer's individual unique green for a given line. Thus, in figure 6, the central vertical line corresponds to the 16 different L/(L + M) values of unique green and all data points are plotted on an abscissal scale relative to this point. In other words, each set of residuals has been shifted laterally on the L/(L + M) axis, so that the empirically measured values of unique green coincide. The near-horizontal line through the data is, in fact, the best-fitting quadratic. There is no evidence for a local minimum near unique green. If such a minimum existed, then at the centre of figure 6 we should expect more points to lie below the zero value than above.

Figure 6.

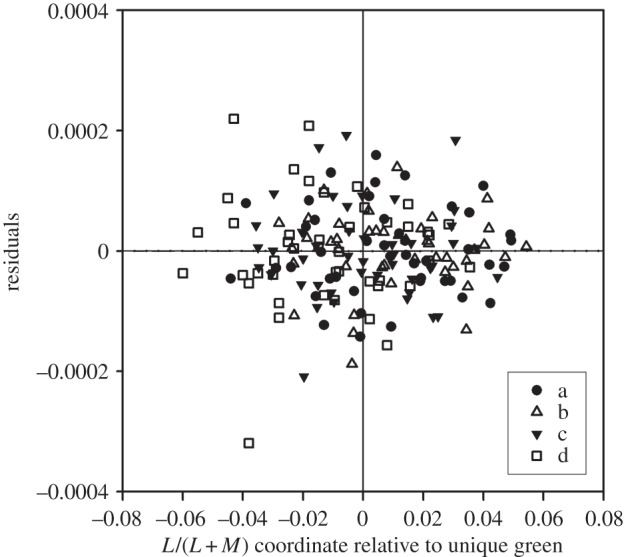
Residuals relative to the functions fitted to the individual data in figure 2. Data points are plotted separately for each referent on each line (a, b, c, d) for each observer. Each subset of data for a given observer and a given line have been plotted relative to the L/(L + M) value of the observer's own estimate of unique green (indicated by the vertical line in the centre of the plot). The near-horizontal line is the quadratic that best fits all the data points. There is no indication of a local minimum near unique green.

Although direct comparisons need caution, owing to the different metrics and conditions (see §1b), the absence of reduced thresholds near unique green is compatible with measurements made in other studies [17,18,43,44].

4. Conclusion

It has often been asked whether discrimination is enhanced at the boundaries of perceptual categories. Examples of such enhancements have been found for speech perception and for discrimination at the unique blue/unique yellow locus (i.e. the boundary between reddish and greenish colours). The present results show firmly that the principle is not a universal one. Under the experimental conditions used here and with practised observers working at the limits of human discrimination, there is no evidence for a local optimum of discrimination at the locus of ‘unique green’ (i.e. at the boundary between yellowish and bluish hues).

Why might discrimination be enhanced at the locus of unique blue and unique yellow, which forms a boundary between reddish and greenish colours [15], and not enhanced at the locus of unique green, which forms a boundary between yellowish and bluish colours? To explain the enhancement at the locus of unique blue and unique yellow, we previously suggested that both phenomenological equilibrium and optimal discrimination might correspond to the neutral point of the same neural channel (see §1c). We envisaged a neural channel that drew inputs of one sign from L and S cones, and of the opposite sign from M cones. However, a hypothesis of this type does not require that discrimination should always be enhanced at a category boundary, since the channel that mediates discrimination may not necessarily be the channel that sets the phenomenological equilibrium. Consider a chromaticity that appears unique green. This chromaticity would conventionally be thought to be one that places in equilibrium a channel in which the L-cone signal was opposed to some weighted combination of S and M cones [8]. The same chromaticity should appear unique green whatever the direction in which one approaches it (i.e. whatever the direction in the chromaticity diagram along which the experimenter allows the stimulus to vary in an adaptive estimate of the equilibrium hue). But it is very unlikely indeed that the same neural channel would mediate difference limens for all these different directions. The different directions modulate the cone signals to different degrees and in different synergies. When chromaticity is varied along a line passing through unique green in the present experiment, then the most sensitive channel—the channel that underlies discrimination performance—appears to be one that extracts the ratio of long- and middle-wave cone excitations. There may well be other lines passing through unique green along which other chromatic channels are the most sensitive at threshold. (A vertical line in the MacLeod–Boynton diagram is necessarily such a line, because the ratio of L and M excitations is constant along such a line.) From the perspective of visual science, there is no intrinsic requirement that discrimination should be optimal at the boundaries of colour categories, but phenomenal equilibria and optimal discrimination may coincide when both depend on the same underlying channel.

The experiments in both Cambridge and St Petersburg were approved by the Psychology Research Ethics Committee of the University of Cambridge.

Funding statement

The research was supported by Royal Society International Exchanges grant no. IE110252 and by Russian Foundation for Basic Research grant no. 12-04-01797.