Switchable S = 1/2 and J = 1/2 Rashba bands in ferroelectric halide perovskites

Significance

Manipulation of electron spins is an important research subject to achieve breakthroughs in current electronics. The Rashba effect is the spin energy level splitting due to broken inversion symmetry and spin–orbit coupling, and the controllability of Rashba splitting is crucial to spin manipulation. Here, we report a theoretical investigation of Rashba band splitting in ferroelectric halide perovskite materials. Since the polarization direction in ferroelectric materials can be switched by external electric fields, Rashba splitting can be controlled conveniently in these materials. Interestingly, ferroelctric polarizations give rise to two distinct Rashba bands of contrasting orbital and spin characters. Taking advantage of the unique band characteristics, these materials prove promising candidates for the switchable Rashba effect.

Abstract

The Rashba effect is spin degeneracy lift originated from spin–orbit coupling under inversion symmetry breaking and has been intensively studied for spintronics applications. However, easily implementable methods and corresponding materials for directional controls of Rashba splitting are still lacking. Here, we propose organic–inorganic hybrid metal halide perovskites as 3D Rashba systems driven by bulk ferroelectricity. In these materials, it is shown that the helical direction of the angular momentum texture in the Rashba band can be controlled by external electric fields via ferroelectric switching. Our tight-binding analysis and first-principles calculations indicate that and Rashba bands directly coupled to ferroelectric polarization emerge at the valence and conduction band edges, respectively. The coexistence of two contrasting Rashba bands having different compositions of the spin and orbital angular momentum is a distinctive feature of these materials. With recent experimental evidence for the ferroelectric response, the halide perovskites will be, to our knowledge, the first practical realization of the ferroelectric-coupled Rashba effect, suggesting novel applications to spintronic devices.

The Rashba effect has been widely investigated in 2D surfaces, interfaces, quantum wells, and 3D bulk systems (1–6). The essential requisite for the Rashba effect is that the spin degeneracy is lifted by the inversion symmetry-breaking (ISB) field in the presence of the spin–orbit coupling (SOC). To date, major concerns have focused on enlarging Rashba strength characterized by the Rashba coefficient (3, 5, 6). The controllability in the direction of the ISB field, on the other hand, has not been seriously considered. In a surface or an interface, the potential gradient generated by the structural inversion asymmetry results in the loss of controllability; the field direction is mainly fixed according to the preformed surface or interface configuration. The situation is similar in recently discovered 3D Rashba material BiTeI (6), because this material has the compositional ISB field between Te and I layers.

Controlling the ISB field and ultimately Rashba-type band splitting can be achieved by using a novel ferroelectric Rashba material (7, 8). In a ferroelectric system, the bulk polarization controlled by external electric fields generates the ISB field. Therefore, the ferroelectric polarization directly couples to the spin splitting and the helical spin texture in the ferroelectric Rashba material, enabling the helicity reversal via the ferroelectric switching. Recent theoretical study suggested GeTe as a possible candidate for this mechanism, but the direct measurement of the ferroelectric polarization and switching is still missing due to the sizable conductivity of bulk GeTe (7, 8).

We consider organic–inorganic hybrid metal halide perovskites as promising ferroelectric Rashba materials. The general formula for this material class is where , i.e., methylammonium (MA); M = Pb and Sn; and X = I and Br. The materials have several advantages over GeTe. Firstly, polar distortions and ferroelectric responses in the halide perovskite have been clearly observed in experiments (9, 10). On the other hand, GeTe inevitably generates Ge vacancies to give considerable bulk conductivity, which in turn hinders the polarization switching (11). Secondly, unlike the multiple band edges and strong hexagonal warping in GeTe (7, 8), the band edge states of the halide perovskites lie at a single point in the Brillouin zone with nearly isotropic Rashba bands. Thus, the halide perovskites have ideal Rashba-split bands with proper material quality. Finally, whereas GeTe has an indirect band gap (11), the halide perovskites have a direct one. This direct gap becomes important when we consider the transition between the valence and conduction bands in optical devices.

Interestingly, the above halide perovskite series has two contrasting types of Rashba bands simultaneously: the and Rashba bands at the valence and conduction bands, respectively (Fig. 1). This originates from the different band characters in terms of the angular momentum at the valance and conduction band edges common in halide perovskite compounds (12). The angular momentum character of the individual band can be affected by relative energy scales of the crystal field and SOC; the crystal field quenches orbital degrees of freedom, whereas SOC entangles spin and orbital degrees. Through the competition between the two energy scales, the band character on which the Rashba Hamiltonian is based can vary from the fully spin–orbital entangled total angular momentum state (J) to the spin state (S) (13), which causes a significant distinction in the angular momentum texture of the Rashba band.

Fig. 1.

Schematic illustration of the switchable Rashba effect. The polarization-coupled Rashba-type band splitting of the and manifolds in hybrid metal halide perovskites.

In this work, we examine the electronic structures of the hybrid metal halide perovskites as candidates for the ferroelectric Rashba materials. By constructing a minimal tight-binding (TB) model Hamiltonian, we can capture the key features of the band structures; the low-energy effective Hamiltonian gives rise to the ferroelectric-coupled and Rashba bands at the valence band maximum (VBM) and the conduction band minimum (CBM), respectively. The Rashba-type splitting of the fully spin–orbital-entangled subspace stems from the bandgap-independent intraorbital as well as the bandgap-dependent interorbital terms. On the contrary, Rashba splitting only consists of the interorbital term (14). We present several examples of possible ferroelectric Rashba materials (β-MAPbI₃, β-MASnI₃, and ortho-MASbBr₃) by adopting first-principles electronic structure calculations based on density functional theory. These halide perovskites are shown to have the characteristic features predicted in the TB model with the sizable Rashba coefficient . A different type of controllability on the relative helicity between the two Rashba bands is also discussed according to the positions of the lateral halide atoms.

Results and Discussion

To reveal the microscopic origin of the ferroelectric-driven Rashba effect, we construct a TB Hamiltonian which contains additional hopping channels allowed by broken inversion symmetry. In the cubic phase of halide perovskites, CBM (VBM) consists of triply degenerate bands (a single band) in the absence of SOC, whose orbital angular momentum L = 1 (L = 0). The triple bands come from the p orbitals of the M-site atom, and the single band from the s orbital of M and p orbitals of the surrounding halogens. In the presence of SOC, the triply degenerate L = 1 states split into lower and upper bands whereas SOC is ineffective in the single band, resulting in the CBM and VBM (Fig. 2A). Under the ISB field, the TB Hamiltonian reads

with the s and p orbital states at the M site as the minimal basis set. Here, the first two terms describe the electronic structure of the high symmetric cubic perovskites (12), and the last term, , breaks the inversion symmetry by ferroelectric polarization. Most importantly, additional orbital mixings between the nearest neighbors emerge in ; for example, the ISB field along the z direction allows the hopping between the nearest s and orbitals, , as well as the nearest (or ) and 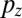orbitals, . The general form of the hopping parameters induced by the ISB field in the arbitrary direction reads ( or ). For simplicity, we omit the on-site mixing of s and p states. (For details on the TB model, see SI Text.)

Fig. 2.

The band structures and angular momentum textures of the TB model. The band structures are depicted (A) without an ISB field and (B) with and having the ferroelectric moment along the [001] direction. In B, the helical direction of the orbital angular momenta is denoted by CW (clockwise) or CCW (counterclockwise) in red color near CBM whereas that of the spin angular momenta is shown in blue near VBM. The orbital (red solid arrows) and spin (blue dotted arrows) angular momenta are presented in (C) VBM and (D) CBM bands near the A point of the Brillouin zone for with the constant energy contours at the horizontal energy cuts in B.

The eight-band TB model in Eq. 1 is solved numerically as shown in Fig. 2. When the ISB term is introduced in the z direction, i.e., with the ferroelectric moment along the [001] direction, Rashba-type band splitting occurs near the A point of the tetragonal Brillouin zone (Fig. 2B). To understand the splitting mechanism, we derive the 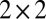effective Hamiltonian for the manifold near VBM up to

with , and the manifold near CBM

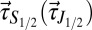with , and , where is the band gap without the ISB term, λ is the SOC strength, t are hopping parameters, I is the identity matrix, and are the Pauli matrices describing the degrees of freedom. The and are functions that describe the parabolic band dispersion. The form of the splitting terms corresponds to the Bychkov–Rashba Hamiltonian (1), where the ISB field term is represented by the ferroelectric polarization and and 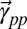determine the direction and magnitude of the splitting. The ferroelectric switching flips the direction of and in turn reverses the helical angular momentum texture of the Rashba band. [This helicity reversal does not depend on the specific form of the effective Hamiltonian (SI Text).]

Although the splitting terms in the effective Hamiltonian for VBM and CBM have the same form as the ferroelectric-coupled Rashba-type band splitting, they have quite different aspects. Firstly, the splitting occurs mainly in the space in VBM whereas it does in the 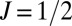space in CBM, which results from the original band characters. Consequently, the spin angular momentum is conspicuous in VBM, whereas the orbital angular momentum dominates in CBM (Fig. 2 C and D). Secondly, the origin of the splitting terms in CBM (Eq. 3) is the intraorbital coupling within the manifold as well as the s–p coupling, whereas that in VBM (Eq. 2) is only the interorbital coupling between the s and p states. It is remarkable that the intraorbital splitting term within the manifold (the 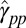term) contains no other energy scale except for , which can survive in a large band gap system. Note that the splitting terms from the s–p coupling (the 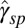terms in Eqs. 2 and 3) inevitably include the prefactors containing the hopping parameter and the energy difference of the s and p states in contrast.

With the qualitative understanding in the TB model, we investigate a series of the ferroelectric metal halide perovskites using first-principles calculations. Perovskites are known to show various structural phase transitions that may include the ferroelectric phase (15). Relative sizes of constituent atoms are important for the ferroelectricity in the perovskite structure (16). Indeed, there have been experimental attempts to establish ferroelectric phases by using organic molecules at the A sites (9, 10, 17). Among them, β-MAPbI₃ was found to have polar distortion, and a clear signature of the ferroelectric response was observed at room temperature (9). Other compounds such as MASnI₃ make transitions to the β-phase at a lower temperature and are expected to show similar behavior. Once the ferroelectricity is established, hybrid metal halide perovskites could be good candidates for ferroelectric Rashba materials due to the large SOC inherent in Pb and Sn.

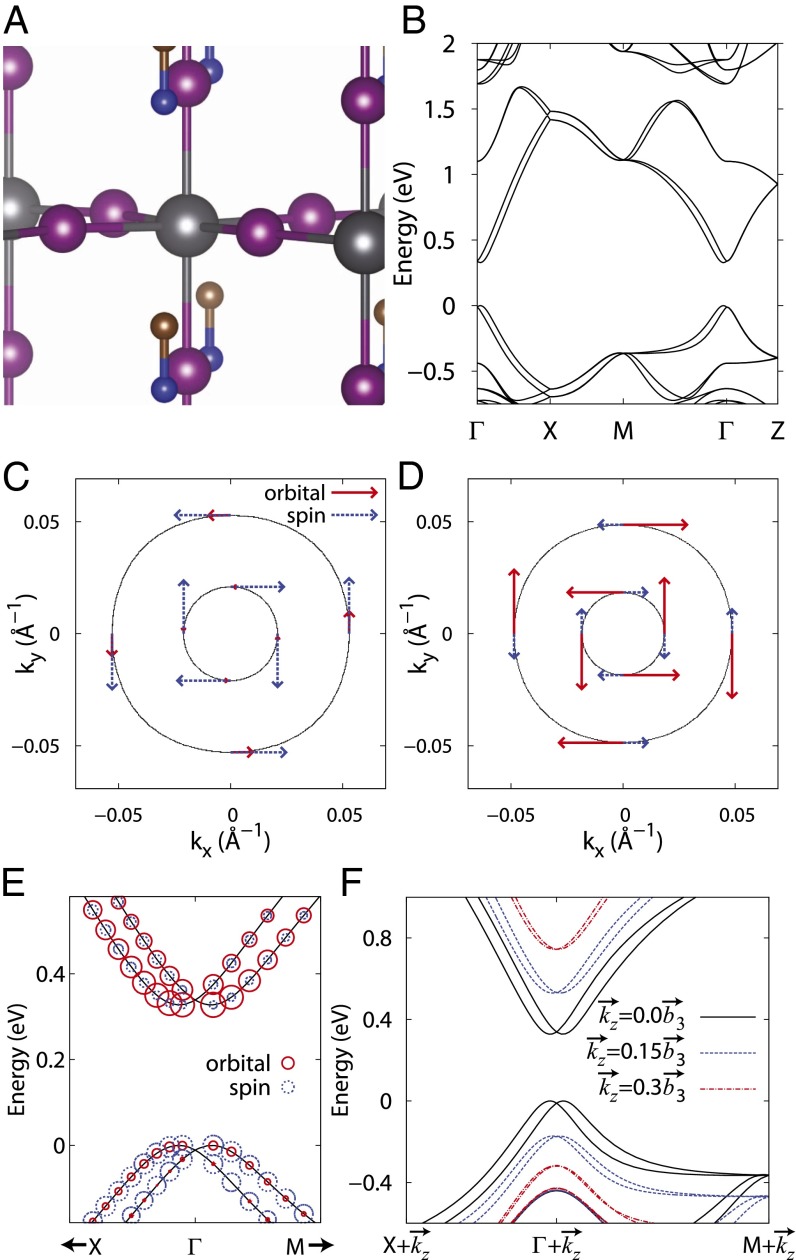
β-MAPbI₃ has a tetragonal unit cell with four formula units. There are octahedron rotations in the basal plane, and small polar distortions occur along the z direction. The difference between the longer and shorter Pb—I bond length resulting from the off-centering of the Pb atom is Å. The atomic and electronic structures of β-MAPbI₃ are depicted in Fig. 3 A and B. VBM and CBM are located near the Γ point where clear Rashba-type band splitting appears. 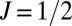Due to the original character of each band, namely valence and conduction bands, main contributions to the angular momenta of VBM come from the spin, whereas CBM is dominated by orbital angular momentum components (Fig. 3 C–E) in accordance with our TB analysis. The two Rashba bands are contrahelical, i.e., they have the opposite helicity and the constant energy contours show a nearly isotropic shape. Here, we assign the helical direction to the spin (orbital) angular momenta in VBM (CBM) as the principal contributions come from the spin (orbital). Because the material intrinsically has a 3D structure, it has a dispersive band without band splitting in the polarization direction as shown in the dispersion along the Γ–Z line (Fig. 3B). To see the 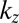dependence of Rashba splitting, the band structures in three different planes are depicted in Fig. 3F. The size of the splitting diminishes as increases.

Fig. 3.

Electronic and atomic structures of β-MAPbI₃ from the first-principles calculations. (A) The atomic and (B) band structures of β-MAPbI₃ are shown. The spin (blue dotted arrows) and orbital (red solid arrows) angular momenta are depicted with the constant energy contours near (C) and (D) with and 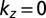. (E) The magnitudes of the spin (blue dotted circles) and orbital (red solid circles) angular momenta for the VBM and CBM bands. (F) The band structure with different values. Here, 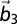is the reciprocal lattice vector along the z direction.

The strength of the Rashba effect is characterized by the Rashba coefficient . By using the energy difference (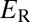, Rashba energy) and the momentum offset 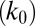between the band crossing point and the band extremum, the Rashba coefficient can be obtained. The estimated values for β-MAPbI₃ near CBM are , , and 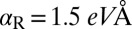for Γ–X. The calculation for Γ–M gives practically the same value, indicating the isotropic structure of the band splitting. Rashba coefficients of other candidates in the hybrid metal halide perovskite series are listed in Table 1, where the Rashba coefficients are of order 1. The sizes of the Rashba coefficients are comparable to those in the giant Rashba materials, BiTeI and GeTe (6–8). When replacing Pb with Sn, various physical quantities (SOC strength, the positions of Sn and I atoms, and the band gap) can affect the amount of the splitting. In β-MASnI₃, the SOC strength is reduced but the off-centering of Sn is slightly larger (the bond length difference ) than β-MAPbI₃, resulting in the similar Rashba coefficient. In case of CBM in ortho-MASnBr₃, the Rashba energy is larger, but the angular momentum texture does not correspond to the characteristic Rashba band, possibly due to the significant distortions in the compound.

Table 1.

Estimated Rashba energy , momentum offset , and Rashba coefficient

Compound	Band	Direction
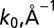β-MAPbI3	CBM	Γ–X	12	0.015	1.5
	VBM	Γ–X	11	0.016	1.4
β-MASnI3	CBM	Γ–X	11	0.011	1.9
	VBM	Γ–X	4	0.006	1.2
ortho-MASnBr3	VBM	X–Γ	15	0.031	1.0
	VBM	X–S	13	0.031	0.84
	VBM	X–Y	14	0.031	0.92

According to the effective Hamiltonians in Eqs. 2 and 3, the helicity of the angular momentum in CBM is determined by both and 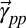, whereas that in VBM depends on 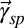only. This provides additional controllability in the relative helicity between VBM and CBM Rashba bands. According to the relative sizes and directions of and , the two Rashba bands can have the same helicity (cohelical) or an opposite one (contrahelical). A series of band structures is plotted from the TB model by varying the value of 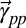but with a fixed ; the relative helicity between VBM and CBM can be tuned from contrahelical (Fig. 2B) to cohelical (Fig. 4B). In the intermediate region, the band crossing occurs in the 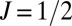manifold (Fig. 4A). In real materials, the positions of the lateral halide atoms can determine the relative helicity (SI Text). It is to be noted that, although the helicity of VBM is determined only by in our simplified model, there might be other terms if the VBM band couples to other bands (for example, the halogen p bands) appropriately. In general, the Rashba splitting term of the effective Hamiltonian can be written as

where originate from the intra- or interband coupling under the ferroelectric-induced ISB field. The relative magnitudes of 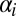and directions of 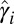will determine the helicity of the Rashba band.

Fig. 4.

Relative helicity change. The band structures of the TB model (A) with and 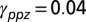, and (B) with 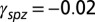and .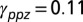

We also want to mention a characteristic aspect of Rashba band splitting in the halide perovskites. In 2D Rashba systems, the asymmetry of the crystal field is relatively large, resulting in, for example, -like surface states with interband Rashba splitting (18). In contrast, the starting point of the effective Hamiltonian near the Fermi energy in the halide perovskites is the high-symmetric cubic structure where the triple degeneracy of CBM is present due to the cubic symmetry. Thus, the inclusion of SOC under the ISB field gives rise to the almost fully spin–orbital entangled 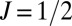Rashba band that contains the bandgap-independent intraband splitting term. In the intraband splitting, the orbital components of the 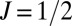states are essential as the ISB field mixes only the orbital part. This unique intraband splitting mechanism would be important in large gap Rashba materials.

It is interesting to consider the effect of low dimensionality in layered perovskite materials. In the case of the 2D limit, the threefold degeneracy at CBM is broken due to the crystal field. For a monolayer of PbI₆ octahedra with polar distortions, we find that CBM states have different orbital composition from the bands in the 3D limit. (The electronic structure calculation for the 2D layer is presented in SI Text.) Thus, in 2D layered structures the Rashba-type splitting near the band edge states occurs with a different band character in CBM. The ferroelectric 2D Rashba system could be realized in hybrid layered halide perovskites experimentally (19, 20).

Conclusions

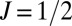In conclusion, we have investigated the electronic structures of hybrid metal halide perovskites with ferroelectric distortions. We have shown that ferroelectric polarization switching enables the angular momentum helicity reversal in the band edge states. The band structure is intriguing in that two contrasting and Rashba bands appear simultaneously and the Rashba band contains the bandgap-independent intraband splitting term. The coexistence of and Rashba bands would critically influence the optical transitions between the two Rashba bands. Thus, the controllable Rashba effect could provide opportunities to exploit the spin and orbital degrees of freedom in the photoinduced effect of photovoltaics (21–24) that has increasing importance in the energy materials research.

Methods

The density functional theory calculations were performed using Vienna Ab initio Simulation Package (25, 26) with projector augmented-wave potentials (27). The PBEsol (Perdew–Burke–Ernzerhof revised for solids) exchange-correlation functional was adopted (28). A plane–wave basis set with the energy cutoff of 520 eV was used. Experimental lattice constants and internal coordinates were used. The effect of the SOC was included using the second variational method (29). The constant energy surfaces were obtained from the interpolated band structures by maximally localized Wannier functions as implemented in the Wannier90 package (30–32).