Visuospatial selective attention in chickens

Significance

Top-down selective attention, which is fundamental to cognition, has been studied extensively in humans and nonhuman primates. Here we report the behavioral hallmarks of selective attention in a nonprimate species, the domestic chicken. When provided with a spatial cue, birds exhibited dramatic improvements in accuracy, faster reaction times, and higher choice certainty in a target localization task. Our results reveal that chickens shift spatial attention rapidly and dynamically following principles remarkably similar to those documented in primates. Given the evolutionary distance (>250 million years) and enormous ethological differences between chickens and primates, our findings suggest that neural mechanisms mediating selective attention appeared early in vertebrate evolution and that they are conserved across phylogeny.

Abstract

Voluntary control of attention promotes intelligent, adaptive behaviors by enabling the selective processing of information that is most relevant for making decisions. Despite extensive research on attention in primates, the capacity for selective attention in nonprimate species has never been quantified. Here we demonstrate selective attention in chickens by applying protocols that have been used to characterize visual spatial attention in primates. Chickens were trained to localize and report the vertical position of a target in the presence of task-relevant distracters. A spatial cue, the location of which varied across individual trials, indicated the horizontal, but not vertical, position of the upcoming target. Spatial cueing improved localization performance: accuracy (d′) increased and reaction times decreased in a space-specific manner. Distracters severely impaired perceptual performance, and this impairment was greatly reduced by spatial cueing. Signal detection analysis with an “indecision” model demonstrated that spatial cueing significantly increased choice certainty in localizing targets. By contrast, error-aversion certainty (certainty of not making an error) remained essentially constant across cueing protocols, target contrasts, and individuals. The results show that chickens shift spatial attention rapidly and dynamically, following principles of stimulus selection that closely parallel those documented in primates. The findings suggest that the mechanisms that control attention have been conserved through evolution, and establish chickens—a highly visual species that is easily trained and amenable to cutting-edge experimental technologies—as an attractive model for linking behavior to neural mechanisms of selective attention.

The capacity to select particular locations or stimuli for differential analysis and decision making is essential for any animal to behave intelligently in a complex environment. It follows that neural mechanisms that enable this capacity must have appeared early in evolution (1). In humans, and nonhuman primates, selective attention enables such adaptive behavior by selecting from all possible information the information that is most relevant for making decisions (2, 3). However, little is known about whether the capacity for selective attention exists in nonprimate vertebrate species.

Studies that were intended to measure selective attention in nonprimate species have produced inconclusive results for several reasons. First, much of the previous work has inferred the capacity for selective attention based on selective learning or selective reporting of specific cue features, both in birds (4) and in rodents (5). For example, in highly cited work on feature-based attention (4), pigeons were reinforced for pecking on targets that contained combinations of two features (e.g., color and shape). In later trials, when the features were presented individually, they pecked almost exclusively on targets with only one of the two features (e.g., color, ignoring shape). The results were interpreted as indicating that the birds had attended selectively, during training, to only one of the two features. However, a follow up study provided evidence that questioned this interpretation (6). The controversy highlights serious caveats with using tasks that do not distinguish selection for attention from selective learning of cue features or a bias for subsequent responses.

Second, previous studies did not distinguish the effects of attention from those of motor preparation. For example, pigeons were shown to be able to anticipate the location of an upcoming target based either on the statistics of target presentation (7) or on the validity of a spatial cue (8). However, these studies measured the effects of cueing only in terms of faster reaction times to the cued location, and faster reaction times can result simply from planning a motor response to a target’s location based on the advance information provided by the cue.

Third, and most importantly, even studies that measured the effects of attention on behavior in terms of percent correct did not distinguish perceptual (d′) improvements at the cued location from increases in choice (or response) bias toward the cued location (3). A fundamental requirement in the design of cued spatial attention tasks is that spatial cues must convey only information that is orthogonal to the task. Otherwise, perceptual effects could be confounded by cue-induced changes in bias toward the cued location (3).

This study measures the effects of top-down spatial attention on perceptual performance in chickens. Extensive research in primates has generated specific experimental protocols for characterizing and quantifying the effects of attention (3). Quantitative metrics that are diagnostic of attention are (i) improvements in perceptual accuracy and (ii) shortening of reaction times. Using these metrics, the benefits of attention have been shown in primates to vary dramatically with the strength of a target stimulus (9, 10), its location relative to the locus of attention (11, 12), and the presence and strength of distracting stimuli (13, 14). In this study, we demonstrate these same benefits of attention in chickens.

A priori, the properties of visual attention might be expected to be substantially different between chickens (an afoveate species with laterally positioned eyes) and humans and nonhuman primates (foveate species with frontal eyes). However, our results document remarkable similarities between chickens and primates regarding the rules that govern selective attention as well as competitive stimulus selection, the core component of attention that determines the information that gains access to working memory (15). The similarities include deleterious effects of bottom-up distracters that increase systematically with distracter strength, perceptual benefits of top-down spatial cueing that diminish the deleterious effects of bottom-up distracters, and improvements in choice certainty with spatial cueing.

Our findings are highly relevant to studies that seek to understand the effects of visual attention on sensory processing in a variety of lateral-eyed, afoveate, nonprimate mammalian model species, such as mice and rats. In addition, given the evolutionary distance (>250 million years) and enormous ethological differences between chickens and primates, these similarities suggest that mechanisms for mediating competitive stimulus selection for attention appeared early in vertebrate evolution and that they are conserved across phylogeny. Thus, our findings strongly encourage the application of comparative neuroscience to the study of mechanisms of attention.

Results

Target Localization in the Presence of a Task-Relevant Distracter.

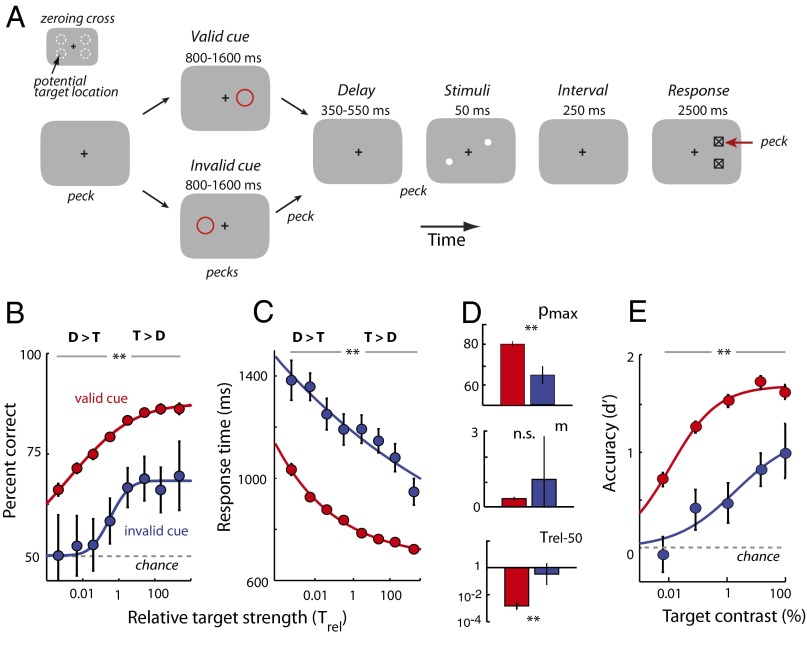
Birds were trained on a task that required them to report the vertical location of a target stimulus in the presence of a distracting stimulus (Fig. 1A). The bird initiated a trial by pecking on a zeroing cross at the center of a touch-sensitive video screen. After a variable delay (depending on the cueing protocol; Methods) the birds pecked again on the cross to trigger the appearance of a stimulus array consisting of two briefly flashed (50-ms) stimuli (positive contrast 2° dots) in opposite hemifields, one to the left and the other to the right (±60° azimuth; Fig. 1A, white dots). The location of each stimulus varied randomly between two possible locations, above or below the visual horizon (±12.5° elevation; Fig. 1A, dashed circles). The locations of the two stimuli were independently sampled, and upper and lower locations were tested with equal probability. The two stimuli were identical except in contrast, which was varied randomly and independently for each stimulus. After the stimulus array was extinguished (250-ms interval), two response boxes appeared to one side. The side of the response boxes designated post hoc which of the stimuli was the target and which the distracter (10); such tasks are referred to as “filtering” tasks (12, 16). In filtering tasks, the distracter is always a potentially task-relevant stimulus, so that an additional stimulus (either a pre or post hoc cue) is necessary to distinguish the target from the distracter. Birds were rewarded for indicating the vertical location of the target by pecking on the response box closest to the target’s elevation (Fig. 1A, red arrow and Movie S1).

Fig. 1.

Top-down spatial cueing improves target localization in a filtering task. (A) The sequence of events in a target localization task with a task-relevant distracter and interleaved spatial cues (see Target Localization in the Presence of a Task-Relevant Distracter for description). The black + is the zeroing cross, the red circle is the cue, white dots are the target and distracter, squares with an inlaid X are the response boxes, and the red arrow is the peck to the response box. (Inset) Dashed circles are the potential target locations (not actually presented on the screen). (B) Percent correct as a function of distracter and target strengths (contrasts) for localization performance without a cue (n = 199 experimental sessions in three birds). Target and distracter contrasts were randomly and independently sampled from one of nine values (0.0033–100%, uniformly spaced on a logarithmic scale). Hotter colors indicate higher percent correct. The dashed white line is the line of equal target and distracter strengths. The arrow indicates the axis of increasing relative target strengths. (C) Same as in B, but with a spatial cue. (D) Response times as a function of distracter and target strengths for correctly localized targets, without a cue. Hotter colors indicate shorter (faster) response times. Other conventions are as in A. (E) Same as in D, but with a spatial cue. (F) Psychometric functions of percent correct, without and with a spatial cue, as a function of relative target strength (T_rel, defined as the target-to-distracter contrast ratio). The strength of the target relative to that of the distracter, plotted on a logarithmic scale, increases from left to right (direction of the arrow in B). Gray data represent uncued performance and red data represent cued performance. The dashed vertical line represents equal target and distracter strengths (T_rel = 1). Curves represent cumulative Gaussian fits. Error bars represent SEM (jack-knife). (G) Psychometric functions of response times without and with a spatial cue, for correctly localized targets, as a function of relative target strength (population data). Lines represent power law fits (Pieron’s law). Other conventions are the same as in F. (H, Left) Schematic showing parameters estimated from cumulative Gaussian fits to psychometric functions of percent correct (shown in F). p_max is the asymptotic performance, m is the slope, T_rel-50 is the value of T_rel at which performance reached half of its maximum value (above chance), r₅₀ is the value of T_rel at which performance reached half of its range. (H, Right) p_max, m, and T_rel-50 estimates from psychometric functions of uncued (gray) and cued (red) performance. Error bars represent SEM (jack-knife). (F–H) Significant differences are indicated by a double asterisk (**P < 0.01 level, bootstrap test with Bonferroni correction for multiple comparisons); n.s., not significant.

We also included in the task, the option for the bird to report an opt-out (“NoGo”) response by pecking twice on the zeroing cross following the appearance of the response boxes. NoGo responses were rewarded with a probability of 0.33 (uncertain reward). NoGo responses were used specifically to provide a measure of the birds’ decision certainty (17), analyzed in Effects of Spatial Cueing on Choice Certainty.

In this first section, we report the effect of varying target and distracter contrasts on target localization performance quantified as percent correct and mean response time. For these analyses, we included only trials in which the bird gave a Go response (peck to response box), and treated the responses as if they were made in a two-alternative forced choice (2-AFC) task; the analysis incorporating NoGo responses is provided in Effects of Spatial Cueing on Choice Certainty. The percentage of correctly localized targets was computed as the proportion of Go responses directed at the correct response box. Response times were measured as the interval between stimulus array onset and the peck on the response box for successfully localized targets.

Uncued target localization.

The uncued filtering task (Fig. 1A, upper sequence) tested the effects of a task-relevant distracter on target localization as a function of the contrasts of the target and distracter stimuli. Localization performance for the various combinations of target and distracter contrasts was plotted as matrices (Fig. 1 B and D; n = 199 experiments in three birds). These matrices revealed the following trends: Localization performance was best when the target was strong and the distracter weak, performance deteriorated as target strength decreased or distracter strength increased, and it was worst when the target was weak and the distracter strong. These data demonstrate a systematic, competitive interaction between the target and the distracter that depended critically on the relative strengths of the target and concurrent distracter stimuli, as has been reported previously for humans engaged in a similar filtering task (12). Therefore, we analyzed the data as a function of relative target strength (T_rel, the ratio of the target’s contrast to the distracter’s contrast) by pooling data from trials with matching T_rel values (lower left to upper right diagonally aligned bins of the matrices in Fig. 1 B and D; SI Methods).

For the uncued trials, percent correct increased systematically with increasing T_rel (axis through the matrices as indicated by the solid white arrow in Fig. 1B). Performance increased steadily from above chance (50%) for the lowest T_rel, to ∼80% for the highest T_rel (Fig. 1F, gray symbols). Performance never approached 100%, perhaps due to the challenging nature of the task: In this task, the target stimulus was not identified until 250 ms after the stimulus array had been extinguished. In addition to the increase in percent correct, mean response times decreased systematically as the relative target strength increased (Fig. 1G, gray symbols). Data from individual birds showed similar trends (Fig. S1).

To quantify the effects of relative target strength on localization performance, we fit parametric functions to the data. Percent correct data were well fit (R² = 0.98) with a three-parameter cumulative Gaussian function (Fig. 1H, asymptotic performance, p_max = 83.9 ± 5.9%; slope, m = 0.26 ± 0.09, T_rel at 50% asymptotic performance, log₁₀ T_rel-50 = −1.33 ± 0.94). The T_rel at which performance reached 50% of its dynamic range (r₅₀) was not significantly different from 1 (target = distracter; log₁₀ r₅₀ = −0.53 ± 0.60, P > 0.1). Mean response times were well fit (R² = 0.99) with a three-parameter power law (Pieron’s law) function (Fig. S2; scale, α = 327 ± 13 ms; slope, β = 0.075 ± 0.006; for a fixed offset, γ = 553 ms; SI Methods).

In addition to computing mean response times, we also computed reaction times, measured as the interval between stimulus array onset and the time of initiation of an orienting response (Fig. S3A, arrows). To control for delays caused by initially mistaken movements toward the distracter, we measured reaction times only for trials in which the bird’s initial movement was made toward the target (SI Methods). Mean reaction times varied in a manner that closely matched mean response times across target contrasts (Fig. S3B, gray), but without the additional time required to execute the response (peck on the response box).

Effect of spatial cueing.

For humans, a spatial cue that is informative about the location of an upcoming target stimulus improves task performance by drawing the subject’s spatial attention to the cued location in anticipation of the stimulus. We tested whether spatial cueing has the same effect on chickens performing the target localization task.

The design of spatial cueing tasks for measuring perceptual accuracy poses a critical challenge: If the cue is highly predictive of the location of an upcoming target in a localization task (task involving reporting the location of a stimulus, or change in a stimulus), an animal is likely to develop a strong response bias toward the cued location. This renders the psychometric function of localization accuracy—percent correct (or d′) as a function of target strength—difficult to measure (or estimate), because responses tend to be overwhelmed by false alarms due to the response bias toward the cued location. This response bias cannot be trained away (e.g., by punishment or “time-outs”), because the animal may then develop an aversion to the cue, thereby diminishing the beneficial effects of spatial cueing.

We designed a task that eliminated any cue-induced bias effect on localization accuracy: We used a spatial cue that provided information about the azimuth of the target, but no information about its vertical location, the parameter upon which the reward depended. In 50% of the trials (which were interleaved with the trials analyzed in the previous section), a spatial cue (10° radius, red annulus) was presented on the horizon (duration: 1,400 [800–1,600] ms; median [68% confidence interval (CI)]), and was extinguished [cue–target interval: 400 (350–550) ms] before the stimulus array appeared (Fig. 1A, lower sequence). The cue predicted the side (azimuth) of the upcoming response boxes, and therefore identified the target stimulus, with 100% validity. However, the cue was completely uninformative about the vertical location (elevation) of the target.

The effect of the cue on target localization performance is shown as matrices of percent correct (Fig. 1C) and of mean response times (Fig. 1E). Comparing the matrices of responses without (Fig. 1 B and D) and with (Fig. 1 C and E) spatial cueing, reveals that the cue substantially reduced the disruptive effects of the distracter on target localization (binned values of percent correct and response times shift to hotter colors) across nearly the entire range of target–distracter contrast combinations.

Quantitative analyses of the effects of the cue on target localization performance are shown in Fig. 1 F–H (red data). The cue increased the proportion of correctly localized targets and decreased mean response times compared with performance on interleaved trials without the cue (Fig. 1 F and G, red vs. gray symbols). The beneficial effects of the cue on percent correct were greatest at low-intermediate relative target strengths (T_rel from 0.01 to 10; Fig. 1F, asterisks indicate significant differences at the P < 0.01 level, bootstrap test with Bonferroni correction for multiple comparisons, unless otherwise stated), and were not significant at the highest relative target strengths (T_rel > 10). On the other hand, the beneficial effects of the cue on mean response (Fig. 1G) and reaction times (Fig. S3B) were apparent even at high relative target strengths. Data from individual birds showed similar effects (Fig. S1).

Parameter estimates from the psychometric functions (cumulative Gaussian fits) supported these conclusions (Fig. 1H). The relative target strengths that yielded 50% of asymptotic performance (T_rel-50) and maximal range (r₅₀), both occurred at significantly lower values in the cued vs. uncued condition (log₁₀ T_rel-50 = −2.72 ± 0.22; log₁₀ r₅₀ = −2.30 ± 0.28, P < 0.01). Thus, the cue facilitated localization of the target at distracter strengths that degraded target localization in the uncued trials. Moreover, the slope of the psychometric function was significantly steeper (m = 0.63 ± 0.16, P < 0.01; Fig. 1H). However, asymptotic performance was not significantly different (p_max = 80.5 ± 1.2%, P > 0.9; Fig. 1H). In addition, mean response times were shorter by up to 100 ms in the cued vs. the uncued condition (Fig. 1G; P < 0.01, bootstrap test). The scale parameter α was significantly smaller (196 ± 12 ms) and the slope parameter β, significantly larger (0.107 ± 0.012) than in the uncued condition (Fig. S2; P < 0.01, γ = 553 ms, fixed).

In summary, spatial cueing of the target greatly reduced the deleterious effects of distracters when target contrasts were similar to or weaker than distracter contrasts. The magnitude of the cueing effect was equivalent to an order of magnitude (∼20-fold) shift in relative target strength for 50% of asymptotic performance. These effects of spatial cueing in chickens parallel those of top-down (learned or endogenous) cueing on psychometric functions in humans (3).

Effect of Spatial Cueing on d′ and Bias.

An increase in percent correct performance that results from spatial cueing could be due to either an improvement in perceptual accuracy (d′) for localizing targets or a change in response bias (b). We applied signal detection theory (SDT) to distinguish the effects of spatial cueing on d′ vs. b (Fig. 2A). For this analysis, hit rates (proportion of correctly localized targets) and false-alarm rates (proportion of incorrectly localized targets) were computed only from those trials in which the animals gave a Go response, and the data were analyzed with a 2-AFC model (Fig. 2A). Rather than averaging percent correct across upper and lower targets, as is conventional in such analyses, we applied an SDT model that provided estimates of response bias for the upper and lower response box, respectively (SI Methods), and thereby provided a bias-free estimate of localization accuracy for discriminating upper from lower targets (18). In these analyses, the estimates of the psychometric functions were conditional on the animal’s decision to give a Go response; for an analysis that incorporates the full cohort of responses (Go and NoGo responses), see Effects of Spatial Cueing on Choice Certainty.

Fig. 2.

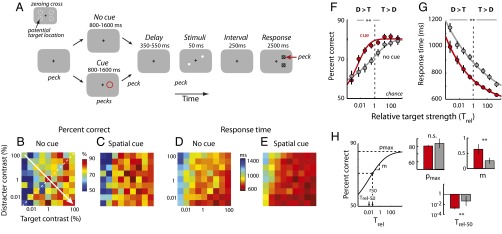
Spatial cueing effects on perceptual localization accuracy (d′) and bias (b). (A) A 2-AFC signal detection model incorporating bias. The solid line is the decision variable (ψ) distribution for a stimulus at the upper location (location 1, ψ|h₁). The dashed line is the ψ distribution for a stimulus at the lower location (location 2, ψ|h₂). As with conventional SDT, the distributions are assumed to be unit normal (Gaussian with unit variance). Localization accuracy, d′, the distance between the means of the two distributions, measures their mutual overlap. Bias, b, represents a criterion (cutoff value for the decision variable) based on which the animal decides to report an upper (ψ > b) vs. lower (ψ < b) target. (B) Psychometric functions of localization accuracy (d′) as a function of relative target strength for performance without (gray) and with (red) the cue (population data). Data averaged across equivalent target-to-distracter contrast ratios (diagonal entries of the performance matrix, Fig. 1 B and C). (Inset) The arrow indicates the axis of increasing T_rel. Curves represent cumulative Gaussian fits. Other conventions are the same as in Fig. 1F. (C) Bias, b, as a function of relative target strength without (gray) and with (red) the cue. Positive values indicate a bias toward the upper response boxes and negative values toward the lower. Curves represent sigmoid fits. Other conventions are the same as in B. (D) Psychometric functions of localization accuracy (d′) as a function of absolute target contrast for performance without (gray) and with (red) the cue. Data averaged across distracter contrasts (columns of the performance matrix, Fig. 1 B and C). (Inset) The arrow indicates the axis of increasing target contrast_. Curves represent Naka–Rushton fits. Other conventions are the same as in B. (E) Bias, b, as a function of absolute target contrast without (gray) and with (red) the cue. Other conventions are the same as in C and D. (B–E) Significant differences are indicated by a single asterisk (*P < 0.05) or double asterisk (**P < 0.01 level, bootstrap test with Bonferroni correction for multiple comparisons).

We computed the psychometric function—d′ as a function of relative target strength (also referred to as the “psychophysical function”)—both with and without spatial cueing (Fig. 2B). These functions were remarkably similar to the psychometric functions based on percent correct (Fig. 1F): In the uncued trials, d′ increased steadily across the range of relative target strengths, whereas on cued trials, d′ increased steeply and reached its asymptotic value at T_rel ≈ 1 (target = distracter). Again, the benefits of spatial cueing were greatest for intermediate relative target strengths, an effect characterized in the attention literature as “contrast gain.”

In a filtering task, the major determinant of distracter effects is the strength of the target relative to that of the concurrent distracter. However, we also analyzed the effects of the distracters as a function of the absolute target strength. For this analysis, we averaged the effects of the distracters across all distracter contrasts (average of matrix columns in Fig. 1 B and C). Psychometric functions of absolute target contrast also revealed substantial improvements in performance with cueing (Fig. 2D). The improvements in d′ were apparent even at the highest target contrasts due to the potency of the distracters for disrupting performance in the uncued condition (Fig. 1B). Cue-induced improvements in d′ were highest for targets of intermediate contrasts (0.1–1%; Fig. S4B, solid line), again consistent with the cueing effect being a contrast gain.

These analyses also revealed that the birds exhibited an increasing bias toward response boxes in the lower hemifield both with decreasing relative and absolute target strengths (Fig. 2 C and E). This trend in choice bias was apparent both in the cued and uncued trials. Such a choice bias, favoring locations in the lower hemifield, has been observed previously both in birds (19) and in humans (20).

The results indicate that cueing-induced improvements in performance cannot be attributed to changes in choice bias alone, and do indeed involve improvements in perceptual localization accuracy.

Effects of Spatial Cueing on Choice Certainty.

For humans, the effect of a spatial cue on choice certainty is controversial: Attentional cues have been found to have either a facilitatory effect (21) or no effect (22) on choice certainty based on post hoc ratings of confidence. Chickens do not provide a comparably explicit rating of their choice certainty. However, in our task, they could give a NoGo (opt-out) response that was occasionally rewarded (with a probability of 0.33). Tasks that include such an opt-out choice have been referred to as “unforced choice,” “free choice,” or “uncertain option” tasks (23–25). As explained below, the unforced-choice design of our task allowed us to estimate the birds’ confidence in their ability to localize target stimuli. For this analysis, we assessed performance as a function of absolute target contrast, to be consistent with convention. However, the results remained the same regardless of the specific representation chosen.

The proportion of NoGo responses decreased systematically with increasing target contrasts (Fig. 3B). In addition, cueing the target consistently decreased the proportion of NoGo responses (Fig. 3B, red vs. gray). What behavioral strategy could explain this pattern of effects?

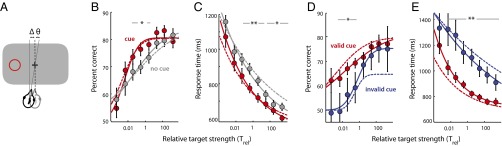
Fig. 3.

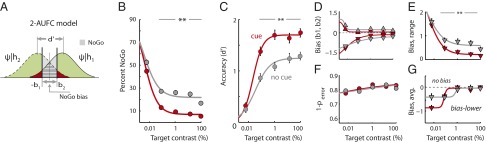
Spatial cueing improves choice certainty. (A) A 2-AUFC signal detection model incorporating NoGo (opt-out) responses. A key difference from the 2-AFC model (Fig. 2A) is that the animal employs two criterion values (biases, b₁ and b₂) to make a decision in one of three ways: reporting an upper target (ψ > b₂), lower target (ψ < −b₁), or for giving a NoGo response (−b₁ ≤ ψ ≤ b₂). Other conventions are as in Fig. 2A. Red shading represents the probability of an incorrect Go response (error), green shading (including area overlaid by red) represents the probability of a correct response (hit), gray shading represents the probability of a NoGo response (miss), and the hatched area represents the region of overlap for the two distributions. (B) Proportion of NoGo responses without (gray) and with (red) the cue, as a function of target contrast (averaged across distracter contrasts). (C) Psychometric functions of localization accuracy, d′, for performance without (gray) and with (red) the cue, computed with the 2-AUFC signal detection model. Other conventions are as in Fig. 2D. (D) Biases, b₁ and b₂, as a function of target contrast for performance without (gray) and with (red) the cue, computed with the 2-AUFC signal detection model. Other conventions are the same as in Fig. 2E. The negative of b₂ is plotted so that a larger magnitude of b₂ corresponds to more negative values. (E) Bias range (or NoGo bias, |b₁| + |b₂|) as a function of target contrast for performance without (gray) and with (red) the cue. (F) Error-aversion certainty, the certainty of avoiding an error (1 − P_error; area of red shaded region in A), as a function of target contrast for performance without (gray) and with (red) the cue. (G) Median bias (average of b₁ and −b₂) as a function of target contrast for performance without (gray) and with (red) the cue. Other conventions are the same as in Fig. 2E.

We hypothesized that the birds were making NoGo responses on trials in which they were not certain of the correct choice. To explore this hypothesis, we developed a signal detection model for the two-alternative unforced-choice (2-AUFC) task, a model that incorporated the animal’s NoGo responses (Fig. 3A). According to this model, a NoGo response resulted whenever the evidence did not strongly favor the presence of a stimulus at either of the two locations (upper or lower). This occurred when the decision variable fell between two criterion values (Fig. 3A, biases b₁ and b₂, thick vertical lines) that represented cutoff values for each decision (for the upper location or the lower location) along the decision axis. A similar signal detection model, called the “indecision model” with asymmetric criteria, has been proposed recently (25).

We refer to the range defined by the two biases (magnitude of biases |b₁| + |b₂|) as the “NoGo bias” (Fig. 3A): the greater the magnitude of the NoGo bias, the greater the tendency for a NoGo response. The 2-AUFC model fit the behavioral performance across target contrasts with remarkable precision (uncued: 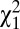= 0.31, P > 0.98; cued: 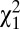= 0.70, P > 0.95; randomization goodness-of-fit test; SI Methods). In addition, we evaluated the predictive ability of the model with leave-one-out fitting (SI Methods); model predictions matched the observed response proportions (Fig. S4A).

In the 2-AUFC model, an increase in the proportion of NoGo responses (Fig. 3A, gray-shaded) can arise from two factors: (i) a change in the NoGo bias by increasing b₁, b₂, or both; and (ii) a change in perceptual (localization) accuracy by decreasing d′. The 2-AUFC model provides a principled approach for decoupling the contributions of these two factors to changes in the proportions of NoGo responses.

Analysis with the 2-AUFC model revealed that the observed increase in the proportion of NoGo responses with decreasing target contrast was associated with a change in both NoGo bias and perceptual accuracy. In addition to a decrease in d′ with decreasing target contrast (Fig. 3C, gray), the magnitudes of the biases (b₁ and b₂) increased with decreasing target contrast (Fig. 3D, gray), thereby increasing the NoGo bias (Fig. 3E, gray). The observed decrease in the proportion of NoGo responses with spatial cueing of the target was also associated with changes in the same two factors: Spatial cueing caused localization accuracy (d′) to increase (Fig. 3C, red vs. gray) and the NoGo bias to decrease (Fig. 3E, red vs. gray). The reduction in NoGo bias was significant for each target contrast for which cueing increased d′ (Fig. 3 C vs. E, P < 0.01, bootstrap test).

Birds and mammals are known to adjust their response strategies to maximize their rate of reward. In our experiments, the average rate of reward for a NoGo response was 0.33, which was considerably less than that for an accurate Go response (1.0) and less than that for a random guess Go response (0.5; to subthreshold target stimuli, for example). Moreover, variance of the reward across trials would be only slightly greater for the random guess Go response than for the NoGo response (guess Go: σ_r = 0.50; NoGo: σ_r = 0.47, Bernoulli process). Thus, if the birds’ goal in our experiments had been to maximize their rate of reward, the ideal strategy would have been to abstain from NoGo responses and to make Go responses (even when based on random guesses) on every trial, cued or uncued. Contrary to this prediction, the birds made many NoGo responses, and the proportion of NoGo responses decreased significantly with spatial cueing (Fig. 3B, red vs. gray). Thus, the birds were not making NoGo responses to maximize their rate of reward. What else might have caused them to make NoGo responses?

To answer this question, we turned to a Bayesian framework of decision making. In the Bayesian framework, the certainty associated with making a correct decision in a 2-AFC task is measured as the probability of making a correct response: P_correct. This definition provides a normative measure of choice certainty for animals, from which explicit confidence ratings cannot be obtained (17, 26). In the signal detection framework, P_correct is directly related to d′ which is inversely related to the overlap between the two signal distributions (Fig. 3A, hatched). In a 2-AFC task, the certainty of making a correct choice is also the certainty of not making an incorrect (error) choice; because these two choices (correct and error) are mutually exclusive and exhaustive, their probabilities must sum to one [P_correct + P_error = 1].

By contrast, in a 2-AUFC task, there is the additional option of making a NoGo choice, so that the probability of making an erroneous Go choice (Go response to an incorrect location; Fig. 3A, red shaded area) is not fully determined by the probability of making a correct Go choice (Go response to the correct location; Fig. 3A, green shaded area). Thus, the NoGo choice decouples erroneous Go choices from correct Go choices. Consequently, the certainty of not making an erroneous Go choice [P_{no error} = 1 − P_error] is separable, in principle, from the certainty of making a correct Go choice [P_correct], unlike in the 2-AFC task. We refer to the certainty with avoiding an erroneous Go response as the “error-aversion certainty.” In the 2-AUFC model, error-aversion certainty [P_{no error}] varies inversely with the probability of making an erroneous Go choice.

According to the 2-AUFC model, a decrease in d′ results in an increase in P_error and, therefore, a decrease in error-aversion certainty [P_{no error}]. On the other hand, an increase in NoGo bias (b₁ + b₂) has the opposite effect: It results in a decrease in P_error and an increase in error-aversion certainty. We observed that for both cued and uncued conditions, changes in the NoGo bias correlated strongly (and negatively) with changes in d′ (Fig. S4C; r = −0.91, P < 0.001). This analysis indicated that the animals adjusted their NoGo bias as their perceptual discriminability (d′) changed. Could this strategy reflect a tendency to keep the proportion of errors, and, hence, the error-aversion certainty, constant during Go choices?

Fig. 3F shows the error-aversion certainty for all of the data, pooled across birds. This value remained remarkably constant across target contrasts (linear fit, error-aversion certainty slope, cued: 1.2 ± 0.4% per decade of contrast; uncued: 0.8 ± 0.4%; not significantly different from zero, P > 0.05) and between the cued and uncued conditions (intercept, cued: 83.9 ± 1.0%; uncued: 82.5 ± 0.9%, P > 0.1, bootstrap test). The same results were observed in all but one bird (two out of three for this task, and three out of four for the task described in Effects of Invalid Cueing) when the data were analyzed separately by individual. This analysis indicates that, rather than maximizing rewards, the birds maintained a constant certainty of avoiding erroneous Go responses: NoGo responses increased proportionately with diminishing hit rates such that the error-aversion certainty remained constant across target contrasts, between cued and uncued conditions, and across birds. While maintaining a constant certainty of avoiding errors, they dramatically increased their certainty of correct choices [P_correct] during Go responses when the target was spatially cued. Taken together, these results indicate that choice certainty with localizing targets increased with spatial cueing.

Finally, the 2-AUFC model revealed a more robust effect of cueing on localization accuracy than did the 2-AFC model: Differences between d′ for the cued vs. uncued conditions were consistently greater when estimated with the 2-AUFC model (Fig. 3C vs. Fig. 2D; Fig. S4B and Discussion). These increases in d′ differences reflect the advantage of incorporating NoGo responses into the estimation of d′. The 2-AUFC model also confirmed the trend in choice bias that was identified earlier using the 2-AFC model (Fig. 3G): The birds exhibited a choice bias for the lower response box when target contrasts were weak.

Effects of Invalid Cueing.

For humans, an invalid cue (one that provides incorrect information about an upcoming target) produces effects on perceptual performance that are opposite to those of valid cues: a significant reduction in localization accuracy and an increase in reaction times (27). We asked whether invalid spatial cueing has similar effects on chickens.

In separate sessions (n = 211 experiments in four birds), we measured performance in the target localization task with interleaved validly cued and invalidly cued trials. In 90% of trials, the cue was presented on the same side as the upcoming response boxes, correctly predicting the side of the upcoming target; in the remaining 10% of trials, the cue was presented on the side opposite to the response boxes, resulting in an invalidly cued target (Fig. 4A). All other parameters of the filtering task remained the same. Because a cue was presented on every trial, the timing of the offset of the cue provided identical information regarding the timing of the imminent stimulus array for both validly and invalidly cued targets.

Fig. 4.

Spatial cueing effects are stronger with invalid cueing. (A) Sequence of events in a task with interleaved invalid (10%) and valid (90%) spatial cues (see Effects of Invalid Cueing for description). Other conventions are the same as in Fig. 1A. (B) Psychometric functions of percent correct with valid (red) and invalid (blue) cues, as a function of relative target strength (T_rel) (n = 211 experimental sessions in four birds). Other conventions are the same as in Fig. 1F. (C) Psychometric functions of response times for correctly localized targets as a function of relative target strength with valid (red) and invalid (blue) cues (population data). Other conventions are the same as in Fig. 1G. (D) p_max, m, and T_rel-50 estimates based on cumulative Gaussian fits to psychometric functions of percent correct, for performance with valid (red) and invalid (blue) cues. Other conventions are the same as in Fig. 1H. (E) Psychometric functions of perceptual localization accuracy (d′) with valid (red) and invalid (blue) cues, as a function of absolute target contrast (averaged over distracter contrasts), computed with the 2-AFC signal detection model (population data). Other conventions are the same as in Fig. 2D.

On invalidly cued trials, the stimulus that was usually the target was identified post hoc to be the distracter. In this condition, the distracter was extremely effective in degrading the bird’s localization accuracy and slowing its mean response time to the target. In particular, when the strength of the distracter exceeded the strength of the invalidly cued target (T_rel < 1), localization accuracy fell to near chance levels (Fig. 4B, blue) and mean response times were exceptionally long (Fig. 4C, blue).

The degradation in localization performance caused by invalid cueing was considerably greater than the difference in performance between cued and uncued targets, described previously: Invalid cueing resulted in a more robust increase in T_rel-50 (P < 0.01 for significant differences between validly and invalidly cued trials, bootstrap test; Fig. 4D), as well as poorer asymptotic performance (P < 0.01; Fig. 4D). In addition, accuracy and response time differences between invalid and valid cues were up to three times greater than the differences between uncued and cued performance (Fig. S5 A and B). The inclusion of invalid cues in a testing session caused performance on the validly cued trials to decrease relative to performance on cued trials in sessions which did not include invalidly cued trials (Fig. 1 F and G, red, vs. Fig. 4 B and C, red), suggesting that the possibility that a cue might be invalid had deleterious effects on responses to cued targets.

The effects of invalid cueing were also apparent in psychometric functions of absolute target contrast. Analysis with the 2-AFC model demonstrated that invalid cueing severely degraded localization accuracy relative to performance on validly cued trials (Fig. 4E); repeating the analysis with the 2-AUFC model (which incorporated NoGo responses) revealed even stronger effects of invalid cueing on localization performance (Fig. S5 C and E). Remarkably, however, invalid cueing caused little change in error-aversion certainty across target contrasts (Fig. S5F), in parallel with the effect observed previously with the cued/uncued paradigm (Fig. 3F). Although a nominally greater error-aversion certainty was associated with valid vs. invalid cueing, the difference was not significant (intercept, valid: 81.6 ± 0.7%, invalid: 78.4 ± 2.5%, P = 0.13, bootstrap test).

The results demonstrate that invalid spatial cueing degrades the target localization performance of chickens in a manner that resembles the effects of invalid cueing on the performance of primates.

Control for Overt Orienting.

Are the effects of spatial cueing due to overt or covert orienting mechanisms? Animals that possess retinal specializations for high visual acuity, such as primates, can improve perceptual performance on visual tasks either by overt orienting (directing the fovea toward a target stimulus) or by covert orienting (covertly monitoring the target stimulus without moving the head or eyes). For these species, orienting the optical axis of the eye to bring a stimulus on to the fovea can have an enormous impact on perceptual performance (28). However, chickens do not have foveas. Overtly orienting the optical axis of the eye toward a stimulus provides only a marginal increase in sensory spatial resolution for chickens, compared with foveate species, such as primates (see also Discussion).

We controlled for putative effects of overt orienting by exploiting a natural, stereotyped action pattern exhibited by ground-foraging birds. When a chicken prepares to peck at an object, it follows a highly stereotyped oculomotor strategy: Immediately before and for 150 ms following a peck, both eyes assume specific (±3°), binocularly converged positions in the orbits and, during this period, the optical axes of the eyes assume stable, predictable orientations in the head and relative to each other (29).

We exploited this stereotyped behavior in our experiments to present stimuli at consistent locations in the visual field: Stimulus arrays (target and distracter) were always triggered by the bird’s peck on the zeroing cross, and the arrays lasted for only 50 ms, well within the postpeck period (150 ms) of binocular stability. Hence, during this brief period the orientation of the eyes can be inferred with high reliability from the location and orientation of the head (beak), which we monitored with high spatial and temporal precision (SI Methods).

Analyzing head positions across trials, we found no positional biases during uncued trials (Fig. S6 gray; data from a representative bird). This is not surprising because, in uncued trials, the identity of the target was not revealed until after the array had disappeared. Because the target’s location varied randomly across sequential trials, there was no systematic motor strategy that could aid localization performance. Consistent with this logical argument, the birds exhibited no systematic biasing of head position relative to the location of the upcoming target on uncued trials, based on measurements of horizontal head displacement (Δ) and rotation (yaw, θ, Fig. 5A).

Fig. 5.

Cueing effects persist after controlling for head position biases. (A) Head position and orientation were monitored for each bird on each trial. Lateral displacement (Δ) and yaw (θ) of the head relative to the vertical plane perpendicular to the display and passing through the zeroing cross. The red annulus represents the side of the cue. (B) Psychometric functions of percent correct without (gray) or with (red) the spatial cue, as a function of relative target strength, after excluding trials in which the head was in a biased position (population data). Solid lines are the cumulative Gaussian fits. Dashed lines are the fits based on the entire dataset (repeated from Fig. 1F). Other conventions are the same as in Fig. 1F. (C) Same as in B, but for response times. Other conventions are as in Fig. 1G. (D) Same as in B, but for percent correct with valid (red) and invalid (blue) cueing. Other conventions are as in Fig. 4B. (E) Same as in D, but for response times. Other conventions are as in Fig. 4C.

On cued trials, the cue predicted the side of the upcoming target stimulus with high validity. Nevertheless, in the majority of cued trials (which were interleaved with uncued trials), the distribution of head positions largely overlapped those in uncued trials (Fig. S6, green).

In a subset of cued trials, however, a clear head position bias was observed (Fig. S6, red vs. gray): The head was translated up to several millimeters toward the side of the cue (Fig. 5A; Δ) and the beak direction was simultaneously counterrotated away from the cue and back toward the zeroing cross (Fig. 5A; θ). The most obvious explanation for this unexpected, counterrotation of the head away from the side of the cue, specifically on these trials, was that the bird was maintaining binocular fixation of the zeroing cross while displacing its head toward the side of the cue. The same behavior was observed in all tested birds.

This overt movement strategy may have conferred some performance advantage on cued relative to uncued or invalidly cued trials. First, this motor strategy may have allowed faster response times. Second, it increased (by up to 0.5° for the 95th percentile of head displacement deviations) the size of the 2° target dot on the retina on the side of the cue. To control for these potential effects of overt differences, we reanalyzed the data after selecting specifically for trials with matching values of head Δ and θ (tolerance: Δ = ±0.5 mm; θ = ±1°) across cued and uncued conditions (Fig. S6, green; for details, see SI Methods). Due to the stringency of this matching process, >50% of trials were eliminated from the analysis.

Reanalysis of the data yielded results (Fig. 5 B–E, solid lines) that closely resembled the original results based on the entire dataset (Fig. 5 B–E, dashed lines). Percent correct was consistently higher for cued compared with uncued or invalidly cued trials, and statistically significant (*P < 0.05, bootstrap test) at low and intermediate values of relative target strength (Fig. 5 B and D; the decrease in statistical significance can, in part, be attributed to the decrease in sample sizes for bootstrap analysis, following the Δ–θ matching procedure). The most conspicuous difference was a higher percent correct on invalidly cued trials for high relative target strengths (Fig. 5D, T_rel > 1).

The effects of cueing on response time also remained robust after the matching procedure (**P < 0.01 or *P < 0.05; Fig. 5 C and E). The reanalysis resulted in a marginal reduction in the magnitude of the response time effect (Fig. 5 C and E; smaller difference between the two solid line fits vs. the two dashed line fits), consistent with the possibility that the lateral head displacement tended to shorten response times (but see Discussion).

Discussion

We measured the effects of spatial cueing on the ability of chickens to report the location of a target stimulus in the presence of a task-relevant distracter. Spatial cueing dramatically increased the accuracy (d′) of target localization and decreased response times, particularly when the contrast of the target was weak relative to that of the distracter. These effects are the signatures of attention in humans and nonhuman primates (2, 3, 30). In addition, in chickens, as in humans, spatial cueing increased choice certainty (21).

Our task design enabled us to quantify the effects of attention in a visuospatial task by overcoming key drawbacks of the experimental designs used in previous studies of nonprimate species. First, because the cue (red circle) and the response boxes (squares with an inlaid X) were distinct from the target and distracter stimuli (dots), the effects of selective attention to the cued location were not conflated with selective learning of specific cue features or with biases for a particular response target. Second, our design permitted the quantification of d′, a measure of perceptual accuracy that is uncontaminated by bias effects and is the metric of choice in human studies (3). Finally, the cue provided spatial information (target azimuth) that was uncorrelated and, quite literally, orthogonal to the information necessary to complete the task (target elevation), thereby controlling for the potential confounds of a cue-induced spatial bias. Our results characterize for the first time to our knowledge, in a nonprimate species, perceptual effects of spatial attention that are distinct from the effects of motor preparation or cue-induced biases.

Unlike primates, which typically make conjugate eye movements (the optical axes of both eyes moving in parallel), chickens (and many lateral-eyed animals) can move their eyes independently (31, 32). In addition, because the axes of the eyes are directed laterally, the left and right eyes have different views of the world (31). This has led to the speculation that such animals could process and attend to stimuli in each monocular visual field independently. In our experiments, the target and distracter stimuli were presented immediately following a zeroing-cross peck on opposite sides of the screen (±60°), well away from the zone of binocular overlap (Fig. 1A). Thus, each stimulus (target/distracter) was viewed monocularly. It is conceivable that the chickens would have been able to process the stimuli in the left and right hemifields independently and attend to both separately. The results disproved this hypothesis. Distracters substantially degraded the ability to localize targets presented in the opposite hemifield (e.g., Fig. 1 B and D) providing compelling evidence for strong competitive (bottom-up) interactions operating across the visual hemifields. In addition, cueing the stimulus on one side resulted in a substantial degradation in localization performance on the opposite side (e.g., Fig. 4 B and C). These results are consistent with a unitary locus of top-down selective attention induced by spatial cueing in our task. These properties of spatial attention in chickens are strikingly similar to those reported in primates.

Covert vs. Overt Orienting.

Humans, and other foveate primates, can orient both covertly and overtly (moving the eyes) to stimuli of interest. In primates, the spatial resolution provided by the retina (density of retinal ganglion cells) varies by a factor of 1,000 to 4,000 from the center of the optical axis (perpendicular through the center of the pupil) to >80° into the periphery (33). In these species, overtly orienting the eye toward a stimulus can provide substantial improvements in perceptual sensitivity or acuity in processing stimuli. On the other hand, many vertebrate species (such as chickens) and nonprimate mammalian species (such as rats and mice) do not have a fovea. In chickens, photoreceptor and retinal ganglion cell density varies by a factor of 2 to 5 across a comparable range of eccentricities (0–100°), and spatial acuity falls off by a factor of <2 between the center and the periphery (34, 35). Thus, for chickens, compared with primates, orienting the eye toward a stimulus of interest does not substantially improve spatial resolution.

In our task, birds viewed the stimulus on each side monocularly. Moreover, the azimuth and the potential elevations of the stimuli on each side were constant across trials and, therefore, known to the bird on every trial. Thus, there was no advantage for differentially orienting either eye toward any particular location on cued vs. uncued trials.

In attempting to distinguish covert vs. overt orienting mechanisms, another important distinction between primates and several nonprimate species must be borne in mind: the position of the eyes in the head, and the corresponding pattern of eye movements. For lateral-eyed species (such as chickens), the conventional definition of overt attention—improvements in perceptual performance by shifting the direction of gaze—is problematic. First, unlike primates (a frontal-eyed species), the optical axes of the two eyes of chickens (a lateral-eyed species) are never mutually aligned. Thus, they never have a single direction of gaze. Second, as mentioned previously, chickens can move the eyes independently (disconjugately). These two characteristics make it difficult to ascertain where a chicken is looking based on the orientation of the eyes. Finally, even when chickens converge the eyes to fixate a stimulus for pecking, the axes of the eyes remain directed >15° to each side of the target object (29), further demonstrating the nebulous relationship between the direction of gaze (optical axes), and the location of the stimulus that is selected for guiding behavior.

Although the eyes of a chicken are always oriented in different directions, they do move to consistent, symmetrical, frontal locations for about 100–150 ms after the bird pecks (29). We took advantage of this behavior to deliver stimuli (targets and distracters) to consistent locations in the bird’s visual field. Stimulus arrays were presented for 50 ms, immediately following a peck on the cross, well within the period of stable, binocular convergence, and when the head was in a consistent orientation relative to the cross. With this approach we sought to ensure that there was as little difference as possible in the locations of the stimuli on the retinas between cued and uncued trials.

On a fraction of cued trials, however, the birds translated the head slightly toward the cued side, while simultaneously counterrotating the head away from the cued side (Fig. S6). This overt behavior tended to maintain binocular fixation of the cross, while bringing the head, and eye adjacent the cued side, slightly closer to the target. We isolated the contribution of responses from this subset of trials to the overall effects by removing all cued and uncued trials that were not matched for head position and rotation at the time of target presentation. Removing these trials decreased somewhat the magnitudes of the effects. Nevertheless, all of the effects remained strong: a contrast-gain effect of the cue on perceptual performance and faster response times toward the cued location (Fig. 5 B–E). We conclude that these effects are due to covert attention.

Several different factors could account for the decrease in the cueing effects that resulted from removing trials that were not matched for head position. First, head displacement and rotation may have conferred sensory resolution or motor reaction time advantages (overt effects) for responses on the cued side (although the cue still provided no information about the vertical location of the impending target). Second, these overt biases may have reflected exceptionally high motivational state and, therefore, may have corresponded to trials in which the animal was attending most strongly to the cued side (covert effects). Third, the reduction in the significance (P values) of the cueing effect could be due, in part, to the decreased number of trials that qualified for the bootstrap analysis following the head-position matching procedure (covert effects). The data do not distinguish between these overt vs. covert contributions to performance. The advantages of covert over overt mechanisms are that they can shift the locus of enhanced sensory processing faster, more frequently, and without breaking camouflage.

Spatial Cueing Modulates Stimulus Priority.

Results from the filtering task show that when confronted by multiple stimuli, chickens retain information about those stimuli that can be recalled a short time later should one of the stimuli become behaviorally relevant. The accuracy of recalled spatial information depends on the contrast of the selected stimulus relative to that of distracting stimuli: Localization performance was excellent as long as the contrast of the selected stimulus was much greater than that of distracting stimuli, but declined steeply as the relative strength of the distracter increased (Figs. 1F and 2B, gray). The data indicate that for chickens, as for primates, the accuracy of retained information depends, in part, on a competitive process based on the relative physical salience of stimuli.

Spatial cueing greatly reduced the effects of distracting stimuli on perceptual performance. When the selected stimulus (target) was of high contrast relative to distracters, cueing provided little perceptual benefit (Figs. 1F and 2B, red). However, as the relative strength of the distracter increased, cueing tended to maintain performance at near-maximum levels, an effect similar to a contrast-gain effect of attention documented in humans (3).

Invalid cueing revealed additional effects on performance accuracy. The accuracy in localizing invalidly cued targets (Fig. 4 B and E, blue) plummeted relative to localization of either cued (Fig. 4 B and E, red) or uncued stimuli (Figs. 1F and 2B, gray) across all target strengths (relative or absolute). Still, the effects on accuracy were maximal at intermediate target strengths (relative, Fig. 4B; or absolute, Fig. 4E and Fig. S4C), again consistent with a contrast-gain effect. In humans, contrast-gain effects are observed when the size of a target is small compared with the size of the attention field (3, 10). The contrast-gain changes we report here are consistent with this interpretation: In our task the cue only indicated the side of the upcoming target stimulus, and it is reasonable to hypothesize that the birds maintained an attention field that encompassed both potential target elevations.

As with humans, the most consistent effects of spatial cueing were on reaction times (30). We found that even for target contrasts at which percent correct was unaffected by spatial cueing, reaction and response times were significantly reduced by spatial cueing (Fig. 1 F vs. G and Fig. 5 B vs. C and D vs. E). This decrease in decision time with attention is consistent with cueing causing a systematic reduction in the decision boundary separation (b₁ to b₂ range, Fig. 3 A and E), as postulated by integration-to-bound models of decision making in humans (30).

The magnitude of the effect of cueing on perceptual performance is estimated most accurately when opt-out (NoGo) responses are included in the analysis (Fig. 3C). The importance and advantages of incorporating such opt-out responses in lieu of the standard 2-AFC design have been highlighted previously (25). Modeling the decision-making process with a 2-AUFC model (indecision model) permitted us to demonstrate that the strategy used by the birds in performing the task was not one of maximizing rewards, but one of maintaining a constant (high) certainty of averting errors when making a Go choice (Fig. 3F). We wish to clarify that the constant proportion of errors (Fig. 3F) is different from motor errors (lapse rates) during the Go responses. Lapse rates are conventionally defined as the proportion of incorrect Go responses as a fraction of the total number of Go responses for the most salient (easiest to localize) targets. On the other hand, the proportion of errors (Fig. 3F) is the proportion of incorrect Go responses as a fraction of the total number of all responses (Go + NoGo). Other models have incorporated lapse rates when fitting data with a 2-AUFC–like model (25). Analyzing our data with such models could result in more accurate estimates of the d′ and bias (absolute values), but would not alter our claim regarding the improvements of d′ (relative values) with cueing.

The opportunity to give NoGo responses enabled the animals to express their confidence in not making an error independently of their confidence in making correct Go choices. As task difficulty increased, animals were faced with the following choice: a random guess (with 50% probability of reward but also an equal probability of making an error) or a NoGo response. Under these conditions, the chickens chose a NoGo response in a large proportion of trials (Fig. 3B). This result has intriguing parallels with human decision making: Loss aversion (the tendency to avoid erroneous choices that may result in losses) rather than gain acquisition powerfully dominates choice behavior in humans (36).

The results reported in this study demonstrate that the capacity of chickens to select particular locations for selective attention is controlled both by the relative physical salience of stimuli (bottom-up information) and by the relevance of stimuli to behavior (top-down information). In our experiments, when a stimulus was identified post hoc as being the behaviorally relevant stimulus, top-down mechanisms largely counteracted the degrading effects of bottom-up competition by distracters and enhanced perceptual performance to the cued stimulus. Thus, in chickens, as in primates, bottom-up and top-down information combine to yield the priority of a stimulus for attention (37).

Methods

Birds.

All procedures were in compliance with the guidelines of the National Institutes of Health for the care and use of laboratory animals and were approved by the Institute Animal Care and Use Committee of Stanford University (Protocol ID 20287). Experiments were performed with four female adult (>12 mo) white leghorn chickens (Gallus domesticus, Hyline strain). The birds were kept on a food-restricted schedule that maintained them at 70% of their free feeding weight. Water was available ad libitum in the home cage.

Details regarding the stimulus presentation, data acquisition, training, and testing, which followed protocols similar to those outlined in (19), are provided in SI Methods.

Filtering Task.

Birds were trained to report the location of a target stimulus in the presence of a distracter (Fig. 1A, upper sequence). The target and distracter were positive contrast dots (∼2° diameter) presented in opposite hemifields, one to the left and the other to the right, each at 60° azimuths (Fig. 1A, white dots). The elevation of each stimulus varied randomly between two possible locations (Fig. 1A, Inset, dashed circles) 12.5° above or below the visual horizon relative to the bird’s head at the time of the peck (for details, see SI Methods and ref. 19). The locations of the two stimuli were independently sampled, and upper and lower locations were tested with equal probability. The target and distracter were identical except in contrast, which was varied randomly, and independently sampled from one of nine different contrast levels (0.0033–100%), uniformly spaced on a logarithmic scale (ratio of 3.631 between successive levels); stimuli were calibrated with an OceanOptics spectrometer (19). After the stimulus array was extinguished (250-ms delay), two response boxes (square boxes with an inlaid X motif) appeared to one side. Birds were rewarded for indicating the location of the target by pecking on the response box (within a 20-mm radius) closest to the target’s location (Fig. 1A, red arrow); reward constituted access to the feeder for 2 s. We also included in the task the option for the bird to report a NoGo (opt-out) response by pecking twice on the zeroing cross. NoGo responses were rewarded with a probability of ∼0.33 (uncertain reward). No catch trials (trials in which no target is displayed) were included in our tasks.

Spatial Cueing.

In 50% of the trials, a spatial cue (10° radius, red annulus) was presented on the horizon for ∼1,400 ms [(800–1,600) ms; 68% CI, see next section] and was extinguished ∼400 ms [(350–550) ms; 68% CI] before the stimulus array appeared. Trials with a spatial cue were pseudorandomly interleaved with trials in which no cue was presented (uncued, previous section). The cue predicted the side and azimuth of the upcoming response boxes and, therefore, the target stimulus with 100% validity (Fig. 1A, lower sequence). The cue was completely uninformative, however, about the vertical location (elevation) of the target.

Distribution of Cue Durations and Cue–Target Intervals.

In both cued and uncued filtering tasks, the timing of the appearance and disappearance of the cue, as well as the timing of stimulus presentation, were locked to the bird’s peck responses to the zeroing cross (Fig. 1A). In the cued filtering task, the cue was presented following the first peck on the zeroing cross. Next, birds pecked a variable number of times (two to four times), following which the cue was extinguished. Following cue offset, birds pecked once more (“Delay” in Fig. 1A) to trigger the stimuli (target and distracter). On average, the interval between pecks was ∼400 ms. The distributions of cue durations (two to four pecks, 800–1,600 ms; median, 1,400 ms) and cue–target intervals (one peck, 350–550 ms; median, 400 ms) reflect integral multiples of the interpeck intervals. In uncued trials, the distribution of pecks before the stimulus array was presented was carefully matched to the cueing protocol (Fig. 1A, upper vs. lower sequence). This permitted matching the interval between trial initiation and stimulus presentation for cued and uncued trials.

Valid/Invalid Cueing.

This task was identical with the cued localization (filtering) task except that a spatial cue (same physical characteristics as described before) was presented on every trial. In 90% of trials, the cue was presented on the side of the upcoming response boxes, and therefore the target; these were termed “validly cued” trials, as the cue correctly predicted the location of the upcoming target. In 10% of interleaved trials, the cue was presented on the side opposite the upcoming response boxes (and target). These were termed “invalidly cued” trials. As before the cue was completely uninformative about the vertical location of the target.

Details regarding the analysis of performance metrics, signal detection models, head position control analysis as well as the bootstrap analyses for estimating significant differences are provided in SI Methods.