How multiplicity determines entropy and the derivation of the maximum entropy principle for complex systems

Significance

The maximum entropy principle (MEP) states that for many statistical systems the entropy that is associated with an observed distribution function is a maximum, given that prior information is taken into account appropriately. Usually systems where the MEP applies are simple systems, such as gases and independent processes. The MEP has found thousands of practical applications. Whether a MEP holds for complex systems, where elements interact strongly and have memory and path dependence, remained unclear over the past half century. Here we prove that a MEP indeed exists for complex systems and derive the generalized entropy. We find that it belongs to the class of the recently proposed (c,d)-entropies. The practical use of the formalism is shown for a path-dependent random walk.

Abstract

The maximum entropy principle (MEP) is a method for obtaining the most likely distribution functions of observables from statistical systems by maximizing entropy under constraints. The MEP has found hundreds of applications in ergodic and Markovian systems in statistical mechanics, information theory, and statistics. For several decades there has been an ongoing controversy over whether the notion of the maximum entropy principle can be extended in a meaningful way to nonextensive, nonergodic, and complex statistical systems and processes. In this paper we start by reviewing how Boltzmann–Gibbs–Shannon entropy is related to multiplicities of independent random processes. We then show how the relaxation of independence naturally leads to the most general entropies that are compatible with the first three Shannon–Khinchin axioms, the -entropies. We demonstrate that the MEP is a perfectly consistent concept for nonergodic and complex statistical systems if their relative entropy can be factored into a generalized multiplicity and a constraint term. The problem of finding such a factorization reduces to finding an appropriate representation of relative entropy in a linear basis. In a particular example we show that path-dependent random processes with memory naturally require specific generalized entropies. The example is to our knowledge the first exact derivation of a generalized entropy from the microscopic properties of a path-dependent random process.

Many statistical systems can be characterized by a macrostate for which many microconfigurations exist that are compatible with it. The number of configurations associated with the macrostate is called the phase-space volume or multiplicity, M. Boltzmann entropy is the logarithm of the multiplicity,

and has the same properties as the thermodynamic (Clausius) entropy for systems such as the ideal gas (1). We set 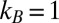. Boltzmann entropy scales with the degrees of freedom f of the system. For example, for N noninteracting point particles in three dimensions, . Systems where scales with system size are called extensive. The entropy per degree of freedom is a system-specific constant. Many complex systems are nonextensive, meaning that if two initially insulated systems A and B, with multiplicities and , respectively, are brought into contact, the multiplicity of the combined system is . For such systems, which are typically strongly interacting, non-Markovian, or nonergodic, and the effective degrees of freedom do no longer scale as N. Given the appropriate scaling for , the entropy is a finite and nonzero constant in the thermodynamic limit, .

A crucial observation in statistical mechanics is that the distribution of all macrostate variables gets sharply peaked and narrow as system size N increases. The reason behind this is that the multiplicities for particular macrostates grow much faster with N than those for other states. In the limit the probability of measuring a macrostate becomes a Dirac delta, which implies that one can replace the expectation value of a macrovariable by its most likely value. This is equivalent to maximizing the entropy in Eq. 1 with respect to the macrostate. By maximizing entropy one identifies the “typical” microconfigurations compatible with the macrostate. This typical region of phase space dominates all other possibilities and therefore characterizes the system. Probability distributions associated with these typical microconfigurations can be obtained in a constructive way by the maximum entropy principle (MEP), which is closely related to the question of finding the most likely distribution functions (histograms) for a given system.

We demonstrate the MEP in the example of coin tossing. Consider a sequence of N independent outcomes of coin tosses, , where is either head or tail. The sequence x contains heads and tails. The probability of finding a sequence with exactly heads and tails is

where is the binomial factor. We use the shorthand notation for the histogram of heads and tails and for the marginal probabilities for throwing head or tail. For the relative frequencies we write . We also refer to θ as the “biases” of the system. The probability of observing a particular sequence x with histogram k is given by . It is invariant under permutations of the sequence x because the coin tosses are independent. All possible sequences x with the same histogram k have identical probabilities. is the respective multiplicity, representing the number of possibilities to throw exactly heads and tails. As a consequence Eq. 2 becomes the probability of finding the distribution function p of relative frequencies for a given N. The MEP is used to find the most likely p. We denote the most likely histogram by and the most likely relative frequencies by .

We now identify the two components that are necessary for the MEP to hold. The first is that in Eq. 2 factorizes into a multiplicity that depends on k only and a factor that depends on k and the biases θ. The second necessary component is that the multiplicity is related to an entropy expression. By using Stirling’s formula, the multiplicity of Eq. 2 can be trivially rewritten for large N,

where an entropy functional of Shannon type (2) appears,

The same arguments hold for multinomial processes with sequences x of N independent trials, where each trial takes one of W possible outcomes (3). In that case the probability for finding a given histogram k is

is the multinomial factor and . Asymptotically holds. Extremizing Eq. 5 for fixed N with respect to k yields the most likely histogram, . Taking logarithms on both sides of Eq. 5 gives

Obviously, extremizing Eq. 6 leads to the same histogram . The term in Eq. 6 is sometimes called relative entropy or Kullback–Leibler divergence (4). We identify the first term on the right-hand side of Eq. 6 with Shannon entropy , and the second term is the so-called cross-entropy . Eq. 6 states that the cross-entropy is equal to entropy plus the relative entropy. The constraints of the MEP are related to the cross-entropy. For example, let the marginal probabilities be given by the so-called Boltzmann factor, , for the “energy levels” , where β is the inverse temperature and α the normalization constant. Inserting the Boltzmann factor into the cross-entropy, Eq. 6 becomes

which is the MEP in its usual form, where Shannon entropy gets maximized under linear constraints. α and β are the Lagrangian multipliers for the normalization and the “energy” constraint , respectively. Note that in Eq. 6 we used to scale . Any other nonlinear would yield nonsensical results in the limit of , either 0 or ∞. Comparing with Eq. 1 shows that indeed, up to a constant multiplicative factor, . This means that the Boltzmann entropy per degree of freedom of a (uncorrelated) multinomial process is given by a Shannon-type entropy functional. Many systems that are nonergodic, are strongly correlated, or have long memory will not be of multinomial type, implying that is not invariant under permutations of a sequence x. For this situation it is not a priori evident that a factorization of into a θ-independent multiplicity and a θ-dependent term, as in Eq. 5, is possible. Under which conditions such a factorization is both feasible and meaningful is discussed in the next section.

Results

When Does a MEP Exist?

The Shannon–Khinchin (SK) axioms (2, 5) state requirements that must be fulfilled by any entropy. [Shannon–Khinchin axioms: SK1, entropy is a continuous function of the probabilities only and should not explicitly depend on any other parameters; SK2, entropy is maximal for the equidistribution ; SK3, adding a state to a system with does not change the entropy of the system; and SK4, entropy of a system composed of two subsystems, A and B, is .] For ergodic systems all four axioms hold. For nonergodic ones the composition axiom (SK4) is explicitly violated, and only the first three (SK1–SK3) hold. If all four axioms hold, the entropy is uniquely determined to be Shannon’s; if only the first three axioms hold, the entropy is given by the -entropy (6, 7). The SK axioms were formulated in the context of information theory but are also sensible for many physical and complex systems.

The first Shannon–Khinchin axiom (SK1) states that entropy depends on the probabilities only. Multiplicity depends on the histogram only and must not depend on other parameters. Up to an N-dependent scaling factor the entropy is the logarithm of multiplicity. The scaling factor removes this remaining N dependence from entropy, so that SK1 is asymptotically fulfilled. In fact, SK1 ensures that the factorization into a θ-independent characteristic multiplicity and a θ-dependent characteristic probability is not arbitrary.

For systems that are not of multinomial nature, we proceed as before: To obtain the most likely distribution function we try to find that maximizes for a given N. We denote the generalized relative entropy by

Note that whenever an equation relates terms containing k with terms containing p, we always assume . The maximal distribution therefore minimizes and is obtained by solving

for all . α is the Lagrange multiplier for normalization of p.

The histogram can be seen as a vector in a W-dimensional space. Let be a W-dimensional vector whose ith component is 1, and all of the others are 0. With this notation the derivative in Eq. 9 can be expressed asymptotically as

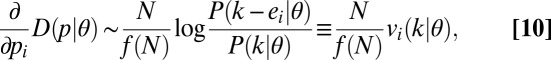where we write for the log term. We interpret as the ith component of a vector . Let be the ith component of the jth basis vector for any given k; then has uniquely determined coordinates ,

has coordinates in any basis . However, as can be easily verified, not all bases are compatible with SK1–SK3 (see condition i in the Theorem below). The problem of factorizing therefore reduces to the problem of finding an appropriate basis. For reasons that become clear below, we choose the following Ansatz for the basis

where the functions are so-called deformed multinomial factors, and are some appropriately chosen constants. is a factor depending on a continuous, monotonic, and increasing function T, with , and . are positive, monotonic increasing functions on the natural numbers. The freedom of choosing , u, and T in this basis provides a well-defined framework that allows us to derive the conditions for the existence of a MEP. Deformed multinomials are based on deformed factorials that are well known in the mathematical literature (8–13) and are defined as

For a specific choice of u, deformed multinomials are then defined in a general form as

where is the largest integer less than x. With the basis of Eq. 12 we can write

Note that this can be done for any process that produces sequences , where takes one of W values. We can now formulate the following:

Theorem.

Consider the class of processes , with , parameterized by the biases θ and the number of elements N. The process produces histograms k with probability . Let N be large and be the histogram that maximizes . Assume that a basis of the form given in Eq. 12 can be found, for which (i) , for all , and (ii) for fixed values of N and θ, the coordinate of in this basis, as defined in Eq. 11, becomes a nonzero constant at . [Condition ii means that the first derivatives of vanish at under the condition , N being constant.] Under these conditions factorizes, , with

Moreover, there exists a MEP with generalized entropy , for some scaling function . The factors in Eq. 16 represent the constraint terms in the MEP. The solution of the MEP is given by .

The physical meaning of the Theorem is that the existence of a MEP can be seen as a geometric property of a given process. This reduces the problem to one of finding an appropriate basis that does not violate axioms SK1–SK3 and that is also convenient. The former is guaranteed by the Theorem, and the latter is achieved by using the particular choice of the basis in Eq. 12.

Condition ii of the Theorem guarantees the existence of primitive integrals and . If condition i is violated, the first basis vector of Eq. 12 introduces a functional in p that will in general violate the second Shannon–Khinchin axiom SK2. Conditions i and ii together determine up to a multiplicative constant , which can be absorbed in a normalization constant. may be difficult to construct in practice. However, for solving the MEP it is not necessary to know explicitly; it is sufficient to know the derivatives of the logarithm for the maximization. These derivatives are obtained simply by taking the logarithm of Eq. 16. For systems that are compatible with the conditions of the Theorem, in analogy to Eq. 6, a corresponding MEP for the general case of nonmultinomial processes reads

has to be chosen such that for large N the generalized relative entropy neither becomes 0 nor diverges for large N. is the generalized entropy, and is the generalized cross-entropy. In complete analogy to the multinomial case, the generalized cross-entropy equals generalized entropy plus generalized relative entropy. Note that in general the generalized cross-entropy will not be linear in . In ref. 14 it was shown that the first three Shannon–Khinchin axioms allow only two options for the constraint terms. They can be either linear or of the so-called “escort” type (15), where constraints are given by specific nonlinear functions in (14). No other options are allowed. For the escort case we have shown in refs. 14 and 16 that a duality exists such that the generalized entropy S, in combination with the escort constraint, can be transformed into the dual generalized entropy with a linear constraint. In other words, the nonlinearity in the constraint can literally be subtracted from the cross-entropy and added to the entropy. Compare with the notion of the “corrector” discussed in ref. 17.

The Generalized Entropy.

We can now compute the generalized entropy from Eq. 17,

where is the derivative with respect to z. Further, we replace the sum over r by an integral that is correct for large N. The resulting generalized entropy is clearly of trace form. In refs. 14, 18, and 19 it was shown that the most general form of trace form entropy that is compatible with the first three Shannon–Khinchin axioms is

where is a so-called generalized logarithm, which is an increasing function with , ; compare refs. 14 and 16. Comparison of the last line of Eq. 18 with Eq. 19 yields the generalized logarithm

with and b constants. By taking derivatives of Eq. 20, first with respect to z and then with respect to N, one solves the equation by separation of variables with a separation constant ν. Setting , we get

By choosing T and ν appropriately one can find examples for all entropies that are allowed by the first three SK axioms, which are the -entropies (6, 7). -entropies include most trace form entropies that were suggested in the past decades as special cases. The expressions and from Eq. 21 can be used in Eqs. 9 and 15 to finally obtain the most likely distribution from the minimum relative entropy,

which must be solved self-consistently. is the inverse function of T. In the case that only the first two basis vectors are relevant (the generalized entropy and one single constraint term), we get distributions of the form

with , . In a polynomial basis, specified by , the equally spaced “energy levels” are given by . Note that , and depends on bias terms.

For a specific example let us specify and . Eqs. 21 and 19 yield

which is the so-called Tsallis entropy (20). for this choice of T. Any other choice of T leads to -entropies. Assuming that the basis has two relevant components and using the same as above, the derivative of the constraint term in the example is obtained from Eq. 16,

This constraint term is obviously nonlinear in and is therefore of escort type. Here the expression plays the role of equidistant energy levels. The example shows explicitly that finding the most likely distribution function by maximization of (minimization of relative entropy) is equivalent to maximizing the generalized entropy of Eq. 24 under a nonlinear constraint term, . In ref. 14 it was shown that a duality exists that allows us to obtain exactly the same result for , when maximizing the dual entropy of Eq. 24, given by , under the linear constraint, .

Example: MEP for Path-Dependent Random Processes.

We now show that path-dependent stochastic processes exist that are out of equilibrium and whose time-dependent distribution functions can be predicted by the MEP, using the appropriate, system-specific generalized entropy. We consider processes that produce sequences x that increase in length at every step. At a given time the sequence is . At the next time step a new element will be added. All elements take one of W different values, . The system is path dependent, meaning that for a sequence x of length N the probability for producing depends on the histogram k and the biases θ only. For such processes the probability to find a given histogram, can be defined recursively by

For a particular example let the process have the transition probability

where is a normalization constant, and . Let us further fix . Note that fixing the biases θ in multinomial systems means that as N gets large one obtains , for all i. Obviously approaches a steady state and N becomes an irrelevant degree of freedom in the sense that changing N will not change . Fixing all asymptotically determines completely and leaves no room for any further constraint. For path-dependent processes the situation can be very different. For example, the relative frequencies of the process defined in Eq. 27 never reach a steady state as N gets larger. [One can show that for such systems the inverse temperature approximately grows (sub)logarithmically with N.] Here, fixing θ for all i still allows to evolve with growing N, such that 1 df remains that can be fixed by an additional constraint. [Additional constraints may become necessary for intermediate ranges of N, where some coordinates that need to vanish asymptotically (in the appropriately chosen basis) are not yet sufficiently small.] The process defined in Eq. 27 is a path-dependent, W-dimensional random walk that gets more and more persistent as the sequence gets longer. This means that in the beginning of the process all states are equiprobable . With every realization of state i in the process, all states become more probable in a self-similar way, and a monotonic distribution function of frequencies emerges as N grows. The process appears to “cool” as it unfolds. Adequate basis vectors can be obtained with deformed multinomials based on , , and a polynomial basis for . For this u, in Fig. 1A (solid lines), we show normalized deformed binomials for and . Dashed lines represent the usual binomial. Clearly, generalized multiplicities become more peaked and narrow as N increases, which is a prerequisite for the MEP to hold. In Fig. 1B the variance of deformed binomials is seen to diminish as a function of sequence length N for various values of ν. The dashed line shows the variance for the usual binomial. Distribution functions obtained for numerical simulations of sequences with W states are shown in Fig. 1C for sequence lengths , 5,000, and 10,000 (solid lines). Averages are taken over normalized histograms from 150 independent sequences that were generated with , and . The distributions follow exactly the theoretical result from Eq. 23, confirming that a basis with two relevant components (one for the entropy one for a single constraint fixing N) is sufficient for the given process with . Dashed lines are the functions suggested by the theory, with , where β is obtained from a fit to the empirical distribution. β determines . α is a normalization constant. Although the power exponent does not change with N, the “inverse temperature” β increases with N (Fig. 1C, Inset), which shows that the process becomes more persistent as it evolves—it “ages.” Because , the observed distribution p can also be obtained by maximizing the generalized entropy S (Eq. 24) under a nonlinear constraint or, equivalently, by maximizing its dual, with a linear constraint, as discussed above. For other parameter values a basis with more than two components might become necessary. Note that the nonlinear (escort) constraints can be understood as a simple consequence of the fact that the relative frequencies p have to be normalized for all N. In particular, the escort constraints arise from and Eq. 23, which states that does not change its functional shape as θ or N is varied.

Fig. 1.

Numerical results for the path-dependent random process determined by the deformed factorial with . (A) Normalized generalized binomial factors (solid lines). Distributions get narrower as N increases, which is necessary for the MEP to hold. Dashed lines show the usual binomial factor ( and ). (B) Variance of the normalized generalized binomial factors (solid lines), as a function of sequence length N, for various values ν and . The dashed line is the variance of the usual binomial multiplicity. (C) Probability distributions for the states i from numerical realizations of processes following Eq. 27, with and for various lengths N (solid lines). Distributions follow the theoretical result from Eq. 23. Dashed lines are with . α and β are obtained from fits to the distributions and clearly dependent on N (Inset). They can be used to determine .

Discussion

We have shown that for generalized multinomial processes, where the order of the appearance of events influences the statistics of the outcome (path dependence), it is possible to constructively derive an expression for their multiplicity. We are able to show that a MEP exists for a much wider class of processes and not only for independent multinomial processes. We can explicitly determine the corresponding entropic form from the transition probabilities of a system. We show that the logarithm of the obtained generalized multiplicity is one-to-one related to the concept of Boltzmann entropy. The expressions for the obtained generalized entropies are no longer of Shannon type, , but assume generalized forms that are known from the entropies of superstatistics (21, 22) and that are compatible with the first three Shannon–Khinchin axioms and violate the fourth (6, 7, 14). Further, we find that generalized entropies are of trace form and are based on known generalized logarithms (14, 16, 18, 23). Our findings enable us to start from a given class of correlated stochastic processes and derive their unique entropy that is needed when using the maximum entropy principle. We are able to determine the time-dependent distribution functions of specific processes, either through minimization of the relative entropy or through maximization of the generalized entropy under nonlinear constraints. A previously discovered duality allows us to obtain the same result by maximization of the dual generalized entropy under linear constraints. Systems for which the new technology applies include out-of-equilibrium, path-dependent processes and possibly even aging systems. In an explicit example of a path-dependent random walk we show how the corresponding generalized entropy is derived. We implement a numerical realization of the process to show that the corresponding maximum entropy principle perfectly predicts the correct distribution functions as the system ages in the sense that it becomes more persistent as it evolves. Systems of this kind often never reach equilibrium as .