Gait synchronization in Caenorhabditis elegans

Significance

How independent agents interact to form collective behavior is of interest in diverse disciplines. Larger animals coordinate their motions via their nervous systems. However, little is known regarding the mechanisms by which microscopic animals coordinate their gaits. We observed that, when in a swarm, clusters of Caenorhabditis elegans synchronize their swimming gait. To identify the mechanism responsible for this behavior, we devised controlled experiments to examine the interactions between pairs of animals. Our studies indicate that steric hindrance is the dominant factor responsible for gait synchronization in C. elegans, and that hydrodynamic interactions and mechanosensation do not play a significant role. We infer that a similar mechanism may apply to other microscopic swimming organisms and self-propelled particles.

Abstract

Collective motion is observed in swarms of swimmers of various sizes, ranging from self-propelled nanoparticles to fish. The mechanisms that govern interactions among individuals are debated, and vary from one species to another. Although the interactions among relatively large animals, such as fish, are controlled by their nervous systems, the interactions among microorganisms, which lack nervous systems, are controlled through physical and chemical pathways. Little is known, however, regarding the mechanism of collective movements in microscopic organisms with nervous systems. To attempt to remedy this, we studied collective swimming behavior in the nematode Caenorhabditis elegans, a microorganism with a compact nervous system. We evaluated the contributions of hydrodynamic forces, contact forces, and mechanosensory input to the interactions among individuals. We devised an experiment to examine pair interactions as a function of the distance between the animals and observed that gait synchronization occurred only when the animals were in close proximity, independent of genes required for mechanosensation. Our measurements and simulations indicate that steric hindrance is the dominant factor responsible for motion synchronization in C. elegans, and that hydrodynamic interactions and genotype do not play a significant role. We infer that a similar mechanism may apply to other microscopic swimming organisms and self-propelled particles.

Collective motion of multiple individuals has been observed in swarms of large and small organisms, in single cells, and in suspensions of self-propelling objects (1). The mechanisms of interactions among individuals leading to collective motion vary among organisms. Large organisms such as fish likely use their nervous system to coordinate their motions (2). At the micrometer scale, swarms of organisms lacking nervous systems exhibit gait synchronization (3) and pattern formation (4–17). Long-range hydrodynamic interactions (18–30) and short-range nonhydrodynamic interactions (17, 31, 32) have been implicated in enabling coordination among swimmers. However, the relative importance of hydrodynamic interactions and nonhydrodynamic interactions remains an open question (32–34).

In comparison with swimming fish at one extreme and single-celled organisms on the other, both of which have been studied extensively, little is known about the interactions among animals, such as the nematode Caenorhabditis elegans, that are too small for inertia to play a significant role (that is, they are low Reynolds number swimmers; ref. 35), large enough for Brownian motion to be irrelevant, and possess a nervous system. Although the ecological niches of C. elegans are not yet precisely known (36), in the laboratory C. elegans often exist in dense populations with ample opportunity for interactions among animals. The fact that most wild-type C. elegans feed in swarms (37) suggests that interactions among individuals are common in nature. However, there are only a very few studies of interaction among individual nematodes (38, 39).

An adult C. elegans is ∼1 mm long and 80 µm in diameter and propels itself at speeds of hundreds of micrometers per second in water by producing a propagating sinusoidal wave (35, 40). The simple posture and nervous system as well as the ease of genetic and physical manipulation make the C. elegans an attractive model organism for studying, among other things, the collective behavior of swimmers and how genotype affects phenotype.

When it is suspended in a low-viscosity medium such as water, C. elegans propels itself by undulatory motion. In this respect, the motion of the C. elegans is somewhat reminiscent of that of the flagella of sperms (41). Coordinated motion in the sperm has been intensely studied. There are, however, important distinctions between the C. elegans and sperm. In sperm, flagella dynamics and synchronization are greatly affected by the high compliance of the flagella. In contrast, C. elegans is rigid (40) and, under normal conditions, its swimming gait is insensitive to hydrodynamic stresses. Additionally, in contrast to sperm, C. elegans has a nervous system that can respond dynamically to external stimuli.

In this study, using C. elegans as a model organism, we examine the interactions among individual swimmers. We observed synchronized swimming in C. elegans swarms. The collaborative behavior facilitates efficient motility and prevents jamming. Jamming avoidance and maintenance of mobility are beneficial to the animal and critical for its survival, enabling search for food and efficient migration away from inhospitable environments. We assess whether the coordination requires mechanosensory nervous-system function, and whether it is caused by long- or short-range interactions. To facilitate controlled experiments, we devised a new apparatus and a method to study interactions between pairs of swimmers. We found that neither sensory input nor hydrodynamic interactions play a significant role in the synchronization of swimmers’ gaits in C. elegans. Instead, steric forces are the dominant factor that governs coordination.

Results and Discussion

Synchronization in Swarms of C. elegans.

When imaging a swarm of wild-type C. elegans in a drop, we observed that clusters of swimmers synchronized their gait (Fig. 1A and Movie S1). In contrast, no such cooperation was observed in dilute suspensions. This collaborative behavior prevented jamming and facilitated a more efficient motility when animals were in close proximity.

Fig. 1.

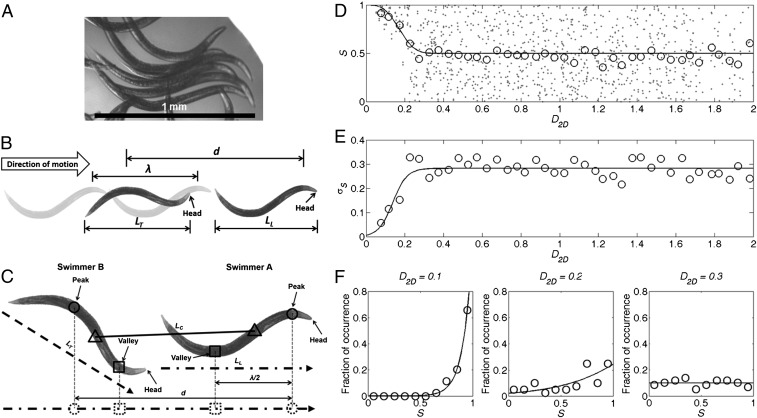
Synchronization in a swarm of animals. (A) When in a swarm, clusters of wild-type C. elegans synchronize their gait. (B) A schematic defining synchronization between collinear swimmers. Both swimmers are depicted in dark shades. The extrapolated wave pattern of the lead swimmer is in light shades. L_T and L_L denote the axial lengths of the trailing and leading animals, respectively; and λ denotes the wavelength of the leading animal and d denotes the horizontal distance between the peaks of the leading and trailing animals. (C) Extension of the definition of synchronization to noncollinear swimmers. The dashed and dash–dotted arrows represent the direction of motion of each swimmer. L_C denotes the distance between midpoints of each swimmer’s peak and valley. (D) The synchronization (S) as a function of the normalized interswimmer distance (D_2D). The dots correspond to data for individual pairs. The open circles correspond to the average values of S. (E) The SD of synchronization (open circles) as a function of D_2D. (F) The probability distribution (circles, n = 3 experiments) of S when D_2D = 0.1 ± 0.05 (Left), 0.2 ± 0.05 (Center), and 0.3 ± 0.05 (Right). The solid lines are fitted curves to guide the eye.

To quantify the interactions among swimmers, we define a synchronization figure of merit. To this end, we consider two swimmers: a leader and a trailer. When the two animals are swimming in the same direction, we say that the two animals are perfectly synchronized when the trailer’s gait is aligned with the extended waveform of the leader’s gait (Fig. 1B). In other words, perfect synchronization implies that the two animals are swimming in phase. To address circumstances when the directions of the two animals’ motions are not the same, we project the instantaneous peaks (circles) and valleys (squares) of both swimmers’ gaits on a line parallel to the leader’s direction of motion (Fig. 1C). We then examine the misalignment between the trailer’s projected peak and the extended waveform of the leader to define the synchronization

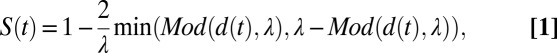where λ is the wavelength of the leader (defined as twice the distance between the projected peak and valley), d is the distance between the projected peaks of the two swimmers, t is time, and Mod is the Modulo (remainder). We use S instead of the phase difference between the two swimmers’ gaits because S can be inferred directly from experimental data. Clearly, 0 ≤ S ≤ 1. S = 1 corresponds to perfect synchronization (0° phase lag), whereas S = 0 corresponds to 180° phase lag. The dimensionless distance D_2D between the pair is defined as the distance between the midpoints of each swimmer’s peak and valley (L_C in Fig. 1C) normalized by the average projected lengths of the swimmers along their directions of motion (L_L and L_T in Fig. 1C). D_2D = 2L_C/(L_L + L_T). In the above, subscripts L and T identify the leader and trailer, respectively.

Fig. 1D depicts the synchronization S as a function of the normalized distance D_2D between pairs of animals (in three different swarms). The dots correspond to data for individual pairs and the hollow circles are the average of S (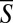) at any interanimal distance D_2D. The mean value 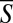was computed using a moving average with an averaging window ΔD_2D = 0.05. Fig. 1E (circles) depicts the SD of S (σ_S) as a function of D_2D. Fig. 1F depicts the probability distribution function (circles) of the synchronization S at interanimal distances D_2D = 0.1 ± 0.05 (Fig. 1F, Left), D_2D = 0.2 ± 0.05 (Fig. 1F, Center), and D_2D = 0.3 ± 0.05 (Fig. 1F, Right). The solid lines represent best-fit curves. When D_2D > 0.3, S is randomly distributed between S = 0 and S = 1 with an average of ∼0.5 and an SD of ∼0.29. This behavior is reminiscent of a uniformly distributed random variable in the domain [0, 1], which has the theoretical mean of 0.5 and the SD of 0.29. When the pairs are sufficiently far apart (D_2D > 0.3), the nematodes’ gaits are uncorrelated. When D_2D decreases from 0.3 to 0, 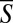increases from 0.5 (uncorrelated) to 1 (perfect synchronization), and the SD σ_S decreases from 0.29 to 0. The experimental data indicates that coordination is exhibited only among proximate swimmers. What, then, are the mechanisms that are responsible for the motion coordination?

Pair Interactions.

The experiment shown in Fig. 1 involves a large population, making it difficult to isolate the dominant factor that controls the interactions among animals. When attempting to understand complex systems, it is convenient to consider pair interactions. To this end, we designed an apparatus to monitor the behavior of pairs of swimmers as a function of the distance between the animals. Our device is comprised of a tapered, microfluidic conduit in which fluid flows from the narrow end to the wide end (Fig. S1). The depth of the conduit is large enough to accommodate uninhibited motion of a single adult animal and small enough to prevent the stacking of multiple adult animals along the conduit’s height. The conduit confines the pair of swimmers, controllably duplicating the confinement imposed by the other animals in the swarm in Fig. 1A. A pair of animals were introduced into the conduit at its wide end and induced to swim upstream by their attraction to the negative pole of a DC electric field, located next to the conduit’s narrow end, a phenomenon termed electrotaxis (42), which is a sensory response. The electric field used to stimulate movement is small and the electrical forces, such as electrophoresis, are insignificant. It does not affect the animals’ swimming gait nor does it harm the animals (43). In later experiments, we realized that once in the conduit, the nematodes retained their original direction of motion and swam upstream even in the absence of an electric field, which allowed us to carry out experiments either in the presence or the absence of the electric fields and establish that the electric field did not significantly affect the animals’ behavior.

As the nematodes progressed upstream in the tapered conduit, the cross-sectional area available to the flow decreased, and the intensity of the adverse flow increased, causing the leading animal to slow down at a faster rate than the trailing one. Thus, the trailing animal could catch up (Movie S2), pass the leader (when having a greater propulsive thrust), or phase lock for a period (10 phase-locked beating cycles are shown in Movie S3). Thus, our device provided a convenient means to examine the motion of two nematodes as a function of the distance between the animals.

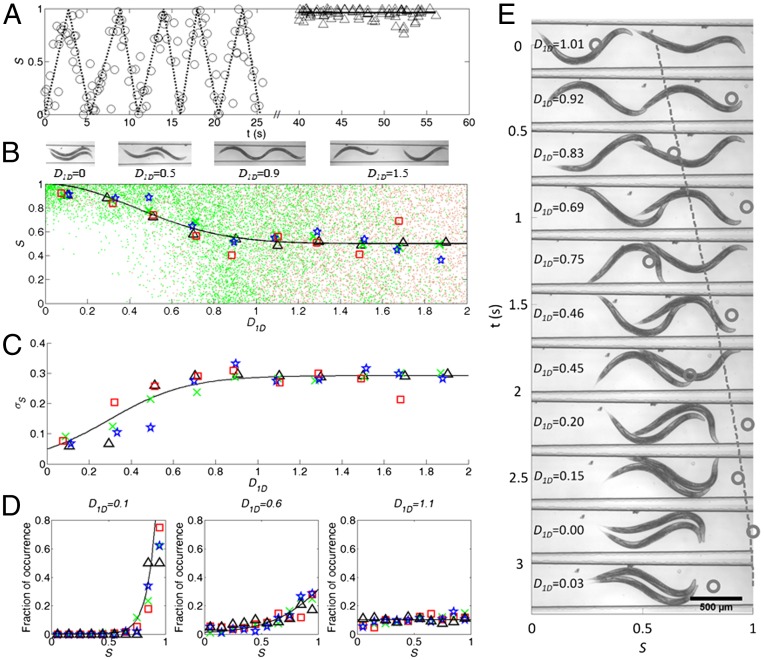
To quantify the interactions between the two swimmers, we use the figure of merit defined in Eq. 1. Fig. 2A is an example of the experimental data obtained in one experiment. The figure depicts S as a function of time as the trailing animal catches up with the leading one. The dimensionless distance between the pair of animals, D_1D, is the axial distance between the midpoints of each swimmer’s head and tail normalized with the average value of L_L and L_T. When the distance between the animals D_1D > 1 (t < 25 s), S fluctuates nearly periodically as a function of time. When D_1D < 1 (t > 40 s), the pair are nearly perfectly in phase (S ∼ 1).

Fig. 2.

Synchronization of pairs of animals. (A)The synchronization S as a function of time as the trailing swimmer catches up with the leading one. When t < 25 s, the distance between the swimmers’ centers of mass exceed one body length. When t > 40 s, the distance between the swimmers’ centers of mass is smaller than one body length. The synchronization S (B) and its SD (C) as functions of the normalized interanimal distance D_1D. The small green and pink dots in B correspond to experimental data (wild-type animals, mec-4 mutants, and mec-3 mutants) and numerical simulations, respectively. The large symbols in B correspond to average values of S. Insets show photographs of animals with different distances between their centers of mass. (D) The probability distribution of S at D_1D = 0.1 ± 0.1 (Left), 0.6 ± 0.1 (Center), and 1.1 ± 0.1 (Right). Green crosses, red squares, blue pentagrams, and black triangles correspond to wild-type N2 (n = 29 pairs), mec-4 mutants (n = 13 pairs), mec-3 mutants (n = 13 pairs), and theoretical (n = 5,000) predictions, respectively. The solid lines are fitted curves to help guide the eye. (E) A time series of frames depicting two C. elegans synchronizing their gaits as the trailer approaches the leader. Witness that, from time to time, the animals make contact, which facilitate synchronization and a better utilization of space. The symbols (open circles) and the dashed line (added to guide the eye) depict the synchronization (horizontal axis) as functions of time (and, indirectly, the distance between the animals). The open circle in each frame corresponds to the level of synchronization of the pair shown in the frame.

The phase difference between the leading and trailing animals’ gaits is

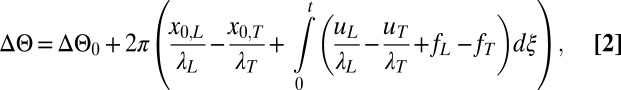where 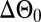is the inherent phase difference, x₀ is the animal’s axial position at time t = 0, u is the animal’s time-dependent axial velocity, λ is the wavelength, and f is the frequency. The synchronization S is closely related to the phase difference.

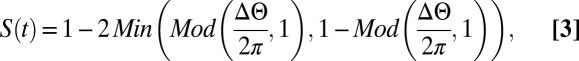when D_1D > 1, S exhibits fluctuations primarily due to variations in the animals’ relative velocity. The differences in two animal’s gaits’ frequencies are relatively small (Fig. S2) and contribute little to the fluctuations in S. The nearly periodic behavior exhibited by S in Fig. 2A (t < 25 s) suggests that when the animals are located sufficiently far apart, their gaits are fixed and unaffected by hydrodynamic interactions. Indeed, due to the relatively high bending rigidity of the C. elegans, one would not expect hydrodynamic interactions to affect the animal’s gait. We will address this issue in more detail later in the paper.

We repeated similar experiments to the ones depicted in Fig. 2A numerous times. Fig. 2B depicts S as a function of D_1D. The (green) dots correspond to individual data points, and the large symbols next to the solid line correspond to the average value of S (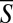) at any D_1D. The mean value 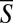was computed using a moving average with an averaging window ΔD_1D = 0.2.

We first experimented with wild-type nematodes (n = 29 pairs). When D_1D > 1, S (green dots) is randomly distributed between S = 0 and S = 1 with an average (green crosses) of ∼0.5. This random distribution results from the arbitrary initial positions of the animals in the experiment. When D_1D < 1 and decreases to 0, S increases to 1. Fig. 2C (symbols) depicts the SD of S as a function of D_1D. Fig. 2D depicts the probability distribution function (green crosses) of S when D_1D = 0.1 ± 0.1 (Fig. 2D, Left), 0.6 ± 0.1 (Fig. 2D, Middle), and 1.1 ± 0.1 (Fig. 2D, Right). The solid lines represent best-fit curves. When D_1D > 1, 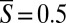, the SD is ∼0.29, and the nematodes’ gaits appear uncorrelated. In other words, when D_1D > 1, the synchronization S (Fig. 2D, Right) behaves like a uniformly distributed random variable in the domain [0, 1], which has the theoretical mean of 0.5 and the SD of 0.29. When 0 < D_1D < 1, the two animals partially overlap (see D_1D = 0.9 and D_1D = 0.5 in Fig. 2B, Insets) and 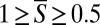. As D_1D decreases, the level of synchronization increases (Fig. 2B) and the SD decreases (Fig. 2C). The peak in the probability distribution function (Fig. 2D, Middle) occurs at S ∼ 0.8 when D_1D = 0.6. When D_1D = 0, the two animals are nearly perfectly in phase (S ∼ 1). The SD is at its smallest value and the peak in the probability distribution function shifts to S ∼ 1 (Fig. 2D, Left). The duration of the synchronized behavior depended on the propulsive thrusts of the animals. When the trailer’s propulsive thrust exceeded that of the leader, it synchronized its gait for a short period while passing the leader (Movie S2). The passer then assumed an equilibrium position upstream of the former leader. When the propulsive thrusts of the two animals were similar, they swam in synch at the same equilibrium position for many periods. For example, Movie S3 features two animals swimming in phase for 10 swimming periods. The experimental data suggests that distant wild-type swimmers (D_1D > 1) do not significantly interact and their gaits are unsynchronized. In contrast, proximate swimmers (D_1D < 1) adjust their gaits and the synchronization increases as the distance between the swimmers decreases. The level of synchronization observed in our apparatus is similar to the one observed in the swarm of swimmers in the drop (Fig. 1), suggesting that the apparatus does not significantly alter the nature of the interactions among animals. The confinement imposed by the conduit was critical, however, to maintain the pair of swimmers in sufficient proximity when passing to allow them to interact. Indeed, two swimmers could co-occupy the same conduit’s cross-section without jamming only when they synchronized their gaits.

Does Mechanosensation Play a Role in Synchronization?

The role of mechanosensation in gait adjustment has been a subject of some debate. Park et al. (44) reported that mechanosensitive nematodes can adjust their gait to enhance their speed when interacting with pillars arranged in arrays with certain pitches, and mec-4 and mec-10 mutants, which are defective in mechanosensation, lacked this capability. Interestingly, Majmudar et al. (45) carried out numerical simulations under conditions similar to Park et al.’s experiments and produced lifelike, genotype-independent, locomotory dynamics similar to that exhibited by the touch-sensitive nematodes in Park et al.’s (44) experiments. Therefore, the role of mechanosensation in C. elegans’ interaction with the patterned medium remains debated. Because, in our experiments, synchronization only takes place when the animals are in close proximity, it is natural to wonder whether this behavior depends on mechanosensation.

To explore this issue, we experimented with touch-insensitive mutants lacking mec-3 (n = 13 pairs) or mec-4 (n = 13 pairs) gene function. The mec-4 null mutants are insensitive to weak mechanical stimuli to the body (46), whereas mec-3 null mutants are insensitive to both weak and harsh mechanical stimuli to the body (47). Both genes are required for the function of the six mechanoreceptor neurons (MRNs) that sense gentle touch along the animal’s body wall (48). The insensitivities of mec-3 and mec-4 null mutants to mechanical probing were verified by lack of backing response to stimulation of the anterior body with a strand of hair. In contrast, the wild-type animals recoiled when similarly probed.

If MRN function were required for synchronization, we should observe reduced synchronization or jamming in mec-3 and mec-4 null mutants. The data for mec-3 and mec-4 null mutants are depicted with cyan pentagrams and red squares, respectively, in Fig. 2 B–D, and behave similarly to the data of the touch-sensitive wild-type animals (green crosses). Therefore, we conclude that defective mechanosensation does not impair synchronization and that sensitivity to touch is not required for synchronization. Although we cannot fully exclude involvement of other sensory mechanisms (outside of the MRNs), our data suggest that the MRNs do not play a role in the synchronization. Our experiments indicate that synchronization takes place only when animals are in close proximity, is genotype-independent, and is not the result of deliberate action. So what causes synchronization?

How Do the Worms Adjust their Gait to Synchronize their Motions?

In colloid systems, proximate particles interact through thermal fluctuations (entropic forces). Given the relatively large size of the C. elegans, thermal fluctuations are not likely to play a significant role. To gain insights into the mechanism that allows the two nematodes to adjust their relative positions so as to optimize their use of space, we analyzed individual video frames when 0 < D_1D < 1. An example of such a time series is shown in Fig. 2E. The worms’ undulatory motion enables them to sample the environment transverse to their direction of motion. As a result, as D_1D decreases below 1, the two animals undergo occasional collisions. These collisions shift the two animals’ locations, resulting in synchronization. This mechanism of synchronization does not require alterations in the animals’ gait, but, instead, adjusts the relative positions of the animals’ centers of masses. It appears, therefore, that in our system nonthermal, muscle-induced forces are the main cause for synchronization. The synchronization process in C. elegans appears to be similar to pattern formation in rod-shaped colloidal systems with the important distinction that in our active suspension, the C. elegans’ muscle-induced periodic fluctuations replace the random thermal fluctuations of the colloids in the colloidal rod suspension.

Is Synchronization Caused by Steric Hindrance?

To examine the role of volume exclusion in our experiments, we borrowed ideas from statistical thermodynamics (a hard sphere model; ref. 49) and carried out simple, 2D Monte Carlo computations to explore objects’ utilization of space in the absence of any hydrodynamic interactions. An agreement between model predictions and the statistics recorded in our experiments would lend support to the hypothesis that short-range repulsion forces are responsible for the synchronization in our system. We generated two virtual (hard) objects shaped like swimming worms (Fig. S3) with a random phase difference between them selected from a uniform distribution in the interval [−π, π]. The virtual swimmers were placed at random axial positions along a conduit of similar dimensions to the one used in our experiments. One virtual swimmer was positioned so that the peak of its gait touched one of the conduit’s walls, and the other was placed so that the valley of its gait touched the other conduit’s walls, which is consistent with the observed positions of the worms in the experiments and which maximizes the utilization of space. We computed the synchronization S as a function of the distance (D_1D) between the two objects’ body centers for all cases in which the simulated swimmers did not overlap and excluded from consideration all occurrences when the objects overlapped, which is consistent with our experiment where the conduit is sufficiently shallow to preclude animals’ stacking in the vertical direction. The computed, individual S values (small pink dots in Fig. 2B), the average of S (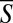, large black triangles in Fig. 2B), and the SD (large black triangles in Fig. 2C) were depicted as functions of D_1D (n = 5,000). The corresponding probability distributions of S at various values of D_1D were depicted in Fig. 2D (large black triangles). The similarity between the computer-simulation results and the experimental data are striking. Because the simulations did not include hydrodynamics or deliberate decisions, they lend credence to the notion that the synchronization occurs primarily due to entropiclike, short-range repulsive forces (volume exclusion).

What Is the Role of Hydrodynamic Forces?

Generally, swimmers can coordinate their motion either by retaining fixed gaits and shifting the relative positions of their centers of mass and/or by adjusting their gaits. The gait adjustment could be the result of hydrodynamic forces or neuronal action.

Can hydrodynamic forces affect the C. elegans’ gait? Although the C. elegans’ undulatory motion resembles that of sperm, there is a critical distinction. The sperms’ flagella are highly compliant while the C. elegans are not. We quantify the swimmer’s rigidity with the “compliance number” (50) 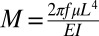that represents the ratio of hydrodynamic stresses and elastic (bending) stresses. In the above, EI, E, and I are the swimmer’s bending rigidity, modulus of elasticity, and moment of inertia for bending, respectively. The μ is the suspending medium’s viscosity. See Supporting Information for the characteristic properties of the flagella and the C. elegans. For the sperm and the C. elegans in water, M ∼ 314 and M ∼ 0.12, respectively. In other words, the sperm is highly compliant, and the C. elegans is 2,600-fold more rigid. When in water, the sperm’s undulatory motion is strongly affected by hydrodynamic forces, and the C. elegans’ gait is negligibly impacted by viscous stresses. This observation is consistent with the experimental data (3), which shows that, in contrast to sperm (51), the C. elegans’ bending frequency and amplitude are independent of the suspending liquid’s viscosity over a broad range of viscosities (40). Our own experiments also indicate that the C. elegans’ gait amplitude and frequency are nearly independent of the position of the animal along the tapered conduit, as long as the conduit’s width exceeds the animal’s swimming amplitude. Moreover, the gait amplitude and frequency are similar when D_1D < 1 and D_1D > 1 (Fig. S4). In other words, even when the animals interact, their gaits remain largely unaltered. The C. elegans’ motion alters the flow field of, but is not affected by, the surrounding liquid.

Can hydrodynamic forces shift the relative positions of C. elegans to facilitate gait synchronization? Although theoretical (19–23) studies of 2D waving sheets demonstrate that the sheets synchronize by hydrodynamic interactions, hydrodynamic forces in two dimensions are much greater than in three dimensions. To further verify that hydrodynamics did not play a significant role in synchronization, we carried out a controlled experiment in which we monitored the motions of an active (live) nematode and a paralyzed nematode suspended in a drop, far from the drop’s boundaries. We found that the velocities of the pair were nearly independent of the distance between the animals unless the two animals were in contact (Fig. S5, n = 31 pairs). See Supporting Information for further details. This suggests that noncontact forces are negligible in our system. Although similar data has not been reported explicitly for other microorganisms, examination of available videos (15, 52) suggests that nonmotile individuals are affected only by direct contact, which suggests negligible hydrodynamic interactions in those systems as well.

Are our Conclusions Applicable to Other Motile (Active) Suspensions?

It has been reported that collective behaviors are apparent in low Reynolds number motile systems only when the group member concentrations exceed certain thresholds C_c (4, 11, 53, 54) (number of members per unit volume or unit area). We define the average distance between individual members at the critical concentration as H = (1/C_c)^1/n, where n = 2 for a planar system and n = 3 for a 3D system; the largest dimension of the object is L; and the “steric number” J = L/H. When J > 1, one would expect significant short-range, steric interactions. Indeed, in many of the circumstances in which collective behavior was observed, ranging from gliding assays of microtubules and actin filaments to chemotaxing bacteria and including our own experiments, J > 1 (Table S1). This suggests that short-range steric effects or avoidance of collision may be one of the key rules that govern the collective behavior in these systems as in the case of the C. elegans.

In summary, we report that when in a swarm, clusters of C. elegans exhibit synchronized behavior and that the level of synchronization depends sensitively on the distance between pairs of animals. We devised an experiment that allowed us to closely examine pair interactions to determine whether synchronization results from deliberate sensory action, long-range hydrodynamic interactions, or short-range contact forces. Variants of the experimental apparatus can be used, among other things, to localize animals without contact restraints for prolonged observations, to study motility, to sort animals according to propulsive thrust, and to estimate their propulsive power.

Our experiments with swarms of swimmers in a drop and with pairs of swimmers in our apparatus show that C. elegans synchronize their swimming gait only when the animals are in close proximity. Gait synchronization allows optimal utilization of available space, prevents jamming, and enables motility, which is critical for the animals’ ability to forage for food and to move away from inhospitable environments. Synchronization appears to be caused primarily by short-range, steric interactions, and does not require mechanosensation. Our experimental observations are in striking agreement with the predictions of a Monte Carlo, volume exclusion (hard-sphere–like) model, supporting the notion that no additional forces, such as hydrodynamic ones, are involved. Indeed, control experiments indicate that hydrodynamic interactions do not play a significant role in the interactions between pairs of animals.

The animals’ transverse, undulatory motion plays a similar role to that of thermal fluctuations in colloidal systems by enabling pairs of animals to interact through collisions. The same mechanism responsible for pair synchronization may also assist the C. elegans in conforming with and taking advantage of obstacles, such as pillars, while navigating their complex native environment.

Materials and Methods

Device Fabrication and Experimental Procedure.

In brief, our experimental apparatus (Fig. S1) was formed with polydimethylsiloxane using standard soft photolithography, and consisted of a 98 ± 4 μm tall conduit with side walls tapered to 0.56° with respect to the conduit’s axis. See Supporting Information for additional details. The conduit was capped by attaching it to a glass slide and was filled with M9 buffer (3 g/L KH₂PO₄, 6 g/L Na₂HPO₄, 5 g/L NaCl, and 1 µM MgSO₄). The narrow end of the tapered conduit connected to a syringe pump and the wide end to an open well. The conduit was just tall enough to accommodate uninhibited motion of a C. elegans adult (body diameter ∼80 μm). An electrode at the conduit’s wide end and another (negative pole) at the narrow end facilitated the application of an electric field of intensity ∼4 V/cm along the conduit’s axis.

A few nematodes were inserted in the well next to the wide end. The pump then induced fluid flow from the wide end to the narrow end until two nematodes entered the tapered conduit. Next, the direction of pumping was reversed to induce fluid motion from the narrow end to the wide end. Due to electrotaxis (42, 43), the nematodes swam upstream, against the flow (Movie S2). As the nematodes progressed upstream in the tapered conduit, the intensity of the adverse flow increased, causing the leading animal to slow down at a faster rate than the trailing one, and allowing the trailing animal to catch up and, occasionally, pass the leader. Eventually, the animals arrived at equilibrium positions, at which their propulsive thrusts balanced the adverse flow resistance.

An upright microscope and a digital camera were used to record the animals’ motion. At the conclusion of each recording, the animals were flushed out from the apparatus, and a fresh group of worms were inserted. The flushing step helped remove any bubbles that may have accumulated during the course of the experiment. Animal cultivation and image processing are described in the Supporting Information.