How Accurate Are Transition States from Simulations of Enzymatic Reactions?

Abstract

The rate expression of traditional transition state theory (TST) assumes no recrossing of the transition state (TS) and thermal quasi-equilibrium between the ground state and the TS. Currently, it is not well understood to what extent these assumptions influence the nature of the activated complex obtained in traditional TST-based simulations of processes in the condensed phase in general and in enzymes in particular. Here we scrutinize these assumptions by characterizing the TSs for hydride transfer catalyzed by the enzyme Escherichia coli dihydrofolate reductase obtained using various simulation approaches. Specifically, we compare the TSs obtained with common TST-based methods and a dynamics-based method. Using a recently developed accurate hybrid quantum mechanics/molecular mechanics potential, we find that the TST-based and dynamics-based methods give considerably different TS ensembles. This discrepancy, which could be due equilibrium solvation effects and the nature of the reaction coordinate employed and its motion, raises major questions about how to interpret the TSs determined by common simulation methods. We conclude that further investigation is needed to characterize the impact of various TST assumptions on the TS phase-space ensemble and on the reaction kinetics.

Introduction

Transition state theory (TST) describes the rates of chemical reactions in terms of the free energy barrier for the process.¹⁻⁴ Although the theory was developed mainly to describe reaction dynamics in the gas phase, it has been applied to activated processes in condensed-phase environments using one of the following forms:⁵⁻⁷

1

In eq 1, ζ is the reaction coordinate, and the dynamical factor ⟨|ζ̇|⟩_ζ^⧧ corresponds to the equilibrium ensemble average of the absolute crossing velocity, ζ̇ ≡ dζ/dt, evaluated at the transition state (TS), where ζ = ζ^⧧. The reaction-coordinate velocity is typically described as the velocity of a free particle: ⟨|ζ̇|⟩_ζ^⧧ = (2/πβM_eff)^1/2, where β = (k_BT)⁻¹, in which k_B is Boltzmann’s constant and T is the temperature, and M_eff specifies the effective (or reduced) mass for motion along the reaction coordinate. Q^⧧ is the reduced classical phase-space density at the dividing hypersurface along the reaction coordinate, and Q_RS is the classical partition function for the reactant state (RS). The ratio Q^⧧/Q_RS is equivalent to the ratio of the equilibrium populations of the system in the TS and the RS, ρ(ζ^⧧)/∫_ζ^RS ρ(ζ) dζ, and represents the probability density that the system will reach ζ^⧧. Specifically, the integration in the denominator of the last term is over values of the reaction coordinate corresponding to the RS. It is this probability ratio, or activation factor, that dominates the rate constant and, most importantly, its temperature dependence. The potential of mean force (PMF), W(ζ), is the classical-mechanical free energy profile along the reaction coordinate averaged over all other (orthogonal) degrees of freedom.

Essential to this theory is the activated complex located at the dividing surface between reactants and products (i.e., the TS ensemble). This activated complex is presumed to be in quasi-equilibrium with the reactant molecules (i.e., the complexes’ concentration is unaffected by the rate of transformation to products or the products concentration) and is calculated by equilibrium theory. In most flavors of traditional TST, a distinct reaction coordinate is separated out from all other degrees of freedom, and the motion of the system along the reaction coordinate leading to the TS is assumed to be separable from these other degrees of freedom at ζ^⧧.^4,8 If the motion along the reaction coordinate is slow relative to the response of the remaining degrees of freedom, equilibrium solvation is assumed. Moreover, TST treats barrier crossing at the TS as a free translational motion, and nuclear quantum effects (NQEs) such as tunneling are ignored. These inherent limitations of traditional TST are well-known and have been reviewed extensively.^9,10

The missing ingredients in TST may be added as correction terms in the generalized version of TST, thus in principle providing the true rate constant. Indeed, prefactors accounting for TS recrossing and NQEs have been added with great success.¹¹⁻¹³ However, the basic assumptions hidden within the TST framework, such as equilibrium solvation and free-particle behavior at the TS, might directly influence the nature of the activated complex. It is not clear that correction terms relying on the TST activated complex are sufficient to obtain the correct rate constant.¹⁴ Moreover, finding an optimal reaction coordinate is extremely challenging when a large number of degrees of freedom is involved in the reaction, such as reactions in water and in enzymes.⁸ Indeed, the choice of reaction coordinate can greatly influence the computed rate constant within TST. Interestingly, a recent work by Peters and co-workers suggested that it might be impossible to remove the recrossing phenomenon even in a fairly simple system such as ion dissociation in water.¹⁵

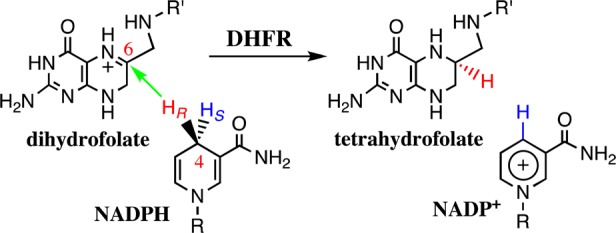
The above-mentioned question regarding the nature of the activated complex obtained from TST-based approaches becomes particularly acute in complex systems such as enzymes.¹⁶ Although our current understanding of enzyme catalysis relies on decades of groundbreaking work within the TST framework,^11,17,18 this understanding assumes in most cases that the environment influences the reaction by means of equilibrium solvation. Moreover, the role of dynamics in condensed-phase reactions is still under intense debate.^13,19−24 In this paper, we scrutinize the nature of the activated complex obtained from standard simulation methods employed in conjunction with TST. In particular, we use umbrella sampling (US)²⁵ and the string method (SM)^26,27 with various reaction coordinates defined on the basis of the reacting species. The US and SM simulations yield minimum-free-energy paths along a set of reaction coordinates in which the environment provides equilibrium solvation (i.e., the effect of the degrees of freedom orthogonal to the reaction coordinate is treated as a Boltzmann-averaged influence on the reaction progress). Typically, US and SM employ some form of biasing potentials to allow barrier crossings. These standard methods in computational enzymology are compared with simulations using transition-path sampling (TPS), which yields a collection of reactive dynamics trajectories.²⁸⁻³⁰ Using TPS, one considers only trajectories connecting the reactant and product basins. As a result of the bias introduced with this requirement, configurations on the transition pathways are not distributed according to the equilibrium distribution of the system. Therefore, configurations with low weight in the equilibrium ensemble might have a much larger weight in the transition-path ensemble if they belong to regions that must be traversed to cross from reactants to products. However, the dynamics of the barrier crossings are unperturbed and independent of the definition of the reaction coordinate. Thus, the present work provides an important benchmark comparing condensed-phase reaction simulations using TST-like methods (i.e., US and SM) and dynamics-based methods (i.e., TPS). The model system for the current study is the enzyme dihydrofolate reductase from Escherichia coli (ecDHFR), which serves as an important test system in enzymology. The hydride transfer in ecDHFR (Scheme 1) has been studied by numerous researchers, both experimentally³¹⁻³⁸ and computationally.^{12,20,22,39−53}

Scheme 1. Hydride Transfer Reaction Catalyzed by DHFR (R = Adenine Dinucleotide 2′-Phosphate; R′ = p-Aminobenzoyl Glutamate).

The current results show that TS ensembles obtained from classical simulations for ecDHFR using standard US or SM techniques with various reaction coordinates are substantially different from those obtained using TPS. In particular, the observed donor–acceptor distances (DADs) at the TS are considerably longer for TPS than US/SM. The present discrepancy between the two sets of approaches warrants further studies to understand the extent to which reaction coordinate dynamics, nonequilibrium solvation, and biasing potentials affect the computed rate constants and kinetic isotope effects.

Methods

Model of the Enzyme–Substrate–Coenzyme Complex

The initial coordinates used to build the model for the present study were based on the crystal structure of a complex of ecDHFR with folate, NADP⁺, and water molecules (PDB ID code 1RX2(54)), where the Met20 loop is in the closed conformation. The original ligands in this structure were exchanged with N5-protonated 7,8-dihydrofolate (henceforth H₃folate⁺) and NADPH to form a model of the reactive Michaelis complex. Of the 159 amino acid residues, all of the ionizable residues were treated as bearing protonation states corresponding to neutral pH.³¹⁻³³ In particular, Asp27 was modeled as deprotonated,⁵⁵⁻⁵⁷ and the specific protonation states of the histidine residues were determined on the basis of hydrogen-bonding interactions. This model was soaked in a pre-equilibrated 65 Å × 65 Å × 65 Å cubic water box and thereafter neutralized by adding 14 sodium ions to allow evaluation of electrostatic interactions using the Ewald summation scheme. The final model was composed of 27 986 atoms. Further details have been provided elsewhere.⁴⁸

Potential Energy Surface

The potential energy surface (PES) in the current study was described by a hybrid quantum mechanics/molecular mechanics (QM/MM) Hamiltonian.⁵⁸⁻⁶⁰ The QM region consisted of 69 atoms, including portions of the substrate and coenzyme in proximity to the reaction center along with two link atoms.⁴⁸ This part was described by a modified AM1 semiempirical Hamiltonian⁶¹ in which the specific reaction parameters (SRPs) were optimized to treat model reactions involving various derivatives of nicotinamide and pterin compounds (denoted AM1-SRP).⁴⁸ The MM part contained the protein, the remaining substrate and coenzyme atoms not described by QM, waters, and ions. The MM atoms were treated using the CHARMM36 force field⁶²⁻⁶⁵ with grid-based energy correction maps (CMAP)⁶⁶ for peptide dihedral angles, and water molecules were represented by the three-point-charge TIP3P model.⁶⁷ QM/MM interactions were treated by electrostatic embedding, wherein the MM partial atomic charges were included in the one-electron Hamiltonian. The QM/MM interaction energies between the reacting fragments (QM) and the protein (MM) were fine-tuned by modifying the van der Waals parameters of the QM hydrogen atoms.⁶⁸ This combined potential energy was shown to yield accuracy comparable to that of density functional theory (DFT), giving accurate results for the hydride transfer reaction in ecDHFR.⁴⁸ All of the simulations employed the CHARMM program.^69,70

Molecular Dynamics Simulations

Periodic boundary conditions were applied, and the Ewald method was employed for reciprocal-space summations between MM sites as well as for the QM/MM interactions (64 × 64 × 64 FFT grid, κ = 0.340 Å^–1).⁷¹ A 13.0 Å group-based cutoff was applied for van der Waals and electrostatic interactions. All atoms were gradually relaxed at the MM level of theory to remove close contacts in the initial protein–ligand–solvent model. The isothermal–isobaric (NPT) ensemble was employed at 298 K and 1 atm using the extended pressure/temperature (CPT) algorithm^72,73 with the Hoover thermostat.⁷⁴ Newton’s equations of motion were integrated with a time step of 1 fs,⁷⁵ and the SHAKE algorithm⁷⁶ was applied to constrain all MM bonds involving hydrogen atoms. The system was heated in a stepwise fashion from 48 K to 298 K over 25 ps and thereafter equilibrated at the target temperature (298 K) over the course of 1 ns at the MM level of theory, with a further 200 ps of equilibration using the QM(AM1-SRP)/MM potential. Further details of the molecular dynamics (MD) simulations are available in ref (48).

Umbrella Sampling

The classical-mechanical PMF was determined using the US technique in order to sample the high-energy regions of the PES.²⁵ The reaction coordinate (ζ) was defined geometrically as the difference between the lengths of the breaking (C4N_NADPH–H4N) and forming (H4N–C6_H3folate⁺) bonds (henceforth denoted as 1D_asym). A total of 17 discrete regions along the reaction coordinate (“windows”) were defined with uniform spacing of 0.25 Å. Each simulation was performed with the addition of a biasing potential (roughly the negative of the computed PMF) and a harmonic restraint centered at each window. Further details may be found in our previous work.⁴⁷

String Method in Collective Variables (SMCV)

The SM simulations were carried out using the implementation by Ovchinnikov et al.⁷⁷ in CHARMM. Two types of collective variables (CVs) were defined. The first one used two distances (the forming and breaking bond distances), and the second one used three distances (the forming and breaking bond distances and the DAD). For each set of CVs, the entire path (called the string) connecting the reactant basin to the transition state and to the product basin was represented by 48 discretized images, with one MD replica assigned to each image. For example, image 0 represented the reactant-state MD replica and image 47 the product-state MD replica. The SMCV simulations were carried out in two steps. First, starting from an initial path generated by the US simulation, an iterative path optimization was carried out for 200 ps. Each iteration was composed of a short (0.5 ps) MD simulation, during which the force on each CV was evaluated, and an update of the CVs. The MD simulation was carried out with a harmonic restraining potential applied to each CV with a force constant of 250 kcal mol^–1 Å^–2. The CV update was carried out by evolving the path in the direction of the negative gradient of the PMF and then reparametrizing the CVs to enforce approximately equal arc lengths between neighboring images. Then the final PMF was evaluated over a 200 ps MD simulation without updating the CVs. During the final PMF simulation, the coordinates were saved every 1 ps for analysis of the geometries. The error of the final PMF values was computed by block-averaging (50 ps) of the entire 200 ps results (Figure S1 in the Supporting Information).

Transition-Path Sampling

The TPS simulations followed the implementation by the group of Schwartz and co-workers.^30,78 A microcanonical ensemble of reactive trajectories was generated employing the TPS method. The initial step in the TPS algorithm is to define the reactant and product basins. Herein we defined the reactant basin as H₃folate⁺ + NADPH and the product basin as H₄folate + NADP⁺ (Scheme 1). The reactive bond lengths were employed as order parameters for each basin, and a bond was considered formed if the distance between the donor or acceptor carbon and the transferring hydride was ≤1.5 Å. An order parameter of ≤1.3 Å was also tested and had no qualitative impact. Initially, a single reactive trajectory was generated using a biasing potential with a gentle harmonic restraint centered at the TS, which was obtained from US simulations.^47,48 This resulted in a 500 fs reactive trajectory connecting the reactant and product basins. Subsequently, a random point along this trajectory was chosen as a seed point for a new trajectory. The momenta of all of the atoms in the system were perturbed by a small amount to generate a new set of velocities. The perturbations were chosen from a zero-mean Gaussian distribution multiplied by a scaling factor in the range 0.10–0.25. The perturbation was then rescaled to ensure that the total energy was conserved and that the system did not acquire net linear or angular momenta. The random seed point with the new momenta was then propagated forward and backward in time for 250 fs, yielding a 500 fs trajectory. If the new trajectory connected the reactant and product basins, it was selected as a new reactive trajectory. If the trajectory was not reactive, it was rejected and a new point along the previous reactive trajectory was chosen. In this way, new trajectories were generated to form an ensemble of reactive trajectories. We simulated eight separate TPS runs until each yielded 400 reactive trajectories, giving a total of 3200 reactive trajectories.

Following the generation of the reactive trajectories, we then turned to locating the TS along each trajectory using committor analysis. The dividing surface was defined as a point in phase space with equal probabilities of ending in the reactant basin and the product basin. For each point along the reactive trajectory, a set of activated dynamics simulations with random initial velocities chosen from a Maxwell–Boltzmann distribution were initiated, and these trajectories were followed as they settled into the reactant or product basins. The numbers of trajectories settling in the reactant basin (N_R) and the product basin (N_P) were then collected. In practice, we performed a bracketing search in the vicinity of the minimum DAD for each trajectory and initiated 30 activated dynamics runs. Points along the trajectories with |N_R – N_P| ≤ 4 were accepted as part of the TS ensemble.

The time step in all of the TPS simulations was 0.5 fs.

Open-Chain Path Integral Simulations

To determine the momentum distribution⁷⁹ of the transferring hydride atom at the dividing surface, we employed the quantum–classical open-chain path integral (QCOPI) method.⁴⁶ The TSs were defined on the basis of the PMF in the case of the US simulations and the committor analysis in the case of the TPS trajectories. The open paths were represented by 33 beads, and the simulations were performed with isotropic sampling. Approximately 10⁴ classical configurations and 100–500 Monte Carlo staging steps were employed in computing the momentum distribution for the TS ensembles.

Results

A representative TPS reactive trajectory is presented in Figure 1. The reactive event is followed by tracing the distances between the transferring hydride and the donor and acceptor atoms as well as by monitoring the DAD. As the reaction occurs, the C4N–H4N distance increases while the C6–H4N distance is reduced. Toward the TS the reactive C–H vibration develops large amplitudes, similar to those of the product C–H shortly after the reaction. This is indicative of thermally hot vibrations, which lie at the edge of the Maxwell–Boltzmann kinetic energy distribution and only dissipate after hundreds of femtoseconds. Concomitant with these changes, a dip in the DAD curve is observed, which is typical for H^–/H⁺/H· transfer reactions (also see the comparison of RS and TS in Table 1). Each chemical event is rapid and occurs within the time frame of a single donor–acceptor symmetric vibration (i.e. on the order of a few hundred fs). This time is considerably shorter than the total simulation time of individual trajectories. It is therefore unlikely that the current TPS simulations are biased toward short transitions. The very fast hydride transfer is facilitated by favorable reactive 6N-dimensional phase-space states (3N for the configuration and 3N for the corresponding momentum, i.e., dynamics). During such fast chemical events it is unlikely that the enzyme environment has sufficient time to fully relax, and quasi-equilibrium is not obeyed.

Figure 1.

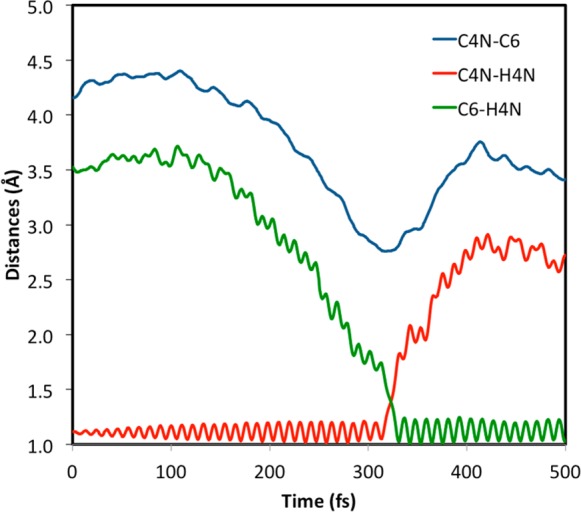
Illustrative geometric features from a reactive event during a transition-path sampling trajectory.

Table 1. Comparative Analysis of Geometric Parameters Obtained with Umbrella Sampling (US), String Method (SM), and Transition-Path Sampling (TPS) Simulations.

	TPS		US 1Dasyma		SM 2D
	RS	TS	RS	TS	RS	TS
C4N–H4N (Å)	1.11 ± 0.05	1.37 ± 0.05	1.12 ± 0.03	1.30 ± 0.03	1.11 ± 0.03	1.35 ± 0.03
C6–H4N (Å)	3.15 ± 0.52	1.41 ± 0.04	2.57 ± 0.17	1.40 ± 0.03	2.76 ± 0.05	1.38 ± 0.03
C4N–C6 (Å)	4.01 ± 0.39	2.75 ± 0.06	3.60 ± 0.18	2.64 ± 0.06	3.79 ± 0.09	2.65 ± 0.06
rehybridization (Å)	–1.13 ± 0.18	–0.09 ± 0.12	–1.14 ± 0.15	–0.10 ± 0.20	–1.12 ± 0.16	–0.40 ± 0.25
C4N–H4N–C6 (deg)	138.1 ± 17.1	164.2 ± 6.4	155.4 ± 11.7	159.8 ± 7.8	156.2 ± 11.4	154.5 ± 6.9
N5–S(Met20) (Å)	3.98 ± 0.16	4.19 ± 0.20	3.96 ± 0.35	3.88 ± 0.60	3.76 ± 0.35	3.65 ± 0.26
N7N–S(Met20) (Å)	4.58 ± 0.20	4.31 ± 0.16	3.79 ± 0.27	4.00 ± 0.58	5.23 ± 0.54	3.87 ± 0.30
N7N–O(Ala7) (Å)	2.95 ± 0.09	2.87 ± 0.09	2.84 ± 0.11	2.97 ± 0.21	2.95 ± 0.14	2.96 ± 0.16
N7N–O(Ile14) (Å)	2.90 ± 0.09	2.88 ± 0.04	3.05 ± 0.20	3.09 ± 0.21	4.40 ± 0.58	3.18 ± 0.24
O7N−N(Ala7) (Å)	3.05 ± 0.10	2.95 ± 0.06	3.09 ± 0.20	3.03 ± 0.20	3.16 ± 0.21	2.97 ± 0.14
N7N–C7N–C3N–C2N (deg)	14.7 ± 9.6	6.1 ± 3.1	13.1 ± 9.7	11.6 ± 9.1	14.0 ± 11.5	10.8 ± 8.6
O7N–C7N–C3N–C2N (deg)	160.8 ± 30.1	173.9 ± 5.2	167.1 ± 9.6	167.9 ± 9.2	167.3 ± 9.9	168.1 ± 9.2

^aFrom ref (47).

To quantify the convergence of the TPS simulations, we used the minimum DAD during the reactive event. Employing this metric, we followed eight independent trajectories as they evolved in trajectory space. The results are displayed in Figure 2. As is readily clear from the figure, the trajectory search converged after ca. 300 trajectories for the combined ensemble of all trajectories. This suggests that considerable trajectory searches are required until enzyme states that are optimal for hydride transfer are found. The final 50 trajectories of each of the eight independent TPS runs were employed in the TS analysis.

Figure 2.

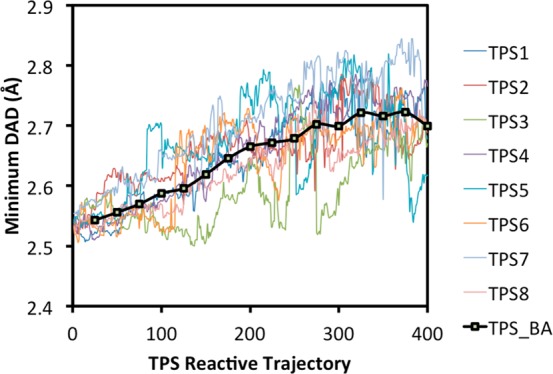
Minimum donor–acceptor distances (DADs) from eight separate TPS reactive trajectory series. Each of the eight trajectory series had 400 reactive trajectories. The block-averaged (BA) minimum DADs are shown in black.

In Table 1 we have collected the average values of key geometric parameters for the RS and TS obtained from the TPS simulations. These are compared with values obtained from US and SM simulations following previously described approaches.⁴⁷ Further details of the SM results are available in Figure S1 in the Supporting Information. The US results are comparable to those of other researchers.^24,51 Analysis of the geometrical parameters of the TS ensembles revealed significant differences between the TPS simulations on the one hand and the US and SM simulations on the other hand. For simplicity, in the following we compare only the TPS and US results, as the US and SM results are similar. At the TS, the average C4N–H4N distance from TPS is 1.37 ± 0.05 Å, while the average C6–H4N distance is 1.41 ± 0.04 Å. The TPS average value for the antisymmetric stretch coordinate (i.e., R_C4N–H4N – R_C6–H4N), which is often employed as a reaction coordinate in standard US simulations, is −0.04 ± 0.07 Å. The corresponding values obtained from US (1D_asym) are 1.30 ± 0.03, 1.40 ± 0.03, and −0.10 Å for R_C4N–H4N, R_C6–H4N, and the antisymmetric stretch coordinate. In our previous work, we defined a rehybridization coordinate⁴⁷ and applied it in multidimensional free energy simulations of several enzyme-catalyzed reactions involving a hydrogen transfer step.^47,80,81 This coordinate quantifies the difference between the orbital hybridization states of the acceptor and donor carbons in geometric means⁴³ and is independent of the position of the transferring hydrogen. The average TS value of the rehybridization coordinate obtained from TPS is −0.09 ± 0.12 Å, compared to −0.10 ± 0.20 Å from US. These values suggest that the TS obtained using TPS is similar to that obtained using US. However, the average TPS DAD is 2.75 ± 0.06 Å, which is considerably longer than that obtained with US (2.64 ± 0.06 Å). The DAD distributions from US and TPS, which are presented in Figure S2 in the Supporting Information, show a wider distribution in the TPS simulations than in the US simulations. In addition, the TPS TS is more linear, with an average C4N–H4N–C6 angle of 164.2 ± 6.4°, while an angle of 159.8 ± 7.8° was obtained with US. We note that an in vacuo model bimolecular TS complex calculated with the same AM1-SRP Hamiltonian has a saddle-point angle of 162.4°.⁴⁸ The van der Waals contact/proximity between the sulfur atom of the Met20 side chain and the N5 and N7N positions of the reactive complex allows the lone pair of the sulfur to maintain interactions with the bound ligands via either hydrogen bonding or dative bonding. Together with the hydrogen bonding between the N7N atom and the carbonyl oxygen of Ile14, these support the nicotinamide ring in its binding site toward the catalytic event. According to the present TPS simulations, the interaction between the pterin N5 nitrogen and the Met20 sulfur atom is slightly weakened during the course of the reaction because the positive charge on the nitrogen is neutralized as the hydride transfer occurs. This latter finding is in contrast to that of Luk and co-workers, who suggested a stronger interaction with Met20 in the TS on the basis of US simulations.^22,51 Indeed, this subtle difference was also not observed in the current US simulations. The hydrogen bonds of the NADPH/NADP⁺ amide group with the backbones of Ala7 and Ile14 are shortened upon reaching the TS, suggesting tighter binding of the TS according to the TPS simulations. Again, this trend was not fully observed in our US simulations. Finally, the TPS simulations predict the angle between the amide moiety and the pyridine ring of the nicotinamide to be 15–20° in the RS, while it is ca. 6° at the TS (similar to that observed in the crystal structure of the DHFR:folate:NADP⁺ ternary complex⁵⁴), significantly increasing the overlap between the π systems within the nicotinamide. Again, this subtle effect is not as significant in our US simulations. Thus, TPS seems to predict that DHFR is an enzyme designed to bind the TS more tightly while enhancing orbital conjugation, although differences between many of the structural parameters are within the standard deviations.

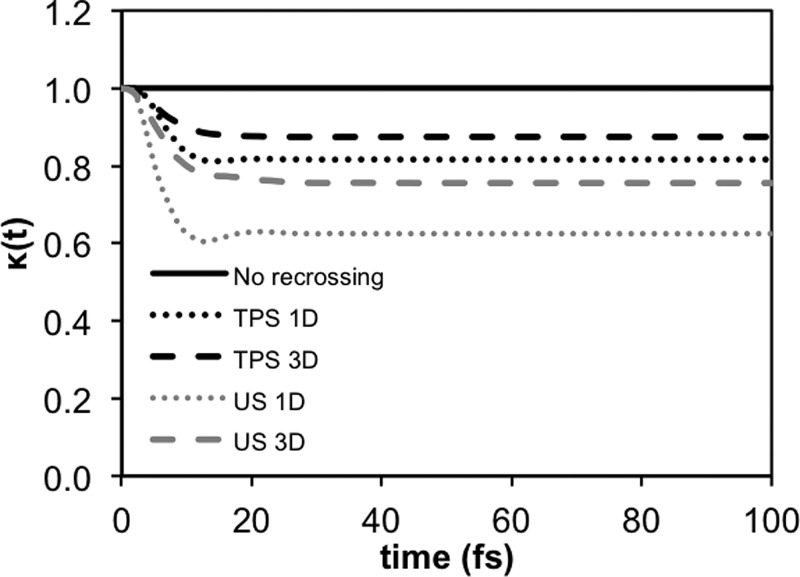
We further note that the classical recrossing transmission coefficients (κ) computed using US and TPS are considerably different (Figure 3). Using US with an antisymmetric stretch coordinate, we obtained a recrossing factor of 0.63, corresponding to a free energy error of 0.3 kcal/mol in the barrier height.⁴⁷ In contrast, using TPS we obtained a transmission coefficient of 0.82, as there is much less recrossing. Similarly, using a 3D coordinate, we obtain transmission coefficients of 0.76 and 0.87 with US and TPS, respectively.

Figure 3.

Time-dependent transmission coefficients, κ(t), for the hydride transfer reaction in ecDHFR computed on the basis of trajectories produced with one- and three-dimensional umbrella sampling simulations with an antisymmetric stretch and collective reaction coordinates (US 1D and 3D, gray) and from transition-path sampling simulations (TPS 1D and 3D, black). In the TPS simulations, the transition states were determined using a committor analysis and κ(t) was computed using the 1D and 3D coordinates as a metric.

We note that using a three-dimensional reaction coordinate composed of an antisymmetric stretch, the DAD, and a rehybridization coordinate gave nearly identical TS geometries as the simple one-dimensional antisymmetric stretch coordinate.⁴⁷ Additionally, SM with an additional collective reaction coordinate gave similar results as US, albeit with a slightly longer DAD. We also note that employing an environmental reaction coordinate based on potential energy in conjunction with a standard antisymmetric stretch coordinate yielded results similar to the current US results.⁵¹ Taken together, the results of the present work suggest that simulations incorporating TST-like assumptions are unable to properly sample long DADs, whereas the dynamics-based TPS method accesses long DADs during barrier crossing.

Finally, we compared the quantum momentum distributions (obtained using the recently developed QCOPI method^46,79) for the transferring hydride at the US and TPS dividing surfaces. The momentum distribution is a highly sensitive reporter of the potential experienced by a particle. In Figure 4 we compare the momentum distributions obtained for dividing-surface configurations from US simulations restrained to different DADs with the TS obtained from TPS simulations. It is clear from inspection of the US curves in Figure 4 that as the DAD increases at the TS, the momentum distribution becomes increasingly narrow, reflecting a wider position distribution. Interestingly, the momentum distribution obtained for the TPS dividing surface is significantly different from all of those attained with US. Careful inspection of the tails of the momentum distributions suggests that the potential experienced by the hydride using US resembles a single-well potential, whereas the potential using TPS corresponds to a small double-well potential. This suggests that the potentials experienced by the transferring hydride at the TS obtained using different techniques are rather different.

Figure 4.

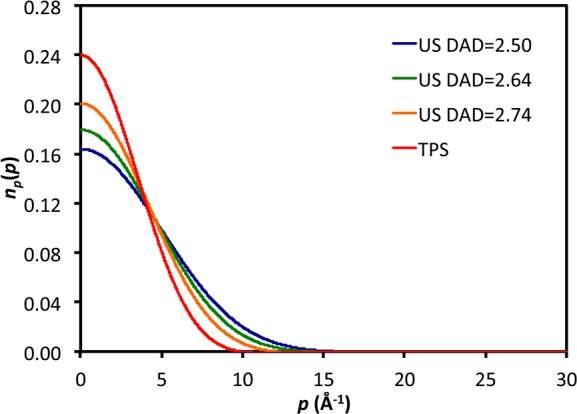
Momentum distributions for the transferring hydride at transition states obtained using umbrella sampling at different donor–acceptor distances and using transition-path sampling.

Discussion

TPS simulations have been applied to various enzyme systems,^{16,19,30,78,82,83} although presently it is not a household method in computational enzymology. In the present work, we performed a comparison between the activated complexes obtained for the enzyme DHFR using the TPS method and two other widely used approaches, US and SM. We found that the TSs obtained using the two families of methods are significantly different. In particular, the TSs obtained using TPS have longer DADs and are more linear than those observed using US and SM. Additionally, the classical recrossing transmission coefficients using US and TPS were found to be significantly different. With US there is considerable recrossing of the TS, whereas with TPS there is much less recrossing. In the current study, we did not compare the free energy profiles associated with the transition-path ensemble. This is not a trivial task, and additional information is required to determine reaction probabilities.⁸⁴ However, the free energy profiles from TPS are not expected to be significantly different from the US and SM profiles because the reaction barrier is less sensitive to the exact location of the TS. Indeed, the free energy surface for DHFR is rather flat in the TS region with respect to the DAD.⁴⁷ A related careful comparison between US and TPS on the rotational barrier in a disaccharide in vacuo showed similar results with the two methods, although additional pathways were found using TPS.⁸⁵ However, certain kinetic parameters such as the kinetic isotope effect and dynamic recrossing at the TS are sensitive to the geometry of the TS. Thus, they require an accurate determination of the TS. In particular, the NQEs responsible for the kinetic isotope effect are highly sensitive to the fine details of the TS. It is not clear that simple corrections to the rate constant via various prefactors can rectify the errors introduced into the computation of kinetic isotope effects using an incorrect TS ensemble.

We stress that the difference between the US/SM and TPS approaches is not merely one of computational strategy. Instead, it is likely that underlying physical assumptions inherent to the methods, such as equilibrium solvation and the nature of the reaction coordinate and its motion, give rise to the different results. The traditional TST-based US and SM techniques assume that the barrier-climbing process is slow relative to the relaxation of the environment, and therefore, at every value of the reaction coordinate the environment is assumed to be fully relaxed to achieve thermodynamic equilibrium throughout the entire system for all degrees of freedom. In contrast, the actual barrier crossing is very rapid in TPS, and the environment is largely unchanged during the reaction. This is consistent with a reaction dynamics model where the system spends most of its time searching for a reactive configuration and set of momenta. Once the proper 6N-dimensional state (3N for the configuration and 3N for the momentum, where N is the number of atoms in the system) suitable for reaction is attained, the reaction occurs rapidly. In this case, if certain protein dynamics are coupled with the chemical step, the effects of such dynamics are naturally taken into account in TPS, whereas they are ignored in the TST-based methods.

An additional fundamental difference between the two families of methods concerns the motion along the reaction coordinate. In US and SM, the motion along the reaction coordinate is unphysical because of the applied bias. The reaction coordinate is assumed to be separable from the other degrees of freedom, and the velocity of the reactive mode is assumed to approach that of a free particle. On the other hand, the reactive trajectories produced from TPS correspond in principle to a true barrier-climbing process. Indeed, in TPS simulations there is a kinetic energy associated with the barrier crossing, similar to what one would expect in the true chemical step. This motion along the reaction coordinate, combined with the lack of time for environmental reorganization during hydride transfer, generates a friction force that influences the nature of the activated complex in multidimensional systems.

We note that additional differences in the details of the current simulations exist. The US and SM simulations were performed in the isothermal–isobaric (NPT) ensemble using a thermostat, while the TPS simulations employed a microcanonical (NVE) ensemble (albeit conforming with NVT conditions). However, US in the NVE ensemble yielded DADs identical to those in the NPT simulations, so this is unlikely to be of significance here.

We believe that it could be of interest to compare biased and unbiased simulations for other activated processes and to explore the validity of the equilibrium solvation assumption inherent to traditional TST as well as the effects of nonequilibrium dynamics on the reaction. Additionally, more advanced tools for analysis of the dividing surface could be employed.¹⁵ We further note that a quantum-dynamical analogue of classical TPS simulations should be used to identify the TS more precisely.⁸⁶ Finally, as noted above, direct rates or kinetic isotope effects were not computed with TPS in the current work. A direct comparison of computed and experimental absolute rates and kinetic isotope effects and their temperature dependence will be necessary to further scrutinize the current TPS and US results.

Supporting Information Available

Figures showing distributions of key geometrical parameters from the SM simulations and DAD distributions obtained using US and TPS. This material is available free of charge via the Internet at http://pubs.acs.org.

This work was supported by a grant to A.K. and D.T.M. from the United States–Israel BSF (Grant 2007256) and grants to A.K. from the NIH (R01 GM65368) and NSF (CHE-1149023). K.N. acknowledges the startup grant from Umeå University and the Swedish National Infrastructure for Computing (SNIC) and the National Energy Research Scientific Computing Center (NERSC) for providing computational resources.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States