Real-time high resolution laser speckle imaging of cerebral vascular changes in a rodent photothrombosis model

Abstract

The study of hemodynamic and vascular changes following ischemic stroke is of great importance in the understanding of physiological and pathological processes during the thrombus formation. The photothrombosis model is preferred by researchers in stroke study for its minimal invasiveness, controllable infarct volume and lesion location. Nevertheless, there is a lack in high spatiotemporal resolution techniques for real time monitoring of cerebral blood flow (CBF) changes in 2D-profile. In this study, we implemented a microscopic laser speckle imaging (LSI) system to detect CBF and other vascular changes in the rodent model of photothrombotic stroke. Using a high resolution and high speed CCD (640 × 480 pixels, 60 fps), online image registration technique, and automatic parabolic curve fitting, we obtained real time CBF and blood velocity profile (BVP) changes in cortical vessels. Real time CBF and BVP monitoring has been shown to reveal details of vascular disturbances and the stages of blood coagulation in photothrombotic stroke. Moreover, LSI also provides information on additional parameters including vessel morphologic size, blood flow centerline velocity and CBF spatiotemporal fluctuations, which are very important for understanding the physiology and neurovascular pathology in the photothrombosis model.

1. Introduction

Watson and colleagues were the first to introduce a photothrombosis model in which cerebral ischemia was induced in rats [1]. This model was later modified for a murine model system [2]. The rodent photothrombosis model has been used to better understand the underlying pathological mechanisms in human stroke [3]. In the rodent model, the thromboembolism is induced by intravenous injection of Rose Bengal in combination with focal illumination of the cortical vessels. This combination leads to a local photochemical reaction between Rose Bengal and light, generating free oxygen radicals that disturb endothelial function, which then leads to platelet aggregation and thrombus formation [4]. The photothrombosis model is preferred by many stroke researchers for its minimal invasiveness, controllable infarct volume and lesion location [5].

When studying stroke, the vascular changes during thrombus formation, including the spatiotemporal changes in blood flow and vessel diameter, are important in understanding the pathophysiology of thrombosis and in developing antithrombotic therapeutics [6, 7]. Parameters related to blood flow, including blood velocity profile (BVP), which describes the blood flow speed distribution across a vessel, and vessel diameter changes, are closely related to vascular shear rates and shear force. These parameters are directly linked to the process of thrombus formation, including growth and stabilization of the thrombus [8], platelet deposition on thrombogenic substrate [9], platelet aggregation [10], etc. In particular, BVP is of great interest for vascular biologists because the changes in BVP not only reflect cellular aggregation inside blood vessels [11], but also the morphology of blood vessels (e.g. the diameter of arterioles) [12] and the blood flow centerline velocity [13]. Nevertheless, most studies on the neurovascular mechanism of thrombus formation are based on modeling due to the lack of high spatiotemporal resolution using in vivo BVP imaging techniques.

In this study, we implemented a 2D cerebral blood flow (CBF) imaging technique, i.e. laser speckle imaging (LSI), to study the changes in CBF and BVP in the rodent photothrombotic stroke model. LSI, as a full-field optical imaging technique, was first applied to study CBF in rat brain by Dunn et al. [14]. This technique was successfully used in the study of functional activation in the rat somatosensory cortex [15], cortical spreading depression in a migraine model [16], and vasoconstrictive vascular coupling during focal ischemic depolarizations [17]. LSI has also been a useful tool in the study of photothrombosis and related physiological and pathological phenomena through the temporal and spatial mapping of CBF distribution [18–20]. Nevertheless, the traditional LSI technique has difficulty resolving BVP information due to insufficient resolution.

In this present work, we implemented a microscopic-LSI system that can monitor CBF and acquire BVP information with a resolution of 2 µm during the process of photothrombosis. By extracting information such as cerebral vascular changes in morphologic factors, blood flow centerline velocity, and CBF fluctuations during the thrombus formation, we have been able to characterize the dynamic spatial and temporal process of photothrombotic stroke in a rodent model.

2. Methods and materials

2.1 Animal preparation

The experimental protocols used in this study were approved by the Animal Care and Use Committee of the Med-X Research Institute of Shanghai Jiao Tong University. One male Sprague-Dawley rat (296 g) was anesthetized with 70 mg/mL chloral hydrate via intraperitoneal (IP) injection (initial dose of 5 mL/kg, IP, then approximate 1.5 mL/kg/h). Standard sterile precautions were taken during surgical procedures. The rat was constrained in a stereotaxic frame (Benchmark Deluxe^TM, MyNeurolab.com, St. Louis, MO, USA) and temperature was measured rectally and maintained at 37°C with a heating pad and DC control module (FHC Inc., Bowdoinham, ME, USA). After being shaved, the rat scalp was disinfected with 70% ethanol and povidone iodine solution. A midline scalp incision was made and the tissues underlying the scalp were cleaned to expose the skull. A 4 × 7 mm² cranial window over the left cortex was thinned to translucency using a high-speed dental drill (Fine Science Tools Inc., North Vancouver, Canada). The cranial window was centered at 3.5 mm posterior to the bregma and 2 mm lateral to the midline. Finally, the thinned area was immersed in mineral oil (Sigma-Aldrich Co., Ontario, Canada) to decrease specular reflections and enclosed by reinforced glass ionomer cements (Dental Materials Factory of Shanghai Medical Instruments Co., Shanghai, China). Before we began image acquisition, an acupuncture needle was placed at the bottom-left corner of the imaging window as the registration reference.

2.2 Imaging system

A schematic representation of our imaging system is shown in Fig. 1 . Two laser beams were used in our experiment. The first laser beam (780 nm, 10 mW, L780P010, Thorlabs, USA) was used as an illuminating source for imaging and the second laser beam (532 nm, 100 mW, 13216-620, Forward Optoelectronics Co., Ltd., Shanghai, China) was used for photothrombosis model induction. The 780 nm laser beam illuminated the thinned area of the skull and the reflected and scattered lights were filtered by a long-pass filter (>750 nm, FEL0750, Thorlabs, USA). The light which passes through the filter was then collected by the microscope (S8 APO, Leica Microsystems, Germany) and imaged using a CMOS camera (avA1000-100gm, Basler, Germany).

Fig. 1.

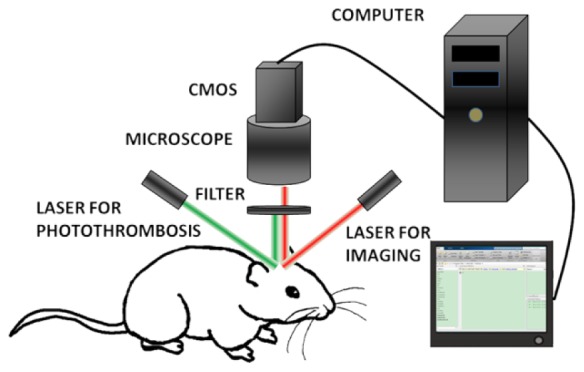
Schematic of the imaging system.

2.3 Photothrombosis procedures

A laser beam (diameter: 1.5 mm, wavelength: 532 nm) was stereotactically directed onto the region of interest (ROI) which contains the middle cerebral artery (MCA). Prior to illumination, Rose Bengal (133 mg/kg body weight, 40 mg/mL saline) was injected intravenously. After that, the ROI was continuously illuminated until the MCA branch was occluded.

2.4 Imaging procedures

Throughout the experiment, we acquired the images at a rate of 60 fps with an exposure time of 5 ms. The ROI contains 640 × 480 pixels and each pixel size is 2 × 2 µm². During the photothrombosis process, the images were captured continuously by the CMOS camera and stored as stacks with 20 frames in each stack.

2.5 Data processing

2.5.1 Registration of raw speckle images

Before we analyzed the CBF changes, the raw images needed to be registered to eliminate motion artifacts created by respiration and heartbeat. Using the microscopic view, motion artifacts in raw speckle images are much more prominent than those observed with the normal view. The acupuncture needle tip introduced over-exposed pixels that could be directly used as the reference for registration, which is a better strategy than the rLASCA that we previously reported [21]. In order to eliminate motion artifacts, the area containing the needle tip without any visible blood vessels in the first frame of the first stack was chosen as a template to register the remainder of the images. Figure 2(a) shows the raw speckle image and the red square marks the template. Each frame was aligned to the first frame by looking for a template-sized window with the highest degree of similarity to the template [22]. Figure 2(b) and 2(c) show the laser speckle contrast images without and with registration, respectively. The blurring of the needle tip in Fig. 2(b) underscores the necessity of registration. The green dashed circle in Fig. 2(c) indicates the focal point for the induction of photothrombosis by the 532 nm laser.

Fig. 2.

Raw speckle image and laser speckle contrast images in microscopic view. (a) Raw speckle image in microscopic view. The white area within the red square is the acupuncture needle tip, which was used as a reference for registration. (b) LSI image calculated without registration. (c) LSI image after registration. The green dashed circle indicates the focus of photothrombosis. It is clear that registration successfully removes motion artifacts and improves spatial resolution.

2.5.2 Calculation of CBF

After registration, we calculated the CBF map. For each image stack with 20 frames, we defined the contrast value K at every pixel $(i,j)$ as

$$K=\frac{{\sigma }_{20}(i,j)}{{\mu }_{20}(i,j)}$$ (1)

where ${\sigma }_{20}$ and ${\mu }_{20}$ are the standard deviation and the mean intensity at pixel $(i,j)$ over 20 frames, respectively. According to the theory behind LSI, K is related to blood flow velocity v through correlation time ${\tau }_c$, which is assumed to be inversely proportional to v as shown in Eq. (2) [23].

$$K^2=\beta \left[\frac{{\tau }_c}{T}+\frac{{\tau }_c{}^2}{2T^2}\left(e^{-\frac{2T}{{\tau }_c}}-1\right)\right]$$ (2)

where T is exposure time, $\beta =1/N$, and N is the number of speckles in each pixel area [24]. In our study, we use $1/K^2$ to represent blood flow velocity v at every pixel. A typical LSI image is shown in Fig. 2(c).

2.5.3 Estimating the BVP

After obtaining the 2D CBF distribution, we were able to extract the BVP along the cross section of a selected vessel, which can be used to study the hemodynamic changes in the thrombosis process. A cross section of the blood vessels close to the focus of thrombosis was manually selected. Then, a five-sample-point median filter was applied for smoothing along the cross section. According to the theory of fluid mechanics, the velocity of an ideal fluid in large glass tubes should have a parabolic distribution. Parabolic curve fitting is commonly used to acquire BVP in retinal blood vessels [25] or cerebral blood vessels [26]. Here, we used a piecewise function $F(x)$ to fit the CBF velocity values along the selected cross section for a single vessel:

$$F(x)=\{\begin{array}{l}Y(x_1),x<x_1\\ P(x),x_1\le x\le x_2\\ Y(x_2),x>x_2\end{array}$$ (3)

where $x_1$ and $x_2$ represent the two boundaries of the vessel, $Y(x)$ represents the CBF velocity value outside the vessel and $P(x)$ is the parabolic function fitting of BVP along the cross session of the vessel. The boundaries $x_1$ and $x_2$ can be automatically detected using the criterion of generating a minimal difference square between $Y(x)$ and $F(x)$. Assuming that the number of pixels along the cross section is L, the boundaries $x_1$ and $x_2$ are determined as:

$$\{x_1,x_2\}=\arg \underset{1\le x_1<x_2\le L}{{\displaystyle \min }}{\displaystyle \sum _{x=1}^L{\left(F(x)-Y(x)\right)}^2,}{x}_1,x_2\in \mathbb{N}$$ (4)

After obtaining the BVP of the blood vessel, the blood vessel diameter (D, in pixels) and centerline velocity ($V_c$, in aspect of $1/K^2$) changes during the thrombosis process can be calculated. $V_c$ is defined as the maximum blood flow velocity on BVP [25], and D is represented by the distance between the two boundaries $(x_1,x_2)$ of BVP.

3. Results and discussions

3.1 BVPs along the cross sections of cerebral blood vessels

3.1.1 Changes in BVP close to the ischemic core

We were able to obtain BVP and single point blood flow information with high spatiotemporal resolution using a microscopic LSI system. Figure 3 shows the LSI images (Fig. 3(a), 3(c), 3(e) and 3(g)) and the corresponding BVPs (Fig. 3(b), 3(d), 3(f) and 3(h)) along the selected cross section C1 (indicated by the red line in Fig. 3(a)) at different stages of thrombus formation.

Fig. 3.

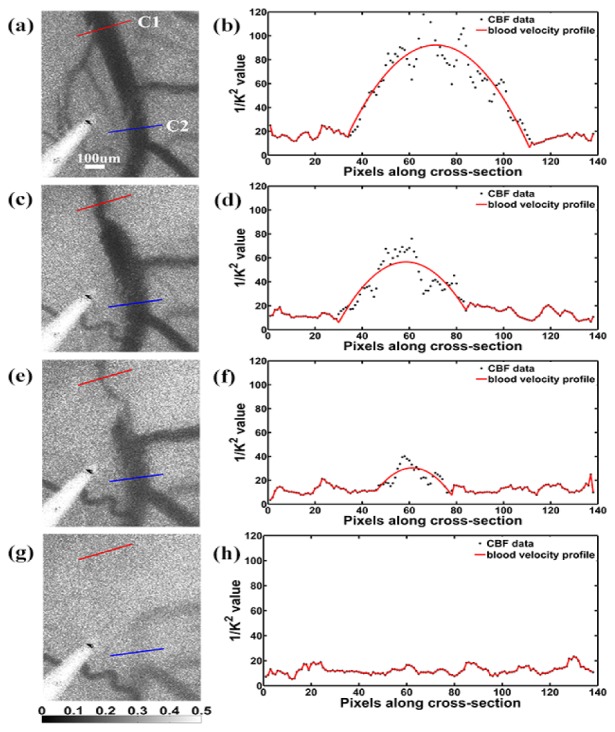
LSI images and the corresponding BVPs. (a), (c), (e) and (g) are LSI images at different time points in the photothrombosis process (t₁ = 0 min, t₂ = 6 min, t₃ = 9 min, t₄ = 10 min). The corresponding BVPs along the selected cross session C1 are shown in (b), (d), (f) and (h), respectively. The BVPs are fitted with parabolic curves. A cross section C2 (blue) far from the focus is selected for further comparison with C1 (red) in aspects of vessel diameter and centerline velocity.

For the purpose of demonstration, images representing four time points are shown, i.e. t₁ = 0 min, t₂ = 6 min, t₃ = 9 min and t₄ = 10 min after initiation of illumination. The supplementary video (see Media 1 ^{(3.4MB, MP4)} ) shows the complete process of thrombus formation and the disturbances in BVP. As shown in Fig. 3, while CBF decreases during the thrombosis process, the overall BVP along the C1 cross section remains flat. This is because during the thrombus formation, the blood vessel experiences dramatic vasoconstriction and vasodilation, resulting in significant changes in the vessel shape as well as the BVP. As the vessel is completely blocked by the thrombi, there is no blood flow through C1 (Fig. 3(h)). Real time high resolution LSI clearly shows dynamic changes in CBF and BVP during the thrombosis process.

After obtaining the overall BVP, we further analyzed the blood flow at selected points along C1, as blood flow is closely related to flow-imposed shear stress at the vessel wall [27] and flow-mediated vasoconstriction and vasodilation [28].

We selected point A and point B, which are close to the vessel wall and the centerline respectively at t₁ = 0 min (Fig. 4(b) ), for analysis. Here, each point refers to a 3 × 3 pixel area. Figure 4(c) shows the blood flow velocity changes at these two points throughout the photothrombosis process. As Fig. 4(c) indicates, we can separate photothrombosis into three phases according to the changes of $V_A$ and $V_B$. In phase I, during the beginning stage of thrombus formation (up to 3 minutes after the start of illumination), $V_A$ and $V_B$ quickly drop due to the newly formed thrombus. $V_A<V_B$ because B is closer to the centerline of the vessel than A. In phase II, during the thrombus formation (from t = 3 min to t = 10 min), both $V_A$ and $V_B$ change dramatically, showing great variances in blood flow velocity due to the complicate dynamics found during blood coagulation. In phase III, following complete occlusion of the artery ($t\ge 10$ min), both $V_A$ and $V_B$ fall to a capillary bed CBF level.

Fig. 4.

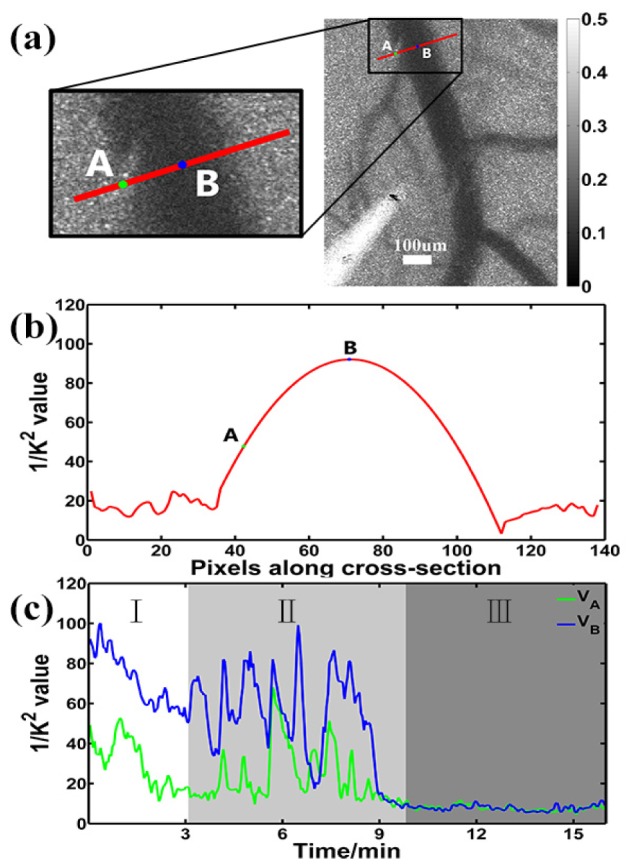
CBF changes at a single point during the photothrombosis process. (a), (b) Two selected points close to the vessel wall (point A) and centerline (point B) at the baseline along the cross section C1 were selected to demonstrate the changes in CBF during the thrombus formation. (c) Blood velocity changes of point A and point B, represented by $V_A$ and $V_B$, are plotted during the photothrombosis process.

3.1.2 Comparison of BVPs at different distances from the ischemic core

Next, we compared the BVPs along two cross sections, i.e. C1 and C2 in Fig. 3(a), at different distances from the ischemic core during the photothrombosis process. C1 was selected as above, close to the focus of illumination, while C2 is on the same artery trunk but far from the focus. We then used these values to estimate the vessel diameter and centerline velocity changes at C1 and C2 during the photothrombosis process based on the BVPs. Vessel diameter D is a commonly used parameter in studying blood flow in physiological and pathological conditions [29–31]. The centerline velocity $V_C$, which is defined as the maximum blood flow value on the BVP, is also of great importance in flow dynamics.

Figure 5(a) illustrates the definitions of vessel diameter D and centerline velocity $V_C$. Figure 5(b) shows the changes in vessel diameter during the photothrombosis process along cross sections C1 ($D_{C1}$) and C2 ($D_{C2}$), while Fig. 5(c) shows $V_C$ changes in the corresponding sections. As the figures show, at the 9 minutes after illumination initiation, both $D_{C1}$ and $V_{C1}$ drop to zero, corresponding to complete occlusion. There is a temporal delay in the drop of $D_{C2}$ and $V_{C2}$, which is as expected since the direction of blood flow is from C1 to C2. Interestingly, after the artery trunk is completely occluded, we observed a rebound in blood flow at C2. $D_{C2}$ completely returned to the baseline level (see Media 2 ^{(2.9MB, MP4)} ) and $V_{C2}$ rebounded to about 1/3 of its baseline level after a short no-flow period. Therefore, BVP changes at C2 clearly show the complementary flow from the branch artery when a vessel is occluded in its upper trunk.

Fig. 5.

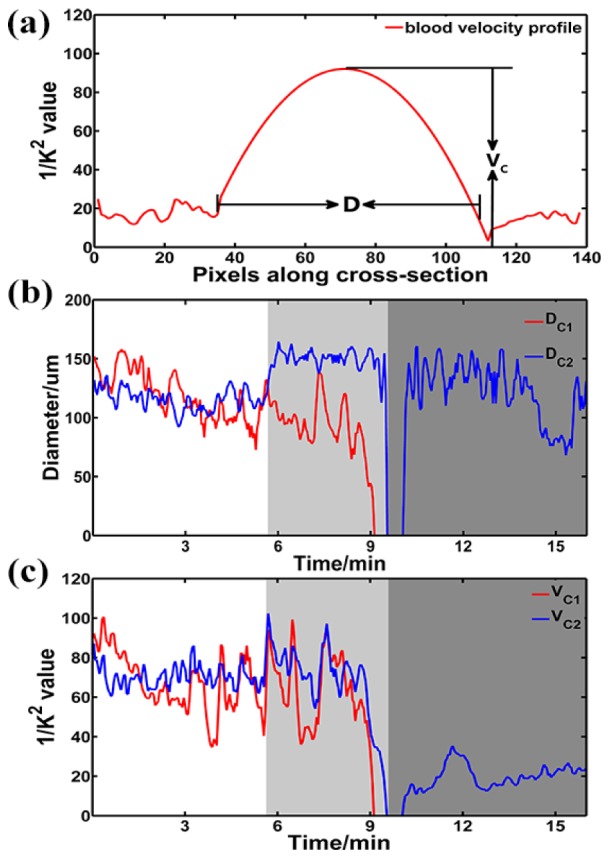
Changes in cerebral vessel diameter and the centerline velocity during the photothrombosis process at different locations. (a) Illustration of the definition of vessel diameter D and centerline velocity $V_C$ on BVP. (b) Vessel diameter changes at cross sections C1 and C2, denoted as $D_{C1}$ and $D_{C2}$. (c) The centerline velocity, i.e. $V_{C1}$ and $V_{C2}$, on cross sections C1 and C2.

By monitoring the BVPs at cross sections at different distances from the thrombotic core, we can record the changes of the blood vessels during coagulation. The CBF varied as a dynamic process with transient rebounds and fluctuations. Moreover, the BVP data enabled a reliable numerical analysis of vascular dynamics. We observed that $V_C$ is sensitive to thrombus formation and the detailed spatiotemporal changes in $V_C$ at different locations showed more comprehensive dynamics, including a time delay in BVP variation, vasoconstriction and vasodilation, and supplementary branch flow. All of these detailed processes could only be observed in real time using a high resolution LSI technique.

3.2 Spatial and temporal distribution of CBF fluctuations

In addition to BVP, we also investigated the distribution of CBF fluctuations. Specifically, we calculated the standard deviation of blood flow velocity $v_t$ in a ROI, denoted as ${\sigma }_t$. The value ${\sigma }_t$ can be used to describe blood flow fluctuation characteristics [32]. Figure 6(a) shows seven selected ROIs along the artery. All ROIs contain the same number of pixels (40 × 25), coded in different colors and labeled S1 to S7. During thrombus formation, the 532 nm laser was focused on ROI S1. The direction of blood flow in the artery of interest is from S1 toward S3, according to the anatomic structure. S6 and S7 are located on the branches of the same artery. In Fig. 6(b), we plotted the changes of ${\sigma }_t$ in all ROIs during thrombus formation. According to changes in ${\sigma }_t$, the entire process of the rat photothrombotic stroke model can be generally separated into four stages (see Fig. 6(b)).

Fig. 6.

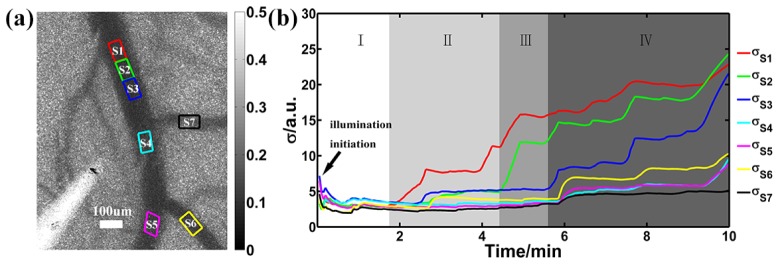
The change of CBF standard deviation ${\sigma }_t$ in the process of thrombus formation. (a) Seven ROIs (40 × 25 pixels each) along the blood vessels were selected (coded by colors and labeled from S1 to S7) to analyze the temporal change of ${\sigma }_t$. (b) ${\sigma }_t$ curves for each ROI. ${\sigma }_t$ curves show four distinct stages of photothrombotic stroke model.

Stage I is the baseline with low blood flow fluctuation, similar to the period before the photochemical reaction. Significant disturbances of CBF are then observed in the ROIs, and the disturbances are greater and earlier in time the closer they are to the ischemic core (i.e. Stage II: S1, Stage III: S2, S3 and then Stage IV: S4, S5, S6, S7). It is interesting to see a step-wise pattern in the change in ${\sigma }_t$, which may be related to thrombus accumulation.

Figure 6 suggests that CBF standard deviation could be a valuable parameter in characterizing the dynamic changes in the photothrombosis process. In combination with BVP, blood vessel diameter and centerline velocity, real time high resolution LSI offers a novel approach with which to study different aspects of the thrombosis process, and further enables in vivo of hemodynamics during photothrombotic stroke.

In recent work by Dunn’s group, multi-exposure speckle imaging (MESI) [33] was used to improve the quantitative accuracy of LSI and monitor the chronic blood flow in a similar photothrombotic stroke model [34]. It should be noted that MESI needs to collect images with multiple exposure durations at the cost of temporal resolution, which, therefore, was less recommended in monitoring the acute change of the CBF during the thrombus formation. Besides, such a multiple exposure approach is sensitive to the motion artifacts from heart beat or breath, which also limited its performance in real-time application. By using on-line registration technique, the microscopic LSI in this study is able to monitor the dynamic vascular changes in the acute stage of stroke.

4. Conclusion

In conclusion, we have implemented a microscopic LSI system to monitor the CBF and BVP of cerebral blood vessels during thrombosis with high spatial and temporal resolution. We calculated blood vessel diameter, centerline velocity of CBF and CBF standard deviation in different areas during thrombus formation. The analysis of our photothrombotic stroke model shows a multi-stage process in vascular occlusion, with different hemodynamics in the main and branch vessels. The techniques described here can potentially be used for real time monitoring of stroke formation or intervention. In the meantime, our ability to obtain high resolution in vivo real time BVP data can also be beneficial to the study of vascular mechanics and hemodynamics.