Abstract
A dendritic spine is a small membranous protrusion from a neuron's dendrite that typically receives input from a single synapse of an axon. Recent research shows that the morphological changes of dendritic spines have a close relationship with some specific diseases. The distribution of different dendritic spine phenotypes is a key indicator of such changes. Therefore, it is necessary to classify detected spines with different phenotypes online. Since the dendritic spines have complex three dimensional (3D) structures, current neuron morphological analysis approaches cannot classify the dendritic spines accurately with limited features. In this paper, we propose a novel semi-supervised learning approach in order to perform the online morphological classification of dendritic spines. Spines are detected by a new approach based on wavelet transform in the 3D space. A small training data set is chosen from the detected spines, which has the spines labeled by the neurobiologists. The remaining spines are then classified online by the semi-supervised learning (SSL) approach. Experimental results show that our method can quickly and accurately analyze neuron images with modest human intervention.
OCIS codes: (100.0100) Image processing, (100.5010) Pattern recognition, (100.6890) Three-dimensional image processing
1. Introduction
In neuron-biology research, the morphological structures of neurons have been proven to have a close correlation with the neuron functional properties. Among all the morphological structures of neurons, the dendrite and the dendritic spines are the most functional parts that draw the concentration of neuron-biology researchers. Most of the dendrites are the tree-like structures of neuronal cells and their spines are small protrusions on the surface of dendrites. Currently, the morphological analysis of dendritic spines is widely used in the neurobiology research such as the one on Alzheimer’s disease [1–3]. With the help of modern fluorescence microscopy methods, the detailed 3D shapes of dendrites and spines can be obtained by confocal laser scanning microscopy (CLSM) or two-photon laser scanning microscopy (2PLSM) [4]. Since dendritic spines have various shapes and their structures correlate highly with their underlying cognitive functions [5], it is crucial to detect and extract dendritic spines from the dendrite, and analyze the spines morphological structure efficiently.
There are mainly two kinds of approaches when dealing with the morphological analysis of neuron structure. One of the most popular analysis methods is conducted on maximal intensity projection (MIP) images, which analyzes the neuron morphological structures based on features extracted from the 2D plane by projecting 3D voxels with maximum intensity that fall in the way of parallel rays traced from the viewpoint to the plane of projection [6–8]. In this approach, intensity of the pixels on the 2D plane is one of the most important features in distinguishing dendrite and spines. Cheng et al. [7] proposed an automated dendrite spines detection in 2PLSM based on MIP image. Bai et al. [8] also used the MIP image to track the backbone of dendrite, and segment the spines from dendrite with a breadth model, but these approaches in the 2D plane cannot guarantee a high accuracy because the information is lost when the original 3D image stacks are projected to a 2D plane. The second kind of approach analyzes the 3D structure of neurons. Among the existing 3D approaches, Janoos et al. [9] proposed a 3D reconstruction and identification of dendritic spines algorithm based on the skeletonization. First, the center line of the whole neuron structure was extracted. Then, the longest line was considered as the backbone of dendrite and the shorter lines were considered as the centerlines of dendritic spines. However, the skeletonization algorithm has two problems that make it weak. First, it is time consuming to get all the centerlines from the 3D volume with complex shapes. Second, for the different shapes of dendritic spines, the skeletonizaiton algorithm always produced too many short branches in one spine and was too inflexible in getting the real centerlines from the branches.
A 3D neuron analysis approach was proposed by Rodriguez et al. [10], which was based on a 3D reconstruction algorithm using the Rayburst diameter [10,11], where Rayburst is defined as casting a multidirectional core of rays from an interior point to the surface of a solid, allowing precise quantification of anisotropic and irregularly shaped 3D structures. The Rayburst diameter in each layer of a spine was calculated and the head and neck of each spine was defined according to the distribution of the diameters. This method detect and classify the spines in an efficient way, but it may not be accurate in dealing with the spines having too complex shapes. First, the spine shape is only defined by the head to neck ratio (HNR). Second, a global threshold of HNR is not adaptive in analyzing different kind of images. Therefore, machine learning approaches are needed to classify dendritic spines with an online neuron morphological analysis strategy.
To solve the dendritic spines morphological analysis problems efficiently, we propose a novel morphological analysis algorithm for dendritic spines based on a SSL approach. In this framework, dendritic spines are detected and segmented from dendrite based on wavelet transform. After the measurement of spines, the SSL approach is conducted on the spine classification. First, the dendrite backbone on a 2D xy plane is tracked and all the dendrites’ surface with meshes in a 3D space are reconstructed. Second, spines are segmented from the dendrite based on wavelet transform, where the segmenting positions are located where the wavelet response on a spine section quickly changes. Features of spines are also extracted after the spines segmentation. Third, a small portion of detected spines are selected by a neurobiology expert, and labeled as the training set for classification. Lastly, the labels of the remaining spines can be calculated after the training process and all the detected spines are classified by the learning framework.
Our strategy is different from previous methods mainly in three ways. First, our approach is totally conducted on the 3D image stacks except for the dendrite backbone extraction. Second, a wavelet transform is applied to detect and segment the spines from the dendrites. Third, a SSL approach is applied in the spine morphological classification. The rest of this paper is organized as follows: In section 2 we introduce the image acquisition and preprocessing. In Section 3 we describe the detection and morphological classification strategy of dendritic spines in a 3D image dataset and show the SSL algorithm in detail, where the SSL approach is applied for the first time to the morphological classification of 3D spines. In section 4 we show experimental results and we conclude our paper and discuss future development in section 5.
2. Image acquisition and preprocessing
Due to fast development in the field of neuron imaging technology, the detailed 3D shape of neuron parts can be obtained by some kinds of modern fluorescence microscopy methods. 2PLSM provides unprecedented capabilities for 3D, spatially resolved photochemistry, particularly photolytic release of caged effector molecules [12–14]. These imaging technologies are powerful tools to study the structure of dendritic spines. In this section, the acquisition of 3D image stacks is described in detail. The preprocessing of raw 3D image stacks acquired from 2PLSM is also introduced. In order to research different neuron morphological structures, the datasets were obtained from a variety of brain regions and treatments of intact animals using 2PLSM. All the 3D acquired image stacks had the resolution of 512×512 pixels in the x-y plane. Since the average spine length was always 1 µm, 3D images with a high definition of 0.05×0.05×0.10 µm/pixel helped to get a clearer geometrical structure of the spines during the detection approach. The image stacks contains 18 slices in the z field on average, and are 16-bit gray-scale images.
The noise and the lighting condition are the two main reasons that cause the degradation of images obtained by optical microscopy. Therefore, before the reconstruction of 3D image stacks, the raw image stacks were preprocessed by de-noising algorithms. A 3D median filter with a 3×3×3 three kernel size and a top-hat filter were applied to the images to remove the noise and correct uneven illumination degradation. The intensity of the dendrites and spines were enhanced, reducing false detection of spines, especially some detached spines from the dendrite. The filters also smoothed the surfaces of the neuron, making the following reconstruction much smoother.
In order to extract spines, the neuron should be segmented from the background first. Since the intensity is not distributed evenly in each spine, there is a problem finding the spine components with low intensities. The neuron, including dendrite and spines, is segmented from the background using the adaptive threshold methods [7], which set a threshold for each pixel. This threshold is then used to test against the pixel intensity value to produce binary images. After segmentation, morphological filtering is performed to remove the noise, fill the holes, and smooth the boundaries. It is notable that some morphological processing, such as filling holes, can distort dendrite structures. To prevent these problems, local intensity information is considered during the processing.
3. Methodology
In this section, we discuss the algorithms we used in the morphological analysis of dendritic spines in the 3D neuron image stacks, including spine detection and classification. The flowchart of dendritic spines morphological analysis is shown in Fig. 1 . First, the neuron is segmented from the background using the adaptive threshold algorithm proposed in [7]. Based on the preprocessing results, we extract the centerline of dendrite from 3D volume in section 3.1. In section 3.2, we introduce the spine detection algorithm based on wavelet transform in details. The detailed measurements of spines are obtained after spines being segmented from the dendrite. Then, we apply the SSL approach on the morphological classification of dendritic spines in section 3.3, and the detected spines are classified into three categories, mushroom, thin, and stubby according to spine morphology definitions in [10,11].
Fig. 1.

Flowchart of the dendritic spine morphological analysis
3.1 Dendrite extraction
Compared to tube-like dendrites, spines have more complex shapes and mostly don’t have distinct segmenting positions from the dendrite. In order to detect dendritic spines correctly, the centerline along the neuron should be extracted. First, the raw 3D neuron images is processed with the method that was proposed in paper [15]. The centerline along the neuron, which is also called dendrite backbone, is extracted by casting rays inside of the neuron. Meanwhile, the approximated radii along the backbone is also calculated based on method of casting rays, which is similar to the Rayburst sampling, an algorithm for automated 3D shape analysis which was first proposed by Rodriguez et al. [10,11]. Fig. 2 illustrates this process and one of the results.
Fig. 2.

Illustration of casting rays sampling. (a) Casting rays inside the dendrite, the green line and the red line represent the longest and shortest diameters casting inside the neuron. (b) Blue circles represent the estimated dendrite with casting rays diameters in different areas while the red curve represents the estimated center line of the dendrite. A magnified figure can be seen in (c).
As shown in Fig. 2, the backbone extraction gets a raw representation of dendrite with a centerline and radii in different parts. However, it cannot separate the spines from the dendrite accurately because most of spines do not have clear boundary between the dendrite. In order to get the accurate measurement of spines for the morphological analysis, dendritic spines should be detected and segmented from the dendrite using our novel approach.
3.2 Dendritic spine detection
Dendritic spines are morphological specializations protruding from the neuronal dendrites, typically 0.5-2 μm in length [16]. In morphologic structure, spines with strong synaptic contacts typically have a large spine head which connects to the dendrite via a membranous neck. In our approach, individual spines are detected by clustering candidate spine voxels, starting from the tip points, moving towards the dendrite, then ending at the segmenting position. According to the backbone tracking results, tip points of each spine are defined as voxels that have the longest distance to the centerline of the dendrite. We pick up a small part of dendrite and describe the detection in details.
On an individual spine, tip points are first detected according to the protocol in [10]. As illustrated in Fig. 3 , a perpendicular line is set from the tip point T to the centerline of dendrite B1B2, and cross each other at the point BS. The junction point between TBS is defined as J. Here we define TJ as the max distance to dendrite surface and TK, the centerline of the spine, is the length of the spine. Starting from the tip point, we cut the spine with planes vertical to the perpendicular at intervals. Meanwhile, the wavelet transform gives an additional way, besides intensity, to determine the center points on each section. The center points and the final segmenting position are defined according to the procedures mentioned below.
-
1)
The sections are selected at intervals of two pixels (0.1-0.2 µm) along the perpendicular. Since the length of a spine can be very short in the image, small interval make the detection more accurate.
-
2)On each section plane, wavelet transform is employed to get the voxels which have the largest response. In practice, a 2D Gabor kernel wavelet is employed on the section plane because Gabor wavelet has transform better localization characters in the time and frequency fields compared with the Fourier transform. On the other hand, Gabor wavelet transform has low computational expense, which is suitable for the online real time use. The core function of Gabor wavelet on the section plane is defined as:
where(1)
Whereiis the plural item, v, u, kdonate the wave length of the Gabor filter, the direction of the kernel function, and the number of all directions (set as 6 in our algorithm), respectively. The parameterdetermines the size of Gaussian window, and here. The variable kernel frequency of waveletis set as and the variable direction is set as .
Fig. 3.
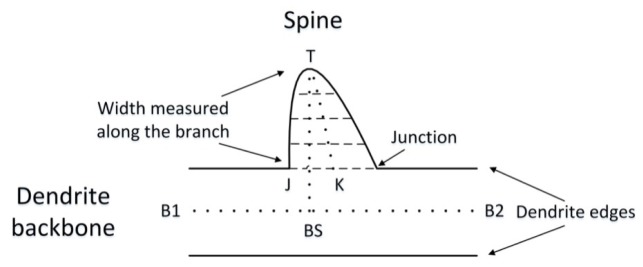
Determination of the segmenting position.
For the input intensity map of numberisection, the evolution of Gabor wavelet is set as:
| (2) |
where is the intensity of the corresponding pixel. Complex number are gotten after the Gabor wavelet transform, , is set as a result of the wavelet transform. Wavelet in six directions are generated from the kernel, where.
For each pixel position and considered scale value, the response with maximum modulus over all possible directions is considered. The centerline of a spine always has the highest intensity, where the wavelet response is centered. In each section of the spine, the point that has the highest value of is considered as the center point of this section. By linking all the center points along the section planes, a more accurate centerline of the spine is detected.
The segmentation position is defined by the sudden change of the wavelet response. In the reconstructed map of wavelet transform, adaptive threshold is set to define the segmentation position of the spine and dendrite. In adaptive threshold methods, a threshold is set for each pixel. This threshold is then used to test against the pixel intensity value to produce a binary image. The basic formulation of adaptive threshold for pixel p is given by
| (3) |
whereis the intensity of pixelpandis the response of pixelpafter the wavelet transform.
As illustrated in Fig. 4 , the wavelet response of one spine has clear boundary with other spines or parts of the dendrite from the sections close to the tip point. With the section approaching to the dendrite, the segmenting position is defined as the location where the boundary of wavelet response quickly increases.
Fig. 4.
Spine detection results after wavelet transform. (a) The original intensity map of each section, (b) The wavelet response map of each section. The sections are along a spine, and have 2 microns at intervals.
Compared with Bai’s algorithm [8], our approach can output a more accurate centerline and segmenting position because we additionally consider the wavelet response along with the intensity. In order to move on to the morphological classification of the spines, many kinds of features are calculated from the detected dendritic spines. Unlike skeletonization, our spine detection approach determines the centerline inside the spine.
3.3 Semi-supervised dendritic spines classification
Dendritic spines play an important role for the structure of neurons and are of functional importance. The main aim of spine morphological classification is to link the phenotypes of different spine classes to different biological functions. In morphological analysis, dendritic spines can be generally classified into three categories: mushroom, thin, and stubby [17]. Examples of the predefined phenotypes for dendritic spines are shown in Fig. 5 .
Fig. 5.

Examples of the predefined phenotypes, mushroom, thin, and stubby.
In a previous study [10], a classification method based on Rayburst diameters inside the dendritic spines was proposed. The Rayburst diameter in each layer of a spine was calculated and the HNR was introduced to define the spine shape analysis. HNR is easy and effective in defining the spine shapes in 2D images. However, since 3D spines always have too complex shapes, classification based on HNR is not accurate.
To solve these problems, we propose a novel morphological classification algorithm for dendritic spines based on a SSL approach. SSL is halfway between supervised and unsupervised learning. The algorithm is provided with some supervision information, which are always the labels associated with some of the samples. This makes it be suitable to classify complicated spine group with a small training dataset selected online. In the framework of dendritic spines classification based on SSL, we first extract morphological features in 3D based on our spine detection method. Second, a neurobiology expert manually selects a small portion of detected spines in each class as the training set. Finally, the labels of the remaining spines can be calculated after the training process and all the detected spines are classified by the learning framework.
SSL is a class of machine learning technique that makes use of both labeled and unlabeled data for training, typically a small amount of labeled data with a large amount of unlabeled data. SSL falls between unsupervised learning (without any labeled training data) and supervised learning (with completely labeled training data). As an efficient algorithm with some prior knowledge, SSL approach is mostly used in the classification [18]. The approach to SSL seeks to design a classifying function which is sufficiently smooth with respect to the intrinsic structure collectively revealed by known labeled and unlabeled points [19]. Consider the whole dataset represented as, and a label set as. Inside the dataset, the firstℓpoints have labelsand the remaining points are unlabeled. The goal is to predict the labelsof the unlabeled data.
In the algorithm, affinity matrix Wplays an important role in the learning, where means the similarity between pointsand. For different features inχ, different features in each column have different effects on the similarity calculation. Effective features are selected before the construction of the datasetχ. A coefficientis introduced to represent the weight ofk-th feature. should be normalized and. The number ofNspines withdfeatures can be looked at as the datasetχwithNrows anddcolumns. Then, some samples belonging to different classes are randomly selected as the training datasetand the label matrix Yis pre-labeled with training samples, where , if dataiis pre-labeled in class c; and in otherwise cases.
Before calculation, the input dataset is normalized in each column and the similarity between same features of different data can be calculated by considering the detected spines as a graph, the SSL algorithm can be described as follows:
-
1)Calculate the affinity matrixW, which is defined as:
(4)
wheremeans different spines data, kmeans thek-th feature of one data, andσis a constant.
-
2)
Construct the matrix, in whichDis a diagonal matrix with its-element equal to the sum of thei-th row ofW.
-
3)Iterate the similarity matrixFuntil convergence, where
(5)
andαis a pre-defined constant equals to 0.9 in our approach.
-
4)Letdenote the limit of the sequence. Label each pointas a label, where
(6) -
5)By the iteration Eq. (5), we get
(7)
since, and the eigenvalues ofSis in,
| (8) |
then the classification matrix is obtained as
| (9) |
Socan be calculated without iteration [19]. After these procedures, the labels of the rest dataset can be obtained.
For the application of spine image transduction, many kinds of 3D features are obtained from the spine detection, such as the head and neck diameter, spine length, volume, etc. In order to get the most reliable features in classification, a feature selection approach is proposed before semi-supervised training.
To get higher performance, two main improvements are applied in this semi-supervised framework. First, in the application of the morphological classification of spines, different 3D features are obtained from the spine detection, such as the head and neck diameter, spine length, volume, etc. To improve the results, features selection should be performed before the learning process. For each of the features, the best set ofcan be calculated. The most effective features can also be selected according to the experimental results. Second, the affinity matrixWplays an important role in the learning algorithm, wherereflects the similarity between the pointsand. Because even after normalization most of features have different orders of magnitude, the distance betweenandis not appropriate to reflect the similarity. Therefore, the value of is introduced to replace the distance. The training performance is highly improved by this new definition.
4. Results and discussions
To validate our proposed algorithm, we use the dataset that includes 20 3D image stacks acquired from a variety of mice brain regions and treatments obtained. Our method was implemented in MATLAB and deployed on a PC with an Intel Duo 3.0 GHz processor and a 4GB RAM. With the training by SSL framework, the unlabeled dendritic spines were assigned to different classes. Since there is no iteration in this frame work, the time consuming part of the semi-supervised framework depends only on the number of features being used. In our practice, the learning process has a relative high speed of 30-40 seconds in classification of one image with about 80-100 spines.
4.1 Results analysis of dendritic spines detection
In order to validate our proposed algorithm, the semi-supervised segmentation results are validated with the manual result images. Dendritic spines are firstly detected, and a neurobiologist manually marked the detected spines on the neuron in all 20 image stacks after 3D reconstruction. Then, the SSL spine detection approach was conducted on the dataset. We also used the NeuronStudio software, which analyzes neurons based on the algorithms in [10,11], to detect and classify the dendritic spines from 3D neuron image stacks. In the validation, we mainly compared the spine detection accuracy between two approaches. Compared with the manually detection results by a neurobiology expert, the number of detected spines, the number of wrong detection, and the number of missing spines are also compared. The detailed spine detection results are shown in Table 1 .
Table 1. Comparison of spine detection results on the whole dataset.
| Strategy | Number of detected spines | False positive (wrong detection) | False negative (missing) | |
|---|---|---|---|---|
| Manual | 939 | |||
| Our algorithm | 927 | 45 | 12 | |
| NeuronStudio | 896 | 52 | 43 | |
From Table 1, we can see that there are some spines missing in the detection of both our algorithm and NeuronStudio. For the our algorithm, most of the missing spines have a small Distance to Centerline (DTC), which means these spines are not obviously protruding from the dendrite. Since our spine detection method calculates the wavelet transform response along the spine, the responses variation is not big and there are fewer sections on the line from tip point to centerline. This is the main reason that spines are missed in our detection approach.
Table 1 also shows that the NeuronStudio missed more dendritic spines during the spine detection than our algorithm. This is because NeuronStudio cannot extract the whole dendrite from the neuron since the dendrites extracted by NeuronStudio are separated lines. The Rayburst diameter algorithm is very sensitive to the intensity of the dendrite. For the image stacks with low intensity, the dendrite will break in the low intensity area so there is no spine that can be detected in the broken area. This is the main reason that the NeuronStudio has a much higher missing rate in dendritic spine detection. To further evaluate the statistical results of two algorithms, we compare the differences of spine detection between our algorithm and NeuronStudio by using Chi Square Test [20]. Assuming the null hypothesis is true, a Chi Square Test is a test in which the sampling distribution can be made to approximate a Chi Square distribution (withkdegrees of freedom is the distribution of a sum of the squares ofkindependent standard normal random variables) as closely as desired by making the sample size large enough. According the Chi Square Test results, the sensitivity of our algorithm and NeuronStudio were 98.7% and 95.2% respectively, showing there was significant difference between them(X2=19.1, P<0.001), and the specificity of our algorithm and NeuronStudio were 95.1% and 94.1% respectively, where no significant difference between them(X2=0.82, P=0.37). Finally, the Youden index of our algorithm and NeuronStudio were 93.8% and 89.4% respectively, there was significant difference between them(X2=11.83, P<0.001).
4.2 Results analysis of spines morphological classification
Prior to the classification of the dendritic spines, typical phenotypes of each class are predefined by a neurobiologist for biology. Some of the features are shown in Table 1 for the different spine phenotypes studied in our experiments. Since those features are essential for the differentiation between the three phenotypes, lager weights ofare applied in the calculation of affinity matrix. A total of 927 spines in 20 image stacks are detected and used for the classification experiments.
In the experiments, in order to get the best accuracy of classification, the feature weight in the affinity matrix can be adjusted automatically. After comparison of the results from a set of training, the best set offor each feature can be calculated. According to the experiment results, features such as head to neck ratio and head to length ratio are proved to be the most effective to the classification results.
The feature values vary a lot as shown in Table 2 , especially 'Angle to XY Plane', which has larger std. deviations than mean values, which means it couldn't be taken as an efficient feature in the classification. Meanwhile, in spine detection, protrusions of the dendrite may be detected as spines and may be classified as the stubby. In fact, these protrusions are parts of the dendrite and are not functional as spines. Therefore, it is necessary to consider the stubby with other two phenotypes separately. Accordingly, we classify the detected spines with two different strategies. The first is to classify all the detected spines into three classes: mushroom, thin, and stubby. The second looks stubby as protrusion and considers the mushroom and thin classes as one group of normal spines. According to literature [21], in a set of more sophisticated morphological classification strategy of dendritic spines, ‘mushroom’ and ‘thin’ both have perforated postsynaptic density (PSDs) located in the cytoplasmic surface of the synaptic membrane, rather than ‘stubby’ with macular PSDs. Therefore, in evaluating the classification performance, we assume that ‘mushroom’ and ‘thin’ could be looked as one class. Afterwards, we validate the classification performance by comparing the results obtained from our automated approach to those of the manual analysis.
Table 2. Average and std. deviation of features in morphological classification of dendritic spines. The unit of length is micron (µm), and the unit of angle is degree.
| Feature | Mushroom | Thin | Stubby |
|---|---|---|---|
| Head to Neck Ratio | 7.26 ± 2.74 | 2.08 ± 1.01 | 0.771 ± 0.438 |
| Head to Length Ratio | 0.212±0.059 | 0.118±0.072 | 0.141±0.103 |
| Head Diameter | 0.726±0.027 | 0.241±0.055 | 0.360±0.092 |
| Neck Diameter | 0.101±0.040 | 0.110±0.053 | 0.467±0.210 |
| Max Distance to dendrite surface | 1.76±0.985 | 1.67±1.13 | 1.49±0.665 |
| Angle to XY Plane | −7.23±26.41 | −10.02±-35.02 | 17.65±15.68 |
| Length | 3.43±1.38 | 2.05±0.761 | 2.56±0.533 |
As shown in Fig. 6 , an increase of the training dataset gradually leads to a higher classification accuracy of the algorithm. However, the error rate decreases slowly. For each class, if at least eight samples are retained in training dataset, the classification accuracy is stable. At the same time, the total number of the training dataset only accounts to a very small portion of the whole dataset. Other semi-supervised algorithms such as Supporting Vector Machine (SVM) [22] need a larger portion of training dataset. Compared to these algorithms, our approach can also produce good performance with a training dataset consisting only of a few samples for each class.
Fig.6.
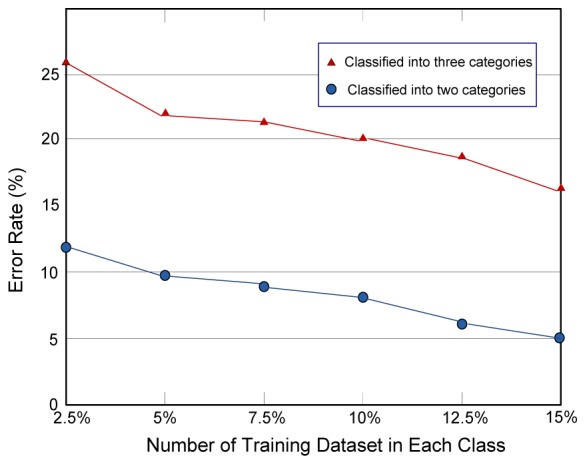
Error rates for morphological classification of dendritic spines. X coordinate denotes the portion of training samples in each class and Y coordinate shows the error rate for classification. The line marked with triangles denotes results classified into 3 categories and the line with circles denotes results obtained by the second classification of the phenotypes into 2 categories
In order to further compare the results with those of the algorithm introduced in [10], another experiment was conducted on the sample datasets of NeuronStudio using our algorithm. The dataset consisted of two image stacks with the resolution 512×512 pixels in each slice and a definition of 0.05×0.05×0.10 µm/pixel. In this experiment, a total of 896 dendritic spines were detected by NeuronStudio and 10% samples for each class were selected for the morphological classification. We also used the features generated from NeuronStudio. The performance of both algorithms is shown below.
Table 3 shows that our learning algorithm has similar accuracy for the classification of the spines into three categories with NeuronStudio and has a higher accuracy in distinguishing protrusions from spines. The results also show that the distance between features in protrusions and normal spines is much larger than that between mushroom and thin classes. This gives some help in the spine detection. Moreover, our approach for the classification of different spine phenotypes can give some useful information for the spine functional analysis.
Table 3. Classification performance for the sample datasets of [10]. The size for the training dataset is set to 10% samples in each class.
| Error Rate | NeuronStudio | SSL Approch |
|---|---|---|
| Error Rate in 2 Classes | 9.0% | 7.8% |
| Error Rate in 3 Classes | 18.6% | 20.1% |
In order to further evaluate the classification result of our SSL approach, we compare the algorithm with the common classification method, the Supporting Vector Machine (SVM). Since the training dataset for SVM should contain a big portion of the original dataset, we used the 50-fold cross validation to validate the classification performance of SVM. The sigmoid function was selected as the kernel. Results show that the best accuracy that SVM can get is 74%. Generally, since the training dataset is more than half of the whole dataset, the classification performance of SVM is not satisfying because there are few features in the dataset.
The experimental results shown above give us a clear impression that our proposed algorithm has good performance of combining the dendritic spine detection and classification. First, our approach detects more spines based on the wavelet transform. Second, with a small training dataset, the SSL algorithm gives convincing labeled outputs for segmentation and classification. Third, the semi-supervised approach gives an efficient way to classify the spines online, which needs neurobiologist to select the most reliable samples for the training. The improvement of classification accuracy is also benefited by the online learning method.
5. Conclusions
In this paper, we propose a novel morphological analysis algorithm for dendritic spines based on a SSL approach. After preprocessing in 3D space, the dendrite is extracted from the neuron based on the casting rays method. Spines are detected with clustering candidate voxels from the tip points and then segmented according to the response to the wavelet transform. Feature vectors of dendritic spines are further classified by the SSL approach. Finally, we get the morphological analysis results of dendritic spines along the neuron.
Since the training dataset is selected by a neurobiologist in our SSL framework, it avoids the error occurring in training dataset selection with manual intervention. An increase of the training dataset gradually leads to a higher classification accuracy of the algorithm. However, the error rate decreases slowly. In the classification stage, if at least 15% for each class are retained in training dataset, the classification accuracy is about 95%, which shows that the SSL framework is more accurate and robust compared to the traditional algorithms.
With the morphological analysis of dendritic spines, the relationship between spine str re and some of the neuron degeneration diseases can be researched deeply. Spine morphology is very diverse and spine size is correlated with the strength of the synaptic transmission. In addition, the spine neck biochemically isolates individual synapses. Therefore, spine morphology directly reflects its function [21]. As shown in the experimental results, the joint framework of spine detection and classification can efficiently analyze the dendritic spines morphology directly in 3D space, which provides a set of useful features for the neurobiologist to delineate the mechanism and pathways of neurological conditions.
The performance of SSL algorithm is highly determined by the features included in training vectors. Therefore, selecting the most representative features will further improve the classification accuracy of SSL. On the other hand, in order to get better detection results, we will apply some mesh structures and extract more efficient features for segmentation in the future. The classification accuracy can also be improved by further research on features extracted from the spine morphological structure. Future research will be conducted on the relationship between the shape variation of dendritic spines and the Alzheimer Disease. It will be an efficient way to analyze 3D dendritic spines in the research of neurological conditions.
References and links
- 1.Knafo S., Alonso-Nanclares L., Gonzalez-Soriano J., Merino-Serrais P., Fernaud-Espinosa I., Ferrer I., DeFelipe J., “Widespread changes in dendritic spines in a model of Alzheimer’s disease,” Cereb. Cortex 19(3), 586–592 (2009). 10.1093/cercor/bhn111 [DOI] [PubMed] [Google Scholar]
- 2.Spires T. L., Meyer-Luehmann M., Stern E. A., McLean P. J., Skoch J., Nguyen P. T., Bacskai B. J., Hyman B. T., “Dendritic spine abnormalities in amyloid precursor protein transgenic mice demonstrated by gene transfer and intravital multiphoton microscopy,” J. Neurosci. 25(31), 7278–7287 (2005). 10.1523/JNEUROSCI.1879-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hartley D. M., Ye C. P., Diehl T., Vasquez S., Vassilev P.M., Teplow D. B., Selkoe D. J., “Protofibrillar Intermediates of amyloid beta-protein induce acute electrophysiological changes and progressive neurotoxicity in cortical neurons,” J. Neurosci. Methods 19(20), 9 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.J. B. Pawley, Handbook of Biological Confocal Microscopy. 3rd ed., Springer, 988 (2006). [Google Scholar]
- 5.Nimchinsky E. A., Sabatini B. L., Svoboda K., “Structure and function of dendritic spines,” Annu. Rev. Physiol. 64(1), 313–353 (2002). 10.1146/annurev.physiol.64.081501.160008 [DOI] [PubMed] [Google Scholar]
- 6.Zhang Y., Zhou X., Witt R. M., Sabatini B. L., Adjeroh D., Wong S. T., “Dendritic spine detection using curvilinear structure detector and LDA classifier,” Neuroimage 36(2), 346–360 (2007). 10.1016/j.neuroimage.2007.02.044 [DOI] [PubMed] [Google Scholar]
- 7.Cheng J., Miller E., Witt R. M., Zhu J., Sabatini B. L., Wong S. T. C., “A novel computational approach for automated dendrite spines detection in two-photon laser scan microscopy,” J. Neurosci. Methods 165(1), 13 (2007). 10.1016/j.jneumeth.2007.05.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bai W., Ji L., Cheng J., Wong S.T.C., “Automated dendritic spine analysis in two-photon laser scanning microscopy images,” Cytometry A 71(10), 9 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Janoos F., Xu X., Machiraju R., Huang K., Wong S. T. C., “Robust 3D reconstruction and identification of dendritic spines from optical microscopy imaging,” Med. Image Anal. 13(1), 167–179 (2009). 10.1016/j.media.2008.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rodriguez A., Dickstein D. L., Hof P. R., Wearne S. L., “Automated three-dimensional detection and shape classification of dendritic spines from fluorescence microscopy images,” PLOS one, 3(4), e1997 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rodriguez A., Ehlenberger D. B., Hof P. R., Wearne S. L., “Rayburst sampling, an algorithm for automated three-dimensional shape analysis from laser scanning microscopy images,” Nat. Protoc. 1(4), 2152–2161 (2006). 10.1038/nprot.2006.313 [DOI] [PubMed] [Google Scholar]
- 12.Matsuzaki M., Ellis-Davies G. C., Kasai H., “Three-dimensional mapping of unitary synaptic connections by two-photon macro photolysis of caged glutamate,” J. Neurophysiol. 99(3), 1535–1544 (2008). 10.1152/jn.01127.2007 [DOI] [PubMed] [Google Scholar]
- 13.Yuste R., Denk W., “Dendritic spines as basic functional units of neuronal integration,” Nature 375(6533), 682–684 (1995). 10.1038/375682a0 [DOI] [PubMed] [Google Scholar]
- 14.Svoboda K., Yasuda R., “Principles of two-photon excitation microscopy and its applications to neuroscience,” Neuron 50(6), 823–839 (2006). 10.1016/j.neuron.2006.05.019 [DOI] [PubMed] [Google Scholar]
- 15.Q. Li, X. B. Zhou, Z. Deng, M. Baron, M. A. Teylan, Y. Kim, and S. T. C. Wong, A Novel Surface-based Geometric Approach for 3D Dendritic Spine Detection from Multi-phonton Excitation Microscopy Images, in The Sixth IEEE International Symposium on Biomedical Imaging. IEEE: Boston, MA, U.S. (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hering H., Sheng M., “Dendritic spines: structure, dynamics and regulation,” Nat. Rev. Neurosci. 2(12), 880–888 (2001). 10.1038/35104061 [DOI] [PubMed] [Google Scholar]
- 17.Hayashi Y., Majewska A. K., “Dendritic spine geometry: functional implication and regulation,” Neuron 46(4), 529–532 (2005). 10.1016/j.neuron.2005.05.006 [DOI] [PubMed] [Google Scholar]
- 18.O. Chapelle and A. Zien, Semi-Supervised Learning (Cambridge: MIT Press 2006). [Google Scholar]
- 19.D. Zhou, T. N. Lal, J. Weston, and B. Scholkopf, Learning with Local and Global Consistency. Advances in Neural Information Processing Systems, 16, 321–8 (2004). [Google Scholar]
- 20.P. E. Greenwood, A Guide to Chi-Squared Testing, 280 (John Wiley & Sons, 1996). [Google Scholar]
- 21.Tashiro A., Yuste R., “Structure and molecular organization of dendritic spines,” Histol. Histopathol. 18(2), 617–634 (2003). [DOI] [PubMed] [Google Scholar]
- 22.J. Shawe-Taylor and N. Crisianini, Support Vector Machines and Other Kernel-Based Learning Methods (Cambridge, UK: Cambridge University Press 2000). [Google Scholar]



