Modeling Longitudinal Drinking Data in Clinical Trials: An Application to the Combine Study

Abstract

Background

There is a lack of consensus in the literature as to how to define drinking outcomes in clinical trials. Typically, separate statistical models are fit to assess treatment effects on a number of summary drinking measures. These summary measures do not capture the complexity of drinking behavior. We used the COMBINE Study to illustrate a statistical approach for examining treatment effects on high-resolution drinking data, which takes into account abstinence and non zero drinking in the same analysis.

Methods

This is a secondary data analysis of COMBINE (n=1195) participants randomly assigned to naltrexone, acamprosate, with medical management and/or Combined Behavioral Intervention (CBI). Using a Poisson hurdle model, abstinence and number of drinks were simultaneously modeled with treatment, prior drinking, week, and study center as covariates. Odds ratios (OR) for abstinence and relative risk (RR) for drinking are reported. A special emphasis was placed on the evaluation of “risky drinking” defined as 3 drinks per day for women and 4 for men.

Results

During treatment, naltrexone increased the odds of abstinence versus placebo naltrexone (OR=1.35[1.06,1.65]) but receiving CBI in addition to naltrexone (versus not) obscured this effect; thus, the naltrexone effect was largest in the group not receiving CBI (OR=1.87[1.29,2.46]). Naltrexone versus placebo naltrexone also reduced the risk of drinking in people who resumed risky drinking, defined as more than 3 and 4 drinks/day for women and men, respectively (RR=0.58[0.24,0.93]) and increased the odds of maintaining low risk drinking (OT=1.99[1.07,2.90]). Both effects were strongest in the absence of CBI when only “medical management” was provided.

Conclusions

Naltrexone promotes both abstinence and reduction in drinking once risky drinking is resumed. The finding that the rate of risky drinking is reduced once a slip has occurred bolsters support for the use of naltrexone, especially since this was observed in the context of a medical management approach that could be delivered in various health care settings. The utilization of a hurdle model adds to prior reports on summary drinking measures, which found no effect of naltrexone on abstinence, did not evaluate its effect closely on risk drinking, and did not analyze weekly drinking behavior.

1. Introduction

The Combined Pharmacotherapies and Behavioral Interventions for Alcohol Dependence (COMBINE) study was the largest study ever performed of pharmacotherapy for alcoholism in the United States (COMBINE Study Group, 2003; Anton et al., 2006). It was designed to assess the benefits of combining behavioral and pharmacological interventions in the treatment of alcohol dependence, a leading preventable cause of morbidity and mortality and a major contributor to health care costs (Mokdad, et al., 2000; Grant, et al., 2004; McKenna et al., 2005). In the COMBINE study, naltrexone (Kranzler and Van Kirk, 2001), acamprosate (Mason, 2003; Mann et al., 2004), and combined behavioral intervention (CBI), were given in combination according to a placebo-controlled 2×2×2 factorial design over 16 weeks (Table 1). It was hypothesized that acamprosate would be effective in promoting abstinence while naltrexone would be effective in reducing the amount of drinking once any drinking had occurred; CBI was proposed to reinforce behaviors towards abstinence and/or to reduce relapse once any drinking had occurred, and it was hypothesized to interact positively with naltrexone (O'Malley et al., 1992; Anton et al., 1999). A medical management (MM) procedure designed to reflect what might occur in primary care practice was provided for participants in all but one study group.

Table 1.

Study design and sample size. ACA= Acamprosate, NTX=naltrexone, CBI = Cognitive Behavioral Intervention

		Placebo ACA	ACA
No CBI	Placebo NTX	153	153
	NTX	154	148
CBI	Placebo NTX	156	151
	NTX	156	157

In the COMBINE study, the two a priori defined primary outcomes were ‘time to the first day of heavy drinking’ and ‘percent days abstinent’ in the 16-week treatment period as derived from calendar recall; these summary measures are the most common primary outcomes specified in clinical trials of alcohol use disorders (Babor et al., 1994; Finney et al., 2003). Naltrexone (+ MM alone) or CBI (+ placebo acamprosate + naltrexone + MM) increased time to first heavy drinking day compared to MM alone + placebo acamprosate but, contrary to expectation, there was no additional advantage of combining CBI with naltrexone over each monotherapy. No effects of either medication on percent days abstinent were found. The failure to find main effects of acamprosate, (alone or in combination with CBI or naltrexone), was unexpected given the positive results from studies of acamprosate (Mason, 2003; Mann et al., 2004) and of the combination of acamprosate and naltrexone conducted in Europe (Kefer et al., 2003; Feeney et al., 2006).

Experts disagree on what are the most relevant summary measures of drinking outcomes in clinical treatment trials (Cisler and Zweben, 1999; Meyer, 2001; Wang et al., 2002; Johnson et al., 2004; Mckay et al., 2006; Shirley et al., 2010; Prisciandaro et al., 2012) and Cochrane reviews have demonstrated a lack of consensus in primary outcome definitions across alcohol trials (Srisurapanont and Jarusuraisin, 2008; Rosner et al., 2009). Further, when drinking outcomes are analyzed as summary measures, for example, when consumption over a 16-week period is summarized into a single endpoint (e.g., percent days abstinent), high resolution information about the complexity of drinking behavior is lost. As a result, the power to detect significant differences in drinking outcomes may be reduced. The limitations of two of the most commonly used summary statistics are illustrated in Figure 1. Figure 1 displays 16 weeks of daily drinking data for 4 patients from the COMBINE study for whom summary measures may be uninformative. Patients 1 and 2 had one early onset heavy drinking day in the entire 16-week treatment period but did not drink any other day in that period. Patients 3 and 4 never officially met a predefined heavy drinking day in those 16 weeks, even though they drank several drinks on many days since the start of the study. Therefore, in the “time to first heavy drinking day” analysis of the original trial report, patient 1 and 2 are considered early treatment ‘failures,’ while patients 3 and 4 are considered a treatment ‘success’. Patients 3 and 4 have similar percent days abstinent even though patient 4 drinks more on non-abstinent days, a behavior that is undetectable when analyzing the summary statistic “percent days abstinent.” These illustrations underscore the limitations of summary endpoints in assessing drinking behavior.

Figure 1.

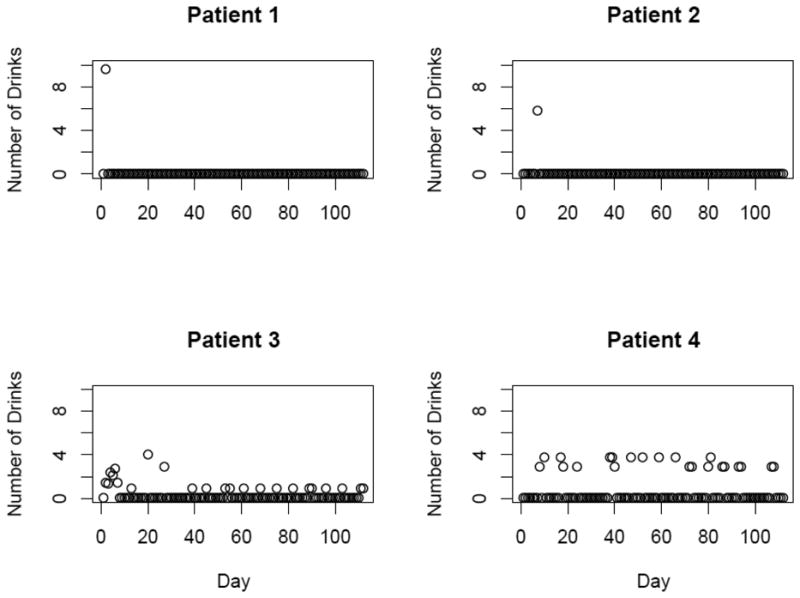
Drinking patterns of 4 representative patients from the COMBINE study.

Instead, abstinence and the number of drinks consumed throughout the study period may be conceptualized as separate but correlated processes. These outcomes are usually analyzed using generalized linear models (GML) but zero-inflated Poisson or binomial (ZIP, ZIB) regression may be used to model consumption if data violate the assumptions of GLMs. There have been several applications of such zero inflated models in the substance use literature (Le and Galea, 2010; Hu et al., 2011; Meszaros et al., 2011; DeSantis et al., 2011; Fielder et al., 2012; Peeters et al., 2012; Walley et al., 2012). However, the statistical assumption of zero inflated models is that zero drinking arises from a set of patients who have zero risk of drinking. Given that all patients in the COMBINE Study are substance-dependent at baseline, this assumption is unreasonable. An alternative 2-part Poisson hurdle model that assumes subjects remain at risk for drinking for the duration of the study is more appropriate (e.g., Mullahy, 1986; McLachlan and Peel, 2000; Bandyopadhyay et al., 2011). Thus, the objective of this paper is to re-analyze the COMBINE data using a two-part hurdle model, to extend this model to accommodate low and high risk drinking definitions, and formally to compare results to those obtained from the original trial report.

2. Methods

2.1 Participants and Procedures

Participants in the COMBINE Study included 1383 eligible alcohol dependent individuals who were randomly assigned to 1 of 9 groups for 16 weeks of treatment. In a 2×2×2 factorial design, all eight groups received MM, 4 groups received more intensive counseling (CBI), and patients in all 8 groups received either active/placebo naltrexone or active/placebo acamprosate yielding 4 medication groups, within each level of counseling (CBI/no CBI). This is illustrated in Table 1. Naltrexone, an opioid receptor antagonist, was studied based on evidence that it reduced the risk of heavy drinking in most studies (Kranzler et al., 2001; Srisurapanont and Jarusuraisin, 2008) while acamprosate, thought to reduce glutamatergic hyperactivity associated with protracted abstinence, was thought to maintain abstinence within varied behavioral treatment frameworks (Mason, 2003; Mann et al., 2004). Medical Management was designed as a means of enhancing medication compliance and reinforcing sobriety that could be used in a primary care or managed care setting by nonspecialists (Pettinati et al., 2004; Miller 2004; Pettinati et al., 2005; Longabaugh, et al., 2005). A ninth group received CBI alone and no pills - as in previous COMBINE reports, this group was not analyzed here since it is outside the 2×2×2 factorial design. This results in a total sample size of 1226 for the current analysis.

2.2 Measures

Individuals were assessed 9 times during the 16 weeks of treatment as well as 3 additional times (i.e., 26, 52, and 68 weeks post-randomization) during the 52 weeks following treatment. Drinking was assessed via Time Line Follow-Back (TLFB), a calendar recall method that has been extensively validated to provide accurate measures of daily drinking. Secondary outcomes including mood and quality of life were also obtained. Primary and secondary analyses of the clinical trial have been reported (Anton et al., 2006; LoCastro et al., 2009; Witkiewitz et al., 2009; Gueorguieva, et al., 2010; Prisciandaro et al., 2012) and data are publicly available for download following registration on the National Institute on Alcohol Abuse and Addiction website. The reader is referred to the primary report for further information on study design and measures (Anton et al., 2006).

2.3 Statistical analyses

Abstinence and reduction in drinking are conceptualized as correlated but separate processes; the former was to be the target of acamprosate and the latter of naltrexone (Littleton and Zieglansberger, 2003). Since it was initially hypothesized that the two medications might affect different facets of the alcohol consumption process (i.e., abstinence violation and subsequent alcohol consumption), the Poisson hurdle model, which promotes a 2-stage decision making process that parallels this conceptualization, is a useful tool to assess treatment effects (Fielder et al., 2012). The first stage involves moving through a zero realization state (i.e., abstinence days). Once this “zero hurdle” is crossed, that is, once drinking has been re-established, the second stage determines the number of subsequent drinks per day. The two processes are modeled via two regressions (logistic and Poisson), i.) generates the “zeros,” i.e., patients who are believed to be at least temporarily abstinent, and ii.) generates counts (drinks consumed) strictly greater than zero. Treatment assignment and covariates are allowed to predict the zeros and the counts in i. and ii. Correlation between the two parts is induced by the introduction of shared random intercept. Covariates enter the model via a logistic regression to predict abstinence, and via a Poisson regression to predict consumption after drinking is resumed. Full model details are shown in the Appendix. The set of regression coefficients are denoted by β and γ for the logistic and Poisson regression components, respectively. The exponent of each component of β is defined (for comparing treatments A:B) as “the odds of abstinence (zero drinking) in treatment A:B” and the exponent of each component of γ is defined as “the risk of increased drinking in treatment A:B after drinking has been resumed.”

To establish a longitudinal outcome variable of reasonable dimension, the TLFB was summarized into average number of drinks per day for each week. This was rounded to the nearest whole number, resulting in a zero inflated outcome since the majority of patients did not drink during the treatment period. Covariates (shown in Table 1 in the Appendix) included ordinal week, three indicators for each of the three active treatments, three interaction terms formed by these treatment indicators, and a three way interaction. To parallel the primary analysis, baseline average number of drinks per day for the past 30 days and study center were also adjusted for (Anton et al., 2006). A hurdle model with shared random effects is subject to computational difficulty if too many covariates are included. Thus, exploratory work that incorporated covariates in both the abstinence and drinking part of the model was performed and determined that study center and prior drinking better predicted abstinence. These covariates were retained in the hurdle part of the model while week better predicted drinking and was retained in the drinking part of the model. Treatments and their interactions were included in both parts of the model.

The NIAAA considers a heavy drinking day as being 5 or more standard drinks for men and 4 or more for women (Falk et al., 2010). Assessing the low level “harmful” or “risky” drinking cutoff adds another dimension to the existent literature. Since a hurdle can be placed at any number of drinks determined by experts, we utilized this NIAAA cutoff to formulate a “low risk drinking hurdle model” rather than a zero hurdle model. To achieve this, a second model was developed and fit using the expert consensus that < 4 drinks/day for women and < 5 drinks/day for men represents non-harmful or low risk drinking. This involves a modification to the denominator of the model likelihood where the support of the hurdle distribution is demarcated at greater than 3 and 4 drinks for women and men. This model formulation and all associated SAS code are shown in the Appendix.

To compare the zero drinking and risky drinking hurdle models to a commonly used longitudinal Poisson regression model (e.g., Le and Galea, 2010; Bandyopadhyay et al., 2011; Walley et al., 2012) three statistics were calculated. The Akaike information criteria (AIC) and Bayesian information criteria (BIC) were used to compare non-nested models. Smaller values of these criteria indicate a better fit. The Vuong likelihood ratio-based test was used to compare nested models. In short, the Vuong test tests the null hypothesis that two models under comparisons are equally close to the “true” model for the data, against the alternative hypothesis that one model is closer (Vuong, 1989). A significant p-value on the Vuong test (p<=0.05) indicates that the model in question is closer to the true model than the reference model (where the longitudinal Poisson regression is the reference model). Hurdle model results are presented in terms of relative risks (RR), odds ratios (OR) and 95% confidence intervals, or regression betas and standard errors (SE).

Finally, to parallel the COMBINE Study's a priori hypotheses, treatment period (weeks 1-16) was analyzed separately from post treatment period (weeks 17-26). The reason for separate modeling is that treatment was expected to be effective during the treatment period but after cessation of treatment, maintenance of the effect is of interest. These are considered two independent a priori tests, thus the 3 models (zero hurdle, risky hurdle, and Poisson) were fit for each period. For each time period assessed, one could envision a correction for multiple testing for the three treatment variables, for the invocation of a 2 part model (ie, 2 correlated regressions each with treatment covariates), or for the other covariates in our model (prior drinking, week, center). However, corrections were not used since the treatment effects were hypothesized a priori, because the utility of the two part model is to help protect against type I error rate inflation in the first place, and because the significance of remaining covariates were not of primary interest.

3. Results

3.1 Treatment period

Table 2 shows parameter estimates, standard errors, and associated p-values for all variables for both hurdle models fit to the treatment period (weeks 1-16). For both models, there is a significant effect of week on consumption, indicating increased alcohol consumption over the treatment period. Although Table 2 reveals which treatment interactions are significant, due to the complicated study design, post hoc contrasts were necessary to obtain the main effect and the pairwise estimates subsequently presented in Table 2. Table 2 displays odds ratios for abstinence and relative risks for consumption, along with 95% confidence intervals, for all contrasts resulting from the zero hurdle model and the low risk drinking hurdle model. The main effects were obtained by averaging estimates over the appropriate cells of the design in Table 1. The main effect estimates are interpreted, for example, as acamprosate versus placebo acamprosate.

Table 2.

The left side contains results from the zero-drink hurdle model and the right side contains results from the <=3 drink and <= 4 drink hurdle model fit to treatment period data (weeks 1-16). ACA=acamprosate, NTX=naltrexone, Prior No. Drink = average number of drinks per day for the month prior to the required abstinence period.

	Zero-drink hurdle model				Low risk drinking hurdle model
Variable	Effect	SE(Effect)	95% CI	P-Value	Effect	SE(Effect)	95% CI	P-Value
Hurdle
Intercept 1	1.29	0.17	0.96,1.62	0.0001	4.95	0.35	4.26,5.64	0.0001
ACA	0.13	0.19	-0.25,0.51	0.50	0.10	0.38	-0.65,0.86	0.79
NTX	0.64	0.19	0.26,1.02	0.001	1.08	0.39	0.32,1.84	0.006
CBI	0.49	0.19	0.11,0.87	0.01	0.99	0.39	0.24,1.76	0.01
ACAxNTX	-0.02	0.22	-0.46,0.42	0.91	0.24	0.45	-0.64,1.11	0.60
ACAxCBI	-0.09	0.22	-0.53,0.35	0.69	-0.27	0.45	-1.15,0.60	0.54
NTXxCBI	-0.67	0.22	-1.11,-0.23	0.003	-1.16	0.45	-2.04,-0.28	0.001
Prior No. Drink	-0.07	0.004	-0.07,-0.06	0.0001	-0.08	0.00	-0.09,-0.07	0.0001
Poisson Regression
Intercept 2	1.80	0.14	1.52,2.08	0.0001	5.05	0.33	4.40,5.70	0.0001
ACA	0.11	0.19	-0.26,0.48	0.55	0.27	0.38	-0.48,1.03	0.47
NTX	0.22	0.19	-0.16,0.59	0.25	1.17	0.39	0.41,1.94	0.002
CBI	-0.11	0.19	-0.47,0.26	0.58	0.58	0.45	-0.18,1.33	0.14
ACAxNTX	-0.24	0.22	-0.67,0.19	0.28	-0.06	0.45	-0.94,0.82	0.89
ACAxCBI	-0.15	0.22	-0.58,0.28	0.49	-0.17	0.45	-1.05,0.71	0.71
NTXxCBI	0.12	0.22	-0.31,0.55	0.60	-1.05	0.45	-1.94,-0.17	0.02
Week	0.02	0.00	0.02,0.02	0.0001	0.01	0.002	0.01,0.02	0.0001

The zero hurdle model showed a significant naltrexone by CBI interaction in the negative direction (β = -0.67, SE=0.22, p =0.003) indicating CBI reduced the effectiveness of naltrexone on abstinence when given with MM only (no CBI). In the presence of significant interactions, main effects must be interpreted with caution, thus all pairwise contrasts were examined (Table 3). There was a significant main effect of naltrexone on abstinence (OR=1.35[1.06,1.65]); however, due to the fact that CBI reduced the naltrexone effect, the comparison with the greatest OR of abstinence was naltrexone + no CBI versus placebo naltrexone + no CBI (OR=1.87[1.29,2.46]). Although there was no main effect of CBI on abstinence, there was an increased odds of abstinence in the CBI + placebo naltrexone group versus the no CBI + placebo naltrexone group (OR=1.56[1.08, 2.05]).

Table 3.

Pairwise odds ratios and risk ratios and 95% Confidence Intervals for the treatment period.

	Zero-drink hurdle model		Low risk drinking hurdle model
Effect	OR[95%CI]	RR[95%CI]	OR[95%CI]	RR[95%CI]
ACA Main Effect	1.08[0.84,1.69]	1.08[0.85,1.31]	1.08[0.57,1.58]	0.84[0.46,1.23]
NTX Main Effect	1.35[1.06,1.65]*	0.86[0.67,1.04]#	1.99[1.07,2.90]*	0.54[0.30,0.79]*
CBI Main Effect	1.15[0.90,1.41]	1.14[0.89,1.38]	1.57[0.84,2.30]	0.88[0.47,1.29]
ACA+NTX vs PLB ACA+PLB NTX	1.46[1.00,1.91]*	0.93[0.65,1.21]	2.21[0.79,3.63]	0.47[0.17,0.76]*
ACA+ PLB NTX vs PLB ACA+PLB NTX	1.09[0.76,1.43]	0.97[0.68,1.27]	1.02[0.37,1.68]	0.81[0.30,1.32]
PLB ACA+ NTX vs PLB ACA+PLB NTX	1.38[0.95,1.80]	0.76[0.53,0.99]*	1.84[0.66,3.03]	0.52[0.19,0.85]*
ACA+CBI vs PLB ACA+no CBI	1.24[0.86,1.62]	1.22]0.85,1.59]	1.65[0.58,2.71]	0.75[0.26,1.24]
ACA+no CBI vs PLB ACA+no CBI	1.13[0.78,1.47]	1.00[0.69,1.31]	1.17[0.40,1.94]	0.77[0.26,1.28]
PLB ACA+CBI vs PLB ACA vs no CBI	1.21[0.83,1.58]	1.06[0.74,1.38]	1.74[0.62,2.86]	0.81[0.29,1.33]
NTX+CBI vs PLB NTX+no CBI	1.49[1.03,1.96]*	0.97[0.68,1.27]	2.45[0.93,3.96]	0.55[0.21,0.90]*
NTX+no CBI vs PLB NTX+no CBI	1.87[1.29,2.46]*	0.91[0.63,1.18]	3.26[1.21,5.31]*	0.32[0.12,0.52]*
PLB NTX+CBI vs PLB NTX+no CBI	1.56[1.08,2.05]*	1.20[0.83,1.56]	2.36[0.90,3.82]	0.61[0.23,0.98]*

^*Indicates significance at p<0.05 and

^#indicates p<0.10.

Once any drinking is resumed, the Poisson part of the model assesses the effects of each treatment on number of drinks consumed (bottom of Table 2). Although there were no significant predictors of consumption in the zero hurdle model, the direction of the naltrexone main effect was to reduce the risk of consumption after drinking had occurred, but this did not reach statistical significance. Thus there is no evidence for the effectiveness of naltrexone in reduction of drinking after drinking is resumed.

The low risk drinking hurdle model also showed a significant naltrexone by CBI interaction in the negative direction (Table 2, β = -1.16, SE = 0.45, p=0.001) indicating that CBI reduced the effect of naltrexone when given with MM only (no CBI) in preventing high risk drinking. There was also a significant negative interaction in the negative direction in the Poisson part of the model (Table 2, β = -1.05, SE = 0.45, p=0.02) indicating that CBI reduced the effect of naltrexone when given with MM only (no CBI) in decreasing the risk of drinking after high risk drinking was resumed. There was a strong significant main effect of naltrexone in increasing the odds of low risk drinking, and in reducing the risk of drinking after high risk drinking was resumed (Table 3). The effects were strongest for the comparison of naltrexone versus placebo naltrexone in the absence of CBI (OR = 3.26[1.21,5.31]; RR = 0.32[0.12,0.53]). To summarize these results, a person on naltrexone has 3.3 times the odds of maintaining low risk drinking and a 68% reduction in the risk of drinking after high risk drinking is resumed, as compared to a person on placebo naltrexone (in the absence of CBI).

All diagnostics indicate that the implementation of the hurdle improves the model fit but that the best fit is provided by the hurdle model for low/high risk drinking. AIC and BIC both favored the hurdle models over the more commonly applied longitudinal Poisson regression model that does not account for zero inflation (Table 5). The Vuong statistic showed that the zero hurdle model did not perform significantly better than the simpler model (V = -1.23, p = 0.22); however, the low risk drinking hurdle model performed significantly better than the simpler model (V = -55.63.73, p < 0.0001). The model fit statistics favoring the low risk drinking hurdle is interesting in light of the findings that the low risk drinking hurdle model resulted in a larger and more significant effect size for naltrexone; thus the placement of the hurdle and 3 or 4 drinks better illustrates naltrexone's effectiveness in decreasing “risky” or “harmful” drinking. This novel finding implies that naltrexone also blunts the progression of drinking once high risk drinking is resumed, which has implications for mechanism and future drug development.

Table 5.

Model diagnostics comparing longitudinal Poisson regression with the two hurdle models.

		AIC	BIC	Vuong Statistic (V)	P -value
Treatment Period	Poisson	54373	54475		----
	Zero-hurdle	53716	53854	-1.23	0.22
	Low Risk-hurdle	25717	25855	-55.63	0.0001
Post-Treatment Period	Poisson	54333	54475		---
	Zero-hurdle	33782	33918	-0.98	0.33
	Low Risk-hurdle	20693	20829	-36.67	0.0001

3.2 Post Treatment Period

The same three models were fit for the follow up period (weeks 17-26). In all models, there was a significant linear effect of time toward increased risk of drinking. No significant treatment main effects or interactions were observed in any model the followup period. The AIC and BIC both favored the hurdle models over the longitudinal Poisson regression model and the Vuong test significantly favored the low risk drinking hurdle model. Main effects on the odds of abstinence and risk of drinking are shown in the Appendix Table 2. Pairwise effects are not shown since no interactions were significant. The zero hurdle model only showed non-significant trends (p<0.10) toward an effect of naltrexone on both abstinence and risk of drinking.

4. Discussion

Alcohol researchers are often interested in understanding how interventions affect abstinence from alcohol as well as amount of drinking once drinking is resumed over the course of treatment. Addressing these two questions usually requires defining multiple summary drinking endpoints, which can increase the probability of a type I error rate. To better address these questions, we presented a novel approach to model treatment effects on abstinence and number of drinks per day utilizing a joint statistical framework. Applied to the COMBINE Study, the approach allowed for the use of all available high resolution outcome data, applied the appropriate modeling assumption that all patients were at risk of drinking throughout the study period, and as a result, was able to detect treatment effects on abstinence and drinking over prior reports.

Results from the present study both complement and add to previous conclusions (Anton et al., 2006; Gueorguieva et al., 2010; Witkiewitz et al., 2010, Falk et al., 2010). As in previous COMBINE reports, naltrexone was found to be effective in positively impacting drinking behavior, and a modifying effect by CBI was observed. However, while the original report found no main effects of naltrexone on percent days abstinent, the current analysis showed that naltrexone promotes abstinence. Furthermore, unlike previous COMBINE reports, the current study demonstrated that naltrexone also promotes (pre-defined) low risk drinking and for those who reach a harmful level of drinking, naltrexone significantly decreases the amount of drinks consumed. Consistent with prior findings, this effect is obscured in the context of CBI, which itself has an effect in the same direction as naltrexone, but is not additive to it. Results derived from the current analytic framework provide greater insight into the mechanism of action of naltrexone on the two part clinical process of abstinence violation and subsequent alcohol consumption.

In addition to showing that naltrexone promotes both abstinence and reduction in drinking when heavy drinking is re-established, the study also adds to previous findings by extending the model in a novel way to evaluate a cut-point for drinking that may be useful for delineating a priori definitions of low from harmful or higher risk drinking. In determining naltrexone's mechanism of impact, there is benefit to conceptualizing low risk (i.e., short of high-risk drinking) rather than assuming low risk drinking equates to zero drinks per day. In fact, regression diagnostics indicated that this model fit was optimal. Results indicated that naltrexone reduces the risk of drinking 68% after high risk drinking is resumed. This large and significant effect size for this supports this cutoff as a meaningful definition of low risk drinking. Of course, further research into a data driven definition of low risk or “acceptable” drinking endpoints is still warranted.

Secondary analyses of these data were warranted for several reasons: 1.) given the degree of conflicting evidence in the literature regarding the effectiveness of naltrexone and acamprosate in reducing drinking and maintaining abstinence, 2.) given the lack of consensus on outcome definitions in alcohol trials, and 3.) due to the misuse of zero inflated models that assume zero-drinking-risk patients in the substance use literature (Bandyopadhyay et al., 2012). The proposed approach has many advantages over commonly used approaches (e.g., Loeys and Moerkerke, 2012; Fielder et al., 2012). First, the hypothesized mechanism of action of acamprosate in promoting abstinence and naltrexone in reducing drinking lends itself to a joint model of abstinence and consumption. Second, clinical “improvement” may signify abstinence or a reduction in quantity of alcohol consumed, both of which are integral parts of a hurdle model. Third, performing many separate analyses of summary endpoints for abstinence and heavy drinking (as reported in the primary paper) reduces the amount of outcome data utilized and may inflate type I error rate. The ease of implementation in SAS software makes the current approach adaptable to other alcohol datasets.

Finally, limitations of this study must be recognized. Since the TLFB reports were heavily zero inflated, i.e., a large number of abstinent days were reported throughout the study, the 2-part model is not expected to be as powerful to detect treatment effects as it would be in a dataset with larger variations in counts. However, a large number of abstinent days is often a statistical issue in substance use clinical trials and resulting parameter estimates achieved here are still valid since the model converged to a sensible maximum. Also, while analysis did not control for the testing of multiple treatments and interactions, interaction p-values were small enough to be deemed significant even after a Bonferroni correction for 3 main effects was employed. Thus, it was justifiable to report results from all pairwise comparisons.

Table 4.

The left side contains results from the zero-drink hurdle model and the right side contains results from the <=3 drink and <= 4 drink hurdle model fit to post-treatment period data (weeks 17-26). ACA=acamprosate, NTX=naltrexone, Prior No. Drink = average number of drinks per day for the month prior to the required abstinence period.

	Zero-drink hurdle model				Low risk drinking hurdle model
Variable	Effect	SE(Effect)	95% CI	P-Value	Effect	SE(Effect)	95% CI	P-Value
Hurdle
Intercept 1	0.93	0.25	0.45,1.42	0.0002	6.63	0.64	5.38,7.88	0.0001
ACA	0.001	0.29	-0.56,0.57	1.00	-0.004	0.58	-1.15,1.14	0.99
NTX	0.65	0.29	0.08,1.22	0.02	0.83	0.57	-0.30,1.95	0.15
CBI	0.34	0.29	-0.23,0.91	0.24	0.85	0.57	-0.27,1.97	0.14
ACAxNTX	-0.38	0.33	-1.03,0.28	0.26	-0.24	0.64	-1.50,1.02	0.71
ACAxCBI	0.10	0.33	-0.55,0.76	0.75	0.04	0.64	-1.22,1.30	0.95
NTXxCBI	-0.27	0.33	-0.93,0.38	0.42	-0.90	0.65	-2.17,0.37	0.16
Prior No. Drink	-0.08	0.005	-0.09,-0.07	0.0001	-0.07	0.007	-0.09,-0.06	0.0001
Poisson Regression
Intercept 2	2.33	0.22	1.90,2.76	0.0001	8.71	0.64	7.46,9.96	0.0001
ACA	0.13	0.28	-0.42,0.68	0.63	-0.01	0.59	-1.06,0.96	0.92
NTX	0.31	0.28	-0.25,0.86	0.28	0.44	0.58	-0.20,1.78	0.12
CBI	-0.16	0.28	-0.71,0.40	0.58	0.35	0.58	-0.27,1.73	0.15
ACAxNTX	-0.24	0.33	-0.88,0.40	0.47	-0.26	0.65	-1.54,1.02	0.69
ACAxCBI	-0.07	0.33	-0.71,0.57	0.84	0.24	0.65	-1.04,1.52	0.71
NTXxCBI	0.10	0.33	-0.54,0.74	0.77	-0.51	0.65	-1.80,0.77	0.44
Week	0.01	0.002	0.01,0.01	0.0001	0.01	0.002	0.01,0.00	0.001

Appendix

Methods: Hurdle Model Description

The hurdle model is written as a mixture of a point mass at zero and a truncated at zero Poisson distribution for the positive counts. The hurdle for the observed number of drinks consumed, denoted y_ij for person i at week j is written as P(Y_ij = y_ij) = p_ij if y_ij = 0 and $P(Y_{ij}=y_{ij})=(1-p_{ij})\frac{f(y_{ij})}{1-f(0)}$ if Y_ij > 0 where f(y_ij)denotes the standard Poisson distribution with rate parameter λ_ij, $f(y_{ij})=\frac{{\lambda }_{ij}{e}^{-{\lambda }_{ij}{y}_{ij}}}{y_{ij}!}$ and p_ij is the probability of “crossing the hurdle” into drinking. Covariates enter the model via logistic regression at the level of the hurdle probability, p_ij and via Poisson risk regression at the level of the Poisson parameter, λ_ij; specifically two separate regression models for fixed time (week) dependent covariate matrices X and Z are specified, with β and γ denoting the associated vectors of regression coefficients for the logistic and Poisson regressions. Each regression also includes the same random effect, u, to induce correlation. The second hurdle model derived using the expert opinion that <= 3 drinks/day for women and <= 4 drinks/day for men represents non harmful or low risk drinking involves truncating the above written model at these values for each sex. This involves a simple modification to the denominator and support of the above equation. First, as P(Y_ij = y_ij) = p_ij if y_ij = 0, 1, 2, or 3 for women and as P(Y_ij =y_ij) = p_ij if y_ij = 0, 1, 2, 3, or 4 for men. Then, $P(Y_{ij}=y_{ij})=(1-p_{ij})\frac{f(y_{ij})}{1-f(0)}$ where f (0) is replaced with f (0) + f (1) + f (2) + f (3) for women and f (0) + f (1) + f (2) + f (3) + f (4) for men with the support of the distribution at y_ij > 3 for women and y_ij > 4 for men.

Appendix Table 1.

These variables were included in all regression models.

Variable	Type	Location
Treatment	Categorical	Hurdle, drinking
Treatment interactions	Categorical	Hurdle, drinking
Week	Ordinal	Drinking
Study center	Categorical	Hurdle
Prior average drinks/day	Count	Hurdle

Appendix Table 2.

Main effect odds ratios and risk ratios [95% confidence intervals] for the follow period.

	Zero-drink hurdle model		Low risk drinking hurdle model
Effect	OR[95%CI]	RR[95%CI]	OR[95%CI]	RR[95%CI]
ACA Main Effect	0.89[0.60,1.18]	1.01[0.68,1.33]	0.91[0.30,1.53]	1.03[0.36,1.70]
NTX Main Effect	1.39[0.94,1.85]#	0.79[0.54,1.04]#	1.40[0.45,2.35]	0.92[0.31,1.53]
CBI Main Effect	1.31[0.88,1.73]	1.16[0.79,1.53]	1.60[0.53,2.67]	0.80[0.28,1.33]

^*Indicates significance at p<0.05 and

^#indicates p<0.10.

Methods: SAS Code

*Poisson 0 hurdle model;

proc nlmixed data=dat method = GAUSS tech = NRRIDG ;

parms b0=0 b1=-.0013 b2=0.33 b3=.171 int4=0 int5=0 int6=0 c0=0 c1=0.024 c2=-.0278 c3=0.172 c4=-.0176 int7=0 int8=0 int9=0 d=0 e1=0 e2=0 e3=0 e4=0 e5=0 e6=0 e7=0 e8=0 e9=0 e10=0 s2=1;

*Hurdle Portion;

eta0= b0+b1*acamprosate + b2*naltrexone + b3*therapy + int4*AN+ int5*AT + int6*NT + d*priordr + e1*centera + e2*centerb +e3*centerc +e4*centerd + e5*centere + e6*centerf + e7*centerg + e8*centerh + e9*centeri + e10*centerj + u1;

expeta0 = exp(eta0);

pB = 1/(1+exp(-eta0));

*Poisson Portion;

etap = c0+ c1*week+ c2*acamprosate + c3*naltrexone + c4*therapy + int7*AN + int8*AT + int9*NT + u1;

expetap = exp(etap);

if count = 0 then l1=log(pB);

else l1= log(1-pB) - expetap+ count1*etap -lgamma(count+1)- log(1-exp(-expetap));

model count general(l1);

random u1 normal (0, s2) subject= id;

run;

*Poisson low risk hurdle model;

*Drink count must be recoded (0-3 as 0 for women, 0-4 as 0 for men);

proc nlmixed data=in.agg_mental method = GAUSS tech = NRRIDG ;

parms b0 = 0 b1= -.0013 b2=0.33 b3=.171 int4=0 int5=0 int6=0, c0 = 0 c1 = 0.024 c2 = -.0278 c3=0.172 c4= -.0176 int7=0 int8=0 int9=0 d=0 e1=0 e2=0 e3=0 e4=0 e5=0 e6=0 e7=0 e8=0 e9=0 e10=0 s2 = 1;

*Hurdle Portion;

eta_0= b0+b1*acamprosate + b2*naltrexone + b3*therapy + int4*AN+ int5*AT + int6*NT + + d*prior_dr +e1*centera + e2*centerb +e3*centerc +e4*centerd + e5*centere + e6*centerf + e7*centerg + e8*centerh+ e9*centeri + e10*centerj + u1;

exp_eta_0 = exp(eta_0);

p_B = 1/(1+exp(-eta_0));

*Poisson Portion;

eta_p = c0+ c1*week+ c2*acamprosate + c3*naltrexone + c4*therapy + int7*AN + int8*AT + int9*NT + u1 ;

exp_eta_p = exp(eta_p);

if gender = “female” then

TRUNC=-log(1

-exp(-exp_eta_p)

-(exp(-exp_eta_p) * exp_eta_p**1)

-(exp(-exp_eta_p) * exp_eta_p**2 / 2)

-(exp(-exp_eta_p) * exp_eta_p**3 / 6));

if gender = “male” then

TRUNC=-log(1

-exp(-exp_eta_p)

-(exp(-exp_eta_p) * exp_eta_p**1)

-(exp(-exp_eta_p) * exp_eta_p**2 / 2)

-(exp(-exp_eta_p) * exp_eta_p**3 / 6)

-(exp(-exp_eta_p) * exp_eta_p**4 / 24));

if count = 0 then l1=log(p_B);

else l1= log(1-p_B) - exp_eta_p+ count*eta_p -lgamma(count+1)-TRUNC;

model count∼general(l1);

random u1∼ normal (0, s2) subject= id_comb;

predict _ll out = LL3;