Calibrationless Parallel Imaging Reconstruction Based on Structured Low-Rank Matrix Completion

Abstract

Purpose

A calibrationless parallel imaging reconstruction method, termed simultaneous auto-calibrating and k-space estimation (SAKE), is presented. It is a data-driven, coil-by-coil reconstruction method that does not require a separate calibration step for estimating coil sensitivity information.

Methods

In SAKE, an under-sampled multi-channel dataset is structured into a single data matrix. Then the reconstruction is formulated as a structured low-rank matrix completion problem. An iterative solution that implements a projection-onto-sets algorithm with singular value thresholding is described.

Results

Reconstruction results are demonstrated for retrospectively and prospectively under-sampled, multi-channel Cartesian data having no calibration signals. Additionally, non-Cartesian data reconstruction is presented. Finally, improved image quality is demonstrated by combining SAKE with wavelet-based compressed sensing.

Conclusion

As estimation of coil sensitivity information is not needed, the proposed method could potentially benefit MR applications where acquiring accurate calibration data is limiting or not possible at all.

INTRODUCTION

Parallel imaging is a powerful method that utilizes multiple receiver elements for reduced scanning time in magnetic resonance imaging (MRI) (1). In this scheme, simultaneous signal receptions through spatially distributed coils provide data redundancy by means of sensitivity encoding. When the sensitivity encoding is applied in conjunction with gradient encoding, the amount of data necessary for proper image reconstruction is greatly reduced. This enables accelerated data acquisition, specifically, under-sampling of k-space data below the apparent Nyquist rate.

The various parallel imaging methods developed so far differ in the way they use sensitivity information to remove aliasing artifacts resulting from the under-sampling. Reconstruction techniques such as SMASH (2) and SENSE (3) expect that the reception profiles from each coil element are known beforehand. However, explicit coil sensitivity measurements often require separate calibration scans, which increases the overall acquisition time. Moreover, any inconsistency due to motion or small errors in the sensitivity estimation manifest as significant visual artifacts in reconstructed images (4).

Auto-calibrating methods avoid the difficulties and inaccuracy associated with explicit estimations by deriving sensitivity information from auto-calibration signals (ACS). In general, ACS are embedded in acquired data as fully sampled center together with under-sampled higher frequency k-space regions. Self-calibrating methods (5, 6, 19) extract sensitivity images from ACS and use the information to reconstruct aliasing artifact free images. Joint estimation techniques, such as JSENSE (7) or the non-linear inversion method (8), attempt to iteratively estimate both the coil sensitivities and image contents while imposing some smoothness constraints on the sensitivity profiles. Data driven auto-calibrating methods, such as GRAPPA (9) and SPIRiT (10), estimate linear relationships within the ACS data (i.e. kernel calibration) and enforce that relationship to synthesize data values in place of unacquired samples (i.e. data reconstruction).

However, in some MR applications, acquiring sufficient ACS for accurate calibration can be limiting or not possible at all. For example, in spectroscopic imaging, matrix sizes in spatial dimensions are relatively small and ACS acquisitions can take up a large portion of total imaging time. In the case of dynamic MRI, repeatedly acquiring ACS over time is also time consuming. For non-Cartesian imaging, such as spirals, acquiring sufficient ACS requires longer readouts, which can result in artifacts due to off-resonance.

In this work, we developed a calibrationless parallel imaging reconstruction framework called SAKE (simultaneous auto-calibrating and k-space estimation). Without performing a separate sensitivity calibration step, the proposed method reconstructs a full k-space from an under-sampled, multi-channel dataset that lacks ACS data. The method jointly manipulates multi-channel data by organizing acquired data into a single, structured matrix. In addition to the structure, this matrix also has low rank due to the linear dependency residing in multi-coil data (11, 12, 13). Therefore, the reconstruction is cast into a structured low-rank matrix completion problem and is formulated as a constraint optimization. Low-rank matrix completion is an active area of research and has much similarity to compressed sensing theory (14, 15). We adopted a projection-onto-sets type algorithm with singular value thresholding (16) to solve the problem iteratively. SAKE can easily incorporate additional a priori information related to underlying MR images, such as sparsity (17), for improved reconstruction performance, and can also be applied on non-Cartesian sampled data.

Theory

In the following, we first define an enhanced data structure called data matrix and describe its structured, low-rank property. Then, GRAPPA-like auto-calibrating methods are discussed in terms of the data matrix. Finally, our proposed method SAKE is explained.

Structured Low-rank Data Matrix

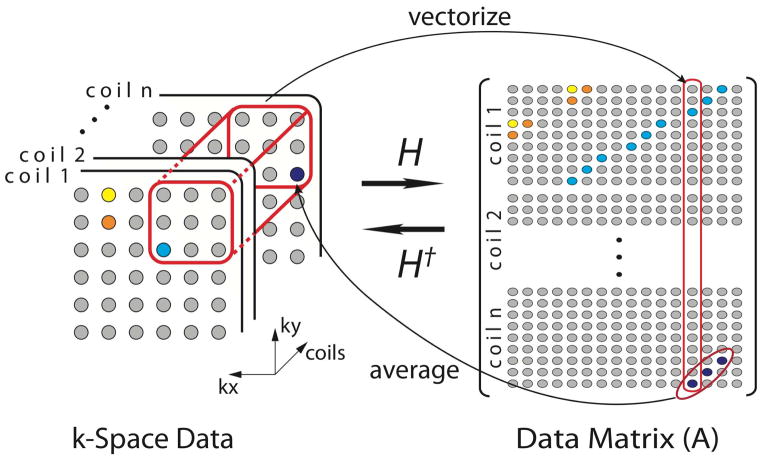
Underlying our approach is a specific data structure that exploits and manifests the correlations within multi-channel MRI k-space data. We structure multi-channel data altogether into a single data matrix of which columns are vectorized blocks selected by sliding a (multi-channel) window across the entire data. A pictorial description of constructing such a matrix with an exemplary 3 × 3 window is shown in Fig. 1. From N_x × N_y sized data with N_c number of coils, we can generate a data matrix having the size of w²N_c × (N_x − w + 1)(N_y − w + 1) by sliding a w × w × N_c window across the entire k-space. Note that due to the nature of the sliding-window operation, the data matrix will have a stacked, block-wise Hankel structure with many of its entries from identical k-space locations being repeated in anti-diagonal directions (emphasized by colored samples in Fig. 1).

Figure 1.

Constructing a data matrix from a multi-channel k-space dataset (H) and vice versa (H^†). A single data block in the k-space is vectorized into a column in the data matrix. Note that the data matrix will have a block-wise Hankel matrix structure. When reversely forming a k-space dataset from a data matrix, multiple anti-diagonal entries are averaged and stored at appropriate k-space locations.

In general, block Hankel matrices are known to possess well-defined subspaces (18). In the Appendix section, under the reasonable assumption that coil sensitivities have compact k-space support, we show that a data matrix in block Hankel form can be structured to become a rank deficient matrix for an appropriately chosen window size w × w. It can be further shown that the rank is bound by rank (A) ≤ (w + s −1)², where A is a data matrix and s is the coil bandwidth measured in k-space pixels. Once we have a rank deficient data matrix, then we can apply a singular value decomposition (SVD) based subspace analysis technique (30) on multi-channel MR data (11, 23) to break the information down into signal and noise subspaces, which are spanned by singular vectors corresponding to dominant singular values and non-dominant ones, respectively. An interesting observation to follow is that the upper bound on rank normalized by the window size (w + s −1)²/w² will approach 1 with increasing window size. For smaller window sizes, the normalized rank will be larger than 1. From a subspace point of view, this means that by using larger windows, we could confine signal components in a relatively compact subspace.

There are several other factors that could lower the rank of the data matrix (11, 23). These include actual values of sensitivity spectrums in k-space, the portion of size of the object within field of views (FOV) and the portion of blank signal within the object (18, 20, 21). A detailed theoretical analysis of the rank behavior, however, is beyond the scope of this manuscript. In the Results, we show empirical evidence that relates rank value with varying window sizes and object supports in the image domain. These results provide a way to estimate the rank for a given coil configuration and window size.

k-Space Based Parallel Imaging Reconstructions

In this section, we discuss a subspace-based view of GRAPPA-like methods based on the structured low-rank data matrix from the previous section. Auto-calibrating, k-space based methods such as GRAPPA or SPIRiT estimate linear dependencies between k-space samples by fitting so-called GRAPPA kernel weights. In the reconstruction step, assuming that the dependencies are the same everywhere in k-space, unacquired data samples are synthesized by applying the linear weights to their nearby k-space points across all coils. The linear weights of GRAPPA/SPIRiT kernels can be easily estimated by organizing multi-channel ACS data into a data matrix (or sometimes referred to as calibration matrix) as shown in Fig. 1. Hereafter, we assume that we have acquired enough auto-calibrating signals. Let A^ACS be the calibration matrix. Then, we can formulate the GRAPPA calibration process of estimating the linear weights into the following equation (9).

$$g_{ir}^H{A}^{\mathit{ACS}}=e_i^H{A}^{\mathit{ACS}}$$ [1]

Here, $g_{ir}^H$ is a GRAPPA kernel for i^th channel that contains linear weights and zeros in appropriate positions. These kernels are also determined by a specific sampling pattern indexed by r. The vector e_i is a vector from the canonical basis that simply selects a row in A^ACS of which linear combinations of neighboring data are being fitted to. We use the notation $g_{ir}^H$ to denote the complex-transpose of g_ir. In the case of SPIRiT (10), linear coefficients for all surrounding samples are found regardless of the sampling pattern, and hence, the index r can be omitted from Eq. 1 to form a SPIRiT kernel $g_i^H$. By rearranging Eq. 1, we get

$${(g_{ir}-e_i)}^H{A}^{\mathit{ACS}}=0.$$ [2]

In other words, GRAPPA/SPIRiT kernels (after subtracting out the vector e_i) are left null vectors of the calibration matrix. Thus, we can view the calibration step as the process of finding a set of representative nulling vectors in the noise subspace (left null space) of A^ACS. As discussed previously, if the kernel window size is chosen appropriately, then A^ACS is low rank and hence always has a non-trivial left null space.

The GRAPPA assumption (9, 10) is that the linear dependencies estimated from the ACS should hold throughout the entire k-space. We can formulate this statement into the following linear equations by extending Eq. 2 to

$${(g_{ir}-e_i)}^{H}A=0,$$ [3]

where A now denotes a data matrix that consists of the entire k-space. Eq. 3 constitutes the most fundamental mechanism in GRAPPA/SPIRiT and provides the foundation for reconstructing unacquired data. It means that any (vectorized) data block in the k-space is nulled by the vector (g_ir − e_i)^H through the inner-product operation and any missing data points should be synthesized in such a way that fulfills this requirement (i.e. calibration consistency condition). In PRUNO (11), the idea of estimating a set of vectors in the noise subspace is extended to identifying a basis that spans the noise subspace itself by performing a SVD on the calibration matrix. Then, missing data samples are synthesized so that k-space data blocks are jointly orthogonal to every element of the basis set. In this perspective, GRAPPA (9), SPIRiT (10) and PRUNO (11) methods can all be viewed as (left) null space formulations. Instead of estimating the noise subspace, ESPIRiT (23) identifies its orthogonal complement, the signal subspace (column space or range) of the calibration matrix and reconstructs data by enforcing each data block to lie in that subspace. It was further shown in (23) that restricting reconstructed data to lie in the signal subspace is implicitly related to making use of coil sensitivities for data reconstruction similar to the SENSE method (3).

Parallel Imaging Reconstruction as Structured Low-rank Matrix Completion

The previously discussed methods all assumed that we have auto-calibration signal to extract subspace information from. However, when the under-sampled dataset does not have ACS, then we cannot estimate the subspaces of the calibration matrix. Consequently, the subspace-based calibration consistency condition cannot be formulated. Instead, we turn to the a priori information that the data matrix is a low-rank matrix. Thus, our approach in formulating SAKE is to recover the structured low-rank data matrix A when only a subset of its entries are given due to under-sampling in k-space.

We first define the following linear operator that generates a data matrix from a multi-channel dataset concatenated in a vector form (Fig. 1).

$$H_w:{ℂ}^{Nx·Ny·Nc\times 1}\to {ℂ}^{w^2{N}_c\times (N_x-w+1)(N_y-w+1)}$$ [4]

Then, a reverse operator that generates a corresponding k-space dataset from a data matrix (possibly without the block-Hankel structure) would be

$$H_w^{†}:{ℂ}^{w^2{N}_c\times (N_x-w+1)(N_y-w+1)}\to {ℂ}^{Nx·Ny·Nc\times 1},$$ [5]

where † denotes a pseudo-inverse operator. In words, the role of H^† is to first enforce the block-wise Hankel structure by averaging the multiple anti-diagonal entries that would have originated from the same k-space locations. Once the data matrix has this structure, H^† stores the averaged values in the appropriate k-space locations (Fig. 1). A detailed discussion on how to implement the linear operators H and H^† in a matrix form is outlined in (16). In practice, due to the large data size and the complexity involved in computing the pseudo-inverse operator, it is recommended to avoid implementing the matrices explicitly. Instead, we implement the pseudo-inverse as an operator that accomplishes the same computation more efficiently. An example is provided in our accompanying source code (see website below).

With Eq. 5, the parallel imaging reconstruction can be formulated into a structured, low-rank matrix completion problem (14, 15).

$$\begin{array}{ll}\mathit{minimize}\hfill & \mathit{rank}(A)\hfill \\ \mathit{subject}to\hfill & x=H^{†}(A),\hfill \\ \hfill & {\Vert Dx-y\Vert }^2<\epsilon .\hfill \end{array}$$ [6]

Here, D is a linear operator that relates reconstructed k-space data x to acquired data y, and ε is a bound on noise. For convenience, we assume the data has been pre-whitened. In other words, we search for a low rank data matrix A (low-rankness), which, when transformed into a k-space data x (structural consistency), is consistent with the acquired data y in relation to sampling mechanism defined by D (data consistency). This formulation is general in the sense that the data consistency constraint applies to both Cartesian and non-Cartesian sampling (see Appendix). It is worthwhile noting that the formulation in Eq. 6 is a variant of the more general low-rank matrix completion setup (14) in the sense that, other than low-rankness and data consistency, we additionally enforce the block Hankel structure (H^†) in the matrix (15).

When the rank of the matrix A is known beforehand, Eq. 6 can be recast into the following formulation (24, 25).

$$\begin{array}{ll}\mathit{minimize}\hfill & {\Vert Dx-y\Vert }^2\hfill \\ \mathit{subject}to\hfill & \mathit{rank}(A)=k,\hfill \\ \hfill & x=H^{†}(A).\hfill \end{array}$$ [7]

In this initial work, we assume that we have an estimate of the rank value (k) of the data matrix and adopt the well-known Cadzow algorithm (16, 26) to solve the problem stated in Eq. 7. The Cadzow algorithm is a simple and intuitive projection-onto-sets type approach in which desired properties of some signal are sequentially enforced within iterations. It is known to produce a quasi-optimal solution that resides in an intersection of composite properties.

In implementing the algorithm, we define the following projection operators that correspond to each of the constraints in Eq. 7:

• Low-rankness projection: hard-threshold singular values of the data matrix constructed from the current estimate of k-space data.

• Structural consistency projection: project the data matrix onto the space of block-wise Hankel matrices. Note that this operation is done implicitly by applying H^† to the data matrix.

• Data consistency projection: project the current estimate of k-space data onto the set of least-squares solutions for the problem Dx = y. See Appendix for details on how this projection is implemented for both Cartesian and non-Cartesian sampling cases.

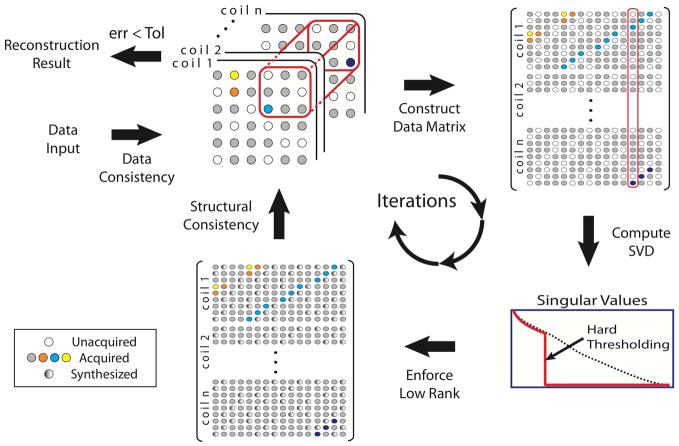
In every loop, these projections are sequentially applied and the iteration is repeated until some convergence criteria are met. For example, the iteration persists until maximum number of repetition is reached or update made on reconstructed data is within a tolerance bound. An intuitive illustration for the algorithm is given in Fig. 2 with pseudo-code in Table 1.

Figure 2.

Diagram of iterative reconstruction in SAKE. Within a single iteration, multiple consistencies are enforced on current estimate of the k-space data. As under-sampling is done the same for all channels, a pseudo-random sampling pattern (white circles) appears repeatedly in the zero-filled data matrix.

Table 1.

Pseudo-code for SAKE

Inputs:	y - acquired (Cartesian/non-Cartesian) data from all channels
	D/D† - operators relating reconstructed data to the acquired data y, and vice versa
	H/H† - operators that construct the data matrix from k-space values, and vice versa
	k - rank of the data matrix
	Tol - tolerance on error
Outputs:	xn - reconstructed data for all channels
Algorithm:	x0 = D†y, n = 0
	do {
	n = n + 1
	An = H(xn−1)% construct data matrix
	[U Σ V] = svd(An) % perform SVD
	An = U|| Σk V||H % hard-threshold singular values (low-rankness projection)
	xn = H†(An) % transform data matrix back to k-space data (structural consistency projection)
	xn = (I − D†D) xn + D†y % data consistency projection (see Appendix for details)
	err = ||xn − xn−1||
	} while err > Tol

METHODS

All our investigations were based on 3D acquisitions from eight-channel coil arrays in which under-sampling is done simultaneously in two phase-encoding directions (k_x − k_y) with through-slice direction (k_z) being the readout. For simplicity, square-shaped windows are assumed.

Hardware and Software

We used Matlab (MathWorks, Inc) to implement SAKE. In the spirit of reproducible research, we provide implementations of the algorithms and examples demonstrating its use. These can be found at (http://www.eecs.berkeley.edu/~mlustig/Software.html). All the programs were run on a Linux machine equipped with an Intel i7-2600K, 3.40GHz CPU and 12 gigabytes of memory.

Structured Low-rank Data Matrix

First, we show the singular value distributions of data matrices generated from a number of simulated and acquired multi-channel data. To generate the simulated data, sensitivity profiles of an eight-channel, circular coil array were calculated based on the principle of reciprocity and the Biot-Savart law in the quasi-static regime (22). Two rectangular phantoms differing in their size relative to the imaging FOV were also generated. To simulate finite extent sampling in k-space, the phantoms and sensitivities were first generated in 1024 × 1024 grid, multiplied pixel-wise in image domain, Fourier transformed to k-space and, finally, cropped to 256 × 256 matrix size.

In addition to the simulated data, two in vivo datasets were used. A brain image of a healthy volunteer was acquired with a T₁-weighted, 3D spoiled gradient echo (SPGR) sequence. Scan parameters were set to TE = 8 ms, TR = 17.6 ms, and flip angle = 20°. Imaging parameters were chosen such that FOV = 20 cm × 20 cm × 20 cm with a matrix size of 200 × 200 × 200 for an isotropic 1 mm³ resolution. A single axial slice was selected from this data set and was used through out the experiments. The scan was performed on a 1.5T MRI scanner (GE, Waukesha, WI) using an eight-channel receive-only head coil. Also, an eight channel, knee image was acquired using a 3D fast spin-echo (FSE) sequence with echo train length 40, first TE = 25.6 ms, and TR = 1.5 s. FOV was set to 15.4 cm × 16 cm × 16 cm with a matrix size of 256 × 320 × 320. In-plane resolution was 0.6 mm × 0.5 mm with a slice thickness of 0.5 mm. A single axial slice from the dataset was selected for our experiment. The scan was performed on a 3T MRI scanner (GE, Waukesha, WI).

For each of the multi-channel datasets, data matrices were constructed from center 80 × 80 part of the data using varying window sizes from 2 × 2 to 15 × 15. Then, SVD on each of the matrices were performed to extract the singular value distributions. The center cropping to 80 × 80 was done to reduce the SVD computation and guarantee that we have fat data matrices for the large window sizes up to 15 × 15.

Calibrationless Parallel Imaging Reconstruction – Retrospective Subsampling

In this experiment, the above head and knee datasets were used. First, to show that calibration and data matrices of real MR data have low rank with compact column space, we extracted center 30 × 30 ACS from each of the Cartesian dataset we acquired, structured them into calibration matrices (Eq. 4), and performed SVD. We also constructed full data matrices for each of the dataset and performed SVD for comparison. We used window size of 6 × 6 in constructing the calibration and data matrices.

To demonstrate the reconstruction capability of SAKE, we under-sampled each Cartesian dataset by a factor of three. A great body of work in matrix completion focuses on sampling the entries of the data matrix randomly (14). To mimic this condition, we have confined all of our experiments to adopt random under-sampling in k-space with elliptical, variable-density (VD) Poisson disk patterns (27). Performing random under-sampling has an additional benefit of having incoherent, noise-like artifacts, as opposed to having coherent aliased objects in the final reconstructed images resulting from uniform under-sampling. This is similar to the case of compressed sensing (17) where random sampling causes very incoherent aliasing that spreads uniformly to other image pixels. For SAKE, the datasets were under-sampled keeping 0 × 0 and 4 × 4 fully sampled center and a 6 × 6 window was used for reconstruction. Iterations in SAKE reconstruction looped until updates made on the k-space data estimate was less than 0.5%. The number of iterations and reconstruction time spent was measured. For comparison, a dataset with 30 × 30 fully sampled center was reconstructed using an auto-calibrating method SPIRiT (10). Additionally, to compare with the reconstructed results, the under-sampled datasets have been density compensated and then Fourier transformed into images.

SAKE Reconstruction on Prospectively Under-sampled Dataset

A prospectively under-sampled, eight-channel phantom dataset with an acceleration factor of three was acquired using a 3D sequence on the 3T scanner. In this case, we chose a transparent commercial MR phantom as the imaging object so that we would have an accurate expectation of exactly how the reconstructed images should appear. This phantom experiment also ruled out motion artifacts. A similar elliptical variable density Possion-disk sampling pattern was adopted. FOV was set to 24 cm × 24 cm × 24 cm with a matrix size of 200 × 240 × 144. As the k_z direction (readout) was fully sampled, Fourier transform in that direction was performed and two slices from k_x − k_y − z data were selected for our experiment.

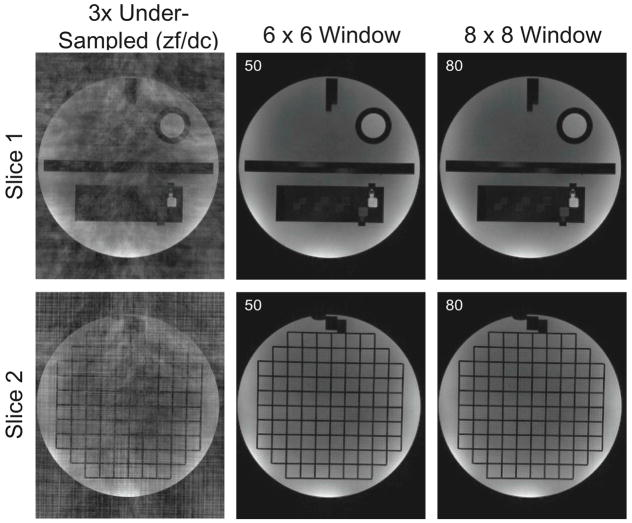
As object support of the phantom data within its FOV was set similar to the knee data, singular value distributions of the knee data were used to estimate the rank value in this experiment. A threshold of 1.4 and 1.25 of window-normalized rank has been used for the 6 × 6 and 8 × 8 window sizes, respectively.

Combination with Compressed Sensing

It is well known that MR images have sparse representation (17) in some transform domain (e.g. wavelet). In order to demonstrate the regularization capability of SAKE, we adopted the joint sparsity model (27), an assumption that multi-channel images are jointly sparse, and added a generalized ℓ₁-norm penalty term into the optimization in Eq. 8.

$$\begin{array}{ll}\mathit{minimize}\hfill & {\Vert D(x)-y\Vert }^2+\lambda \sum _r\sqrt{\sum _c{\mid \mathrm{\Psi }\{\mathit{IFFT}(x)\}\mid }^2}\hfill \\ \mathit{subject}to\hfill & \mathit{rank}(A)=k,\hfill \\ \hfill & x=H^{†}(A).\hfill \end{array}$$ [11]

Here, Ψ denotes a wavelet transform of an MR image with r and c indexing the spatial and coil dimensions, respectively. λ is a parameter that creates a balance between the data consistency and the a priori penalty. In the iterative reconstruction, the aforementioned penalty has been implemented as iterative soft-thresholding on the transform coefficients (10, 17, 27).

Non-Cartesian Multi-channel Reconstruction

To demonstrate non-Cartesian reconstruction capability, we used phantom data acquired with a spiral gradient echo sequence using an 8-channel cardiac coil. The spiral trajectory consists of 60 interleaves for 0.75 mm in-plane resolution over a 30 cm × 30 cm FOV. We have retrospectively under-sampled the spiral dataset by a factor of three to have 20 equally spaced interleaves. The under-sampled dataset was reconstructed using gridding with density compensation, non-Cartesian SPIRiT and SAKE reconstruction for comparison. The SAKE reconstruction ran over 30 iterations resulting in a 260 × 360 sized final image. The window-normalized rank value for the reconstruction was set to 1.3 for a 6 × 6 window.

Results

Structured Low-rank Data Matrix

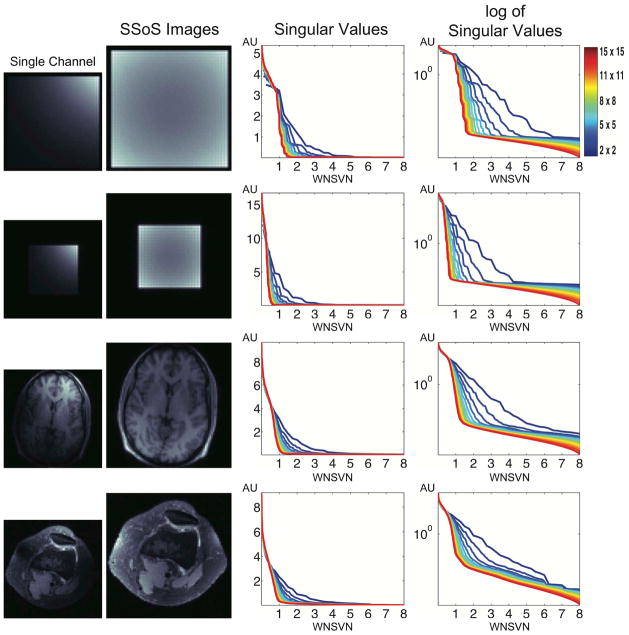
Fig. 3 shows a set of square root of sum of squared (SSoS) images (80 × 80) of the simulated and in vivo objects together with reduced single channel images on their side. Corresponding singular value distributions of data matrices and their semi-log versions are also shown. Graphs of varied window sizes from 2 × 2 (blue) to 15 × 15 (red) have been plotted. Each x-axis represents window-normalized singular vector numbers (WNSVN) and y-axes are all in arbitrary units (AU). First and foremost, the data shows that the data matrices have decreasing window-normalized rank with increasing window sizes. If the window size gets larger than a certain value, than the data matrices start possessing compact column spaces. The window-normalized rank shows convergence to 1 or less (depending on length of object support) with increasing window sizes as anticipated. Note from our previous discussion that, only when we have a compact column space for a data matrix (i.e. the left null space exists), can we do stable GRAPPA calibration. Next, the results from the square phantoms show that, under the same coil configuration, object support has effect on rank values. More specifically, smaller objects tend to have lower rank. Also, the head and knee data together show that while specific singular values from different image contents might differ, the rank values are nearly the same as long as they have similar length of image support and similar coil geometry. Based on this experiment, we conjecture that a rank value from one object can be adopted to estimate rank for a different imaging subject if they share similar length of image support. We tested this assumption by extracting the rank value from a fully sampled knee data and applying it to prospectively under-sampled phantom data (see below), which does not have calibration data to extract subspace information from. Estimation of the image support can be done at a pre-scan stage.

Figure 3.

Singular value distributions of data matrices generated from different imaging objects. SSoS together with single channel images are shown in the left columns. Corresponding singular value distributions (middle column) and their logarithms (right column) are also plotted. The x-axes represent window-normalized singular vector number (WNSVN) and y-axes are in arbitrary units (AU). Singular value distributions of the data matrix were constructed using window sizes between 2 × 2 (blue) and 15 × 15 (red). All graphs share the same color bar representing the window sizes. Note that as window size gets larger, the window-normalized rank approaches one.

Calibrationless Parallel Imaging Reconstruction – Retrospective Subsampling

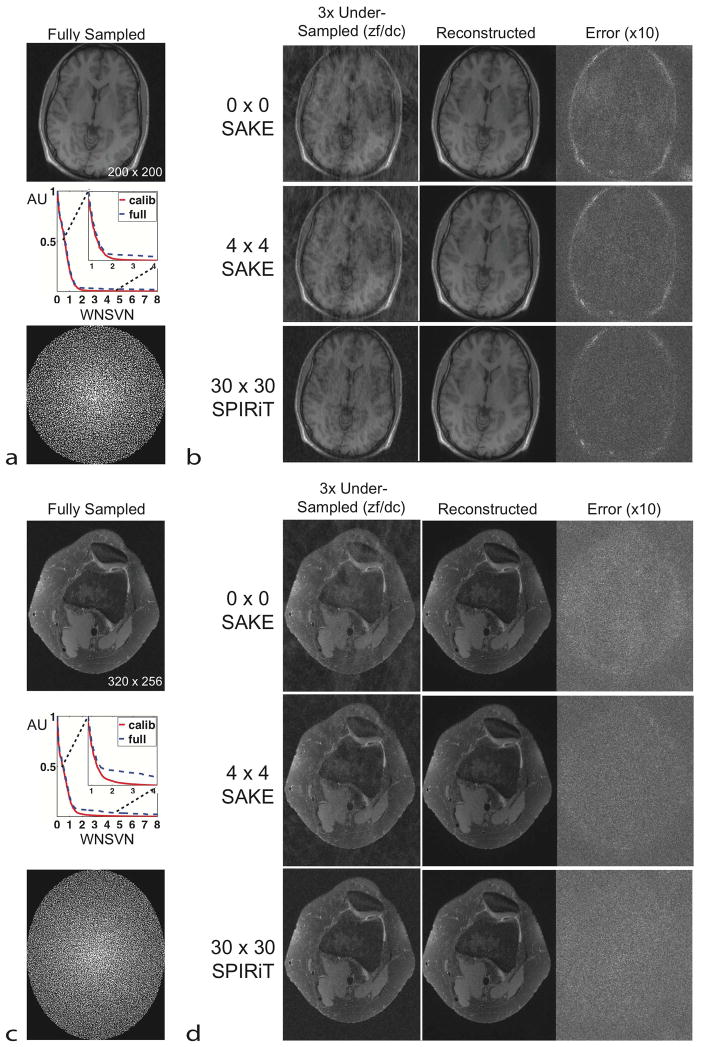
SSoS images and their corresponding singular value distributions of the calibration matrices (solid line) and the data matrices (dashed line) are shown in Fig. 4a and 4c for brain and knee data, respectively. First, it can be observed that the two matrices share similar number of dominant singular values. However, there is a point where deviations are observed in between the singular value distributions of the calibration matrix and the data matrix. This deviation exists because the data matrix has lifted singular values due to noise (28, 29, 30). We estimated window-normalized rank values to be 1.5 for the brain data and 1.4 for the knee data. The estimated ranks were used in the SAKE reconstruction.

Figure 4.

SAKE reconstruction results and comparison to SPIRiT. a, c) Top: SSoS combined fully sampled images (brain and knee). Middle: singular value plots for the calibration matrices (solid line) and the data matrices (dashed line). The inset shows a part from the graph magnified. Bottom: 3× elliptical, variable-density Possion disk random sampling pattern. b, d) Top row: SAKE reconstruction results with no fully sampled center k-space. Middle row: SAKE reconstruction results with 4 × 4 fully sampled center k-space. Bottom row: SPIRiT reconstruction results with 30 × 30 fully sampled calibration area.

Data under-sampled by 3-fold, SAKE reconstruction results and error images (×10 windowed) are shown in Fig. 4b and 4d for brain and knee data, respectively. The number of iterations and the reconstruction time needed for all three experiments are listed in Table 2. The reconstruction results of SAKE with 0 × 0 and 4 × 4 fully sampled center show similar performance and they are comparable to the result acquired with auto-calibrating reconstruction method SPIRiT for both the brain and knee data. When the 4 × 4 center k-space data is given, however, SAKE reconstruction time decreases showing faster convergence.

Table 2.

Number of iterations and time spent in retrospective reconstruction

Data Type	Brain			Knee
Recon. Type	0 × 0 SAKE	4 × 4 SAKE	30 × 30 SPIRiT	0 × 0 SAKE	4 × 4 SAKE	30 × 30 SPIRiT
# of Iter.	63	56	20	28	14	20
Recon. Time (sec)	618	550	2	633	319	2.7

SAKE Reconstruction on Prospectively Under-sampled Dataset

Reconstruction results for the prospectively under-sampled phantom data are shown in Fig. 5. The number of iterations and time spent in performing SAKE reconstruction for each slice and different window sizes are listed in Table 3. As the phantom data were acquired with similar object support length comparable to the knee data, the dominant window-normalized singular values estimated from the knee data for 6 × 6 and 8 × 8 windows were used for this experiment, which were 1.4 and 1.25, respectively. Two reconstruction results based on 6 × 6 and 8 × 8 windows show excellent quality with no visible residual aliasing. However, in the case of 8 × 8 window, reconstruction time increases. This is mainly due to the larger data matrix size resulting from adopting larger window size.

Figure 5.

SAKE reconstruction results for prospectively under-sampled phantom data. Zero-filled and density compensated reconstruction (left column) and reconstruction results from two different window sizes (middle, right column) are shown for two different slices (top, bottom rows). The singular values used for the reconstruction are written in the figures. Note that SAKE reconstruction results show no visual artifacts.

Table 3.

Number of iterations and time spent in prospective reconstruction

Data Type	Slice 1		Slice 2
Window Size	6 × 6	8 × 8	6 × 6	8 × 8
# of Iter.	29	32	33	36
Recon. Time (sec)	370	805	420	911

Combination with Compressed Sensing

Fig. 6a and 6d shows SAKE reconstruction results without and with the ℓ₁-norm penalty, respectively, from the 3-fold accelerated sampling pattern. The zoomed images (Fig. 6b and 6c) clearly show the effect of applying an additional sparsity constraint, which suppresses the over-fitting to noise and generates higher signal-to-noise images. The data was normalized to set the maximum image intensity equal to 1 and the regularization parameter λ was set to 0.007. In general, choosing smaller λ values in regularization would result in images with more noise and applying large λ values might destroy fine structures in reconstructed images (17, 27). The regularization parameter should also be adjusted if images are normalized in different scales.

Figure 6.

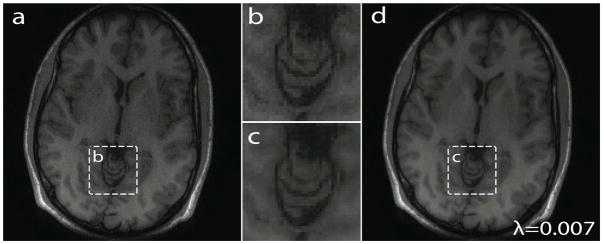
Regularization using ℓ₁-wavelet spatial sparsity with 3-fold acceleration. a) SSoS combined image with no regularization. b) and c) are magnified versions of square boxes in a) and d), respectively. d) SSoS combined image with ℓ₁-wavelet (Daubechies 4) regularization. Note that the images without regularization are much more grainy, while fine spatial features are well preserved with regularization.

Non-Cartesian Multi-channel Reconstruction

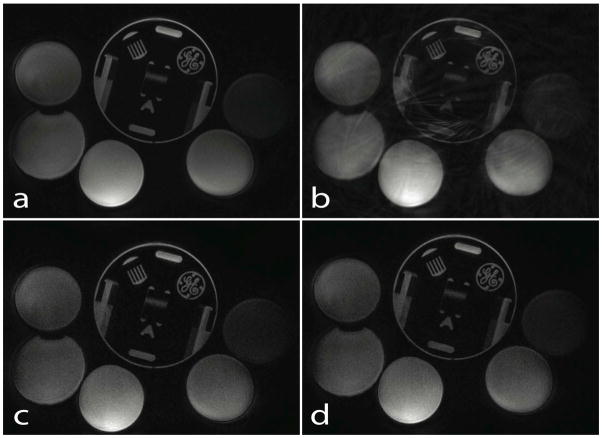
Fig. 7 shows a) fully sampled spiral acquisition image, b) 3-fold under-sampled gridding reconstructed image, c) non-Cartesian SPIRiT reconstruction, and d) SAKE reconstructed image. By comparing b) and d), we can clearly see that aliasing artifacts have been removed by SAKE reconstruction. The result d) is also comparable to that of auto-calibrating reconstruction shown in c).

Figure 7.

SAKE reconstruction result for non-Cartesian parallel imaging. a) Fully sampled, and b) 3-fold under-sampled spiral phantom images gridded and SSoS combined. Note the aliasing artifacts. c) and d) show reconstruction results from SPIRiT and SAKE, respectively. The SAKE reconstruction shows good result with removed artifacts and is comparable to that of SPIRiT shown in c).

Discussion

In general, auto-calibrating parallel imaging reconstructions are done in two steps: a calibration process followed by data interpolation. The calibration step is where either linear weights relating blocks of k-space data or explicit sensitivity estimation is done using ACS in the center of acquired k-space data. Once the calibration information is extracted, it is used in the data reconstruction step where missing k-space samples are interpolated. In the SAKE method developed in this project, calibration is done implicitly by enforcing the data matrix to be a structured low rank matrix. As a result of sensitivity encoding, any (vectorized) blocks of k-space data lie in a low dimensional subspace. Here, we have shown that calibration can be done without explicitly extracting the subspace information by exploiting the low dimensionality of the signal subspace.

As the overall mathematical formulation of restricting the rank of data matrix is not convex (24), it is crucial that we start the reconstruction with an initial estimate (usually, this is the under-sampled data itself) that lies close to the global optimum to ensure a fast convergence. In our approach, we adopted random under-sampling pattern to ensure this condition. Uniformly under-sampled datasets did not show reliable convergence behavior. A theoretical work relating the sampling pattern to convergence condition is beyond the scope of this paper.

In this work, we have adopted a simple thresholding scheme (Cadzow’s algorithm) to estimate the dominant singular values for a number of datasets. We also showed empirical results that support theoretical bounds on the rank of a data matrix and that window-normalized rank value is closely related to object support in image domain. These findings can be used to estimate thresholding parameters. For example, here we used estimates from other scans to predict the rank value for prospectively under-sampled dataset. Although our approach for estimating the rank seems sufficient for practical purposes, we believe that further research on the exact behavior of the rank in relation to changes of imaging subject, coil geometries, and other factors in data acquisition are important and, together with more in vivo studies, are worthy goals for future research. Most of the reconstruction time in SAKE is spent in performing SVD on the large data matrix in every single loop. The computational complexity will increase with a higher rank value, larger window size, and larger image size (28, 29). To reduce the computational load, one could adopt faster SVD implementations such as PROPACK (31) that computes a few singular values and corresponding singular vectors based on Lanczos bidiagonalization. Adopting GPU-based computing (32) is also a possibility. Other approaches in reducing the reconstruction time include using SAKE to reconstruct only a portion of k-space as a synthesized calibration data. Once the calibration data is at hand, many other auto-calibrating methods can be adopted for full data reconstruction.

In some ways, the iterative iGRAPPA algorithm (33) is similar to SAKE. In iGRAPPA, a new GRAPPA kernel is calibrated every iteration from the reconstructed data and then applied to obtain a better approximation. Calibrating a new kernel is similar to learning the low dimensional signal subspace. Our approach is more general as it captures the entire signal subspace using SVD.

Conclusions

In this work, we have presented a calibration data-free parallel imaging reconstruction method called SAKE. The proposed method formulates the parallel imaging reconstruction as a structured low-rank matrix completion problem and solves it by iteratively enforcing multiple consistencies (which can include sparsity). We have shown that SAKE produces reliable reconstruction results in terms of accurate de-aliasing and noise performance. Lastly, the reconstruction with non-Cartesian data shows the flexibility of SAKE.

Appendix

Upper Bound on Rank of Data Matrix

Here, we give an upper bound on the rank value of a data matrix. We consider a multi-channel acquisition case in which image size is set to N_x × N_y with N_c number of coils and further assume that coil sensitivity profiles have compact support of s × s pixels in k-space. For simplicity, we have chosen a square window. Under this condition, multi-channel parallel acquisition can be formulated into a linear equation,

$$a=Em,$$ [A.1]

where a is a vectorized k-space data block across all coils (Fig. 1), E is a sensitivity encoding matrix that implements multiple convolution operations for each channel, and m is a column vector representing a block of corresponding source MR signal in k-space. If we choose the block window size of a to be w × w, the size of the encoding matrix E becomes w²N_c × (w+ s − 1)². As sensitivity encoding is essentially a shift-invariant operation in k-space, Eq. A.1 holds for any data block within the acquired multi-channel data. Thus, we can extend Eq. A.1 into

$$A=EM$$ [A.2]

where A is a data matrix of which every column represents a distinct data block satisfying Eq. A.1 and M is a source signal matrix constructed in a block Hankel form. The size of A and M is given by w²N_c × (N_x − w + 1) (N_y − w + 1) and (w + s − 1)² × (N_x − w + 1) (N_y − w + 1), respectively.

From Eq. A.2, rank(A) is bound by the following equation (29),

$$\mathit{rank}(A)\le min\{\mathit{rank}(E),\mathit{rank}(M)\}.$$ [A.3]

For a given number of channels N_c and a large enough image size N_x × N_y, we can freely set the value of w so that the following relations hold.

$$\begin{array}{l}{w}^2{N}_c>{(w+s-1)}^2\\ {(w+s-1)}^2<(N_x-w+1)(N_y-w+1)\end{array}$$

Note that this effectively makes E a tall matrix and M a fat one. Altogether with Eq. A.3, rank of the data matrix A is bound by

$$\mathit{rank}(A)\le {(w+s-1)}^2$$ [A.4]

Thus, the data matrix A is always rank deficient for an appropriately chosen block window size w × w and has a non-trivial left null space, which, in turn, guarantees the GRAPPA calibration (Eq. 3) to hold.

Implementation of Data Consistency Condition

We rewrite Eq. 7 for convenience.

$$\begin{array}{ll}\mathit{minimize}\hfill & {\Vert Dx-y\Vert }^2\hfill \\ \mathit{subject}to\hfill & \mathit{rank}(A)=k,\hfill \\ \hfill & x=H^{†}(A).\hfill \end{array}$$ [A.5]

This section defines the projection operator that corresponds to the data consistency (||Dx − y||²) in Eq. A.5 and discusses the actual implementation for both Cartesian and non-Cartesian cases.

Given the current estimate x_n, the projection operator onto the set of least-squares solutions for the problem Dx = y is given by the following equation (34).

$$x_{n+1}=(I-D^{†}D)x_n+D^{†}y.$$ [A.6]

In the case of Cartesian sampling, y is acquired data concatenated into a vector form, and D is a matrix that selects sampled locations from the full k-space grid. Note that D is a fat matrix due to under-sampling and consists of linearly independent rows of which are vectors from the canonical basis. Under this definition, D^H becomes an operator that generates a zero-filled full k-space (in a vector form) from the acquired data. It is easy to see that DD^H = I, and, since D has full row rank, D^† reduces to D^† = D^H (DD^H)⁻¹ = D^H (28, 29). Let D_c be an operator that selects non-acquired locations in k-space. Then, Eq. A.6 reduces to

$$\begin{array}{l}{x}_{n+1}=(I-D^{†}D)x_n+D^{†}y\\ =(I-D^{H}D)x_n+D^{H}y\\ =D_c^H{D}_c{x}_n+D^{H}y.\end{array}$$ [A.7]

This update rule is equivalent to replacing estimates of k-space samples with the acquired data at the sampled locations (10).

For the non-Cartesian sampling (e.g. spiral), D is an interpolator that interpolates reconstructed Cartesian data onto non-uniformly sampled k-space locations (35, 36). In this case, computing D^† in Eq. A.6 becomes a non-trivial task. As an alternative, we replace the pseudo-inverse with the adjoint operator D^H and take a gradient descent step.

$$\begin{array}{l}{x}_{n+1}=(I-D^{†}D)x_n+D^{†}y\\ =x_n-D^{†}({Dx}_n-y)\\ \approx x_n-D^H({Dx}_n-y).\end{array}$$ [A.8]

In other words, the update rule in Eq. A.8 is to 1) inversely grid the current estimate of k-space data, 2) calculate residual between the acquired data and the inversely-gridded estimate, 3) grid the residual back to Cartesian grid, and 4) add the result from 3) to the current estimate. This process can be repeated a few times to take more than one gradient descent step. For the spiral data used in this work, we empirically found out that taking two gradient steps produced good results. We adopted the non-uniform fast Fourier transform (NUFFT, 36) for efficient implementation of the gridding process D and D^H Also, the LSQR package was used to calculate the update rule in Eq. A.8 (37). Of course, an appropriate form of density compensation (38) can be adopted in formulating the data consistency constraint as a weighted, least-squares problem that would result in a faster convergence. A detailed discussion on the subject, however, is beyond the scope of this paper.