Biomembrane-mimicking lipid bilayer system as a mechanically tunable cell substrate

Abstract

Cell behavior such as cell adhesion, spreading, and contraction critically depends on the elastic properties of the extracellular matrix. It is not known, however, how cells respond to viscoelastic or plastic material properties that more closely resemble the mechanical environment that cells encounter in the body. In this report, we employ viscoelastic and plastic biomembrane-mimicking cell substrates. The compliance of the substrates can be tuned by increasing the number of polymer-tethered bilayers. This leaves the density and conformation of adhesive ligands on the top bilayer unaltered. We then observe the response of fibroblasts to these property changes. For comparison, we also study the cells on soft polyacrylamide and hard glass surfaces. Cell morphology, motility, cell stiffness, contractile forces and adhesive contact size all decrease on more compliant matrices but are less sensitive to changes in matrix dissipative properties. These data suggest that cells are able to feel and respond predominantly to the effective matrix compliance, which arises as a combination of substrate and adhesive ligand mechanical properties.

Introduction

Adherent cells actively probe the mechanical properties of the extracellular matrix by imposing traction forces and detecting the resulting mechanical responses (ECM). These mechanical signals are converted into intracellular biochemical signals by a process termed mechano-transduction [1, 2]. By this process, cells are able to mechanically adapt to the substrate they adhere to. The influences of matrix mechanical properties on cells have been extensively studied using polyacrylamide (PAA) or structured polydimethylsiloxane (PDMS) substrates. These studies showed that the matrix elasticity has implications on cell morphology [3-5], cell mechanical properties [6, 7], migration [8, 9], adhesion [5, 10], contractile force generation [8, 11, 12], and differentiation [13].

In addition to substrate rigidity, the anchorage and binding details of the adhesion ligands may also play an important role in cellular mechano-sensing. For instance, softer PAA gels are more porous and, therefore, provide sparser anchoring points to adhesive ligands compared to stiffer PAA gels [14]. It has been argued that sparsely anchored adhesive ligands on soft PAA gels stretch differently and behave more compliant when exposed to lateral force than ligands anchored firmly to stiffer PAA gels. Thus, the mechanical cue to which cells respond may not be the stiffness of the underlying matrix but instead the amount of ligand extension or possibly the opening of cryptic binding sites as the ligands unfold under force [14, 15]

The purely elastic PAA and PDMS substrates with immobilized, static adhesive ligands used in previous studies fall short of replicating the viscoelastic and dynamic nature of tissues and cells [16-20]. In contrast to elastic substrates where deformations come to a halt when cell tractions reach a steady state, cell adhesion ligands anchored to viscoelastic or plastic substrates remain mobile and thus provide a different mechanical stimulus. It has been shown that cellular traction forces decrease with increasing mobility of adhesion ligands anchored non-covalently to different polymeric substrates [21], although the bulk mechanical properties of the polymeric substrates were not characterized in that report.

We use a biomembrane-mimicking cell substrate based on a polymer-tethered multi-lipid bilayer system to study cell behavior in response to viscoelastic matrix properties [22]. As a cell adhesion ligand, laminin is coupled to the top lipid layer via amine-to-sulfhydral crosslinkers. The material properties of the multi-bilayer cell substrate can be tuned by increasing the number of bilayers in the stack, which decreases the frictional coupling between the top layer and the supporting glass substrate and, therefore, increases substrate fluidity. Importantly, stacking does not alter the density or binding properties of adhesive ligands. Therefore, any responses of cells grown on bilayers with different stacking numbers can be attributed solely to changes in substrate bulk mechanical properties. Preliminary experiments revealed that the number of stacked bilayers affect fibroblast spreading, morphology, and migration [23], but the viscoelastic properties of the multi-bilayer systems had also not been studied thus far.

To characterize the mechanical properties of the bilayer substrates, we measure the creep response by applying lateral forces onto magnetic microbeads coupled to the laminin ligands. As a reference, we compare these properties to those of laminin-coated glass as well as polyacrylamide substrates. The responses of mouse embryonic fibroblasts (MEFs) to changes in matrix compliance of these substrates are studied in terms of spreading area, motility, cytoskeletal prestress, cell stiffness and focal adhesion size. Finally, the relative influence of matrix elastic versus dissipative properties on cell behavior is analyzed.

Materials and methods

Cell culture

Mouse embryonic fibroblasts (obtained from Dr. W. Ziegler, University of Leipzig) [24] are maintained at 37°C and 5% CO₂ in low glucose (1 g/L) Dulbecco's modified Eagle's medium supplemented with 10% fetal calf serum, 2mM L-glutamine, and 100 U/ml penicillin-streptomycin. Before plating, cells are rinsed with PBS and trypsinized with 0.05% trypsin/EDTA.

Bilayer assembly

Bilayers are fabricated as described in [22]. In brief, small unilamellar vesicles (SUVs) or giant unilamellar vesicles (GUVs) are used. SUVs are prepared by sonication [25, 26] and GUVs by the sucrose hydration method [27]. Two complementary chloroform lipid stock solutions consisting of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC, Avanti Polar lipids) with either 5 mol% 1,2-dihexadecanoyl-sn-glycero-3-phosphothioethanol (sodium salt) (DPTE, Avanti Polar lipids) or 5 mol% 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-{maleimide(polyethyleneglycol)-2000} (ammonium salt) (DSPE PEG2000-Maleimide, Avanti Polar lipids) are prepared as SUVs and GUVs. To produce GUVs, the stock solution is dried, resuspended in 0.1 mM sucrose / 1 mM CaCl₂ solution, heated for 2 h and then cooled down to room temperature. SUV vesicles are formed by resuspending the dried stock solution in Milli-Q water, followed by sonication for 10 min. For the first layer of every stack, SUVs are added to a solid glass support. They adsorb to the glass and break due to intrinsic instabilities to form a lipid bilayer [28, 29]. Additional layers are formed through GUV fusion (Fig. 1). For these layers, GUVs are added in a 0.1 mM glucose / 1 mM CaCl₂ solution and are allowed to bind for 2 hours. Stacking is achieved by adding complementary GUV solutions, which are linked covalently by sulfhydral-maleimide coupling chemistry, linking thiolated lipid DPTE with maleimide-functionalized lipopolymer PEG2000-Maleimide. Adding additional layers increases lateral linker mobility [22] and decreases frictional coupling of the top layer with the glass substrate [30] (Fig.1). The top layer of the stacks is labeled with Texas Red, allowing us to monitor the quality of the formed bilayer deposition through diffusion measurements (fluorescent recovery after photo bleaching, FRAP). Each final substrate is tested for defects by laser bleaching of several 20 μm diameter spots at different locations and observing the subsequent fluorescence recovery. Substrates that did not fully recover within two minutes were discarded. The top layer always contains DPTE, allowing for the layers to be coated with cell-substrate linkers (here: laminin) that are linked via heterobifunctional quantum dots functionalized with PEG-Mal and PEG-NHS.

Figure 1. Phospholipid bilayer stack assembly and properties.

Bilayer substrates are built by stacking alternating GUV solutions on top of each other and linking them via sulfhydral-maleimide coupling chemistry. Previous work suggests that with increasing number of layers, frictional coupling to the solid support decreases, and linker mobility increases [22]. The top layer is functionalized with laminin as a ligand for cell adhesion. Each bilayer has a thickness of 4 nm, and each polymer layer has a thickness of 3.4 nm [22].

Polyacrylamide gels

Polyacrylamide gels are cast using a 40% acrylamide/bisacrylamide (ratio 37.5:1) Solution (Sigma Aldrich). The solution is mixed with water at a final concentration of 4% or 6.1% acrylamide. To initiate polymerization, 0.2% tetramethylendiamin (TEMED) and 0.5% amoniumpersulfat (APS) were added. For traction measurements, gels are prepared by the same protocol at a concentration of 6.1% acrylamide/bisacrylamide, and fluorescence beads are embedded in the gel (see below under traction microscopy).

Live cell imaging

Cells are imaged using an inverted microscope (DMI6000B, Leica) and kept at 37°C and 5% CO₂ within an incubation chamber during measurements. To monitor the changes in cell spreading area, cells are plated for 24 h prior to measurements. Phase contrast images of the cells are obtained and analyzed using a customized Matlab program.

For measuring cell migration, cells are monitored in Hoffmann contrast mode using a 20x 0.4 NA objective with a 0.5x video coupler. Images are taken every 300s over a time period of up to 24h. Cell movements are tracked with custom image processing software written in Matlab. From the cell trajectories, the mean squared displacement (MSD) is calculated [31] and described with a power-law relationship of the form

$$\text{MSD}=\mathrm{D}\ast {(\mathrm{t}/{\mathrm{t}}_0)}^{\mathrm{\beta }}$$ (Eq. 1)

with D denoting the apparent diffusivity (the MSD at the reference time t₀ = 1 min), and β denoting the power-law exponent. The time interval Δt ranges from 300s to 300 min. D characterizes the speed of cell movements at short time intervals, and β characterizes the persistence of cell movement at long time intervals [32]. β typically ranges from a value of 1 for randomly migrating cells to a value of 2 for persistent, ballistically migrating cells [32]. As D is log-normal distributed [32], the geometric mean and geometric standard error of D is computed for each measurement condition. For each trajectory, we also compute the cosine of the turning angle of cell movements between subsequent time intervals Δt ranging from 300 s to 300 minutes [32]. A value near unity characterizes a persistent motion; a value near zero characterizes a random motion.

Magnetic tweezer microrheology

Magnetic tweezers are used to characterize the mechanical properties of substrates and cells [33]. In brief, the magnetic tweezer device is attached to an inverted microscope equipped with a 40x, 0.6 NA objective. The device consists of a solenoid with 250 turns of 0.4 mm diameter copper wire around a high-permeability μ-metal core (HyMu80 alloy, Carpenter, Reading, PA) with a sharp tip.

Magnetic pulling forces in the horizontal direction are exerted on superparamagnetic beads (epoxylated 4.5 μm Dynabeads, Invitrogen). For coupling the beads to the substrates or cells, beads are coated with laminin or fibronectin (Roche Diagnostics), respectively, at a concentration of 5 μg protein in 1 ml PBS for 1×10⁷ beads, at 4°C overnight in a shaker. Prior to measurements, beads are sonicated for 10 s and added to the substrate or the cells at a density of 3,000 beads per mm². After 30 minutes of incubation, unbound beads are gently washed off.

Cells are seeded at a density of 4,000 cells / cm². Measuring time is limited to 30 minutes per dish since the cells are kept at 37°C b ut without CO₂ on the microscope stage. For measuring the mechanical properties of the bilayer substrates, a series of 3 force steps (amplitude 0.5 - 10 nN, duration 5 s with 5 s pauses) is applied. For measuring cells, a stepwise increasing force from 0.5 nN to 10 nN is applied, with each force step lasting 1 s. The resulting bead motion is recorded with a CCD camera (ORCA ER, Hamamatsu, Japan) at a rate of 40 frames/s for cell studies, or at 8 frames/s for substrate studies. Bead displacement d(t) is extracted from the bright-field images with a center-of-mass algorithm (accuracy ∼ 10 nm (rms)) [33]. The creep compliance J(t) (the displacement of beads normalized to the applied force (d(t)/f)) in units of μm/nN is fitted by a power-law,

$$\mathrm{J}(\mathrm{t})={\mathrm{J}}_0{(\mathrm{t}/{\mathrm{t}}_0)}^{\mathrm{\beta }}$$ (Eq. 2)

with time t normalized to t₀ = 1 s as described in [19, 34]. J₀ is the creep compliance at t₀ and corresponds to the inverse magnitude of the cells' dynamic shear modulus (stiffness) [35]. β describes the fluidity of the material, with 0 corresponding to an elastic solid and 1 to a viscous fluid.

Traction microscopy

To study the influence of the different bilayer stacks on the forces that cells exert on their environment, we use traction microscopy. Traction forces are computed from the displacements of beads embedded in a polyacrylamide gel with a Young's modulus of 11.3 kPa. Gels are functionalized using Sulfo SANPHA (Thermo Scientific). For plating cells directly onto gels, the gels are coated with laminin at a concentration of 15 μm/cm². For adding a lipid bilayer to the polyacrylamide substrate, the gels are firsts coated with fibronectin (15 μg/cm²) and then treated with Sulfo-GMBS 10 mg/ml in DMSO. Additional layers, if needed, are stacked according to the layer fabrication protocol described above (Fig. 1).

Next, the cells are plated at a density of 1000 cells/cm² and incubated at 37°C and 5% CO₂ overnight. Throughout the measurement, the cells were kept in a custom-made incubation chamber at 37°C in a humidified 5% CO₂ atmosphere. A bright field image of the cell is taken to record the cell shape and position. Bead positions are recorded using fluorescence imaging. Subsequently, cells are relaxed or detached from the substrate by adding a 100 μl cocktail of 80 μM cytochalasin D in 0.25% trypsin. With no cell forces applied, the gel relaxes back to its stress-free configuration, and a second fluorescent image is taken. Bead displacements due to cell tractions are estimated with an unconstrained deconvolution, and cell tractions are computed using the Fourier transform traction cytometry method described in [36]. From the displacement field and the traction force, we calculate the strain energy U as

$$\mathrm{U}=\stackrel{1}{}/\underset{2}{}\int (\text{Traction}\ast \text{displacement})\text{dx}\text{dy}$$ (Eq. 3)

[37].

Immunofluorescence and TIRF

For immunofluorescence imaging, cells are cultured in a 35 mm petri dish with a 15 mm diameter glass bottom in which the cells grow on laminin-coated glass or on multi-bilayer stacks. Cells are then fixed for 10 min in 4% formaldehyde, permeabilized for 10 min with 0.5% Triton X solution, rinsed with PBS and incubated in 1% BSA in PBS for one hour. Primary antibodies against paxillin (349/Paxillin BD Biosciences, Europe) are added for one hour at a dilution of 1:500, rinsed with PBS, and incubated for 5 min with 3% BSA in PBS. The secondary IgG1 antibody (Biolegend) at a dilution of 1:1000 together with phalloidin-TRITC (Sigma) and Hoechst are added for one hour. Afterwards, the samples are washed with PBS and 3% BSA in PBS. Focal adhesions are imaged using total internal reflection microscopy. Focal contact numbers and areas are analyzed with a Matlab program based on a watershed algorithm as described in [38, 39].

Results

Substrate properties

To characterize substrate rheology, we use a magnetic tweezer microrheometer. During the application of a force step of approximately 1nN, beads attached to the bilayer substrates via laminin-laminin coupling rapidly move towards the tweezer needle tip but then slow down and continued to creep towards the needle tip with decreasing speed. When the force is removed, the beads reverse direction with an initially high speed that continuously declines. The beads return only partially to their starting positions. When the force is turned on again, the beads retrace- their movements from the first force cycle, with a small additional gain in distance towards the needle tip. When the second force cycle is turned off, the beads nearly return to the starting position of the second force cycle, plus the additional movement it has gained during the second force cycle. The bead movement during the third force cycle closely resembles that of the second force cycle, with an even smaller additional gain in distance towards the needle tip (Fig. 2a). This behavior can be described by the superposition of an elastic and a non-elastic deformation of the substrate. The non-elastic components are not consistent with a purely viscous behavior, as only the first force step but much less so the subsequent force cycles cause a permanent bead displacement towards the needle tip. The non-elastic component of the bead displacement is consistent with a structural plasticity that originates from the same matrix components that also determines the substrate elasticity (Fig. 2c). The bead displacement d(t) versus time t in response to a force step with amplitude ΔF is captured by a structural damping behavior of the form

Figure 2. Viscoelastic substrate properties.

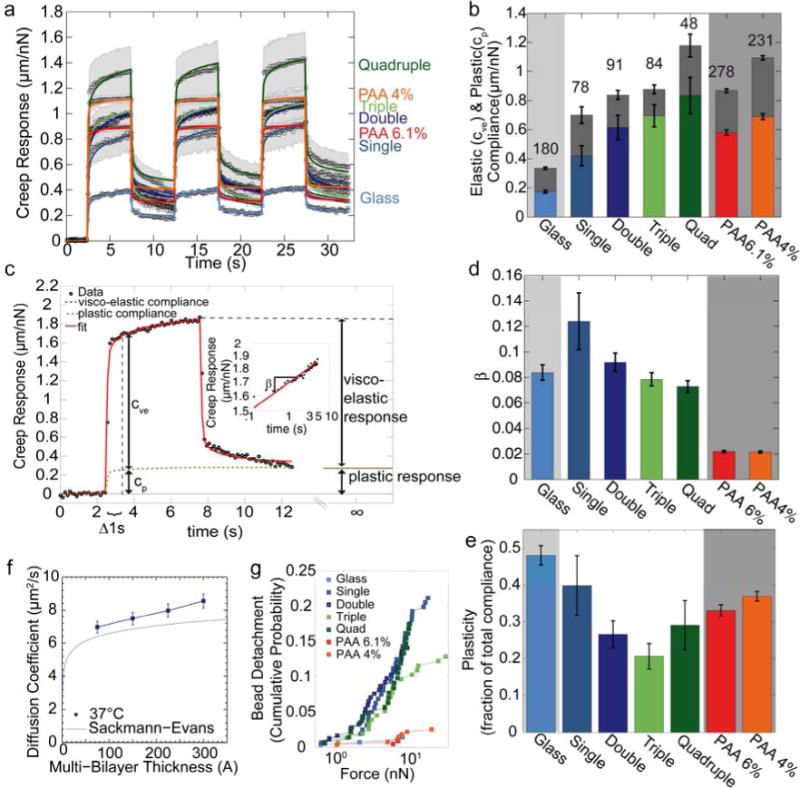
(a) Creep behavior (bead displacement normalized by lateral force) measured with superparamagentic beads bound to laminin on glass, polyacrylamide, or on stacked lipid bilayers. Data points are average values from n>48 individual measurements. The shaded area indicates one standard error of the mean. Solid lines are the fit of Eq. 4 to the data. (b) Elastic compliance c_ve (colored) and plastic compliance c_p (gray) for different substrates. The lower error bars are standard errors of the elastic compliance, the upper error bars are the standard errors of the plastic compliance. The sum of elastic compliance and plastic compliance represents the total creep compliance (bead displacement at t₀ = 1 s normalized to force). (c) Example of bead displacement on quadruple bilayer (black symbols) for a lateral force of 1 nN. The red line indicates the fit of Eq. 4 to the data. Elastic compliance c_ve and plastic compliance c_p are determined at t₀ = 1 s. (d) Power-law exponent β (a measure of substrate fluidity) for different substrates. (e) Plasticity as a fraction of total compliance. (f) Diffusion coefficient of Texas Red-labeled lipids of the top bilayer at 37°C m easured with FRAP (mean ± se from 15 independent measurements). The blue line indicates the theoretical expectations from the Sackmann-Evans-theory for supported bilayers [29, 30]. (g) Cumulative probability of bead detachment from the substrate as a function of pulling force on laminin-coated beads. Bead detachment probability is similar for all bilayer substrates, but is lower on glass and PAA.

$$d(t)/\Delta F=(c_{\mathit{\text{ve}}}+c_p){(t/t_0)}^{\beta }$$ (Eq. 4)

where d(t)/ΔF is the creep modulus J(t), c_ve is the viscoelastic compliance of the substrate (inverse of stiffness), c_p is the plastic compliance of the substrate, t₀ is a reference time arbitrarily set to 1 s, and β is a power-law exponent that is related to the mechanical damping coefficient η (also called loss tangent) of the matrix by the relationship η = tan (π/2 β) [35] (Fig. 2c). In a viscous liquid, bead displacement during force application follows ∼ t¹; in an elastic structure, bead displacement would be described by ∼ t⁰.

From the fit of Eq. 4 to the data, we find that both the viscoelastic and the plastic compliance increase with increasing number of stacked bilayers (Fig. 2b), while the power-law exponent is approximately 0.1, independent of the number of stacked bilayer (Fig. 2d). The plastic compliance is a fraction of approximately 0.3 of the total compliance (Fig. 2g). The predominantly elastic behavior of beads on lipid bilayer stacks is unexpected. With fluorescence recovery after photobleaching (FRAP) of Texas-Red labeled lipids in the top bilayer membrane of each stack, we observe an increase of the lateral diffusivity of Texas-Red labeled lipids with increasing numbers of stacked bilayers (Fig. 2e), consistent with recent TRITC-DHPE lateral diffusion data on comparable single and multi-bilayer systems obtained using wide-field single molecule fluorescence microscopy [22, 40]. Therefore, the predominantly elastic behavior of the beads is attributable to their coupling to the laminin ligands, as further explored below.

For comparison, we also characterize laminin-coated PAA substrates of different densities. The creep modulus of a 4% PAA gel has a total compliance close to that of a quadruple bilayer, whilst a 6.1% PAA gel has a total compliance close to that of a double bilayer. As expected, the power-law exponent for the purely elastic PAA is close to zero.

From the tweezer measurements, we can further infer the adhesion strength between the bead and the laminin-coated bilayer substrate. At a force of 10 nN, approximately 20% of the beads detached from the bilayer surfaces, independent of the number of bilayer stacks (Fig. 2f). This finding supports the notion that bilayer stacking does not alter the density or binding properties of adhesive ligands. On glass and PAA substrates, adhesion of the beads to the surface was stronger, with only 2% of the beads detaching at 10 nN. This result may indicate a higher binding strength of laminin to the underlying glass or PAA matrix compared to the amine-to-sulfhydral crosslinker on the bilayers. More likely, however, these finding points to a higher ligand density on glass or PAA compared to bilayers where only 5% of the DPTE lipids are functionalized with the amine-to-sulfhydral crosslinker for laminin binding.

To further test the influence of the laminin coating on the bilayer substrate properties, we study the creep response for different laminin concentrations. We notice a small increase in the creep modulus of bilayers functionalized with higher laminin concentrations (Fig. 3a,b), suggesting that the bilayer substrate is largely saturated with adhesive ligands at a laminin concentration of 15 μg/cm² used for cell experiments. In addition, these data suggest that part of the creep response originates from the laminin. Indeed, for practically undeformable glass with a laminin coating, we find appreciable creep (Fig. 2a) and a relatively high fluidity with a power-law exponent of 0.1.

Figure 3. Influence of laminin on creep response.

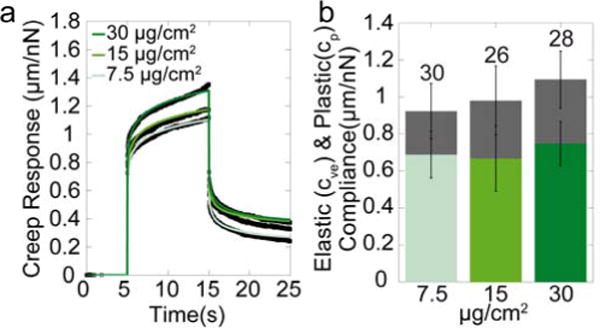
(a) Creep Response of double bilayer substrates coated with different concentrations of laminin. (b) Elastic and plastic compliance of the double bilayer coated with different laminin concentrations.

Cell reaction to different substrates

Cell area

Previous reports demonstrated that cells decrease their spreading area on softer substrates [4, 5, 41]. Here, we show that cell area decreases with increasing number of bilayer stacks. Cells were also smaller on the softer 4.0% PAA substrates compared to cells on the stiffer 6.1% PAA substrates or on glass (Fig. 4). Cell area shows a statistically significant (p<0.05) inverse correlation with the elastic compliance (Fig. 4g), with a correlation coefficient of r²= 0.87. Cell area changes are also inversely correlated with substrate plasticity and fluidity (SI Fig. 1), but the correlation coefficient is small in both cases, and not statistically significant.

Figure 4. Cell spreading area.

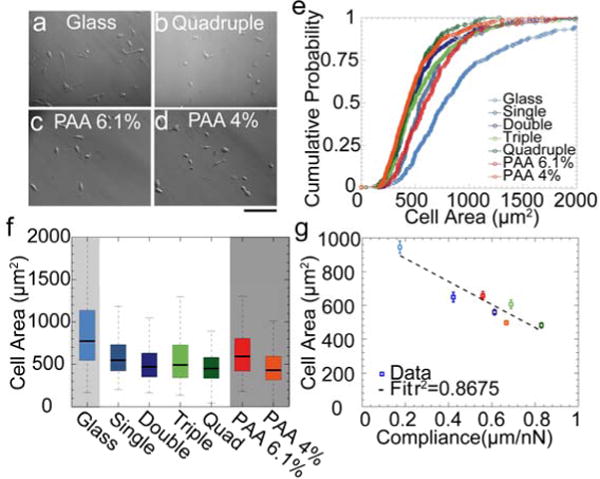
Hoffman modulation contrast images of mouse embryonic fibroblasts after 24 hours of plating on laminin-coated glass (a), quadruple bilayer (b), 6.1 % PAA (c) and 4% PAA (d). Scale bar is 100 μm. (e) Cumulative probability of cell size distribution on different substrates. (f) Same data as in e) plotted as box-plot (5, 25, 50, 75 and 95 percentile). (g) Cell area (mean ± se) decreases with substrate compliance.

Cell motility

Since differences in spreading area have been linked to differences in motility [42, 43], we also analyze the cell motility and persistence. With increasing number of bilayers, cell trajectories shorten and become less persistent (Fig. 5a-j). Cells on 6.1% PAA gels show cell trajectories comparable to those on triple and quadruple bilayer. On 4% PAA gels, cells move with a particularly low persistence. For a quantitative comparison, we analyze the mean squared displacements (MSD) of the cell over a time course of 6 h. Cells plated on laminin-coated bilayer substrates show a reduced MSD compared to cells cultured on glass (Fig. 5k). The MSD increases according to a power-law in time (Eq. 1), with a super-diffusive (β>1) power-law exponent for cells on glass, a diffusive (β ∼1) exponent for cells on bilayer substrates and 6.1% PAA gels, and a sub-diffusive (β<1) exponent for the cells on 4% PAA gels. The increased exponent of the MSD versus time has been previously shown to be correlated with the persistence of movements [32]. Thus, we expect that cells plated on bilayer substrates move less directed than cells on glass substrate but more directed than cells on soft 4% PAA gels. This is confirmed by measurements of the turning angle and its time evolution that show increasing turning angles, hence a less persistent motion, with increasing substrate compliance (Fig. 5m).

Figure 5. Cell motility.

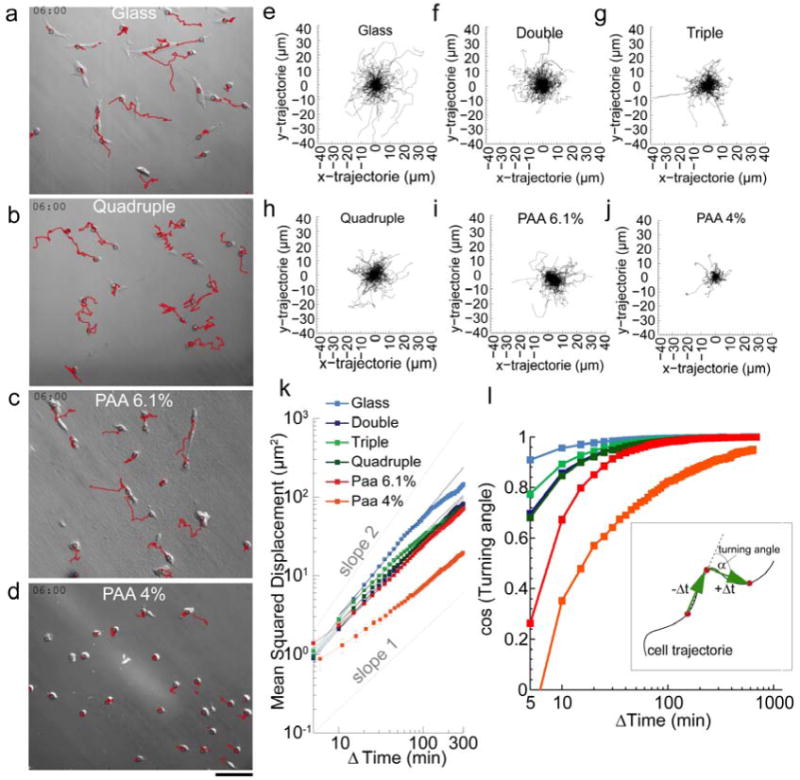
Trajectories (red) of cells plated on laminin-coated glass (a), quadruple bilayer substrates (b), 6.1% PAA (c) and 4% PAA (d) are observed for 6 hours. Scale bar is 100 μm. (e-j) Windrose plot of cell trajectories on different substrates for 250 cells over 5 hours. (k) The MSD of cell movements increase with time according to a power-law with exponents (slopes) of: glass=1.3, double=1.1, triple=1.0, quadruple=1.0, PAA 6.1%=1.0, PAA 4%=0.78. (l) Cosine of the turning angle of cell movements versus lag time. Cells move with smaller turning angles (more directed) on glass (light blue) than on the bilayer substrates and PAA gels. Inset: Schematic of turning angle calculation for a fixed lag time Δt.

Cell stiffness

Cells were shown to soften and to form fewer stress fibers on softer substrates [7, 10, 13]. To measure changes in cell stiffness, we use a magnetic tweezer to apply forces to superparamagnetic beads attached to the cells. From the bead displacement data, we obtain the cell stiffness and fluidity by fitting with a power-law (Eq. 2)[7]. Cell stiffness decreases and cell fluidity increases with increasing number of stacked bilayer and hence with substrate compliance (Fig. 6). The stiffness and fluidity of cells on substrates with comparable compliance (elastic and plastic) is similar, e.g. for cells on the soft 4% PAA gels and on quadruple bilayers, or for cells on stiffer 6.1% PAA gels and on double bilayers.

Figure 6. Cell rheology.

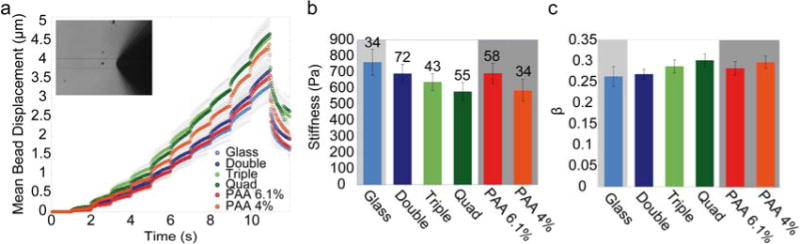
(a) Displacement of beads attached to cells grown on different substrates (mean ± se) in response to force steps (0.5-10 nN). Bead displacement in response to applied force increases with number of stacked bilayers. Inset: Bright field image of a MEF cell with superparamagnetic bead and magnetic tweezer needle tip (black with white outline). (b) Cell stiffness (mean ± se, n as indicated above bars) decreases with increasing number of stacked bilayers. (c) Cell fluidity (power-law exponent of the creep modulus) increases with increasing number of stacked bilayers (mean ± se) .

Cell tractions

Cell stiffness has been shown to scale with the contractile cytoskeletal prestress [19, 44]. We measure how cell contractility changes with bilayer stacking using traction force microscopy. Cells are plated either directly on 6.1% PAA gels, or on single or triple bilayers that are coupled to a 6.1% PAA gel through fibronectin and amine-to-sulfhydral linkers (Fig. 7a). Since cell tractions are counter-balanced by equal and opposite substrate forces, the displacement of marker beads at the top of the elastic PAA layer can be used to compute cell tractions, irrespective of the coupling details between the layer and the force-generating contractile machinery of the cell [44]. We also calculate the strain energy stored in the substrate for each cell (Eq. 3), which is a measure of total cell contractility (Fig. 7d). Maximum cell tractions and strain energy both decrease on single bilayers and even more so on triple bilayer substrates (Error! Reference source not found.. b, c).

Figure 7. Cell tractions.

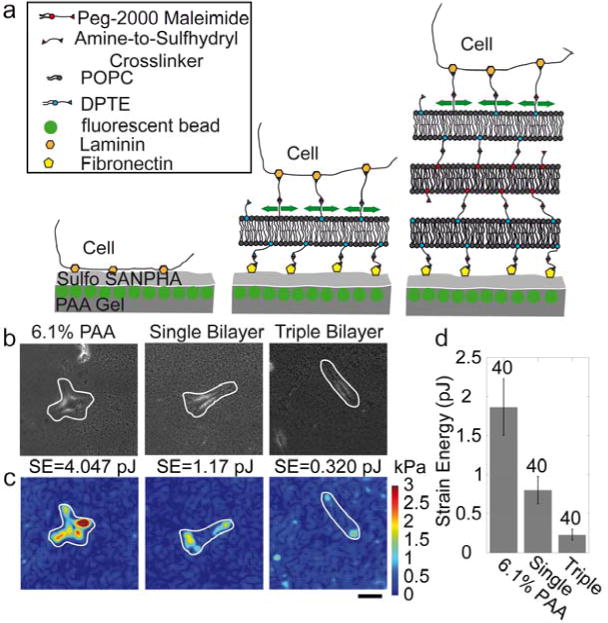
(a) Schematics of the method for measuring tractions of cells on stacked bilayers. (b) Bright field images of MEF cells cultured directly on a 6.1% PAA gel (left), on a single bilayer (middle) and a triple bilayer (right), both on top of a 6.1% PAA gel. (c) Corresponding traction maps (white lines indicate the cell outlines). Scale bar is 20 μm. (d) Elastic strain energy calculated with Eq. 3 from tractions and matrix displacements (mean ± se, n as indicated above bars) decreases with the number of stacked bilayers.

Focal adhesion

Focal adhesions are the points where contractile forces from the cell are transmitted to the substrate. It has been shown that on softer substrates, focal adhesions are more dynamic and irregularly shaped [10]. Bilayer substrates, due to their small thickness, allow us to use TIRF microscopy to monitor focal adhesions (Fig. 8). Focal adhesion size decreases with the number of stacked bilayers (Error! Reference source not found.. a,b), while the density (numbers per area) increases. The latter finding is mainly an effect of the smaller spreading area of cells on the stacked bilayers, as the total number of focal adhesions per cell remains approximately constant for all substrates. Furthermore, the focal adhesions change from an elongated shape on glass and single bilayers to a round morphology on triple and quadruple bilayers (Fig. 8c).

Figure 8. Focal adhesions.

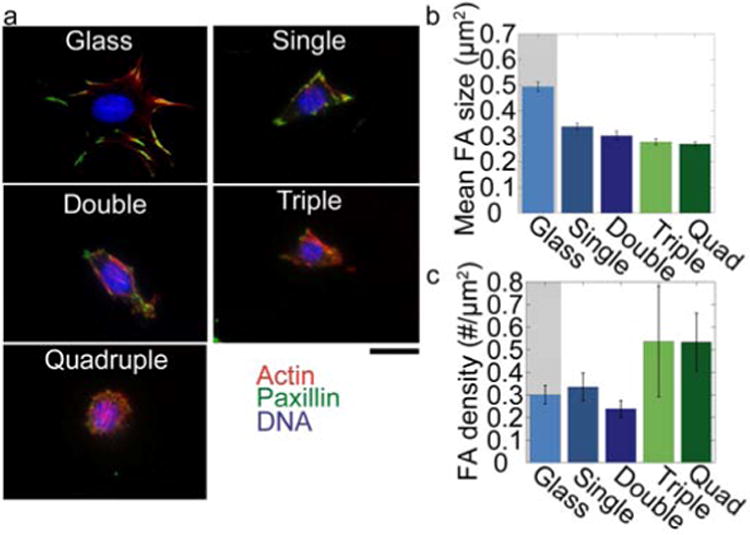
(a) Cells cultured on different substrates stained for paxillin (green), actin (red) and the nucleus (blue). Scale bar is 20 μm. (b) Mean focal adhesion size decreases with number of stacked bilayers (mean ± se from > 8 cells) (c) Number of focal adhesions per cell area increases with number of stacked bilayers.

Discussion

Lipid bilayers are known to be fluid-like [45, 46] and therefore, are used in this study to investigate the response of cells to a viscous matrix. We confirm a fluid-like behavior of Texas-Red labeled lipids in bilayer stacks by fluorescence recovery after photobleaching (FRAP) (Fig. 2e). The increase in diffusivity with increasing number of bilayers closely follows the Sackmann-Evans theory for supported bilayer membranes without polymer tethers [29, 30]. In the magnetic tweezer measurements, however, we find predominantly elastic behavior. The important difference between FRAP and magnetic tweezer measurements is that the magnetic beads are not coupled to the lipids but to the laminin coating. Our findings, therefore, suggests that the laminin coating on top of the bilayers forms crosslinked networks with predominantly elastic properties. This is also in agreement with earlier findings for laminin networks [47-49].

Elastic behavior requires a stable inter-bilayer coupling between the laminin on the surface with the glass substrate at the bottom that may include coupling by lipopolymer-enriched inter-bilayer connections previously reported on similar fluid membrane-based hydrogels [50], percolation of linker clusters in polymer-tethered membranes [51] and strong interleaflet coupling of immobilized membrane constituents (e.g., clusters of immobilized lipids) in lipid bilayer architectures [40, 52]. Elastic network formation is further confirmed by the increase in the creep modulus (lower stiffness) that we find when bilayer substrates are coated with higher concentrations of laminin. We interpret this as the result of a 3-dimensional laminin network that forms when higher concentrations of laminin molecules are unable to bind to an already saturated lipid surface. In fact, the creep modulus of laminin on a glass support is qualitatively similar to that of laminin on lipid bilayers, giving further support to the notion that cells on lipid bilayers predominately feel the elastic response of the laminin and not the viscous response of the lipids.

With increasing number of stacked bilayers, the overall compliance of the substrate increases. It is difficult, however, to extract absolute values for the elastic modulus of the substrate from these measurements, because the contact area between the magnetic probe and the substrate (which sets the total applied stress for a given applied force) as well as the substrate thickness (which sets the total strain) is unknown. Moreover, beads attached to a flat surface can rotate in response to lateral forces and indent a soft substrate at larger rotational angles, which gives rise to a non-linear relationship between force and bead displacement [53]. Therefore, the compliance reported in this study is given in units of bead displacement per unit of force, and is not corrected for these unknown geometrical factors so that it indicates only relative changes in substrate mechanical properties. Nonetheless, the creep modulus measured with 4.5 μm magnetic beads reflects the relevant local mechanical response of the matrix that cells feel.

For comparison, we perform magnetic tweezer creep experiments on laminin-coated glass and laminin-coated polyacrylamide gels with different acrylamide concentrations (4% and 6.1%). Creep responses of these substrates show surprisingly little differences, given the fact that the differences in the shear moduli are large (order of tens of GPa for glass, 600 Pa for 4% gels, and 2800 Pa for 6.1 % gels) [54]. This is because the effective mechanical response of the substrate arises from a combination of the laminin network response on top, and the substrate response (PAA, lipid bilayer, or glass) at the bottom. The considerable compliance of the laminin network, therefore, sets an upper limit for the effective stiffness of any laminin-coated substrate. The mechanical behavior of the base substrate is shielded by the mechanical response of the top coating, which has consequences for the resulting cellular response, as shown below and pointed out previously [14].

Upon closer inspection, the creep modulus of all substrates shows viscoelastic and plastic behavior that is best described by a weak power-law in time (Eq. 4), with a power-law exponent of around 0.1. A power-law exponent of 0 would be expected for a purely elastic material, while an exponent of unity would be expected for a purely viscous material. We argue that the exponent of 0.1 reflects foremost the response of the laminin coating, because laminin-coated glass substrates also show a power-law creep response. Bulk rheology measurements of laminin networks have not been performed thus far, but bulk rheology measurements of self-assembled collagen biopolymer networks show a weak power-law behavior with an exponent of 0.08 over a large range of probing frequencies [37]. When laminin is coated on top of a purely elastic, soft PAA gel, the overall creep response is dominated by the softer PAA gel, and the power-law exponent of the creep response falls to values around 0.02. For increasing numbers of bilayer stacks, the overall material response also becomes softer, and the power-law exponent also falls slightly.

The cells show a clear response to substrates with different mechanical properties. Compared to a laminin-coated glass substrate, cell area decreases with increasing number of stacked bilayers (Fig. 4). We attribute this behavior to the increasing compliance of bilayers with higher stacking number, in agreement with the decreasing spreading area of cells on the softer PAA gel. This finding is also in line with previous reports [1, 3]. It is unlikely that the decrease in spreading area is caused by the only marginally larger plasticity of the substrates with a higher number of lipid bilayer stacks. In fact, the relative contribution of plastic deformations to the total matrix deformations, as well as the power-law exponent of the creep modulus, both decrease with bilayer numbers (Fig. 2d,g). Hence, the more compliant bilayer substrates are at the same time more solid-like and less dissipative. Indeed, the cell spreading area shows a strong correlation with substrate compliance for all matrices including glass and PAA (correlation coefficient r²=0.87, Fig. 4g), while correlations of the spreading area with other parameters are considerably weaker (SI Fig. 1).

We observe a similar trend for the persistence of cell migration on different substrates. This can be seen both by the larger power-law exponent of the MSD and hence by a more super-diffusive behavior (Fig. 5k), and by smaller turning angles (Fig. 5m) of cells on the stiffer substrates. This finding seems in apparent conflict with reports of smaller migration speeds for cells on stiffer substrates [10]. Note however, that given enough time, slow cells with a more super-diffusive and persistent behavior can outrun any other cell. Indeed, cells on the stiffer substrates tend to have a slightly lower speed compared to cells on the softer substrates when evaluated at the shortest time interval of 5 min (Fig. 5k), although cells on the softest PAA gels also show a particularly poor migration at short time intervals.

Cell stiffness was consistently higher on the stiffer substrates (Fig. 6c). As cell stiffness scales with contractile prestress [19, 44], we expect higher traction forces for cells on the stiffer substrates, which indeed is confirmed by our traction measurements (Fig. 7). Note that the force balance implies that all traction forces of the cells are fully transmitted to the elastic polyacrylamide substrate, irrespective of any layer with dissipative properties below the basal cell surface such as a lipid bilayer stack. Therefore, the smaller traction forces of cells on the softer and more dissipative bilayer stacks are caused by a decreased cytoskeletal (contractile) prestress [44], which is in line with the cell behavior on elastic polyacrylamide substrates [8, 10, 55, 56].

The thickness of the bilayer substrates of less than 100 nm allows for TIRF imaging of focal adhesions, which gives it a clear advantage over polyacrylamide and other soft hydrogel or polymer substrates. The reduced traction force of cells on the softer bilayers with higher stacking number is accompanied by smaller and less elongated focal adhesions. This is in agreement with earlier findings that cells strengthen focal complexes in response to internal or external forces [12, 57, 58]. The smaller tractions and smaller focal adhesions on the softer bilayer stacks are consistent with the observed changes in morphology towards a less polarized phenotype, a less persistent cell migration, and reduced cellular prestress.

Conclusion

Contrary to the expectation that laminin-functionalized stacked lipid bilayers behave predominantly dissipative, we find predominantly elastic behavior. However, polyacrylamide (PAA) substrates, which have been previously thought of as purely elastic, also show substantial dissipative properties when functionalized with laminin. Similarly, glass substrates, which have been thought of as rigid, are in fact quite compliant when coated with laminin. Stacked bilayer substrates allow us to alter the base substrate mechanics without altering the binding details of the adhesive ligand. Therefore, bilayer stacks provide an alternative to changing the polyacrylamide concentration as a means to alter substrate compliance. Bilayer stacking does not affect the mesh size of the hydrogel substrate or the details of adhesive ligand binding. We show here that cells respond mostly to the total compliance, which arises as a combination of the mechanical properties of the base substrate together with the mechanical properties of the adhesive ligand. In particular, cell spreading area, cell stiffness, traction forces, and size of focal adhesions scale with the elastic compliance but not with the plasticity or fluidity.