Abstract
Gleevec, a well-known cancer therapeutic agent, is an effective inhibitor of several tyrosine kinases, including Abl and c-Kit. But it displays less potency to inhibit closely homologous tyrosine kinases, such as Lck and c-Src. Because many structural features of the binding site are highly conserved in these highly homologous kinases, the molecular determinants responsible for the binding specificity of Gleevec remain poorly understood. To address this issue, free energy perturbation molecular dynamics (FEP/MD) simulations with explicit solvent was used to compute the binding affinity of Gleevec to Abl, c-Kit, Lck, and c-Src. The results of the FEP/MD calculations are in good agreement with experiments, enabling a detailed and quantitative dissection of the absolute binding free energy in terms of various thermodynamic contributions affecting the binding specificity of Gleevec to the kinases. Dominant binding free energy contributions arises from the van der Waals dispersive interaction, compensating about two-third of the unfavorable free energy penalty associated with the loss of translational, rotational, and conformational freedom of the ligand upon binding. In contrast, the contributions from electrostatic and repulsive interactions nearly cancel out due to solvent effects. Furthermore, the calculations show the importance of the conformation of the activation loop. Among the kinases examined, Abl provides the most favorable binding environment for Gleevec via optimal protein-ligand interactions and a small free energy cost for loss of the translational, rotational, and conformational freedom upon ligand binding. The FEP/MD calculations additionally reveal that Lck and c-Src provide similar non-binding interactions with the bound-Gleevec, but the former pays less entropic penalty for the ligand losing its translational, rotational, and conformational motions to bind, examining the empirically observed differential binding affinities of Gleevec between the two Src-family kinases.
Introduction
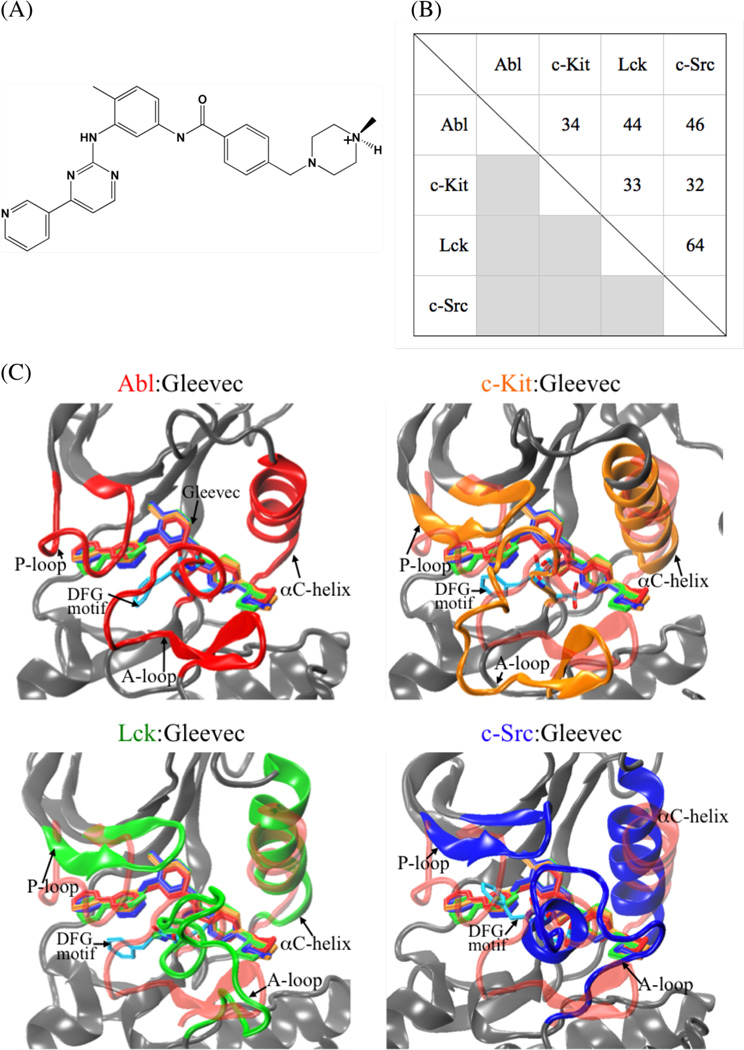
The kinase inhibitor Gleevec,1–3 also known as STI-571 or Imatinib (Figure 1, A), exhibits excellent clinical efficacy in the treatment of patients with certain cancers, such as chronic myelogenous leukemia (CML) and gastrointestinal stromal tumors (GISTs).4–8 CML is attributed to a fusion gene that encodes a constitutively active Abl tyrosine kinase,9, 10 while GIST is caused by the abnormally elevated activity of mutant c-Kit tyrosine kinase.8, 11–13 The clinical success of Gleevec in the treatment of these cancers is attributed to the fact that the drug is a potent inhibitor of Abl (Ki = 0.013 µM14 or IC50 = 0.025 µM15) and c-Kit (IC50 = 0.41 µM15).16, 17 However, Gleevec does not inhibit other closely-related tyrosine kinases such as Lck (Ki = 0.43 µM14 or IC50 = 9.0 µM15) and c-Src (Ki = 31.1 µM14 or IC50 > 100 µM15) despite their high similarity.15, 18, 19 Abl, c-Kit, Lck, and c-Src are members of a large family of non-receptor tyrosine kinases, which are responsible for the regulation of numerous cellular signaling pathways in eukaryotes.20 A better understanding of the underlying physical basis for the binding specificity of Gleevec to these various tyrosine kinases may help in the refinement of specific inhibitors.
Figure 1.
(A) Schematic diagram of Gleevec. (B) Pairwise percentage of sequence identity of Abl, c-Kit, Lck, and c-Src based on multiple sequence alignment of Clustalw2 program. (C) Superimposing the conformation of Gleevec bound to the kinase domains of Abl (colored in red), c-Kit (in orange), Lck (in green), and c-Src (in blue). Gleevec is represented by thick sticks.
Gleevec binds within the catalytic ATP-binding cleft located between the small N-terminal lobe (N-lobe) and the large C-terminal lobe (C-lobe) of the catalytic domain of the kinase to an inactive state, thus preventing a transition back to the active state. The residue sequences near the substrate-binding pocket (Figure 1, B) and their binding profiles to Gleevec (Figure 1, C) are highly similar. While a number of site-directed mutagenesis studies on Abl and c-Kit in the last decade have examined the basis for binding resistance to Gleevec,21–27 the high sequence similarity of the binding pocket among the different kinases highlights the fact that simple structural arguments often fail to explain the wide variations in specificity.14, 17, 28–30 These difficulties are illustrated by the work of Seeliger et al.14 who attempted to re-engineer the binding sensitivity of the kinase domain of c-Src to Gleevec by substituting c-Src residues into Abl to recover favorable interactions. However, none of the mutations significantly increased the sensitivity of c-Src to Gleevec, except for F405A in the conserved Asp-Phe-Gly (DFG) motif of c-Src that is expected to destabilize the inactive apo conformation of c-Src. Hence, site directed mutagenesis was unsuccessful to engineer the desired binding specificity. This suggests that understanding the contribution from homologous residues in difference is difficult. Furthermore, the quantitative impact of the activation (A) loop conformation of c-Src kinase on ligand binding remains unclear. In the X-ray crystallographic structure of c-Src in complex with Gleevec, the A-loop of 13 amino acids near the ligand-binding pocket is unresolved in the electron density.14 It has been suggested that a clash of Tyr416 on the loop with Arg388 prevents the loop from adopting a folded conformation similar to that observed in the Abl, c-Kit, and Lck X-ray structures.14 Differing from the folded loop conformation, an extended A-loop conformation has been observed in the crystal structure of unphosphorylated c-Src, which is similar to the conformation of this loop in other active kinases.14 These empirical observations bring up an interesting question of how the two different A-loop conformations, folded and extended, affect the binding affinity of c-Src to Gleevec.
Detailed computations may help shed light on the determinants of binding specificity of Gleevec and a number of studies have been aimed at this issue. Simonson and Aleksandrov31 analyzed the relative binding free energies of Gleevec to Abl, c-Kite, Lck, and c-Src using alchemical FEP/MD simulations and the molecular-mechanics Poisson-Boltzmann with surface area32, 33 (MM/PBSA) approximation. They concluded that the binding free energies in these inactive apo kinases are essentially comparable and suggested that the differences in binding specificity could arise exclusively from the relative stability of the Gleevec-bound conformation for the kinases. Ojha and Dubey34 used a quantum mechanics extension to MM/PBSA (QMMM/PBSA) method to compute the binding free energy of Gleevec to Abl kinase, where the drug was treated quantum mechanically such that the electronic and polarization contributions of the ligand were considered. In addition, Ojha and Dubey34 and Lee et al.35, 36 calculated the binding free energies of Gleevec to the wild-type and mutant Abl kinases using the MM/PBSA approach. Shan et al.37 carried out unbiased micro-second MD simulations to visualize the spontaneously binding processes of Dasatinib and PP1 to c-Src tyrosine kinase. Rajasekaran and Sethumadhavan38 carried out computations on point mutations of c-Kit to investigate the conformational change of the mutant proteins with respect to the wild-type structure and docking Gleevec to the mutants to explain the drug tolerances. In a previous study, we carried out detailed all-atom alchemical FEP/MD simulations and umbrella sampling simulations to further understand the molecular basis of the binding specificity of Gleevec to the Abl and c-Src tyrosine kinase domains.39 The calculations showed that the relative binding free energy of Gleevec for Abl and c-Src results in part from the differences in intrinsic affinity of the ligand to the binding pockets in these two kinases.
Numerous critical questions about the molecular determinants underlying the binding specificity of Gleevec to inactive apo conformation of Abl, c-Kit, Lck, and c-Src remain unanswered. The goal of the present effort is to identify the main factors driving Gleevec recognition by the tyrosine kinases and to investigate the reasons behind the binding specificity to the different homologs. In addition, we are interested in understanding the impact of the A-loop conformation on the binding affinity of Gleevec. To answer these questions, we employ alchemical FEP/MD simulations to compute the absolute binding free energies of Gleevec to Abl, c-Kit, Lck, and c-Src kinase domains, in which solute and solvent atoms are treated explicitly with an atomic force-field description. Calculations considering different A-loop structures in c-Src kinase are carried out to address how different conformation of the A-loop affects on the drug binding to c-Src. As in a previous FEP/MD study of Gleevec binding,39 the methodology is extended by a combination of restraining potentials and umbrella sampling (US) techniques, and a global replica-exchange molecular dynamics (REMD) simulation scheme is applied to enhance the conformational sampling and improve the convergence of the calculated binding free energies. While a dissection of binding free energy is difficult to access experimentally, the computational methodology used here allows the identification of the molecular determinants controlling the protein-ligand recognition. The study demonstrates that the MD simulations, when combined with a rigorous step-by-step formulation of absolute binding free energy together with extensive sampling methodologies, can provide critical information underlying protein-ligand interactions to help guide rational de novo drug design.
COMPUTATIONAL DETAILS
Atomic Systems
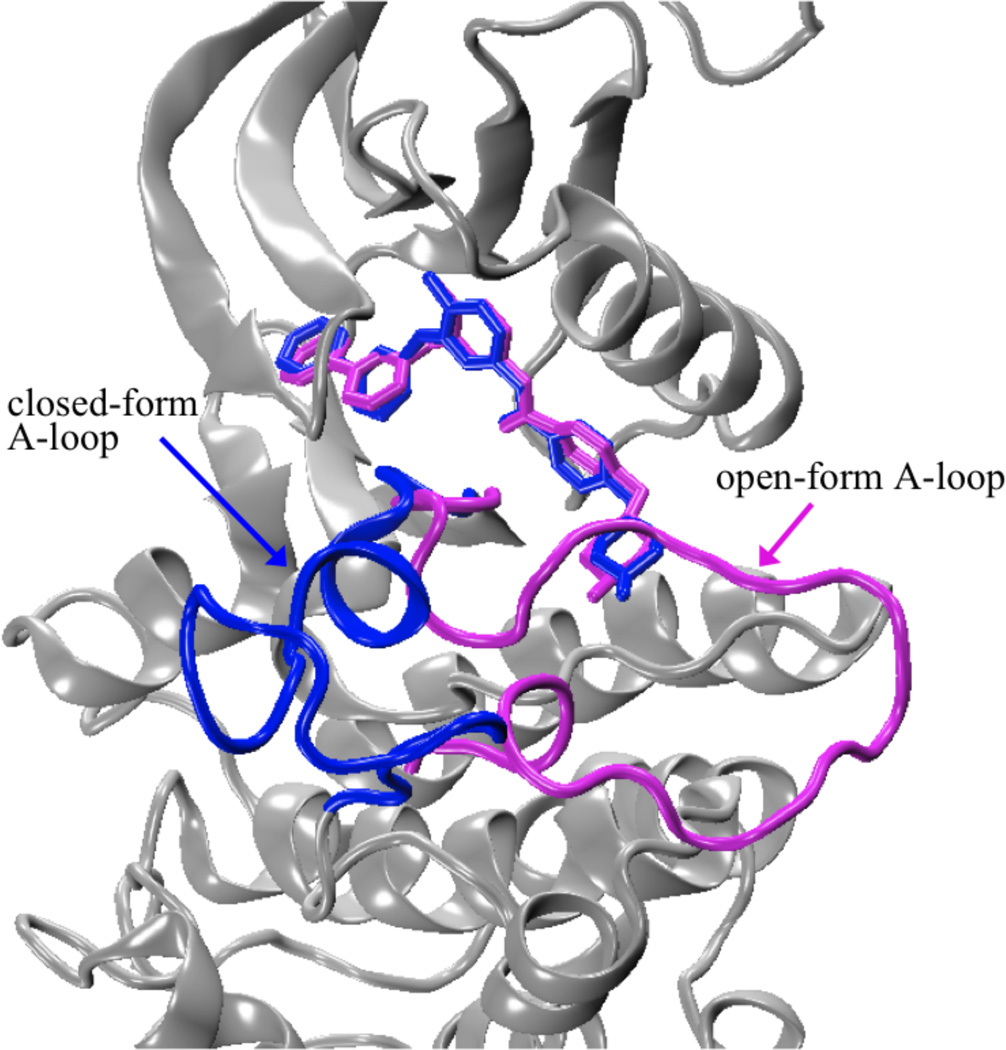
The initial structures of Abl, c-Kit, Lck, and c-Src for the simulations were the crystal structures of the proteins in complex with Gleevec in the ATP-binding pockets (PDB id: 1IEP28 for Abl, PDB id: 1T4617 for c-Kit, PDB id: 2PL030 for Lck, and PDB id: 2OIQ14 for c-Src). By means of pH potentiometric and NMR-pH titrations, the piperazinyl nitrogen atom of Gleevec have shown that its pKa was established to be 7.7 in water, indicating that the piperazine group is either neutral or positively charged in bulk solution.40 Additionally, the crystal structures intimate that there are hydrogen bonds between the piperazinyl nitrogen of Gleevec and the backbone carbonyl oxygen atoms of the kinases (I360 and H361 in Abl; I789 and H790 in c-Kit; I361 and H362 in Lck, and V383 and H384 in c-Src). Recent simulations have further shown that Gleevec is expected to be protonated in the kinase binding pockets.41 Altogether, the above experimental observations and theoretical calculations suggest that Gleevec is protonated in the binding pockets of the kinase complexes, as shown in Figure 1(A). In the Gleevec-bound c-Src complex, thirteen residues of the A-loop (residues 404–420) were disordered in the electron density map. Further structural studies of c-Src in complex with ligands (such as crystal structures PDB id: 3EL8,84 3G6G,85 and 3OEZ) also show that the A-loop in the ligand-bound c-Src is not resolved in the crystal structures. To address this issue, two different A-loop conformations were modeled in silico (Figure 6). The extended open-form A-loop in c-Src, referred to as c-Src(o), was transferred from DFG-in inactive c-Src structure (PDB id: 1Y5786). The other A-loop conformation was closed-form adopted from Gleevec-bound Lck complex structure (spanning from residues 386–398, PDB id: 2PL030) because they have a very high sequence similarity of 64%, referred to as c-Src(c). In the c-Kit complex, the missing residues 690–694 and 753–761 were transplanted from the inactive DFG-out structure (PDB id: 1T4517). Histidine residues in these ligand-bound complex systems were treated as neutral by protonated at Nδ1 or Nε2 according to their local environment. The remaining titratable residues were treated corresponding to ionization states at physiological pH. The HBUILD42 module in CHARMM43 was used to build the missing hydrogen atoms in the X-ray structures. The hydrogen-built structures were afterwards subjected to 500 steps of the energy minimization using the steepest descents44 (SD) method, followed by the adopted-basis Newton-Raphson44 (ABNR) method, with the re-constructed residues and all the other residues held fixed using CHARMM. Each energy-minimized structure was then solvated in a truncated octahedral water box with square edge of length 80 Å. Water molecules at distances less than 2.6 Å from the protein or inhibitor heavy atoms were removed. The systems were neutralized with Na+ and Cl− counter ions at physiological salt concentration of 150 mM. Finally, the hydrogen-built systems for the solvated Gleevec-bound complex with Abl, c-Kit, Lck, and c-Src consist of 36753, 37356, 37227, and 36699 atoms, respectively, and were adopted as the initial structures in the following simulations. All simulations employed the all-atom CHARMM22 force field45 with the CMAP backbone dihedral46, 47 for the protein residues and ion species. The three-point-charge TIP3P48 model was chosen to describe water molecules. The topology and parameter files used to represent the potential function of Gleevec herein were adopted from Simonson’s work.41
Figure 6.
Structurally defined A-loop conformations in c-Src kinase domain. Blue: closed confirmation of A-loop in c-Src(c); magenta: open-form A-loop in c-Src(o). Gleevec is represented by thick sticks.
Simulations Protocol
Periodic boundary conditions at constant temperature and pressure of 300 K and 1 atm were applied within the isothermal-isobaric (NPT) ensemble. Long-range electrostatic interactions were treated using the particle-mesh Ewald49 (PME) method. The non-bonded interaction list was updated on every integration step using a cutoff of 14 Å. The van der Waals energies were switched to zero between 10 Å and 12 Å with a shift function. The dynamics was propagated using the velocity-Verlet (VV2) integration scheme with a time step of 2 fs and all bonds involving hydrogen atoms were considered to their equilibrium distances and the TIP3P water geometry were kept rigid using the SHAKE50 algorithm. Each fully solvated system was energy-minimized for 200 steps with SD, followed by additional 200 steps with ABNR to reduce initial close contacts. The system was then equilibrated for 2 ns under harmonic constraints of a force constant of 100 kcal·mol−1·Å−2 on the non-hydrogen atoms to ensure that the configuration of the protein and of the ligand remains close to the X-ray structure. Afterwards, the system was equilibrated for additional 4 ns with no constraints, and the resulting structure was used to perform the set of free energy simulations. For the solvated system of Gleevec-bound c-Src, the system was first equilibrated for 2 ns under harmonic constraints of a force constant of 25 kcal·mol−1·Å−2 on the backbone heavy atoms of the enzyme as well as all non-hydrogen atoms of the ligand. Afterwards, the system was further equilibrated for additional 26 ns with no constraints. The overall stability of MD simulations for the solvated protein complex systems is shown in Figure S1 in Supporting Information. The stability for the two modeled c-Src complexes over a 200 ns MD is additionally depicted in Figure S9, confirming that both A-loop conformations in the Gleevec-bound c-Src complex system are stable.
For Gleevec in bulk solution, the center-of-masses of the ligand was placed at the center of a cubic water box with side-length of 45 Å, and one chloride counter ion was added to neutralize the system, resulting a total of 8734 atoms. The solvated system was equilibrated for 200 ps with a conformational restrain (k = 10 kcal·mol−1·Å−2) applied on all the heavy atoms of the solute near its reference conformation in the bound state. All the MD simulations of equilibration at this stage were run by NAMD51 program with Langevin dynamics performed at a friction of 5 ps−1. The van der Waals energies were feathered to zero in the region between 12 Å and 13 Å with a smooth switching function.
Absolute Binding Free Energy Calculations
The absolute binding free energies of Gleevec to Abl, c-Kit, Lck, and c-Src kinases calculations are based on the staged FEP/MD simulation protocol with biasing restraints that was introduced in refs. 52–55 and was previously applied to T4 Lysozyme,54 FKBP12,53 and the bacterial ribosome.56, 57 The approach was recently extended by a global replica-exchange molecular dynamics scheme with respect of the thermodynamic coupling parameters “λ” implemented in the program CHARMM version c36a643 via the parallel-parallel REPDSTR58–61 module.60, 61 We refer to this method as FEP/λ-REMD simulations. Details of the REPDSTR implementation in FEP/λ-REMD and in umbrella sampling US/REMD as well as the swap replica-exchange protocol are explained in refs. 60 and 61. In the present set of calculations, replica-exchange was attempted at every 100 steps throughout all the FEP/λ-REMD and US/REMD simulations. All FEP calculations were carried out with the PERT module of CHARMM.
The absolute binding free energy for transferring ligand from bulk solution (bulk) to the binding site of the kinases (site), , can be expressed as follows:52–55, 62, 63
| (1) |
is the interaction (int) free energy difference associated with removing the ligand from bulk solution and inserting it in the binding site. is the free energy cost while introducing and removing the translational (t) and rotational (r) restraints on the ligand in bulk solution and in the binding site. is the conformational (c) free energy associated with transferring the ligand with its bound-state conformation in bulk solution to the same conformation in the binding site. It may be noted that the standard concentration C° cancels the unit in Ft, required to yield a correct standard (absolute) binding free energy. The translational and rotational factors, Ft and Fr, correspond to simple numerical integrals over restraining quadratic potentials used to define the position and the orientation of the bound ligand that have been defined previously.53, 54
The non-bonding interaction energy can be further separated into three major contributions:
| (6) |
where , and correspond to the free energy difference in terms of repulsive (rep), dispersive (dis), and electrostatic (elec) interactions, respectively, while sequentially decoupling the ligand from bulk solution and placing it in the binding pocket. The Weeks-Chandler-Andersen64 (WCA) decoupling scheme was utilized to separate the Lennard-Jones 6–12 potential into purely repulsive and dispersive parts.52 The insertion of the ligand into the binding pockets, or the deletion from bulk solution, was carried out as a stepwise reversible work with alchemical FEP/λ-REMD simulations, staged by the three thermodynamic coupling parameters, λrep (λrep = 0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1), λdis (λdis = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0), and λelec (λelec = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0) controlling the repulsive (ΔGrep), dispersive (ΔGdis), and electrostatic (ΔGelec) interactions of the ligand with its environment, respectively. The FEP/λ-REMD simulations at this stage consist of 40 replicas (windows): 18, 11, and 11 windows were for repulsion, dispersion, and electrostatics stages, respectively. In the λ-swap replica-exchange protocol of FEP/REMD implementation, the configuration of the last λ-staging replica of the repulsion term is able to exchange with that of the first λ-staging replica of the dispersion term.61 Same role applies to the last λ-staging window of dispersion term and the first λ-staging window of electrostatics term. For each run of calculation, the simulation length of each replica window was 220 ps from various initial velocities, and all data points were collected in the meanwhile. The data was post-processed using the weighted histogram analysis method65, 66 (WHAM) to obtain the unbiased free energy of each step upon ligand binding in the proteins or dehydration in bulk solution.
Restraining potentials are introduced for the translational and rotational movements of the ligand relative to the binding site while the ligand is gradually annihilated from bulk solution, and then are released once the ligand is fully interacting with the binding site residues. The free energies corresponding to the removals of the orientational (translational/rotational) restraints on the ligand in the binding sites were performed using FEP/λ-REMD simulations to introduce a coupling parameter that controls the strength of restraining potentials. The FEP/λ-REMD simulations at this stage comprises 15 replicas (windows) with the translation-rotation thermodynamic staging parameter, λt+r, to 0, 0.0025, 0.005, 0.0075, 0.01, 0.015, 0.024375, 0.04, 0.06, 0.08, 0.1, 0.2, 0.4, 0.6, 0.8, and 1. A set of atoms, summarized in Supporting Information Table S1, was selected randomly from each kinase and the ligand to define the anchoring points for the translational and rotational restraints used in the λt+r-staged FEP/REMD calculations.53, 54 As shown in Supporting Information Figure S3, the positions and orientations of the ligand in the binding sites of the enzymes were well defined by those internal coordinates. For each bound complex, the average of last 1-ns MD trajectory was used as the reference values of r0, θ0, ϕ0, α0, β0, and γ0 for the distance, angle, and dihedral restraints, respectively. For the FEP calculations, force constant kd was set to 10 kcal·mol−1·Å−2 for the distance restraints and ka was set to 200 kcal·mol−1·rad−2 for the angle and dihedral restraints. The translational and rotational restraints were combined in one stage with a single coupling parameter, λt+r, to yield . The simulation length of each replica window in the orientational FEP/λ-REMD calculations was 100 ps for each run of sampling, followed by WHAM to compute the orientational contribution of the ligand to the binding.
The free energies associated with adding or removing the conformational restrains of the ligand in bulk solution or in the binding sites relative to its reference conformation were carried out by computing the potentials of mean force (PMFs) as a function of RMSD using umbrella sampling technique with REMD (US/REMD). Twenty-one replicas centered on RMSD offsets increasing from 0.0 to 5.0 Å in steps of 0.25 Å were used. For each ligand-bound kinase, the reference structure of Gleevec used in the US/REMD simulations was obtained from the average of the last 1-ns MD trajectory of Gleevec bound to the protein, followed by an energy minimization of 100 steps. Each replica window of the conformational simulations consisted of 200 ps with a force constant of 10 kcal·mol−1·Å−2 for data collection. WHAM was performed to unbias the results and compute the PMFs as a function of RMSD, i.e. and . It is noteworthy that no translational and rotational restraining potentials were applied during the US/REMD simulations.
To ensure the statistical convergence of the calculations as well as to eliminate the influence of structural relaxation on the calculated free energy, a series of 25 independent FEP/λ-REMD and US/REMD simulation cycles (runs) for each complex and 15 runs for the Gleevec-hydrated system were carried out consecutively, starting from the last configuration saved in the previous run for all corresponding windows (replicas). Each trajectory of the simulations started from different initial velocity. Trajectories were collected every 1000 simulation steps for all simulation windows.
RESULTS AND DISCUSSION
In principle, all-atom alchemical FEP/MD simulations based on the double-annihilation method (DAM) offer an effective approach to compute the absolute binding free energy of a ligand to a protein.67 In DAM, one only needs to calculate the free energy for de-materializing the ligand in bulk solvent and re-materializing it in the binding pocket (relative to a spatially restricted volume to account for the standard state concentration). However, when a binding process is strongly coupled to slow conformational changes associated with the ligand or protein, straight brute-force alchemical FEP/MD simulations can encounter severe convergence problems, and may even lead to erroneous results. In such a situation, a more effective strategy is to first identify all the slow degrees of freedom, and then deliberately control them latter during alchemical FEP/MD simulations using special techniques such as umbrella sampling. Such alchemical FEP/MD simulations carried out in the presence of biasing restraint potentials,53, 54, 63 which is sometimes referred to as “confine-and-release”,68 can be rigorously corrected to yield a properly unbiased binding free energy. Particularly, the strategy is very advantageous to circumspectly control the conformation of Gleevec, a fairly large molecule able to undergo considerable conformational fluctuations over long timescales, via a biasing restraint potential based on the root-mean-square deviation (RMSD) relative to the bound configuration of the ligand.62 These well-established methods are part of the arsenal of FEP/MD simulation techniques that can be used to enhance the statistical convergence of absolute binding free energy calculations. Previous studies39, 56, 57 have demonstrated the overall reliability of this computational methodology combining FEP/MD and umbrella sampling simulations.
In the following, first we carry out alchemical FEP/λ-REMD simulations using a step-by-step reversible work staging procedure to determine the binding affinity of Gleevec to Abl, c-Kit, Lck, and c-Src, respectively, in which the conformation of the A-loop is folded and closed-form. We also carry out umbrella sampling simulations to compute the PMF of Gleevec as a function of RMSD relative to its bound conformation both in bulk solution and in the kinase binding pocket. Combining the results of the RMSD-PMF and the alchemical FEP/λ-REMD yields the absolute binding free energy of Gleevec to a kinase. We additionally model Gleevec binding to c-Src kinase, in which the A-loop conformation is extended and open-form, and compute its binding free energy with Gleevec using the aforementioned strategy. The impact of the two A-loop conformations in c-Src, i.e. c-Src(c) (denoted as with closed-form A-loop) v.s. c-Src(o) (denoted as with open-form A-loop), on the results of the binding affinity for Gleevec to the protein is discussed. In the following, c-Src represents the c-Src(c) conformation, unless otherwise indicated. All the MD simulations were carried out on the basis of atomic models with explicit solvent molecules.
A) Binding Affinity of Gleevec to Abl, c-Kit, Lck, and c-Src
The absolute binding free energy was computed using 25 independent cycles of alchemical FEP/λ-REMD simulations, representing a total of 5.5-ns sampling for each system. The results begin to converge after a few cycles and appear to fluctuate around a mean value after 15 cycles (the progression of the free energy during successive computational cycles is shown in Figure S4). The data points of the last 5 cycles were collected to compute the block average of the absolute binding free energies of Gleevec with the kinases, yielding −10.8, −9.0, −7.3, and −4.6 kcal/mol for Abl, c-Kit, Lck, and c-Src, respectively, as shown in Table 1. The calculated binding affinity of Gleevec to the kinases is in good accord with experimental estimates by measuring the dissociation constant (Ki) of unphosphorylated form of the protein and the ligand.14 Thus, the present computational results are sufficiently accurate to support the conclusions about Gleevec’s binding specificity.
Table 1.
Absolute binding free energy of Gleevec with Abl, c-Kit, Lck, and c-Src tyrosine kinases.a The conformation of the A-loop in c-Src is open-form (o) or closed-form conformation (c).
| site |
|
expt. b | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abl | 1.2 | −29.4 | 0.5 | −27.7 | 5.6 | 11.3 | −10.8 | −10.8 | |||||||
| c-Kit | 7.0 | −28.3 | −4.7 | −26.0 | 4.8 | 12.2 | −9.0 | ||||||||
| Lck | 0.4 | −25.3 | 0.0 | −24.9 | 5.2 | 12.4 | −7.3 | −8.7 | |||||||
| c-Src(c) | 0.0 | −25.1 | 0.9 | −24.2 | 6.3 | 13.3 | −4.6 | −6.2 | |||||||
| c-Src(o) | 4.0 | −23.0 | 0.1 | −18.9 | 4.6 | 7.5 | −6.8 |
Unit in kcal/mol.
The values were derived from the experimentally measured inhibitory potency of Gleevec for unphosphorylated Abl, Lck, and c-Src kinase domain, which is 0.013, 0.43, and 31.1 µM, respectively.14
Direct protein-ligand interactions play a prominent role in all classic ligand docking/scoring schemes. While such schemes may lead to an intuitively reasonable picture of binding specificity, a quantitative assessment of the different statistical mechanical contributions from the molecular interactions must, however, be rigorously accounted for in the binding free energy. The step-by-step alchemical FEP strategy and the RMSD-PMF approach used here naturally dissect the absolute binding free energy of ligand into five components associated with the repulsive, dispersive and electrostatic interactions between the ligand and the environment, as well as the contributions from restricting the translational, rotational, and conformational movements of the ligand upon binding to a target protein, as summarized in Table 1. Accordingly, the detailed dissection of the absolute binding free energy of the ligand with a kinase provides meaningful information to understand the molecular determinants responsible for the differential binding affinity of Gleevec to the homologous kinase binding sites in terms of the chemical features. In the following, we determine and analyze each of these contributions.
Repulsive Contribution Opposes Binding
The progression of the repulsive free energy is plotted in Figure S5(A) as a function of the thermodynamic coupling parameter, λrep. The total reversible work to switch on the repulsive part of the potential function corresponds to a fairly large free energy, both in the bulk solution and in the binding cleft of the kinases. Nevertheless, it is of interest to note that the variation of the free energy with respect to λrep in bulk solution is close, but not quite equivalent, to that in the binding site. As a consequence, the repulsive component upon Gleevec binding is 1.2, 7.0, 0.4, 0.0 kcal/mol for Abl, c-Kit, Lck, and c-Src, respectively. The results imply that the work required for the apo kinases to pre-void the binding cavity for the insertion of Gleevec disfavors the binding.
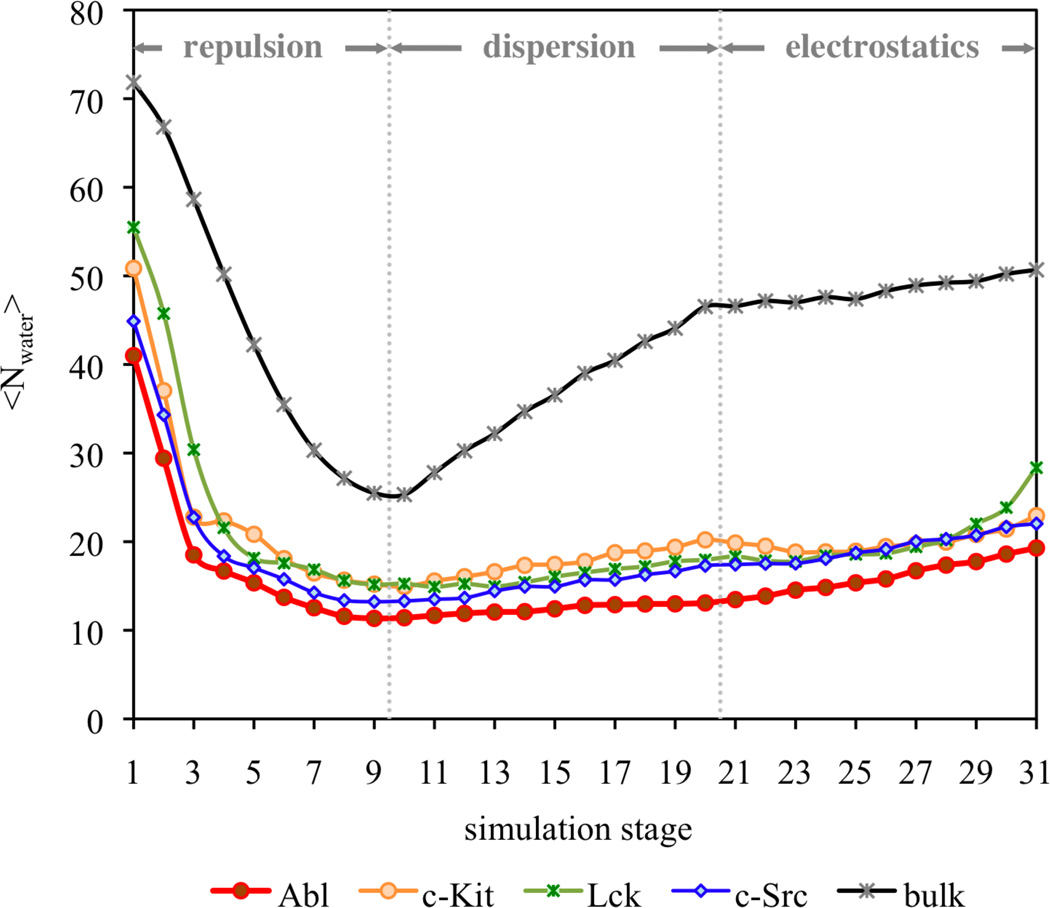
The unfavorable repulsive interactions to the binding could be attributed to desolvation effect upon binding. Because of the fairly large size of Gleevec, the ligand displaces a considerable number of water molecules. The progression of the solvent configurations can be naturally monitored during the staged FEP/λ-REMD simulations with explicit representation of solvent molecules. Figure 2 shows the variations of the average number of water molecules within the binding pockets of the tyrosine kinases during the non-bonded interaction components along the FEP/MD calculations. When the repulsive part of the LJ potential (stages 1–10) is introduced stepwise, a considerable number of 30 to 40 water molecules are expelled from the binding pockets due to the insertion of Gleevec, suggesting that the binding process could incur a substantial free energy penalty to accommodate the ligand.
Figure 2.
Progression of the number of water molecules in the Gleevec-binding pockets of Abl, c-Kit, Lck, and c-Src in response to binding during the FEP calculations. The simulations are divided into 31 stages, starting from repulsive stage 1 and progressing to fully interacting ligand in stage 31. In stages 1–9, the ligand repulsion is gradually switched on. In stages 10–20, the ligand dispersion is turned on. In the stages 21–31, the charges of the ligand are added progressively.
The binding pocket of the kinase should also slightly rearrange itself with certain penalty to complement the bulky ligand. Displacement of the binding site residues or torsion motions of the flexible side chains in the binding pocket could contribute to this local conformational change due to ligand occupation. The local conformational flexibility upon binding could be intimated by the analyses of the radius of gyration for the binding site residues. Radius of gyration, Rg, described as mass-weighted scalar length of each atom of selected amino acid residues from their centroid, has been widely used as an indicator that characterizes compactness/looseness of protein structure. Here, the average radius of gyration for the non-hydrogen atoms of the binding site residues was computed as it changes over λrep along the FEP simulations (Figure S6). The results clearly show that the magnitude of the radius of gyration is increasing as the ligand gradually materialized in the binding pocket, indicating that the binding site residues attempt to deviate from their center to eschew undesired steric clash. Indeed, the environment provided by proteins for binding is more complex and inhomogeneous than bulk solvent. Targeted proteins ought to undergo a fine-tuning feature in modulating ligand binding. Altogether, it is important to consider the alterations of the local flexible behavior as well as the desolvation penalty of the binding pocket upon ligand binding to appropriately evaluate ligand binding affinity, although the resulting repulsive contributions in the binding sites could be close to that in bulk solution in some cases as shown in the present study.
Dispersive Contribution Governs the Gleevec Recognition by the Kinases
The present calculations show that a major factor governing the binding affinity is the dispersive component,69–73 which is −29.3, −28.3, −25.3, and −25.1 kcal/mol for Abl, c-Kit, Lck, ad c-Src, respectively. In addition, the progressions of the dispersive free energies of Gleevec as a function of the coupling parameter λdis show that the slop of the linear progression of the dispersive interaction in the binding site is greater than that in bulk solution (Figure S5, B), revealing vividly that the protein, relative to bulk solvent, provides an environment with a higher density of van der Waals centers to stabilize Gleevec in the binding pocket. Of interest is that the dispersive component reflects the trend of the binding affinity, regarding the dispersive contribution as a key molecular determinant responsible for the binding specificity of Gleevec to the tyrosine kinases.
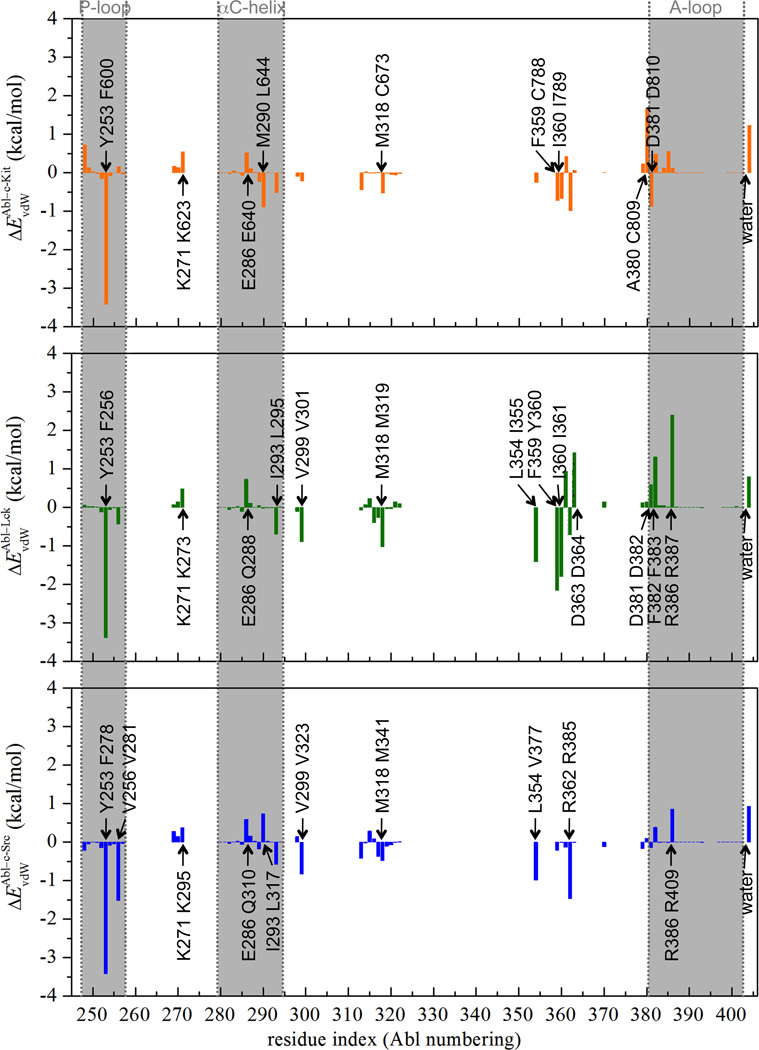
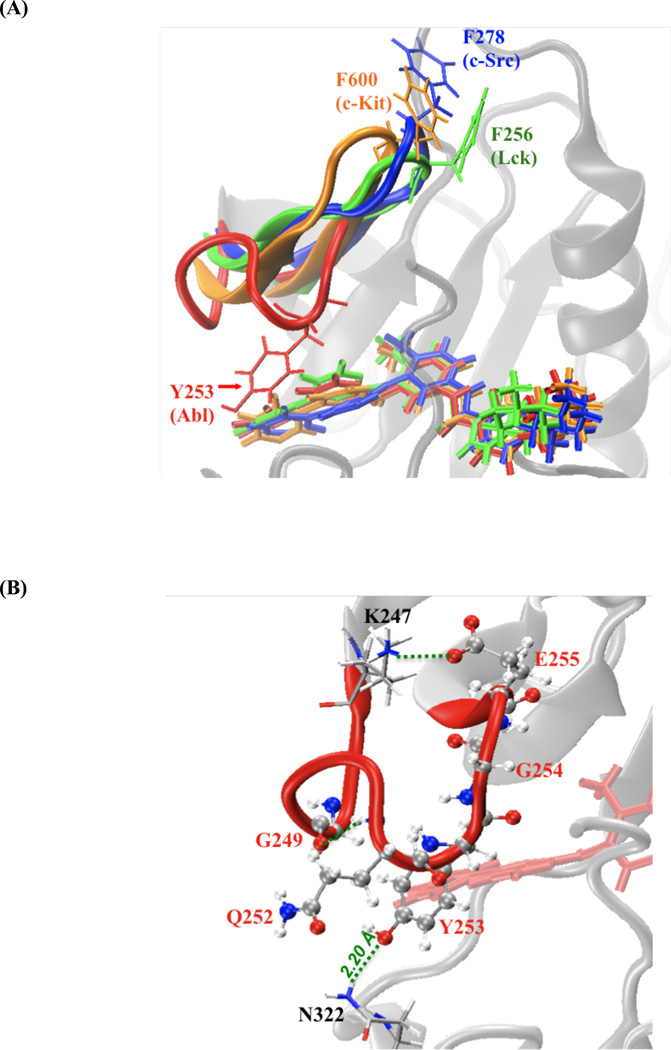
The residual decomposition of the dispersive contribution helps to identify the key molecular determinants responsible for the binding specificity of Gleevec to the kinases. It is achieved by analyzing the average end-point dispersive interaction between the ligand and each amino acid residue in the complex system due to the nearly linear correlation between ΔGdis and λdis. Such end-point analysis is meaningful here because the progression of the dispersive contribution as a function of λdis is essentially linear. Figure 3 shows the van der Waals interaction energies between Gleevec and individual residue in c-Kit, Lck, and c-Src relative to the corresponding residue in Abl. Negative value indicates that the residue of Abl kinase makes favorable van der Waals contacts with the ligand over the corresponding residue (by sequence alignment) of the other kinases, and vise versa. The dispersive interaction energies of the residues comprising the ligand-binding pocket in each complex system are listed in Table S2. The residual decomposition results show that Abl Tyr253 on the phosphate-binding loop (P-loop) makes a significant contribution to stabilizing Gleevec binding in Abl over the corresponding residue of Phe600 in c-Kit, Phe256 in Lck, and Phe278 in c-Src, leading up to 3–4 kcal/mol. This can be attributed to the distinctive conformations of the P-loop in the tyrosine kinases. In Abl, the P-loop (red-colored tube model in Figure 4(A)) adopts a kinked shape that enables Tyr253 to form favorable van der Waals interactions with the pyridinyl ring and pyrimidine group of the ligand. Additionally, this specific P-loop conformation appearing in Abl kinase is held in place by conserved hydrogen bonds between Tyr253 and Asn322 during the simulations (Figure 4, B). These phenomena are lacking in Gleevec-bound c-Kit, Lck, and c-Src, where the P-loop postures an extended conformation. Hence, the kinked-shape P-loop of Abl kinase enables the kinase to hold and make enjoyable van der Waals contacts with the ligand in the binding pocket and this locally conformational difference could correlates to the binding specificity of Gleevec to these kinases. Although the conformation of the P-loop with bound Gleevec in c-Kit (residues 595–604), Lck (residues 251–260), and c-Src (residues 273–282) is similar, the decomposition of the dispersive contribution further shows important differences in the interaction energy with bound Gleevec among the various kinases. In c-Kit the dispersive interaction energy is estimated to be −7.1 kcal/mol, which is larger than the values of −5.8 and −4.2 kcal/mol, obtained for Lck and c-Src, respectively. The energy decomposition illustrates a key feature explaining the variations in inhibitor specificity and how the hydrophobic surface of Gleevec is accommodated by the P-loop of the different kinases.
Figure 3.
Differential van der Waals (ΔEvdW) interaction energies (in kcal/mol) between each individual kinase residue and Gleevec in c-Kit (in color of orange), Lck (in color of green), and c-Src(c) (in color of blue) relative to the corresponding residue in Abl. In each text box, Abl residue is at the bottom and the corresponding c-Kit/Lck/c-Src(c) residue is on the top.
Figure 4.
(A) Superposition of P-loop in the equilibrated complexes of Abl (in red), c-Kit (in orange), Lck (in green), and c-Src (in blue). P-loops are represented by cartoon and Gleevec is shown in thick sticks. (B) Snapshot of the interactions of the P-loop with surrounding residues in Gleevec-bound Abl kinase.
Abl kinase provides an exceptional environment favoring close packing to bind Gleevec among the others. This can be rationalized by summing up the dispersive interaction energy of each binding site residue of the kinases (data shown in Table S2). The calculations show that Abl kinase has the largest total protein-ligand dispersive interaction energy contributing to the stabilization of Gleevec in the binding pocket, which is estimated to be −71.1 kcal/mol. The corresponding contributions for c-Kit, Lck, and c-Src are −67.0, −66.9, −63.5 kcal/mol, respectively, indicating that Abl yields the most optimal van der Waals contacts with bound Gleevec.
Electrostatic Contributions on Gleevec Binding Nearly Cancel Out
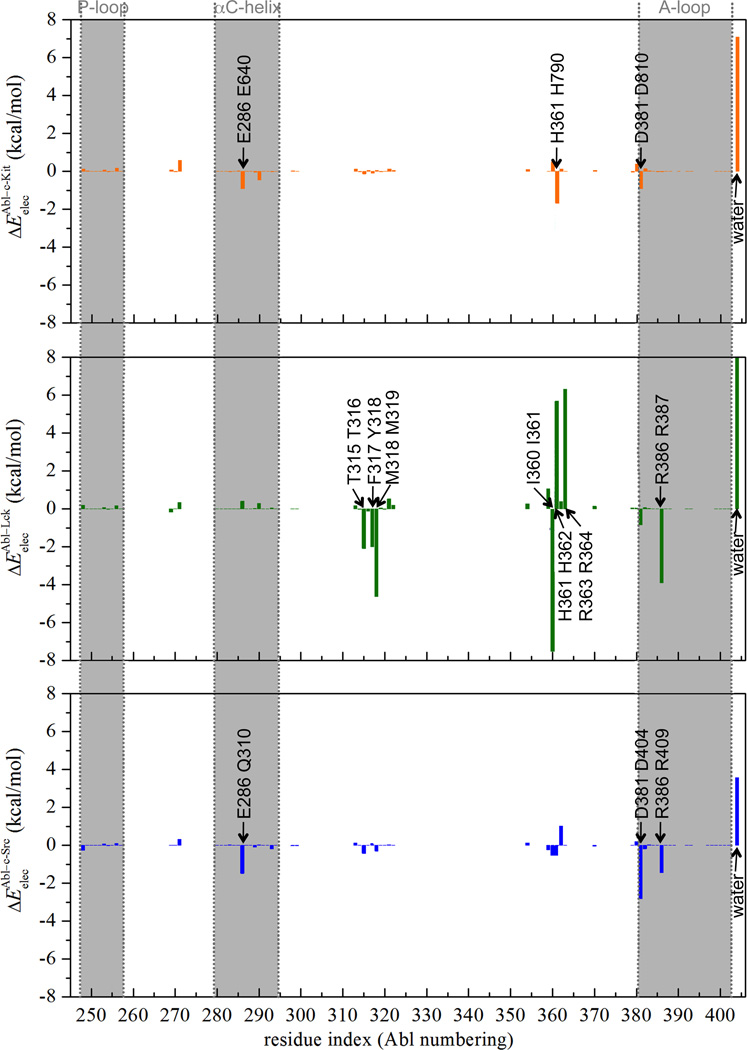
The progression of the electrostatic free energy contribution is plotted as a function of the thermodynamic coupling parameter, λelec (Figure S5, C). In contrast to the van der Waals interactions, which consistently favor the binding process, the contribution of electrostatic interactions nearly cancel out on average. This does not imply, however, that electrostatic interactions are not important for the binding of Gleevec to the kinases. In fact, a closer examination shows that the variations in electrostatic interactions associated with the changes in hydrogen-bonding, charge-charge, and charge-dipolar interactions in the binding pockets is roughly offset by the loss of solvent-ligand interactions in bulk solution. Although the electrostatic contribution to the binding is almost negligible, it is still important for the kinases to properly and precisely anchor the ligand posture in the binding cavity via forming several hydrogen-bonding and charge-charge protein-ligand interactions to enhance the van der Waals interactions with the ligand. In the kinase binding pocket, Gleevec is held in place via a network of hydrogen-bonding and charge-charge interactions. In Abl, strong electrostatic interactions arise from Glu286, Thr315, Met318, Ile360, and His361 (Figure S7 and data are listed in Table S3), consistent with the X-ray structure.16, 29 Glu286 makes favorably electrostatic contribution to the binding by directly forming hydrogen bonds with the amide nitrogen atom of Gleevec via its carboxylate side chain. Additionally, the presence of negatively charged Glu286 and Asp381 nearby the positively-charged piperazine ring of Gleevec contributes favorable charge-charge interactions for the stabilization of the bound ligand. Thr315 makes use of its hydroxyl side chain to accept hydrogen-bonding interaction from Gleevec. Met318, Ile360, and His361 contribute to the electrostatic stabilization by forming hydrogen bonds with the pyridinyl nitrogen atom and protonated piperazine nitrogen atom of Gleevec through their backbones. All these phenomena observed in Gleevec-bound Abl kinases are retained in c-Kit, Lck, and c-Src with conserved or chemically associated amino acid residues, except Lck Asp364 that has favorable electrostatic stabilization to the positively-charged Gleevec over the corresponding aspartate residue in Abl but Abl kinase compensates for the lack via nearby Arg387 on the A-loop (Figure 5). The simulation findings herein are consistent with the experimental observations.14, 17, 28, 30 Of interest is that, by simply summing up the individual electrostatic interaction energy of the binding site residue, Abl kinase has the most favorable total protein-ligand electrostatic interactions among the kinases, suggesting that Abl makes the largest electrostatic stabilization to the ligand binding.
Figure 5.
Differential electrostatic (Eelec) interaction energies (in kcal/mol) between each individual kinase residue and Gleevec in c-Kit (in color of orange), Lck (in color of green), and c-Src (in color of blue) relative to the corresponding residue in Abl. In each text box, Abl residue is at the bottom and the corresponding c-Kit/Lck/c-Src residue is on the top. The actual ΔEelec of water in Lck, which is 16.4 kcal/mol, is truncated for the consideration of figure resolution.
The electrostatic component of the c-Kit binding free energy is estimated to be −4.7 kcal/mol, plays a significant role in the binding affinity. It could be attributed to the hydration of the c-Kit binding pocket that encourages the substrate binding. Undoubtedly, switching on the electrostatic contribution of the positively charged Gleevec (stages 21–31 in Figure 2) further attracts about 3–10 water molecules to the kinase pockets. By computing the electrostatic energy of water molecules within 3 Å of the ligand in the protein binding sites, it shows that the hydration effect in c-Kit provides favorable electrostatic stabilization to the binding over than that in Abl by 7 kcal/mol (Figure 5). The respective terms for Lck and c-Src are 13.6 and 3.6 kcal/mol, also larger than Abl. This observation is consistent with the trend of the hydration states of the binding sites when the λelec coupling parameter is scaled to 1 (i.e., stage 31 in Figure 2) that are 19, 23, 28, and 22 for Abl, c-Kit, Lck, and c-Src, respectively. Altogether, among the studied tyrosine kinases, Abl indeed has the optimal electrostatic feature in response to the stabilization of Gleevec in the binding cavity relative to c-Kit, Lck, and c-Src. However, Abl has the least gain from electrostatic solvation effect in the binding pocket upon binding, resulting in a comparable comparing with the other kinases. This observation, which is consistent with the variations in the number of water molecules within the binding pockets during the FEP simulations, highlights the influence of hydration on the binding process. Thus, the findings reemphasize the importance of sampling solvent configurations upon binding to obtain statistically meaningful estimates of the binding affinity.
When Gleevec is bound to the kinases, the positively charged piperazine ring commonly makes specific interactions with the arginine residue in the HRD motif, where the central arginine is at position 362 in Abl, 791 in c-Kit, 363 in Lck, and 385 in c-Src (Figure S10). Notably, Abl uniquely packs the piperazine ring of the ligand tightly against Arg362, the side chain of which is poised to form salt bridges with the side chains of Glu282 in the αC helix and Arg386 in the A-loop. This is in contrast to the situation observed in c-Kit, Lck, and c-Src where such salt bridge interactions nearby the piperazine ring are absent, which partly accounts for Gleevec’s specificity towards Abl. To evaluate the energetic contribution of the salt bridges to the stabilization of Gleevec in the binding pockets, the non-bonded interactions between the bound ligand and the residues/water molecules within 5 Å of the HRD arginine residue were computed, yielding values of −11.3, −6.6, −3.8, and −4.6 kcal/mol for Abl, c-Kit, Lck, and c-Src, respectively. The calculation shows that these pairs of charged residues in Abl are important for the stabilization of the ligand within the binding pocket. This suggests that the position of Arg362/Glu286/Arg386 amino acid pair in Abl may represent an important design element to aid in rational inhibitor design as well as tuning binding selectivity.
Loss of Translational, Rotational, and Conformational Freedom Upon Binding
It has been shown previously that the relative free energies, calculated from switching-on the restraining potentials when the ligand is in bulk solution and switching-off the latter when the ligand is in the binding pocket, can then be interpreted in terms of a loss of translational, orientational and conformational freedom of the ligand.54, 62, 63 It is expected that a ligand can access a wider range of stable conformations in bulk solution than in the binding pocket, and that a considerable free energy cost must be associated with the loss of conformational freedom. This free energy penalty is commonly neglected or implicitly assumed to be constant in most endpoint docking/scoring schemes such as MM/PBSA. It is noteworthy that the step-by-step reversible work framework adopted here to compute the binding affinity of the ligand to its targeted protein allows us to quantitatively evaluate the free energy associated with the loss of translational and rotational entropy of ligand accompanying binding, i.e. in Table 1. It is achieved by applying strong harmonic restraints to the translational and rotational degrees of freedom of the ligand in bulk solution and then releasing the restraints on the ligand in the binding site. The present strategy also counts the loss in the conformational entropy of the ligand for its binding, by computing PMF as a function of the RMSD of the ligand relative to its bound conformation in bulk solution as well as in the binding sites.62 The free energy associated with the loss of conformational freedom corresponds to the work to restrain the bound ligand in the binding site minus the work to restrain the ligand in the bulk, yielding .
The PMF of Gleevec in bulk water is, undoubtedly, broader than that in the kinase binding pocket, consistent with the notion that the ligand has more freedom to explore a wide range of conformation in bulk solution while it is more restricted and forced to adopt a smaller number of conformations in the binding pocket (Figure S8). The PMF results also clearly reveal a reduction in the number of accessible low-energy-well conformations of the ligand from free to bound state, resulting in the loss of conformational entropy in response to binding. The calculations estimate the free energy penalty due to the decreased degree of freedom in conformational flexibility of Gleevec upon binding is 11.3, 12.2, 12.4, and 13.3 kcal/mol to Abl, c-Kit, Lck, and c-Src, respectively. As a consequence, a considerable thermodynamic penalty is brought on restricting Gleevec from the ensemble of accessible configurations in bulk solution to the confinement of the kinase binding pocket. It is of interest to note that the trend of the free energy cost for the conformational restriction of the ligand reflects the reverse order of the binding affinity. Thus, the loss of the conformation entropy for Gleevec upon binding could be another key indicator for determining its binding specificity to tyrosine kinases.
The restriction on the translational and rotational motions of Gleevec as required for binding to Abl, c-Kit, Lck, and c-Src all lead to a free energy cost by the same order of ~4–6 kcal/mol, disfavoring the binding. As a consequence, a considerable thermodynamic penalty brought on restricting the ligand from its ensemble of translation and rotation and accessible conformation in bulk solution to the binding site is 16.9, 17.0, 17.6, and 19.6 kcal/mol in Abl, c-Kit, Lck, and c-Src, respectively, strongly disfavor ligand binding in these systems. These findings clearly emphasize the importance of considering the restriction of the translational, orientational and conformational motions of the ligand while computing binding affinity of ligand because the magnitude of these free energy cost cancel about two-third of the contribution from the favorable non-bonded interactions.
Lck Binding Pocket Provides Less Spatial Restriction than c-Src
Lck and c-Src have very similar primary sequences with 64% sequence identity. They also adopt similar binding site scaffold while contact with Gleevec (Figure 1). Gleevec, however, is a fairly potent inhibitor of Lck kinase but does not potently inhibit c-Src.14, 19 Thus, the difference in Gleevec binding affinity to Lck and c-Src cannot be solely identified by the X-ray structures. It has been proposed that Lck may adopt a Gleevec-bound apo conformation more easily than c-Src, suggesting that the binding specificity of Gleevec between Lck and c-Src is governed by a conformational selection mechanism.39, 74 The FEP simulations here show that the binding affinity of Gleevec to Lck is −7.3 kcal/mol and is −4.6 kcal/mol to c-Src, revealing that the difference in protein-ligand interactions is a contributor to the inhibitory discrepancy. It is not surprising that the non-bonded interaction component makes similar contribution to Gleevec binding with Lck and c-Src because they have very similar ligand-binding features. The free energy decomposition shows that the entropic penalty for the ligand losing its translational, rotational, and conformational motion upon binding is larger when binds to c-Src, by ~2 kcal/mol over to Lck, suggesting that the different inhibitory efficacy originates from the flexibility/rigidity of the binding pockets. In generally, the translational and rotation motions of a bound ligand depend exactly on how tightly it is held, and this can vary from one complex to another. The MD simulations show that the volume of the binding cavity within the complex system, estimated using VOIDOO75 with a probe radius of 1.4 Å, is 190.7 Å3 for Lck, and is 133.5 Å3 for c-Src, implying that the capacity of the binding cavity in Lck could be more spacious than that in c-Src. In other words, bound Gleevec could be potentially less geometrically restricted in Lck than in c-Src, resulting in losing less degree of freedom in flexibility upon binding with Lck.
B) Impact of the c-Src A-loop Conformation on Gleevec Binding
The conformation of thirteen residues on the A-loop of the Gleevec-bound c-Src complex is unsolved in the crystal structure.14 This mobile loop controls access to the substrate-binding cleft and catalytic site. Using X-ray crystallography, two different conformations of the A-loop have been identified in the tyrosine kinase domains, namely, the folded (closed-form) and extended (open-form) structures (Figure 6). In the Gleevec-bound Abl, c-Kit, and Lck complex structures, the A-loop adopts the folded conformation, however, the alternative of the extended conformation is observed in inactive apo c-Src structure.76 Based on these empirical observations, the binding of Gleevec to c-Src with the two different A-loop structures is modeled (see Materials and Methods for details). In Table 1, the binding free energies of the ligand in c-Src kinase with the closed- and open-form A-loop are denoted as c-Src(c) and c-Src(o), respectively. It is noteworthy that c-Src(o) has less favorable non-bonded interaction contribution than c-Src(c) to stabilize the binding by ~5 kcal/mol, mainly due to the repulsive contribution. However, c-Src(o) compensates this unfavorable contribution by paying less cost to lose translational, rotational, and conformational degree of freedom upon binding than the latter by −7.5 kcal/mol. As a consequence, the offsets makes c-Src(o) have more favorable binding free energy to Gleevec than c-Src(c) by −2.2 kcal/mol. Thus, the present findings suggest that the pliability of the A-loop is clued to substantially play a role in Gleevec binding affinity.
C) Therapeuthic Implications
The accurate prediction of binding affinity is a long-standing goal in the field of computer-aided drug design. The FEP/λ-REMD and US/REMD simulation methodology with explicit solvent molecules applied herein to study the association of Gleevec to various tyrosine kinases permits a realistic depiction of the thermodynamics of binding at the atomic level. This computational methodology naturally incorporate critical factors that are generally ignored in conventional docking and binding scoring functions, such as protein reorganization, receptor/ligand flexibility between bound and unbound states, entropic effects, and desolvation/solvation of the binding pocket. Dissection of the FEP results shed light on the determinant of binding specificity. As suggested by the results from the calculations, the inhibitory potency of a kinase inhibitor could be increased by enlarging the hydrophobic contact surface in a targeted binding site and/or and reducing the desolvation cost in bulk solution. In addition, to improve drug selectivity, non-conserved residues in the binding pockets of tyrosine kinases that display particularities could be exploited to allow the optimization of binding specificity of a potential kinase inhibitor. Lastly, an analysis of the energetic contributions from the non-conserved kinase residues at positions key to ligand binding may be valuable for chemical modifications of a potential compound in order to improve potency and selectivity. In the long term, deepening our understanding of the molecular factors governing the binding specificity of Gleevec to the family highly homologous tyrosine kinases will hopefully lead to the design of improved drugs with greater clinical activity.
CONCLUSION
The development of new agents against CML requires detailed atomic-level information about the drug-binding site of the targeted receptor. While the static structures provided by X-ray crystallography allow a visualization of Gleevec in the binding pockets of the different tyrosine kinases, they do not readily provide information about the microscopic interactions giving rise to variations in binding specificity to these structurally homologous targets. The present study shows that computations based on FEP/λ-REMD and US/REMD simulations with explicit solvent can accurately reproduce the absolute binding affinities of Gleevec for the kinase domain of Abl, c-Kit, Lck, and c-Src, thereby providing a virtual route to examine the interactions responsible for the ligand specificity. The MD simulations reliably show that the calculated absolute binding affinity of Gleevec for the kinases yield good agreement with the experimental measurements, and among these kinases, Gleevec binds to Abl most favorably, as observed empirically. Based on a step-by-step reversible work dissection of the free energy calculations, we were further able to identify the key factors that dictate the specificity of Gleevec binding to the tyrosine kinases, mainly the contribution of dispersive interactions as well as the conformational and orientational entropy costs upon binding. The present MD simulations allow additional insights into the roles of the key kinase residues in the vicinity of the binding pockets bringing on the binding specificity, summarized as follows.
The computational analysis shows that the contribution from the van der Waals dispersive interaction plays a major role, dominating the binding affinity and specificity of Gleevec to the tyrosine kinases. The implication is that close packing and shape complementarity of the environment of the protein binding pocket to Gleevec is critical. The binding pocket provides a higher density of attractive van der Waals interactions relative to the bulk solvent to stabilize the ligand. Unlike the dispersive contribution, the electrostatic contribution of the protein environment upon binding is about neutralized by the loss of the solvent-ligand hydrogen-binding interactions in bulk solution. The free energy contribution from the repulsive interaction corresponding to the penalty for moving bulky Gleevec out of water and inserting it into the binding pocket of the kinases nearly cancels out. Gleevec displays considerable flexibility with multiple accessible conformations in bulk solution. As a consequence, the restriction from the binding pocket is associated with a considerable free energy penalty for the loss of translational, rotational, and conformational freedom. This unfavorable free energy contribution nearly cancels about half to two-third of the total favorable dispersion contribution upon binding.
An apparent requirement for tyrosine kinase to strongly bind Gleevec is to optimize the favorable dispersive van der Waals energy of the aliphatic/aromatic residues in the binding pocket. One way that Abl kinase achieves this is by positioning the phenol side chain of Tyr253 on the P-loop of its kinase domain to make hydrogen bonds with the side chain of Asn322 to uniquely fold a kinked P-loop conformation, in such a way to allow favorable van der Waals interactions with the 2-phenylaminopyrimidine moiety of Gleevec as well as to increase surface complementarity with the drug via an induced fit interactions.16 The situation in c-Kit, Lck, and c-Src, however, differs from that in Abl with respect to two important features. First, the tyrosine residue at position 253 in Abl is a phenylalanine residue in these kinases. Second, the conformation of the P-loop in c-Kit, Lck, and c-Src is more extended and, as a result, the phenylalanine side chain points away from the binding pocket and is exposed to the solvent. Interestingly, the mutation Tyr253Phe in Abl has been correlated with Gleevec resistance in relapsed patients of CML.77–82 The present calculations are suggestive that mutations in the P-loop of Abl kinase might generally result in a decrease of the binding affinity to the kinase by disrupting critical contacts between Gleevec and Tyr253 and undermining the shape complementarity of the pocket to bind Gleevec. Although the conformation of the P-loop in c-Kit, Lck, and c-Src is similar, the loop of c-Kit has tighter binding with Gleevec in the binding site than that of Lck and c-Src due to dispersive van der Waals interactions. This observation further points to the importance of the P-loop as a key feature explaining the binding specificity of the inhibitors for the different kinases.
In addition, among these kinases, Abl provides the most favorable binding environment for Gleevec via optimal electrostatic and attractive van der Waals interactions. Moreover, Abl and c-Kit kinases incur the smallest free energy penalty for the loss of the conformational, translational, and rotational freedom upon Gleevec binding. Lck and c-Src kinases, both classified as members of the Src family, have similar non-bonded interactions with the ligand in the binding pockets; however, Lck pays less entropic penalty on restricting the ligand from bulk solution to the binding site, making a significant contribution to stabilizing the ligand binding in Lck over in c-Src.
The conformationally flexible A-loop of the tyrosine kinases interacts directly with Gleevec in the binding site via the side chains of the aspartate and phenylalanine residues of the DFG motif.14, 17, 28, 30 The present findings show that there is an energetic balance required to accommodate Gleevec in the binding site of tyrosine kinase in the context of different A-loop conformations. For example, the A-loop of c-Src kinase provides more structural contact to stabilize the drug binding when the loop adopts a folded and closed conformation than when it adopts an extended and open-form conformation. On the other hand, however, the former is associated with a larger conformational and orientational free energy penalty upon binding than the latter. These observations suggest that the flexibility and conformational plasticity of the A-loop play a substantial role in the binding affinity of Gleevec.
Conformational selection via the DFG motif in the active site of the tyrosine kinase domain has been suggested as an explanation for the preference of Gleevec binding to Abl and c-Kit over Lck and c-Src.14, 31, 39, 74, 77 In the mechanism, the formers have an intrinsic ability to favorably stabilize the DFG motif to adopt an “out” conformation in the absence of Gleevec, whereas the later, especially c-Src, appears to pay intrinsic energy penalty for adopting the DFG-out conformation to effectively exclude the ligand from the catalytic pocket.39 In the present study, Gleevec binding to the DFG-out inactive conformation of the kinases is studied, and the calculated binding affinities are in good agreement with the experiments. It shows that the Gleevec-protein interactions are different in the kinases, shedding light on the contributions of the distinct protein-ligand interactions to the selectivity of Gleevec. It additionally implies that the free energy difference associated with the conformational selection of the DFG motif was not sufficient to alter the trend observed in the present calculation. Further investigation of the active-to-inactive conformational transition of the DFG flip in the kinases will be necessary to quantify the role of conformational selection to the drug binding in the near future.
The present analysis explains why Abl, c-Kit, Lck, and c-Src display very different specificity for Gleevec despite their close sequence similarity and structural homology and clarifies the physical principles that should guide the design of specific inhibitors. The computational methodology applied in this study takes into consideration of the local conformational changes of drug-targeting site that is accompanied by drug binding. In other words, any impacts on conformational alteration and change of hydration structure of ligand-binding cavity in protein-ligand binding process are carefully taken into account in binding free energy calculations, which is normally lacking in widely used docking/scoring schemes.83 The results suggest that subtle alterations of the drug might be able to counter the spontaneous occurrence of kinase inhibitor resistance in cancer patients in order to prolong the effectiveness of therapeutic treatments. Ultimately, the long-term goal of such analysis will be to help fine-tune the inhibitory profile of specific compounds by optimizing the interactions of unique residues surrounding the drug-binding site, and rationally improve the ability of a selective inhibitor to target a specific kinase by optimizing specific interactions. It is our hope that the physical insight gained by these computations will facilitate the discovery and rational design of novel lead compounds.
Supplementary Material
ACKNOWLEDGMENTS
This research was supported by the National Cancer Institute of the National Institutes of Health (NIH) through Grant CAO93577, and by National Science Foundation (NSF) through Grant MCB-0920261. The computations were made possible by the Extreme Science and Engineering Discovery Environment (XSEDE) supported through NSF Grant OCI-1053575, and by additional resources provided by the Computation Institute and the Biological Sciences Division of the University of Chicago and Argonne National Laboratory through NIH Grant S10 RR029030-01. The authors are grateful to Dr. Yilin Meng and Dr. Yun Lao for helpful discussions and two anonymous reviewers for their constructive comments.
Footnotes
ASSOCIATED CONTENT
Supporting Information
Definitions of the anchoring points used in the λt+r-staged FEP/λ-REMD calculations are listed in Table S1. Averaged dispersive (Edis) and electrostatic (Eelec) interaction energies between protein residues and Gleevec in the kinase binding pockets are listed in Tables S2 and S3, respectively. Time evolutions of RMSD fluctuation of Gleevec-bound Abl, c-Kit, Lck, and c-Src complexes in bulk solution are plotted in Figure S1. Figures S2 shows the superposition of the equilibrated and the starting conformations of Gleevec in the binding pocket of Abl, c-Kit, Lck, and c-Src. Time evolutions of the fluctuations of the six internal coordinates used for the energy restraints of the ligand in the bound complex during the translational and rotational free energy simulations are shown in Figure S3. Convergence of the binding affinity of Gleevec with Abl, c-Kit, Lck, and c-Src kinases is depicted in Figure S4. Progression of the free energy components with respect to the coupling parameters of (A) λrep, (B) λdis, (C) λelec, and (D) λt+r for Gleevec in the binding sites or in bulk solution are shown in Figure S5. Radius of gyration, Rg, for the binding site residues of the kinases as a function of the coupling parameter λrep, are plotted in Figure S6. Hydrogen-bonding interactions between Gleevec and key amino acid residues in the Gleevec-bound Abl kinase are illustrated in Figure S7. PMF profiles on the conformational restraints for Gleevec in bulk solution as well as in the binding pockets of the tyrosine kinases are shown in Figure S8. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Buchdunger E, Zimmermann J, Mett H, Meyer T, Muller M, Druker BJ, Lydon NB. Cancer Res. 1996;56:100. [PubMed] [Google Scholar]
- 2.Druker BJ, Lydon NB. J. Clin. Invest. 2000;105:3. doi: 10.1172/JCI9083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lydon N. Nat. Med. 2009;15:1153. doi: 10.1038/nm1009-1153. [DOI] [PubMed] [Google Scholar]
- 4.Druker BJ, Tamura S, Buchdunger E, Ohno S, Segal GM, Fanning S, Zimmermann J, Lydon NB. Nat. Med. 1996;2:561. doi: 10.1038/nm0596-561. [DOI] [PubMed] [Google Scholar]
- 5.Sawyers CL, Hochhaus A, Feldman E, Goldman JM, Miller CB, Ottmann OG, Schiffer CA, Talpaz M, Guilhot F, Deininger MW, Fischer T, O'Brien SG, Stone RM, Gambacorti-Passerini CB, Russell NH, Reiffers JJ, Shea TC, Chapuis B, Coutre S, Tura S, Morra E, Larson RA, Saven A, Peschel C, Gratwohl A, Mandelli F, Ben-Am M, Gathmann I, Capdeville R, Paquette RL, Druker BJ. Blood. 2002;99:3530. doi: 10.1182/blood.v99.10.3530. [DOI] [PubMed] [Google Scholar]
- 6.Capdeville R, Buchdunger E, Zimmermann J, Matter A. Nat. Rev. Drug Discov. 2002;1:493. doi: 10.1038/nrd839. [DOI] [PubMed] [Google Scholar]
- 7.Buchdunger E, Cioffi CL, Law N, Stover D, Ohno-Jones S, Druker BJ, Lydon NB. J. Pharmacol. Exp. Ther. 2000;295:139. [PubMed] [Google Scholar]
- 8.Demetri GD, von Mehren M, Blanke CD, Van den Abbeele AD, Eisenberg B, Roberts PJ, Heinrich MC, Tuveson DA, Singer S, Janicek M, Fletcher JA, Silverman SG, Silberman SL, Capdeville R, Kiese B, Peng B, Dimitrijevic S, Druker BJ, Corless C, Fletcher CD, Joensuu H. N. Engl. J. Med. 2002;347:472. doi: 10.1056/NEJMoa020461. [DOI] [PubMed] [Google Scholar]
- 9.Nowell PC, Hungerford DA. J. Natl. Cancer Inst. 1960;25:85. [PubMed] [Google Scholar]
- 10.Rowley JD. Nature. 1973;243:290. doi: 10.1038/243290a0. [DOI] [PubMed] [Google Scholar]
- 11.Heinrich MC, Griffith DJ, Druker BJ, Wait CL, Ott KA, Zigler AJ. Blood. 2000;96:925. [PubMed] [Google Scholar]
- 12.Blanke CD, Eisenberg BL, Heinrich MC. Curr. Treat. Options Oncol. 2001;2:485. doi: 10.1007/s11864-001-0070-0. [DOI] [PubMed] [Google Scholar]
- 13.van Oosterom AT, Judson I, Verweij J, Stroobants S, Donato di Paola E, Dimitrijevic S, Martens M, Webb A, Sciot R, Van Glabbeke M, Silberman S, Nielsen OS. Lancet. 2001;358:1421. doi: 10.1016/s0140-6736(01)06535-7. [DOI] [PubMed] [Google Scholar]
- 14.Seeliger MA, Nagar B, Frank F, Cao X, Henderson MN, Kuriyan J. Structure. 2007;15:299. doi: 10.1016/j.str.2007.01.015. [DOI] [PubMed] [Google Scholar]
- 15.Deininger M, Buchdunger E, Druker BJ. Blood. 2005;105:2640. doi: 10.1182/blood-2004-08-3097. [DOI] [PubMed] [Google Scholar]
- 16.Schindler T, Bornmann W, Pellicena P, Miller WT, Clarkson B, Kuriyan J. Science. 2000;289:1938. doi: 10.1126/science.289.5486.1938. [DOI] [PubMed] [Google Scholar]
- 17.Mol CD, Dougan DR, Schneider TR, Skene RJ, Kraus ML, Scheibe DN, Snell GP, Zou H, Sang BC, Wilson KP. J. Biol. Chem. 2004;279:31655. doi: 10.1074/jbc.M403319200. [DOI] [PubMed] [Google Scholar]
- 18.Manley PW, Cowan-Jacob SW, Buchdunger E, Fabbro D, Fendrich G, Furet P, Meyer T, Zimmermann J. Eur. J. Cancer. 2002;38(Suppl 5):S19. doi: 10.1016/s0959-8049(02)80599-8. [DOI] [PubMed] [Google Scholar]
- 19.Namboodiri HV, Bukhtiyarova M, Ramcharan J, Karpusas M, Lee Y, Springman EB. Biochemistry. 2010;49:3611. doi: 10.1021/bi100070r. [DOI] [PubMed] [Google Scholar]
- 20.Manning G, Plowman GD, Hunter T, Sudarsanam S. Trends Biochem. Sci. 2002;27:514. doi: 10.1016/s0968-0004(02)02179-5. [DOI] [PubMed] [Google Scholar]
- 21.Gorre ME, Mohammed M, Ellwood K, Hsu N, Paquette R, Rao PN, Sawyers CL. Science. 2001;293:876. doi: 10.1126/science.1062538. [DOI] [PubMed] [Google Scholar]
- 22.Sirulink A, Silver RT, Najfeld V. Leukemia. 2001;15:1795. doi: 10.1038/sj.leu.2402267. [DOI] [PubMed] [Google Scholar]
- 23.Tipping AJ, Mahon FX, Lagarde V, Goldman JM, Melo JV. Blood. 2001;98:3864. doi: 10.1182/blood.v98.13.3864. [DOI] [PubMed] [Google Scholar]
- 24.Gambacorti-Passerini CB, Gunby RH, Piazza R, Galietta A, Rostagno R, Scapozza L. Lancet Oncol. 2003;4:75. doi: 10.1016/s1470-2045(03)00979-3. [DOI] [PubMed] [Google Scholar]
- 25.Hochhaus A, Kreil S, Corbin AS, La Rosee P, Muller MC, Lahaye T, Hanfstein B, Schoch C, Cross NC, Berger U, Gschaidmeier H, Druker BJ, Hehlmann R. Leukemia. 2002;16:2190. doi: 10.1038/sj.leu.2402741. [DOI] [PubMed] [Google Scholar]
- 26.Campbell LJ, Patsouris C, Rayeroux KC, Somana K, Januszewicz EH, Szer J. Cancer Genet. Cytogenet. 2002;139:30. doi: 10.1016/s0165-4608(02)00615-5. [DOI] [PubMed] [Google Scholar]
- 27.Growney JD, Clark JJ, Adelsperger J, Stone R, Fabbro D, Griffin JD, Gilliland DG. Blood. 2005;106:721. doi: 10.1182/blood-2004-12-4617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nagar B, Bornmann W, Pellicena P, Schindler T, Veach DR, Miller WT, Clarkson B, Kuriyan J. Cancer Res. 2002;62:4236. [PubMed] [Google Scholar]
- 29.Vajpai N, Strauss A, Fendrich G, Cowan-Jacob SW, Manley PW, Grzesiek S, Jahnke W. J Biol Chem. 2008;283:18292. doi: 10.1074/jbc.M801337200. [DOI] [PubMed] [Google Scholar]
- 30.Jacobs MD, Caron PR, Hare BJ. Proteins. 2007;70:1451. doi: 10.1002/prot.21633. [DOI] [PubMed] [Google Scholar]
- 31.Aleksandrov A, Simonson T. J. Biol. Chem. 2010;285:13807. doi: 10.1074/jbc.M110.109660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jorgensen WL, Buckner JK, Boudon S, Tiradorives J. J. Chem. Phys. 1988;89:3742. [Google Scholar]
- 33.Roux B, Nina M, Pomes R, Smith JC. Biophys. J. 1996;71:670. doi: 10.1016/S0006-3495(96)79267-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dubey KD, Ojha RP. J. Biol. Phys. 2011;37:69. doi: 10.1007/s10867-010-9199-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lee T-S, Potts SJ, Kantarjian H, Cortes J, Giles F, Albitar M. Cancer. 2008;112:1744. doi: 10.1002/cncr.23355. [DOI] [PubMed] [Google Scholar]
- 36.Lee T-S, Potts SJ, Albitar M. Rec. Pat. Anti-Canc. Drug Disc. 2009;4:1. doi: 10.2174/157489209788452867. [DOI] [PubMed] [Google Scholar]
- 37.Shan Y, Kim ET, Eastwood MP, Dror RO, Seeliger MA, Shaw DE. J. Am. Chem. Soc. 2011;133:9181. doi: 10.1021/ja202726y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rajasekaran R, Sethumadhavan R. Amino Acids. 2010;39:651. doi: 10.1007/s00726-010-0486-6. [DOI] [PubMed] [Google Scholar]
- 39.Lin YL, Meng Y, Jiang W, Roux B. Proc. Natl. Acad. Sci. USA. 2013;110:1664. doi: 10.1073/pnas.1214330110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Szakács Z, Béni S, Varga Z, Örfi L, Kéri G, Noszál B. J. Med. Chem. 2005;48:249. doi: 10.1021/jm049546c. [DOI] [PubMed] [Google Scholar]
- 41.Aleksandrov A, Simonson T. J. Comput. Chem. 2010;31:1550. doi: 10.1002/jcc.21442. [DOI] [PubMed] [Google Scholar]
- 42.Brunger AT, Karplus M. Prot. Struct. Funct. Genet. 1988;4:148. doi: 10.1002/prot.340040208. [DOI] [PubMed] [Google Scholar]
- 43.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 2009;4:187. [Google Scholar]
- 44.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187. [Google Scholar]
- 45.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J. Phys. Chem. B. 1998;102:3586. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 46.Mackerell AD, Jr, Feig M, Brooks CL., 3rd J. Comput. Chem. 2004;25:1400. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 47.MacKerell AD, Jr, Feig M, Brooks CL., 3rd J. Am. Chem. Soc. 2004;126:698. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 48.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 49.Darden T, York DM, Pedersen I. J. Chem. Phys. 1993;98:10089. [Google Scholar]
- 50.Rychaert JP, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;32:327. [Google Scholar]
- 51.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J. Comput. Chem. 2005;26:1781. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Deng Y, Roux B. J. Phys. Chem. B. 2004;108:16567. [Google Scholar]
- 53.Wang J, Deng Y, Roux B. Biophys. J. 2006;91:2798. doi: 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Deng Y, Roux B. J. Chem. Theory Comput. 2006;2:1255. doi: 10.1021/ct060037v. [DOI] [PubMed] [Google Scholar]
- 55.Deng Y, Roux B. J. Chem. Phys. 2008;128:115103. doi: 10.1063/1.2842080. [DOI] [PubMed] [Google Scholar]
- 56.Ge X, Roux B. J. Phys. Chem. B. 2010;114:9525. doi: 10.1021/jp100579y. [DOI] [PubMed] [Google Scholar]
- 57.Ge X, Roux B. J. Mol. Recognit. 2010;23:128. doi: 10.1002/jmr.996. [DOI] [PubMed] [Google Scholar]
- 58.Woodcock HL, III, Hodošček M, Sherwood P, Lee YS, Schaefer HF, III, Brooks BR. Theor. Chem. Acc. 2003;109:140. [Google Scholar]
- 59.Woodcock HL, III, Hodošček M, Gilbert ATB, Gill PMW, Schaefer HF, III, Brooks BR. J. Comput. Chem. 2007;28:1485. doi: 10.1002/jcc.20587. [DOI] [PubMed] [Google Scholar]
- 60.Jiang W, Hodoscek M, Roux B. J. Chem. Theory Comput. 2009;5:2583. doi: 10.1021/ct900223z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Jiang W, Roux B. J. Chem. Theory Comput. 2010;6:2559. doi: 10.1021/ct1001768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Woo HJ, Roux B. Proc. Natl. Acad. Sci. USA. 2005;102:6825. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Deng Y, Roux B. J. Phys. Chem. B. 2009;113:2234. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Weeks JD, Chandler D, Andersen HC. J. Chem. Phys. 1971;54:5237. [Google Scholar]
- 65.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. J. Comput. Chem. 1992;13:1011. [Google Scholar]
- 66.Souaille M, Roux B. Comput. Phys. Comm. 2001;135:40. [Google Scholar]
- 67.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys. J. 1997;72:1047. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mobley DL, Chodera JD, Dill KA. J. Chem. Theory Comput. 2007;3:1231. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kauzmann W. Adv. Prot. Chem. 1959;14:1. doi: 10.1016/s0065-3233(08)60608-7. [DOI] [PubMed] [Google Scholar]
- 70.Chothia C, Janin J. Nature. 1975;256:705. doi: 10.1038/256705a0. [DOI] [PubMed] [Google Scholar]
- 71.Horton N, Lewis M. Prot. Sci. 1992;1:169. doi: 10.1002/pro.5560010117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Froloff N, Windemuth A, Honig B. Prot. Sci. 1997;6:1293. doi: 10.1002/pro.5560060617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Noskov SY, Lim C. Biophys. J. 2001;81:737. doi: 10.1016/S0006-3495(01)75738-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Levinson NM, Kuchment O, Shen K, Young MA, Koldobskiy M, Karplus M, Cole PA, Kuriyan J. PLos Biology. 2006;4:753. doi: 10.1371/journal.pbio.0040144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kleywegt GJ, Jones TA. Acta Crystallogr. D. 1994;50:178. doi: 10.1107/S0907444993011333. [DOI] [PubMed] [Google Scholar]
- 76.Cowan-Jacob SW, Fendrich G, Manley PW, Jahnke W, Fabbro D, Liebetanz J, Meyer T. Structure. 2005;13:861. doi: 10.1016/j.str.2005.03.012. [DOI] [PubMed] [Google Scholar]
- 77.Shah NP, Nicoll JM, Nagar B, Gorre ME, Paquette RL, Kuriyan J, Sawyers CL. Cancer Cell. 2002;2:117. doi: 10.1016/s1535-6108(02)00096-x. [DOI] [PubMed] [Google Scholar]
- 78.Azam M, Latek RR, Daley GQ. Cell. 2003;112:831. doi: 10.1016/s0092-8674(03)00190-9. [DOI] [PubMed] [Google Scholar]
- 79.Hochhaus A, La Rosee P. Leukemia. 2004;18:1321. doi: 10.1038/sj.leu.2403426. [DOI] [PubMed] [Google Scholar]
- 80.Carter TA, Wodicka LM, Shah NP, Velasco AM, Fabian MA, Treiber DK, Milanov ZV, Atteridge CE, Biggs WH, 3rd, Edeen PT, Floyd M, Ford JM, Grotzfeld RM, Herrgard S, Insko DE, Mehta SA, Patel HK, Pao W, Sawyers CL, Varmus H, Zarrinkar PP, Lockhart DJ. Proc. Natl. Acad. Sci. USA. 2005;102:11011. doi: 10.1073/pnas.0504952102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.O'Hare T, Eide CA, Deininger MW. Blood. 2007;110:2242. doi: 10.1182/blood-2007-03-066936. [DOI] [PubMed] [Google Scholar]
- 82.La Rosee P, Deininger MW. Semin. Hematol. 2010;47:335. doi: 10.1053/j.seminhematol.2010.06.005. [DOI] [PubMed] [Google Scholar]
- 83.Shoichet BK. Nature. 2004;432:862. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Dar AC, Lopez MS, Shokat KM. Chem. Biol. 2008;15:1015. doi: 10.1016/j.chembiol.2008.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Seeliger MA, Ranjitkar P, Kasap C, Shan Y, Shaw DE, Shah NP, Kuriyan J, Maly DJ. Cancer Res. 2009;69:2384. doi: 10.1158/0008-5472.CAN-08-3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Cowan-Jacob SW, Fendrich G, Manley PW, Jahnke W, Fabbro D, Liebetanz J, Meyer T. Structure. 2005;13:861. doi: 10.1016/j.str.2005.03.012. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.