VARIABLE SELECTION IN LINEAR MIXED EFFECTS MODELS

Abstract

This paper is concerned with the selection and estimation of fixed and random effects in linear mixed effects models. We propose a class of nonconcave penalized profile likelihood methods for selecting and estimating important fixed effects. To overcome the difficulty of unknown covariance matrix of random effects, we propose to use a proxy matrix in the penalized profile likelihood. We establish conditions on the choice of the proxy matrix and show that the proposed procedure enjoys the model selection consistency where the number of fixed effects is allowed to grow exponentially with the sample size. We further propose a group variable selection strategy to simultaneously select and estimate important random effects, where the unknown covariance matrix of random effects is replaced with a proxy matrix. We prove that, with the proxy matrix appropriately chosen, the proposed procedure can identify all true random effects with asymptotic probability one, where the dimension of random effects vector is allowed to increase exponentially with the sample size. Monte Carlo simulation studies are conducted to examine the finite-sample performance of the proposed procedures. We further illustrate the proposed procedures via a real data example.

1. Introduction

During the last two decades, linear mixed effects models (Laird and Ware, 1982; Longford, 1993) have been widely used to model longitudinal and repeated measurements data, and have received a considerable amount of attention in the fields of agriculture, biology, economics, medicine, and sociology. See Verbeke and Molenberghs (2000) and references therein. With the advent of data collection technology, many variables can be easily collected in a scientific study, and it is typical to include many of them in the full model at the initial stage of modeling in order to reduce model approximation error. Due to the complexity of the mixed effects models, the inferences and interpretation of estimated models become challenging as the dimension of fixed or random components increases. Thus, the selection of important fixed effect covariates or random components becomes a fundamental problem in the analysis of longitudinal data or repeated measurements data using mixed effects models.

Variable selection for mixed effects models has become an active research topic in the literature. Lin (1997) considers testing a hypothesis on the variance component. The testing procedures can be used to detect whether an individual random component is significant or not. Based on these testing procedures, a stepwise procedure can be constructed for selecting important random effects. Vaida and Blanchard (2005) propose the conditional AIC, an extension of the AIC (Akaike, 1973), for mixed effects models with detailed discussion on how to define degrees of freedom in the presence of random effects. The conditional AIC has further been discussed in Liang et al. (2008). Chen and Dunson (2003) develop a Bayesian variable selection procedure for selecting important random effects in the linear mixed effects model using the Cholesky decomposition of the covariance matrix of random effects, and specify a prior distribution on the standard deviation of random effects with a positive mass at zero to achieve the sparsity of random components. Pu and Niu (2006) extend the generalized information criterion to select linear mixed effects models and study the asymptotic behavior of the proposed method for selecting fixed effects. Bondell et al. (2010) propose a joint variable selection method for fixed and random effects in the linear mixed effects model using a modified Cholesky decomposition in the setting of fixed dimensionality for both fixed effects and random effects. Ibrahim et al. (2011) propose to select fixed and random effects in a general class of mixed effects models with fixed dimensions of both fixed and random effects using maximum penalized likelihood method with the SCAD penalty and the adaptive least absolute shrinkage and selection operator penalty.

In this paper, we develop a class of variable selection procedures for both fixed effects and random effects in linear mixed effects models by incorporating the recent advances in variable selection for linear regression models. We propose to use the regularization methods to select and estimate fixed and random effects. As advocated by Fan and Li (2001), regularization methods can avoid the stochastic error of variable selection in stepwise procedures, and can significantly reduce computational cost compared with the best subset selection procedure and Bayesian procedures. Our proposal differs from existing ones in the literature mainly in two aspects. First, we consider the high-dimensional setting and allow dimensions of fixed and random effects to grow exponentially with the sample size. Second, our proposed procedures can estimate the fixed effects vector without knowing or estimating the random effects vector and vice versa.

We first propose a class of variable selection methods for the fixed effects using penalized profile likelihood method. To overcome the difficulty of unknown covariance matrix of random effects, we propose to replace it with a suitably chosen proxy matrix. The penalized profile likelihood is equivalent to a penalized quadratic loss function of the fixed effects. Thus, the proposed approach can take advantage of the recent developments in the computation of the penalized least-squares methods (Efron et al., 2004; Zou and Li, 2008). The optimization of the penalized likelihood can be solved by the LARS algorithm without extra effort. We further systematically study the sampling properties of the resulting estimate of fixed effects. We establish conditions on the proxy matrix and show that the resulting estimate enjoys model selection oracle property under such conditions. In our theoretical investigation, the number of fixed effects is allowed to grow exponentially with the total sample size, provided that the covariance matrix of random effects is nonsingular. In the case of singular covariance matrix for random effects, one can use our proposed method in Section 3 to first select important random effects and then conduct variable selection for fixed effects. In this case, the number of fixed effects needs to be smaller than the total sample size.

Since the random effects vector is random, our main interest is in the selection of true random effects. Observe that if a random effect covariateis a noise variable, then the corresponding realizations of this random effect should all be zero and thus the random effects vector is sparse. So we propose to first estimate the realization of random effects vector using a group regularization method and then identify the important ones based on the estimated random effects vector. More specifically, under the Bayesian framework, we show that the restricted posterior distribution of the random effects vector is independent of the fixed effects coefficient vector. Thus, we propose a random effect selection procedure via penalizing the restricted posterior mode. The proposed procedure reduces the impact of error caused by the fixed effects selection and estimation. The unknown covariance matrix is replaced with a suitably chosen proxy matrix. In the proposed procedure, random effects selection is carried out with group variable selection techniques (Yuan and Lin, 2006). The optimization of the penalized restricted posterior mode is equivalent to the minimization of the penalized quadratic function of random effects. In particular, the form of the penalized quadratic function is similar to that in the adaptive elastic net (Zou and Hastie, 2005; Zou and Zhang, 2009), which allows us to minimize the penalized quadratic function using existing algorithms. We further study the theoretical properties of the proposed procedure and establish conditions on the proxy matrix for ensuring the model selection consistency of the resulting estimate. We show that, with probability tending to one, the proposed procedure can select all true random effects. In our theoretical study, the dimensionality of random effects vector is allowed to grow exponentially with the sample size as long as the number of fixed effects is less than the total sample size.

The rest of this paper is organized as follows. Section 2 introduces the penalized profile likelihood method for the estimation of fixed effects and establishes its oracle property. We consider the estimation of random effects and prove the model selection consistency of the resulting estimator in Section 3. Section 4 provides two simulation studies and a real data example. Some discussion is given in Section 5. All proofs are presented in Section 6.

2. Penalized profile likelihood for fixed effects

Suppose that we have a sample of N subjects. For the i-th subject, we collect the response variable y_ij, the d × 1 covariate vector x_ij, and q × 1 covariate vector z_ij, for j = 1, … , n_i, where n_i is the number of observations on the i-th subject. Let $n={\sum }_{i=1}^N{n}_i,m_n={\max }_{1\le i\le N}{n}_i$, and ${\tilde{m}}_n={\min }_{1\le i\le N}{n}_i$. We consider the case where ${\lim \sup }_n\frac{m_n}{{\tilde{m}}_n}<\infty$, i.e., the sample sizes for N subjects are balanced. For succinct presentation, we use matrix notation and write y_i = (y_i1, y_i2, … , y_ini)^T, X_i = (x_i1, x_i2, … , x_ini)^T, and Z_i = (z_i1, z_i2, … , z_ini)^T In linear mixed effects models, the vector of repeated measurements y_i on the i-th subject is assumed to follow the linear regression model

$${\mathrm{y}}_i={\mathbf{X}}_i\beta +{\mathbf{Z}}_i{\gamma }_i+{\epsilon }_i,$$ (1)

where β is the d × 1 population-specific fixed effects coefficient vector, γ_i represents the q × 1 subject-specific random effects with γ_i ~ N(0, G), ε_i is the random error vector with components independent and identically distributed as N(0, σ²), and γ₁, …, γ_N, ε₁, …, ε_N are independent. Here, G is the covariance matrix of random effects and may be different from the identity matrix. So the random effects can be correlated with each other.

Let vectors y, γ, and ε, and matrix X be obtained by stacking vectors y_i, γ_i, and ε_i, and matrices X_i, respectively, underneath each other, and let Z = diag{Z₁, …, Z_N} and $\mathcal{G}=\mathrm{diag}\{G,\dots ,G\}$ be block diagonal matrices. We further standardize the design matrix X such that each column has norm $\sqrt{n}$. The linear mixed effects model (1) can be rewritten as

$$\mathrm{y}=\mathbf{X}\beta +\mathbf{Z}\gamma +\epsilon .$$ (2)

2.1. Selection of important fixed-effects

In this subsection, we assume that there are no noise random effects and $\mathcal{G}$ is positive definite. In the case where noise random effects exist, one can use the method in Section 3 to select the true ones. The joint density is

$$\begin{array}{cc}\hfill f(\mathrm{y},\gamma )& =f(\mathrm{y}\mid \gamma )f\left(\gamma \right)={\left(2\pi \sigma \right)}^{-(n+qN)∕2}{\mid \mathcal{G}\mid }^{-1∕2}\hfill \\ \hfill & \times \exp \left\{-\frac{1}{2{\sigma }^2}{(\mathrm{y}-\mathrm{X}\beta -\mathrm{Z}\gamma )}^T(\mathrm{y}-\mathrm{X}\beta -\mathrm{Z}\gamma )-\frac{1}{2}{\gamma }^T{\mathcal{G}}^{-1}\gamma \right\}.\hfill \end{array}$$ (3)

Given β, the maximum likelihood estimate (MLE) for γ is

$$\widehat{\gamma }\left(\beta \right)={\mathrm{B}}_z(\mathrm{y}-\mathrm{X}\beta ),$$

where ${\mathbf{B}}_z={({\mathbf{Z}}^T\mathbf{Z}+{\sigma }^2{\mathcal{G}}^{-1})}^{-1}{\mathbf{Z}}^T$. Plugging $\widehat{\gamma }\left(\beta \right)$ into f(y, γ) and dropping the constant term yield the following profile likelihood function

$$L_n(\beta ,\widehat{\gamma }\left(\beta \right))=\exp \left\{-\frac{1}{2{\sigma }^2}{(\mathrm{y}-\mathrm{X}\beta )}^T{\mathrm{P}}_z(\mathrm{y}-\mathrm{X}\beta )\right\},$$ (4)

where ${\mathbf{P}}_z={(\mathbf{I}-{\mathbf{ZB}}_z)}^T(\mathbf{I}-{\mathbf{ZB}}_z)+{\sigma }^2{\mathbf{B}}_z^T{\mathcal{G}}^{-1}{\mathbf{B}}_z$ with I being the identity matrix. By Lemma 3 in Section 6, P_z can be rewritten as ${\mathbf{P}}_z={(\mathbf{I}+{\sigma }^{-2}\mathbf{Z}\mathcal{G}{\mathbf{Z}}^T)}^{-1}$. To select the important x-variables, we propose to maximize the following penalized profile log-likelihood function

$$\log \left(L_n(\beta ,\widehat{\gamma }\left(\beta \right))\right)-n{\Sigma }_{j=1}^{d_n}p{\lambda }_n\left(\mid {\beta }_j\mid \right),$$ (5)

where p_λn(x) is a penalty function with regularization parameter λ_n ≥ 0. Here, the number of fixed effects d_n may increase with sample size n.

Maximizing (5) is equivalent to minimizing

$$Q_n\left(\beta \right)=\frac{1}{2}{(\mathrm{y}-\mathrm{X}\beta )}^T{\mathrm{P}}_z(\mathrm{y}-\mathrm{X}\beta )+n{\Sigma }_{j=1}^{d_n}p{\lambda }_n\left(\mid {\beta }_j\mid \right).$$ (6)

Since P_z depends on the unknown covariance matrix $\mathcal{G}$ and σ², we propose to use a proxy ${\tilde{\mathbf{P}}}_z={(\mathbf{I}+\mathbf{Z}\mathcal{M}{\mathbf{Z}}^T)}^{-1}$ to replace P_z, where $\mathcal{M}$ is a pre-specified matrix. Denote by ${\tilde{Q}}_n\left(\beta \right)$ the corresponding objective function when ${\tilde{\mathbf{P}}}_z$ is used. We will discuss in the next section on how to choose $\mathcal{M}$.

We note that (6) does not depend on the inverse of $\mathcal{G}$. So although we started this section with the non-singularity assumption of $\mathcal{G}$, in practice our method can be directly applied even when noise random effects exist, as will be illustrated in simulation studies of Section 4.

Many authors have studied the selection of the penalty function to achieve the purpose of variable selection for the linear regression model. Tibshirani (1996) proposes the Lasso method by the use of L₁ penalty. Fan and Li (2001) advocate the use of nonconvex penalties. In particular, they suggest the use of the SCAD penalty. Zou (2006) proposes the adaptive Lasso by using adaptive L₁ penalty, Zhang (2010) proposes the minimax concave penalty (MCP), Liu and Wu (2007) propose to linearly combine L₀ and L₁ penalties, and Lv and Fan (2009) introduce a unified approach to sparse recovery and model selection using general concave penalties. In this paper, we use concave penalty function to conduct variable selection. We make the following assumption on the penalty function.

Condition 1. For each λ > 0, the penalty function p_λ(t) with t ∈ [0, ∞) is increasing and concave with p_λ(0) = 0, its second order derivative exists and is continuous, and $p_{\lambda }^{\prime }(0+)\in (0,\infty )$. Further, assume that ${\sup }_{t>0}{p}_{\lambda }^{″}\left(t\right)\to 0$ as λ → 0.

Condition 1 is commonly assumed in studying regularization methods with concave penalties. Similar conditions can be found in Fan and Li (2001) and Lv and Fan (2009). Although it is assumed that $p_{\lambda }^{″}\left(t\right)$ exists and is continuous, it can be relaxed to the case where only $p_{\lambda }^{\prime }\left(t\right)$ exists and is continuous. All theoretical results presented in later sections can be generalized by imposing conditions on the local concavity of p_λ(t), as done in Lv and Fan (2009).

2.2. Model selection consistency

Although the proxy matrix ${\tilde{\mathbf{P}}}_z$ may be different from the true one P_z, solving the regularization problem (6) may still yield correct model selection results at the cost of some additional bias. We next establish conditions on ${\tilde{\mathbf{P}}}_z$ to ensure the model selection oracle property of the proposed method.

Let β₀ be the true coefficient vector. Suppose that β₀ is sparse and denote s_1n = ||β₀||₀ i.e., the number of nonzero elements in β₀. Write

$${\beta }_0={({\beta }_{1,0},\cdots ,{\beta }_{d_n,0})}^T={({\beta }_{1,0}^T,{\beta }_{2,0}^T)}^T,$$

where β_1,0 is an s_1n-vector and β_2,0 is a (d_n – s_1n)-vector. Without loss of generality, we assume that β_2,0 = 0, that is, the nonzero elements of β₀ locate at the first s_1n coordinates. With a slight abuse of notation, we write X = (X₁,X₂) with X₁ being a submatrix formed by the first s_1n columns of X and X₂ being formed by the remaining columns. For a matrix B, let Λ_min(B) and Λ_max(B) be its minimum and maximum eigenvalues, respectively. We make a few assumptions on the penalty function pλ_n(t) and the design matrices X and Z.

Condition 2.

(A) Leta_n = min₁≤j≤s_1n |β_{0, j}|. It holds that a_nn^T (log n)^−3/2 → ∞ with τ ∈ (0, $\frac{1}{2}$) being some positive constant, and ${\sup }_{t\ge a_n∕2}{p}_{{\lambda }_n}^{″}\left(t\right)=o\left(n^{-1+2\tau }\right)$.

(B) There exists a constant c₁ > 0 such that ${\Lambda }_{min}(c_1\mathcal{M}-{\sigma }^{-2}\mathcal{G})\ge 0$ and ${\Lambda }_{min}(c_1{\sigma }^{-2}\left(\log n\right)\mathcal{G}-\mathcal{M})\ge 0$ (C) The minimum and maximum eigenvalues of matrices $n^{-1}\left({\mathbf{X}}_1^T{\mathbf{X}}_1\right)$ and $n^{\theta }{\left({\mathbf{X}}_1^T{\mathbf{P}}_z{\mathbf{X}}_1\right)}^{-1}$ are both bounded from below and above by c₀ and c₀⁻¹ respectively, where θ ∈ (2τ, 1] and c₀ > 0 is a constant. Further, it holds that

$${\Vert {\left(\frac{1}{n}{\mathbf{X}}_1^T{\tilde{P}}_z{\mathbf{X}}_1\right)}^{-1}\Vert }_{\infty }\le n^{-\tau }\left(\log n\right)∕p_{{\lambda }_n}^{\prime }(a_n∕2)$$ (7)

$${\parallel {\mathrm{X}}_2^T{\tilde{\mathrm{P}}}_z{\mathrm{X}}_1{\left({\mathrm{X}}_1^T{\tilde{\mathrm{P}}}_z{\mathrm{X}}_1\right)}^{-1}\parallel }_{\infty }<p_{{\lambda }_n}^{\prime }(0+)∕p_{{\lambda }_n}^{\prime }(a_n∕2),$$ (8)

where || · ||∞ denotes the matrix infinity norm.

Condition 2(A) is on the minimum signal strength a_n. We allow the minimum signal strength to decay with sample size n. When concave penalties such as SCAD (Fan and Li, 2001) or SICA (Lv and Fan, 2009) are used, this condition can be easily satisfied with λ_n appropriately chosen. Conditions 2(B) and (C) put constraints on the proxy $\mathcal{M}$. Condition 2(C) is about the design matrices X and Z. Inequality (8) requires noise variables and signal variables not highly correlated. The upper bound of (8) depends on the ratio $p_{{\lambda }_n}^{\prime }(0+)∕p_{{\lambda }_n}^{\prime }(a_n∕2)$. Thus, concave penalty functions relax this condition when compared to convex penalty functions. We will further discuss constraints (7) and (8) in Lemma 1.

If the above conditions on the proxy matrix are satisfied then the bias caused by using ${\tilde{\mathbf{P}}}_z$ is small enough and the resulting estimate still enjoys the model selection oracle property described in the following theorem.

Theorem 1. Assume that $\sqrt{n}{\lambda }_n\to \infty$ as n → ∞ and $\log d_n=o\left(n{\lambda }_n^2\right)$. Then under Conditions 1 and 2, with probability tending to 1 as n → ∞, there exists a local minimizer $\widehat{\beta }={({\widehat{\beta }}_1^T,{\widehat{\beta }}_2^T)}^{T}of{\tilde{Q}}_n\left(\beta \right)$ which satisfies

$${\parallel {\widehat{\beta }}_1-{\beta }_{0,1}\parallel }_{\infty }<n^{-\tau }\left(\log n\right),\text{and}{\widehat{\beta }}_2=0.$$ (9)

Theorem 1 presents the weak oracle property in the sense of Lv and Fan (2009) on the local minimizer of $\tilde{Q}\left(\beta \right)$. Due to the high dimensionality and the concavity of p_λ(·), the characterization of the global minimizer of $\tilde{Q}\left(\beta \right)$ is a challenging open question. As will be shown in the simulation and real data analysis, the concave function $\tilde{Q}\left(\beta \right)$ will be iteratively minimized by the local linear approximation method (Zou and Li, 2008). Following the same idea as in Zou and Li (2008), it can be shown that the resulting estimate poesses the properties in Theorem 1 under some conditions.

2.3. Choice of proxy matrix $\mathcal{M}$

It is difficult to see from (7) and (8) on how restrictive the conditions on the proxy matrix $\mathcal{M}$ are. So we further discuss these conditions in the lemma below. We introduce the notation $\mathbf{T}={\sigma }^2{\mathcal{G}}^{-1}+{\mathbf{Z}}^T{\mathbf{P}}_x\mathbf{Z}$ and $\mathbf{E}={\sigma }^2{\mathcal{G}}^{-1}+{\mathbf{Z}}^T\mathbf{Z}$ with ${\mathbf{P}}_x=\mathbf{I}-{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1$. Correspondingly, when the proxy matrix $\mathcal{M}$ is used, define $\tilde{\mathbf{T}}={\mathcal{M}}^{-1}+{\mathbf{Z}}^T{\mathbf{P}}_x\mathbf{Z}$ and $\tilde{\mathbf{E}}={\mathcal{M}}^{-1}+{\mathbf{Z}}^T\mathbf{Z}$. We use || · ||₂ to denote the matrix 2-norm, that is, ||A||₂ = {Λ_max(AA^T)}½.

Lemma 1. Assume that ${\parallel {\left(\frac{1}{n}{\mathbf{X}}_1^T{\mathbf{P}}_z{\mathbf{X}}_1\right)}^{-1}\parallel }_{\infty }<n^{-\tau }\sqrt{\log n}∕p_{{\lambda }_n}^{\prime }(a_n∕2)$ and

$${\parallel {\mathbf{T}}^{-1∕2}\tilde{\mathbf{T}}{\mathbf{T}}^{-1∕2}-\mathbf{I}\parallel }_2<{(1+n^{\tau }{s}_{1n}{p}_{{\lambda }_n}^{\prime }(a_n∕2){\parallel {\mathbf{ZT}}^{-1}{\mathbf{Z}}^T\parallel }_2)}^{-1}.$$ (10)

Then (7) holds.

Similarly, assume that ${\parallel {\mathbf{X}}_2^T{\mathbf{P}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\mathbf{P}}_z{\mathbf{X}}_1\right)}^{-1}\parallel }_{\infty }<p_{{\lambda }_n}^{\prime }(0+)∕p_{{\lambda }_n}^{\prime }(a_n∕2)$, and there exists a constant c₂ > 0 such that

$${\parallel {\mathbf{T}}^{-1∕2}\tilde{\mathbf{T}}{\mathbf{T}}^{-1∕2}-\mathbf{I}\parallel }_2<{[1+n^{-1}{\parallel {\mathbf{ZT}}^{-1}{\mathbf{Z}}^T\parallel }_2\times \max \{c_2{n}^{\theta },2c_0{s}_{1n}{\lambda }_n^{-1}{p}_{{\lambda }_n}^{\prime }(a_n∕2){\parallel {\mathbf{X}}_2^T{\mathbf{P}}_z{\mathbf{X}}_1\parallel }_2\}]}^{-1},$$ (11)

$${\parallel {\mathbf{E}}^{-1∕2}\tilde{\mathbf{E}}{\mathbf{E}}^{-1∕2}-\mathbf{I}\parallel }_2<{[1+{\lambda }_n^{-1}{s}_{1n}\left(\log n\right)p_{{\lambda }_n}^{\prime }(a_n∕2)\times {\parallel \mathbf{Z}\mathcal{G}{\mathbf{Z}}^T\parallel }_2{\left\{{\parallel {\left({\mathbf{X}}_1^T{\mathbf{P}}_z{\mathbf{X}}_1\right)}^{-1}\parallel }_2{\parallel {\mathbf{X}}_2^T{\mathbf{P}}_z{\mathbf{X}}_2\parallel }_2\right\}}^{1∕2}]}^{-1},$$ (12)

then (8) holds.

Equations (10), (11) and (12) show conditions on the proxy matrix $\mathcal{M}$. Note that if penalty function used is flat outside of a neighborhood of zero, then $p_{{\lambda }_n}^{\prime }(a_n∕2)\approx 0$ with appropriately chosen regularization parameter λ_n, and conditions (10) and (12) respectively reduce to

$${\parallel {\mathbf{T}}^{-1∕2}\tilde{\mathbf{T}}{\mathbf{T}}^{-1∕2}-\mathbf{I}\parallel }_2<1,{\parallel {\mathbf{E}}^{-1∕2}\tilde{\mathbf{E}}{\mathbf{E}}^{1∕2}-\mathbf{I}\parallel }_2<1.$$ (13)

Furthermore, since Z is a block diagonal matrix, if the maximum eigenvalue of ZT⁻¹Z^T is of the order o(n^1−θ), then condition (11) reduces to

$${\parallel {\mathbf{T}}^{-1∕2}\tilde{\mathbf{T}}{\mathbf{T}}^{-1∕2}-\mathbf{I}\parallel }_2<1.$$ (14)

Conditions (13) and (14) are equivalent to assuming that ${\mathbf{T}}^{-1∕2}\tilde{\mathbf{T}}{\mathbf{T}}^{-1∕2}$ and ${\mathbf{E}}^{-1∕2}\tilde{\mathbf{E}}{\mathbf{E}}^{-1∕2}$ have eigenvalues bounded between 0 and 2. By linear algebra, they can further be reduced to ${\parallel {\mathbf{T}}^{-1}\tilde{\mathbf{T}}\parallel }_2<2$ and ${\parallel {\mathbf{E}}^{-1}\tilde{\mathbf{E}}\parallel }_2<2$. It is seen from the definitions of T, $\tilde{\mathbf{T}}$, E and $\tilde{\mathbf{E}}$ that if eigenvalues of ZP_xZ^T and ZZ^T dominate those of ${\sigma }^2{\mathcal{G}}^{-1}$ by a larger order of magnitude, then these conditions are not difficult to be satisfied. In fact, note that both ZP_xZ^T and ZZ^T have components with magnitudes increasing with n, while the eigenvalues of ${\sigma }^2{\mathcal{G}}^{-1}$ are independent of n. Thus as long as both matrices ZP_xZ^T and ZZ^T are non-singular, these conditions should easily be satisfied with the choice $\mathcal{M}=\left(\log n\right)\mathbf{I}$ when n is large enough.

3. Identifying important random effects

In this section, we allow the number of random effects q to increase with sample size n and write it as q_n to emphasize its dependency on n. We focus on the case where the number of fixed effects d_n is smaller than the total sample size $n={\sum }_{i=1}^N{n}_i$. We discuss the d_n ≥ n case in the discussion Section 5. The major goal of this section is to select important random effects.

3.1. Regularized posterior mode estimate

The estimation of random effects is different from the estimation of fixed effects, as the vector γ is random. The empirical Bayes method has been used to estimate the random effects vector γ in the literature. See, for example, Box and Tiao (1973), Gelman et al. (1995), and Verbeke and Molenberghs (2000). Although the empirical Bayes method is successful in estimating random effects in many situations, it cannot be used to select important random effects. Moreover, the performance of empirical Bayes estimate largely depends on the accuracy of estimated fixed effects. These difficulties call for a new proposal for random effects selection.

Patterson and Thompson (1971) propose the error contrast method to obtain the restricted maximum likelihood of a linear model. Following their notation, define the n×(n–d) matrix A by the conditions AA^T = P_x and A^TA = I, where P_x = I − X(X^TX)⁻¹X^T. Then the vector A^T ε provides a particular set of n – d linearly independent error contrasts. Let w₁ = A^T y. The following proposition characterizes the conditional distribution of w₁:

Proposition 1. Given γ, the density function of w₁ takes the form

$$f{\mathrm{w}}_1({\mathrm{A}}^T\mathrm{y}\mid \gamma )={\left(2\pi {\sigma }^2\right)}^{-(n-d)∕2}\exp \left\{-\frac{1}{2{\sigma }^2{(\mathrm{y}-\mathrm{Z}\gamma )}^T{\mathrm{P}}_x(\mathrm{y}-\mathrm{Z}\gamma )}\right\}.$$ (15)

The above conditional probability is independent of the fixed effects vector β and the error contrast matrix A, which allows us to obtain a posterior mode estimate of γ without estimating β and calculating A.

Let ${\mathfrak{m}}_0\subset \{1,2,\dots ,q_n\}$ be the index set of the true random effects. Define

$${\stackrel{‒}{\mathfrak{m}}}_0=\{j:j=i{q}_n+k,\text{for}i=0,1,2,\cdots ,N-1\text{and}k\in {\mathfrak{m}}_0\}$$

and denote by ${\overline{\mathfrak{m}}}_0^c=\{1,2,\cdots ,N{q}_n\}\backslash {\overline{\mathfrak{m}}}_0$. Then ${\overline{\mathfrak{m}}}_0$ is the index set of nonzero random effects coefficients in the vector γ, and ${\overline{\mathfrak{m}}}_0^c$ is the index set of the zero ones. Let $s_{2n}={\parallel {\mathfrak{m}}_0\parallel }_0$ be the number of true random effects. Then ${\parallel {\overline{\mathfrak{m}}}_0\parallel }_0=N{s}_{2n}$. We allow Ns_2n to diverge with sample size n, which covers both the case where the number of subjects N diverges with n alone and the case where N and s_2n diverge with n simultaneously.

For any $\mathcal{S}\subset \{1,\cdots ,q_{n}N\}$ we use ${\mathbf{Z}}_{\mathcal{S}}$ to denote the (q_nN)×|$\mathcal{S}$| submatrix of Z formed by columns with indices in $\mathcal{S}$ and ${\gamma }_{\mathcal{S}}$ to denote the subvector of γ formed by components with indices in $\mathcal{S}$. Then ${\gamma }_{{\overline{\mathfrak{m}}}_0}~N(0,{\mathcal{G}}_{{\overline{\mathfrak{m}}}_0})$ with ${\mathcal{G}}_{{\overline{\mathfrak{m}}}_{\mathrm{O}}}$ a submatrix formed by entries of $\mathcal{G}$ with row and column indices in ${\overline{\mathfrak{m}}}_0$.

In view of (15), the restricted posterior density of ${\gamma }_{{\overline{\mathfrak{m}}}_0}$ can be derived as

$$f{\mathrm{w}}_1(\gamma {\stackrel{‒}{\mathfrak{m}}}_0\mid {\mathrm{A}}^T\mathrm{y})\propto f{\mathrm{w}}_1({\mathrm{A}}^T\mathrm{y}\mid \gamma {\stackrel{‒}{\mathfrak{m}}}_0)f\left(\gamma {\stackrel{‒}{\mathfrak{m}}}_0\right)\propto \exp \left\{-\frac{1}{2{\sigma }^2}{(\mathrm{y}-{\mathrm{Z}}_{{\stackrel{‒}{\mathfrak{m}}}_0}{{\gamma }_{\stackrel{‒}{\mathfrak{m}}}}_0)}^T{\mathbf{P}}_x(\mathrm{y}-{\mathrm{Z}}_{{\stackrel{‒}{\mathfrak{m}}}_0}{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0})-\frac{1}{2}{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0}^T{\mathcal{G}}_{{\stackrel{‒}{\mathfrak{m}}}_0}^{-1}{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0}\right\}.$$

Therefore, the restricted posterior mode estimate of ${\gamma }_{{\overline{\mathfrak{m}}}_0}$ is the solution to the following minimization problem:

$$\min \left\{(\mathrm{y}-{\mathrm{Z}}_{{\stackrel{‒}{\mathfrak{m}}}_0}{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0})+{\sigma }^2{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0}^T{\mathcal{G}}_{{\stackrel{‒}{\mathfrak{m}}}_0}^{-1}{\gamma }_{{\stackrel{‒}{\mathfrak{m}}}_0}\right\}.$$ (16)

In practice, since the true random effects ${\overline{\mathfrak{m}}}_0$ are unknown, the formulation (16) does not help us estimate γ. To overcome this difficulty, note that ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}{\gamma }_{{\overline{\mathfrak{m}}}_0}={\mathbf{Z}}_{\gamma }$ and ${\gamma }_{{\overline{\mathfrak{m}}}_0}^T{\mathcal{G}}_{{\overline{\mathfrak{m}}}_0}^{-1}{\gamma }_{{\overline{\mathfrak{m}}}_0}={\gamma }^T{\mathcal{G}}^{+}\gamma$ with ${\mathcal{G}}^{+}$ the Moore-Penrose generalized inverse of $\mathcal{G}$. Thus, the objective function in (16) is rewritten as

$${(\mathrm{y}-\mathrm{Z}\gamma )}^T{\mathrm{P}}_x(\mathrm{y}-\mathrm{Z}\gamma )+{\sigma }^2{\gamma }^T{\mathcal{G}}^{+}\gamma ,$$

which no longer depends on the unknown ${\overline{\mathfrak{m}}}_0$. Observe that if the k-th random effect is a noise one, then the corresponding standard deviation is 0 and the coefficients γ_ik for all subjects i = 1, … ,N should equal to 0. This leads us to consider group variable selection strategy to identify true random effects. Define ${\gamma }_{.k}={\left({\sum }_{i=1}^N{\gamma }_{ik}^2\right)}^{1∕2},k=1,\cdots ,q_n$ and consider the following regularization problem

$$\frac{1}{2}{(\mathrm{y}-\mathrm{Z}\gamma )}^T{\mathrm{P}}_x(\mathrm{y}-\mathrm{Z}\gamma )+\frac{1}{2}{\sigma }^2{\gamma }^T{\mathcal{G}}^{+}\gamma +n{\Sigma }_{k=1}^{q_n}p{\lambda }_n(\gamma \cdot k),$$ (17)

where pλ_n(·) is the penalty function with regularization parameter λ_n ≥ 0. The penalty function here may be different from the one in Section 2. However, to ease the presentation, we use the same notation.

There are several advantages to estimating the random effects vector γ using the above proposed method (17). First, this method does not require knowing or estimating the fixed effects vector β, so it is easy to implement, and the estimation error of β has no impact on the estimation of γ. In addition, by using the group variable selection technique, the true random effects can be simultaneously selected and estimated.

In practice, the covariance matrix $\mathcal{G}$ and the variance σ² are both unknown. Thus, we replace ${\sigma }^{-2}\mathcal{G}$ with $\mathcal{M}$, where $\mathcal{M}=\mathrm{diag}\{M,\cdots ,M\}$ with M a proxy of G, yielding the following regularization problem

$${\tilde{Q}}_n^{\ast }\left(\gamma \right)=\frac{1}{2}{(\mathrm{y}-\mathrm{Z}\gamma )}^T{\mathbf{P}}_x(\mathrm{y}-{\mathrm{Z}}_{\gamma })+\frac{1}{2}{\gamma }^T{\mathcal{M}}^{-1}\gamma +n\sum _{k=1}^{q_n}p{\lambda }_n(\gamma \cdot k).$$ (18)

It is interesting to observe that the form of regularization in (18) includes the elastic net (Zou and Hastie, 2005) and the adaptive elastic net (Zou and Zhang, 2009) as special cases. Furthermore, the optimization algorithm for adaptive elastic net can be modified for minimizing (18).

3.2. Asymptotic properties

Minimizing (18) yields an estimate of γ, denoted by $\widehat{\gamma }$ . In this subsection, we study the asymptotic property of $\widehat{\gamma }$. Because γ is random rather than a deterministic parameter vector, the existing formulation for the asymptotic analysis of a regularization problem is inapplicable to our setting. Thus, asymptotic analysis of $\widehat{\gamma }$ is challenging.

Let $\mathbf{T}={\mathbf{Z}}^T{\mathbf{P}}_x\mathbf{Z}+{\sigma }^2{\mathcal{G}}^{+}$ and $\tilde{\mathbf{T}}={\mathbf{Z}}^T{\mathbf{P}}_x\mathbf{Z}+{\mathcal{M}}^{-1}$. Denote by ${\mathbf{T}}_{11}={\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}+{\sigma }^2{\left({\mathcal{G}}_{{\overline{\mathfrak{m}}}_0}\right)}^{-1}$, ${\mathbf{T}}_{22}={\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}$, and ${\mathbf{T}}_{12}={\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}$. Similarly, we can define submatrices ${\tilde{\mathbf{T}}}_{11}$, ${\tilde{\mathbf{T}}}_{22}$, and ${\tilde{\mathbf{T}}}_{12}$ by replacing ${\sigma }^{-2}\mathcal{G}$ with $\mathcal{M}$. Then it is easy to see that ${\tilde{\mathbf{T}}}_{12}={\mathbf{T}}_{12}$. Notice that if the oracle information of set ${\overline{\mathfrak{m}}}_0$ is available and $\mathcal{G}$ and σ² are known, then the Bayes estimate of the true random effects coefficient vector ${\gamma }_{{\overline{\mathfrak{m}}}_0}$ has the form ${\mathbf{T}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x\mathbf{y}$. Define ${\gamma }^{\ast }={({\left({\gamma }_1^{\ast }\right)}^T,\cdots ,{\left({\gamma }_N^{\ast }\right)}^T)}^T$ with ${\gamma }_j^{\ast }={({\gamma }_{j1}^{\ast },\cdots ,{\gamma }_{j{q}_n}^{\ast })}^T$ for j = 1, … ,N as the oracle-assisted Bayes estimate of the random effects vector. Then ${\gamma }^{\ast }{\overline{\mathfrak{m}}}_0^c=0$ and ${\gamma }^{\ast }{\overline{\mathfrak{m}}}_0={\mathbf{T}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x\mathbf{y}$. Correspondingly, define ${\tilde{\gamma }}^{\ast }$ as the oracle Bayses estimate with proxy matrix, i.e., ${\tilde{\gamma }}_{{\overline{\mathfrak{m}}}_0^c}^{\ast }=0$ and

$${\tilde{\gamma }}_{{\stackrel{‒}{\mathfrak{m}}}_0}^{\ast }={\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\stackrel{‒}{\mathfrak{m}}}_0}^T{\mathrm{P}}_x\mathrm{y}.$$ (19)

For k = 1, … , q_n, let ${\gamma }_{.k}^{\ast }={\left\{{\sum }_{j=1}^N{\left({\gamma }_{jk}^{\ast }\right)}^2\right\}}^{1∕2}$. Throughout we condition on the event

$${\Omega }^{\ast }=\{{\min }_{k\in {\mathfrak{m}}_0}{\gamma }^{\ast }\cdot k\ge \sqrt{N}{b}_0^{\ast }\}$$ (20)

with $b_0^{\ast }\in (0,{\min }_{\in {\mathfrak{m}}_0}{\sigma }_k)$ and ${\sigma }_k^2=\mathrm{var}\left({\gamma }_{jk}\right)$. The above event Ω* is to ensure that the oracle-assisted estimator ${\gamma }_{.k}^{\ast }∕\sqrt{N}$ of σ_k is not too negatively biased. We will need the following assumptions.

Condition 3. (A) The maximum eigenvalues satisfy ${\Lambda }_{max}\left({\mathbf{Z}}_{i}G{\mathbf{Z}}_i^T\right)\le c_3{s}_{2n}$ for all i = 1, … ,N, and the minimum and maximum eigenvalues of $m_n^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}$ and $G_{{\mathfrak{m}}_0}$ are bounded from below and above by c₃ and c₃⁻¹ respectively with m_n = max_1≤i≤N n_i, where c₃ is a positive constant. Further, assume that for some δ ∈ (0, ½),

$${\parallel {\tilde{\mathbf{T}}}_{11}^{-1}\parallel }_{\infty }\le \frac{\sqrt{N}{n}^{-1-\delta }}{p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)},$$ (21)

$$\underset{j\in {\mathfrak{m}}_0^c}{\max }{\parallel {\tilde{Z}}_j^T{\mathbf{P}}_x{\mathbf{Z}}_{{\stackrel{‒}{\mathfrak{m}}}_0}{\tilde{\mathbf{T}}}_{11}^{-1}\parallel }_2<\frac{p_{{\lambda }_n}^{\prime }(0+)}{p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)},$$ (22)

where ${\tilde{\mathbf{Z}}}_j$ is the submatrix formed by the N columns of Z corresponding to the j-th random effect.

(B) It holds that ${\sup }_{\{t\ge \sqrt{N}{b}_0^{\ast }∕2\}}{p}_{{\lambda }_n}^{″}\left(t\right)=o\left(N^{-1}\right)$.

(C) The proxy matrix satisfies that ${\Lambda }_{min}(\mathcal{M}-{\sigma }^{-2}\mathcal{G})\ge 0$.

Condition 3(A) is about the design matrices X, Z, and covariance matrix $\mathcal{G}$. Since ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}$ is a block diagonal matrix and $\lim \sup \frac{{\max }_i{n}_i}{{\min }_i{n}_i}<\infty$, the components of ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}$ have magnitude of the order m_n = O(n/N). Thus, it is not very restrictive to assume that the minimum and maximum eigenvalues of ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}$ are both of the order mn. Condition (22) puts an upper bound on the correlation between noise covariates and true covariates. The upper bound of (22) depends on the penalty function. Note that for concave penalty we have $p_{{\lambda }_n}^{\prime }(0+)∕p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)>1$, whereas for L₁ penalty $p_{{\lambda }_n}^{\prime }(0+)∕p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)=1$. Thus, concave penalty relaxes (22) when compared with the L₁ penalty. Condition 3(B) is satisfied by many commonly used penalties with appropriately chosen λ_n, for example, L₁ penalty, SCAD penaty, and SICA penalty with small a. Condition 3(C) is a restriction on the proxy matrix $\mathcal{M}$, which will be further discussed in the next subsection.

Let $\gamma ={({\gamma }_1^T,\cdots ,{\gamma }_N^T)}^T$ with γ_j = (γ_j1, … , γ_jqn)^T being an arbitrary (N_qn)-vector. Define ${\gamma }_{.k}={\left({\sum }_{j=1}^N{\gamma }_{jk}^2\right)}^{1∕2}$ for each k = 1, … , q_n. Let

$$\mathfrak{m}\left(\gamma \right)=\{k\in \{1,\cdot ,q_n\}:\gamma \cdot k\ne 0\}.$$ (23)

Theorem 2 below shows that there exists a local minimizer of ${\tilde{Q}}_n^{\ast }\left(\gamma \right)$ defined in (18) whose support is the same as the true one ${\overline{\mathfrak{m}}}_0$ and that this local minimizer is close to the estimator ${\tilde{\gamma }}^{\ast }$.

Theorem 2. Assume that Conditions 1 and 3 hold, $b_0^{\ast }{n}^{\delta }∕\sqrt{N}\to \infty$, $\log \left(N{q}_n\right)=o(n^2{\lambda }_n^2∕\left(N{s}_{2n}{m}_n\right))$, and $n^2{\lambda }_n^2∕\left(N{m}_n{s}_{2n}\right)\to \infty$ as n → ∞. Then, with probability tending to 1, there exists a strict local minimizer $\widehat{\gamma }\in {\mathbf{R}}^{N{q}_n}$ of ${\tilde{Q}}_n^{\ast }\left(\gamma \right)$ such that

$$\mathfrak{m}\left(\widehat{\gamma }\right)={\mathfrak{m}}_0\text{and}\underset{k\in {\mathfrak{m}}_0}{\max }{\left\{\frac{1}{N}\sum _{j=1}^N{({\widehat{\gamma }}_{jk}-{\tilde{\gamma }}_{jk}^{\ast })}^2\right\}}^{1∕2}<n^{-\delta },$$

where δ is defined in (21).

Using similar argument to that for Theorem 1, we can obtain that the dimensionality N_qn is also allowed to grow exponentially with sample size n under some growth conditions and with appropriately chosen λ_n. In fact, note that if the sample sizes n₁ = … N ≡ m_n/N, then the growth condition in Theorem 2 becomes $\log \left(N{q}_n\right)=o\left(n{s}_{2n}^{-1}{\lambda }_n^2\right)$. Since the lowest signal level in this case is $\sqrt{N}{b}_0^{\ast }$, if $b_0^{\ast }$ is a constant, a reasonable choice of tuning parameter would be of the order $\sqrt{N}{n}^{-\kappa }$ with some κ ∈ (0, ½). For s_2n = O(nν) with ν ∈ [0, ½) and Nn^1–2κ–ν → ∞, we obtain that N_qn can grow with rate exp(Nn^1−2κ−ν).

3.3. Choice of proxy matrix $\mathcal{M}$

Similarly as for the fixed effects selection and estimation, we discuss (21) and (22) in the following lemma.

Lemma 2. Assume that ${\parallel {\mathbf{T}}_{11}^{-1}\parallel }_{\infty }<\frac{\sqrt{N}{n}^{-1-\delta }}{p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)}(1-\frac{1}{\sqrt{\log n}})$ and

$${\parallel {\mathbf{T}}_{11}^{-1}{\tilde{\mathbf{T}}}_{11}-\mathbf{I}\parallel }_2\le {(1+{\sqrt{N\log ns}}_{2n}{n}^{1+\delta }{p}_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2){\parallel {\mathbf{T}}_{11}^{-1}\parallel }_2)}^{-1}.$$ (24)

Then (21) holds.

Similarly, assume that ${\max }_{j\in {\mathfrak{m}}_0^c}{\parallel {\tilde{\mathbf{Z}}}_j^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}{\mathbf{T}}_{11}^{-1}\parallel }_2<\frac{p_{{\lambda }_n}^{\prime }(0+)}{2p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)}$ with ${\tilde{\mathbf{Z}}}_j$ defined in (22) and

$${\parallel {\mathbf{T}}_{11}{\tilde{\mathbf{T}}}_{11}^{-1}-\mathbf{I}\parallel }_2\le 1.$$ (25)

Then (22) holds.

Conditions (24) and (25) put restrictions on the proxy matrix $\mathcal{M}$. Similarly to the discussions after Lemma 1, if $p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)\approx 0$, then these conditions become ${\parallel {\mathbf{T}}_{11}{\tilde{\mathbf{T}}}_{11}^{-1}-\mathbf{I}\parallel }_2<1$. If ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}$ dominates ${\sigma }^2{\mathcal{G}}_{{\overline{\mathfrak{m}}}_0}^{-1}$ by a larger magnitude, then conditions (24) and (25) are not restrictive, and choosing $\mathcal{M}=\left(\log n\right)\mathbf{I}$ should make these conditions as well as Condition 3(C) satisfied for large enough n.

We remark that using the proxy matrix $\mathcal{M}=\left(\log n\right)\mathbf{I}$ is equivalent to ignoring correlations among random effects. The idea of using diagonal matrix as a proxy of covariance matrix has been proposed in other settings of high dimensional statistical inference. For instance, the naive Bayes rule (or independence rule), which replaces the full covariance matrix in Fisher’s discriminant analysis with a diagonal matrix, has been demonstrated to be advantageous for high dimensional classifications both theoretically (Bickel and Levina, 2004; Fan and Fan, 2008) and empirically (Dudoit et al., 2002). The intuition is that although ignoring correlations gives only a biased estimate of covariance matrix, it avoids the errors caused by estimating a large amount of parameters in covariance matrix in high dimensions. Since the accumulated estimation error can be much larger than the bias, using diagonal proxy matrix indeed produces better results.

4. Simulation and application

In this section, we investigate the finite-sample performance of the proposed procedures by Monte Carlo simulations and an empirical analysis of a real data set. Throughout, the SCAD penalty with α = 3.7 (Fan and Li, 2001) is used. For each simulation study, we randomly simulate 200 data sets. Tuning parameter selection plays an important role in regularized methods. For fixed effect selection, both AIC and BIC-selectors (Zhang, Li and Tsai, 2010) are used to select the regularization parameter λ_n in (6). Our simulation results clearly indicate that the BIC-selector performs better than the AIC-selector for both the SCAD and the LASSO penalties. This is consistent with the theoretical analysis in Wang, Li and Tsai (2007). To save space, we report the results with the BIC-selector. Furthermore the BIC-selector is used for fixed effect selection throughout this section. For random effect selection, both AIC- and BIC-selectors are also used to select the regularization parameter λ_n in (18). Our simulation results imply that the BIC-selector outperforms the AIC-selector for the LASSO penalty, while the SCAD with AIC-selector performs better than the SCAD with BIC-selector. As a result, we use AIC-selector for the SCAD and BIC-selector for the LASSO random effect selection throughout this section.

Example 1. We compare our method with some existing ones in the literature under the same model setting as that in Bondell et al. (2010), where a joint variable selection method for fixed and random effects in linear mixed effects models is proposed. The underlying true model takes the following form with q = 4 random effects and d = 9 fixed effects

$$y_{ij}=b_{i1}+{\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+b_{i2}{z}_{ij1}+b_{i3}{z}_{ij2}+{\epsilon }_{ij},{\epsilon }_{ij}\sim i.i.d.N(0,1),$$ (26)

where the true parameter vector β₀ = (1, 1, 0, … , 0)^T , the true covariance matrix for random effects

$$G=\left(\begin{array}{ccc}\hfill 9\hfill & \hfill 4.8\hfill & \hfill 0.6\hfill \\ \hfill 4.8\hfill & \hfill 4\hfill & \hfill 1\hfill \\ \hfill 0.6\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right),$$

and the covariates x_ijk for k = 1, … , 9 z_ijl for l = 1, 2, 3 are generated independently from a uniform distribution over the interval [−2, 2]. So there are three true random effects and two true fixed effects. Following Bondell et al. (2010), we consider two different sample sizes N = 30 subjects and n_i = 5 observations per subject, and N = 60 and n_i = 10. Under this model setting, Bondell et al. (2010) compared their method with various methods in the literature, and simulations therein demonstrate that their method outperforms the competing ones. So we will only compare our methods with the one in Bondell et al. (2010).

In implementation, the proxy matrix is chosen as $\mathcal{M}=\left(\log n\right)\mathbf{I}$. We then estimate the fixed effects vector β by minimizing ${\tilde{Q}}_n\left(\beta \right)$, and the random effects vector γ by minimizing (18). To understand the effects of using proxy matrix $\mathcal{M}$ on the estimated random effects and fixed effects, we compare our estimates with the ones obtained by solving regularization problems (6) and (17) with the true value ${\sigma }^{-2}\mathcal{G}$.

Table 1 summarizes the results by using our method with the proxy matrix $\mathcal{M}$ and SCAD penalty (SCAD-P), our method with proxy matrix $\mathcal{M}$ and Lasso penalty (Lasso-P), our method with true ${\sigma }^{-2}\mathcal{G}$ and SCAD penalty (SCAD-T). When SCAD penalty is used, the local linear approximation (LLA) method proposed by Zou and Li (2008) is employed to solve these regularization problems. The rows “M-ALASSO” in Table 1 correspond to the joint estimation method by Bondell et al. (2010) using BIC to select the tuning parameter. As demonstrated in Bondell et al. (2010), the BICselector outperforms the AIC selector for M-ALASSO. We compare these methods by calculating the percentage of times the correct fixed effects are selected (%CF), and the percentage of times the correct random effects are selected (%CR). Since these two measures were also used in Bondell et al. (2010), for simplicity and fairness of comparison, the results for M-ALASSO in Table 1 are copied from Bondell et al. (2010).

Table 1. Fixed and random effects selection in Example 1 when d = 9 and q = 4.

Setting	Method	%CF	%CR
N = 30	Lasso-P	51	19.5
Hi = 5	SCAD-P	90	86
	SCAD-T	93.5	99
	M-ALASSO	73	79
N = 60	Lasso-P	52	50.5
ni = 10	SCAD-P	100	100
	SCAD-T	100	100
	M-ALASSO	83	89

It is seen from Table 1 that SCAD-P greatly outperforms the method with Lasso penalty as well as the M-ALASSO method. We also see that when the true covariance matrix ${\sigma }^{-2}\mathcal{G}$ is used, SCAD-T has almost perfect variable selection results. Using the proxy matrix $\mathcal{M}$ makes the results slightly inferior, but the difference vanishes when the sample size is large, i.e., N = 60, n_i = 10.

Example 2. In this example, we consider the case where the design matrices for fixed and random effects overlap. The sample size is fixed at n_i = 8 and N = 30, and the numbers for fixed and random effects are chosen to be d = 100 and q = 10, respectively. To generate the fixed effects design matrix, we first independently generate ${\tilde{\mathbf{X}}}_{ij}$ from N_d(0, Σ), where Σ = (σ_st) with σ_st = ρ^|s–t| and ρ ∈ (−1, 1). Then for the j-th observation of the i-th subject, we set $x_{ijk}=\mathit{I}({\tilde{x}}_{ijk}>0)$ for covariates k = 1 and d, and set $x_{ijk}={\tilde{x}}_{ijk}$ for all other values of k. Thus, 2 out of d covriates are discrete ones and the rest are continuous ones. Moreover, all covariates are correlated with each other. The covariates for random effects are the same as the corresponding ones for fixed effects, i.e., for the j-th observation of the i-th subject, we set z_ijk = x_ijk for k = 1, … , q = 10. Then the random effect covariates form a subset of fixed effect covariates.

The first six elements of fixed effects vector β₀ are (2, 0, 1.5, 0, 0, 1)^T and the remaining elements are all zero. The random effects vector γ is generated in the same way as in Example 1. So the first covariate is discrete and has both fixed effect and random effect. We consider different values of correlation level ρ, as shown in Table 2.

Table 2. Fixed and random effects selection and estimation in Example 2 when m = 8, N = 30 and design matrices for fixed and random effects overlap.

		Random Effects				Fixed Effects
Setting	Method	FNR (%)	FPR	MRL2	MRL1	FNR (%)	FPR	MRL2	MRL1
d = 100	Lasso-P	11.83	9.50	0.532	0.619	62.67	0.41	0.841	0.758
q = 10	SCAD-P	0.50	1.07	0.298	0.348	0.83	0.03	0.142	0.109
p = 0.3	SCAD-T	3.83	0.00	0.522	0.141	0.33	0.02	0.102	0.082
d = 100	Lasso-P	23.67	7.64	0.524	0.580	59.17	0.41	0.802	0.745
q = 10	SCAD-P	1.83	0.71	0.308	0.352	0.67	0.05	0.141	0.109
p = -0.3	SCAD-T	3.17	0.00	0.546	0.141	0.17	0.02	0.095	0.078
d = 100	Lasso-P	9.83	10.07	0.548	0.631	60.33	0.48	0.844	0.751
q = 10	SCAD-P	1.67	0.50	0.303	0.346	0.17	0.05	0.138	0.110
p = 0.5	SCAD-T	5.00	0.00	0.532	0.149	0.50	0.02	0.113	0.091

Since the dimension of random effects vector γ is much larger than the total sample size, as suggested at the beginning of Subsection 2.1, we start with the random effects selection by first choosing a relatively small tuning parameter λ and use our method in Section 3 to select important random effects. Then with the selected random effects, we apply our method in Section 2 to select fixed effects. To improve the selection results for random effects, we further use our method in Section 2 with the newly selected fixed effects to reselect random effects. This iterative procedure is applied to both Lasso-P and SCAD-P methods. For SCAD-T, since the true ${\sigma }^{-2}\mathcal{G}$ is used, it is unnecessary to use the iterative procedure and we apply our methods only once for both fixed and random effects selection and estimation.

We evaluate our new method by calculating the relative L₂ estimation loss, which is defined as

$$RL2\left(\widehat{\beta }\right)={\parallel \widehat{\beta }-{\beta }_0\parallel }_2∕{\parallel {\beta }_0\parallel }_2,$$

where $\widehat{\beta }$ is an estimate of the fixed effects vector β₀. Similarly, the relative L₁ estimation error of $\widehat{\beta }$ , denoted by $RL1\left(\widehat{\beta }\right)$, can be calculated by replacing the L₂-norm with the L₁-norm. For the random effects estimation, we define $RL2\left(\widehat{\gamma }\right)$ and $RL1\left(\widehat{\gamma }\right)$ in a similar way by replacing β₀ with the true γ in each simulation. We calculate the mean values of RL2 and RL1 in the simulations and denote them by MRL2 and MRL1 in Table 2. In addition to mean relative losses, we also calculate the percentages of missed true covaritates (FNR), as well as the percentages of falsely selected noise covariates (FPR), to evaluate the performance of proposed methods

From Table 2 we see that SCAD with the true covariance matrix has almost perfect variable selection results for fixed effects, while SCAD-P has highly comparable performance, for all three values of correlation level ρ. Both methods greatly outperform the Lasso-P method. For the random effects selection, both SCAD-P and SCAD-T perform very well with SCAD-T having slightly larger false negative rates. We remark that the superior performance of SCAD-P is partially because of the iterative procedure. In these high-dimensional settings, directly applying our random effects selection method in Section 3 produces slightly inferior results to the ones for SCAD-T in Table 2, but iterating once improves the results. We also see that as the correlation level increases, the performance of all methods become worse, but the SCAD-P is still comparable to SCAD-T and both perform very well in all settings.

Example 3. We illustrate our new procedures through an empirical analysis of a subset of data collected in the Multi-center AIDs Cohort Study. Details of the study design, method, and medical implications have been given by Kalsow et al. (1987). This data set comprises the human immunodeficiency virus (HIV) status of 284 homosexual men who were infected with HIV during the follow-up period between 1984 and 1991. All patients are scheduled to take measurements semiannually. However, due to the missing of scheduled visits and the random occurrence of HIV infections, there are an unequal number of measurements and different measurement times for each patients. The total number of observations is 1765.

Of interest is to investigate the relation between the mean CD4 percentage after the infection (y) and predictors smoking status (x₁, 1 for smoker and 0 for non-smoker), age at infection (x₂), and pre-HIV infection CD4 percentage (Pre-CD4 for short, x₃). To account for the effect of time, we use a five dimensional cubic spline b(t) = (b₁(t), b₂(t), … , b₅(t))^T . We take into account the two-way interactions b(t_ij)x_i3, x_i1x_i2, x_i1x_i3, and x_i2x_i3. These eight interactions together with variables b(t_ij ), x_i1, x_i2, and x_i3 give us 16 variables in total. We use these 16 variables together with an intercept to fit a mixed effects model with dimensions for fixed and random effects d = q = 17. The estimation results are listed in Table 3 with rows “Fixed” showing the estimated β_j’s for fixed effects, and rows “Random” showing the estimates ${\gamma }_{.k}∕\sqrt{N}$. The standard error for the null model is 11.45, and it reduces to 3.76 for the selected model. From Table 3, it can be seen that the baseline has time-variant fixed effect and Pre-CD4 has time-variant random effect. Smoking has fixed effect while age and Pre-CD4 have no fixed effects. The interactions smoking×Pre-CD4 and age×Pre-CD4 have random effects with smallest standard deviations among selected random effects. The boxplot of the selected random effects is shown in Figure 1.

Table 3. The estimated coefficients of fixed and random effects in Example 3.

	Intercept	b1(t)	62 (t)	63 (t)	64 (t)	65 (t)	x 1	x 2
Fixed	29.28	9.56	5.75	0	-8.32	0	4.95	0	0
Random	0	0	0	0	0	0	0	0	0
	b 1 (t)x 3	b2(t)x3	b3(t)x3	b4(t)x3	b5(t)x3	x1x2	x1x3	x2x3
Fixed	0	0	0	0	0	0	0	0
Random	0.163	0.153	0.057	0.043	0.059	0	0.028	0.055

Fig 1.

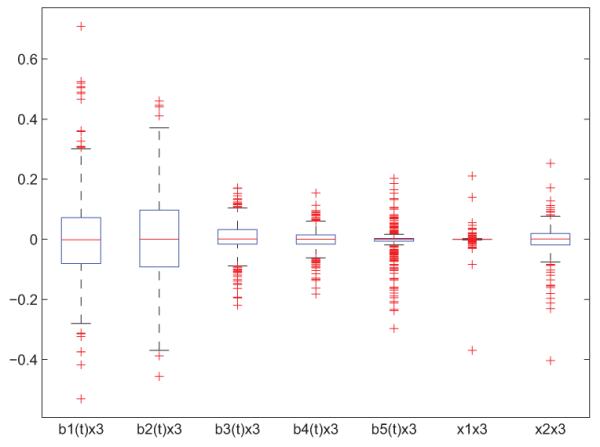
Boxplots of selected random effects. From left to right: b_i(t)x₃, i = 1, 2, … , 5, x₁x₃, x₂x₃, where x₁ is the smoking status, x₂ is the age at infection, x₃ is Pre-CD4 level, and b_i(t)’s are cubic spline basis functions of time.

Our results have close connections with the ones in Huang et al (2002) and Qu and Li (2006), where the former used bootstrap approach to test the significance of variables and the later proposed hypothesis test based on penalized spline and quadratic inference function approaches, for varying-coefficient models. Both papers revealed significant evidence for time-varying baseline, which is consistent with our discovery that basis functions b_j(t)’s have nonzero fixed effect coefficients. At 5% level, Huang et al (2002) failed to reject the hypothesis of constant Pre-CD4 effect (p-value 0.059), while Qu and Li (2006)’s test was weakly significant with p-value 0.045. Our results show that Pre-CD4 has constant fixed effect and time-varying random effect, which may provide an explanation on the small difference of p-values in Huang et al (2002) and Qu and Li (2006).

To further access the significance of selected fixed effects, we refit the linear mixed effects model with selected fixed and random effects using the Matlab function “nlmefit”. Based on the t-statistics from the refitted model, the intercept, the baseline functions b₁(t) and b₂(t) are all highly significant with t-statistics much larger than 7, while the t-statistics for b₄(t) and x₁ (smoking) are −1.026 and 2.216, respectively. This indicates that b₄(t) is insignificant and smoking is only weakly significant at 5% significance level. This result is different from those in Huang et al (2002) and Qu and Li (2006), where neither paper found significant evidence for smoking. A possible explanation is that by taking into account random effects and variable selection, our method has better discovery power.

5. Discussion

We have discussed the selection and estimation of fixed effects in Section 2, providing that the random effects vector has nonsingular covariance matrix, while we have discussed the selection and estimation of random effects in Section 3, providing that the dimension of fixed effects vector is smaller than the sample size. We have also illustrated our methods with numerical studies. In practical implementation, the dimensions of the random effects vector and fixed effects vector can be both much larger than the total sample size. In such case, we suggest an iterative way to select and estimate the fixed and random effects. Specifically, we can first start with the fixed effects selection using the penalized least squares by ignoring all random effects to reduce the number of fixed effects to below sample size. Then in the second step, with the selected fixed effects, we can apply our new method in Section 3 to select important random effects. Thirdly, with the selected random effects from the second step, we can use our method in Section 2 to further select important fixed effects. We can also iterate the second and third steps several times to improve the model selection and estimation results.

6. Proofs

Lemma 3 is proved in the online supplemental file.

Lemma 3. It holds that ${\mathbf{P}}_z={(I-{\mathbf{ZB}}_z)}^T{\mathcal{R}}^{-1}(I-{\mathbf{ZB}}_z)+{\mathbf{B}}_z^T{\mathcal{G}}^{-1}{\mathbf{B}}_z={(\mathcal{R}+\mathbf{Z}\mathcal{G}{\mathbf{Z}}^T)}^{-1}$

6.1. Proof of Theorem 1

Let ${\mathcal{N}}_0=\{\beta ={({\beta }_1^T,{\beta }_2^T)}^T:{\parallel {\beta }_1-{\beta }_{0,1}\parallel }_{\infty }\le n^{-\tau }{\left(\log n\right)}^{3∕2},{\beta }_2=0\in {\mathbf{R}}^{d_n-s_{1n}}\}$. We are going to show that under conditions 1 and 2, there exists a local minimizer $\widehat{\beta }\in {\mathcal{N}}_0\text{of}{\tilde{Q}}_n\left(\beta \right)$ with asymptotic probability one.

For a vector $\beta ={({\beta }_1,\cdots ,{\beta }_p)}^T,\text{let}{\stackrel{‒}{p}}_{{\lambda }_n}^{\prime }\left(\beta \right)$ be a vector of the same length whose j-th component is $p_{{\lambda }_n}^{\prime }\left(\mid {\beta }_j\mid \right)\mathrm{sgn}\left({\beta }_j\right),j=1,\cdots ,d_n$. By Lv and Fan (2009), the sufficient conditions for $\widehat{\beta }={({\widehat{\beta }}_1^T,0^T)}^T\in {\mathbf{R}}^{d_n}$ with ${\widehat{\beta }}_1\in {\mathbf{R}}^{s_{1n}}$ being a strict local minimizer of ${\tilde{Q}}_n\left(\beta \right)$ are

$$-{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z(\mathrm{y}-{\mathbf{X}}_1{\widehat{\beta }}_1)+n{\stackrel{‒}{p}}_{{\lambda }_n}^{\prime }\left({\widehat{\beta }}_1\right)=0,$$ (27)

$${\parallel {\mathrm{v}}_2\parallel }_{\infty }<n{p}_{{\lambda }_n}^{\prime }(0+),$$ (28)

$${\Lambda }_{\min }\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)>-n{p}_{{\lambda }_n}^{″}\left(\mid {\widehat{\beta }}_j\mid \right),j=1,\cdots ,s_{1n},$$ (29)

where ${\mathbf{v}}_2={\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z(\mathbf{y}-{\mathbf{X}}_1{\widehat{\beta }}_1)$. So we only need to show that with probability tending to 1, there exists a $\widehat{\beta }\in {\mathcal{N}}_0$ satisfying conditions (27) – (29).

We first consider (27). Since y = X₁β_0,1 + Z_γ + ε, equation (27) can be rewritten as

$${\widehat{\beta }}_1-{\beta }_{0,1}={\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )-n{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\stackrel{‒}{p}}_{{\lambda }_n}^{\prime }\left({\widehat{\beta }}_1\right).$$ (30)

Define a vector-valued continuous function $g\left({\beta }_1\right)={\beta }_1-{\beta }_{0,1}-{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z({\mathbf{Z}}_{\gamma }+\epsilon )+n{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\stackrel{‒}{p}}_{{\lambda }_n}^{\prime }\left({\beta }_1\right)$ with β₁ ∈ R^s_1n. It suffices to show that with probability tending to 1, there exists $\widehat{\beta }={({\widehat{\beta }}_1^T,{\widehat{\beta }}_2^T)}^T\in {\mathcal{N}}_0$ such that $g\left({\widehat{\beta }}_1\right)=0$. To this end, first note that

$${\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )\sim N(0,{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{P}}_z^{-1}{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}).$$

By Condition 2(B), the matrix $c_1{\tilde{\mathbf{P}}}_z-{\tilde{\mathbf{P}}}_z{\mathbf{P}}_z^{-1}{\tilde{\mathbf{P}}}_z={\tilde{\mathbf{P}}}_z\mathbf{Z}(c_1\mathcal{M}-{\sigma }^{-2}\mathcal{G}){\mathbf{Z}}^T{\tilde{\mathbf{P}}}_z\ge 0$, where A ≥ 0 means the matrix A is positive semi-definite. Therefore,

$$\mathbf{V}\equiv {\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{P}}_z^{-1}{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}\le c_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}.$$ (31)

Thus, the j-th diagonal component of matrix V in (31) is bounded from above by the j-th diagonal component of $c_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}$. Further note that by Condition 2(B), ${\tilde{\mathbf{P}}}_z^{-1}-c_1\left(\log n\right){\mathbf{P}}_z^{-1}\le \mathbf{Z}(\mathcal{M}-c_1\frac{\left(\log n\right)}{{\sigma }^2}\mathcal{G}){\mathbf{Z}}^T\le 0$. Recall that by linear algebra, if two positive definite matrices A and B satisfy A ≥ B, then it follows from the Woodbury formula that A⁻¹ ≤ B⁻¹. Thus, $\left(c_1\log n\right){\tilde{\mathbf{P}}}_z\ge {\mathbf{P}}_z$ and ${\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}\le \left(c_1\log n\right){\left({\mathbf{X}}_1^T{\mathbf{P}}_z{\mathbf{X}}_1\right)}^{-1}$. So by Condition 2(C), the diagonal components of V in (31) are bounded from above by O(n^−θ(log n)). This indicates that the variance of each component of the normal random vector ${\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )$ is bounded from above by O(n^−θ(log n)). Hence, by Condition 2(C),

$$\begin{array}{cc}\hfill & {\Vert {\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )\Vert }_{\infty }\hfill \\ \hfill & =O_p(n^{-\theta ∕2}\sqrt{\left(\log n\right)\left(\log s_{1n}\right))}=o_p(n^{-\tau }\left(\log n\right)).\hfill \end{array}$$ (32)

Next, by Condition 2(A), for any $\beta ={({\beta }_1,\cdots ,{\beta }_{d_n})}^T\in {\mathcal{N}}_0$ and large enough n, we can obtain that

$$\mid {\beta }_j\mid \ge \mid {\beta }_{0,j}\mid -\mid {\beta }_{0,j}-{\beta }_j\mid \ge a_n∕2,j=1,\cdots ,s_{1n}.$$ (33)

Since $p_{{\lambda }_n}^{\prime }\left(x\right)$ is a decreasing function in (0, ∞), we have ${\max }_{1\le j\le s_{1n}}{p}_{{\lambda }_n}^{\prime }\left(\mid {\beta }_j\mid \right)\le p_{{\lambda }_n}^{\prime }(a_n∕2)$. This together with Condition 2(C) ensures that

$$\begin{array}{cc}\hfill & {\Vert n{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{p}_{{\lambda }_n}^{-\prime }\left({\beta }_1\right)\Vert }_{\infty }\le {\Vert n{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}\Vert }_{\infty }{\Vert p_{{\lambda }_n}^{-\prime }\left({\beta }_1\right)\Vert }_{\infty }\hfill \\ \hfill & \le n{\Vert {\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}\Vert }_{\infty }{p}_{{\lambda }_n}^{\prime }(a_n∕2)=o\left(n^{-\tau }\right(\log n\left)\right).\hfill \end{array}$$ (34)

Combining (32) and (34) ensures that with probability tending to 1, if n is large enough,

$$\Vert {\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )+n{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{p}_{\lambda }^{-\prime }\left({\beta }_1\right){\Vert }_{\infty }\le n^{-\tau }\left(\log n\right).$$

Applying the Miranda’s existence theorem (Vrahatis, 1989) to the function g(β₁) ensures that there exists a vector ${\widehat{\beta }}_1\in {\mathbf{R}}^{s_{1n}}$ satisfying ${\parallel {\widehat{\beta }}_1-{\beta }_{0,1}\parallel }_{\infty }\le n^{-\tau }\log n$ such that $g\left({\widehat{\beta }}_1\right)=0$.

Now we prove that the solution to (27) satisfies (28). Plugging y = X₁β_0,1 + Zγ + ε into v in (28) and by (30), we obtain that

$${\mathbf{v}}_2={\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1({\beta }_{0,1}-{\widehat{\beta }}_1)+{\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z(\mathbf{Z}\gamma +\epsilon )={\mathbf{v}}_{2,1}+{\mathbf{v}}_{2,2}.$$

where ${\mathbf{v}}_{2,1}=[-{\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z+{\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z](\mathbf{Z}\gamma +\epsilon )$ and ${\mathbf{v}}_{2,2}={\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\stackrel{‒}{p}}_{{\lambda }_n}\left({\widehat{\beta }}_1\right)$. Since $(\mathbf{Z}\gamma +\epsilon )~N(0,{\mathbf{P}}_z^{-1})$, it is easy to see that v_2,1 has normal distribution with mean 0 and variance

$${\mathbf{X}}_2^T(\mathbf{I}-{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T){\tilde{\mathbf{P}}}_z{\mathbf{P}}_z^{-1}{\tilde{\mathbf{P}}}_z(\mathbf{I}-{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z){\mathbf{X}}_2.$$ (35)

Since ${\mathbf{P}}_z^{-1}\le c_1{\tilde{\mathbf{P}}}_z^{-1}$, $\mathbf{I}-{\tilde{\mathbf{P}}}_z^{1∕2}{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z^{1∕2}$ is a projection matrix, and ${\tilde{\mathbf{P}}}_z$ has eigenvalues less than 1, it follows that for the unit vector e_k,

$$\begin{array}{cc}\hfill {\mathbf{e}}_k^T\mathrm{var}\left({\mathbf{v}}_{2,1}\right){\mathbf{e}}_k& \le c_1{\mathbf{e}}_k^T{\mathbf{X}}_2^T({\tilde{\mathbf{P}}}_z-{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}{\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z){\mathbf{X}}_2{\mathbf{e}}_k\hfill \\ \hfill & \le c_1{\mathbf{e}}_k^T{\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_2{\mathbf{e}}_k\le {\mathbf{e}}_k^T{\mathbf{X}}_2^T{\mathbf{X}}_2{\mathbf{e}}_k=c_{1}n,\hfill \end{array}$$

where the last step is because each column of X is standardized to have L₂-norm $\sqrt{n}$. Thus, the diagonal elements of the covariance matrix of v_1,2 are bounded from above by c₁n. Therefore, for some large enough constant C > 0,

$$\begin{array}{cc}\hfill P\left({\Vert {\mathbf{v}}_{2,1}\Vert }_{\infty }\ge \sqrt{2\mathit{Cn}\log d_n}\right)& \le (d_n-s_{1n})P\left(\mid N(0,c_{1}n)\ge \sqrt{2\mathit{Cn}\log d_n}\right)\hfill \\ \hfill & =(d_n-s_{1n})\exp (-c_1^{-1}C\log d_n)\to 0.\hfill \end{array}$$

Thus, it follows from the assumption $\log d_n=o\left(n{\lambda }_n^2\right)$ that ${\parallel {\mathbf{v}}_{2,1}\parallel }_{\infty }=O_p\left(\sqrt{n\log d_n}\right)=o_p\left(n{p}_{{\lambda }_n}^{\prime }(0+)\right)$. Moreover, by Condition 2(B) and (C),

$${\Vert {\mathbf{v}}_{2,2}\Vert }_{\infty }\le n{\Vert {\mathbf{X}}_2^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1{\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)}^{-1}\Vert }_{\infty }{p}_{{\lambda }_n}^{\prime }(a_n∕2)<n{p}_{{\lambda }_n}^{\prime }(0+).$$

Therefore, the inequality (28) holds with probability tending to 1 as n → ∞.

Finally we prove that $\widehat{\beta }\in {\mathcal{N}}_0$ satisfying (27) and (28) also makes (29) hold with probability tending to 1. By (33) and Condition 2(A),

$$0\le -{\mathit{np}}_{{\lambda }_n}^{″}(\mid {\widehat{\beta }}_j\mid )\le -n{\sup }_{t\ge a_n∕2}{p}_{{\lambda }_n}^{″}\left(t\right)=o\left(n^{2\tau }\right).$$

On the other hand, by condition 2(C), ${\Lambda }_{\min }\left({\mathbf{X}}_1^T{\tilde{\mathbf{P}}}_z{\mathbf{X}}_1\right)\ge c_0{n}^{\theta }$. Since θ > 2τ , the inequality (34) holds with probability tending to 1 as n → ∞.

Combing the above results, we have shown that with probability tending to 1 as n → ∞, there exists $\widehat{\beta }\in {\mathcal{N}}_0$ which is a strict local minimizer of ${\tilde{Q}}_n\left(\beta \right)$. This concludes the proof.

6.2. Proof of Theorem 2

Let $\gamma ={({\gamma }_1^T,\cdots ,{\gamma }_N^T)}^T$ with ${\gamma }_j^T=({\gamma }_{j1},\cdots ,{\gamma }_{j{q}_n})$ a R^Nq_n-vector satisfying $\mathfrak{m}\left(\gamma \right)={\mathfrak{m}}_0$. Define $\mathbf{u}\left(\gamma \right)={({\mathbf{u}}_1^T,\cdots ,{\mathbf{u}}_N^T)}^T\in {\mathbf{R}}^{N{q}_n}$ with u_j = (u_j1, … , u_jqn)^T , where for j = 1, … ,N,

$${\lambda }_n{u}_{\mathit{jk}}=p_{{\lambda }_n}^{\prime }(\gamma \cdot k){\gamma }_{\mathit{jk}}∕\gamma \cdot k\text{if}k\in \mathfrak{M}\left(\gamma \right),$$ (36)

and λ_nu_jk = 0 if $k\notin \mathfrak{m}\left(\gamma \right)$. Here, ${\gamma }_{.k}={\left\{{\sum }_{j=1}^N{\gamma }_{jk}^2\right\}}^{1∕2}$. Let ${\tilde{\gamma }}^{\ast }$ be the Bayes estimate defined in (19). By Lv and Fan (2009), the sufficient conditions for γ ∈ R^q_nN with ${\gamma }_{{\overline{\mathfrak{m}}}_0^c}=0$ being a strict local minimizer of (18) are

$${\tilde{\gamma }}_{{\overline{\mathfrak{M}}}_0}^{\ast }-{\gamma }_{{\overline{\mathfrak{M}}}_0}=n{\lambda }_n{\tilde{\mathbf{T}}}_{11}^{-1}\mathbf{u}\left({\gamma }_{{\overline{\mathfrak{M}}}_0}\right),$$ (37)

$${\left({\Sigma }_{j=1}^N{w}_{\mathit{jk}}^2\right)}^{1∕2}<{\mathit{np}}_{{\lambda }_n}^{\prime }(0+),k\in {\mathfrak{M}}_0^c,$$ (38)

$${\Lambda }_{\min }\left({\tilde{\mathbf{T}}}_{11}\right)>n{\Lambda }_{\max }\left(-\frac{{\partial }^2}{\partial {\gamma }_{\overline{{\mathfrak{M}}_0}}^2}\left({\Sigma }_{j=1}^{\mathit{qn}}{p}_{{\lambda }_n}\right(\gamma \cdot k\left)\right)\right),$$ (39)

where $\mathbf{w}\left(\gamma \right)={({\mathbf{w}}_1^T,\cdots ,{\mathbf{w}}_N^T)}^T\in {\mathbf{R}}^{N{q}_n}$ with w_j = (w_j1, … , w_jqn)^T , and

$$\mathbf{w}\left(\gamma \right)={\mathbf{Z}}^T{\mathbf{P}}_x(\mathbf{y}-\mathbf{Z}\gamma )-{\mathcal{M}}^{-1}\gamma .$$ (40)

We will show that, under Conditions 1 and 3, the above (37) – (39) are satisfied with probability tending to 1 in a small neighborhood of ${\tilde{\gamma }}^{\ast }$.

In general, it is not always guaranteed that (37) has a solution. We first show that under Condition 3, there exists a vector ${\widehat{\gamma }}^{\ast }$ with $\mathfrak{m}\left({\widehat{\gamma }}^{\ast }\right)={\mathfrak{m}}_0$ such that ${\widehat{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }$ makes (37) hold. To this end, we constrain the objective function ${\tilde{Q}}_n^{\ast }\left(\gamma \right)$ defined in (18) on the (Ns_n2)-dimensional subspace $\mathcal{B}=\{\gamma \in {\mathbf{R}}^{q_{n}N}:{\gamma }_{{\overline{\mathfrak{m}}}_0^c=0}\}\text{of}{\mathbf{R}}^{q_{n}N}$. Next define

$$\begin{array}{c}\hfill {\mathcal{N}}_1=\{\gamma ={({\gamma }_{11},\cdots ,{\gamma }_{1q_n},\cdots ,{\gamma }_{N1},\cdots ,\gamma N_{q_n})}^T\in \mathcal{B}:\hfill \\ \hfill {\max }_{k\in {\mathfrak{M}}_0}{\left\{{\Sigma }_{j=1}^N{({\gamma }_{\mathit{jk}}-{\tilde{\gamma }}_{\mathit{jk}}^{\ast })}^2\right\}}^{1∕2}\le \sqrt[]{N}{n}^{-\delta }\}.\hfill \end{array}$$

For any $\tilde{\gamma }\in {\mathcal{N}}_1$ and each $k\in {\mathfrak{m}}_0$, we have

$$\begin{array}{cc}\hfill & {\Vert \tilde{\gamma }-{\tilde{\gamma }}^{\ast }\Vert }_{\infty }\le \underset{k\in {\mathfrak{M}}_0}{\overset{\max }{}}{\left\{\sum _{j=1}^N{({\gamma }_{\mathit{jk}}-{\tilde{\gamma }}_{\mathit{jk}}^{\ast })}^2\right\}}^{1∕2}\le \sqrt[]{N}{n}^{-\delta },\text{and}\hfill \\ \hfill & {\tilde{\gamma }}_{{\cdot }_k}^{\ast }={\left\{\sum _{j=1}^N{\left({\tilde{\gamma }}_{\mathit{jk}}^{\ast }\right)}^2\right\}}^{1∕2}\le {\left\{\sum _{j=1}^N{({\tilde{\gamma }}_{\mathit{jk}}^{\ast }-{\tilde{\gamma }}_{\mathit{jk}})}^2\right\}}^{1∕2}+{\left\{\sum _{j=1}^N{\left({\tilde{\gamma }}_{\mathit{jk}}\right)}^2\right\}}^{1∕2}\le \sqrt[]{N}{n}^{-\delta }+\tilde{\gamma }{\cdot }_k.\hfill \end{array}$$ (41)

Note that by Condition 3(C), we have ${\tilde{\mathbf{T}}}_{11}^{-1}\ge {\mathbf{T}}_{11}^{-1}$. Thus it can be derived using linear algebra and the definitions of ${\tilde{\gamma }}_{.k}^{\ast }$ and ${\gamma }_{.k}^{\ast }$ that ${\tilde{\gamma }}_{.k}^{\ast }\ge {\gamma }_{.k}^{\ast }$. Since we condition on the event Ω* in (20), it is seen that for large enough n,

$$\tilde{\gamma }{\cdot }_k\ge \tilde{\gamma }{.}_k^{\ast }-\sqrt[]{N}{n}^{-\delta }\ge \gamma {\cdot }_k^{\ast }-\sqrt[]{N}{n}^{-\delta }\ge \sqrt[]{N}{b}_0^{\ast }∕2$$ (42)

for $k\in {\mathfrak{m}}_0$ and $\tilde{\gamma }\in {\mathcal{N}}_1$. Thus, in view of the definition of u(γ) in (36), for $k\in {\mathfrak{m}}_0$, we have

$${\Vert {\lambda }_n\mathbf{u}\left({\tilde{\gamma }}_{{\overline{\mathfrak{M}}}_0}\right)\Vert }_{\infty }\le {\max }_{k\in {\mathfrak{M}}_0}{p}_{{\lambda }_n}^{\prime }\left(\tilde{\gamma }{\cdot }_k\right)\le p_{{\lambda }_n}^{\prime }(\sqrt[]{N}{b}_0^{\ast }∕2)$$

where the last step is because $p_{{\lambda }_n}^{\prime }\left(t\right)$ is decreasing in t ∈ (0, ∞) due to the concavity of p_λn(t). This together with (21) in Condition 3 ensures

$${\Vert n{\lambda }_n{\tilde{\mathbf{T}}}_{11}^{-1}\mathbf{u}({\tilde{\gamma }}_{{\overline{\mathfrak{M}}}_0}\Vert }_{\infty }\le n{\Vert {\tilde{\mathbf{T}}}_{11}^{-1}\Vert }_{\infty }{p}_{{\lambda }_n}^{\prime }(\sqrt[]{N}{b}_0^{\ast }∕2)\le \sqrt[]{N}{n}^{-\delta }.$$ (43)

Now define the vector-valued continuous function $\Psi \left(\xi \right)=\xi -{\tilde{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }-n{\lambda }_n{\tilde{\mathbf{T}}}_{11}^{-1}\mathbf{u}\left(\xi \right)$, with ξ a R^Ns_2n-vector. Combining (41) and (43) and applying Miranda’s existence theorem (Vrahatis, 1989) to the function Ψ(ξ), we conclude that there exists ${\widehat{\gamma }}^{\ast }\in {\mathcal{N}}_1$ such that ${\widehat{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }$ is a solution to equation (37).

We next show that ${\widehat{\gamma }}^{\ast }$ defined above indeed satisfies (39). Since ${\widehat{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }\in {\mathcal{N}}_1$, by (42) we have ${\widehat{\gamma }}_{.k}^{\ast }>\sqrt{N}{b}_0^{\ast }∕2$ for $k\in {\mathfrak{m}}_0$. Since pλ_n(t) is concave in t ∈ [0, ∞), we know that $-p_{{\lambda }_n}^{\prime }\left(t\right)$ is negative and increasing in (0, ∞). Note that for any vector x,

$$\frac{{\partial }^2}{\partial {\mathrm{x}}^2}{p}_{{\lambda }_n}(\Vert \mathrm{x}{\Vert }_2)=p_{{\lambda }_n}^{″}(\Vert \mathrm{x}{\Vert }_2)\frac{{\mathrm{xx}}^T}{\Vert \mathrm{x}{\Vert }_2}+p_{{\lambda }_2}^{\prime }(\Vert \mathrm{x}{\Vert }_2)(\frac{1}{\Vert \mathrm{x}{\Vert }_2}-\frac{{\mathrm{xx}}^T}{\Vert \mathrm{x}{\Vert }_2^3}).$$ (44)

Thus,

$${\Lambda }_{\max }(-\frac{{\partial }^2}{\partial {\mathrm{x}}^2}{p}_{{\lambda }_n}(\Vert \mathrm{x}{\Vert }_2\left)\right)\le -p_{{\lambda }_n}^{″}(\Vert \mathrm{x}{\Vert }_2)+\frac{p_{{\lambda }_n}^{\prime }(\Vert \mathrm{x}{\Vert }_2)}{\Vert \mathrm{x}{\Vert }_2}-\frac{p_{{\lambda }_n}^{\prime }(\Vert \mathrm{x}{\Vert }_2)}{\Vert \mathrm{x}{\Vert }_2}=-p_{{\lambda }_n}^{″}(\Vert \mathrm{x}{\Vert }_2).$$

This together with (20) indicates that with probability tending to 1, the maximum eigenvalue of the matrix $-\frac{{\partial }^2}{\partial {\gamma }_{{\overline{\mathfrak{m}}}_0}^2}\left({\sum }_{j=1}^{q_n}{p}_{{\lambda }_n}\left({\widehat{\gamma }}_{.k}^{\ast }\right)\right)$ is less than

$${\max }_{j\in {\mathfrak{M}}_0}(-p_{{\lambda }_n}^{″}({\widehat{\gamma }}_{\cdot j}^{\ast }\left)\right)=o\left(N^{-1}\right)=o(m_n∕n).$$

Further, by Condition 3 (A) and (B), $\frac{1}{n}{\Lambda }_{\min }\left({\tilde{\mathbf{T}}}_{11}\right)=\frac{1}{n}{\Lambda }_{\min }\left({\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}\right)\ge c_3\frac{m_n}{n}$. Thus, the maximum eigenvalue of the matrix $-\frac{{\partial }^2}{\partial {\gamma }_{{\overline{\mathfrak{m}}}_0}^2}\left({\sum }_{j=1}^{q_n}{p}_{{\lambda }_n}\left({\widehat{\gamma }}_{.k}^{\ast }\right)\right)$ is less than $n^{-1}{\Lambda }_{\min }\left({\tilde{\mathbf{T}}}_{11}\right)$ with asymptotic probability 1, and (39) holds for ${\widehat{\gamma }}^{\ast }$

It remains to show that ${\widehat{\gamma }}^{\ast }$ satisfies (38). Let $\widehat{\mathbf{v}}={\widehat{\gamma }}^{\ast }-{\tilde{\gamma }}^{\ast }$. Since ${\widehat{\gamma }}^{\ast }$ is a solution to (37), we have $\widehat{\mathbf{v}}=n{\lambda }_n{\tilde{\mathbf{T}}}_{11}^{-1}\mathbf{u}\left({{\widehat{\gamma }}_{\overline{\mathfrak{m}}}}_0\right)$. In view of (40), we have

$$\begin{array}{cc}\hfill & \mathbf{w}\left({\widehat{\gamma }}_{{\overline{\mathfrak{M}}}_0^c}^{\ast }\right)=\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T-{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}^T\right){\mathbf{P}}_x\mathbf{y}+{\tilde{\mathbf{T}}}_{12}^T{\widehat{\mathbf{v}}}_{{\overline{\mathfrak{M}}}_0}\hfill \\ \hfill & =\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T-{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}^T\right){\mathbf{P}}_x(\mathbf{Z}\gamma +\epsilon )+{\tilde{\mathbf{T}}}_{12}^T{\widehat{\mathbf{v}}}_{{\overline{\mathfrak{M}}}_0}\equiv {\tilde{\mathbf{w}}}_1+{\tilde{\mathbf{w}}}_2.\hfill \end{array}$$ (45)

Since $\mathbf{Z}\gamma +\epsilon ~N(0,{\mathbf{P}}_z^{-1})$, we obtain that ${\tilde{\mathbf{w}}}_1~N(0,\mathbf{H})$ with $\mathbf{H}=({\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}^T-{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T){\mathbf{P}}_x{\mathbf{P}}_z^{-1}{\mathbf{P}}_x({\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}-{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}{\tilde{\mathbf{T}}}_{11}^{-1}{\tilde{\mathbf{T}}}_{12})$. Note that ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}$ is a block diagonal matrix and the i-th block matrix has size n_i×(q_n–s_2n). By Condition 3(A), it is easy to see that ${\Lambda }_{\max }\left(\mathbf{Z}\mathcal{G}{\mathbf{Z}}^T\right)\le {\max }_{1\le i\le N}{\Lambda }_{\max }\left({\mathbf{Z}}_{i}G{Z}_i^T\right)\le c_1{s}_{2n}$. Thus, ${\mathbf{P}}_x{\mathbf{P}}_z^{-1}{\mathbf{P}}_x={\mathbf{P}}_x({\sigma }^2\mathbf{I}+\mathbf{Z}\mathcal{G}{\mathbf{Z}}^T){\mathbf{P}}_x\le ({\sigma }^2+c_1{s}_{2n}){\mathbf{P}}_x^2=({\sigma }^2+c_1{s}_{2n}){\mathbf{P}}_x$. Further, it follows from ${\tilde{\mathbf{T}}}_{12}={\mathbf{T}}_{12}$ and ${\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0}\le {\tilde{\mathbf{T}}}_{11}$ that

$$\begin{array}{cc}\hfill & \mathbf{H}\le ({\sigma }^2+c_1{s}_{2n})\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T-{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}^T\right){\mathbf{P}}_x\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}-{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}{\tilde{\mathbf{T}}}_{11}^{-1}{\tilde{\mathbf{T}}}_{12}\right)\hfill \\ \hfill & ({\sigma }^2+c_1{s}_{2n})\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}+{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}{\tilde{\mathbf{T}}}_{11}^{-1}{\tilde{\mathbf{T}}}_{12}-2{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0}{\tilde{\mathbf{T}}}_{11}^{-1}{\tilde{\mathbf{T}}}_{12}\right)\hfill \\ \hfill & \le ({\sigma }^2+c_1{s}_{2n})\left({\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}-{\tilde{\mathbf{T}}}_{12}^T{\tilde{\mathbf{T}}}_{11}^{-1}{\tilde{\mathbf{T}}}_{12}\right)\le ({\sigma }^2+c_1{s}_{2n}){\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{M}}}_0^c}.\hfill \end{array}$$

Thus, the i-th diagonal element of H is bounded from above by the i-th diagonal element of $({\sigma }^2+c_1{s}_{2n}){\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}^T{\mathbf{P}}_x{\mathbf{Z}}_{{\overline{\mathfrak{m}}}_0^c}$, and thus bounded by ${\tilde{c}}_1{s}_{2n}{m}_n$ with ${\tilde{c}}_1$ some positive constant. Therefore by the normality of ${\tilde{\mathbf{w}}}_1$ we have

$$\begin{array}{cc}\hfill & P\left(\Vert {\tilde{\mathbf{w}}}_1{\Vert }_{\infty }\ge {\left\{2{\tilde{c}}_1{s}_{2n}{m}_n\log \right(N(q_n-s_{2n})\left)\right\}}^{1∕2}\right)\hfill \\ \hfill & \ge N(q_n-s_{2n})P(\mid N(0,{\tilde{c}}_1{s}_{2n}{m}_n)\mid \le \left\{2{\tilde{c}}_1{s}_{2n}{m}_n\log \right(N(q_n-s_{2n})\left)\right\}{}^{1∕2})\hfill \\ \hfill & =O(\left(\log \right(N(q_n-s_{2n})\left)\right){}^{-1∕2})=o(1).\hfill \end{array}$$

Therefore, ${\parallel {\tilde{\mathbf{w}}}_1\parallel }_{\infty }=o_p\left({\left\{s_{2n}{m}_n\log (N(q_n-s_{2n})\right\}}^{1∕2}\right)=o_p\left(n{N}^{-1∕2}{\lambda }_n\right)$ and

$$\underset{j>s_{2n}}{\max }{\left\{{\Sigma }_{k=1}^N{\tilde{w}}_{1,\mathit{jk}}^2\right\}}^{\frac{1}{2}}\le \sqrt[]{N}\Vert {\tilde{\mathrm{w}}}_1{\Vert }_{\infty }=o_p\left(n{\lambda }_n\right)=o_p\left(1\right){\mathit{np}}_{{\lambda }_n}^{\prime }(0+),$$ (46)

where ${\tilde{w}}_{1,jk}$ is the ((j – 1)q_n + k)-th element of N_qn-vector ${\tilde{\mathbf{w}}}_1$.

Now we consider ${\tilde{\mathbf{w}}}_2$. Define ${\tilde{\mathbf{Z}}}_j$ as the submatrix of Z formed by columns corresponding to the j-th random effect. Then, for each j = s_2n +1, … , q_n, by Condition 3(A) we obtain that

$${\left\{\sum _{k=1}^N{\tilde{w}}_{2,\mathit{jk}}^2\right\}}^{\frac{1}{2}}=n{\lambda }_n{\Vert {\tilde{\mathrm{Z}}}_j^T{\mathrm{P}}_x{\mathrm{Z}}_{{\overline{\mathfrak{M}}}_0}{\tilde{\mathrm{T}}}_{11}^{-1}\mathrm{u}\left({\widehat{\gamma }}_{{\overline{\mathfrak{M}}}_0}^{\ast }\right)\Vert }_2\le n{\Vert {\lambda }_n\mathrm{u}\left({\widehat{\gamma }}_{{\overline{\mathfrak{M}}}_0}^{\ast }\right)\Vert }_2{\Vert {\tilde{\mathrm{Z}}}_j^T{\mathrm{P}}_x{\mathrm{Z}}_{{\overline{\mathfrak{M}}}_0}{\tilde{\mathrm{T}}}_{11}^{-1}\Vert }_2$$

where ${\tilde{w}}_{2,jk}$ is the ((j – 1)q_n + k)-th element of N_qn-vector ${\tilde{\mathbf{w}}}_2$. Since ${\widehat{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }\in {\mathcal{N}}_1$, by (36), (42) and the decreasing property of $p_{{\lambda }_n}^{\prime }(\cdot )$ we have ${\parallel {\lambda }_n\mathbf{u}\left({\widehat{\gamma }}_{{\overline{\mathfrak{m}}}_0}^{\ast }\right)\parallel }_2\le p_{{\lambda }_n}^{\prime }(\sqrt{N}{b}_0^{\ast }∕2)$. By (22) in Condition 3(A),

$$\underset{j\le s_{2n}+1}{\max }{\left\{{\Sigma }_{k=1}^N{\tilde{w}}_{2,\mathit{jk}}^2\right\}}^{\frac{1}{2}}<{\mathit{np}}_{{\lambda }_n}^{\prime }(0+).$$

Combing the above result for ${\tilde{\mathbf{w}}}_2$ with (45) and (46), we have shown that (38) holds with asymptotic probability one. This completes the proof.