A comparative study of variable selection methods in the context of developing psychiatric screening instruments

Abstract

The development of screening instruments for psychiatric disorders involves item selection from a pool of items in existing questionnaires assessing clinical and behavioral phenotypes. A screening instrument should consist of only a few items and have good accuracy in classifying cases and non-cases. Variable/item selection methods such as Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net, Classification and Regression Tree, Random Forest, and the two-sample t-test can be used in such context. Unlike situations where variable selection methods are most commonly applied (e.g., ultra high-dimensional genetic or imaging data), psychiatric data usually have lower dimensions and are characterized by the following factors: correlations and possible interactions among predictors, unobservability of important variables (i.e., true variables not measured by available questionnaires), amount and pattern of missing values in the predictors, and prevalence of cases in the training data. We investigate how these factors affect the performance of several variable selection methods and compare them with respect to selection performance and prediction error rate via simulations. Our results demonstrated that: (1) for complete data, LASSO and Elastic Net outperformed other methods with respect to variable selection and future data prediction, and (2) for certain types of incomplete data, Random Forest induced bias in imputation, leading to incorrect ranking of variable importance.We propose the Imputed-LASSO combining Random Forest imputation and LASSO; this approach offsets the bias in Random Forest and offers a simple yet efficient item selection approach for missing data. As an illustration, we apply the methods to items from the standard Autism Diagnostic Interview-Revised version.

1. Introduction

In psychiatry, where there are no blood tests or other biological measures for diagnosing illness, diagnosis is based on questionnaires consisting of items that probe subjects’ behaviors and feelings. For most psychiatric conditions, typically there exist one or more standardized diagnostic instruments. For example, Autism Spectrum Disorder (ASD) can be diagnosed with the interview-based Autism Diagnostic Interview-Revised (ADI-R) [1], the self-report Social Communication Questionnaire (SCQ) [2], or the Autism Diagnostic Observation Schedule (ADOS) [3], which is based on clinical observations. These instruments consist of numerous items, are time-consuming, and often require trained persons to administer them. For these reasons, they are not appropriate for screening purposes.

Researchers are often interested in the development of brief screening tools based on questions or items from existing diagnostic instruments (see, e.g., [4] using various machine learning classifiers). The purpose of such tools could be, for example, to rapidly identify potential participants for research studies, to be included as a subsection in a national survey, or to offer a screening instrument to be used universally in general clinical practice. Therefore, only a few items need to be selected from existing questionnaires for inclusion in a brief screening instrument.

Multiple statistical methods can be used for item selection. In this paper, we focus on the following five commonly used feature selection methods: (1) two-sample t-test [5], (2) Classification and Regression Tree (CART) [6]; (3) Random Forest [7]; (4) Least Absolute Shrinkage and Selection Operator (LASSO) [8]; and (5) Elastic Net [9]. The first method is a typical item selection method in psychometric research. The latter four methods are widely applied in genetic research, imaging studies, and other high-dimensional feature selection setups [10, 11], and a tremendous amount of research has been carried out to assess their performance in cases where the number of variables is exponentially higher than the number of subjects, that is, the large-p-small-n problem (or n ≪ p), [12–14]. In addition to those five methods, we propose a new method called Imputed-LASSO, which combines imputation based on Random Forest and LASSO, as a sixth method targeting variable selection on data with missing values in the predictors.

Here, we are interested in the performance of those methods in a typical situation of developing screening instruments in psychiatric research: the data sets usually consist of around a hundred items (often coded as 0, 1, 2, 3, etc) and tens to hundreds of subjects; the number of items p is typically smaller than the number of subjects n. However, the characteristics of the data in this situation could be quite different from those in genomic studies and present distinct challenges. First, subjects often omit one or more of the items in a questionnaire – this could create problems with methods that require complete observations, such as LASSO and Elastic Net. Second, often sets of items can be highly correlated because of attempting to measure the same aspects of a psychiatric condition. For example, the diagnostic instruments in autism try to assess two major aspects typical for this condition – social interactions/communications and repetitive/odd behaviors. Finally, although in many cases the more items in a diagnostic instrument, the higher the accuracy of the instrument, the final decision of the number of variables to be selected should be appropriate for inclusion in the screening tool under development, particularly depending on the purpose and the application of the individual instrument. For example, in order to develop a 5-min telephone-based screener for autism, approximately 10 items would be ideal to select from existing questionnaires (e.g., ADI-R, SCQ, etc).

In this paper, we investigate the performance of the abovementioned variable selection methods for the purposes of developing psychiatric screening instruments using simulations. Let Y denote the diagnostic status (Y = 1 for cases, and Y = 0 for non-cases), and let X be the vector of p observed predictors (i.e., the set of items to select from). We assume that the data-generating model is a logistic regression:

$$\text{logit}P(Y=1|\mathbf{X},\mathbf{Z})=\mathbf{Z}\mathit{\beta }$$ (1)

where Z indicates the set of true predictors, which might be a subset or a function of a subset of X, or it might contain variables that are not part of X.

It would appear that when attempting to shorten a diagnostic instrument, the target should be prediction accuracy, and thus, no subjective judgement should play a role in selecting the items that optimize these criteria. However, incorporation of expert knowledge, which cannot always be formally included in the analysis, is essential in developing such diagnostic tools, and therefore, we also focus on variable selection. We further explain the role of substantive area experts in Section 5. We compare the variable selection methods with respect to selection of true predictors and test classification errors, under different scenarios for Z from Equation (1), missing data patterns, and prevalence of cases in the training data.

We organize the paper as follows. Section 2 contains a brief summary of the five common variable selection methods listed previously. There we also introduce the proposed method of combining Random Forest and LASSO when there are missing values in the predictors. In Section 3, we present the simulation design for assessing the effect of various factors typically characterizing the data available for development of a screener. This section also gives the algorithm and criteria for comparing the methods. In Section 4, we show the simulation results and conduct a comparison between the methods. Section 5 reports the results from the application of the variable selection methods on real data from individuals with and without ASD diagnosis, who were interviewed with a full diagnostic instrument, and illustrates how the results from the simulation studies informed the process of shortening the measure. The paper concludes with a discussion in Section 6.

2. Variables selection methods

We first give a brief introduction of each of the five commonly used feature selection methods. In our context, a feature refers to an item from the questionnaires and we use these terms interchangeably.

Two-sample t-test is a classic method for prioritizing variables based on their importance in distinguishing between two groups. It tests how different two groups of subjects (e.g., cases and non-cases) are on an individual item, and items with the least significant differences can be eliminated. In psychometric studies, it is applied as a standard item selection method for the purpose of constructing tests for classifying groups of subjects, such as the criterion-keyed test [5]. Note that for other high-dimensional feature selection problems, it is not usually employed as a variable selection method but rather as a prescreener (e.g., [15]) with Sure Independence Screening property (i.e., in cases when p ≫n, it can reduce high dimensionality p to a scale p^* < n, while all important variables still remain with an overwhelming probability [16]). In terms of predicting the outcomes, a common way is to calculate a score based on the average or sum of the selected variables and to classify as cases subjects with scores higher than a certain cutoff point. The cutoff is usually determined by sensitivity/specificity analysis.

CART [6] is a nonparametric technique that selects variables parsimoniously by building a series of logical questions, in order to separate subjects into subsets and then classify (in classification) or predict (in regression) subjects’ outcomes within each subset. At each node, it recursively partitions the predictor space, searches for all possible partitions among those based on all possible features, and chooses the one that gives maximum reduction in ‘impurity’ for a new split at that node. There are different types of impurity measures, and the most commonly used ones are Gini index and cross entropy, which are defined by 2π(1 − π) and − π logπ − (1 − π) log(1 − π), respectively, for two-class classification problems, where π is the proportion of one of the classes. Different definitions of impurity in the sets yield different optimization criteria. An important benefit of the CART methodology is that it can detect interactions among features, as well as non-monotonic relations in predicting the outcome. In addition, the CART algorithm can handle missing values in a principled way by surrogate splits.

Random Forest [7] is based on CART, but rather than one tree, it grows a large number of trees (usually hundreds) to build a forest. It is random in two aspects: First, it takes a number of bootstrap samples from the original data and grows one tree on each sample; second, at each node within each tree, it randomly chooses a set of the candidate variables to split a new branch. The overall prediction/classification of the forest is derived by averaging the predictions/votes from the individual trees. The accuracy of prediction/classification can be estimated from the so-called out-of-bag (OOB) sample, which comprised observations that are in the original data but are not used when building one individual tree. The OOB error is the mean square error (for prediction) or misclassification error (for classification) averaged over observations from all trees for which they have been OOB. Random Forest often yields a favorable error rate, and it can assess variable importance by some internal measurements (e.g., [7, 17, 18]). Studies have illustrated that there is bias in Random Forest variable importance measures in situations where potential predictors vary in their scale of measurement or their number of categories [18]. Although this is not an issue in the current context, because items within a questionnaire are typically measured on the same scale, in cases where items have widely different number of categories, it is recommended ([18]) that the conditional framework of [19] be used instead. Finally, when there are missing data, Random Forest imputes the missing observations by a weighted average of the non-missing observations, where the weights are calculated by proximity, which measures the similarity between two subjects by the proportion of times they end up in a same final leaf [20].

LASSO [8] is a regularized regression method with L₁ penalty and is frequently used to handle largep-small-n problems. In addition to the restriction of the ordinary least squares, it adds constrains to the coefficient parameters, which shrinks the coefficients and sets some of them to be zero. In particular, it minimizes the residual sum of squares subject to an L₁ penalty term:

$$\mathit{\beta ̂}=\text{arg min}{\Vert \mathbf{Y}-\mathbf{X}\mathit{\beta }\Vert }_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1$$ (2)

where λ in Equation (2) is called tuning parameter and is often selected by cross-validation. This method has lower variance than regular regression models but is biased, and in order to compensate for the bias, when the shrinkage parameter is selected by a data-driven rule, LASSO tends to result in a more complex model then necessary; that is, it selects more ‘false positive’ variables [21]. LASSO is sign consistent if and (almost) only if an irrepresentable condition is satisfied; that is, LASSO consistently selects the true model with correct signs if and (almost) only if the ‘fake’ predictors that are not in the true model are irrepresentable by the true predictors [22]. LASSO has selection inconsistency if there is a group of highly correlated true variables; that is, LASSO tends to arbitrarily select only one correlated variable from the group [9, 23]. Finally, this method requires complete data, and in the case when some subjects are missing some of the predictors, LASSO works with the subset of cases that have no missing values. In the case of shortening a psychiatric diagnostic questionnaires, this is a serious disadvantage, as data used for such purposes rarely contain complete observations on all subjects.

Elastic Net [9] is similar to LASSO but is a subject to a weighted sum of L₁ and L₂ penalties; that is, it solves the following optimization problem:

$$\mathit{\beta ̂}=\text{arg min}{\Vert \mathbf{Y}-\mathbf{X}\mathit{\beta }\Vert }_2^2+{\lambda }_2{\Vert \mathit{\beta }\Vert }_2^2+{\lambda }_1{\Vert \mathit{\beta }\Vert }_1.$$ (3)

Denoting $\alpha =\frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}$ and λ = λ₁ + λ₂, Equation (3) is equivalent to

$$\mathit{\beta ̂}=\text{arg min}{\Vert \mathbf{Y}-\mathbf{X}\mathit{\beta }\Vert }_2^2+\lambda [\alpha {\Vert \mathit{\beta }\Vert }_2^2+(1-\alpha ){\Vert \mathit{\beta }\Vert }_1].$$ (4)

This method is less aggressive in reducing the number of selected correlated variables than LASSO and thus might include more variables in the model. It also encourages some grouping effects, meaning that strongly correlated predictors tend to be selected or not selected together. In the context of shortening a psychiatric diagnostic instrument, on the one hand, including more variables might be considered a disadvantage. On the other hand, because diagnostic instruments typically use many items to assess one or just a few latent constructs, items are expected to be correlated, and selecting a small number of correlated items together might be beneficial in the sense of improving reliability. Like LASSO, this method requires complete data on all subjects.

Imputed-LASSO is a method that we propose to address the shortcomings of LASSO in situations where large proportion of units have incomplete data, such as those typical in psychiatric research. This approach utilizes Random Forest to impute the missing data and obtains complete data on all units (subjects) [20]. It then uses LASSO to select variables based on the imputed (complete) data set.

3. Simulations design

In the context of developing screening instruments, the major questions of interest are the following. First, which method selects variables correctly (i.e., selects more true variables that are in the data-generating process, as well as fewer false positives). Second, which method predicts future data accurately (i.e., results in lower misclassification rate, and higher sensitivity and specificity, or area under the receiver operating characteristic curve (AUC)). In addition, various factors characterizing typical psychiatric data used for developing screening instruments may affect the selection of features and prediction performance of a variable selection method. Such factors are the following: (i) the correlation among predictors; (ii) possible interactions between the predictors in determining the outcome; (iii) unobservability of important variables (i.e., some true variables are not measured by available instruments); (iv) the amount and pattern of missing data in the predictors; and (v) the prevalence of cases in the data. We performed a simulation study to assess how the feature selection methods perform depending on the factors characterizing the available data.

3.1. Generating the predictors

Informed by research on mental disorders such as autism, we simulated a training data set (n = 400) and a test data set (n = 200). Let X_ij, i = 1, …, n subjects and j = 1, …, p (for p = 60 or 70) be the pool of predictor variables from which we want to select a subset. For all i = 1, …, n, and all j = 1, …, p, X_ij = 0, 1, 2 with probabilities π₀, π₁, π₂, respectively, $({\sum }_{k=0}^2{\pi }_k=1)$. Of the p predictor variables, the first 10, X₁, …, X₁₀, are true predictors, and X₁₁, …, X₅₀ are noises (also refer to as ‘fake’ predictors); these 60 variables are presumed observed when we fit the models. X₆₁, …, X₇₀ are additional predictors that might be a part of the data-generating process in some scenarios (to be further explained later); these variables are true predictors but are not observed. That is, they are omitted when we apply the variable selection methods. We consider six scenarios for the predictors X (see Table I for summary).

• C1. Independent: X₁, …, X₁₀ are true predictors; X₁₁, …, X₆₀ are noises; all variables are independent of each other.

• C2. Correlated (True, Noise): X₁, …, X₁₀ are true predictors and are independent of each other ; X₁₁, …, X₆₀ are noises that are independent of each other, but X₁₁, …, X₂₀ are pairwisely correlated with X₁, …, X₁₀, that is, Corr(X₁, X₁₁) = … = Corr.X₁₀, X₂₀) = ρ (ρ = 0.8).

• C3. Correlated (True, True): X₁, …, X₁₀ are true predictors, of which X₁, …, X₅ are mutually correlated (ρ = 0.75), X₆, …, X₁₀ are mutually correlated (ρ = 0.75), and the two blocks of items are independent; X₁₁, …, X₆₀ are independent noises.

• C4. Omitted interactions: As C1, but all two-way interactions of the 10 true predictors X₁, …, X₁₀ are added to the model generating the outcomes; the interactions are omitted when applying all methods.

• C5. Unobserved true predictors: As C1, but 10 additional independent true variables, X₆₁, …, X₇₀, are included in the model to generate the outcomes; these variables are assumed to be unobserved and thus omitted when applying all methods.

• C6. Complex: All of the previously mentioned scenarios are combined in this scenario. X₁, …, X₁₀, X₆₁, …, X₇₀, are true predictors, of which (X₁, X₂, X₆₁, X₆₂), (X₃, X₄, X₆₃, X₆₄), …, (X₉, X₁₀, X₆₉, X₇₀) are within-block correlated (ρ = 0.7), and X₆₁, …, X₇₀ are unobserved; X₁₁, …, X₅₀ are noises, of which (X₁₁, X₁₂), …, (X₁₉, X₂₀) are pairwisely correlated, and they are also highly correlated with (X₁, X₂), …, (X₉, X₁₀), respectively, (ρ = 0.7); (X₂₁, X₂₂), …, (X₂₉, X₃₀) are pairwisely correlated (ρ = 0.7), and they are also slightly correlated with (X₁, X₂), …, (X₉, X₁₀).ρ = 0.3); all two-way and three-way interactions of X₁, …, X₁₀ are included in the outcome-generating model but omitted when applying the selection methods; X₃₁, …, X₆₀ are independent noises.

Table I.

Simulation scenarios.

#	Scenario	True predictors	Noise terms	f(Z)
C1	Independent	X1, …, X10, independent	X11, …, X60, independent	$b_{10}+b_{11}{\sum }_{j=1}^{10}{X}_j$ (b10 = −5, b11 = 0.5)
C2	Correlated (True, Noise)	X1, …, X10, independent	X11, …, X20 are correlated with X1, …, X10, respectively, (ρ = 0.8); X21, …, X60 are independent noises.	$b_{20}+b_{21}{\sum }_{j=1}^{10}{X}_j$ (b20 = −5, b21 = 0.5)
C3	Correlated (True, True)	X1, …, X5 and X6, …, X10 are block-wisely correlated (ρ = 0.75).	X11, …, X60, independent	$b_{30}+b_{31}{\sum }_{j=1}^{10}{X}_j$ (b30 = −3, b31 = 0.3)
C4	Omitted interactions	X1, …, X10, independent; all two-way interactions, omitted	X11, …, X60, independent	$$b_{40}+b_{41}{\sum }_{j=1}^{10}{X}_j+b_{42}{\sum }_{1\le j<k\le 10}{X}_j{X}_k$$ (b40 = −5, b41 = 0.1, b42 = 1/45)
C5	Unobserved true predictors	X1, …, X10, independent; X61, …, X70, independent and unobserved	X11, …, X60, independent	$b_{50}+b_{51}{\sum }_{j\in [1,10]\cup [61,70]}{X}_j$ (b50 = −5, b51 = 0.25)
C6	Complex	(X1, X2, X61, X62), (X3, X4, X63, X64), …, (X9, X10, X69, X70) are block-wisely correlated (ρ = 0.7) of which X61, …, X70 are unobserved; all two-way and three-way interactions of X1, …, X10	X11&X12, …, X29&X30 are pairwisely correlated (ρ = 0.7), of which X11&X12, …, X19&X20 are highly correlated with X1&X2, …, X9&X10, respectively, (ρ = 0.7), and X21&X22, …, X29&X30 are slightly correlated with X1&X2, …, X9&X10(ρ = 0.3) X31, …, X60 are independent noises.	$b_{60}+b_{61}{\sum }_{j\in [1,10]\cup [61,70]}{X}_j+b_{62}{\sum }_{1\le j<k\le 10}{X}_j{X}_k+b_{63}{\sum }_{1\le j<k\le 10}{X}_j{X}_k{X}_l$ (b60 = −3.4, b61 = 0.1, b62 = b63 = 1/825)

Z denotes the set of true predictors.

In the last column, the b’s are constants.

Note that the value of these constants are chosen so that the distribution of P(Y = 1) is similar across different scenarios.

3.2. Generating the outcome

We generated the outcome variable Y (Y = 1 if a case and Y = 0 if a non-case) based on the logistic regression model in Equation (1) in the following three steps:

• Step 1.Generate a predictor matrix X_n×p(n = 400 or 200, p = 60 or 70);

• Step 2.Generate _Pi = Pr (subject i is a case) by equation

  $$P_i=\mathit{\text{Pr}}(Y_i=1|{\mathbf{Z}}_{\mathbf{i}})=\frac{e^{f({\mathbf{Z}}_{\mathbf{i}})+{\epsilon }_i}}{1+e^{f({\mathbf{Z}}_{\mathbf{i}})+{\epsilon }_i}},$$

  where Z_i is the vector of true predictors for subject i, which is a subset of all generated predictors X (or, as in the scenario C4, contains interactions between variables in X), f is some function of Z (see Table I for details), and εi ~ 𝒩(0; 0:001), i = 1, …, n, where 𝒩 denotes the Gaussian distribution;

• Step 3.Generate 1000 replications of the response variable Y_i by Y_i ~ Bernoulli(P_i), keeping X_i and P_i fixed, i = 1, …, n. By doing so, each subject (i) has 1000 simulated outcomes Y_i (derived from their true predictor vector Z_i, which will be predicted later by all observed predictors X₁, …, X₆₀.

3.3. Missing data pattern and case prevalence

For all six predictor scenarios in Section 3.1, we consider the effect of missing values and case prevalence. In particular, in addition to the complete data cases, we introduced missing values among the predictors in the training data. Overall, 5% of observations in the predictors is missing, and 50% of the rows (i.e., half of the subjects) has at least one missing observation. The missingness is formed in two patterns: (M1) all 60 potential predictor variables have equal probability of missing observations, and (M2) some predictors are four times more likely to be missing than the rest (these variables are X, X₆, X₁₁, X₁₆, …, X₅₆). Missingness is independent of the outcome variable and is random across predictors. Also, we considered two case prevalence levels, that is, the proportion of cases, in the training data set: 0.5 and 0.3. Therefore, we simulated six scenarios for predictors, three types of missingness, and two prevalence levels, resulting in altogether 36 situations.

3.4. Models to be fitted on the data

To compare the variables selection methods, we fitted the following list of models to the simulated data:

• Generalized linear model (GLM): We first apply a regular logistic regression on the simulated data, modeling the outcome as a function of all 60 observed predictors, and we select predictors with p-values less than 0.05. This is as a reference model for scenarios C1–C3, where all true predictors are among the observed ones, while in scenarios C4–C6, the GLM is the correct model form, but it omits some true predictors.

• Two-sample t-test: For each predictor X_j, j = 1, …, 60, perform two-sample t-test, and calculate t-statistic adjusted by sample size:

  $$t_{j,\mathit{\text{adj}}}=t_j\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$$

  where n₁ and n₂ are the sample sizes for the groups of cases and non-cases, respectively, and t_j is the usual t -statistic. This modification to the usual t-test statistic is necessary to account for varying sample sizes because of missing predictors. We sort the predictors by |t_j,adj| from largest to smallest and select the top 10 variables. As for prediction, we calculate the average of the selected 10 variables for all subjects and transform them into the range of [0,1] via dividing by the maximum of the means. We treat these scores as predicted probabilities of being a case and used a cutoff point of 0.5 to classify the subjects.

• CART: We apply CART on the training data and find the variables that appear in the tree as selected variables (multiple occurrence for one variable is considered being selected only once). The tree is pruned based on the criterion of Cp = 0:01. We predict the test data based on the tree obtained on the training data.

• Random Forest: Sort the variables by Mean Decrease Accuracy from largest to smallest, and select the top 10 variables. Here, Mean Decrease Accuracy is a permutation-based internal measure that can assess variable importance and works as follows: For a specific predictor X_j, for each tree in the forest, calculate the difference between the OOB errors with X_j randomly permuted and that on the original data (i.e., without X_j permuted), and average the differences over the entire forest [20]. Notice that although Random Forest can assess variable importance, its prediction is based on the entire variable space, that is, all predictors in X. Thus, in order to investigate the prediction performance of the selected variables, we use normalized scores based on the average of the top 10 variables, just like for the two-sample t-test (again, the cutoff point is set at 0.5.).We also show the Random Forest prediction based on all variables to provide a benchmark of how low the prediction error can be. The prediction using all variables is not to be compared with prediction from the other methods.

• LASSO: Apply LASSO and select variables on the training data. Use cross-validation to find the optimal tuning parameter λ defined in Equation (2). Predict test data by the selected model. Note that when there are missing predictors, LASSO uses only units (i.e., subjects) with complete data.

• Elastic Net: Similar to LASSO, but use cross-validation to find λ, fixing α at 0.5 to save computational time (λ and α are defined in Equation (4)).

• Imputed-LASSO: This is the method we propose for situations with missing observations, such as M1 and M2. The method consists of utilizing Random Forest to perform missing data imputation before applying a variable selection method. The imputation procedure is iterative and works as follows: For the initial iteration, median imputation is applied, and a forest is built based on the imputed data, for which proximities (defined in Section 2) are calculated and new imputations are obtained by the average or vote weighted by these proximities; for each of the rest iterations, a new forest is built on the data imputed in the previous iteration, and proximities and imputations are updated accordingly. For our study, we used four iterations. We apply LASSO to select variables based on the imputed training data set.

3.5. The algorithm for fitting and the criteria for comparing the methods

The algorithm to fit each model and the criteria to compare the methods with regard to selection and prediction performances are as follows. For each of the 36 situations and for each of the 1000 repetitions of the outcome variable Y :

1. Apply the methods for variable selection by predicting the outcome from the observed first 60 predictors X₁, …, X₆₀ in the training data set, and select a subset of the predictors; calculate the number of times each predictor is selected out of the 1000 repetitions, and obtain the average number of true and false variables selected by each method;

2. Predict the outcome in the test set by the model selected on the training data; obtain test error (i.e., misclassification error) and receiver operating characteristic (ROC) curve, more specifically, the area under the ROC curve (AUC).

We utilized the following R packages in the simulations: rpart, Random Forest, and glmnet. We also used Efron’s R function stat.stanford.edu/~;omkar/monograph/simz.R to simulate block-wisely correlated continuous variables with pre-assigned correlation coefficients.We then categorize the continuous variables by desired probabilities to create correlated categorical variables with levels 0, 1, and 2. The change in correlation between variables after categorization is minor.

4. Simulation results

We discuss some interesting results in this section. A more detailed report is available in the supporting material available online.^‡

4.1. Complete data and equal prevalence

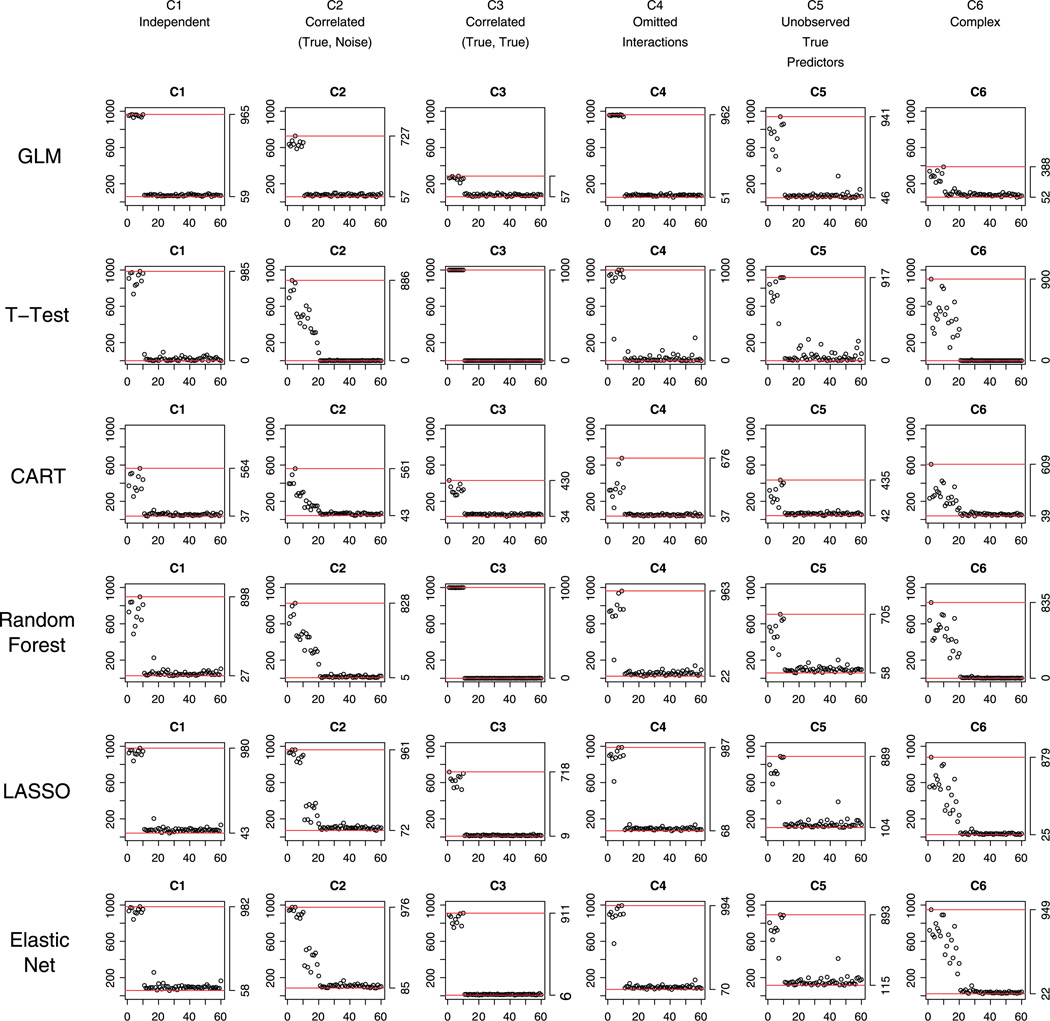
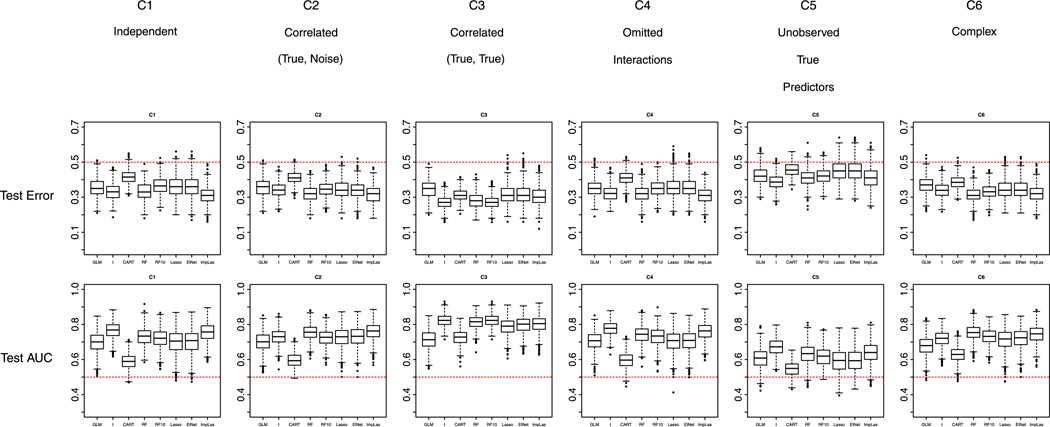
Starting from the simplest situation with complete data and equal prevalence of cases and non-cases in the training data set, Figure 1 shows the variable selection performance for all methods (row) for all scenarios (column). For each plot, on the horizontal axis is the index of the first 60 observed predictors X₁, …, X₆₀, and on the vertical axis is the number of times each of the 60 variables is selected out of the 1000 fits; horizontal lines show the maximum and minimum number of times the variables are selected.

Figure 1.

Complete data and equal prevalence of cases and non-cases in the training data set: performance of the methods with respect to selecting correct variables under the six scenarios C1 to C6.

Under C1 Independent, the reference GLM, which is the model under which the outcomes are generated, seemed to be the best in selecting the true variables (all true variables were selected with over 90% probability), as well as reducing false positives (all noises were selected with less than 10% probability).

Under C2 Correlated (True, Noise), GLM seemed to have multicollinearity problem, although false positives were kept low. Two-sample t -test, CART, and Random Forest were also problematic: They selected the true variables with much less probability and included many fake predictors. LASSO and Elastic Net selected true variables accurately, just as the result under the independent situation C1; nevertheless, they also included some false positive variables, especially Elastic Net (Elastic Net and LASSO selected approximately 3–4 and 2–3 noises that are correlated with the true predictors, respectively.). This is likely due to the fact that Elastic Net has grouping effect when selecting correlated variables (as was discussed in Section 2).

Under C3 Correlated (True, True), GLM suffers even more severe multicollinearity. LASSO seemed to be too aggressive in excluding correlated true predictors (approximately only six true variables were selected), although false positive was desirably low. This illustrates the potential limitation of LASSO to simultaneously select a group of highly correlated true variables (as was discussed in Section 2). Elastic Net, in contrast, was less aggressive than LASSO and selected true variables well, again because of its grouping effect. Under this scenario, however, the grouping effect is credited as a benefit (as opposed to as a disadvantage in C2). Interestingly, two-sample t-test and Random Forest selected the true predictors perfectly – all 10 true variables were never missed. This is because Y, generated by the linear model in Equation (1), is related to the sum of the true predictors (see Table I for details). Thus, when the true predictors are positively correlated with each other as in scenario C3, the correlation between this sum and an individual true predictor is much larger than the correlation between the outcome (Y) and a noise variable, and as a result, the t-test picks all 10 true variables. Compared with scenario C1, where the true predictors are independent of each other, the correlation between an individual true predictor and the sum of all true predictors under C3 is larger, which explains why the t-test does better in C3 than in C1.

Under C4 Omitted Interactions, interactions had little effect on selecting important main effects – except for CART, all methods selected the true main effects and reduced the noise terms satisfactorily.

Under C5 Unobserved True Predictors, where the additional 10 variables X₆₁, …, X₇₀ are true but unobserved, all methods became worse in selecting true variables – larger than 30% probability that important observed variables would be missed. Moreover, false positives were also greater than under previous scenarios. GLM, t -test, LASSO, and Elastic Net performed somewhat better than CART and Random Forest.

Under the last scenario C6 Complex, where all factors (correlations, interactions, and unobservability) are included, all models became worse in selecting true variables and reducing the selection of noise variables. The first 10 noises that are highly correlated with the 10 true variables were selected with high probability. Compared to other methods, both LASSO and Elastic Net selected true predictors better and simultaneously selected fewer noises.

Across all six scenarios for the relationships between the predictors, LASSO and Elastic Net seemed to outperform other methods in selecting true variables. While there are strong effects of the between-predictor relationships on the selection performance of all methods, these regularized regression methods consistently selected true variables with large probability (84% on average) and selected fewer fake predictors. Given that in psychiatric research, CART is used quite often (e.g., [24–26]), for understanding the mechanisms of action of treatments or to identify factors that contribute to the heterogeneity in the presentation of various mental illnesses, it is instructive to notice CART’s poor performance in this regard, not only when the outcome and the covariates of interest have the association in a linear form but also when the true model contains interactions between the observed predictors.

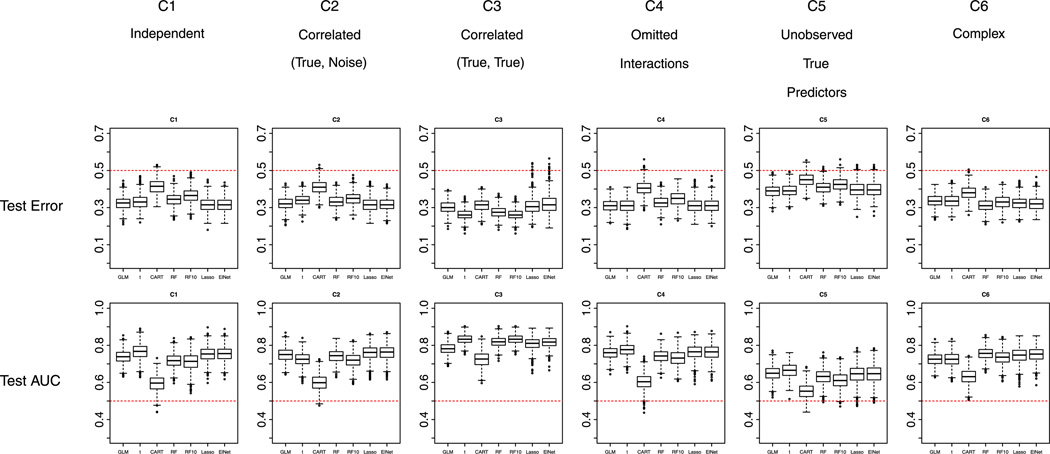
Similarly, for prediction performance, LASSO and Elastic Net did not differ much, and best prediction (i.e., lowest test error and highest AUC) is achieved with either one of them under most scenarios. As mentioned earlier, in the situation of shortening a psychiatric instrument (where items are typically highly correlated and more items usually lead to more reliable total score), it is not immediately clear whether the inclusion of several correlated items by Elastic Net, or the selection of only one from a set of correlated predictors by LASSO would be better. Two-sample t-test and Random Forest using top 10 variables outperformed other methods under C3 condition, where true variables are correlated within groups and noise terms are independent. This is consistent with the selection performance of these two methods under this scenario: they selected all 10 true variables and no other noise terms. Figure 2 shows the boxplots of test errors and test AUC’s for all scenarios for all methods. Dotted red lines in the plots show the prevalence of cases (here 0.5).

Figure 2.

Complete data and equal prevalence of cases and non-cases in the training data set: performance of the methods with respect to misclassification error and area under the receiver operating characteristic curve (AUC) in the test data set under the six scenarios C1 to C6. RF refers to Random Forest; RF10 refers to Random Forest with 10 variables selected; ElNet refers to Elastic Net. Note: Random Forest should not be compared with other methods.

4.2. Missing observation (M1 & M2) and equal prevalence

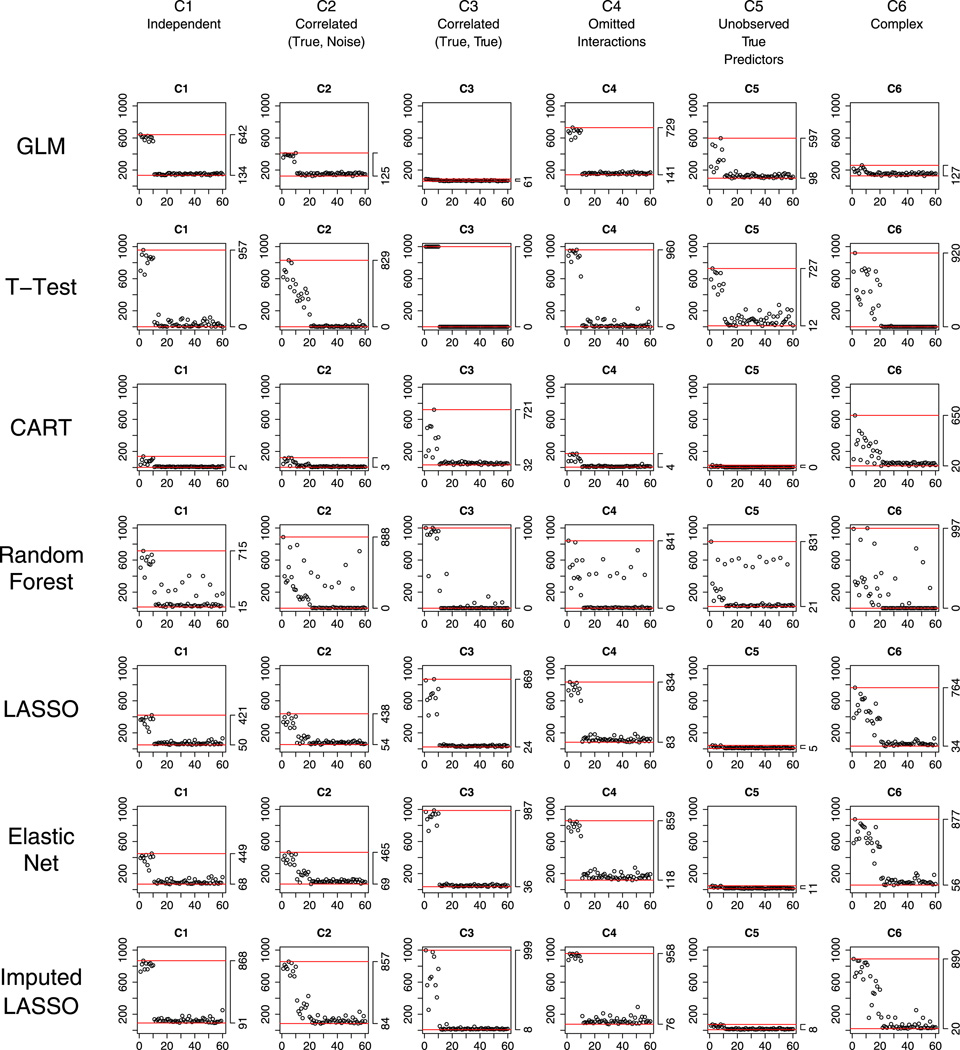
When some of the observations are missing, linear models (GLM, LASSO, and Elastic Net) use only observations on subjects with complete data (here, this is a half of the observations in the training and test data sets); CART uses surrogates splits to assign subjects to branches when the splitting variable is missing at a certain node; Random Forest and Imputed-LASSO impute missing data by proximity before selecting variables.

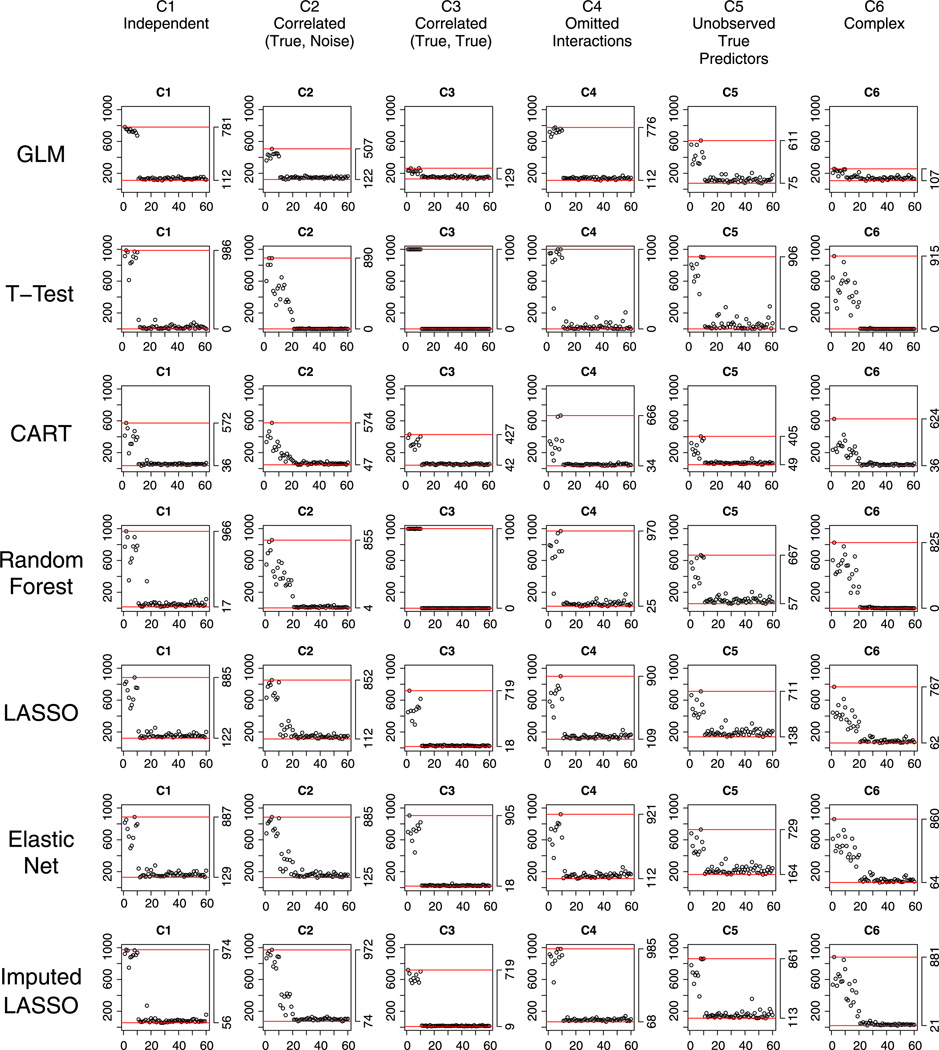
We consider two situations, where the probabilities of missing observations are equal (M1) and unequal (M2) across the predictors and do not depend on the outcome. Under both situations, linear models (GLM, LASSO, and Elastic Net) ignored subjects with incomplete data and performed similarly – the performance was worse compared to the complete data case (Section 4.1) because of smaller sample size. Here, we are more interested in the other methods that include mechanisms for dealing with missing data or sample size changes and that may behave differently between the two missing patterns of the data. Figures 3 and 4 show the selection performance under M1 and M2 (for M2, the selection results for GLM, LASSO, and Elastic Net are similar to M1 and thus not shown).

Figure 3.

Equal proportion of missing data in all predictors M1 and equal prevalence of cases and non-cases in the training data set: performance of the methods with respect to selecting correct variables under the six scenarios C1 to C6.

Figure 4.

Unequal proportion of missing data in predictors M2 and equal prevalence of cases and non-cases in the training data set: performance of the methods with respect to selecting correct variables under the six scenarios C1 to C6.

4.2.1. Robustness to sample size decrease of the two-sample t-test and CART

The two-sample t-test and CART were not affected by missingness in the predictors under either M1 or M2. For two-sample t-test, the resistance to the decrease of the sample sizes in the two groups for both equal and unequal missingness across the predictors is due to the fact that it is sample-size adjusted and does not rely on sampling scheme if the missingness in the predictors is independent of the outcome. For CART, the selection of a variable to split at a node is based on the reduction in impurity (in particular, we used Gini index in the simulation study), which only depends on the proportion of each class (group) at each level of the variable, rather than the sample size in that class [6]. Because the probability of missingness is the same for cases and non-cases, the proportions of the two classes remained unchanged, and the trees that CART built on incomplete data were similar to those on complete data.

4.2.2. The bias of random forest imputation

Under M1 situation, for both Random Forest and Imputed- LASSO, the selection results were very similar to those on complete data, showing the benefit of Random Forest imputation on equal-probability missingness. In fact, studies have suggested that because the Random Forest imputation uses proximity-based nearest neighbor approach, it will be valid under missing completely at random mechanism [27].

However, for M2, where variables X₁, X₆, X₁₁, …, X₅₆ are four times more likely to be missing than other variables, after imputation, Random Forest tended to select more often the noise variables with large probability of missingness (i.e., X₁₁, X₁₆, …, X₅₆). We found that this is due to the bias of Random Forest imputation when there is a difference in the prevalence of missing values among the predictors. To impute one missing observation for a specific variable, Random Forest utilizes proximities, which count the number of times two subjects end up in a same final leaf, as the weights to sum over other non-missing observations on that variable. Although in general the covariances among predictors and between predictors and the outcome are preserved by the Random Forest imputation, for variables that have higher probability of missingness, the correlations with the outcome tend to increase as iteration goes on. For this reason, in the M2 case, Random Forest selected the variables with higher proportion of missingness most often. One exception is scenario C3, where the true predictors are correlated among each other but not with the noise variables: Here, Random Forest selected the noises with higher missing proportions, but at much lower rate than it selected the true predictors. In this case, of the true predictors X₁, …, X₁₀, the most often selected are X₁ and X₆, showing again the imputation bias in favor of variables with more missingness.

4.2.3. Imputed-LASSO: LASSO offsets the problem of random forest imputation

Surprisingly, Imputed- LASSO was only slightly affected by the unequal missingness in the predictors – it still excelled in selecting true variables and was relatively good in reducing the noise variables, especially under the complex scenario C6. In Section 2, we have seen that LASSO selected noise variables that are correlated with true predictors with 20%–30% probability (in C2), and was aggressive in reducing correlated true predictors (in C3) on the complete data. However, for M2, LASSO seemed to offset the bias of Random Forest imputation, and it prevented the noise terms with large missingness from appearing important. For variables that have more missing observations, after Random Forest imputation, the correlation between them and the outcome variable increased more than those with less missingness (see the previous text). However, this increment had limited effect on the variable selection of LASSO. Moreover, the Imputed- LASSO performed better than regular LASSO in terms of selecting the true variables, likely because more information was used. This suggests the merit of Imputed-LASSO on data similar to M2. The only exceptional case is C3 Correlated (True, True) scenario, where the Imputed-LASSO was much more likely to select the true variables with larger missingness only (i.e., X₁ and X₆). In other words, the increment in correlation between predictors and response due to Random Forest imputation illustrates the inconsistency in selecting correlated true variables that characterizes LASSO.

For prediction performance, under M1, best prediction was achieved most of the time with two-sample t-test or Imputed-LASSO, and in the scenario of correlated true predictors C3, by Random Forest based on the 10 most important variables. Under M2, however, because of the bias of Random Forest imputation, the prediction by the 10 Random Forest selected variables was not as successful. This shows that when sample size is reduced because of missingness in the data like those in M1 and M2, two-sample t-test is a good back-up method even for prediction and Imputed-LASSO works well (especially for more complicated situations such as C6). Figure 5 shows the prediction performance for M1 with equal prevalence of cases and non-cases (the plot for M2 is provided in web-based supporting material).

Figure 5.

Equal proportion of missing data in predictors M1 and equal prevalence of cases and non-cases in the training data set: performance of the methods with respect to misclassification error and area under the receiver operating characteristic curve (AUC) in the test data set under the six scenarios C1 to C6. RF refers to Random Forest; RF10 refers to Random Forest with 10 variables selected; ElNet refers to Elastic Net; ImpLas refers to Imputed-LASSO. Note: Random Forest should not be compared with other methods.

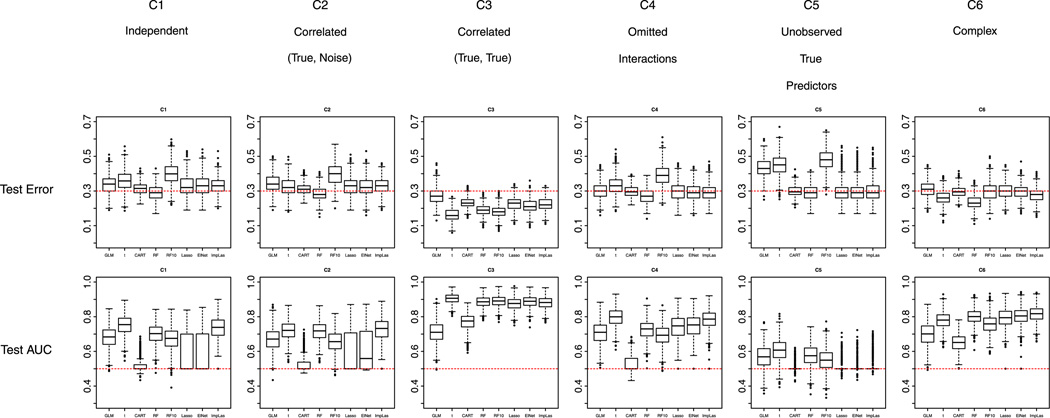
4.3. Unequal prevalence of cases and non-cases

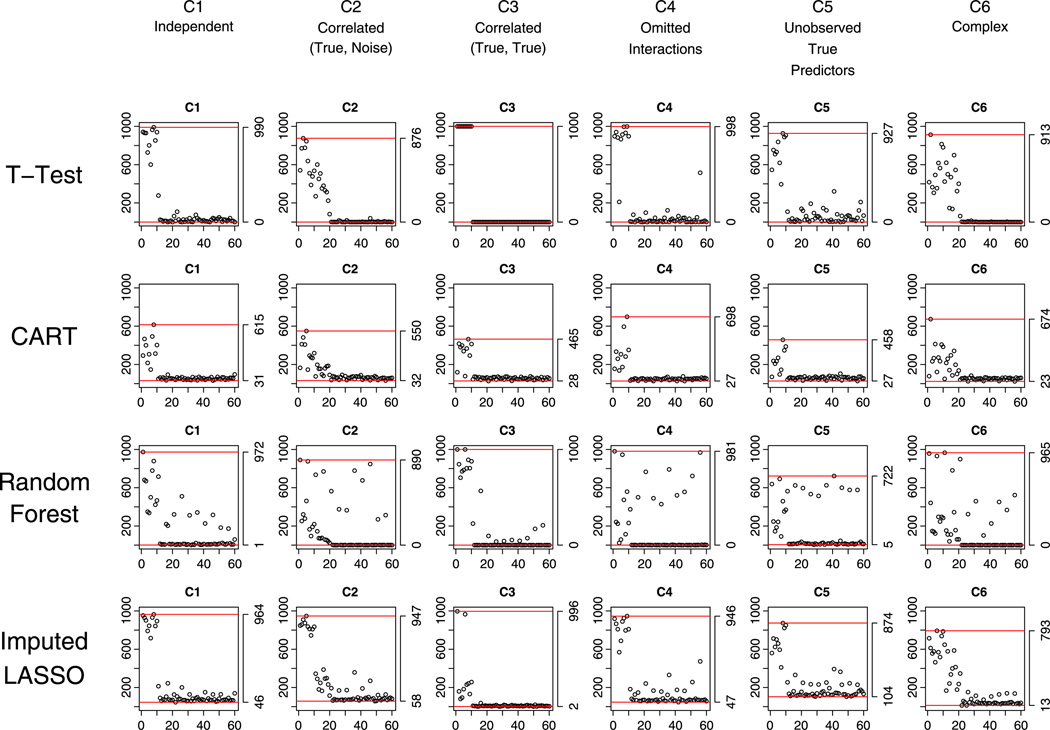
In many studies, the data sets used for developing screening instruments would not have equal prevalence of cases and non-cases, with non-cases typically constituting a higher proportion of the data. We considered a prevalence level of cases 0.3 with complete data, equal missingness (M1) and unequal missingness (M2) in the predictors (results are the same for prevalence of cases equal to .7 = 1– .3). The results from the simulations showed that the prevalence of cases in the training data can have strong effect on most methods: Linear models (GLM, LASSO, and Elastic Net) selected true variables with approximately 20% less probability than in the equal prevalence situations; CART almost completely failed to select any variables; Random Forest imputation was, again, problematic in the case of unequal-probability missingness (M2). The exceptions were two-sample t-test and Imputed-LASSO. Under scenario C5 where half of the true predictors are unobserved and cannot be represented by any other observed variables, penalized regression methods (i.e., LASSO, Elastic Net, and Imputed-LASSO) selected only a few variables in the unbalanced data case, although they did well under balanced data. Two-sample t-test, however, is not affected by prevalence and still selected seven (of the 10) true variables on average, suggesting, again, a good back-up method. On the other hand, if the data are unbalanced in prevalence and if penalized regression methods result in tiny models that contain few predictors, this might suggest that there are missing true predictors whose information cannot be obtained through observed data. Except for C5, Imputed-LASSO worked well across different scenarios for both M1 and M2, showing that it was not affected by either prevalence or missingness for most scenarios, and was thus quite stable. Figure 6 shows the variable selection charts for M2 with 30% case prevalence (for complete data and M1 with unequal prevalence, see supplementary document online).

Figure 6.

Unequal proportion of missing data in predictors M2 and prevalence of cases 30% in the training data set: performance of the methods with respect to selecting correct variables under the six scenarios C1 to C6.

With respect to prediction, the results are quite similar for complete data, M1 and M2 situations: Prevalence had strong effect in that further reduction in error rate (from 30% false negative without any predictors) was limited. For most scenarios, median test error was slightly below the prevalence level of 0.3, except for scenario C3, where approximately 5%–10% reduction could be made. Test AUC, on the other hand, could be quite high with t-test and Imputed-LASSO, showing again the benefit of Imputed-LASSO and the back-up property for t-test in predicting future data. Figure 7 shows the boxplots of predictive errors and AUC’s for M2 with unequal prevalence of cases and non-cases (plots for complete data and M1 with unequal prevalence are provided in the web-based supporting material).

Figure 7.

Unequal proportion of missing data in predictors M2 and unequal prevalence of cases and non-cases in the training data set: performance of the methods with respect to misclassification error and area under the receiver operating characteristic curve (AUC) in the test data set under the six scenarios C1 to C6. RF refers to Random Forest; RF10 refers to Random Forest with 10 variables selected; ElNet refers to Elastic Net. Note: Random Forest should not be compared with other methods.

4.4. Summary of simulation results

In summary, for complete data, both LASSO and Elastic Net seemed to be performing the best in selecting important variables. As discussed in Section 2, in the context of shortening psychiatric instruments, there is a tension between selecting ‘important’ correlated items, which would potentially increase the reliability of the measure, and selecting only ‘important’ items that contribute independent information, which would result in a shorter instrument. Because of its constraints on the coefficients with both L1 and L2 norms, Elastic Net tends to select more variables than LASSO, and thus, it includes more noise terms when those terms are correlated with the true predictors, giving an advantage to LASSO. However, Elastic Net’s grouping effect could be viewed as an advantage when true predictors are in fact correlated, which is a common situation in designing psychiatric questionnaires, thus giving an advantage to Elastic net in such cases. When there are missing values in the predictors, Imputed-LASSO selected true variables most efficiently and consistently. It eliminates the problem of Random Forest imputation on data with unequal probability of missingness.

Moreover, in data configurations when most methods were not able to select variables such as scenario C5 with unequal prevalence, where the data are unbalanced and some information is completely unavailable (in contrast with C6, where the lost information contained in X₆₁, …, X₇₀ can still be recovered by correlated variables available in the data sets), two-sample t-test was not severely affected by the lost information and could still select the observed true variables relatively well. Table II shows the comparison with respect to variable selection among the methods for all scenarios, missing data patterns, and prevalence levels.

Table II.

Comparison of all six methods with respect to the average number of true and noise variables selected under all case-prevalence levels, all scenarios for data configuration, and all missing data patterns.

Scenario	Missing pattern	GLM	t-test	CART	Random Forest	LASSO	Elastic Net	Imputed LASSO
Prevalence = 0.5
C1.Independent	Complete	9.5 (3.7)	9	4.1 (2.8)	7.3	9.3 (4)	9.3 (4.8)	–
	M1	7.3 (6.6)	8.9	3.9 (2.8)	7.4	7 (7.8)	7.2 (8.3)	9.1 (4.2)
	M2	7.2 (7)	8.7	3.7 (2.6)	6	7.6 (6.8)	7.8 (8.2)	8.8 (4.4)
C2.Correlated (True, Noise)	Complete	6.4 (3.8)	6.4	3.6 (4)	6	9 (6.7)	9.2 (8.2)	–
	M1	4.3 (7.3)	6.3	3.5 (4)	5.9	7.3 (8)	7.7 (9.4)	8.7 (7.1)
	M2	4 (6.8)	6.3	3.3 (3.6)	3.8	7.1 (9.3)	7.5 (10.8)	8.4 (6.6)
C3.Correlated (True, True)	Complete	2.6 (3.8)	10	3.3 (2.8)	10	6.2 (0.9)	8.4 (0.7)	–
	M1	2.3 (7.5)	10	3.3 (2.8)	10	4.8 (1.4)	7.1 (1.2)	6.3 (0.8)
	M2	2.4 (8.1)	10	3.3 (2.8)	8.5	4.8 (1.3)	7.2 (1.2)	3.3 (0.4)
C4.Omitted interactions	Complete	9.6 (3.6)	8.8	3.7 (2.5)	7.3	8.9 (4.5)	8.9 (4.8)	–
	M1	7.3 (6.8)	8.7	3.5 (2.5)	7.2	6.6 (7.1)	6.9 (7.6)	8.7 (4.7)
	M2	7.3 (6.8)	8.5	3.3 (2.4)	3.8	7.2 (8.4)	7.4 (9.3)	8.2 (5.1)
C5.Unobserved true predictors	Complete	7.1 (3.5)	7.7	2.9 (3.1)	5.2	7.2 (7)	7.4 (7.7)	–
	M1	4.3 (6)	7.5	2.7 (3.5)	5	5.1 (9.6)	5.4 (10.8)	7 (7.5)
	M2	4.5 (5.5)	7.3	2.5 (3)	3.4	4.4 (8.9)	4.7 (10.3)	6.8 (8.2)
C6.Complex	Complete	2.9 (4.1)	5.9	3.4 (4.2)	5.9	6.5 (5.2)	7.7 (6.5)	–
	M1	2.2 (7)	5.8	3.3 (3.8)	5.9	4.9 (6.6)	5.9 (8.1)	6.6 (5.2)
	M2	2.2 (7)	5.6	3.1 (3.8)	3.9	4.5 (6)	5.6 (7.2)	6.3 (6.2)
Prevalence = 0.3
C1.Independent	Complete	9.2 (4)	8.6	1.2 (0.6)	6.9	8.9 (5.6)	9 (8.1)	–
	M1	5.8 (8)	8.6	0.9 (1.4)	6.9	5 (4)	5.5 (5.5)	8.7 (5.5)
	M2	6 (7.5)	8.3	0.8 (0.4)	5.8	3.4 (3.5)	3.8 (4.8)	8.1 (6.2)
C2.Correlated (True, Noise)	Complete	5.9 (3.9)	6.2	0.9 (0.7)	5.7	8.2 (7.5)	8.5 (10.1)	–
	M1	3.8 (7.5)	6.2	0.9 (0.8)	5.8	3.4 (4.2)	4 (6.2)	7.8 (7.6)
	M2	4 (7.8)	6	0.7 (0.6)	4.2	3.4 (4.9)	3.9 (6.6)	7.9 (8)
C3.Correlated (True, True)	Complete	4.3 (4.9)	10	3.9 (3)	10	8.3 (1.1)	9.7 (1.1)	–
	M1	0.6 (2.6)	10	3.9 (2.8)	10	6.4 (1.6)	8.9 (1.9)	8.4 (1.1)
	M2	0.8 (3.4)	10	3.7 (2.6)	9	6.6 (1.8)	9 (2.5)	6.8 (1)
C4.Omitted interactions	Complete	9.7 (3.9)	9	1.6 (0.8)	7.3	9.5 (5.8)	9.7 (8.2)	–
	M1	6.2 (7.5)	8.8	1.3 (0.7)	7.2	6.1 (5.3)	6.3 (7)	9.4 (5.9)
	M2	6.7 (8)	8.8	1.2 (0.6)	4.9	7.4 (5.8)	7.8 (8.3)	9.2 (6)
C5.Unobserved true predictors	Complete	5.1 (3.8)	6.1	0.1 (0.1)	3.8	0.5 (0.6)	0.4 (0.6)	–
	M1	3.1 (6.5)	6	0.1 (0.1)	3.6	0.3 (0.6)	0.3 (0.6)	0.4 (0.6)
	M2	3.7 (6.2)	5.7	0.1 (0.1)	2.9	0.3 (0.6)	0.3 (0.8)	0.6 (0.8)
C6.Complex	Complete	3.6 (4.3)	5.9	3.6 (3.5)	6.1	8.1 (6.5)	9.2 (9.2)	–
	M1	2.4 (7.9)	5.9	3.3 (3.4)	6.2	5.8 (7)	7.5 (9.9)	8.1 (6.5)
	M2	2 (7.2)	5.6	3.3 (3.8)	4.3	5.6 (6.4)	7.3 (9.7)	7.8 (7.2)

Average number of selected noise terms are shown in parentheses.

Bold cells correspond to the methods that selected the most true predictors under each condition.

Two-sample t-test and Random Forest rank all variables in each simulation, and we selected the top 10 of them. Thus, the average number of noise variables selected is 10 minus the average number of true variables, and they are not shown for these two methods.

GLM, generalized linear model; CART, Classification and Regression Tree; LASSO, Least Absolute Shrinkage and Selection Operator.

For prediction performance, we found that Elastic Net and LASSO worked the best in predicting future data in the situations of complete data. As is expected under incomplete data situation, Imputed- LASSO was superior to the other methods. Two-sample t-test prediction based on average of selected variables also performed well under certain cases (e.g., correlated true predictors). Tables III and IV show the prediction results.

Table III.

Comparison of all six methods with respect to mean test error under all case-prevalence levels, all data configuration scenarios, and all missing data patterns.

Scenario	Missing pattern	GLM	t-test	CART	Random Forest	RF10	LASSO	Elastic Net	Imputed LASSO
Prevalence = 0.5
C1.Independent	Complete	0.324	0.311	0.412	0.343	0.366	0.316	0.316	–
	M1	0.355	0.331	0.416	0.334	0.365	0.361	0.361	0.311
	M2	0.363	0.348	0.418	0.362	0.391	0.361	0.362	0.332
C2.Correlated (True, Noise)	Complete	0.322	0.342	0.409	0.332	0.348	0.316	0.316	–
	M1	0.356	0.34	0.413	0.322	0.345	0.344	0.341	0.317
	M2	0.356	0.357	0.413	0.342	0.448	0.344	0.343	0.33
C3.Correlated (True, True)	Complete	0.302	0.26	0.313	0.274	0.26	0.31	0.32	–
	M1	0.345	0.269	0.313	0.279	0.269	0.315	0.314	0.305
	M2	0.352	0.265	0.313	0.284	0.282	0.324	0.326	0.32
C4.Omitted interactions	Complete	0.311	0.31	0.405	0.328	0.346	0.31	0.311	–
	M1	0.352	0.323	0.41	0.323	0.35	0.356	0.355	0.309
	M2	0.337	0.305	0.412	0.345	0.402	0.342	0.342	0.311
C5.Unobserved true predictors	Complete	0.389	0.392	0.45	0.408	0.424	0.398	0.398	–
	M1	0.423	0.387	0.457	0.408	0.42	0.447	0.449	0.411
	M2	0.433	0.413	0.457	0.442	0.446	0.455	0.455	0.422
C6.Complex	Complete	0.337	0.336	0.382	0.313	0.33	0.325	0.32	–
	M1	0.373	0.34	0.386	0.313	0.333	0.348	0.344	0.323
	M2	0.371	0.332	0.386	0.332	0.37	0.353	0.35	0.33
Prevalence = 0.3
C1.Independent	Complete	0.313	0.344	0.312	0.298	0.366	0.317	0.316	–
	M1	0.353	0.351	0.312	0.313	0.38	0.348	0.345	0.325
	M2	0.338	0.358	0.313	0.29	0.399	0.33	0.331	0.33
C2.Correlated (True, Noise)	Complete	0.31	0.316	0.308	0.284	0.328	0.324	0.322	–
	M1	0.343	0.324	0.309	0.282	0.337	0.327	0.324	0.324
	M2	0.343	0.325	0.31	0.285	0.394	0.327	0.323	0.328
C3.Correlated (True, True)	Complete	0.219	0.164	0.229	0.181	0.164	0.21	0.204	–
	M1	0.288	0.186	0.231	0.201	0.186	0.241	0.229	0.233
	M2	0.273	0.162	0.232	0.188	0.18	0.226	0.215	0.221
C4.Omitted interactions	Complete	0.286	0.342	0.297	0.282	0.362	0.292	0.292	–
	M1	0.32	0.334	0.297	0.292	0.356	0.316	0.312	0.299
	M2	0.304	0.333	0.298	0.272	0.391	0.298	0.294	0.289
C5.Unobserved true predictors	Complete	0.422	0.448	0.299	0.297	0.465	0.306	0.304	–
	M1	0.418	0.457	0.299	0.295	0.48	0.304	0.302	0.303
	M2	0.431	0.452	0.299	0.291	0.483	0.297	0.298	0.3
C6.Complex	Complete	0.274	0.265	0.291	0.234	0.263	0.266	0.264	–
	M1	0.311	0.265	0.293	0.213	0.26	0.271	0.26	0.26
	M2	0.314	0.262	0.296	0.234	0.297	0.299	0.295	0.276

Bold cells correspond to the methods that resulted in the smallest test error under each condition.

Random Forest should not be used for comparison against the other methods.

RF10, Random Forest using the top 10 selected variables; GLM, generalized linear model; CART, Classification and Regression Tree; LASSO, Least Absolute Shrinkage and Selection Operator.

Table IV.

Comparison of all six methods with respect to mean test area under the receiver operating characteristic curve (AUC) under all case-prevalence levels, all scenarios, and all missing data patterns.

Scenario	Missing pattern	GLM	t-test	CART	Random Forest	RF10	LASSO	Elastic Net	Imputed LASSO
Prevalence = 0.5
C1.Independent	Complete	0.739	0.766	0.594	0.718	0.711	0.752	0.753	–
	M1	0.699	0.767	0.589	0.732	0.72	0.699	0.701	0.756
	M2	0.688	0.755	0.588	0.69	0.678	0.705	0.707	0.737
C2.Correlated (True, Noise)	Complete	0.749	0.725	0.599	0.742	0.719	0.76	0.76	–
	M1	0.701	0.729	0.595	0.755	0.725	0.726	0.73	0.761
	M2	0.701	0.71	0.594	0.728	0.605	0.726	0.729	0.745
C3.Correlated (True, True)	Complete	0.781	0.833	0.724	0.819	0.833	0.809	0.817	–
	M1	0.713	0.823	0.726	0.813	0.823	0.786	0.797	0.801
	M2	0.705	0.826	0.725	0.803	0.805	0.782	0.794	0.779
C4.Omitted interactions	Complete	0.76	0.776	0.604	0.742	0.731	0.762	0.762	–
	M1	0.706	0.776	0.596	0.743	0.731	0.702	0.705	0.76
	M2	0.726	788	0.596	0.718	0.641	0.729	0.731	0.758
C5.Unobserved true predictors	Complete	0.649	0.664	0.553	0.63	0.611	0.643	0.644	–
	M1	0.607	0.671	0.547	0.632	0.617	0.594	0.595	0.639
	M2	0.595	0.645	0.545	0.586	0.583	0.567	0.568	0.609
C6.Complex	Complete	0.726	0.724	0.631	0.755	0.734	0.745	0.751	–
	M1	0.678	0.72	0.628	0.753	0.73	0.712	0.719	0.743
	M2	0.681	0.733	0.626	0.739	0.685	0.717	0.724	0.742
Prevalence = 0.3
C1.Independent	Complete	0.738	0.757	0.53	0.722	0.706	0.742	0.744	–
	M1	0.67	0.755	0.522	0.726	0.703	0.643	0.65	0.741
	M2	0.681	0.751	0.52	0.701	0.672	0.595	0.599	0.72
C2.Correlated (True, Noise)	Complete	0.736	0.72	0.531	0.739	0.713	0.73	0.733	–
	M1	0.669	0.715	0.529	0.736	0.709	0.603	0.612	0.721
	M2	0.669	0.72	0.525	0.717	0.656	0.603	0.609	0.714
C3.Correlated (True, True)	Complete	0.863	0.91	0.774	0.898	0.91	0.896	0.903	–
	M1	0.712	0.891	0.772	0.883	0.891	0.864	0.878	0.882
	M2	0.712	0.905	0.769	0.886	0.889	0.874	0.887	0.88
C4.Omitted interactions	Complete	0.764	0.791	0.544	0.748	0.738	0.779	0.783	–
	M1	0.705	0.797	0.539	0.751	0.747	0.653	0.659	0.782
	M2	0.706	0.797	0.529	0.726	0.692	0.724	0.73	0.779
C5.Unobserved true predictors	Complete	0.588	0.596	0.502	0.577	0.563	0.506	0.506	–
	M1	0.56	0.6	0.503	0.57	0.56	0.504	0.503	0.506
	M2	0.567	0.607	0.502	0.576	0.549	0.504	0.504	0.508
C6.Complex	Complete	0.792	0.776	0.652	0.817	0.788	0.823	0.829	–
	M1	0.718	0.779	0.647	0.828	0.793	0.799	0.813	0.832
	M2	0.7	0.78	0.646	0.799	0.758	0.783	0.797	0.816

Bold cells correspond to the methods that resulted in the largest test AUC under each condition.

Random Forest should not be compared to the other methods.

RF10, Random Forest using the top 10 selected variables; GLM, generalized linear model; CART, Classification and Regression Tree; LASSO, Least Absolute Shrinkage and Selection Operator.

5. Autism Diagnostic Interview-Revised example

We illustrate the benefits and drawbacks of the previously discussed variable selection methods in developing psychiatric diagnostic instruments by a real example. The ADI-R [1] is a well-known instrument that is widely used for autism diagnosis. This interview-based questionnaire is typically used with parents and consists of 93 items, some of which are relevant only for certain children’s age groups and language ability levels. The authors were involved in the work of experts in ASD on shortening and modifying ADI-R for the purpose of developing a brief interview over the phone, appropriate for screening subjects for research studies. Separate interviews were to be developed for different age groups and levels of language abilities. A large database of responses to ADI-R questions from individuals with diagnosis made on the basis of an array of questionnaires, including the gold standard for ASD diagnosis ADOS [3], was available to the authors. Individuals were classified as either having or not having ASD diagnosis; about half of the later class consisted of subjects with no diagnosis, and the rest had some other developmental diagnosis but not ASD. The adopted strategy was to use the available data as a ‘selection’ sample and by applying some variable selection methods to identify a handful of items (around 10) that provide a reasonable predictive accuracy. Thus selected items would then be vetted by experts, modified (if necessary) for the purposes of administering them over the phone as opposed to in person, and used to develop a telephone screen. This telephone screen would then be applied to a new sample of individuals, that is, a ‘validation’ sample, which would also undergo the entire battery of tests for obtaining accurate diagnosis. The quality of the new telephone screen would be based on results from the validation sample.

Here, we illustrate how one might approach the question of selecting a subset of a few items for the purposes of rapid screening. This is the first stage of the previous strategy, using the available data as a ‘selection’ sample. Suppose one is interested in developing a telephone-based 5-min screening tool for a specific group of children from age 2 to 4 years and 11 months and with language ability level less than five words, based on a portion of current version items in the original ADI-R questionnaire. For this specific age and language group, we have data on n = 475 subjects and 44 items of interest, from which around 10 items are expected to be selected to form the screening tool. For the purpose of comparing the applications of all six methods on real data, we randomly separated the ‘selection’ sample into a training set (n₁ = 316, n_1,case = 221, n_1,control = 95) and a test set (n₂ = 159, n_2,case = 103, n_2,control = 56). The proportion of subjects who have at least one missing observation on the 44 items are quite high (over 80%), and the missing probability is uneven across items (from 0% to 39%, median=1.5%). The prevalence of ASD cases is around 0.7 for both data sets.

On average, the six methods selected 11 variables. Table V later shows the results from selection and prediction for the analytic methods applied to the ADI-R data. For two-sample t-test and Random Forest, we selected the top 10 variables according to the rules in the simulation study. CART selected the fewest items (eight variables), and Elastic Net selected the most (14 variables). The 10 items selected most frequently included child’s age when parents were first concerned (ACON), showing and directing attention (CSHOW), stereotyped utterances and delayed echolalia (CSTEREO), reciprocal conversation (CCONVER), and a few others. Elastic Net selected all of them. Ranked second were Imputed-LASSO and two-sample t-test, which selected 8 of the 10 most frequently selected items. GLM did not select any variables in that the number of predictors was large relative to the number of complete cases and a linear separation occurred.

Table V.

Comparison of variable selection methods on Autism Diagnostic Interview-Revised data.

	GLM	Two-sample t-test	CART	Random Forest / RF10	LASSO	Elastic Net	Imputed LASSO
ntraining	50	316	316	316	50	50	316
ncase	35	221	221	221	35	35	221
ncontrol	15	95	95	95	15	15	95
Prevalence	0.7	0.7	0.7	0.7	0.7	0.7	0.7
		ACON	ACON	ACON	ACON	ACON	ACON
		CCHAT	APHRASE	CCONVER	CCONVER	CCONVER	APHRASE
		CCONVER	CIMIT	CGAZE	CHSHAKE	CGAZE	CCONVER
		CINR	CINSGES	CINAPPQ	CINSGES	CHSHAKE	CGAZE
		CINSGES	CNEOID	CINR	COSHARE	CINR	CINR
		CNOD	CNOD	COCOMF	CRESIS	CINSGES	CNOD
		CQRESP	CSHOW	CSHOW	CRESPSH	CNOD	CQRESP
		CRESPSH	CSTEREO	CSTEREO	CSHOW	COSHARE	CRESPSH
		CSHOW		CUATT	CSTEREO	CRESIS	CSHOW
		CSTEREO		ELSKIL	CUATT	CRESPSH	CSOPLAY
					CVERRIT	CSHOW	CSTEREO
						CSTEREO	CUNPROC
						CUATT	ELSKIL
						CVERRIT
nvariable	0	10	8	10	11	14	13
Test error		0.371	0.252	0.222/0.415	0.405	0.379	0.333
Test AUC		0.721	0.659	0.765/0.71	0.731	0.726	0.7

Variables in italic font are selected most frequently across all methods.

GLM did not select any variables because of large number of predictors relative to the number of observations.

GLM, generalized linear model; CART, Classification and Regression Tree; LASSO, Least Absolute Shrinkage and Selection Operator; AUC, area under the receiver operating characteristic curve.

Using insights from the simulation study about the performance of the variable selection methods in similar situations, we gave to the experts for vetting the list of variables selected by the Imputed-LASSO plus the two variables from the 10 most frequently selected that were not picked by the Imputed-LASSO (CUATT) and (CINSGES). The validation sample is currently collected, and results are not yet available.

6. Discussion

We compared five variable selection methods (two-sample t-test, CART, Random Forest, LASSO, and Elastic Net) with respect to their performance in shortening psychiatric diagnostic instruments. In addition, we proposed the Imputed-LASSO, a method designed to deal with situations when large number of the units contain missing data. The Imputed-LASSO used Random Forest to impute the missing observations and form a set of complete data; for feature selection, we apply LASSO on the imputed data. We performed the comparison via a simulation study to investigate how those methods would perform in the selection of items from data typically available for this purpose. Psychiatric diagnosis is based on questionnaires consisting of 20 to 100 items, characterized by correlations between them, frequently missing data on at least a few items for each individual and varying prevalence of cases and non-cases in the data set available for analysis.

From the simulations, we found that there were several advantages and disadvantages for certain methods in variable selection. LASSO, which has a lot of good properties in variable selection and is one of the most often used approaches for feature selection, is known to aggressively reject predictors correlated with already selected ones. In some situations, this is considered as a disadvantage, and alternative approaches have been developed to deal with it, such as Elastic Net and regularized methods with grouped property. In the particular case discussed here, it is not obvious if this property of LASSO is a strength or a weakness. Elastic Net seemed to do better under correlated true variables situations, did worse in the case of correlated true and noise predictors, and performed similar to LASSO in both selecting important variables and predicting future data when there were no missing data in the training data set.

For missing data, Random Forest, after the imputation, was biased in calculating variable importance, which resulted in high selection of noise variables (i.e., false positives) when the probabilities of missing observations were different across the predictors. Nevertheless, the Imputed-LASSO, combining Random Forest imputation with LASSO, was shown to be an easy, efficient, and stable method that was not affected by probability of missingness in predictors or prevalence of cases in the data. We also found that the two-sample t-test is a good back-up method even under some extreme situations when most other methods did not work.

• Several issues need attention:

• α in Elastic Net, see Equation (4): For Elastic Net, we fixed α at 0.5 to save computation time, although, in some other cases, it might be more appropriate to use certain algorithms (e.g., cross-validation) to select this parameter.

• Imputed-GLM and imputed-Elastic Net:For incomplete data cases, after Random Forest imputations, one can also apply GLM or Elastic Net on the imputed data. The choice of presenting only the results from imputed-LASSO was based first on the observation that the comparisons between LASSO, GLM, and Elastic Net from the complete cases were carried over their imputed versions, and second, as discussed earlier in Sections 2 and 4.4, at least in the case of shortening psychiatric questionnaires, the advantage of choosing several correlated items together versus only one item from a group of correlated items is not clear. The imputed versions of these regularized regression methods compare similarly to their performance on complete data. In the online supplementary material, we show the results of a small simulation study comparing Imputed-GLM, Imputed-Elastic Net, and Imputed-LASSO in the case of equal case prevalence and M2 missingness with respect to variables selection and prediction. In general, linear models with shrinkage or sparsity constraints tend to eliminate the problem of Random Forest imputation, which selects fake variables with high missingness.

• Single versus multiple imputation: The results for Imputed-LASSO presented here are based on a single imputation, which was chosen for its simplicity. However, to evaluate the effect of this decision on the variability of the results, we performed a small simulation study, in which we used 10 imputed data sets. For each of the scenarios C1 to C6, the proportion of times a variable was selected was obtained also by averaging over the 10 imputed data sets. Aside from random variation, we observed no systematic effect. We conclude that there is no evidence for the benefit of multiple imputation over a single one in the setup considered here.

• Cost of false negative and false positive: We assumed equal cost of false negative and positive. If this is not the case, one might change the priors for tree-based methods or the cutoffs in the linear models. However, the question remains what criteria one wants to optimize. The case when the goal is to maximize the AUC is considered in [28].

• More unbalanced prevalences: We also tried more unbalanced prevalences of cases (e.g., 10%) in the training data set, and the performance of most methods became quite unsatisfactory, suggesting that sufficient balance of cases and non-cases in the training data is required for a good performance of variable selection methods.

• Selection versus prediction: As is known, the criteria to select the right variables and to perform good prediction sometimes may conflict. Because prior information of which variables are true is usually unavailable, the typical way to select variables by LASSO and Elastic Net is through cross-validation, which is based on future prediction, rather than the accuracy of variable selection. This might lead to mistakes in some situations. However, through our simulation results, we observed that the effect was not very significant and that using cross-validation in LASSO or Elastic Net was a feasible way for item selection, at least on psychiatric data similar to the ones we generated.

• Negative correlation: In our simulation, the correlations among variables in the generated data were all positive, and negative correlations were not considered as a factor to affect method performance. This might not be problematic for psychiatry type of variable selection because all items are usually pre-processed into the same direction with regard to their scientific meaning and their association with the corresponding disorder (e.g., typically in a questionnaire for all items, the higher the score, the more serious the disease). For other analysis (e.g., genetic research), however, the effects of negative correlations need to be considered.

• Inconsistency of test error and AUC: Frequently, the test error and test AUC are consistent in the sense that minimizing the error rate maximizes AUC. However, this is not always the case (e.g., [28, 29]), and it might be better to use both measures instead of just one.

• Varying number of categories in the items: In this paper, we considered the case of categorical predictors with the same number of categories, which were treated as continuous variables. This special case is likely to be appropriate in many similar situations of shortening psychiatric instruments. In cases where the diagnostic tool consists of items measured on different scales, having different number of categories, or some being nominal and other ordinal, care needs to be taken to accommodate this variation. For example, variants of LASSO algorithm for ordinal and nominal predictors should be used that have been developed especially for such cases, for example, [30, 31].

We derive all the results and conclusions in the paper through a simulation study, and theoretical proofs of the merits and drawbacks of the variable selection methods need further pursuit.

Finally, although only mentioned here in passing, the importance of involving substantive area experts in the process of shortening diagnostic instruments cannot be overemphasized. The real challenge is to incorporate human judgement without letting human bias influence the statistical analyses.