Gap junction networks can generate both ripple-like and fast ripple-like oscillations

Abstract

Fast ripples (FRs) are network oscillations, defined variously as having frequencies of > 150 to > 250 Hz, with a controversial mechanism. FRs appear to indicate a propensity of cortical tissue to originate seizures. Here, we demonstrate field oscillations, at up to 400 Hz, in spontaneously epileptic human cortical tissue in vitro, and present a network model that could explain FRs themselves, and their relation to ‘ordinary’ (slower) ripples. We performed network simulations with model pyramidal neurons, having axons electrically coupled. Ripples (< 250 Hz) were favored when conduction of action potentials, axon to axon, was reliable. Whereas ripple population activity was periodic, firing of individual axons varied in relative phase. A switch from ripples to FRs took place when an ectopic spike occurred in a cell coupled to another cell, itself multiply coupled to others. Propagation could then start in one direction only, a condition suitable for re-entry. The resulting oscillations were > 250 Hz, were sustained or interrupted, and had little jitter in the firing of individual axons. The form of model FR was similar to spontaneously occurring FRs in excised human epileptic tissue. In vitro, FRs were suppressed by a gap junction blocker. Our data suggest that a given network can produce ripples, FRs, or both, via gap junctions, and that FRs are favored by clusters of axonal gap junctions. If axonal gap junctions indeed occur in epileptic tissue, and are mediated by connexin 26 (recently shown to mediate coupling between immature neocortical pyramidal cells), then this prediction is testable.

Introduction

Very fast oscillations (VFOs; more than ~80 Hz) in cortical neuronal populations are divided into two classes, ripples (more than ~250 Hz) and fast ripples (FRs; more than ~250 Hz; Bragin et al., 1999; Staba et al., 2002, 2004b; Worrell et al., 2004; Urrestarazu et al., 2007; Engel et al., 2009; Blanco et al., 2010), with putatively different pathophysiological correlates. FR frequencies occur normally, nested on somatosensory evoked potentials (Curio et al., 1994; Jones & Barth, 2002), and abnormally – in epilepsy patients (Engel et al., 2009), in hippocampal kainate-injected rodents (Bragin et al., 1999, 2002), in the pilocarpine temporal lobe epilepsy model (Lévesque et al., 2012), and in the tetanus toxin epilepsy model (Jiruska et al., 2010). FRs constitute a useful localising indicator for seizure initiation (Jacobs et al., 2008, 2009; Schevon et al., 2009; Andrade-Valenca et al., 2011).

Concerning cellular mechanisms, four points are relevant

First, in a dentate gyrus recording, after kainate injection in vivo (Engel et al., 2009), a ripple (~175 Hz) is immediately followed by an FR (~260 Hz). Both this recording and observations that as little as 1 mm³ can generate FRs (Bragin et al., 2002) and that principal cell firing increases during FRs (Le Van Quyen et al., 2008; Engel et al., 2009) suggest that a small principal cell network could generate both ripples and FRs.

Second, numerous observations indicate that neither ripples (Nimmrich et al., 2005; Traub et al., 2010; Bähner et al., 2011) nor FRs (Jones & Barth, 2002) require phasic GABA_A receptors (Behrens et al., 2007; Liotta et al., 2011). Therefore, it makes sense to examine models not containing interneurons.

Third, there is evidence for involvement of gap junctions in ripples (Draguhn et al., 1998) and FRs. In vivo evidence includes halothane block of ripples during physiological sharp waves (Ylinen et al., 1995) and seizures (Grenier et al., 2003), and FRs produced by whisker stimulation (Staba et al., 2004a,b). In models, VFO only emerges when coupling between neurons is strong enough for a spike to propagate from one to the other (Traub & Whittington, 2010); such coupling is realisable when it is axonal (Traub et al., 1999; Schmitz et al., 2001).

Fourth, although somatic depolarisation is permissive for VFO (e.g. Grenier et al., 2003), a concept embedded in network models (Traub & Bibbig, 2000; Munro, 2008; Munro & Börgers, 2010), such somatic permissiveness cannot be a general requirement – VFO occurs during in vitro sharp waves, when pyramidal cells can be strongly hyperpolarised (Bähner et al., 2011; Maier et al., 2011; Traub et al., 2012).

Axonal networks can oscillate via: (i) a series of waves, each initiated by a spontaneous action potential (ripple-like; Traub et al., 1999, 2010; Lewis & Rinzel, 2000; Munro & Börgers, 2010; Vladimirov et al., 2011); and (ii) an FR-like re-entrant oscillation (Lewis & Rinzel, 2001; Munro, 2008; Munro & Börgers, 2010; Vladimirov et al., 2012). Re-entry begins by breaking the symmetry of spike propagation in different directions around a cycle (see further below). Here, we use a small network (256 multicompartment cells) to permit analysis of the cyclic structure of the network, and to investigate the mechanism of FR onset.

Materials and methods

Patient recordings

Data from slice studies were derived from 18 patients (eight males; 10 females; mean age, 40.9 ± 4.1 years; range, 16–71 years; median, 42 years) with medically intractable epilepsy undergoing elective neurosurgical tissue resection (Roopun et al., 2010; Cunningham et al., 2012). All patients gave their written informed consent, before surgery, for use of the resected brain tissue. This study was approved by the County Durham & Tees Valley 1 Local Research Ethics Committee (06/Q1003/51; date of review 3 July 2006), and had clinical governance approved by the Newcastle Upon Tyne Hospitals NHS Trust (CM/PB/3707). All aspects of the study conformed with The Code of Ethics of the World Medical Association (Declaration of Helsinki), printed in the British Medical Journal (18 July 1964). Details on these 18 patients are as summarised in Table 1.

Table 1.

Summary of patient data

	Age (years)	Gender	Seizure semiology	Pathology	Brain region	Surgical outcome	Antiepileptic medication
1	44	M	Focal dyscognitive with occasional secondary generalisation	Mesial temporal lobe sclerosis	Temporal lobe	Seizure-free	CBZ, PGB
2	20	M	Focal dyscognitive seizures	Hippocampal sclerosis	Temporal lobe	Seizure-free	CBZ, VAL
3	32	F	Daily complex partial seizures with déjà vu, automatisms, occasional secondary generalisation	Oligodendroglioma, epileptic focus resection	Temporal lobe	Reduction in seizure frequency	LEV
4	54	M	Focal dyscognitive seizures	Glioma	Temporal lobe	Reduction in seizure frequency	CBZ, VAL
5	28	F	Epileptic seizures (unknown semiology)	Hippocampal sclerosis	Temporal lobe	Seizure-free	CBZ, GBP, LEV
6	71	M	Focal dyscognitive seizures	Glioblastoma	Temporal lobe	No information	No information
7	60	M	Status epilepticus	Grade 4 glioblastoma	Occipital lobe	Seizure-free	PHE
8	21	F	Focal dyscognitive with secondary generalisation	Grade 2 astrocytoma	Temporal lobe	Seizure-free	CBZ
9	37	F	Focal dyscognitive seizures	Hippocampal sclerosis	Temporal lobe	Seizure-free	CLB, VAL, ZON
10	40	F	Focal dyscognitive seizures with secondary generalisation	Hippocampal sclerosis	Temporal lobe	Persisting focal dyscognitive seizures	PHE, ZON
11	16	M	Focal dyscognitive seizures	Hippocampal sclerosis	Temporal lobe	Persisting focal dyscognitive seizures	LEV, VAL
12	70	F	Single seizure (unknown semiology)	Glioblastoma	Temporal lobe	No information	VAL
13	16	F	Focal dyscognitive with secondary generalisation	Mild cortical dysplasia	Temporal lobe	Persisting nocturnal seizures	No information
14	53	F	Single generalised tonic clonic seizure	Cavernous angioma	Temporal lobe	Seizure-free	LEV
15	44	F	Focal dyscognitive seizures	Hippocampal sclerosis, anterior temporal lobectomy	Temporal lobe	No reduction in seizure frequency	OXC
16	2	F	Focal dyscognitive seizures	Mesial temporal sclerosis	Temporal lobe	Two seizures since surgery	LTG
17	48	M	Focal dyscognitive seizures, occasional secondary generalisation	Hippocampal sclerosis	Temporal lobe	Seizure-free	CLB, LAC, OXC
18	55	M	Focal dyscognitive seizures	Craniotomy for space-occupying lesion	Temporal lobe	Seizure-free	No information

CBZ, carbamazepine; CLB, clobazam; F, female; GBP, gabapentin; LAC, lacosamide; LEV, levetiracetam; LTG, lamotrigine; M, male; OXC, oxcarbazepine; PGB, pregabalin; PHE, phenytoin; VAL, valproate; ZON, zonisamide.

In vitro human neocortex recordings

Human slices were derived from material removed as part of the surgical treatment of medically intractable cortical epilepsy from the left and right temporal and occipital regions. Anesthesia was induced with intravenous remifentanil with or without alfentanil (0.2–0.4 and 1 mg/kg, respectively). At induction, a bolus dose of propofol (1–2 mg/kg) was administered intravenously. The patient also received a muscle relaxant, vecuronium (0.1 mg/kg). Anesthesia was maintained with remifentanil, oxygen, and desflurane at a minimum alveolar concentration volume of 0.5–1.0. Resected tissue was immediately transferred to sucrose-containing artificial cerebrospinal fluid containing: 252 mM sucrose, 3 mM KCl, 1.25 mM NaH₂PO₄, 2 mM MgSO₄, 2 mM CaCl₂, 24 mM NaHCO₃, and 10 mM glucose. Neocortical slices containing all layers were cut at 450 µm (Microm HM 650 V), incubated at room temperature for 20–30 min, and then transferred to a standard interface recording chamber (34–36 °C) perfused with oxygenated artificial cerebrospinal fluid containing: 126 mM NaCl, 3 mM KCl, 1.25 mM NaH₂PO₄, 1 mM MgSO₄, 1.2 mM CaCl₂, 24 mM NaHCO₃, and 10 mM glucose. The time between resection and slice preparation was < 5 min. Single-electrode extracellular recordings (DC, 500 Hz) were conducted with artificial cerebrospinal fluid-filled glass microelectrodes (2 MΩ) connected to an extracellular amplifier (EXT-10-2F; NPI Electronic, Tamm, Germany). The GABA_A receptor blockers gabazine and picrotoxin, and the N-methyl-d-aspartate receptor blocker D-(-)-2-amino-5-phosphopentanoic acid, were obtained from Tocris (UK). The gap junction blocker carbenoxolone (disodium salt) was obtained from Sigma (UK). Multi-electrode array recordings were conducted with UTAH arrays (96 electrodes; electrode pitch, 400 µm) connected to a Cerebus (Blackrock Microsystems, Salt Lake City, UT, USA) data acquisition system. Signals were amplified and digitised (10–30 kHz) with the Cerebus system, and down-sampled to 1 kHz for subsequent offline analysis with MATLAB (MathWorks, Natick, ME, USA).

Post hoc immunocytochemistry

Upon termination of electrophysiological recordings, slices were immediately fixed in 4% buffered paraformaldehyde solution and stored overnight at 4 °C. Slices were resectioned at 40 µm with a vibratome (VT-1000S; Leica Microsystems, UK), and immunoper-oxidase-stained for non-phosphorylated neurofilaments (a marker for large pyramidal neurons that delineates layers III and V), with a monoclonal antibody for SMI-32 (Covance, Princeton, NJ, USA) and standard histological procedures (Gibson & Clowry, 2003). Immunostained sections were digitally scanned with a Leica SCN 400 slide scanner (Leica Microsystems), and archived on a Digital Image Hub (Leica Biosystems).

FR detection

Data were filtered with an equiripple finite impulse response filter, with bandpass settings to isolate FRs (for these experimental observations, defined as 180–500 Hz) activity (Fig. 2). The remaining activity mostly resembled brief trains of small population spikes of variable amplitude. We used a simple trough-detection algorithm and calculated inter-event intervals over time to detect FR events. The spatial location and extent of this FR activity was determined by calculating the overall FR power (> 200 Hz) for each electrode in the Utah arrays, and overlaying this on the stained slice used for the recording.

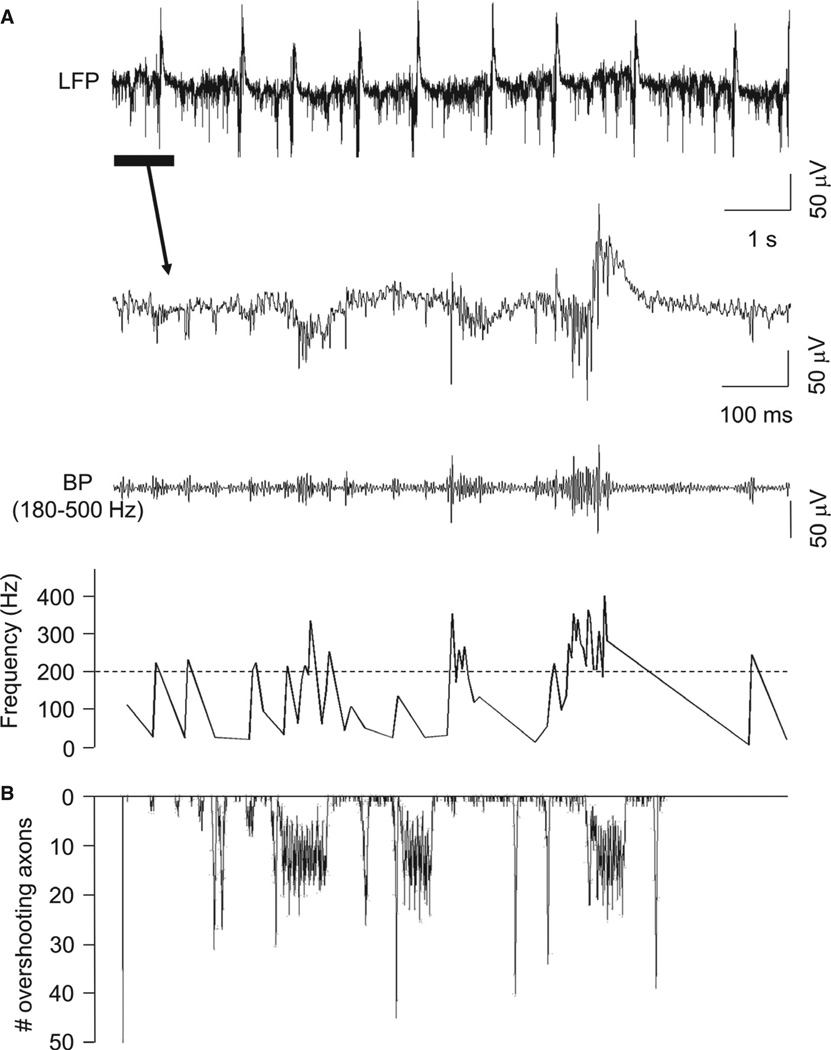
Fig. 2.

Human epileptic cortex shows brief, spontaneous epochs of FRs in vitro. (A) Upper trace – example of broadband (0.1 Hz to 1 kHz), spontaneous epileptiform activity in an LFP recording from a slice of epileptic human temporal cortex maintained in vitro (Patient 14; see Table 1). The expanded portion of the trace (below) illustrates epochs of rapid population spikes occurring off baseline or associated with slower LFP components (see Roopun et al., 2010). These high-frequency events could be isolated by bandpass (BP) filtering at 180–500 Hz (lower trace). Inter-event intervals showed instantaneous frequencies between approximately 200 and 400 Hz. (B) Model simulations captured the essence of this epileptiform behavior, including spontaneous, large-amplitude population spikes and brief runs of FRs when the number of active (i.e. generating full action potentials) axons was plotted against time (see Modeling methods).

Modeling methods

For the sake of conceptual simplicity, and because of data suggesting that VFO can be generated without chemical synapses (e.g. Draguhn et al., 1998; Traub et al., 2010; Cunningham et al., 2012), we simulated networks containing only pyramidal cells, coupled only by gap junctions, without chemical synapses and without interneurons. Gap junctions were, in the present model, located on axonal branches [for data supporting this feature, see Bähner et al. (2011) and Traub et al. (2012)]. Networks of 256–8000 neurons were simulated; the simulation data illustrated here were from 256-cell networks, which were the easiest to analyse. Five hundred milliseconds of neuronal activity was simulated in each run. The data base consisted of > 100 network simulations.

Structure and membrane properties of single neurons

We used the pyramidal neuron model described in detail in Traub et al. (2012). Each ‘neuron’ has a soma, branching dendrites, and a 24-compartment axon. The axon has two four-compartment branches, a proximal one and a distal one (see Fig. 1 of Traub et al., 2012). The relevant active conductances for the present study are – transient sodium [g_Na(F)]; delayed rectifier [g_K(DR)]; the transient ‘A’ type of potassium conductance [g_K(A)]; and the cholinergically gated ‘M’ conductance [g_K(M)]. [Both A and M conductances are known to be present in axons (Debanne et al., 1997; Pan et al., 2006).] Heterogeneity was introduced by slight variations in axonal bias currents and A-conductance densities, across different neurons. In the present model implementation, many of the other conductances are small enough to be negligible – slow sodium conductances, slow afterhyperpolarisations, and calcium conductances.

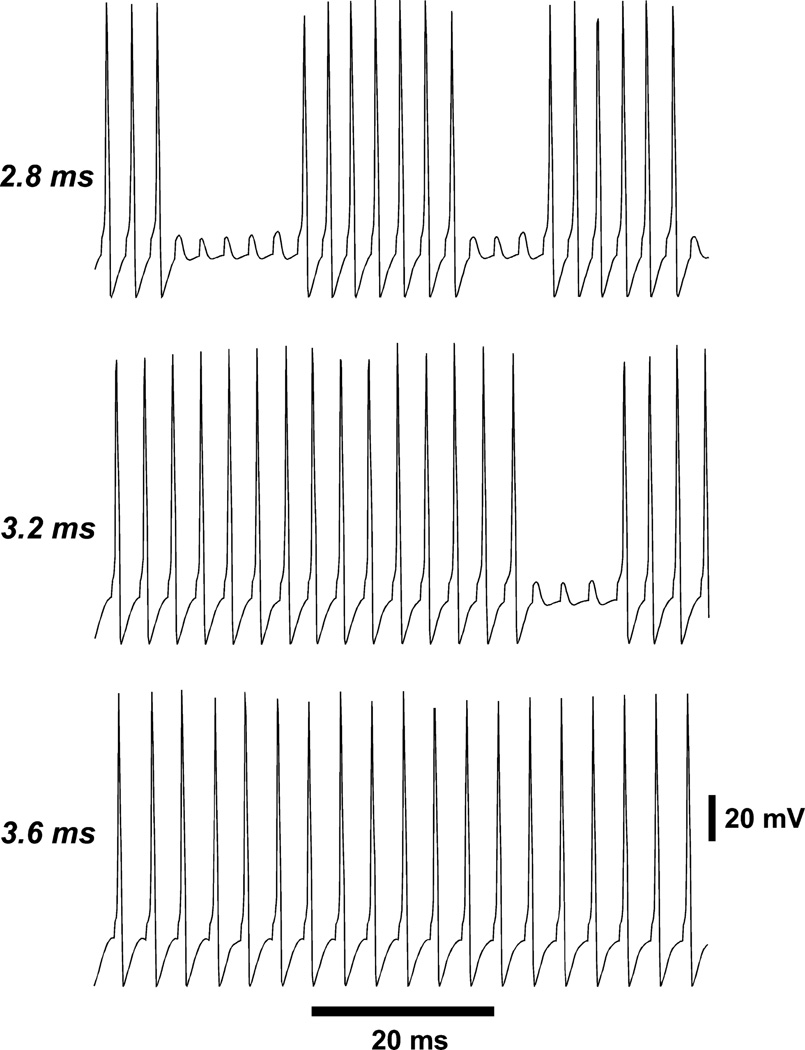
Fig. 1.

Response of a distal axon to strong periodic current pulses (3 nA, 0.4 ms, five compartments). At stimulation intervals of 2.8 and 3.2 ms, sequences of 1 : 1 firing are interrupted by an intermittent firing block [owing to axonal g_K(M)]; this intermittency does not occur here with a stimulation interval of 3.6 ms, which instead causes 1 : 1 following. Thus, the axonal refractory time is somewhat over 3 ms for this type of stimulation.

In some simulations, we increased distal axonal excitability relative to baseline conditions. This was done by doubling axonal R_M (from 1000 to 2000 Ω-cm²), and by increasing distal g_Na(F) density by 33 or 40%. Both of these manipulations tend to make the axons more excitable, and to promote passage of action potentials from one axon to another.

Background on ‘re-entry’

The mechanism that we shall propose for FR is called ‘re-entry’. We employ this term in a manner used in cardiac electrophysiology (specifically, ‘re-entrant circus movement’; Moe, 1975; Janse & D’Alnoncourt, 1987; Spach & Josephson, 1994). Heart tissue consists of myocardial cells, specialised conduction cells, AV nodal cells, sinoatrial cells, etc., all of which are excitable cells that can generate action potentials. The cardiac cells are also coupled by gap junctions, which allow spike propagation from one cell to another coupled cell, or at least from many cells to many other coupled cells (the experimental literature on this precise point is limited). Normal cardiac activity consists of periodic impulses, generated within a small region, that propagate reproducibly along a defined, branching pathway (i.e. without cycles), in such a way that each impulse ‘dies’ after it reaches the end of the branches – allowing, after a refractory period, the opportunity for the next impulse to propagate. During a re-entrant circus rhythm (which is abnormal), activity instead propagates around a cycle of excitable cells; from this cycle, activity can branch out to the rest of the heart. Cardiac re-entry is favored by certain abnormalities, either structural (aberrant pathways within the heart) or functional (e.g. inhomogeneities in refractory times). Such abnormalities are permissive for activity to begin propagating around a cycle in one direction only – a requirement for annihilation to be avoided – a neural example of annihilation would be a squid axon preparation, with two action potentials propagating in opposite directions towards each other, that meet, with both then failing to propagate further. With one-directional propagation around a cycle, however, re-entry can continue for a number of periods, until, perhaps, slower refractoriness, or an external stimulus, stops it. An axonal network, as we model it, is not a tissue like the heart, in the sense of being a three-dimensional syncytium of cells, and is better modeled as a network. Analogous physical ideas still apply, however.

Repetitive firing of isolated neurons

When cyclic (‘circus’) activity is modeled in abstract, cellular-automaton networks, either with neuronal-like (Traub et al., 1999, 2010; Lewis & Rinzel, 2000; Vladimirov et al., 2011, 2012) or with more general abstract elements (Singh et al., 2011), it becomes clear that the minimal cycle length is equal to the total number of ‘refractory’ plus ‘resting’ plus ‘active’ states. ‘Refractoriness’ in a cellular-automaton model, however, does not have a precise correlate in more physiologically realistic neuronal models with Hodgkin–Huxley-like ionic conductances. There are two reasons for this. First, the membrane variables that determine whether a cell (more precisely here, an axon) will fire are continuous, and not discrete. That is, firing behavior is not truly ‘all-or-none’. Second, M-current kinetics are slow enough that ‘refractoriness’ can accumulate over several closely spaced action potentials – a type of dynamics not generally included in cellular-automaton models. In spite of this, it is necessary to have some estimate of the ‘refractory period’ of our model neurons. We obtained estimates in two ways: (i) when steady currents (up to 0.4 nA) were injected into the distal axonal branch, then spikes could be generated in that branch at frequencies up to ~850 Hz; (ii) however, when the distal axonal tip was phasically and periodically stimulated at different frequencies, the distal branch was only able to fire 1 : 1 with the stimuli at frequencies up to ~280 Hz (Fig. 1). Intervals of 1 : 1 firing at higher frequency could be observed, but these intervals were interrupted by periods of failure (Fig. 1). When axonal g_K(M) was blocked, 1 : 1 following would occur reliably at frequencies up to ~420 Hz (not shown). Phasic stimulation has more relevance to our network simulations than does tonic stimulation, because what the networks do is allow spikes to jump from cell to cell across gap junctions. Thus, we can estimate the relevant ‘axonal refractory period’ as approximately 2.4–3.6 ms, depending on axonal potassium conductance densities.

Gap junction locations and conductances

In any one simulation, gap junctions were all located at homologous compartments in the axons. The gap junction site could be in the proximal axonal branch, but, in almost all cases, was in the distal axonal branch. Gap junction conductances were voltage-independent and non-rectifying. Conductances of 1–12 nS were tried. In the illustrations for this article, values of 4 or 6.5 nS were used.

Ectopic spikes

When gap junctions were located on the proximal axonal branch, then ectopic spikes were generated by 2.7-nA, 0.4-ms current pulses to the distal two compartments of the proximal branch, at random intervals (mean, 50 Hz per axon). When gap junctions were located on the distal branch, ectopic spikes were generated by 3.0-nA, 0.4-ms current pulses to the distal six compartments of the axonal trunk. The mean frequency was 50 Hz per axon when the network size was 256 neurons, but lower frequencies were used for larger networks (e.g. 1 Hz per axon for an 8000-cell network). Ectopic spikes were present from time 0 until 375 ms, and then stopped; this was in order to determine whether any present population activity would continue on its own, without ongoing ectopic spikes.

Network sizes and topologies

We performed simulations in networks of 240–8000 cells. The cells were organised into rectangular arrays. Most of the simulations were performed in 256-cell (16 × 16) networks, because this was the smallest size (given other parameters) in which we were able to observe periodic (re-entrant) behavior. Gap junction connectivity was random, subject to constraints:

1. The mean index (i.e. the mean number of gap junctions on an axon) was 2.

2. Connectivity was spatially localised. Thus, a cell at lattice position (i,j) could connect to a cell at lattice position (k, l) only if |i − k| ≤ 4 and |j − l| ≤ 4. Values for localisation constraint were varied in some instances.

3. In some cases, there was a limitation on connectivity for individual neurons. For example, all neurons might be constrained to have four or fewer gap junctions (respectively – five or fewer, or six or fewer). In a representative 256-cell network without any such constraint, one particular neuron had eight gap junctions, even though the average was two. [In general, in a random network, the mean number of gap junctions per neuron will be Poisson-distributed (Erdös & Rényi, 1960). With constraints on spatial localisation, however, the degree distribution will be binomial – of course, approximating a Poisson distribution as the constraint becomes larger and larger. When an additional connectivity constraint is imposed, we do not have an analytical formula for the degree distribution; qualitatively, however, one can see that it will start to approximate to a uniform distribution, as branches at highly connected nodes are removed and redistributed to nodes with lower connectivity.]

The structure of a portion of smaller networks was sometimes drawn by hand. Specifically, we would remove isolated cells and small subnetworks, as well as any cell lying on a tree (i.e. cells that do not lie on any cycle). What was left was the ‘cyclic core’, in which re-entrant activity (if present) must be generated.

Spike propagation times

In cellular-automaton models of network activity (e.g. Traub et al., 1999), there is a basic time step that corresponds physically to the time that it takes for a spike in one cell to propagate to a connected cell. However, just as is the case for ‘refractoriness’, such a ‘spike propagation time’ is an approximation in a network that contains ionic conductances, differences in the number of gap junctions per neuron, and heterogeneity in intrinsic properties. The reason, of course, is that propagation time, across a gap junction, will not be constant but will depend on membrane conditions and shunts from other gap junctions. In one simulation (256-cell network), we used explicit network connectivity, as well as axonal spike times (time resolution, 0.1 ms) during a wave of activity, to measure propagation delays across the system. Most propagation delays were 0.1 ms, but delays of 0.2 ms and even 0.3 ms were also observed. If we take 0.1 ms as the basic time step, and 300 Hz (~3.3-ms period) as a re-entrant population frequency, cycles of length ≥ 30 must be driving the re-entrant rhythm.

Analysis of loop structure

In order to make sense of re-entrant activity in a particular network, it is essential to know the properties of the loops (cycles) that are present (Vladimirov et al., 2012). In random networks that are sufficiently large, it is possible to estimate the number of loops of length L (N_L) by analytical methods (Dorogovtsev et al., 2008), when L is much less than log(N) (N = number of cells in the network). N_L follows an exponential law, with exponent L. Strangely, when N is large enough, N_L is independent of N. In the present case, however, we are mostly looking at networks where N = 256 and L = 30 or even more, so that it is not true that L is much less than log(N). Indeed, 30 is larger than log(256) ~ 5.5. Therefore, we used a different method. In a sample 256-cell network, we explicitly listed the loops up to length 20, using an algorithm whose MATLAB code was kindly provided by J. J. Howbert. As expected, the distribution of N_L (L = 5, …, 20) followed an exponential law, with N₂₀ = 12 486. Extrapolating this exponential law, we estimate that the representative network contains an astonishing 2.14 million different cycles of length 30. It is important, in interpreting the results, to appreciate the enormous complexity of a network having only 256 cells and that is connected sparsely (mean of only two connections per cell).

Comment on randomness and noise in the simulated system

Our simulations use a pseudorandom noise generator (‘durand’), and are therefore deterministic and reproducible (on the same computer with the same compiler), provided that the same ‘seeds’ are used for the noise generator. The program uses noise in two distinct fashions – first, to generate network topology (i.e. gap junction connectivity); and second, to generate ectopic spikes. In some cases, we generated different realisations of a given set of network parameters, by varying the first seed; in other cases, we varied dynamical behaviors of a given fixed network realisation, by varying the second seed. It is essential to emphasise that a given network realisation might, or might not, generate FRs, depending on the second seed (the one used for random ectopic spike generation) – the transition between different collective types of activity in our system has an essential stochastic component. The reasons why this should be true will be clarified below.

Rhythmicity

We define rhythmicity here as the ratio of the first side peak to the central peak, in autocorrelations of 50 ms of data – data either for total axonal firing, or for individual axonal firing times (which were binned at 0.5 ms).

Computation details

Simulation code was written in Fortran, for the mpi parallel environment, and compiled with the mpxlf command. Programs ran on 20 nodes of an IBM 7040-681 AIX parallel machine. Simulation of 50 ms of activity for a 256-cell network took ~1.8 h. Power spectra were computed for 500 ms of total axonal activity (i.e. the number of axons at the gap junction site that were firing overshooting action potentials), with a fast Fourier transform algorithm. We plotted the axonal activity because it yielded the most direct summary of what the network as a whole was doing. Source code is available from R. D. T. (rtraub@us.ibm.com).

Results

Distinction between ‘ripples’ and ‘fast ripples’ in this article

Because the frequency threshold between ripples and FRs is elastic when different studies are compared, how is one to define a useful and practical value for this threshold? [The origins of the various different thresholds are complex, and include numerous possibilities: (i) patient-to-patient variability; (ii) human vs. experimental animal differences; and (iii) different temperature, extracellular fluid composition, etc. between in vitro and patient data. There may also be genuine differences in FR mechanisms, patient-to-patient, or patient-to-experiment.] We have tried to take a logical approach as follows. Our model networks often showed a sudden switch in oscillation frequency (and other oscillation properties), with frequencies straddling some threshold value that lies between 200 and 300 Hz – that is, a value similar to the cutoff between ripples and FRs often seen in the literature. There is one mechanism for oscillations at the lower frequencies (presumably corresponding to ripples), and a different mechanism for oscillations at the higher frequencies (presumably corresponding to FRs). The problem is that, in human tissue, one does not have the same access to oscillation mechanisms as one does in the model; in the model, almost all aspects of the mechanism are (at least in principle) accessible. In contrast, with human tissue, one can only draw certain partial experimental correspondences (with pharmacology, multiple extracellular recordings, intracellular recordings, imaging, etc.) between biological data and simulation data. We shall therefore assume – and admit, for now, that it is just an assumption – that FRs are occurring in human tissue when there is an abrupt transition from a lower frequency (presumed ripple) to a higher frequency (presumed FR), with the threshold at ≥ 180 Hz (Fig. 3Bii), or if the field is oscillating at > 250 Hz.

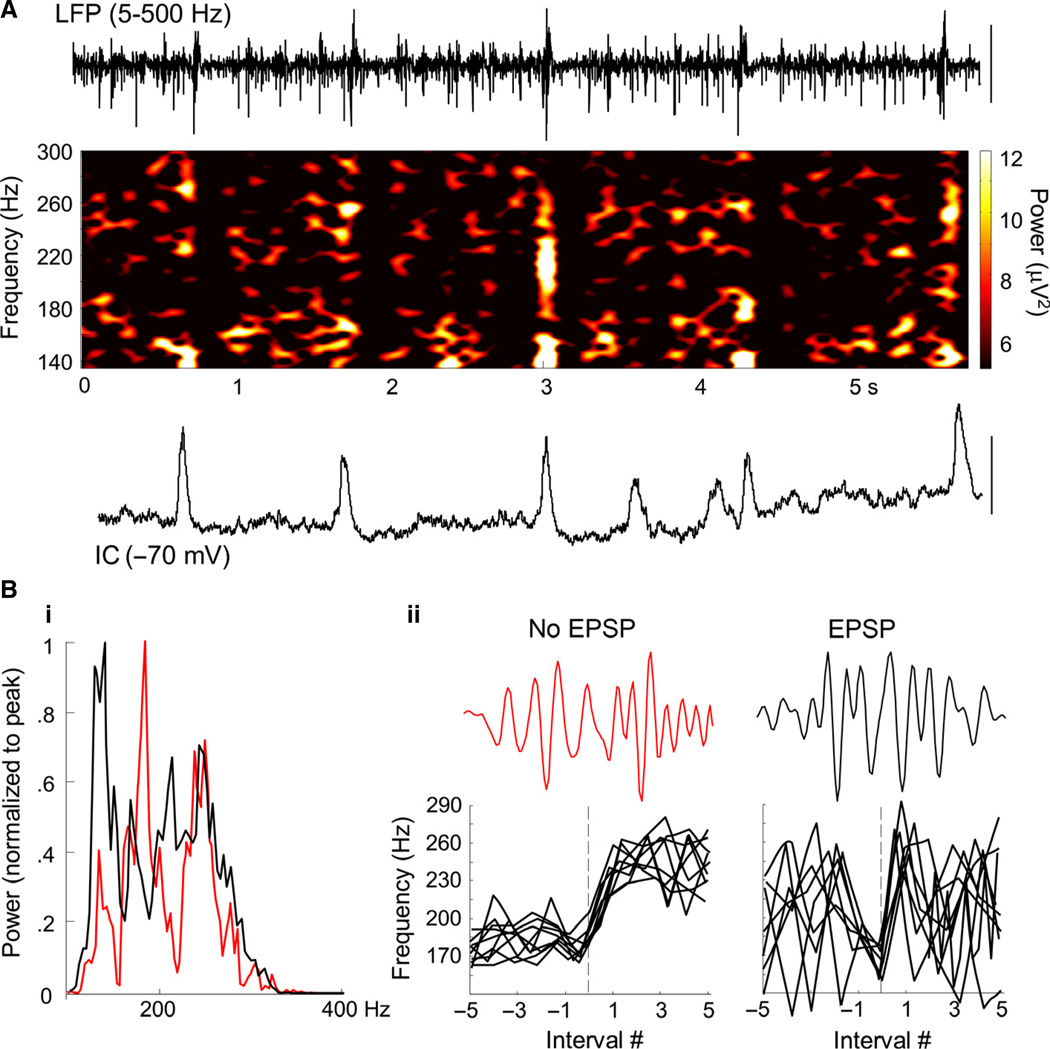
Fig. 3.

Ripple and FR discharges in human epileptic neocortex in vitro are modified by, but do not depend upon, synaptic excitation. [Data from Patients A, B and C of Roopun et al. (2010).] (A) Example LFP from layer 3 neocortex (5–500-Hz bandpass) and concurrent intracellular (IC) recording from a layer 3 pyramidal cell hyperpolarised to −70 mV mean membrane potential, to expose spontaneous excitatory synaptic inputs. Note the near-continuous presence of epochs of activity in the ripple/FR frequency range demonstrated in the corresponding LFP spectrogram. Scale bars – 200 µV (field LFP), 6 mV (IC). (B) (i) Mean power spectra plotted from 100 to 400 Hz for 200-ms epochs of data (10 each from three), for intervals between spontaneous EPSPs (red) or during EPSP events (black). Note that the ~200-Hz ripple frequency peak is replaced by a lower-frequency ~150-Hz peak, and delineation of ripple and FR (> 200 Hz) events is abolished by EPSP generation. (ii) Examples of rapid transitions from ripple to FR activity in the absence of EPSPs, and the more erratic, unstable frequencies seen during EPSPs. Nine examples (three each from three slices) are aligned to a transition from ripple to FR, below single examples of LFP high-frequency activity.

Ripple-like and FR-like behavior in human epileptic cortex maintained in vitro

Spontaneous, transient high-frequency local field potential (LFP) events were recorded in slices from all 18 patients included in this study (Table 1). High-frequency events were seen alone or superimposed on larger, lower-frequency LFP events as reported previously in Roopun et al. (2010). High-pass filtering of the recordings (> 180 Hz) revealed these events to be composed of runs of variable-amplitude population spikes (Fig. 2). Instantaneous frequencies derived from population spike event detection rasters demonstrated a range of frequencies from approximately 200 to 400 Hz, along with larger, single population spikes occurring alone. Bath application of the GABA_A receptor antagonist gabazine (500 nM) to slices showing FRs did not alter the occurrence of these events [modal peak – control, 212.5 ± 12.5 Hz; gabazine, 213.5 ± 12.5 Hz (n = 2)]. Initial experiments with a Utah array also demonstrated that antagonism of GABA_A receptors with picrotoxin (at concentrations up to 30 µM) did not abolish FR activity (not shown). In addition, addition of the N-methyl-d-aspartate antagonist D-APV (50 µM) did not alter the FR behavior (n = 1; data not shown). This pattern of events was captured in the model detailed above when the number of axons firing full action potentials (overshooting axons) was plotted over time.

FR events and ripple–FR transitions in human cortex can occur without synaptic depolarisation

Data in which concurrent recordings from layer 3 pyramidal cells (n = 3; Roopun et al., 2010) allowed a comparison of synaptic excitation and high-frequency field events were reanalysed. To determine any differential relationship between ripples or FRs and excitatory postsynaptic potentials (EPSPs), epochs of field activity in superficial layers were separated into those associated with EPSPs and those where no EPSP was present (Fig. 3A). In general, no significant difference in mean frequency was seen (Roopun et al., 2010). However, a broader frequency range of activity was seen when synaptic excitation was present, including both higher and lower frequencies, than for transient high-frequency events arising from ‘baseline’ activity, i.e. when synaptic excitation was not present. Spectral analysis showed no significant difference in the peak power of FR events (18 ± 4 vs. 16 ± 4 µV₂, EPSP vs. no EPSP, 200–400 Hz; Fig. 3Bi). In contrast, the spectral peak in the ripple frequency range was significantly reduced when events occurred coincident with EPSPs (152 ± 14 vs. 185 ± 12 Hz, EPSP vs. no EPSP). Examination of period-by-period instantaneous frequency immediately before and after transitions from ripple (< 200 Hz) to FR (> 200 Hz) activity suggested relatively stable events in these two frequency bands in the absence of somatic EPSPs (Fig. 3Bii).

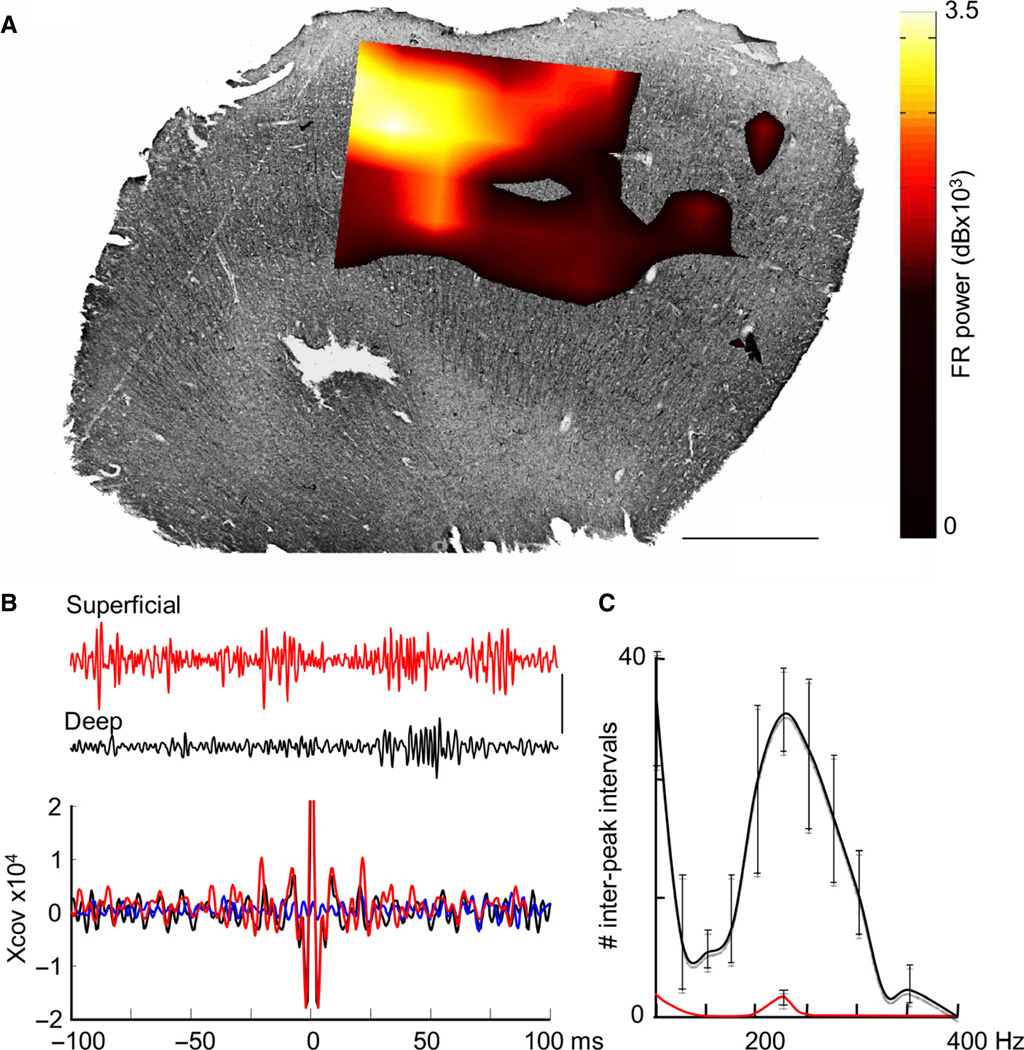
FR-like behavior alone occurred predominantly in the superficial (layers 2–4) cortex, with a clear modal peak at 226 ± 14 Hz (67 439 events; 18 patients). An example is illustrated in Fig. 4A. Note the patchy appearance in this example, with a spatial scale of order 1 mm. High-frequency transient events were also observed in layer 5, but occurred far less frequently and at a lower mean frequency than in superficial layers (185 ± 11 Hz). Autocorrelations revealed a near-absence of FR activity in deep layers, and this frequency difference accompanied very weak cross-covariance between layers (Fig. 4B). Bath application of 0.2 mM carbenoxolone to slices showing FRs reduced the incidence of FR events from 29 ± 3.1 to 1.3 ± 1.2 (n = 3), suggesting a gap junction-mediated mechanism (Fig. 4C). In order to understand how FRs can occur, and their relationship with more common, lower-frequency ripples, the model that captured this type of behavior is examined in detail below.

Fig. 4.

Ripple and FR discharges dominate in the superficial neocortex and are blocked by carbenoxolone. (A) Example of the spatial distribution of > 200-Hz activity in a slice from human neocortex stained for non-phosphorylated neurofilament. FR power is represented as a colormap hard-thresholded at 6 9 10³ dB. Scale bar – 1 mm. (B) Concurrently recorded LFPs (100–400 Hz, 0.5-s epochs) from superficial (red) and deep (black) electrodes, showing a greater incidence of activity in the frequency range in superficial layers. Mean autocorrelations of activity in the two layers (n = 10, 0.5-s epochs each from three slices), showing a greater incidence of FR activity in superficial layers. Cross-correlations between superficial and deep layers (blue) revealed very poor temporal interaction across the layers. Scale bar – 50 µV. (C) Data from three slices from three patients, demonstrating FR in control conditions (black line), and in the presence of carbenoxolone (0.2 mM). Ripple and FR frequency events were almost completely abolished by the gap junction blocker carbenoxolone.

Summary of model results

The simulation results suggest that gap-junctionally connected networks of neurons – where the electrical coupling allows spikes to cross from neuron to neuron (Mercer et al., 2006) – can generate ripples or FR-like events, and that certain structural network features are expected to favor FRs. However, in our model, FRs are triggered by randomly occurring ectopic spikes, unlike in the re-entry models that are usually studied (e.g. Gansert et al., 2007). Thus, a given network – with fixed topology, neuronal intrinsic properties, and electrical coupling parameters – observed only over a finite time interval may or may not actually exhibit a transition to FRs. This will be the case even if the given network is, in principle, capable of generating such a transition. The occurrence of the transition is expected to depend on initial conditions, and on stochastic properties of the ectopic spikes. As a consequence, establishing rigorous causal relationships between network properties and FR occurrence through simulations alone is extremely difficult; impractically numerous simulations are required. The following examples are therefore intended to provide heuristic understanding, and to illustrate physical principles, as well as to point to experimental tests – but not to provide quantitative predictions.

Ripple-like behavior in a small network

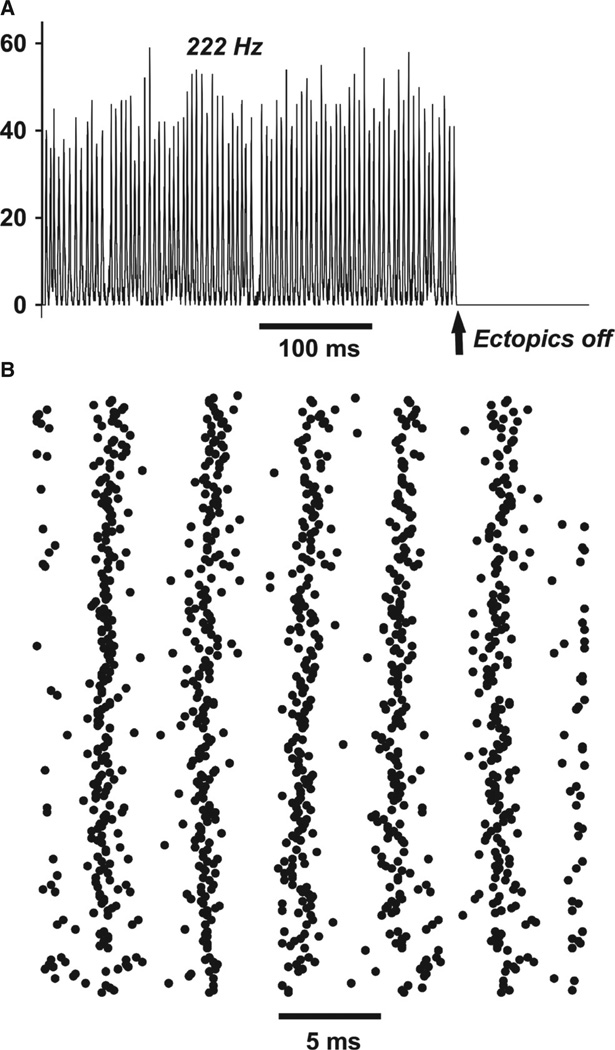
Figure 5 illustrates ripple-like oscillations in a 256-cell network [mean of two gap junctions per cell, but no more than four in any one cell; gap junction conductance 4 nS; axons with enhanced excitability as in Materials and methods – axonal R_M = 2000 Ω-cm², and distal axonal g_Na(F) on the high side]. Figure 5A shows the net population activity, i.e. the total number of axons whose gap junction site membrane voltage was ≥ 0 mV. This activity was regular, although not perfectly so, with a power spectral peak at 222 Hz; the activity stopped as soon as ectopic spikes were shut off. The data simply show that the present model, at least in part of its parameter regime, and despite its relatively small size, is able to replicate previous simulation studies of ripple-like very fast oscillations (Traub et al., 1999, 2010; Lewis & Rinzel, 2001; Munro & Börgers, 2010).

Fig. 5.

Ripple-like behavior in a network of only 256 axons. No axon was allowed to couple to five or more other axons, limiting the possibilities for spike transmission failure. The mean index (number of gap junctions per axon) was 2. (A) Number of axons firing overshooting action potentials at the gap junction site. Population activity is roughly periodic, at 222 Hz, and stops when spontaneous ectopic action potentials stop. (B) Raster of axonal firing during a portion of the ‘ripple’, showing the irregularity of activity at the single-cell level. This type of population rhythm, mostly in larger networks and using axons without branches, has been described in previous models (Traub et al., 1999, 2010; Lewis & Rinzel, 2001; Munro & Börgers, 2010; Cunningham et al., 2012).

The model is small enough, however, to allow examination of some of its ‘microscopic’ behavior, i.e. the details of spike timings of all of the axons (Fig. 5B) – the raster plot brings out the variability (quantified later) in spike timing of individual axons, despite the highly organised population activity. Once it becomes possible to measure (e.g. by optical imaging) multiple axons simultaneously, such an experimental prediction may become testable.

FR-like behavior in a small network

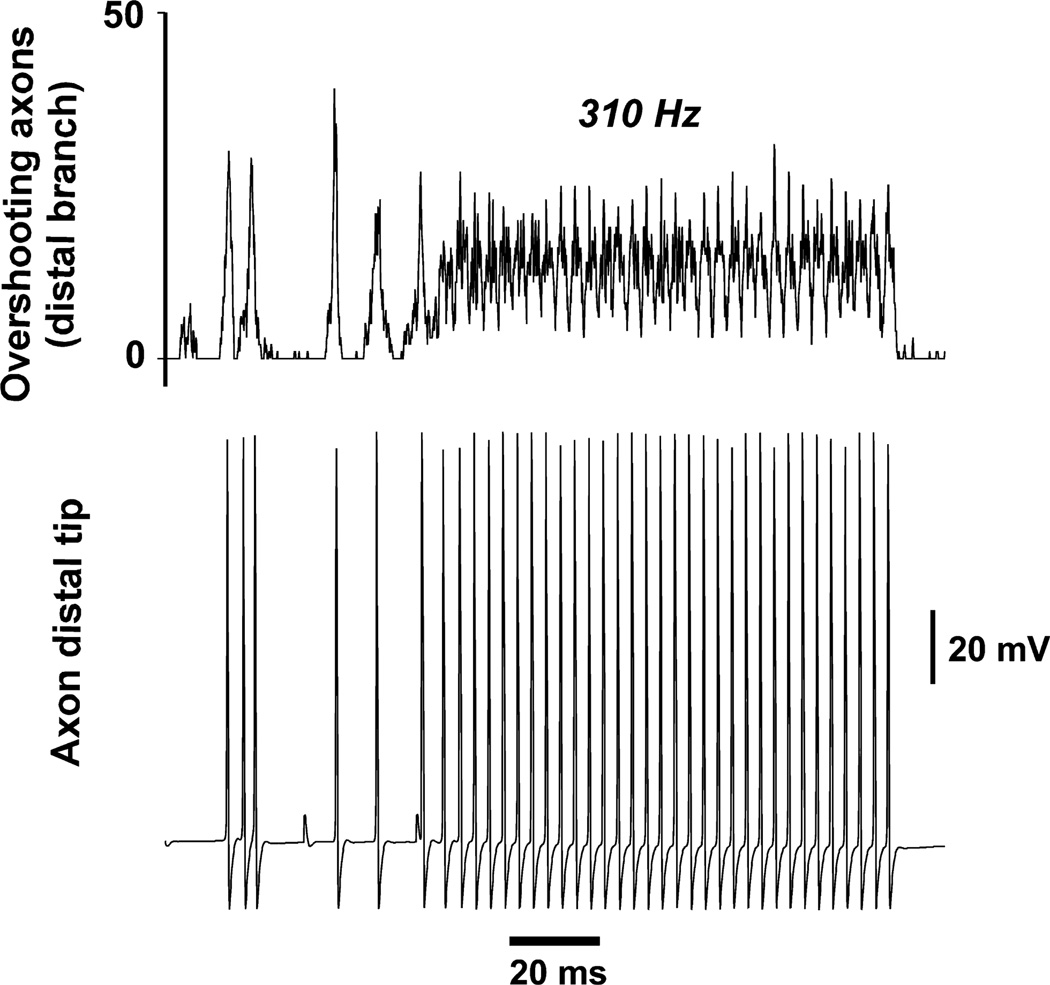
The network used to generate the data for Fig. 6 contained 256 neurons, as in Fig. 5, but there were the following differences (all of which would tend to favor spike propagation failure at certain axons): (i) there was no constraint on the number of gap junctions on any one axon – some axons had six gap junctions, and one even had eight; (ii) gap junction conductance was higher (6.5 vs. 4.0 nS); (iii) axonal R_M was lower (1000 Ω-cm²); and (iv) distal axonal g_Na(F) was on the low side (see Materials and methods). In the present case, ripple-like waves at the start of the simulation did not organise into a regular rhythm, but, after four or five such waves, there was the sudden onset of an extremely regular, faster rhythm at 310 Hz – an FR-like rhythm. The net population activity during this FR-like rhythm never fell to zero, unlike the case for the ripple-like rhythm in Fig. 5. Interestingly, in this example, the FR-like rhythm stopped abruptly (even though ectopic spikes continued), with individual axons suddenly halting their firing, without obvious hyperpolarisation (Fig. 6, lower trace). When the simulation was repeated with axonal g_K(M) blocked, the FR-like rhythm simply continued apace (not shown), suggesting that intrinsic axonal properties can contribute to the termination of FRs; conversely, when g_K(M) density was doubled with respect to that used in Fig. 6, then multiple FR-like events occurred, each of which lasted only for tens of milliseconds (not shown). Even with the simulation of Fig. 6, the FR-like rhythm restarted later in the simulation (not shown here), and then persisted after ectopic spiking was shut off.

Fig. 6.

Onset of FR-like behavior, in a network of 256 neurons. Ectopic spikes are present. Axonal R_m was 1000 Ω-cm² (vs. 2000 Ω-cm² for the simulation of Fig. 5), and distal axon g_Na density was also reduced as compared with Fig. 5 (see Materials and methods). As a result, spike propagation across gap junctions is unreliable, and ripple-like activity at the beginning of the simulation is broken up. This gives, to the FR-like activity, the appearance of arising de novo, or after a population spike, as can happen in vitro (Fig. 2). Note that the FR-like oscillation stops spontaneously towards the end of the illustration, even though ectopics continue; FR-like activity resumes later on (not shown). Blockade of axonal g_K(M) prevents the spontaneous termination of FR-like activity (not shown).

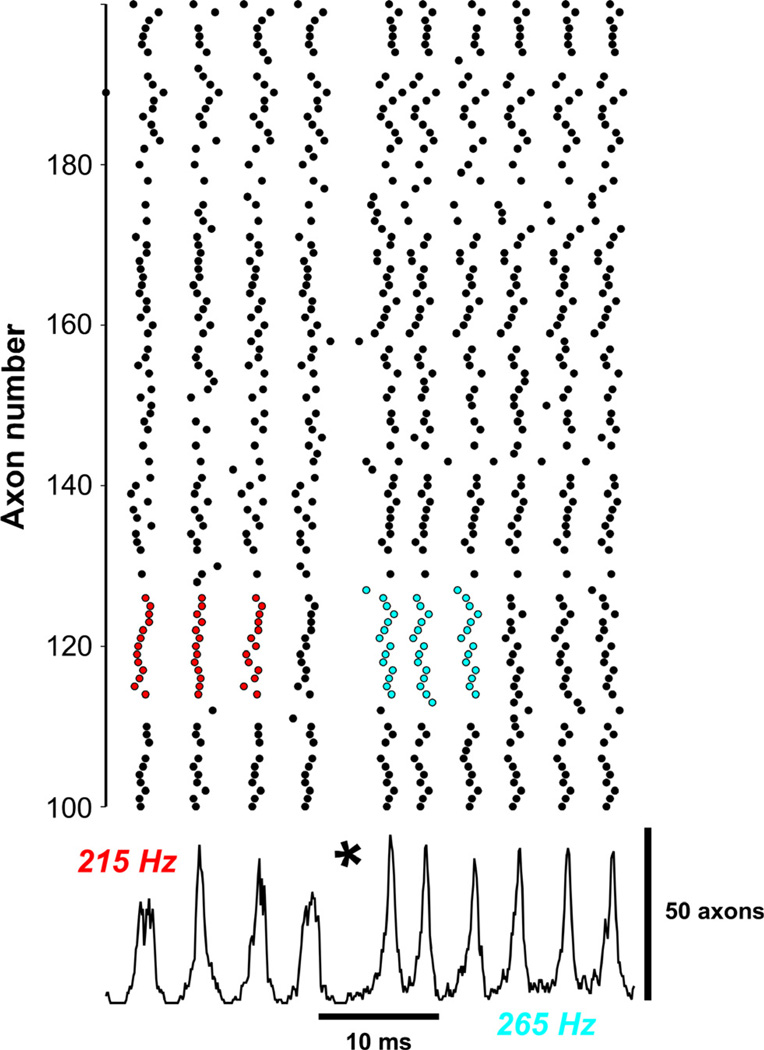
Switch from ripple-like to FR-like behavior

Up to now, we have illustrated ripple-like behavior alone, or FR-like behavior alone. We show in Fig. 7 the sudden transition from a brief epoch of ripple-like activity at 215 Hz to FR-like activity (at higher amplitude) at 265 Hz. (These data can be compared with those of Engel et al., 2009). A portion of the axonal raster is shown above, and total axonal activity below, with the asterisk marking the transition. The colored portions of the raster are examples of irregularity (at the level of small ensembles of cells) during the ripple-like rhythm (red circles, left), as compared with more regular patterns during FR-like activity (blue circles, right). The 256-cell network used to generate Fig. 7 had a network configuration that was intermediate between the configurations used for Fig. 5 (ripple-like; no axon could have more than four gap junctions) and Fig. 6 (FR-like; no constraint on the number of gap junctions on any one axon) – in the case of Fig. 7, there was a constraint, but it was weaker than for Fig. 5 – in Fig. 7, no axon could have more than six gap junctions. The network realisation used contained exactly three axons that each had six gap junctions, all lying on the cyclic core; there were other axons with six gap junctions, only some of which lie on the cyclic core.

Fig. 7.

Transition from ripple-like oscillation (215 Hz) to FR-like oscillation (265 Hz) – compare Engel et al. (2009). Shown is a 256-cell network with mean index 2, with no cell allowed to couple to seven or more other cells – coupling to six cells is allowed, and occurs three times in the network. Gap junction conductance (4 nS), axonal R_m and distal g_Na had ‘high’ values (as in Fig. 4), allowing stable rippling to occur (beginning of the simulation). Nevertheless, a transition to FR-like activity occurs at the time marked by *. A partial raster of axonal activity is shown above, and the number of overshooting axons below. The raster shows irregularity of single-axon patterns during ripple-like activity (red) vs. more regular activity during FR-like activity (blue). The FR-like activity continues after ectopic spiking is terminated (not shown). Details of how the FR transition occurs are shown in Fig. 8.

We consider next a critical aspect of how this switch in behavior, from ripple-like to FR-like, could come about.

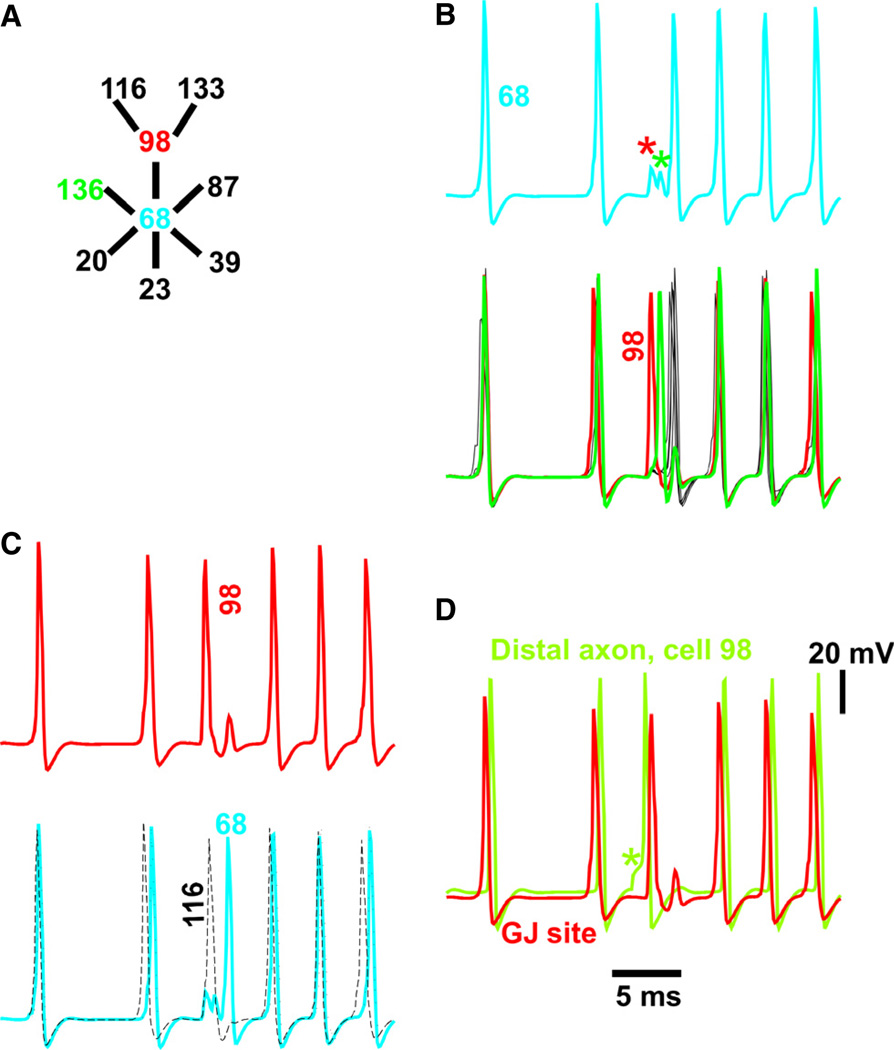
Because a change in network behavior takes place as constraints on the number of gap junctions allowed on individual axons are weakened, even with the total number of gap junctions held constant [an observation consistent with the data of Lewis & Rinzel (2001) and Munro & Börgers (2010)], it made sense to examine in detail the events in those few cells of high connectivity. As noted above, there were exactly three cells that each contained six gap junctions, all on the cyclic core, so we repeated the simulation of Fig. 7, recording the axonal membrane potentials (gap junction sites) of these three cells, and of all of the cells coupled to them. [Note that, in our simulation program, ectopic spikes are computed by a pseudorandom number generator, so it is possible to repeat a simulation and obtain the same outputs.] For two of the three ‘high-index’ or ‘hub’ cells, nothing unusual was noted, but for one of these cells – cell 68 – there was a conduction block of a very particular sort.

FR-like behavior can be initiated when there is an ectopic spike in an axon coupled to another axon, if the second axon is ‘highly connected’

Figure 8A shows some of the gap-junctional connectivity around hub cell 68 (blue, index = 6), including two other cells of interest – cell 136 (green) and cell 98 (red). The records in Fig. 8B–D show details of what was happening in these cells around the ripple–FR transition of Fig. 7 (*). Figure 8B shows hub cell 68 (above, axonal gap junction site) and the six cells coupled to it below (cell 98 in red; cell 136 in green; other cells in black). At the transition point, spikes in cells 98 and 136 failed to propagate into hub cell 68 (asterisks), and evoked spikelets instead. Immediately after the spikelets, hub cell 68 and its other four coupled cells fired almost synchronously. This – the occurrence of spikelets instead of full action potentials in cell 68 – is the expected spike transmission failure at a high-index cell.

Fig. 8.

Cellular events putatively leading to the onset of FR-like behavior in Fig. 7 – failure of spike propagation into a highly connected cell (cell 68, a hub with six gap junctions). (A) The relevant subnetwork, with thick lines, or edges, representing axonal gap junctions. (B) Axonal potentials, at the transition to FR-like activity, in the high-index hub cell (cell 68, above), and the six cells electrically coupled to it (below). Action potentials in cell 98 (red, the ectopic-generating cell; see below) and cell 136 (green) induce only pikelets in cell 68. (C) The spike in cell 98 (red, above) fails to propagate into hub cell 68 (blue, below), as shown in B, but the spike in cell 98 does propagate into the connected cell 116 (dots, below), and also to the connected cell 133 (not shown). The delayed spike in hub cell 68, in turn, fails to propagate back to cell 98. These are the well-known appropriate conditions for starting re-entry – although it is impossible to be certain, with our present methods, that propagation failure at this particular cell (cell 68) is what sets off re-entry in the whole network. (D) The spike in cell 98 that fails to propagate to cell 68 is ectopic, as can be determined from the potential at the distal axon (green, *), the axonal site where ectopic spikes are initiated in this model. GJ, gap junction.

Figure 8C shows cell 98 (a neighbor of hub cell 68, and one whose spike does not invade cell 68’s axon), along with another neighbor of cell 98 – cell 116 (black dashes). The point here is that, around the rhythm transition point, the axonal spike in cell 98 was blocked at hub cell 68, but did propagate into its neighboring cell, cell 116; it also propagated to the other neighbor (Fig. 6A), cell 133 (not shown). This is important. If hub cell 98’s spike were blocked in all directions, the initiation of re-entry would not be possible; but, in fact, cell 98’s spike was only blocked in one direction. The general concept illustrated here is, of course, well known.

Finally, Fig. 8D shows that the spike in cell 98 originated at the tip of the distal axon, and hence was ectopic – the voltage response to the current pulse that initiated an ectopic spike is obvious in the distal axon voltage trace (*), and the ectopic spike preceded the spike at the gap junction site – whereas, in all other cases, the reverse was true – spikes at the gap junction site (coming as they did from spikes in coupled axons) preceded the spike in the distal axon.

Thus, the data in Fig. 8 show that the transition to FR-like activity might arise when a random event occurs in the right place (adjacent to a high-index hub cell) at the right time. Specifically, concerning time, the ectopic spike (which is to initiate re-entry) must occur late enough after the previous wave for propagation to take place (i.e. axonal membranes are not refractory), but before too many cells get ‘caught up’ in a new noise-driven wave. The data do not prove, however, that the ectopic spike illustrated in Fig. 8 actually succeeds in establishing re-entry. We see that one step of propagation is present (into cells 116 and 133), but do not show the precise complete path that leads to a successful return to cell 98 – a matter of some complexity (see Vladimirov et al., 2012). Computational analysis of the present network structure showed that there are 2698 distinct cycles that contain both hub cell 68 and hub cell 98; thus, there are many possibilities available. Furthermore, other ectopic spikes in the system might be the one(s) that initiate re-entry. (Again, this highlights the enormous complexity of electrically coupled systems with even a few hundred neurons.)

In order to examine this latter point in more detail, we first repeated the simulation of Fig. 8, saving the axonal (gap junction site) voltage of each of the 106 neurons that lie on the cyclic core. There were two other neurons of index 6 that showed spikelets, indicative of conduction block, around the time of the FR transition. With our current visualisation methods, we cannot determine which precise event was the one to start FR. Another manipulation was to repeat the simulation of Fig. 8, but with one of the gap junctions, lying on hub cell 68, now blocked (so that cell 68 had index 5 instead of index 6). In that case, an FR transition nevertheless took place, at approximately the same time as in Fig. 8 – but without conduction block at cell 68. Thus, conduction block at that particular neuron is not essential for the FR transition. We found, however, conduction block around the FR transition in three other cells (two having index 6, and one having index 4). Identifying, in actual neural tissue, the precise site (at the single-neuron level) of an FR transition may thus prove difficult or impossible.

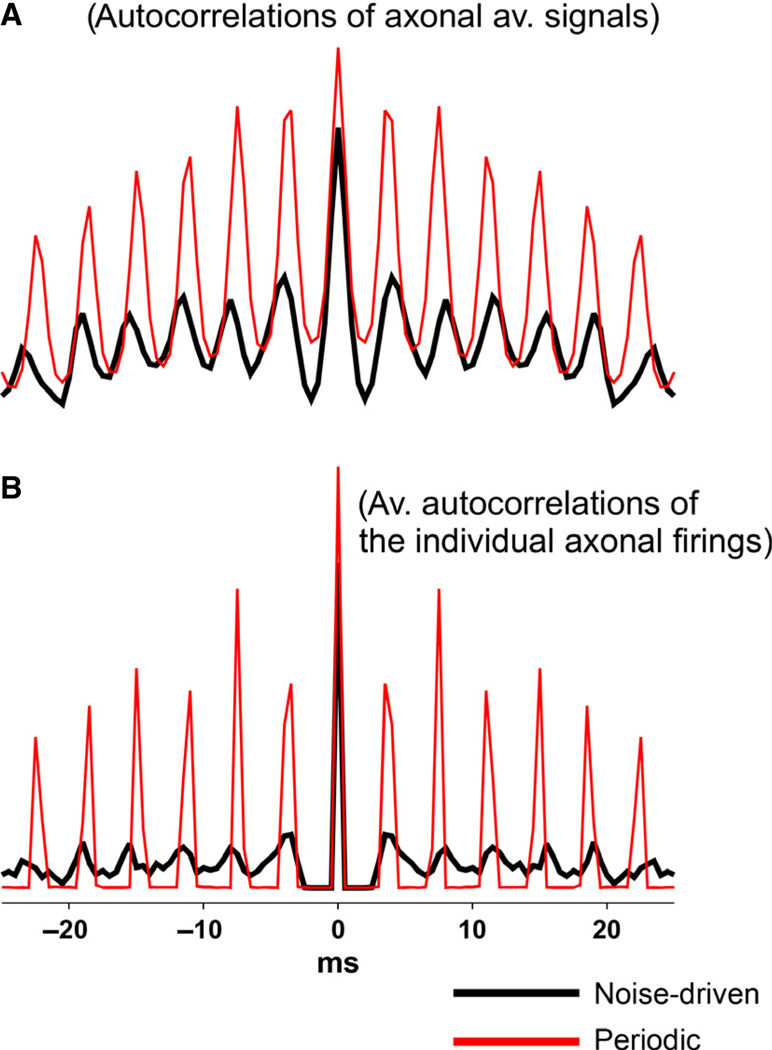
Quantification of the differences in rhythmicity between model ripple-like and FR-like behaviors

In Fig. 9, we provide an example of how one might quantify what is obvious to the naked eye. Figure 9 compares 50 ms of data from a network ripple-like oscillation (Fig. 5) and an FR-like oscillation (Fig. 7). Figure 9A shows autocorrelations of the total axonal activity signal (ripple-like noise-driven activity in black; FR-like, more periodic, activity in red). Clearly the FR-like activity was more rhythmic. However, in Fig. 9B, we also compare autocorrelations for the same simulations, but this time using averages (across the entire axonal populations) of autocorrelations of the individual spike firing times, binned at 0.5 ms. Again, as expected, the FR simulation data were more rhythmic; but the difference in rhythmicity was much greater for the single-cell data than when the average axonal activities were compared. This observation is consistent with one’s visual impression of the respective axonal raster data (e.g. Fig. 7).

Fig. 9.

Differences in rhythmicity for ripple-like behavior (black) and FR-like behavior (red). To obtain ripple-like behavior in a 256-cell network (total of 256 gap junctions) of mean index 2, all cells had index ≤ 4. To obtain FR-like behavior, all cells had index ≤ 6. All other parameters were identical. (A) Autocorrelations of 50 ms of total axonal activity. Rhythmicity (amplitude of first side peak/amplitude of central peak) was 52% for ripplelike activity and 84% for FR-like behavior. (B) Summed autocorrelations of all of the individual axonal firings over 50 ms, with a bin width of 0.5 ms. Rhythmicity was 16% for ripple-like activity and 48% for FR-like activity – a striking difference.

Discussion

In this article, we have presented a conceptually simple model of how a relatively small network (256 neurons) can generate either ripples, FRs, or a transition from ripples to FRs – all patterns that are observed in vivo and in vitro, particularly as repeated, transient events in the absence of overt synaptic excitation of pyramidal cells in superficial neocortical layers. The model can explain how FRs could arise in tiny volumes of tissue (Bragin et al., 2002), and suggests that an axonal M-current could help to terminate FRs. We would expect that cholinergic excitation, by blocking M-currents, would therefore prolong FRs.

The main postulate of the model is that both ripples and FRs are generated by gap junctions, independently of phasic chemical synaptic actions; the gap junctions must allow spikes to pass from neuron to neuron, and are most probably located in axons (Schmitz et al., 2001; Hamzei-Sichani et al., 2007). There is considerable evidence that ripples can be generated in this manner, including the recent experimental verifications of the predicted antidromic nature of somatic spikes during sharp wave–ripples (Papatheodoropoulos, 2008; Bähner et al., 2011). On the other hand, evidence for gap junctions playing a crucial role in FRs is more limited; such evidence stems from halothane suppression of FRs evoked by whisker stimulation, FRs that are superimposed on a slower somatosensory potential (which itself is not blocked by halothane; Staba et al., 2004a,b). However, the data in Figs 2–4 of the present study show that FRs can occur spontaneously in small regions of epileptic human cortex in a carbenoxolone-dependent, pyramidal neuron EPSP-independent manner, as seen for ripple-frequency oscillations previously (Roopun et al., 2010). Thus, if both types of high-frequency local population activity share the same gap junction-related pharmacological sensitivity, then we need to consider how the two rhythms may be formed – are they simply different frequency manifestations of the same underlying mechanism (as seen for glissandi; Cunningham et al., 2012), or are they fundamentally different at the network level? An important implication of the model, in the context of the above question, is that ectopic axonal action potentials sustain ripple-like oscillations; in contrast, ectopic spikes are also required to initiate FRs (Fig. 8), but are not needed to sustain FRs once they start. We predict a role for GABA_A receptors in axons (Trigo et al., 2008; Pugh & Jahr, 2011) in both ripples and FRs, because axonal GABA_A receptors can: (i) trigger ectopic activity (Stasheff et al., 1993a,b); (ii) induce gap junction-dependent VFO in axonal networks (Traub et al., 2003); and (iii) potentiate somatic firing during in vitro sharp wave–ripples (Bähner et al., 2011).

A conceptual understanding of how re-entry can work in a complicated network that contains multiple cycles comes from the work of Vladimirov et al. (2012) and Singh et al. (2011) (see also Gansert et al., 2007). (There are differences in detail in the approaches of these two studies – Vladimirov et al. employed a few gap junctions, or links, with special properties, and used brief stimuli applied to a subset of cells; the second study examined the behavior after one or another set of initial conditions, in networks without stimuli and where the links had uniform properties.) Here is the nub of the conceptual problem – it is easy to picture a neuronal (or cardiac) action potential propagating in one direction around a cycle of cells, each connected to two neighbors, and forming a circle – provided that the initial conditions are right for propagation to proceed in one direction only, and provided that propagation from one cell to a connected, non-refractory, neighboring cell is reliable. And, of course the cycle must be long enough for the propagating action potential to return (around the cycle) and to find and re-invade cells that have recovered from refractoriness. However, what will happen when one or more other cycles intersect our basic cycle, something that will surely happen in a random network?

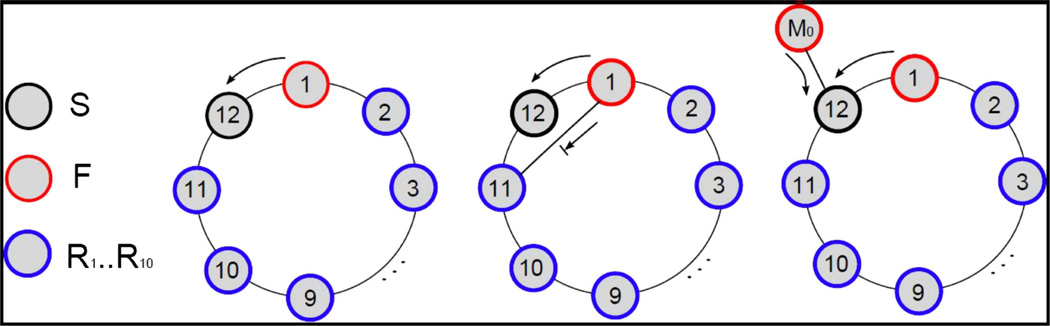
This question is most readily addressed in a network of cellular-automaton- like elements, rather than in a network of ‘realistic’ neurons. To be specific, suppose that our model neurons have a resting state (S), a firing state (F, the action potential), and 10 (to pick a number) refractory states (R₁, R₂, …, R₁₀) – 12 states in all (Fig. 10, left). The normal sequence of events for a cell will be: S → F → R₁ → R₂ → … → R₁₀ → S. Suppose that we have a cycle of 12 nodes, N₁, N₂, …, N₁₂, and to start (at time 1) we have N₁ = F, N₂ = R₁, …, N₁₁ = R₁₀, N₁₂ = S. Propagation can only go in one direction (counter-clockwise in Fig. 10) – N₁ cannot propagate to N₂ (because N₂ is refractory), but it can propagate to N₁₂. Hence, at time 2, we have N₁ = R₁, N₂ = R₂, …, N₁₀ = R₁₀, N₁₁ = S, N₁₂ = F, and so forth, in a persistent reentry, or circus, movement. Clearly, a cycle of length < 12 cannot support continuing activity, because the propagating firing will hit a refractory ode. On the other hand, what happens if we introduce a new link (a gap junction, in effect), say between N₁ and N₁₁? If N₁ is in state F (i.e. is firing; Fig. 10, middle), then N₁₁ must be refractory; likewise, if N₁₁ is firing, then N₁ is refractory. Thus, intersecting cycles make no difference once re-entry has actually started.

Fig. 10.

Periodic activity in a cycle of minimal length, for a cellular automaton-like model. ‘Cells’ can (left) be in a resting state S (green), a firing state F (red), or refractory states R₁, …, R₁₀ (blue). Left – a cycle of length 12 has the minimal length for supporting re-entry. In the situation shown, cell 1 is firing and about to excite cell 12, which is at rest. Other cells are refractory. Middle – a ‘shortcut’ (straight arrow) has no effect on re-entry around a minimal cycle. In this case, firing cell 1 can excite resting cell 12, as before, but cannot excite refractory cell 11. Right – cells connecting into a minimal cycle have no effect on re-entry. In this case, firing cell M₀ is ready to excite cell 12, but cell 12 is being excited by cell 1 in any case; if an outside firing cell is connected to any other cell in the cycle, that cell would either be firing (and hence be oblivious to external inputs) or refractory (also oblivious). [See text for discussion of what can happen in cycles longer than the minimal length.]

Now suppose the cycle of length 12, with activity proceeding around it, is embedded in a larger network. For example, another node, M₀, is connected to N₁₂ (Fig. 10, right). Can activity from M₀ ‘invade’ our cycle and perturb it? For M₀ to invade, N₁₂ must be at rest, in state S. But then, as above, N₁ will be firing, in state F. In this case, N₁₂ would fire anyway, on the next time step – the input from M₀ does not change anything. Thus, our 12-cycle is not disturbed, either by ‘internal’ links between its cells, or by something trying to enter from the ‘outside world’.

Finally, suppose that activity in our 12-state ‘neurons’ is cycling around a loop of length > 12, perhaps of length 14, with nodes N₁, N₂, …, N₁₄. We could then have, at some time or other, this arrangement of states: N₁ = F, N₂ = R₁, N₃ = R₂, …, N₁₁ = R₁₀, N₁₂ = S, N₁₃ = S, N₁₄ = S. In the isolated loop of length 14, the next cell to fire would be N₁₄; however, if an intersecting loop crosses N₁₂, or N₁₃, ‘invasion’ can occur. This argument shows how re-entrant cycles that are longer than the minimal length are unstable, and can be ‘taken over’ by shorter cycles (Vladimirov et al., 2012), providing a reason why the shortest feasible cycles will dominate periodic network behaviors.

Unfortunately, in extrapolating these arguments (based on rigorously defined cellular automaton-like models) to models with membrane conductances, one must be cautious – ‘refractoriness’ is not precisely defined with voltage-dependent membrane conductances. Additional complexities arise because links between adjacent nodes (i.e. gap junctions between coupled neurons) are no longer exactly equivalent, owing to shunting effects (Fig. 8), and because re-entry in our current model arises spontaneously, not as a result of imposed initial conditions (as in Singh et al., 2010). We also observed, in a very large network (8000 neurons), two different frequencies that were simultaneously present (not shown) – as though parts of the network could act as though they were functionally uncoupled. In situations like this, there seems to be no recourse but to use simulations.

The present model is quite distinct from that of Ibarz et al. (2010) – the latter model depends on fast excitatory chemical synapses, and does not contain gap junctions. The model of Ibarz et al., so far as we can determine, does not account for ripples, or the ripple–FR transition. Indeed, there are fundamental structural, dynamic and predicted experimental features that differ between the Ibarz et al. (2010) study and the present study. For example, the time scales of cell–cell interaction are of order 0.1 ms in the present study (spike propagation time) and 2 ms in Ibarz et al. (2010) (time to peak of unitary synaptic conductance). Collective activity in the present study is generated by spreading waves and/or cycles of axonal firing, as opposed to intrinsic bursting in a population of strongly depolarised neurons in Ibarz et al. (2010). Oscillation periods in the present study are determined primarily by axonal network properties, and in Ibarz et al. (2010) by intrinsic refractory periods of neuronal membrane conductances (with the possibility of period halving in the network as a whole). Experimentally, the present model predicts FR occurrence without an underlying sharp wave or interictal burst, in agreement with our current and previous (Roopun et al., 2010) epileptic human neocortical data. In contrast, the Ibarz et al. (2010) model was based on an interictal spike model (Traub & Wong, 1982), so that large intracellular depolarisations were present, and used in the context of experimental hippocampal kainate epilepsy. These fundamental differences in models can be assessed in future with specific experiments, including testing the sensitivity of FRs to selective AMPA receptor blockade, and additional intracellular recordings during FRs to determine whether somatic bursting, with strong depolarisation, continues during FRs [present in the Ibarz et al. (2010) model, but absent in our model, as well as in the actual pyramidal neuron shown in Fig. 3].

Finally, it is clear that gap junction shunting, which allows re-entry to start (data above; Lewis & Rinzel, 2001; Gansert et al., 2007; Munro & Börgers, 2010), can work only if multiple gap junctions, putatively on axons, are close together, perhaps even on the same axonal branch (as in the present model). Once the putative gap junction protein is identified, it will be possible to test this anatomical prediction of the model in epileptic vs. normal human tissue. Given that connexin 26 has recently been shown to be present in developing neocortical pyramidal neurons (Yu et al., 2012), and that cells can dedifferentiate after an injury, one could hypothesise that neurons within an epileptogenic lesion overexpress (or re-express) connexin 26 in axons.

Abbreviations

EPSP

excitatory postsynaptic potential

FR

fast ripple

LFP

local field potential

VFO

very fast oscillation