Canonical Granger Causality between Regions of Interest

Abstract

Estimating and modeling functional connectivity in the brain is a challenging problem with potential applications in the understanding of brain organization and various neurological and neuropsychological conditions. An important objective in connectivity analysis is to determine the connections between regions of interest in the brain. However, traditional functional connectivity analyses have frequently focused on modeling interactions between time series recordings at individual sensors, voxels, or vertices despite the fact that a single region of interest will often include multiple such recordings. In this paper, we present a novel measure of interaction between regions of interest rather than individual signals. The proposed measure, termed canonical Granger causality, combines ideas from canonical correlation and Granger causality analysis to yield a measure that reflects directed causality between two regions of interest. In particular, canonical Granger causality uses optimized linear combinations of signals from each region of interest to enable accurate causality measurements from substantially less data compared to alternative multivariate methods that have previously been proposed for this scenario. The optimized linear combinations are obtained using a variation of a technique developed for optimization on the Steifel manifold. We demonstrate the advantages of canonical Granger causality in comparison to alternative causality measures for a range of different simulated datasets. We also apply the proposed measure to local field potential data recorded in a macaque brain during a visuomotor task. Results demonstrate that canonical Granger causality can be used to identify causal relationships between striate and prestriate cortex in cases where standard Granger causality is unable to identify statistically significant interactions.

1. Introduction

An important objective in brain research is to understand how information propagates between different regions (Jirsa & McIntosh, 2007). Electrophysiological measurements of brain activity can be useful for achieving this goal, since they provide rich information about the location and temporal dynamics of spontaneous and task-related brain networks. In particular, invasive local field potential (LFP) and electrocorticography (ECoG) measurements as well as noninvasive electroencephalography (EEG) and magnetoencephalography (MEG) data allow for the modeling of brain connectivity, with wide ranging implications for addressing neuroscientific questions (Astolfi et al., 2007; Bressler et al., 2007; Schoffelen & Gross, 2009), understanding mechanisms of neuropathology (Lin et al., 2009; Wilke et al., 2009), and studying neuropsychological conditions (Hesse et al., 2003). Many connectivity models require assumptions regarding the behavior of the relationship between signals from different regions; for example, autoregressive models try to find areas of the brain whose electrical activity co-varies with past activity in other areas of the brain (Cheung et al., 2010; Hesse et al., 2003).

This paper focuses on models based on Granger causality (GC) (Granger, 1969). Causal models estimate the strength and directionality of signal interactions by analyzing the joint distributions of their time series under appropriate modeling assumptions. Classical methods for causal modeling analyze causality between multiple time series in a pairwise fashion, using bivariate models (Geweke, 1982). However, pairwise analysis is not ideal for functional brain mapping experiments in which multiple time series are available from different sensors, voxels (in a reconstructed source volume), or vertices (from a reconstructed source surface). Usually, such time series can be spatially correlated because of the limited spatial resolution of the mapping techniques or because functional activation is spatially distributed across a larger region of cortex. One approach could be to remove the influence of these confounds via partial measures of causality (Guo et al., 2008), but such partial measures usually require the estimation of a complex parametric model and may be hard to interpret (Eichler, 2006; Kuś et al., 2004; Zhou et al., 2009).

Rather than analyzing causality independently between pairs of time series, in some cases it may be more desirable to analyze causality between regions of interest (ROIs) that each include multiple correlated time series (d’Alessandro et al., 2003). Grouping multiple time series together can reduce the number of variables to estimate in a parametric model, can improve the signal-to-noise ratio of the resulting causality measure, and can help in identifying long-range connectivity that might previously have been obscured by larger apparent short-range connectivity that is artificially introduced by crosstalk within the ROI (Bin et al., 2009).

Many methods have been proposed to assess connectivity between ROIs. One popular method is canonical correlation (Hotelling, 1936), which estimates an undirected model of connectivity by maximizing the correlation between weighted linear combinations of signals from two ROIs. In addition to providing a measure of connectivity, canonical correlation also provides an estimate of the relative contribution of each signal from each ROI to the correlation between the ROIs (Deleus & Van Hulle, 2011; Kuylen & Verhallen, 1981). Canonical correlation analysis, however, is not a causal model and provides no information about the direction of information flow between ROIs.

Models of directed interaction between ROIs often use the concept of GC. Multivariate Granger causality (MGC) (Barrett & Seth, 2010) relies on multivariate autoregressive models of the signals between each ROI. While MGC can be accurate when the data records are sufficiently long, MGC involves substantially more parameters to estimate than do bivariate methods and can be prone to overfitting and sensitive to noise. A possible way to reduce this effect is to use penalized autoregression to promote certain desirable qualities in the estimation of causality such as spatial smoothness or sparse connectivity (Valdés-Sosa et al., 2005). Another approach is Granger canonical correlation analysis (GCCA), (Wu et al., 2011) which aggregates signals in each ROI much like canonical correlation analysis. This approach results in a reduction of the number of parameters to estimate relative to methods like MGC and penalized autoregression, although it does not estimate the amount of causality or the underlying signals responsible for the causal connection (Sato et al., 2010), and can only identify the presence or absence of causality.

In this paper we formulate, develop, and apply a novel directed causal connectivity measure called canonical Granger causality (CGC) that combines the strengths of canonical correlation with the directionality of GC. Our CGC measure combines the strengths and overcomes the disadvantages of GC and MGC by using an optimized weighted linear combination of the time series to parsimoniously represent each ROI with a single time series. This is similar to the idea of canonical correlation, where the signal dimensionality is reduced by considering the weighted sum of signals (Correa et al., 2010). Subsequently, CGC computes standard bivariate GC between the two representative time series.

While CGC and MGC both summarize causal influences between ROIs, CGC is a more parsimonious model and thus is more stable for short timeseries as shown in the following sections. CGC and penalized autoregression both estimate causal models with low complexity, but CGC uses the a priori information to select regions of interest while penalized autoregression simply looks for sparse causal interactions without addressing problems related to crosstalk between signals. Finally, similar to GCCA, CGC also uses weighted sums to represent each region when estimating causality. However, CGC estimates the strength of causality between those regions; results from our simulations will show that CGC can thus better estimate the underlying connectivity betweeen the signals of interest in reach region.

A preliminary version of CGC was presented by Ashrafulla et al. (2012). This paper expands substantially upon the results presented in that work, presenting a refined procedure for computing CGC, using extensive simulations to evaluate and characterize the approach relative to methods like MGC and GCCA, and applying the method to identify causality in real LFP data.

This paper is organized as follows. In section 2 we review GC and MGC to establish the groundwork for CGC, and we describe GCCA for comparison. The CGC measure and associated algorithms are presented in section 3. A simulation study is described in section 4 that illustrates the advantages and disadvantages of the proposed approach. In section 5, the proposed measure is applied to real brain data acquired from a macaque performing a visuomotor task (Bressler et al., 1993), where we show that CGC can identify causal interactions between striate and prestriate regions of the occipital lobe. Finally, discussions and conclusions are presented in sections 6 and 7, respectively.

2. Review of Granger Causality Measures

2.1. Granger Causality (GC)

Let x₁ and x₂ be two time series of length N. If the past values of x₂ substantially improve the prediction of x₁, then x₂ is said to “Granger cause” x₁ (Granger, 1969). GC thus attempts to measure the extent to which past values of x₂ can be used to predict the present value of x₁ (Sims, 1972). Mathematically, calculation of GC from x₂ to x₁ considers two different P^th order autoregressive (AR) models given by:

$$x_1\left[n\right]=\sum _{p=1}^{P}b\left[p\right]x_1[n-p]+r_1\left[n\right]$$ (1)

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\hfill x_1\left[n\right]\hfill \\ \hfill x_2\left[n\right]\hfill \end{array}\right]=& \sum _{p=1}^P\mathbf{A}\left[p\right]\left[\begin{array}{c}\hfill x_1[n-p]\hfill \\ \hfill x_2[n-p]\hfill \end{array}\right]+\left[\begin{array}{c}\hfill s_1[n-p]\hfill \\ \hfill s_2[n-p]\hfill \end{array}\right]\hfill \\ \hfill n=& 1,\dots ,N\hfill \end{array}$$ (2)

where the AR coefficients $b\left[p\right]\in \mathbb{R}$ and $\mathbf{A}\left[p\right]\in {\mathbb{R}}^{2\times 2}$, p = 1, … , P, are estimated by minimizing the variance or 2-norm of the prediction errors r₁[n] and [s₁[n] s₂[n]]^T in equations (1) and (2) respectively. The quantities

$${\rho }_1^2=\frac{1}{N-1}\sum _{n=1}^N{\left(r_1\right[n\left]\right)}^2\mathrm{and}{\sigma }_{2\to 1}^2=\frac{1}{n-1}\sum _{n=1}^N{\left(s_1\right[n\left]\right)}^2$$ (3)

measure the total AR prediction errors under the two different models. ${\rho }_1^2$ is a measure of how well the past of x₁ can be used to predict its future values, while ${\sigma }_{2\to 1}^2$ is a measure of how well the past of both x₁ and x₂ can be used to predict future values of x₁. GC is computed as the ratio of these two residual errors:

$$G_{x_2\to x_1}=\ln \frac{{\rho }_1^2}{{\sigma }_{2\to 1}^2}.$$ (4)

GC takes values between 0 and ∞, with large values of GC indicating that the past of x₂ contributes significantly to the prediction of x₁.

GC requires the estimation of a modest number (P+4P = 5P) of AR coefficients, which makes estimation of GC relatively stable for short time series (low N) or more complex models (high P). Granger causality does not provide a mechanism for analyzing causality between three or more time series. In addition, when GC is applied pairwise to spatially-correlated signals from multiple areas in the brain, GC is biased towards finding higher causality between spatially-adjacent areas (Wang et al., 2007).

2.2. Multivariate Granger Causality (MGC)

MGC is one method to extend GC for analyzing causality between two sets of multiple time series (Barrett & Seth, 2010). Given the vector-valued time series y₁ (with M₁ values at each time point) and the vector-valued time series y₂ (with M₂ values at each time point), MGC attempts to measure the extent to which past values of y₂ can be used to predict the present value of y₁. Analogous to the two AR models used by GC, MGC considers two P^th order multivariate autoregressive (MVAR) models given by:

$${\mathbf{y}}_1\left[n\right]=\sum _{p=1}^P\mathbf{B}\left[p\right]{\mathbf{y}}_1[n-p]+{\mathbf{r}}_1\left[n\right]$$ (5)

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\hfill {\mathbf{y}}_1\left[n\right]\hfill \\ \hfill {\mathbf{y}}_2\left[n\right]\hfill \end{array}\right]& =\sum _{p=1}^P\mathbf{A}\left[p\right]\left[\begin{array}{c}\hfill {\mathbf{y}}_1[n-p]\hfill \\ \hfill {\mathbf{y}}_2[n-p]\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\mathbf{s}}_1\left[n\right]\hfill \\ \hfill {\mathbf{s}}_2\left[n\right]\hfill \end{array}\right]\hfill \\ \hfill n& =1,\dots ,N\hfill \end{array}$$ (6)

where $\mathbf{B}\left[p\right]\in {\mathbb{R}}^{M_1\times M_1}$ and $\mathbf{A}\left[p\right]\in {\mathbb{R}}^{(M_1+M_2)\times (M_1+M_2)}$, p = 1, … , P, denote the MVAR coefficient matrices which are estimated to minimize the variances of the prediction errors r₁[n] and [s₁[n]^T s₂[n]^T]^T. Similar to GC, MGC is defined as the ratio between the sizes of these two prediction errors and is given by:

$$M_{{\mathrm{y}}_2\to {\mathrm{y}}_2}=\ln \frac{\mid {\mathbf{P}}_1^2\mid }{\mid {\Sigma }_{2\to 1}^2\mid }$$ (2)

where ∣·∣ denotes the matrix determinant and

$${\mathbf{P}}_1^2=\frac{1}{N-1}\sum _{n=1}^N\left({\mathbf{r}}_1\left[n\right]{\mathbf{r}}_1^T\left[n\right]\right)$$ (8)

$${\Sigma }_{2\to 1}^2=\frac{1}{N-1}\sum _{n=1}^N\left({\mathbf{s}}_1\left[n\right]{\mathbf{s}}_1^T\left[n\right]\right).$$ (9)

As with GC, MGC takes values between 0 and ∞, with large values indicating that the past of y₂ contributes significantly to the prediction of y₁. Relative to GC, MGC enables the estimation of causality between two ROIs, with each ROI containing multiple time series. However, MGC requires the estimation of many more $(M_1^{2}P+{(M_1+M_2)}^{2}P)$ coefficients, which makes it less stable than GC, particularly when the number of samples is small.

2.3. Granger canonical correlation analysis (GCCA)

GCCA (sometimes named cluster Granger causality (Sato et al., 2010)) is an alternate measure of regional causality which is based on lagged correlations. Considering the vector-valued time series y₁ and y₂ above, and the order P which corresponds to the maximum lag in the causal interaction, GCCA is computed as (Wu et al., 2011)

$$\left(\widehat{\alpha },\widehat{\beta }\right)=\underset{\begin{array}{c}\hfill \alpha \in {\mathbb{R}}^{M_1},\beta \in {\mathbb{R}}^{M_2}\hfill \\ \hfill {\mid \mid \alpha \mid \mid }_{{\ell }_2}={\mid \mid \beta \mid \mid }_{{\ell }_2}=1\hfill \end{array}}{\arg \max }\mathrm{corr}\left({\alpha }^T{\mathbf{y}}_1\left[n\right],{\beta }^T{\mathbf{y}}_2^T[n-P]\right)$$ (10)

$${\mathit{R}}_{{\mathbf{y}}_2\to {\mathbf{y}}_1}=G_{{\widehat{\beta }}^T{\mathbf{y}}_2\to {\widehat{\alpha }}^T{\mathbf{y}}_1}$$ (11)

where corr(a, b) is the correlation between two processes a and b, and G represents the GC defined in (4). GCCA takes values between 0 and 1, with a zero value implying no causality. Since the only parameters to estimate are the weights, GCCA only requires the estimation of M₁ + M₂ parameters. In addition, GCCA can be solved simply via singular value decomposition techniques similar to those used for canonical correlation (Kuylen & Verhallen, 1981). GCCA is able to detect causality relatively well (Sato et al., 2010), but as we will demonstrate in simulation in section 4, GCCA is not effective in determining the strength of causality.

3. Canonical Granger Causality (CGC)

This section introduces a new measure, CGC, that combines ideas from canonical correlation analysis and GC analysis. Like MGC, CGC enables the estimation of causality between two ROIs containing multiple time series. However, CGC uses a more parsimonious model than MGC, which makes it less sensitive to noise and less prone to overfitting. Like canonical correlation and GCCA, CGC uses weighted sums of time series to represent each region. However, CGC measures the amount of Granger causality and thus is able to better measure the strength of regional interactions.

Considering the vector-valued time series y₁ and y₂ introduced above, we define CGC as:

$$C_{{\mathrm{y}}_2\to {\mathrm{y}}_1}=\underset{\begin{array}{c}\hfill \alpha \in {\mathbb{R}}^{M_1},\beta \in {\mathbb{R}}^{M_2}\hfill \\ \hfill {\mid \mid \alpha \mid \mid }_{{\ell }_2}={\mid \mid \beta \mid \mid }_{{\ell }_2}\hfill \end{array}}{\max }{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}.$$ (12)

where G represents the Granger causality defined in equation (4). CGC is obtained by computing the standard GC on scalar-valued time series ${\widehat{x}}_1={\alpha }^T{\mathbf{y}}_1$ and ${\widehat{x}}_2={\beta }^T{\mathbf{y}}_2$ obtained from a linear combination of the original time series from each ROI. The linear combination weights for each ROI, α and β, are optimized to maximize the GC between ${\widehat{x}}_1$ and ${\widehat{x}}_2$. Note that we have constrained α and β to have unit norm because GC is invariant to rescaling of the data.

Given the unit-norm constraint, the estimation of α and β requires estimation of M₁ + M₂ − 2 parameters. Combined with the estimation of 5P AR coefficients for standard GC (cf. section 2.1), CGC requires the estimation of M₁ + M₂ − 2 + 5P parameters. Note that CGC has substantially fewer parameters to estimate compared to the $M_1^{2}P+{(M_1+M_2)}^{2}P$ parameters that must be estimated for MGC (cf. section 2.2), and that this difference is particularly pronounced for large values of P, M₁, or M₂. As we will demonstrate in section 4, this reduction in the number of parameters results in CGC being more stable and accurate in identifying ROI-to-ROI causality than MGC for short data records. However, we note that CGC is an ROI-wise measure that finds the strongest causal interaction between the two ROIs, and hence may not provide direct insight into the individual signal interactions if there are multiple causal connections between ROIs.

Computation of CGC requires optimization with respect to weight vectors α and β. Due to the unit-norm constraints, α lies on the (M₁ − 1)-sphere ${\mathcal{S}}^{M_1-1}$, and β lies on the (M₂ − 1)-sphere ${\mathcal{S}}^{M_2-1}$. In the appendix we exploit the structure of these constraint sets to introduce a numerical algorithm to optimize these weights, using a variation of a technique developed for optimization on the Steifel manifold (Edelman et al., 1998).

4. Simulations

We compared the properties of the CGC, MGC, and GCCA measures using multiple different simulated time series. Performance was evaluated by examining each method’s ability to find true causality while avoiding false causality. We tested all measures on simulated time series with varying numbers of samples (N), model order (P), and noise levels as described below.

4.1. Simulation models

We simulated directed networks of 2 ROIs (ROI₁ and ROI₂) with M₁ = M₂ = 4. Simulations were constructed from AR models, and included interference and noise (described in section 4.1.2). Simulations were generated for model orders P ∈ {2, 4, 6, 8, 10}, number of time points N ∈ {100, 200, 400}, signal-to-interference ratios SIR ∈ {1, 5, 25}, and signal-to-noise rations SNR ∈ {1, 5, 25}, with a fixed number of interferers (I = 2).

4.1.1. Simulated Signals of Interest

Each ROI has one underlying time series involved in information transfer between the ROIs, denoted by x₁ and x₂ respectively. We simulate these signals using bivariate AR processes according to:

$$\left[\begin{array}{c}\hfill x_1\left[n\right]\hfill \\ \hfill x_2\left[n\right]\hfill \end{array}\right]=\sum _{p=1}^P\left[\begin{array}{cc}\hfill D\left[p\right]\hfill & \hfill A\left[p\right]\hfill \\ \hfill 0\hfill & \hfill D\left[p\right]\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_1[n-p]\hfill \\ \hfill x_2[n-p]\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\eta }_1\left[n\right]\hfill \\ \hfill {\eta }_2\left[n\right]\hfill \end{array}\right].$$ (13)

Here, the past of x₁ has no effect on x₂ because the corresponding coefficients in the AR model are zero. The only possible causal information transfer is then from ROI₂ to ROI₁, with the amount of causality modulated by A[p], p = 1, … , P. The process is driven by simulated zero-mean white Gaussian innovations η₁ and η₂.

These AR models are generated randomly in such a way that (1) we consistently obtained stable AR models, and (2) the resulting P^th-order AR signals cannot be accurately modeled by another AR model with order smaller than P. To test the ability of the three measures to detect causality, we generated two types of processes: those for which there is no causality (A[p] = 0, p = 1, … , P) and those for which there is causality from x₂ to x₁ (A[p] ≠ 0 for some p = 1, … , P). In each case, we generated the coefficients for a given order P using the following steps:

1. We constructed two sequences:

   $$\begin{array}{cc}\hfill d\left[p\right]& =\frac{1}{p},p=1,\dots ,P,\hfill \\ \hfill a\left[p\right]& =\mathrm{Uniform}[0.15,0.3],p=1,\dots ,P,\hfill \end{array}$$

   where Uniform [j, k] is a uniformly-distributed random variable between real numbers j and k.

2. We set D[p] equal to 0.3 · d[p]. For no causality, we set A[p] = 0, P = 1, … , P. For causality, we set A[p] equal to d[p] · a[p]. Combined with the previous step, this procedure was found to always generate a stable process for our simulation parameters.

3. Using monotonically descending d[p] coefficients may admit lower-order AR modeling of signals (e.g. an AR model with P = 2 may sufficiently fit signals from an AR process simulated above without reordering for P = 4). So, to ensure the signals require order-P AR modeling, we randomly reordered the AR matrices:

   • (a) We let (q₁, q₂, … , q_P) be a random shuffling of the indices {1, … , P}.
   • (b) We assigned D[q₁] → D[1], D[q]₂ → D[2], … , D[q_P] → D[P].
   • (c) We applied the same reordering to A[p], p = 1, … , P.

4.1.2. Observation Model

Given the underlying signals x₁ and x₂, we simulated the measured vector-valued time series for each ROI according to

$${\mathbf{y}}_{\mathit{r}}\left[n\right]={\mathbf{g}}_{\mathit{r}}{x}_r\left[n\right]+\frac{{\delta }_{\mathit{r}}\left[n\right]}{\mathbf{SIR}}+\frac{{\epsilon }_{\mathit{r}}\left[n\right]}{\mathbf{SNR}}r=1,2,$$ (14)

where ${\mathbf{g}}_{\mathit{r}}\in {\mathbb{R}}^4$ is a vector describing the relative contribution of x_r to each of the 4 time series in ROI_r (drawn uniformly from ${\mathcal{S}}^4$ in our simulation), δ_r represents simulated interference, and ε_r is simulated measurement noise (white Gaussian with unit variance in our simulation).

The interference signals δ₁ and δ₂ are vector-valued time series used to emulate background brain activity that is not associated with causality between the two ROIs. To emulate within-region brain activity, we want the signals to be sums of causally related time series that are independent from signals in other regions of activity. The time series δ₁[n] and δ₂[n] are each simulated as a sum of randomly generated scalar AR time series z_r,i[n], i = 1, 2 according to:

$${\delta }_{\mathit{r}}\left[n\right]={\Sigma }_{i=1}^2{\mathbf{h}}_{r,\mathit{i}}{z}_{r,i}\left[n\right]r=1,2,$$ (15)

where h_r,i represent the contribution of each interferer to each time series with its corresponding region, and are drawn uniformly at random from ${\mathcal{S}}^4$. For region r ∈ {1, 2}, we enforce the desired within-region causality by generating the scalar AR time series z_r,1 and z_r,2 with autoregression of the same order P as the source model:

$$\left[\begin{array}{c}\hfill z_{r,1}\left[n\right]\hfill \\ \hfill z_{r,2}\left[n\right]\hfill \end{array}\right]=\sum _{p=1}^P\left[\begin{array}{cc}\hfill D\left[p\right]\hfill & \hfill B\left[p\right]\hfill \\ \hfill B\left[p\right]\hfill & \hfill D\left[p\right]\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\gamma }_1\left[n\right]\hfill \\ \hfill {\gamma }_2\left[n\right]\hfill \end{array}\right].$$ (16)

We choose the coefficients D[p] and B[p] using the same procedure described in section 4.1.1 for generating D[p] and A[p].

4.2. Detecting Causality

We used receiver operating characteristics (ROCs) to evaluate the performance of CGC and MGC. The ROC curve is a plot of the true positive versus false positive rate computed from a test statistic as a function of a decision threshold (Metz, 1978). For the simulation setup in section 4.1, we define a “true positive” as occuring when the causality from ROI₂ to ROI₁ exceeds the decision threshold applied to the Granger measure when A[p] is nonzero, while a “false positive” occurs when the causality from ROI₂ to ROI₁ exceeds the decision threshold when A[p] = 0, p = 1, … , P.

We performed T = 1500 Monte Carlo simulations, computing for each simulation

• CGC: C_y2→y1 and C_y1→y2,

• MGC: M_y2→y1 and M_y1→y2, and

• To establish a best case performance limit, we also computed bivariate GC using a linear combination of signals based on the true weights (g₁ and g₂) used to generate the multivariate data from the bivariate signals of interest: $G_{{\mathrm{g}}_2^T{\mathrm{y}}_2\to {\mathrm{g}}_1^T{\mathrm{y}}_1}$ and $G_{{\mathrm{g}}_1^T{\mathrm{y}}_1\to {\mathrm{g}}_2^T{\mathrm{y}}_2}$.

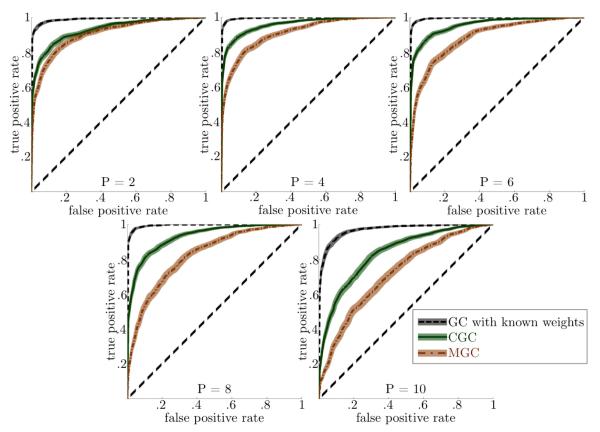
The empirical ROC curves for each measure derived from these simulations are shown in Figure 2 for the simulations where N = 400, SIR = 5 and SNR = 1. It can be seen from each of the plots that CGC shows a higher true positive rate than MGC for a given false positive rate. Increasing the order P of the simulated AR processes amplifies the difference between CGC and MGC, due to the increasing difference in the number of parameters between the two measures. Specifically, for P = 8 the number of parameters required for MGC is (4² · 8 + (4 + 4)² · 8)/(4 + 4 + 5 · 8) = 40/3 times more than the number of parameters required for CGC. Additionally, our simulations show that applying GC to ROI signals formed using perfect prior knowledge of the original weights g₁ and g₂ yields better performance than CGC, as expected. We note that with GCCA, we found ROCs and AUCs nearly equal to CGC for all simulations.

Figure 2.

CGC has a higher true positive rate for a given false positive rate than MGC. The dark lines are the mean ROCs, with the shadows indicating the 95% confidence intervals after bootstrapping. Knowing the true weights is better than CGC because CGC has an upward bias in the condition of no causality due to its maximization procedure, but such weights are not known in most practical applications.

In order to further compare the performance of CGC to MGC, we summarize the ROCs by calculating the area under the ROC curve (AUC). The AUC measures the ability of each measure to discern true directions of causality, averaged over all possible choices of the false positive rate. In order to estimate a 95% confidence interval of AUC non-parametrically, we performed 1000 bootstrap simulations (Efron & Tibshirani, 1993).

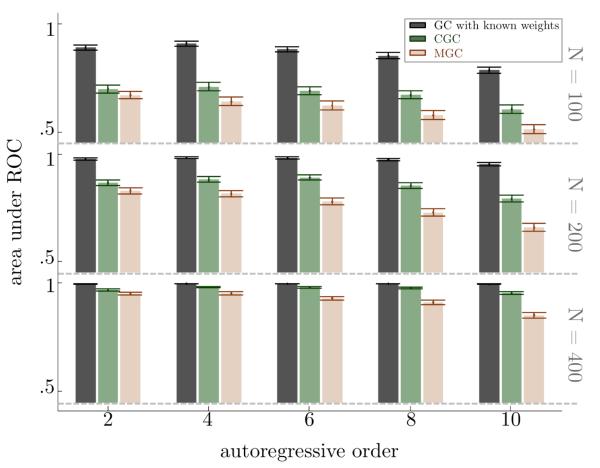
In Figure 3 the AUC is plotted, along with its bootstrapped confidence intervals, as a function of P and N, for a case with SIR = SNR = 5. As N decreases, the performance of MGC deteriorates substantially, while CGC is still able to reasonably differentiate true causality from false causality. Similar to the previous results, the difference between the performances of CGC and MGC grows even more as P increases. As before, the performance of MGC and CGC is surpassed by the performance of GC with known weights, though the performance of both MGC and CGC approach that of GC with known weights as N increases. Additional results in Table 1 of the supplementary material show that as SIR and SNR decrease, the gap in performance of CGC over MGC decreases, but CGC always has a larger mean AUC; in fact, for most cases CGC also has a 95% AUC confidence interval that has no overlap with the corresponding 95% AUC confidence interval for MGC.

Figure 3.

CGC can better differentiate between causality and non-causality over MGC, and that difference is amplified as the autoregressive order increases. For each method, length of timeseries, and autoregressive order, the height of the bar corresponds to the mean AUC while the error bars describe the 95% confidence interval of the AUC.

CGC does not perform as well as GC with known weights due to the upward bias in CGC: by calculating a maximum over weights, CGC is guaranteed to be higher than GC with known weights. For long time series, the difference between estimated causalities in true and false directions is significantly larger than this bias. However, for short time series, the bias increases and therefore the ROC performance of CGC deteriorates. We do not show results comparing CGC to GCCA, as they showed nearly equal AUC confidence intervals for all simulation parameter choices.

4.3. Estimating Causality

In addition to CGC’s ability to detect the presence of causality, we also evaluated its ability to quantify the strength of causality. In particular, we analyzed the error of CGC and GCCA with respect to the ground truth of bivariate GC with known weights. We do not analyze MGC as MGC showed much larger bias than CGC or GCCA for most cases. For each simulation, we calculate how well CGC and GCCA match the bivariate causality by taking the squared difference:

$${\mathrm{error}}_{\mathrm{CGC}}={\left(C_{{\mathrm{y}}_2\to {\mathrm{y}}_1}-G_{{\mathbf{g}}_2^T{\mathrm{y}}_2\to {\mathbf{g}}_1^T{\mathrm{y}}_1}\right)}^2,$$ (17)

$${\mathrm{error}}_{\mathrm{GCCA}}={\left(R_{{\mathrm{y}}_2\to {\mathrm{y}}_1}-G_{{\mathbf{g}}_2^T{\mathrm{y}}_2\to {\mathbf{g}}_1^T{\mathrm{y}}_1}\right)}^2.$$ (18)

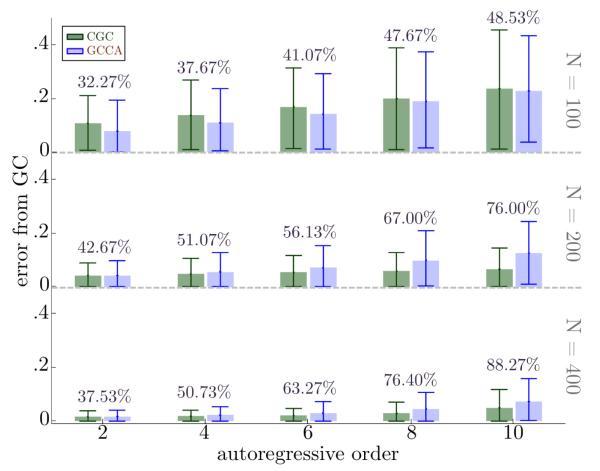
Mean and 95% confidence intervals for these errors are plotted in Figure 4 for multiple N and P values, for the case where SIR = SNR = 5. For low model orders, both CGC and GCCA track the ground truth bivariate GC well; in addition, it can be seen that GCCA has less error than CGC for these cases. For large N, CGC produces more accurate estimates of causality than GCCA. For small N, GCCA perofrms better than CGC in accuracy. However, at small N it can also be seen that neither estimate is an accurate estimator of the underlying causality. The benefit of GCCA is in fact much smaller than its error from the true causality. Additional results shown in the supplementary material in Table 2 and Table 3 indicate that errors rates for both CGC and GCCA is relatively unaffected by SIR, but that CGC is generally more accurate than GCCA as SNR decreases.

Figure 4.

As the autoregressive order increases, for moderate timeseries lengths, CGC becomes much more adept at estimating the underlying true bivariate causality than GCCA. For each choice of method, length of timeseries N, and autoregressive order R, the bar is the mean error over simulations and the error bars describe the 95% confidence interval of error. For short timeseries, CGC seems to perform worse, but the mean value and variance of errors show that this drawback is minimal because both CGC and GCCA are equally inadequate at estimating the strength of the true causality.

5. Real Experimental Data

We also applied CGC and MGC to estimate causality between brain regions using data collected during a visuomotor task performed by a macaque. This data is a prototypical example of a case with real brain data where we are interested in ROIs rather than individual channels (Goldberg et al., 2002; Turi et al., 2012). The data for this task was made available by Dr. Steven Bressler (Florida Atlantic University, Boca Raton, FL, USA) and consisted of local field potential (LFP) recordings as explained below.

5.1. Experimental Setup

A macaque was implanted with transcortical bipolar electrodes to record LFPs at multiple brain locations on one hemisphere, including multiple recordings in the striate and prestriate. The macaque was also trained to perform a visuomotor decision making task (Bressler et al., 1993). The macaque initiated each trial of the experiment by depressing a lever, after which a visual stimulus appeared for 100ms. The visual cue would inform the monkey to either let go of the lever (“Go”) or keep the lever down (“NoGo”).

Voltages were recorded at a 200Hz sampling rate. Defining the lever’s initial descent to be at time t = 0, we focus on a time interval up to 300ms after stimulus (t = 300ms). After pooling together multiple runs, we have 480 trials for each condition “Go” (corresponding to a stimulus image of 4 dots in the shape of a diamond) and “NoGo” (corresponding to a stimulus image of 4 dots in the shape of a line).

5.2. Preprocessing

In order to examine causality in visual cortex, we computed time-varying estimates of causality over the period 0-300ms, using the windowing parameters described by Ding et al. (2000). The 6 electrodes located in the visual cortex naturally form two anatomical ROIs: S ₁, S ₂ and S ₃ form a striate ROI and IT, P1 and P2 form a prestriate ROI, as illustrated in Figure 5. These ROIs and their connectivity have been associated with visual pattern recognition (Liang et al., 2000; Mishkin et al., 1983). The ability to cluster electrodes into anatomically constrained ROIs in this manner is typical of multielectrode invasive recordings.

Figure 5.

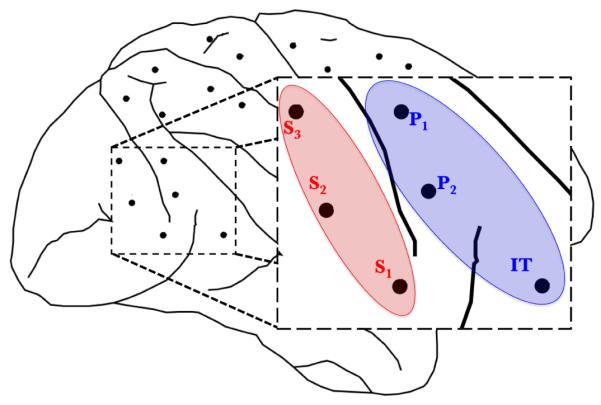
Location of the 6 LFP channels in the monkey recorded during the experiment. We analyzed striate-prestriate causal interactions related to the stimulus: a visual cue to perform a motor task.

The focus of our analysis was on alpha and beta band activity because of previous work that studied these bands with this data (Bressler et al., 1999; Chen et al., 2006); therefore, we applied a 14th-order elliptical filter to the data with a passband of 8–30 Hz and a stopband attenuation of 60 dB for frequencies below 5 Hz and above 40 Hz. Such filtering may lead to spurious causality (Florin et al., 2010) so for each autoregressive model estimated below we used a model selection procedure using the Akaike Information Criterion to determine the order of the autoregression model. Such a procedure, under the constraint that the same filter is used for every signal, will reduce the amount by which filtering affects causality estimates (Barnett & Seth, 2011). We also subtracted the ensemble mean from the signals to remove a cause of 2^nd order non-stationarity, and scaled each time series to have unit power.

The CGC and MGC measures were computed between the striate and prestriate ROIs for each time point using a sliding time-window of duration 55ms, yielding time series of causality values. We chose an intermediate window length to heuristically balance between the benefits of short windows (capturing short-time causality, avoiding non-stationarity) and the benefits of long windows (reducing the effects of trial-to-trial ERP variability (Wang et al., 2008), decreasing the variance in causality estimation). Separate causality measures were obtained for the trials corresponding to the “Go” response and the trials corresponding to the “NoGo” response. Bootstrapping with 1000 resamples was used to compute confidence intervals on all estimates.

5.3. Striate-Prestriate Causality

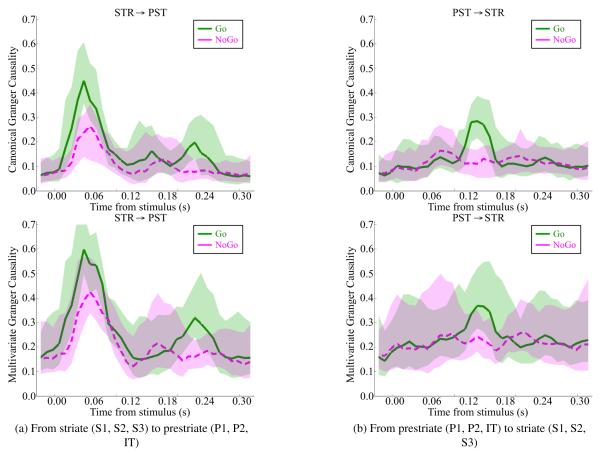
The resulting CGC and MGC measures for each condition are plotted as a function of time in Figure 6. Both measures indicate that the peak causality from striate to prestriate occurs in both tasks at 57.5ms. However, the difference between the two tasks is more pronounced for CGC than MGC; in fact, for CGC there is a statistically significant (p ≤ 0.02) difference in causality between the two tasks when correcting for multiple comparisons across time through the Benjamini-Hochberg procedure (Benjamini & Hochberg, 1995). The task-related difference in causality may be attributed to the increased complexity in the stimulus image of a diamond as opposed to the stimulus image of a line (Bressler et al., 1999).

Figure 6.

Both CGC (top row) and MGC (bottom row) find causality at 57.5ms from striate to prestriate (left column), but CGC finds a statistically significant difference in causality between the two conditions. In addition, both CGC and MGC find some causality at 137.5ms from prestriate to striate (right column) under the “Go” condition, though only CGC finds a statistically significant difference in causality between the two conditions. This prestriate to striate causal interaction may be part of visuomotor processing, as “Go” requires visuomotor interaction while “NoGo” only requires visual processing.

In addition, both measures indicate an increase in causality from prestriate to striate specific to the “Go” task at 137.5ms. Again, the difference between “Go” and “NoGo” at this time point is quite pronounced for CGC. There is a statistically significant (p ≤ 0.01) difference between the causality between these two conditions for CGC when correcting for multiple comparisons as before, while MGC does not demonstrate such statistically significant differences at this level between the two conditions at any point during the experiment. Note that signal propagation from the prestriate to striate has been observed in previous literature on visuomotor processing when visual stimulation leads to a motor action response (Lock et al., 2003). The differences in connectivity as observed using CGC for “Go” and “NoGo” can be explained as a result of this signal interaction since “Go” involves visual and visuomotor networks, while “NoGo” involves only visual networks.

5.4. Electrode Weights

The computation of CGC also yields linear combination weights and the signals of interest for each ROI. We analyzed the weights at the two time points, 57.5ms and 137.5ms, corresponding to peak differences in causality between “Go” and “NoGo.” Results are only shown for the “Go” task, which demonstrated causality at both time points. In Figure 7 we plot the weight vectors estimated in CGC in each direction of causality. At each sensor, we also plotted the confidence interval using the previous bootstrap procedure.

Figure 7.

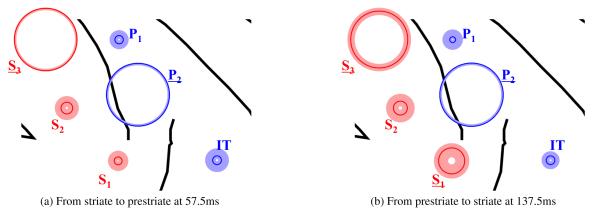
Most of the causality in both timepoints of interest are driven by the relationship between two recording sites: S ₃ and P₂. The main plot shows the relative magnitude of the weight estimated for each channel; the larger the circle radius, the larger the magnitude of the weight for that channel. The dark line shows the mean magnitude of the weight over the full set of trials, while the shaded region shows the bootstrapped confidence interval. The analysis also indicates that S ₁ has a higher weight in causality from prestriate to striate at 137.5ms than from striate to prestriate at 57.5ms.

At the first time of large causality (57.5ms), the signals from S ₃ for the striate and P₂ for the prestriate contribute substantially to the linear combination used in CGC, as indicated by the large magnitude of the weights at those sensor locations. Later at 137.5ms, only P₂ contributes substantially to the linear combination for the prestriate, while both S ₁ and S ₃ contribute for the striate. The presence of S ₃ and P₂ is consistent with previous analysis of this data (Liang et al., 2000). However, in the causality of interest at 137.5ms, we found that there was a significant increase in the weight for S ₁ with respect to the first time of large causality. Using a two-sample t-test, we found that there was a significant difference (p ≤ 0.05) in the weight of S ₁ between the two timepoints and directions of causality. The presence of S ₁ is not found with bivariate GC (Liang et al., 2000) and therefore needs to be further investigated.

6. Discussion

We propose a new measure, CGC, that models directed connectivity between two ROIs by estimating optimal weighted sums of the signals from each ROI. The resulting scalar-valued weighted sum can be viewed as a regional signal representing the ROI. In each ROI, the signals of interest are the ones that participate in a causal interaction between ROIs, with the weights representing the spatial topography of these signals.

With simulated and LFP data, we find CGC to be more robust to sample size and model order than an alternative method for calculating regional causality (MGC). In simulation, CGC showed improved causality detection performance compared to MGC as shown by the difference in AUC and TPR between causality measures. In LFP data, CGC showed short-time task differences in causality between the striate and prestriate; such statistically significant differences were not observed with MGC. This striate-prestriate causality has previously been associated with tasks involving visual pattern recognition (Liang et al., 2000; Mishkin et al., 1983) and visuomotor processing where the visual stimulus causes a motor action (Lock et al., 2003). CGC is more able to discriminate between causal and non-causal interactions for shorter sample sizes and higher autoregressive model orders partially because CGC simplifies the model of regional causality by taking a weighted sum of the signals in each region.

We found in simulation that CGC was a better estimate of the underlying bivariate causality than GCCA whenever there was a large number of samples, high model order, and/or low SNR. This is the result of the differences between the way the two measures estimate their weight vectors: CGC is maximizing Granger causality while GCCA is only maximizing lagged cross-correlation at order P. As a result, GCCA degrades in performance relative to CGC as model order increases, because GCCA only analyzes correlations of lag equal to the model order while CGC summarizes the correlations of lags from 0 up to the model order. One consequence of our simulation results is that GCCA may have a difficult task in differentiating between two unequally strong causal interactions, while CGC differentiates between those unequally strong interactions due to the subsequent change in the underlying Granger causality. For low model order, both CGC and GCCA have low error in estimating the underlying bivariate causality. In those cases, GCCA shows less error for most of the simulations, but differences were overshadowed by the inaccuracy of CGC and GCCA to estimate GC as shown in Figure 4.

CGC provides, in addition to causality, the weights used to estimate the signals in each region related to that causality. In simulations, we saw that for larger sample size (N = 400) and smaller model order (P = 2, 4, 6), CGC estimated causality with similar accuracy to the causality using the correct (known) weights. In the causal network in the macaque, high weights were observed at S ₃ and P₂, consistent with previous analysis of this data. However, in the portion of the response related to the visuomotor network, the sensor S ₁ also had significant weight which is inconsistent with earlier findings (Liang et al., 2000).

CGC depends on predefined ROIs. In the macaque data, the LFP recordings include two sets of electrodes grouped in two well-defined anatomical ROIs: the striate and prestriate. However, anatomical ROIs are not required for CGC; we can use decompositions such as principal components (PCA) or associations such as correlation to cluster recordings into distinct functional ROIs. Whether the ROIs are defined anatomically or functionally, CGC is able to more robustly detect causal interactions between ROIs without the need to specify which specific subregions are involved. Moreover, the weight vectors obtained during model fitting provide an estimate of the relative contribution of these subareas to the causal interaction.

In some cases, it might be of interest to apply CGC to ROIs that each contain a large number of signals. However, CGC should be used with caution in these settings. In particular, CGC is just like other canonical correlation-type methods, and requires that the number of time samples be much larger than the number of signals in each ROI to avoid degeneracies. If this condition is not satisfied, then CGC will spuriously estimate infinite causality in both directions. In our simulations, we used 8 signals, much smaller than the minimum of 100 samples simulated, to avoid this issue. In addition, the computational complexity of CGC is linear in the number of signals in each ROI, as shown in section 3. Hence, CGC may require a lot of runtime to find the optimal weights when measuring regional causality between ROIs.

With LFP signals we have shown CGC’s ability to find inter-regional connectivity as well as signals of interest in a region. We can extend this work to other functional brain modalities such as electrocorticography (ECoG), electroencephalography (EEG) and magnetoencepahlography (MEG). While the LFP signals are directly related to local neuronal populations, the sensors in ECoG, EEG and MEG are sensitive to much larger areas of neuronal activity. If two ROIs are widely separated then CGC should produce meaningful results for EEG and MEG data. However, in cases where there is significant crosstalk or linear mixing between ROIs, the causality measures can be compromised (Hui et al., 2010). In that case, it may be possible to modify the CGC approach to first remove linear mixing between ROIs (Brookes et al., 2011; Hipp et al., 2012; Soto et al., 2010) before computing causality.

CGC could also potentially be applied to reduce the effects of linear mixing in other modalities with poor spatial resolution like cortical current density mapping. Cortical current density map ROIs typically contain many vertices, so a dimensionality reduction step would need to be used before applying CGC. With appropriate preprocessing and data reduction, then, regional measures such as CGC would potentially model dynamic causality on the brain by incorporating the distributed nature of cortical current density maps through weighted sums.

Currently, since we do not know the distribution of CGC under the assumption of no causality, we have used resampling procedures such as permutation testing or bootstraps to test for significant CGC. However, it should be noted that canonical correlation, through its reformulation as a maximum eigenvalue problem, has an associated parametric null distribution that can derived using random matrix theory (Mardia et al., 1980). It might be possible to use similar techniques to derive a null distribution for CGC, though our attempts to do this have not yet been successful.

The CGC model presented here can be extended to the frequency domain methods of finding causality (Geweke, 1982; Kaminski et al., 2001). By computing causality at different frequencies, we may be able to discover significant causality over restricted frequency bands when there is no significant overall causality. In many cases, it has been found that causal interactions are localized in frequency (Lin et al., 2009; Wilke et al., 2009; Wu et al., 2008); however, frequency measures are difficult for all but the simplest of cases as it is hard to find a frequency domain measure that is both interpretable and can be summarized easily by the original measure (Chicharro, 2012). Another extension of CGC would allow more than one interaction between the two ROIs by computing two more more sets of weight vectors; hence a measure of causality could be determined that lies somewhere between CGC and MGC. This extension may better approximate causal relations in the brain, where it may be expected that multiple signals in one ROI, none uniquely determined by any channel in that ROI, are interacting with multiple signals in a second ROI.

In this paper, CGC is proposed as a bivariate model: the only signals being analyzed are those in the two ROIs. If there are other signals that may be driving or influencing signals from the two ROIs, we can attempt to remove the influences of these other signals by simple linear regression (Guo et al., 2008), as was done in partial GCCA (Wu et al., 2011) and partial MGC (Barrett & Seth, 2010). However, removing the effects of all signals not in the two ROIs can increase the variance in causality estimation. Often, when computing partial causality, it is thus prudent to use some data reduction (e.g. principal components) on all signals not in the two ROIs before calculating partial causality (Zhu et al., 2009). A similar data reduction approach may have to be incorporated into a partial CGC formulation.

In addition, partial causality measures suffer from the artifact of redundancy (Angelini et al., 2010). Redundancy is the presence of the same signal of interest in multiple recordings. CGC is different from partial causality measures, in that it responds to redundancy in a different way. Redundancy refers to the presence of the same signal of interest in multiple signals, and leads to spuriously low causality in methods like partial GCCA and partial MGC when the shared signal is removed during the regression process. CGC does not regress away redundant signals of interest and will not suffer from spuriously low causality if there is shared information between signals from the same ROI. However, CGC can suffer from spuriously high causality if the same signal of interest is present in both ROIs.

7. Conclusion

The analysis of brain imaging data often focuses in anatomically or functionally defined ROIs, rather than discrete cortical locations. However, most existing methods of causal functional connectivity analysis from electrophysiological data focus on interactions between individual pairs of signals or multivariate models of interaction between all electrodes. This paper presents a novel measure, CGC, that models the causal interaction between ROIs by borrowing ideas from canonical correlation and Granger causality. With this new measure, causality between ROIs is modeled through weighted sums of the signals in the individual ROIs. We also presented a numerical method to determine the weights and corresponding causality from one ROI to another. In simulation, we demonstrated that CGC can effectively differentiate both the presence and strength of causality for complex model order, moderate noise levels and low data sizes. In an application to macaque LFP data from a visuomotor task, we demonstrated CGC’s ability to determine dynamic differences in causality in the occipital lobe corresponding to the type of visual stimulus and visuomotor response.

Figure 1.

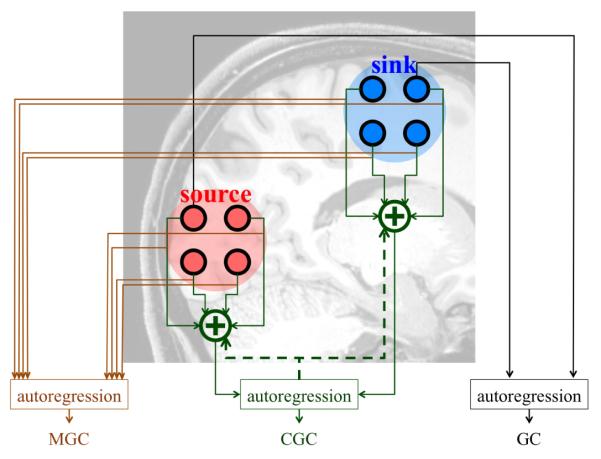
We want to estimate the causality from the source region to the sink region via the time series recordings (represented by dark circles) from each region. GC analyzes the causality between pairs of recordings using univariate and bivariate autoregressive models. MGC fits much larger parametric autoregressive models to collections of time series. CGC parsimoniously represents each ROI using a single signal formed through an optimized weighted linear combination of signals from the ROI. CGC then applies standard GC analysis to these parsimonious representations.

Appendix A. Numerical Implementation

To simplify notation in the sequel, we define the vector w from the set $\mathcal{S}$ as:

$$\mathbf{w}=\left[\begin{array}{c}\hfill \alpha \hfill \\ \hfill \beta \hfill \end{array}\right]\in \mathcal{S}\triangleq {\mathcal{S}}^{M_{1^{-1}}}\times {\mathcal{S}}^{M_{2^{-1}}}.$$ (A.1)

We assume that we have the ability to compute the unconstrained gradient (i.e., ignoring the unit-norm constraints) of the CGC measure in (12), G_{β^Ty2→α^Ty1}, with respect to w:

$${\nabla }_{\mathrm{w}}{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}=\left[\begin{array}{c}\hfill {\nabla }_{\alpha }{\mathit{G}}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}\hfill \\ \hfill {\nabla }_{\beta }{\mathit{G}}_{{\beta }^2{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}\hfill \end{array}\right]$$ (A.2)

where the subscripts indicate the components of the gradient corresponding to the weight vectors α and β. In our implementation, this gradient computation is performed numerically using an adaptive finite-difference method, with the AR coefficients for GC estimated using a modified version of Burg’s algorithm as described by de Waele & Broersen (2003).

Due to the properties of $\mathcal{S}$, it can be shown (Absil et al., 2008) that the constrained gradient of G_{β^Ty2→α^Ty1} with respect to $\mathcal{S}$ is a projection of the unconstrained gradient:

$${\nabla }_{\mathrm{w}}^{\mathcal{S}}{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}=\left[\begin{array}{c}\hfill (\mathbf{I}-\alpha {\alpha }^T){\nabla }_{\alpha }{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}\hfill \\ \hfill (\mathbf{I}-\beta {\beta }^T){\nabla }_{\beta }{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}\hfill \end{array}\right]$$ (A.3)

We use a nonlinear conjugate gradient algorithm with Polak-Ribière updates (Edelman et al., 1998) to maximize G_{β^Ty2→α^Ty1}. The algorithm requires the specification of two termination criterion parameters (ε for the weights and δ for the value of G_{β^Ty2→α^Ty1}), a conjugate gradient restart parameter Q, and an initial point ${\mathbf{w}}_0=\left[\begin{array}{c}\hfill {\alpha }_0\hfill \\ \hfill {\beta }_0\hfill \end{array}\right]\in \mathcal{S}$ (which we choose randomly).

Initialization

Let ${\mathbf{g}}_0={\nabla }_{{\mathbf{w}}_0}^{\mathcal{S}}{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^2{\mathrm{y}}_1}$ be the initial gradient and ${\mathbf{d}}_0=\left[\begin{array}{c}\hfill {\mathbf{d}}_0^{\alpha }\hfill \\ \hfill {\mathbf{d}}_0^{\beta }\hfill \end{array}\right]={\mathbf{g}}_0$ be the initial ascent direction, where we have split d₀ into two components of length M₁ and M₂ corresponding to the weight vectors α and β.

Main Loop

For iteration k = 1, … , Q, we optimize over successive search paths in $\mathcal{S}$:

Search Path

Form the one-dimensional curve

$$\mathrm{w}\left(t\right)=\left[\begin{array}{c}\hfill {\alpha }_{k-1}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)+\frac{{\mathbf{d}}_{k-1}^{\alpha }}{{\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}}\sin \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)\hfill \\ \hfill {\beta }_{k-1}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\beta }\mid \mid }_{{\ell }_2}t\right)+\frac{{\mathbf{d}}_{k-1}^{\beta }}{{\mid \mid {\mathbf{d}}_{k-1}^{\beta }\mid \mid }_{{\ell }_2}}\sin \left({\mid \mid {\mathbf{d}}_{k-1}^{\beta }\mid \mid }_{{\ell }_2}t\right)\hfill \end{array}\right]$$ (A.4)

The normalization of the two components of the gradient is required to allow the entire path to lie in $\mathcal{S}$. Geometrically, the path represents the traversal of great circles around the two spheres in $\mathcal{S}$, starting at w_k–1 and moving along the direction d_k–1.

Search

Find the maximal value of G_{β^Ty2→α^Ty1} over the search path using the golden section search (Kiefer, 1953), with the location of the maximum given by $\widehat{t}$.

Update

1. Update ${\mathbf{w}}_k=\mathbf{w}\left(\widehat{t}\right)$.

2. Update ${\mathbf{g}}_k={\nabla }_{{\mathbf{w}}_k}^{\mathcal{S}}{G}_{{\beta }^T{\mathrm{y}}_2\to {\alpha }^T{\mathrm{y}}_1}$.

3. Define the step size γ_k (Polak & Ribière, 1969) using the modified gradient ${\overline{\mathbf{g}}}_{k-1}$,

   $${\gamma }_k={({\mathbf{g}}_k-{\overline{\mathbf{g}}}_{k-1})}^T{\mathbf{g}}_{k-1}$$ (A.5)

   $${\overline{\mathbf{g}}}_{k-1}=\left[\begin{array}{cc}\hfill \mathbf{I}-{\alpha }_{k-1}{\alpha }_{k-1}^T\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \mathbf{I}-{\beta }_{k-1}{\beta }_{k-1}^T\hfill \end{array}\right]{\mathbf{g}}_{k-1}$$ (A.6)
4. Update the search direction d_k using the transported previous search direction ${\overline{\mathbf{d}}}_{k-1}$:

   $${\mathbf{d}}_k={\mathbf{g}}_k+{\gamma }_k{\overline{\mathbf{d}}}_{k-1}$$ (A.7)

   $${\overline{\mathbf{d}}}_{k-1}=\left[\begin{array}{c}\hfill -{\alpha }_{k-1}\sin \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)+\frac{{\mathbf{d}}_{k-1}^{\alpha }}{{\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)\hfill \\ \hfill -{\beta }_{k-1}\sin \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)+\frac{{\mathbf{d}}_{k-1}^{\beta }}{{\mid \mid {\mathbf{d}}_{k-1}^{\beta }\mid \mid }_{{\ell }_2}}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}t\right)\hfill \end{array}\right]$$ (A.8)

Termination

Exit the process if

$${\mid \mid {\mathbf{w}}_k-{\mathbf{w}}_{k-1}\mid \mid }_{{\ell }_2}<\epsilon$$ (A.9)

or

$$G_{{\beta }_k^T{\mathrm{y}}_2\to {\alpha }_k^T{\mathrm{y}}_1}-G_{{\beta }_{k-1}^T{\mathrm{y}}_2\to {\alpha }_{k-1}^T{\mathrm{y}}_1}<\delta .$$ (A.10)

Repeat

Go to iteration k + 1

Reset

If we reach the last iteration in the loop, so that k = Q, and neither of the termination criterion are satisfied, set k = 0, α₀ = α_Q, and β₀ = β_Q, and repeat the algorithm from the beginning.

By using this modified version of the nonlinear conjugate gradient method designed for the constraint set $\mathcal{S}$, the algorithm converges faster than the standard conjugate Sgradient descent method (Edelman et al., 1998). We observed that setting ε = δ = 10⁻⁶ and Q = M₁ + M₂ − 2 allowed the optimization to converge. We also observed a substantial decrease in algorithm runtime by modifying the search path in each iteration from a one-dimensional curve (dependent on t) to a two-dimensional curve dependent on t₁ and t₂:

$$\mathbf{w}(t_1,t_2)=\left[\begin{array}{c}\hfill {\alpha }_{k-1}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}{t}_1\right)+\frac{{\mathbf{d}}_{k-1}^{\alpha }}{{\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}}\sin \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}{t}_1\right)\hfill \\ \hfill {\beta }_{k-1}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}{t}_2\right)+\frac{{\mathbf{d}}_{k-1}^{\beta }}{{\mid \mid {\mathbf{d}}_{k-1}^{\beta }\mid \mid }_{{\ell }_2}}\cos \left({\mid \mid {\mathbf{d}}_{k-1}^{\alpha }\mid \mid }_{{\ell }_2}{t}_2\right)\hfill \end{array}\right]$$ (A.11)

and then optimizing over this curve first in t₁ and then in t₂, in each case using a golden section search.

Note that the cost function for CGC is non-convex because reversing the sign of either set of weights does not affect the variances in the Granger causality computation. This sign ambiguity leads to equivalent solutions for the optimal weights in CGC. However, in simulation we found that this optimization algorithm consistently converges to the same maximum found via a multiresolution grid search.