An Iterative Spherical Mean Value (iSMV) Method for Background Field Removal in MRI

Abstract

Purpose

The Sophisticated Harmonic Artifact Reduction for Phase data (SHARP) method has been proposed for the removal of background field in MRI phase data. It relies on the spherical mean value (SMV) property of harmonic functions, and its accuracy depends on the radius of the sphere used for computing the SMV and truncation threshold needed for deconvolution. The goal of this work is to develop an alternative SMV based background field removal method with reduced dependences on these parameters.

Methods

The proposed background field removal method (termed iterative SMV or iSMV) consists of applying the SMV operation repeatedly on the field map and it was validated in a phantom and in vivo brain data of five healthy volunteers.

Results

The iSMV method demonstrates accurate background field removal in the phantom. Compared to SHARP, the iSMV method shows a significantly reduced dependence on the SMV radius both in phantom and in human data. Because a smaller radius can be chosen, the iSMV method allows retaining a larger part of the region of interest, compared to SHARP.

Conclusion

The iSMV method is an effective background field removal method with a reduced dependence on method parameters.

INTRODUCTION

There has been increasing interest in the use of MRI signal phase and quantitative susceptibility mapping (QSM) (1-13) for the study of tissue magnetic properties (11,14-24). The MRI signal phase reflects the total magnetic field experienced by water proton spins, which is the superposition of the local magnetic field, generated by susceptibility sources within the chosen region of interest (ROI), and the background field, generated by susceptibility sources outside the ROI. A precise estimation of the local field map is essential for obtaining an accurate map of tissue magnetic susceptibility. Therefore, the background field must be removed through a separate background removal procedure. Three commonly used methods are the High-Pass Filter (HPF) method (25), the Projection onto Dipole Fields (PDF) method (26), and the Sophisticated Harmonic Artifact Reduction for Phase Data (SHARP) method (18).

The background field corresponds to the magnetic field measured on a uniform phantom whose shape is identical to the ROI. Consequently, it is a harmonic function, i.e., a solution to the Laplace equation (9,27,28). The HPF method exploits the fact that such a background field tends to be very smooth by removing the low spatial frequency components. It is effective and has the advantage of being very straightforward to implement but, since the Fourier basis functions are not solutions to the Laplace equation, the HPF method may give rise to noticeable artifacts (26). Additionally, the size of the low-pass filter must be chosen carefully, since it affects the final local field. The PDF method fits the total field using a set of dipole functions centered at locations outside the ROI, such that the fitted field is, by construction, a harmonic function. It is more computationally expensive and accuracy of the local field suffers near the boundary of the ROI, because the assumed orthogonality between the dipole field originating inside and those outside the ROI is only approximate. The SHARP method relies on the fact that a harmonic field satisfies the following property. For any given sphere at any given location within the ROI, the mean value of a harmonic function over that sphere is equal to the function value at the center of that sphere (27). It is referred to in the following as the Spherical Mean Value (SMV) property. The SHARP method is straightforward to implement and computationally efficient. However, in practice, the local field obtained with the SHARP method depends on the radius used in the SMV operation and on the threshold needed for the subsequent deconvolution (see below). Additionally, since the SMV cannot be computed for voxels that are less than a radius away from the ROI border, the local field is only available on a modified ROI that is smaller than the original ROI.

Here, we propose an alternative SMV based background removal method that overcomes these shortcomings by repeatedly applying the SMV operation on the field map. The proposed method, named iterative Spherical Mean Value (iSMV), is validated in both phantom experiment and in vivo.

THEORY

For a given ROI denoted by R, let F₀ be the total field map, which can be estimated from MRI phase data after proper spatial unwrapping. The total field can be separated into two components: F₀ = F_nh + F_h, with F_nh the non-harmonic component or the local field, and F_h the harmonic component or background field. Both the SHARP method and the proposed iSMV method utilize the SMV property of harmonic functions. In this section, we include the definition of the SMV operation, a short review of the SHARP method, and the theory of the proposed iSMV method.

The SMV operation

We use B(x₀, r) to denote a sphere with radius r centered at a location x₀ within region R. For a given function f defined on R and a given ragius r, the SMV_r at a point x₀ is given by

$$\left({\mathrm{SMV}}_{r}f\right)\left({\mathit{x}}_0\right)=\frac{1}{V}{\int }_{B\left({\mathit{x}}_{0,r}\right)}f\left(\mathit{x}\right)dV,$$ (1)

where V is the volume of the ball B(x₀, r). The SMV_r operation is only defined for locations x₀ for which the ball B(x₀, r) lies completely within R. If f is harmonic in R, then, according to the SMV property, f(x₀) = (SMV_rf)(x₀).

If the SMV operation is applied to every point x in R, we get the function (SMV_rf)(x). This SMV operation is simply an average filter and can be efficiently implemented using Fourier Transform. Note that for points near the boundary of R, the SMV_r operation cannot be faithfully calculated since it would require data outside R, which we assume is not available. This is, for instance, the case when the ROI is chosen such that only air is present outside the ROI, where MRI phase measurements are either not possible or unreliable. We thus distinguish two non-overlapping regions within R: 1) R_r, defined as the region where the SMV_r operation does not require data outside R, and 2) R′, defined as the region whose voxels are less than a distance r away from the boundary of R. Note that R_r becomes smaller as r increases.

The SHARP method

The SHARP method calculates the local field using a three-step process, consisting of a convolution, a point-to-point multiplication with a mask M_r, and a deconvolution, i.e.,

$$F_{nh}={(1-{\mathrm{SMV}}_r)}^{-1}{M}_r(1-{\mathrm{SMV}}_r)F_0.$$ (2)

Here, the convolution of the total field F₀ with the (1 – SMV_r) kernel removes the harmonic background field, the point-to-point multiplication with M_r sets the value of all voxels outside of R_r to zero, and the deconvolution (1 – SMV_r)^–1 is computed in Fourier space using a point-to-point division with the Fourier Transform of the (1 – SMV_r) kernel. This kernel vanishes at k = 0, such that truncation is needed before applying the division to avoid noise amplification (18,28). In principle, the effect of an average filter cannot be reverted unless careful treatment of the boundary values of F_nh is carried out. This thresholded k-space division leads to loss of information and accuracy. Additionally, results are available only on the smaller ROI R_r, where the SMV_r can be faithfully calculated. Overall, the local field generated by the SHARP method depends on the chosen radius r and on the chosen truncation threshold for the deconvolution process (28).

The iSMV method

For functions f defined on the ROI R, we define the operator S_r as follows

$$\left(S_{r}f\right)\left(\mathit{x}\right)=\{\begin{array}{cc}f\left(\mathit{x}\right)\hfill & \mathit{x}\in R^{\prime }\hfill \\ \left({\mathrm{SMV}}_{r}f\right)\left(\mathit{x}\right)\hfill & \mathit{x}\in R_r\hfill \end{array}\phantom{\}}.$$ (3)

Let us now fix the radius r and make the assumption that the background field F_h is known on the border R′. Define a modified field map F̃₀ that is equal to F_h on the border R′ and equal to F₀ on the inner (cropped) region R_r. Define the function $S_r^{\infty }{\tilde{F}}_0$ as the result of applying the operator S_r an infinite number of times on F̃₀. The function $S_r^{\infty }{\tilde{F}}_0$ satisfies the following properties:

1. It is equal to F_h on the border R′ by definition, and

2. For all $\mathit{x}\in R_r:\left({\mathrm{SMV}}_r\left(S_r^{\infty }{\tilde{F}}_0\right)\right)\left(\mathit{x}\right)={\mathrm{SMV}}_r\left({\mathrm{SMV}}_r^{\infty }{\tilde{F}}_0\right))\left(\mathit{x}\right)=\left({\mathrm{SMV}}_r^{\infty }{\tilde{F}}_0\right)\left(\mathit{x}\right)=\left(S_r^{\infty }{\tilde{F}}_0\right)\left(\mathit{x}\right)$, such that $S_r^{\infty }{\tilde{F}}_0$ satisfies the SMV property for radius r everywhere inside R_r. Therefore, $S_r^{\infty }{\tilde{F}}_0$ must be a harmonic function itself (29). Since the solution to the Dirichlet problem of finding a harmonic function inside a given region that satisfies a given boundary condition is unique for a closed ROI (30), it is found that $S_r^{\infty }{\tilde{F}}_0=F_h$. The local field on R_r can then be calculated as

   $$F_{nh}=F_0-S_r^{\infty }{\tilde{F}}_0.$$ (4)

   The proposed method depends now only on the choice of the radius r.

METHODS

SHARP Implementation

SHARP was reported to achieve the best result with a radius equal to 6 to 7 voxels (28). In this paper, we chose to compute iSMV and SHARP with a 1 voxel radius and a 6 voxels radius to investigate the radius dependences of both methods. For SHARP, we used the recommended values for the truncation threshold: 0.15 for the 1 voxel radius and 0.0225 for the 6 voxels radius (28).

iSMV Implementation

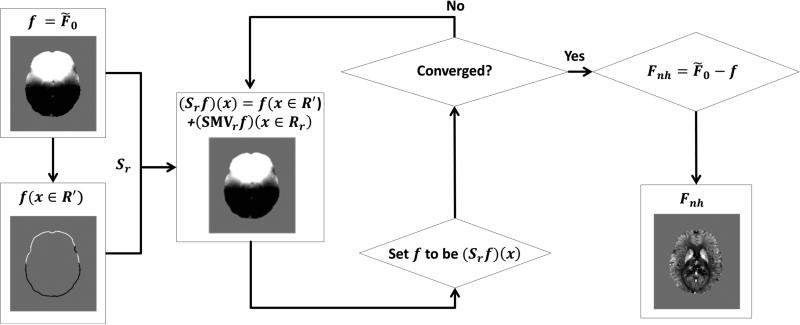
In order to compute the local field using the iSMV method, knowledge of the background field at the boundary of the ROI is required. In practice, the local field is often much smaller than the background field. Therefore, in this study, it was assumed that the local field was zero at the boundary and, consequently, the background field was equal to the total (measured) field at the boundary. If other prior information about the boundary values is known, it can be easily incorporated in the method. The operator S_r was implemented by first performing the SMV_r over the entire field of view (FOV), which can be done efficiently in Fourier space, followed by the replacement of the boundary values (those within the region R′) with the corresponding boundary values of the total field F₀. The repeated application of the S_r operator implemented in this fashion was halted once the relative error between the norms of two successive iterations was smaller than 5 × 10^–5. The visual interpretation of the algorithm is shown in Figure 1.

Figure 1.

A flow chart of iSMV algorithm.

Since iSMV is an iterative method, it is important to use an accurate SMV_r kernel for the convolution. In the construction of the SMV_r kernel, each voxel was weighted according to the volume of the intersection of that voxel with the sphere with radius r.

Phantom experiments

A water phantom was constructed by placing two vials of 0.025% and 0.016% Gadolinium solutions in a container filled with water. This phantom was scanned using a 3D multi-gradient echo sequence on a 1.5-T scanner (GE Excite HD) with a 5-inch surface coil for signal reception. The imaging parameters were TE/△TE/#TE/TR/FA/BW/FOV/matrix size = 3.1ms/ 3.1ms/ 10/52.3ms/15°/±62.50kHz/24×24×9.6 cm³/256×256×80. The scan was repeated after the two vials were removed and the equivalent volume of water was added to replace the removed volume. The second scan was used to obtain the reference background field, to which the computed background fields from the first scan were compared. The ROI was segmented by signal thresholding of the magnitude images. The background field was estimated in the data from the first scan using the SHARP and iSMV methods, using two different radii (1 voxel and 6 voxels). The accuracies of both methods were evaluated by calculating the relative error of the computed local field with respect to the reference (true) local field. The relative error was defined as the norm of the difference between the estimated field and the reference field divided by the norm of the reference field, evaluated on the cropped region of interest R_r:

$$\text{relative error}={\Vert F_{reference}-F_{estimated}\Vert }_{R_r}∕{\Vert F_{reference}\Vert }_{R_r}$$ (5)

with F the field for which the error was calculated (either the local or the background field).

In vivo Human Brain

Five healthy volunteers were scanned using a 3D multi-gradient echo sequence on a 3T scanner (GE Excite HD), under approval by the Institutional Review Board. Imaging parameters were TE/△TE/#TE/TR/FA/BW/FOV/matrix size=5ms/5ms/8/50ms/20°/±62.50kHz/21.75×24×12.8 cm³/232×256×64. A visual comparison was performed between the estimated local fields obtained by SHARP and iSMV using two different radii (1 voxel and 6 voxels).

RESULTS

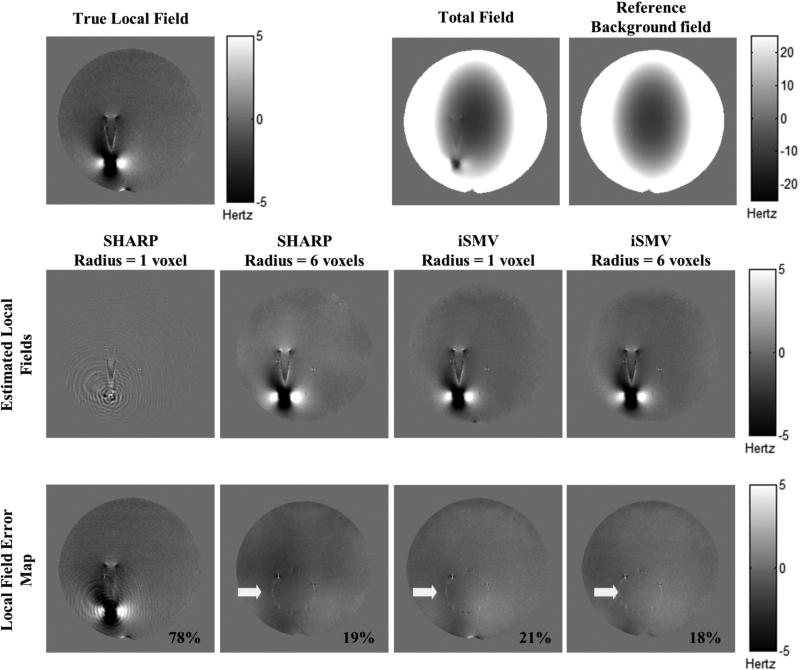
Figure 2 shows the results obtained in the phantom experiment. The local field estimated using SHARP with a radius of 6 voxels is noticeably different from that using a radius of 1 voxel, whereas the iSMV estimated local fields are consistent between the two radii. The relative error of the local field was substantially larger for SHARP using a 1 voxel radius, compared to SHARP using a 6 voxel radius and iSMV using a 1 or 6 voxel radius, all of which resulted in similar errors.

Figure 2.

Phantom results. The top row shows the true local field, the total field, and the reference background field. The middle row shows the estimated local fields using SHARP and iSMV with both 1 voxel and 6 voxels radii. The bottom row shows the difference between the fields on the second rows and the true local field. The corresponding relative errors, calculated using Eq.5, are located on the bottom right hand corner. Adequate background field removal was obtained using SHARP with a 6 voxels radius, while the 1 voxel radius leads to significant error in the estimated background field. The local fields estimated using iSMV with 1 and 6 voxels radii are similar to the 6 voxels radius SHARP result. The residual artifact indicated by the white arrow is caused by an imperfect subtraction of the plastic support structure due to a slight error in registration between the actual and the reference acquisition.

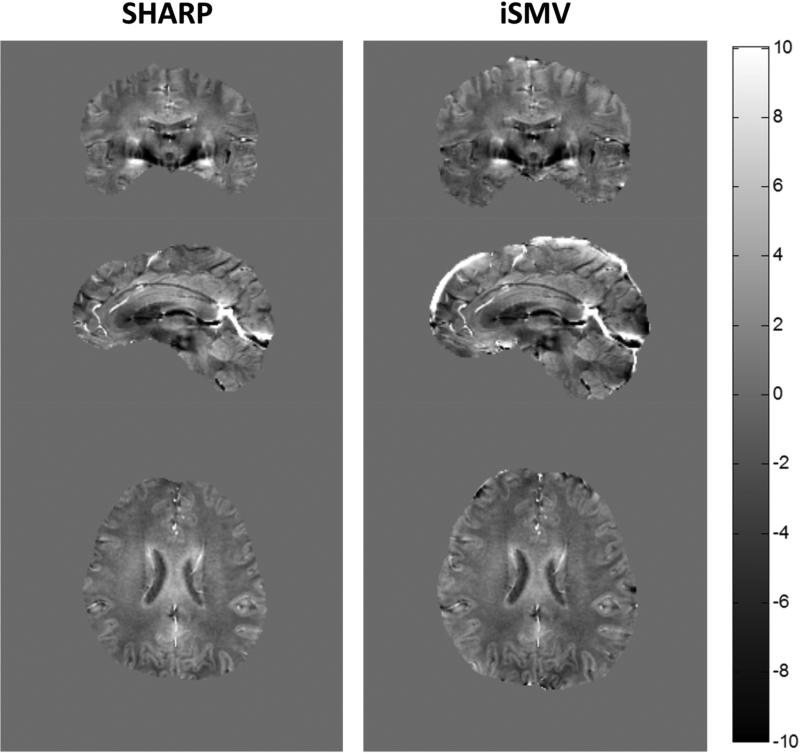
Figure 3 presents a comparison between the SHARP and iSMV results in a healthy subject using a 1 voxel radius and a 6 voxel radius. For the local fields estimated using the SHARP method (top row), a noticeable difference was seen between the two radii. Using SHARP with a 6 voxel radius as a reference, the relative error (Eq. 5) between the two SHARP results was 78%. The local fields estimated using iSMV method (bottom row) produced consistent results: using iSMV with a 6 voxel radius as a reference, the relative error (Eq. 5) between the two iSMV results was 9%.

Figure 3.

In vivo human brain comparison between SHARP and iSMV using both 1 and 6 voxels radii. The third column shows the difference between the 1 and 6 voxels radii results for both methods, and presented on the cropped ROI when using a 6 voxels radius.

Over all subjects, the relative error between the 1 and 6 voxel radius iSMV results was 11%±2%. Using the 6 voxel radius SHARP as the reference, the relative errors of the 1 voxel radius SHARP, 1 voxel radius iSMV, and 6 voxel radius iSMV were 78%±2%, 17%±2%, and 17%±3% respectively.

Computation times for the in vivo brain data were 3s for both the 1 voxel radius and the 6 voxel radius SHARP, 105s for the 1 voxel radius iSMV, and 76s for the 6 voxel radius iSMV. The algorithm was implemented with MATLAB 2009a (MathWorks, Natick, MA, USA) on an Intel® Xeon W3530 @ 2.80GHz with 8GB RAM.

Figure 4 shows a comparison between SHARP using a 6 voxel radius and iSMV using a 1 voxel radius in a second healthy subject in three orthogonal planes. A high degree of similarity between the two estimated local fields was observed, but the iSMV estimate was available on a larger ROI.

Figure 4.

In vivo comparison of SHARP (6 voxels radius) and iSMV (1 voxel radius) in a second healthy volunteer. Note that the iSMV retains more data near the ROI boundary because it allows the use of a smaller radius. Inside the cropped ROI, the estimated local fields are similar for both methods.

DISCUSSION

In this paper, an iterative spherical mean value (iSMV) method is described for the removal of the background field in MRI. Our phantom and human data show that the background fields estimated using iSMV are similar to those obtained with the SHARP method, but are much less dependent on the choice of radius when performing the SMV operation. In both the phantom and the in vivo human brain, significant changes in the SHARP results were observed when a different radius of the sphere was used. Generally, a larger radius increases the accuracy of the SHARP estimates but comes at the cost of a further cropping of the ROI for which the local field can be computed (denoted by R_r in the current work). Consequently, SHARP inherently has a tradeoff between accuracy of the result and loss of voxels near the boundary. With iSMV, however, an estimate of the local field can now be obtained for an ROI that is only slightly smaller than the original ROI. A limitation of this work is that the relative error of the in vivo data is computed using the SHARP method with a 6 voxels radius as reference, since the true local field is not available. This makes it difficult to assess the accuracy of the iSMV results on the human data, compared to the experiments, where the true local field is available.

The iSMV method fundamentally treats the problem of separating harmonic and non-harmonic components as a boundary value problem for estimating a background field in a closed region. In this work, it was assumed that, at the boundary, the background field was equal to the total field. In many instances, the chosen ROI will be at or close to the air-tissue interface (~9 ppm susceptibility difference w.r.t. water, ~2 ppm for bone), which induces a magnetic field that is up to an order of magnitude larger than those generated by local sources of susceptibility, such as venous blood (~ 0.3 ppm), cortex grey matter (~ 0.05 ppm), substantia nigra (~0.12 ppm), and globus pallidus (~0.2 ppm) (5,8,31). For brain imaging on healthy subjects, the background field caused by the air-tissue boundary and bone dominates the local field generated by brain tissue due to their susceptibility difference. For patients with hemorrhage close to the skull, it may happen that the local field is similar in magnitude compared to the background field. Unless additional information is available about the local field at the ROI boundary, this can lead to an erroneous estimation of the local field near the boundary.

Compared to iSMV, the SHARP method uses the same SMV property of harmonic functions, but does not specify an assumed ROI boundary condition explicitly. Additionally, the SHARP method utilizes a thresholded k-space division to undo the effect of the SMV operation on the local field, and thus introduces another parameter that needs to be chosen carefully, since it influences the final result. The HPF method exploits the fact that the sought-after harmonic fields are generally smooth and it does not use a boundary condition. Additionally, the local field estimate obtained with HPF does not need the choice of an ROI and is available over the entire FOV. The obtained background field is not necessarily harmonic and the size of the low pass filter is an additional parameter to be optimized. Both SHARP and HPF are computationally more efficient than the initial implementation of iSMV in this work, though improvements may be expected by borrowing methods used in boundary value problems. Compared to iSMV, the PDF method retains data of the entire ROI (26), but relies on the approximate orthogonality between local and background field dipoles. The estimated background field is a harmonic function but it does not use a boundary condition. Its computational burden is lower than iSMV but higher than SHARP and HPF. In this note of limited scope, we have focused on developing an alternative SMV based method with a reduced dependence of the SMV radius on the final result. A comparison of all these methods using rigorous mathematical analyses and experimental evaluations is a natural continuation of this work in future research.

CONCLUSION

We have demonstrated that the iterative spherical mean value (iSMV) method is accurate for background field removal in MRI. When compared to SHARP, the dependence of the estimated local field on the radius used for SMV is strongly reduced, and allows the estimation of the local field on a larger region of interest.