Conformational Flexibility of Human Casein Kinase Catalytic Subunit Explored by Metadynamics

Abstract

Casein kinase CK2 is an essential enzyme in higher organisms, catalyzing the transfer of the γ phosphate from ATP to serine and threonine residues on protein substrates. In a number of animal tumors, CK2 activity has been shown to escape normal cellular control, making it a potential target for cancer therapy. Several crystal structures of human CK2 have been published with different conformations for the CK2α catalytic subunit. This variability reflects a high flexibility for two regions of CK2α: the interdomain hinge region, and the glycine-rich loop (p-loop). Here, we present a computational study simulating the equilibrium between three conformations involving these regions. Simulations were performed using well-tempered metadynamics combined with a path collective variables approach. This provides a reference pathway describing the conformational changes being studied, based on analysis of free energy surfaces. The free energies of the three conformations were found to be close and the paths proposed had low activation barriers. Our results indicate that these conformations can exist in water. This information should be useful when designing inhibitors specific to one conformation.

Introduction

Kinases are an important protein family involved in numerous pathophysiological processes. CK2 casein kinase catalyzes the transfer of the γ phosphate from ATP to serine and threonine residues on protein substrates. In a number of tumors, CK2 activity escapes normal cellular control, making it a potential target for cancer therapy (1). From a structural point of view, CK2 crystallizes as a tetramer composed of two catalytic alpha subunits (CK2α) and two regulatory beta subunits (CK2β) (2). Although at first glance CK2α is a rigid molecule not undergoing phosphorylation or other characteristic mechanism to alter its activity, human CK2α has been shown to display a surprising plasticity of ATP binding elements. Several crystal structures of this protein have been published with different conformations (3–5). Currently, ∼45 human CK2α/α′ structures have been deposited in the Protein Data Bank. These conformations indicate that two regions near the ATP binding site are particularly flexible. The first of these regions (hereafter known as the hinge region, see Fig. 1) is formed by the interdomain hinge and the αD helix connecting the N- and C-terminal domains of CK2α. The hinge region interacts with the adenine group of the donor ATP molecule. In contrast to maize CK2α, where the hinge region is always in an open conformation, human CK2α has both a closed and an open conformation (6). The second highly flexible region in human CK2α is the p-loop (or glycine-rich loop), located between the first two strands, β1 and β2. The two glycine residues in this loop confer its flexibility (7). Finally, a third region at the CK2α/CK2β interface, the β4β5 loop, can also adopt several conformations (8).

Figure 1.

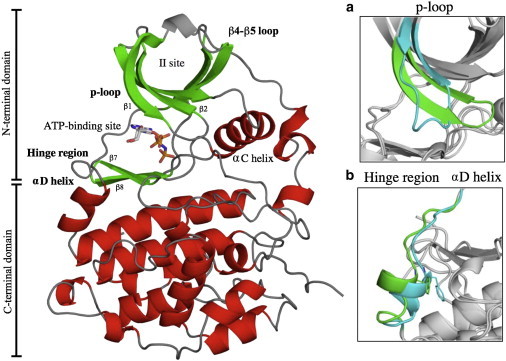
Overview of the flexible regions near the ATP binding site of the catalytic subunit of protein kinase in the totally active conformation (PDB: 2PVR). (a) Two conformations are superposed: in blue the collapsed p-loop, in green the stretched p-loop conformation. (b) The two conformations superposed are the closed and the open hinge region conformation respectively in blue and green. Figures were prepared with PYMOL (DeLano Scientific, San Carlos, CA, http://www.pymol.org). To see this figure in color, go online.

Elucidating these conformational rearrangements will provide helpful clues for the design of effective and selective inhibitors. To explain the high number of crystal structures obtained for human CK2α, Niefind et al. (4,9) propose a dynamic equilibrium between three conformations of the protein in its unbound form. Each of these conformations corresponds to a crystallographic structure obtained experimentally with a given specific activity. Scheme 1 illustrates these three structures. In the central conformation indicated in Scheme 1, the hinge region is closed and two of its amino acids, Asn-118 and Asp-120, can form H-bonds with the ATP ribose moiety of the donor ATP. This results in a ribose’s displacement far from its functional position, leading to a partially (in)active state (9). In contrast, the first conformation shown in Scheme 1 is an active conformation, with an open hinge region. The final conformation is a totally inactive CK2α, with a closed hinge region and collapsed p-loop preventing ATP binding.

Scheme 1.

Hypothetical equilibrium of CK2α proposed by Niefind et al. (9)

Molecular dynamics (MD) has become a widely used, precious tool in many branches of science, particularly biology and chemistry. Thanks to advances in computer technology, we are now able to simulate biological systems and elucidate even complex mechanisms. However, it remains difficult to explore configurations separated by high free energy barriers. In recent years, many methods have been proposed to overcome this limitation of MD. These methods are often based on enhanced sampling techniques (10). We have used the metadynamics method developed by Parrinello and co-workers (11). With this technique, the sampling is accelerated by the addition of repulsive Gaussians to the potential energy surface, for some degrees of freedom known as collective variables (CVs). Several formulations of metadynamics have been developed besides the direct version (11), including the well-tempered variant (12).

This approach has previously been successfully used to simulate rare events and to reconstruct free energy surfaces (FESs) based on a suitably selected set of CVs (13–15). When studying protein conformational changes, specific degrees of freedom must be taken into account. Several strategies have been developed to avoid using a high number of CVs, which increases computational time and makes interpretation of the FES difficult (12,16). The first group of these strategies combines metadynamics with other algorithms, such as parallel tempering (17), bias-exchange (18), etc. The second consists of path-based methods such as the nudged elastic band method, string method, or transition path sampling. For this study, we chose to use metadynamics with path collective variables (PCVs) (19). This method allows us to reconstruct the free energy path connecting an initial and a final state. This approach has been successfully used to study protein conformational rearrangements (20), protein folding (21), drug-receptor interactions (22); and in particular, it has been used to study other kinases, elucidating a closure mechanism (23) and in simulations of inhibitor undocking (24).

CK2α is a potential target for cancer therapy (1) and we have previously reported a theoretical method to estimate protein-ligand interactions in CK2α inhibitors (25). In this article, we study the conformational rearrangements of the CK2α. PCVs are used to study the equilibrium of CK2α proposed by Niefind et al. (4,9), as illustrated in Scheme 1. The work has been separated into two parts: i), the equilibrium between the partially (in)active and the totally inactive state, in which the conformational change is the collapse of the glycine-rich loop; ii), the equilibrium between the totally active and the partially (in)active state, which corresponds to an open-to-close transition of the hinge region. For each equilibrium, a guess path was constructed using metadynamics with several CVs. FESs were then computed using path collective variables. The difference in free energy between the three conformations was evaluated and is discussed, and a mechanism connecting one conformation to another is proposed. These results should be useful in the research of new inhibitors, specific to one conformation.

Computational Details

Setup of the system: MD

The structures chosen to model the conformations from Scheme 1 were obtained from three crystal structures of human CK2α(1–335) from the Protein Data Bank. The chosen fully active structure with an open hinge region is 2PVR (26). The partially (in)active structure, which has been chosen, is 3H30 (8) with a closed hinge region and a stretched glycine-rich loop. The resolved structure of inactive CK2α is 3FWQ (7). It has a glycine-rich loop collapsed and a closed hinge region. All the ligands in the remote cavity or in the ATP binding site were removed to study paths without ligand.

The RX structures were equilibrated by preliminary MD. MD were carried out with AMBER10 (27) and the AMBER force field (amber99SB) (28). In these entire MD, periodic boundary conditions were used. Structures were solvated with a TIP3P water rectangular box. The dimensions of the box were chosen to be at least 10 Å larger than the solute in every direction. No counter ions are needed because the protein is neutral. Long-range electrostatic interactions were computed using the particle-mesh Ewald method with a cutoff value of 10 Å. The time step was set at 1 fs. After minimization, a two-step heating was carried out with small constraints on CK2α: in a NVT ensemble heat from 0 to 100 K in 50 ps and from 100 to 300 K in 200 ps with a Langevin thermostat with a collision coefficient of 5 ps⁻¹. All the constraints were then lifted and MD was run in NPT ensemble at 300 K during 1 ns. After equilibration the final size of the box was 87.7 × 76.1 × 72.7 Å³. Root mean-square deviation (RMSD) analysis was performed to check that the structures remained stable.

Building a guess path: Metadynamics with several CVs

For each equilibrium, we have taken as initial and final structures the RX structures equilibrated by MD simulations as starting points.

In metadynamics, sampling is accelerated by biasing the system through the addition to the potential energy of a sum of repulsive Gaussian terms along the trajectory followed by a set of CVs. This allows the system to explore other regions of the configurational space through low energy paths and prevents from returning in minima, which have already been visited. The sum of Gaussian terms as a function of CVs during the simulation is the negative of the FES (see the Supporting Material for more details). The choice of CVs is critical to build the correct FES.

Several combinations of relevant CVs were used. For the p-loop equilibrium, the CVs were the distances between Arg-47 and His-160, Arg-47 and Asp-120, Lys-49 and Asp-156, Tyr-50 and Asp-156, and the dihedral angle Arg-47(Cβ, Cα, C),Gly-48(N). For the hinge region equilibrium, they were the distances between Thr-119 and Ile-164, Phe-121 and Val-162, and the dihedral angle Phe-121(Cγ, Cβ, Cα, and C). Atoms chosen to calculate the distance for the CVs, parameters of the metadynamics performed with AMBER10 patched with PLUMED (29) are given in the Supporting Material.

With these collective variables, we did not successfully connect the initial and the final conformations. Therefore, these simulations could not be used to build the FESs of the two conformational changes. It justifies the use of path collective variables to describe the transitions. However, these metadynamics gave several intermediate structures between the end points of the two equilibriums. These structures have been useful to construct a first path for the two conformational changes.

Building of the FES: Metadynamics with PCVs

The first path obtained previously gives us a guess path used to define two orthogonal CVs, called path collective variables, to construct the FESs. These two CVs can be written as

$$\begin{array}{l}s\left(R\right)=\frac{1}{P-1}\frac{\sum _{i=1}^P\left(i-1\right)e^{-\lambda {\left[R-R\left(i\right)\right]}^2}}{\sum _{i=1}^P{e}^{-\lambda {\left[R-R\left(i\right)\right]}^2}},\hfill \\ z\left(R\right)=-\frac{1}{\lambda }\ln \left(\sum _{i=1}^P{e}^{-\lambda {\left[R-R\left(i\right)\right]}^2}\right),\hfill \end{array}$$

s(R) represents the progress along the guess path and has no dimension. z(R) represents the distance from the guess path and has the dimension of square length. P is the total number of frames of the guess path. A suitable metric must be defined to calculate the distances between conformations in the configurational space. Among the metrics available, there are the RMSD in Cartesian coordinates, the RMSD in distances, the contact map distance, and a chirality measure. In this study, R–R(i) is the RMSD in Cartesian coordinates between a set of atoms, which have been carefully chosen for the two equilibrium studied. The RMSD is calculated after alignment of the structures between all the carbon atoms in the carbonyl group of the backbone from residues 20 to 260. This choice is made to ensure a correct alignment with a reasonable time of calculation. The parameter λ is comparable to the inverse of the mean-square displacement between successive frames. It controls the smoothness of the s(R) function.

The choice of the set of atoms, which was used to calculate the RMSD, is critical. For the p-loop equilibrium, several atoms of the p-loop were considered: Cα, N, and C atoms of residues (Arg-43-Phe-54) and some atoms from the side chains of Arg-47, Lys-49, Tyr-50, Asp-120, Asp-156, and His-160. For the second equilibrium, atoms were chosen from the hinge region: several Cα, N, and C atoms of residues (Val-112-Leu-128) and (His-160-Ile-164) and the side chains of Asn-117, Asn-118, Thr-119, Asp-120, and Phe-121 (see Table S1 in the Supporting Material).

The path is defined by a series of frames. They must be taken as equidistant as possible relative to the metric used, to avoid unphysical events on the FES. Other paths than the guess path can be explored, even if the guess one is not optimal. The collective variable z(R) allows the system to relax to a free energy minimum path. For the two equilibriums, the first path obtained previously and used to define the PCVs contains five frames. Several metadynamics with PCVs were then made to improve the paths and to increase the number of the frames. The final path, for the two equilibriums, contained 16 frames.

First, FESs with different Gaussian parameters had been built with the direct version of metadynamics. The values of the λ parameter were 3.42 Å⁻² for the p-loop equilibrium and 4.13 Å⁻² for the hinge equilibrium. The Gaussian deposition rate was 1 ps, the height of 0.7 kcal/mol (simulations have also been performed with 1 and 0.5 kcal/mol), and the Gaussian widths were δs = 0.3 and δz = 0.05 Å². The SHAKE algorithm (30) was used to constrain all bonds involving hydrogens and the time step was 2 fs. The collective variable, z(R), was constrained to be <2.0 Å². It is necessary to save time and prevent the system from going far away from the reference path, but it is large enough to let the system explore conformations different from the guess path.

The convergence of the calculated FES was tested: the free energy difference between two basins, the initial and the final conformations of the equilibrium, was plotted as a function of the simulation progress (31,32). However, the analysis of the convergence rate for the simulations performed in the direct version of metadynamics even after several recrossing events still give us a large deviation and the convergence was not reached. One of the drawbacks of metadynamics in its direct version is that the free energy does not converge to a value but oscillates around the correct result, leading to an average error, which is proportional to the square root of the bias potential deposition rate (33). A solution is to use the well-tempered version of metadynamics (12). In this variant of metadynamics, the height of the Gaussians gradually decreases in each position (see equations in the Supporting Material), which prevents the problem of ‘overfilling’ in one region and reduces errors. Simulations with this variant of metadynamics were performed during respectively 55 and 58 ns for the p-loop and the hinge region equilibriums. The FESs were obtained with an adaptive bias of 3300 K, an initial height of 0.7 kcal/mol, and the same parameters as the first simulations.

Results and Discussion

To understand the flexibility of CK2α, the two conformational changes were studied separately. This allowed us to focus on one flexible region of the enzyme at a time. The main steps of the two transitions and the FESs obtained are presented and discussed below.

Collapse of the p-loop

The first equilibrium studied is between the partially (in)active state, with the p-loop stretched, and the inactive state, with the p-loop collapsed. Throughout this transition the hinge region remains closed. The p-loop is known to be highly flexible and has been shown to be distorted in other kinases (34). Metadynamics analysis with PCVs reveals a FES, which can be divided into several domains, characterized by energy minima and corresponding to the main steps of the process linking the two states (Fig. 2). Typical structures encountered in the different energy minima, or basins, are illustrated in Fig. 3, a–e.

Figure 2.

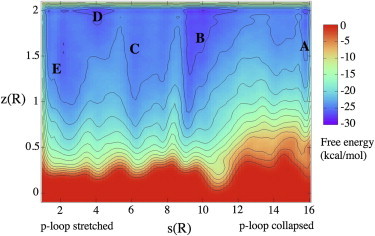
FES reconstructed as a function of s and z of the p-loop equilibrium. The energy separation between contours is 2 kcal/mol. Basins A–E are referring to the conformations in Fig. 3, a–e. To see this figure in color, go online.

Figure 3.

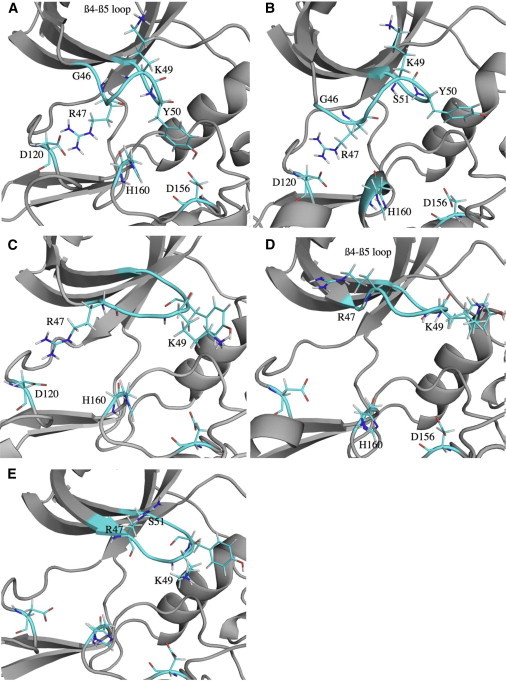
(a–e) Steps of the p-loop collapse. Typical structure of basins A–E defined in Fig 2. Figures were prepared with PYMOL (DeLano Scientific, http://www.pymol.org). To see this figure in color, go online.

The conformations found in basin A (Fig. 3 a) correspond to the inactive state, where the p-loop has collapsed into the ATP cavity, preventing access to the active site. This conformation is induced by the movement of three amino acids in this loop: Arg-47, Lys-49, and Tyr-50. In the collapsed conformation, Lys-49 points at the β4/β5 loop, whereas Arg-47 and Tyr-50 are folded such that they form salt bridges and H-bonds with Asp-120 and His-160 (Arg-47) and with Asp-156 (Tyr-50). In the first step of transformation to the partially (in)active form (Fig. 3 b), the H-bond between Tyr-50 and Asp-156 breaks as the distance increases from ∼2 to 8 Å. This corresponds to an upward shift of the p-loop as the Lys-49(Cα)-His-160(Cα) distance increases from 10 to 13 Å, and a general unfolding of this loop as the Lys-49(Cα)-Gly-46(Cα) distance increases from 7 to 8–9 Å. The main feature connecting basin B to basin C (Fig. 3 c) is the breaking of the H-bonds between Arg-47 and Asp-120, Arg-47 and His-160 (distances increase from 2 to 9 Å). This gives rise to a conformation with a larger p-loop: the distance between Cα of Arg-47 and Ser-51 is 7–9 Å, whereas it is 5–6 Å in both the initial and final states. In basin D (Fig. 3 d), the side chain of Arg-47 rotates, changing the orientation of its peptide backbone so that it points at the β4/β5 loop. At the same time, Lys-49 shifts to face in the opposite direction, pointing at His-160/Asp-156. This results in the Lys-49(Nz)-His-160(Cα) distance dropping from 14 to 11 Å. The final step in this rearrangement (basin E, Fig. 3 e) is the enlargement of the β1 and β2 strands, with the integration of Arg-47 into strand β1, and of Glu-52 into strand β2. Basin E describes the partially (in)active state. In this conformation, the p-loop is stretched and extended as much as possible.

Our simulation reveals the two conformations, with the p-loop collapsed and with the p-loop stretched, to have similar free energy. According to this metadynamics, the stretched loop conformation has approximatively the same energy as the collapsed loop conformation. The highest free activation energy barrier is very small, ∼3 kcal/mol, between basin B and basin C. This transition corresponds to the beginning of Arg-47 rotation, which will ultimately lead to breaking the interactions with Asp-120 and His-160. In the first simulations performed with the direct version of metadynamics and with the same PCVs, energies of the two conformations have been found close and the highest activation barrier was also due to the rotation of Arg-47. These results show that the conformational change to the p-loop of CK2α is possible in water.

Because the barrier is very low, we have performed a 40 ns dynamics on the partially (in)active structure to see if the transition can be studied by classical dynamics. No spontaneous conformational change of the p-loop in the collapse conformation has been observed. Similarly, as energy basin B is deep compared with the other basins in the landscape, a MD run of 5 ns was performed on one structure. The stability of the conformation was checked. To compare with initial and final conformations (basins A and E), RMSD during the dynamics was calculated with the same atoms chosen for the path collective variables definition and the equilibrated stretched p-loop conformation as the reference structure. We find an average RMSD value of 3.2 Å, 2.8 Å, and 1 Å for the simulations of respectively the basins A, B, and E, showing the differences between the three structures.

To test the convergence of the calculated FES, the free energy difference between the initial and the final conformations of the equilibrium is plotted as a function of the simulation progress (Fig. S1 and Fig. S2). The energy difference shown is the difference between the minimum energy in the collapsed and the stretched p-loop conformation. The simulation was performed until two recrossing events occurred leading to a simulation of ∼55 ns. The estimation of the error is ∼1–2 kcal/mol.

Closure of the hinge region

The second equilibrium studied is between the conformation with an open hinge region and the conformation with a closed hinge region. For these two conformations, the p-loop is stretched. The three-dimensional plot of the free energy as a function of the CVs s and z and the structures encountered in the different basins are given in Fig. 4.

Figure 4.

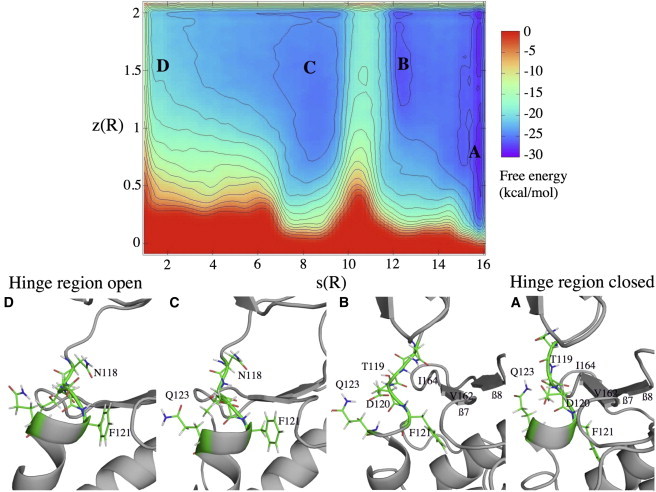
FES reconstructed as a function of s and z of the hinge region equilibrium. The energy separation between contours is 2 kcal/mol. Basins A–D are referring to the conformations below the FES. Figures were prepared with PYMOL (Delano Scientific, http://www.pymol.org). To see this figure in color, go online.

Basin A corresponds to the closed hinge region conformations (Fig. 4 a). In this conformation, some amino acids from the hinge region are found to penetrate the ATP binding site. Thus, Thr-119 and Phe-121 form H-bonds with Ile-164 and Val-162 on strand β7. This is possible because Phe-121 can bury its aromatic side chain in a hydrophobic cavity. We suggest a mechanism for the closed-to-open transition beginning with breaking the H-bonds between the hinge region and strand β7. The H-bonds Thr-119-Ile-164 and Phe-121-Val-162 break as the distance between residues increases from ∼2 to 4–5 Å. The aromatic side chain of Phe-121 remains in the cavity, in a position called in, whereas the αD-helix shifts with Thr-119, Asp-120, and Phe-121. These conformations form basin B (Fig. 4 b). To change from here to basin C (Fig. 4 c), Phe-121 rotates from an in position to an out position. Meanwhile, a H-bond in the hinge region, linking the side chain of Gln-123 and Asp-120, is broken, increasing the distance between these residues from 2 to 6 Å. The last step before reaching basin D 4 is rotation of Asn-118 so that its side chain points toward the interior of the active site. The final open hinge conformation (Fig. 4 d) leaves rather more space in the ATP binding site than the closed conformation as Phe-121 points to the surface in its out position.

This metadynamics simulation indicates that the free energy is similar for the initial and final conformations, i.e., those corresponding to basins A and D with the open and closed hinge region. The closed state is 8 kcal/mol lower in free energy than the open state. The first activation barrier for the proposed mechanism is ∼4 kcal/mol, corresponding to the transition from basins A to B when the αD-helix shifts with Thr-119, Asp-120, and Phe-121. The second and the highest activation barrier, ∼8 kcal/mol, is the Phe-121 flip between the basins B to C. For the final basins, C and D, the FES is quite flat. Asn-118 rotation seems to require little energy. Thus, basin D is not clearly delimited. This could be explained by the absence of ligand, leaving a large space in the ATP binding pocket. This leaves Asn-118 free to move. In addition, in conformations with an open hinge region, because the interaction between segment Thr-119-Phe-121 and the β7/β8 strands is weaker than in the closed structures, the regions are more flexible.

For information, in some of the first metadynamics performed with the direct version and with the same PCVs, the rotation of Phe-121 and the shift of the αD-helix with Thr-119, Asp-120, and Phe-121 were separated, as described previously, whereas in others they occurred at the same time. The convergence assessments of the FES presented in Fig. 4 are given in Fig. S3 and Fig. S4. Consequently, the two conformations are close in free energy and can exist in equilibrium in water.

Conclusion

This study describes metadynamics simulations with path collective variables used to study the flexibility of a human casein kinase, CK2. Two conformational changes to human CK2α were considered: the collapse of the p-loop, and the open-to-closed transition of the hinge region. Niefind et al. (9) had previously suggested equilibrium between three conformations linking the two functional states. Our simulations indicate that the structure with a stretched p-loop and a closed hinge region has indeed the same free energy as the structure with a collapsed p-loop, and is 8 kcal/mol lower than the conformation with an open hinge region. We suggest a mechanism for these two conformational changes. The highest activation barrier is ∼3 kcal/mol for the p-loop equilibrium, corresponding to the beginning of Arg rotation. For the hinge region equilibrium, the highest barrier involves a rotation of Phe-121, and requires 8 kcal/mol. Our results indicate that the conformational changes between the three states entail reasonable barriers, and so that the three conformations can exist in water.

Each of the three conformations has a different specific activity: the conformation with the p-loop collapsed is inactive; the conformation with the p-loop stretched and the hinge region closed is partially (in)active; and the conformation with the hinge region opened is active. The results presented here should help in the design of new CK2 inhibitors. Our data indicate that, before the binding interaction, human CK2α exists as an ensemble of conformations in dynamic equilibrium. The presence of a ligand can influence this equilibrium by stabilizing one of the conformations, as in a conformation selection model (35). Several classes of inhibitors of this enzyme have already been developed (36), some of which target the ATP binding site. Depending on whether and where they form H-bonds, these inhibitors may stabilize the open or the closed hinge region conformation. Thereby, the hinge region is found in a closed conformation for the CK2α^1–335-resorufin but in an open conformation for the inhibitor CX-4945 and the CK2α^1–325/CK2α′^327–350−AMPPN(P) complex (4). Similarly, small molecules could be found that occupy the remote cavity, as CK2β-derivated cyclopeptides, which corresponds to the CK2α/CK2β interface (37). This type of interaction could stabilize the inactive conformation, where the p-loop is collapsed into the ATP binding site. Thus, new strategies may now emerge in the search for CK2 inhibitors, taking the flexibility of this kinase into account to develop inhibitors selective for one of the three conformations.