Abstract
The unique viscoelastic nature of axons is thought to underlie selective vulnerability to damage during traumatic brain injury. In particular, dynamic loading of axons has been shown to mechanically break microtubules at the time of injury. However, the mechanism of this rate-dependent response has remained elusive. Here, we present a microstructural model of the axonal cytoskeleton to quantitatively elucidate the interaction between microtubules and tau proteins under mechanical loading. Mirroring the axon ultrastructure, the microtubules were arranged in staggered arrays, cross-linked by tau proteins. We found that the viscoelastic behavior specifically of tau proteins leads to mechanical breaking of microtubules at high strain rates, whereas extension of tau allows for reversible sliding of microtubules without any damage at small strain rates. Based on the stiffness and viscosity of tau proteins inferred from single-molecule force spectroscopy studies, we predict the critical strain rate for microtubule breaking to be in the range 22–44 s−1, in excellent agreement with recent experiments on dynamic loading of micropatterned neuronal cultures. We also identified a characteristic length scale for load transfer that depends on microstructural properties and have derived a phase diagram in the parameter space spanned by loading rate and microtubule length that demarcates those regions where axons can be loaded and unloaded reversibly and those where axons are injured due to breaking of the microtubules.
Introduction
Mild traumatic brain injury (mTBI), alternatively called “concussion”, is now recognized as a major health issue. Selective damage to axons throughout the white matter is thought to be the key pathological substrate of mTBI, with significant work devoted to characterizing the biochemical degradation of the axons after injury (1,2). However, emerging evidence suggests that primary mechanical forces play an important role in triggering these biochemical cascades (1,3,4). In particular, it has been observed that the axonal ultrastructure can rupture during dynamic loading at strain rates found in TBI, resulting in transport interruption (5–7). This mechanical vulnerability of axons is thought to be due to their uniquely viscoelastic properties, with the axonal cytoskeleton consisting of microtubule bundles that are cross-linked by the microtubule-associated protein (MAP), tau (Fig. 1).
Figure 1.
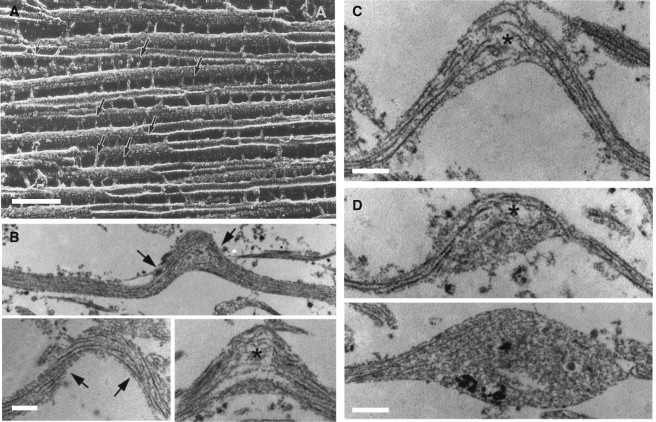
(A) Electron microscopy image of porcine brain MTs polymerized with tau protein. (Arrows) Cross-linkers between the MTs. Scale bar = 100 nm. (Reprinted with permission from ©1988 Rockefeller University Press. Originally published in Hirokawa et al. (8).) (B) Experimental results for injury of cultured 2-mm-long axons (5). A controlled air pulse (with duration <50 ms) is applied to the axon and the increase in the length is used to infer tensile stretch of the axon. (Arrows) Intact straight MTs inside the axon; (asterisk) broken ends of the MTs at the peak of the generated undulations. (C) Due to the interruption of the axonal transport, swelling starts to appear at the end of the broken MTs (asterisks) (D) The swelling grows and becomes more apparent in the transmission electron microscopy micrographs (taken at 1–2 h after injury). Scale bars in panels B–D = 500 nm. Reprinted with permission from Tang-Schomer et al. (5).
Over several years, a micropatterned cell culture system has been used to examine the immediate effects of dynamic stretch applied exclusively to axons (5–10). Under slow loading rates of stretch (strain rates ∼0.01 s−1), axons easily tolerate stretching up to twice their original length and returned back to their prestretch length with no evidence of damage. However, under dynamic loading conditions (strain rates > 26 s−1), multiple regions of undulating distortions were observed along the length of the axons (6). Notably, undulating axonal profiles are also found in the white matter acutely following TBI in humans (7), suggesting the same mechanical mechanism of cytoskeletal disruption occurs in real-world conditions.
To characterize the mechanical damage to the axonal ultrastructure that follows stretch injury in vitro, longitudinal sections of the axons were examined using transmission electron microscopy (5). Interestingly, significant alterations of microtubule configurations were found in the undulated regions of the axon. Specifically, physical breaks of microtubules were observed at the peak of the undulations, with the conspicuous free ends displaying a frayed appearance similar to a microtubule undergoing catastrophic depolymerization (Fig. 1). The breaking and buckling of microtubules were found to physically impede relaxation of the axon until the regional microtubules were subsequently chemically depolymerized (4). In consideration of constructing a mathematical model of this process, in what follows, the same mechanical loading conditions are employed as well as strain-rate-dependent responses of whole axons that have been reported by other authors (11–13).
Notably, these studies show that although microtubules are the stiffest structural components of axons (14), they, nonetheless, become the weakest-link at large strain rates (5). To examine the mechanism behind this mechanical breaking of microtubules, we developed a viscoelastic micromechanical model of the axon to study its response to dynamic loading. It has previously been shown that the overall response of the axon to mechanical forces during stretch and stretch growth is viscoelastic (15,16). This observed viscoelastic response has been modeled by treating the axon with spring and dashpot models that do not account for the internal structure (15,16). The model we have developed here to study failure, consists of staggered arrays of microtubules cross-linked by MAP tau proteins, mimicking the normal architecture in vivo (17).
Although we treat microtubules as elastic elements, the tau protein is treated as a viscoelastic spring, based on previous characterization (18). The viscosity of tau, representing the rate dependence of the breaking of intramolecular bonds in the protein, has been recently measured using single-molecule force spectroscopy studies (18). By including these components, we derive a set of coupled partial differential equations to study the competition between stretching of the microtubules and the sliding of microtubules relative to their neighbors. We find that the former dominates over the latter at large strain rates, providing a quantitative mechanism of why microtubules can break, despite being much stiffer than the other cytoskeletal components. Our equations allow us to study the variation of the stretch along the length of the microtubule, hence enabling us to determine the locations where breaks in the microtubule lattice occur. We also predict the critical strain rate at which microtubules break as a function of their length by only using material parameters determined from experimental measurements (8,19–21).
Model and Governing Equations
As discussed in detail in Burgoyne (17) and Brady et al. (22), the axon structure consists of microtubules (MTs) cross-linked with short side-arm biopolymers called tau proteins. Among the components of the neuronal cytoskeleton, MTs serve both as organelle transport tracks and neuronal structural elements (22). For simplicity, we have not included another major cytoskeletal structure, neurofilaments, because the MTs are larger and stiffer than neurofilaments. Indeed, recent work has shown that the mechanical stiffness of the axon was most reduced in MT-disrupted axons compared to neurofilament-disrupted axons, confirming that MTs contribute the most to the mechanical properties of the axon (23). Because the focus of this work is on the mechanical response and failure of the axon during dynamic loading, following previous work (24), we adopt a hexagonal microtubule lattice cross-linked by tau proteins shown in Fig. 2 a.
Figure 2.
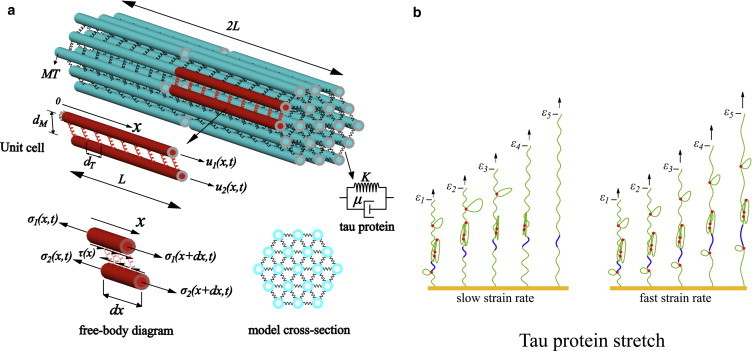
(a) The microstructure of the axon consists of MTs cross-linked by tau proteins (springs). The unit cell used in the mathematical analysis with staggered neighbors is also shown. The viscoelastic model considered for the tau protein consists of a spring (stiffness K) and a dashpot (viscosity μ). (Free-body diagram) Axial and shear components of forces acting on the MTs. (b) The response of the tau protein to different pulling rates at five different strains, ε1–ε5. (Red dots) Intramolecular bonds; (green solid-curve) backbone of the tau protein. At slow strain rates, the intramolecular bonds rupture at smaller force levels (magnitude of the force is proportional to arrow lengths), whereas at fast strain rates, larger force levels are needed to stretch the protein. (Blue segment) Section of the protein backbone that stretches at fast rates of pulling, whereas its length is nearly constant at slow rates. To see this figure in color, go online.
As suggested by electron micrography studies (17), we assume a staggered distribution of MTs, where alternate rows of MTs are staggered with respect to their neighbors by a distance L (refer to Fig. 2 a). For each MT, a hollow cylindrical cross-section with outer and inner radii and RI, respectively, and Young’s modulus EM (typically RO = 12.5 nm, RI = 7 nm, and EM = 1.9 GPa (19)), is assumed. Each MT is surrounded by near-neighbor MTs, where the α-value of four and six results in the square and hexagonal distribution of the MTs in the axon. The distance between neighboring MTs is denoted by dM (typically 23–38 nm (20)) and the spacing between the adjacent tau proteins is denoted by dT (typically 20–40 nm (8)).
To study the mechanical response of the axon for different loading rates, a viscoelastic shear-lag model for tau-mediated sliding of the microtubules is derived and numerically solved. As we discuss below, recent experiments (18) clearly show that the mechanical response of tau proteins is characterized by both elastic and viscous contributions. To capture these features of the mechanical response, a Kelvin viscoelastic model (shown in Fig. 2 a) consisting of a spring with stiffness K in parallel with a dashpot with viscosity μ is used for tau proteins. For this viscoelastic element, the force F-displacement δ relation satisfies
| (1) |
where the dot represents the time derivative, and
| (2) |
As the axon is loaded, forces are transferred from one MT to neighboring MTs through the stretching of the tau proteins, which leads to sliding of the MTs relative to each other. To compute the shear stress on the surface of the MTs due to stretching of the tau-proteins, we place a Cartesian coordinate system at the center of one MT, in such a way that the x axis is oriented along the length of the MT (refer to Fig. 2 a). We define a unit cell made up of two adjacent staggered MTs, with longitudinal displacement fields denoted by u1(x,t) and u2(x,t). With this definition, the elongation of the tau protein connecting the two points of the two adjacent MTs is
| (3) |
From this elongation, the force generated in each tau protein can be converted to a shear stress τ(x,t) acting on the surface of the MTs through the relation (Fig. 2 a)
| (4) |
where β is the angle between the tau protein and the MT. Next, by considering force balance in the axial direction of the MT, this shear stress can be converted to the normal/axial stress, σ(x,t), in the MTs by using the relation (see the free-body diagram shown in Fig. 2 a and also Ahmadzadeh et al. (25))
| (5) |
Combining Eqs. 1–5 results in the governing system of partial differential equations,
| (6) |
where v1(x,t) = (x,t) and v2(x,t) = (x,t) and
| (7) |
As we discuss below, Lc gives the length over which stresses are transferred between the microtubules. To allow us to determine the dimensionless combination of material parameters that govern mechanical response, we rescale the spatial and temporal coordinates using the equations X = x/L and T = t. Similarly, the displacement and fields are rescaled as Ui(X,T) = ui(x,t)/L and Vi(X,T) = (x,t)/L, respectively (i = 1,2). In terms of these variables, Eq. 6 can be rewritten as
| (8) |
The mechanical response of the model can be obtained by specifying the displacement of one end of the unit cell as a function of the strain rate, while holding the other end fixed. Specifically U1(0,T) = 0 and U2(1,T) = T, where is the applied strain rate. In addition, at the two free ends of the MTs present in the unit cell, the traction-free boundary conditions ∂U2(0,T)/∂X = ∂U1(1,T)/∂X = 0 are applied.
A recent computational model for the mechanical response of the axon (24), dealt with the rate-independent response of the axon to axial strains. In this study, the following sets of parameters were adopted:
which gives Lc = 0.22 μm (Eq. 7), and ϕ = 0.13 (Eq. A2). For these parameters, Eq. A1 of our model predicts the normalized Young’s modulus E(T)/ϕEf of ∼0.8, which agrees well with the corresponding normalized Young’s modulus ∼1.2 for strains close to 1%. To go beyond the quasi-static regime and to study dynamic effects not considered in any previous computational studies, we solve the governing Eq. 8 numerically with the finite element-package COMSOL 4.3a (COMSOL, Palo Alto, CA).
Model response depends on two dimensionless parameters
Based on the scaled governing equations (see the expressions in Eq. 8), we can infer that the mechanical response of the axon depends on two dimensionless parameters, namely, L/Lc (scaled half-length of the MTs) and (scaled rate of loading); note that the boundary conditions are independent of these parameters. Each of these parameters depends on the geometric and material parameters of the axon (Eqs. 2 and 7). We present estimates for these parameters, obtained primarily from experiments, in Table 1 (see also Janmey et al. (26)).
Table 1.
List of symbols in the viscoelastic shear-lag model
| Parameter | Quantity | Value | Ref. |
|---|---|---|---|
| RO | MT outer radius | 12.5 nm | (19) |
| RI | MT inner radius | 7 nm | |
| EM | MT Young’s modulus | 1.9 GPa | (19) |
| dM | MT spacing | 23–38 nm | (20) |
| dT | Tau protein spacing | 20–40 nm | (8) |
| 2L | MT length | 2–10 μm | (21) |
| — | MT rupture tensile strain | 50% | (26) |
| K | Tau protein spring constant | 0.25 pN/nm | (18) |
| η | Tau protein dashpot timescale | 0.35 s | (18) |
The lengths of the axons in the brain are in the range 1–10 μm (27). In this case the MT length distribution has been extensively studied by Yu and Baas (21), who analyzed axons (∼60 μm in length) from embryonic rat hippocampal neurons. They showed that the lengths of MTs in the axon vary between 0.05 and 40.14 μm (with an average length of 4.02 μm, and a standard deviation of 5.28 μm). Based on this work, we consider MT length that is in the range 2L = 2–10 μm.
To observe the onset of MT failure and axotomy in our simulations, we have to consider the critical strain at which MTs break. Janmey et al. (26) examined a MT network deformed under shear and showed that MTs in this network can withstand 50% of extensional strain before failure. Other studies with dual-optical tweezers on the fluorescently-labeled MTs obtain a 30% failure strain for MTs, which is consistent with the work of Janmey et al. (26), because it is known that fluorescently labeling the MTs reduces their mechanical strength to some degree (28). Schaap et al. (29) examined the effect of the MT incubation with tau protein on the mechanical strength of the MT wall and showed that the tau protein forms a 1-nm layer circumferentially along the outer ridges of the MT protofilaments. Whereas this added layer does not change the radial spring constant of the MTs in the indentation experiments, due to the stabilizing effect of the tau protein the failure load modestly increases by15%. These studies suggest that the maximum strain the MTs can withstand before failure is close to 50%.
The other key parameters in our model are the stiffness and viscosity of the tau protein. Recently, Wegmann et al. (18) carried out AFM based single-molecule force microscopy on nonaggregated human tau proteins and derived the force-elongation behavior of the longest tau isoform (hTau40 with 441 residues and contour length of 151 ± 14 nm). They pulled a single tau molecule with an AFM tip until the tip detached from the molecule. During this process, they observed the rupture of the intramolecular bonds within the tau protein in the form of sharp peaks in the force-extension curve. We used the breaking statistics of these intramolecular bonds to deduce the viscoelastic properties of tau proteins. As shown schematically in Fig. 2 b, under slow rates of pulling the protein, these intramolecular hydrogen bonds rupture easily, leading to overall elongation of the protein without the need to stretch the backbone. On the other hand, under a fast pulling rate, the stiffness of these intermolecular bonds increases rapidly; according to Bell’s theory (30), the rupture force of intermolecular bonds increases logarithmically with loading rate. Thus, for fast loading, the strain applied to protein elongation is accommodated by elongation of the backbone, resulting from variations in the bond angles and lengths.
Both the stiffness and viscosity of the protein can be inferred from the mentioned AFM experiment (18). From the average slopes of the force-elongation curve of the tau protein, we estimate the stiffness to be K ≈ 0.25 pN/nm, which is comparable to stiffness of related proteins reported in the literature (31,32). The viscosity of the elastic response arises from the rate dependence of rupture of intermolecular bonds within the protein. For each of the observed force peaks, by analyzing the statistics of unbinding events, an intrinsic unfolding rate at zero applied force (κ0 ∼ 0.14 s−1) and the distance between the bound and transition energy states (xu ∼ 0.14 nm) have been extracted in Wegmann et al. (18). These values have been used to obtain the rate constant κ, for rupture at each of the peak forces, using the Bell equation (30),
| (9) |
where Fp is the peak force, kB is the Boltzmann constant, and T is the absolute temperature. As shown in Bell (30), the average rate for breaking of each of the unfolding events provides a direct estimate for the viscoelastic parameter η; based on the rates given in Wegmann et al. (18), we obtain η ∼ 0.35 s, comparable to viscoelastic timescales observed for related proteins (31,32).
Experiments on dynamic stretching of axons (5,6) show that, under quasi-static loading (strain rate= 0.01 s−1), the axon can be stretched up to 100% strain without any evidence of damage of MTs, whereas MTs break at strain rates in the range ≅ 22–44 s−1 and when strains exceed 65%. Using these values of strain rates and η (Table 1), we determined that ≅ 8–15 should simulate dynamic loading conditions (Smith et al. (6)) that would lead to axotomy, whereas ≅ 0.001 should correspond to quasi-static loading response.
Finally, for the hexagonal lattice of MTs, the number of neighbors as α = 6, and estimating the angle β = 60°, and spacing of tau proteins dT = 30 nm (Fig. 2 a and Table 1), we obtain the characteristic length for load transfer to be Lc = 3.57 μm. Then, based on the two MT lengths considered here, namely, 2L = 2 μm and 2L = 10 μm, we obtain L/Lc = 0.28 and L/Lc = 1.40, respectively. In the next section, we use these parameter values to study the response of the axon to mechanical loading at different strain rates.
Results
Relative sliding versus stretching of the MTs is controlled by L/Lc and
As the axon is stretched, the deformation can be accommodated either by relative sliding of the MTs (caused by stretching of tau proteins) or by the stretching of the MTs. The dimensionless form of the governing equations (Eq. 8) show that the particular mode of deformation depends on two dimensionless parameters, L/Lc and . We first study the variation of the stretch of the tau proteins along the length of the MTs. To this end, we consider two MT lengths, one short L/Lc = 0.28, and the other long L/Lc = 1.40. The MTs are pulled at quasi-static ≅ 0.001, rate and dynamic loading rates ≅ 15. The distribution of the elongation of the tau proteins and the stretching of the MTs at an overall strain level of 10% is plotted in Fig. 3.
Figure 3.
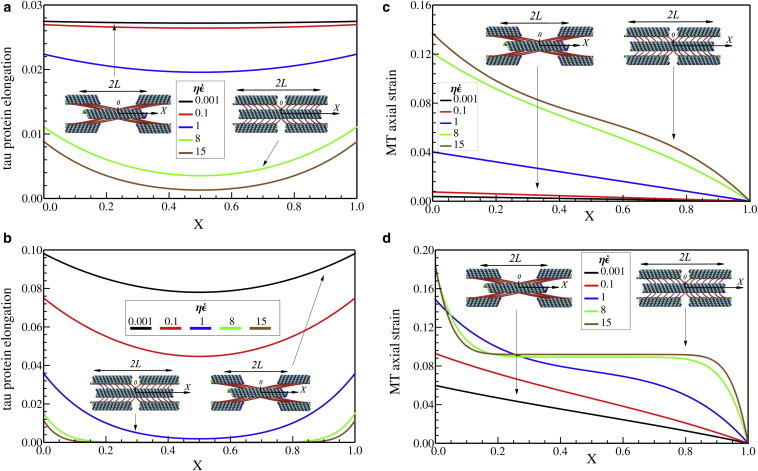
Elongation of tau proteins along the MTs, U2(X,T) – U1(X,T), with (a) L/Lc = 0.28 and (b) L/Lc = 1.40 and also axial strain along microtubules, ∂U1(X,T)/∂X, with (c) L/Lc = 0.28 and (d) L/Lc = 1.40, when overall elongation of the axon is 10%. The centers of the MTs stretch more with increasing strain rate and increasing length. To see this figure in color, go online.
We find a strong dependence of the stretch of the tau proteins on 1), their position relative to the ends of the MTs, 2), the overall length of the MTs, and 3), the strain rate. While the tau proteins located at X = 0 and X = 1 (which correspond to the ends of the two adjacent MTs) elongate considerably, the elongation is smaller at the center, X = 0.5. The extent to which the strain of the tau proteins at the center is smaller than the strain at the ends depends on both the rate of stretch and the length. This decrease in the stretch of the cross-linking proteins in regions between the force-free ends of the MTs is a general feature of shear-lag models (25). For quasi-static loading, the length scale over which this transfer takes place is the characteristic length, Lc (Eq. 7); when the microtubules are smaller or comparable to this characteristic length, there is no drop in the stretch of the tau proteins (black curve in Fig. 3 a) and the load transfer is primarily due to the sliding of the MTs. On the other hand, for longer MTs, sliding of the MTs is greater at the free ends and the mode of load transfer transitions to a stretching of the MTs, as seen in Fig. 3 b.
With increasing strain rate, the effective stiffness of the tau proteins increases due to contributions from the viscoelastic effects. Because the characteristic length scale for transitioning from sliding of MTs to stretching of MTs (Eq. 7) decreases with the effective stiffness of the tau proteins, stretching of the MTs becomes the dominant load-bearing mechanism over the MT sliding. This is clearly seen for the case of long MTs (L/Lc = 1.40), under fast loading, ≅ 15, where the tau proteins in the region 0.2 ≤ X ≤ 0.8 have negligible elongation. On the other hand, at low rates of deformation, the sliding of the MTs is larger; by decreasing the applied strain rate from ≅ 15 to ≅ 0.001, the MT sliding is increased by 250% (Fig. 3 a) and 500% (Fig. 3 b) for short and long MTs, respectively. This result shows that under a quasi-static loading, MTs start to slide and transfer the load in the axon through the tau protein elongation.
Plots of the axial strains in the MTs as a function of strain rate for different lengths are shown in Fig. 3, c and d. Consistent with the discussion in the preceding paragraph, stretch in the MTs is larger at larger strain rates and longer MTs experience larger stretch. Further, our calculations show that the stretch in the microtubules vanishes at the free ends and is largest at the center. Thus, longer MTs are more prone to breaking by initiation of failure at their midpoints. Next, we load the axon at different rates to determine the threshold strain at which the MTs break, resulting in axotomy (disconnection).
MTs break at fast strain rates
The maximum strain in the MTs, ∂U1(0,T)/∂X, as a function of the overall axonal strain for short L/Lc = 0.28 and long L/Lc = 1.40 MTs loaded at different strain rates is shown in Fig. 4, a and b. When the axons contain short MTs, they can easily be elongated to very large strains under quasi-static loading conditions. In this case, the deformation is accommodated by sliding of the MTs and strain in the MTs is negligible, which allows for reversible loading and unloading of axons as observed in experiments. On the other hand for dynamic loads, = 15, MTs fail at the overall axon strain of 75% (Fig. 4 a), consistent with experimental observations (5,6).
Figure 4.
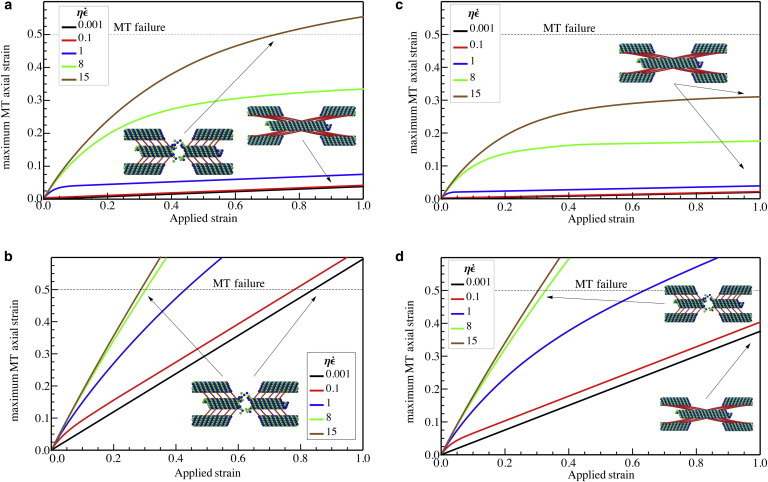
The maximum axial strain in the MTs, when the spacing between the tau proteins is 30 nm, with (a) L = 1 μm, L/Lc = 0.28 and (b) L = 5 μm, L/Lc = 1.40 and also when the spacing between the tau proteins is increased to 60 nm with (c) L = 1 μm, L/Lc = 0.20 and (d) L = 5 μm, L/Lc = 1.00, as a function of the total axonal strain. To see this figure in color, go online.
Also, for the axons with longer MTs, strain in the MTs is larger and therefore these longer MTs are more prone to failure. In this case, L/Lc = 1.40, under quasi-static loading, the axon can be stretched up to 82% strain without failure (Fig. 4 b). However, under dynamic loading, strains close to 29% result in the breaking of the MTs (Fig. 4 b) with swelling at the axon. Our results also show that when the MTs in axon have different lengths, longer MTs are more susceptible to failure compared to the shorter MTs.
Critical strain for microtubule failure increases with decrease in the linear density of tau proteins along the MTs
Another key parameter that controls the characteristic length scale for load transfer, Lc (Eq. 7), is the spacing between tau proteins. In this section, we consider the effects of increasing this spacing on the critical strain for axon failure. Because the characteristic length scale increases with increasing spacing between the tau proteins, sliding of the MTs becomes more prevalent over stretching compared to the case studied earlier. Subsequently, the failure of the MTs occurs at larger overall strain levels applied to the axon. By doubling the spacing of the tau proteins compared to the previous subsection, the magnitude of Lc increases to 5.06 μm; for MT lengths 2L = 2 μm and 2L = 10 μm, we obtain L/Lc = 0.20 and L/Lc = 1.00, respectively. In this case, the axial strain in the MTs as a function of the overall applied strain for short and long MTs is plotted in Fig. 4, c and d.
Fig. 4, c and d, shows that upon decreasing the linear density of tau proteins, the threshold strain for MT failure generally increases in all the cases. This increase is more pronounced when the loading is quasi-static and when the MT length is small; when the loading rate is fast and the MTs are long, this increase is less apparent. As an example, when the MT’s length is L = 5 μm, an increase in the tau protein spacing by a factor of two does not alter the dynamic threshold strain for breaking of the MTs. This fact can be explained based on our previous observations, where, for the long MTs and under fast loading rates, many of the tau proteins are force-free and redundant, particularly those distal from the free MT ends. Therefore, decreasing the density of tau proteins does not have a significant impact on the failure strains.
Discussion
In summary, we have implemented a viscoelastic shear-lag model to elucidate the mechanical response of the axon under dynamic loading conditions. We assumed that the axon structure consists of uniformly staggered MTs cross-linked by tau proteins, which we treat as a Kelvin viscoelastic element as suggested by recent AFM experiments (18). We then studied the mechanical response and breaking of the MTs for slow (strain rate = 0.01 s−1) and fast loading rates (strain rate = 44 s−1) relevant for axonal stretch injury. The key predictions of our models can be summarized as follows:
-
1.
The tau proteins located at different points along a MT stretch to differing extents: the proteins located at the end of the MTs elongate considerably, whereas the elongation of proteins located away from the free-ends is less in long MTs and at fast loading rates.
-
2.
The applied strain is accommodated along the axon by either sliding (due to the elongation of tau proteins) or stretching of the MTs. When the axon is loaded quasi-statically, MT sliding is more pronounced and the axial strain in the MTs is small. On the other hand, under fast loading of the axon, MT stretch is large and the sliding of the MTs is negligible.
-
3.
Under quasi-static loading, axons can withstand large uniaxial strains without failure of the MTs, whereas fast loading leads to mechanical breaking of the MTs. In addition, when the average length of the MTs inside an axon is larger, this threshold strain for axotomy is smaller.
-
4.
Based on the stiffness and viscosity of tau proteins deduced from AFM experiments (18), our model predicts that MTs will break when loaded at strain rates in excess of 22–44 s−1, in excellent agreement with observations (5,6). Thus, our model is able to predict the transition from reversible loading-unloading of the axons to failure with no fitting parameters.
-
5.
For a given level of axonal strain and strain rate, stretching of the longer MTs in an axon is larger compared to that of short MTs. Subsequently, longer MTs fail before the short ones and we predict failure to occur away from the free ends and near the midpoints of the MTs.
Based on our numerical simulations and the asymptotic analysis for the mechanical response in limiting cases (presented in Eq. A2), we have obtained a phase diagram that demarcates regions where axons can be stretched and where microtubules in the axons break (Fig. 5).
Figure 5.
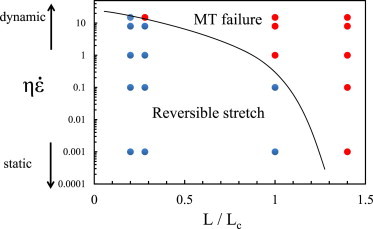
Phase-diagram that demarcates regions where MTs break and where axon can be reversibly deformed. The symbols (red = MT breaking, blue = MT sliding) are from numerical solutions presented in Fig. 4. To see this figure in color, go online.
The model presented in this article takes into account the microstructure of the axon (Fig. 2) to mimic the axonal failure in TBI. To capture the interruption of the cargo transport in TBI, it is essential to consider the actual load-transfer mechanism between the MTs (mediated by tau proteins). The amount of load transferred between the microtubules varies along their length, which behooves us to consider a model that reflects the ultrastructure of the axon. We believe that the model shown in Fig. 2 (motivated by experimental micrographs in Fig. 1) represents the simplest possible model of the axonal microstructure. Based on this model, we have shown that the response of the axon to stretch depends only on two variables, as shown in a phase diagram form in Fig. 5. None of the more generic models, including inelastic wormlike chain or generic binding site models, can predict strain rate-dependent failure criteria for the axon because they lack microstructural details necessary to capture load distribution.
In our model, we assume that the tau proteins remain bound to MTs and participate in the load-transfer mechanism over the entire duration of the loading process. Makrides et al. (33) have shown that tau proteins can either be bound tightly to the MT lumen forming irreversible bonds with a half-life on the order of several hours, or alternatively bind to the surface of the MT and form a dynamic bond with a very fast association (kon = 294 μM−1.s−1) and relatively slow dissociation (koff = 2.5 s−1) rates (33). Indeed the electron micrographs in Fig. 1 clearly show tau proteins penetrating the lumen of the MTs, which is consistent with our assumption that the tau proteins remain bound during the loading process. In the latter case, where tau can potentially dislodge from the MT, the time needed for subsequent rebinding is ∼1 ms (for a physiological concentration 1 μM of tau), which is much faster than the characteristic cross-over loading timescale of 1/20 s for breaking of MTs.
Thus, even in this case, our assumption is reasonable because of the fast rebinding timescales. Also, at low strain rates, the axon can stretch more than what we predict based on this model because the tau proteins have enough time to unbind over the timescales of loading. However, this is not directly relevant to our work here, because our interest is in large-strain rate response, where tau proteins will not unbind over the timescales of loading. In addition to binding and unbinding, diffusion of tau proteins along MTs has recently been observed by Hinrichs et al. (34). For the loading rates of 20 s−1, the diffusion length (, where t is time and D is diffusion constant ∼ 0.15 μm2.s−1 (34)) over the relevant timescale of ∼0.05 s is 120 nm, which is negligible compared to the overall length of the axon. Therefore, we are justified in neglecting the effect of diffusion of tau proteins that are not bound to the MT lumens at fast rates of loading. The MTs bound to the lumens (which is the case for majority of the proteins shown in Fig. 1) of course cannot diffuse along the MTs.
In our model, the lengths and elastic moduli of the MTs in the axon are assumed to be constant throughout the course of the stretching. However, it is well known that the MTs constantly alternate between polymerization (or rescue) and depolymerization (or catastrophe) states (35). In addition, different stabilizing drugs (such as taxol) and destabilizing drugs (such as nocodazol) are shown to alter the instability dynamics of MTs (36). Future extensions of the model should consider coupling between microtubule polymerization and mechanical effects to shed light on the role of MT stabilizing/destabilizing agents. As an example, it is known that the structural MAPs (such as tau proteins) promote MT stability and inhibit MT catastrophe considerably. The reported polymerization rate (growth rate) and depolymerization rate (shrinkage rate) for the MTs in the presence of the tau protein is ∼1.5 μm/min and 0.088 μm/min, respectively (37).
It is evident that these timescales are much larger than the timescales for failure at large strain rates and, therefore, for this case the effect of polymerization dynamics on failure should not be significant. However, at quasi-static strain rates (with duration 1–2 min), the growth/shrinkage of the MTs should be relevant. A simple approach to handle this effect is to assume a time-dependent MT half-length (L(t)), obtained from MT dynamics) and to solve the governing equation (Eq. 8) numerically. A more involved approach may be to carry out stochastic simulations that account for the statistics of MT catastrophes. We hope to address these extensions of our model in future publications.
Diffuse axonal injury is the one of the most common and important consequences of all severities of TBI and is thought to be the predominant pathological feature of mTBI (concussion). While it is generally accepted that accelerations or sudden loads to the head cause diffuse axonal injury throughout the white matter, how this load at the macroscale leads to the damage at the cellular level is poorly understood. Most computational models of TBI treat the white and gray matter uniformly as viscoelastic, hyperelastic, or fiber-reinforced materials (3,27,38). However, the origin of viscoelasticity, nonlinearity, or the cause of injury are not typically linked to vulnerable cellular constituents, such as focusing down to the micro- and nanoscale level of white-matter axons. Therefore, we have developed an approach that includes fundamental mechanical units of specific subcellular structures, microtubules, and tau proteins that contribute to the rate dependence of failure.
By incorporating the information on the failure criteria and the analytical solutions in the limiting cases (Eq. A2) summarized in the phase diagram (Fig. 5) in three-dimensional finite-element models of head injury (38), it may be possible to extrapolate the patterns of failure or recovery at the subcellular level to the macroscale response to tissue loading. Note that the state of strain in head models can be complex; however, what matters for injury is the component of the strain tensor projector along the axonal axis. Thus, the injury criterion can be applied if the strain rate in Fig. 5 is replaced by the projected strain rate.
Acknowledgments
H.A. and V.B.S. thank Dr. Louis Soslowsky, Brianne Connizo, and Benjamin Freedman for discussions on the applications of the shear-lag model to biocomposites.
This study was supported by National Science Foundation grant No. NSF-CMMI-1312392 (to V.B.S.), by National Institutes of Health grant Nos. NS R01-038104 and NS P01-056202, and by Department of Defense grant No. PT110785 (to D.H.S.).
Appendix I: Young’s Modulus for the Axon
The instantaneous Young’s modulus for the axon E(T), at a specific strain , can be calculated from the generated effective average stress to the overall strain , of the axon as
| (A1) |
Here ϕ is the volume fraction of the MTs in the axon, which in the case of the hexagonal distribution of the MTs is
| (A2) |
Appendix II: Analytical Solutions for Elastic Fields in Limiting Cases
As discussed earlier, the mechanical response of the axon to loading at different strain rates depends on two dimensionless parameters, L/Lc and . If we take the extreme limits of these two parameters, analytical solutions to the governing equations (Eq. 8) can be obtained. The goal of this section is to derive a phase diagram for axon response based on these analytical solutions. Specifically, for very fast >> 0, and quasi-static ≈ 0 loading rates, we consider the response of very long L/Lc >> 1 and a very short L/Lc << 1 MTs and find the analytic solution to Eq. 8.
η ≈ 0
In this case, the axon is subjected to a static strain rate, and the tau protein element (Fig. 2 a) is reduced to an elastic spring with stiffness K. Mathematically, by ignoring the first term on the right-hand side of Eq. 8, we obtain
| (A3) |
This form of the governing equations is identical to the classic shear-lag model where the cross-linkers between the MTs are assumed to be elastic. The general displacement field in the classic shear-lag model is (25)
| (A4) |
| (A5) |
Here, ψ is the axial strain in the MTs (in the range 0 < ψ < T), and can be obtained as
| (A6) |
With the above solution in hand, we now consider two extreme values for the MT length, as follows:
L/Lc << 1 (very short MTs)
In this case, one can show that ψ = 0, which means that MT stretch is zero and
| (A7) |
| (A8) |
In this limit, MT sliding is the main load transfer mechanism in the axon. This fact has also been observed in our numerical results, where for the short MTs and under quasi-static loading the MT sliding is found to be large (Fig. 3 a, = 0.001) and the stretch in the MT is negligible (Fig. 3 c, = 0.001).
L/Lc >> 1 (very long MTs)
Taking the limit of the above displacement fields (Eqs. A4 and A5) for L/Lc >> 1 results in ψ = T and
| (A9) |
This solution shows that MT stretching is the primary mechanism for load transfer in the axon and the MT sliding is negligible in this limit. This behavior has already observed in our numerical simulations, where, under the quasi-static loading rates, the axon with longer MTs show larger MT stretches (Fig. 3 d, = 15).
η >> 1
In this case, the axon is subjected to a very rapid dynamic strain, and accordingly the dashpot presented in the tau protein unit (Fig. 2 a) will not have enough time to respond. Here, the governing Eq. 8 simplifies to
| (A10) |
| (A11) |
We can find the displacement fields obtained from this equation with the boundary conditions U1(0,T) = 0, U2(1,T) = T,
| (A12) |
These solutions show that the MT stretch is the primary load-transfer mechanism and that the displacement fields are independent of the MT length. In our numerical results we see that for both the long and short MTs under a dynamic loading, MT sliding is negligible (Fig. 3, a and b, for = 15) and MT stretch is pronounced (Fig. 3, c and d, for = 15).
Based on these results, we can conclude that the approximate criterion that demarcates regions where MTs break and regions where they slide is
| (A13) |
where the right-hand side is a constant of order unity. A phase diagram that shows the response of the axon as a function of the scaled length of the MTs and the scaled rate of stretching is given in Fig. 5. We find that this phase diagram satisfactorily captures the trends observed in the numerical calculations presented in Fig. 4.
References
- 1.Johnson V.E., Stewart W., Smith D.H. Axonal pathology in traumatic brain injury. Exp. Neurol. 2013;246:35–43. doi: 10.1016/j.expneurol.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Knöferle J., Koch J.C., Lingor P. Mechanisms of acute axonal degeneration in the optic nerve in vivo. Proc. Natl. Acad. Sci. USA. 2010;107:6064–6069. doi: 10.1073/pnas.0909794107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cloots R.J.H., van Dommelen J.A.W., Geers M.G.D. Multi-scale mechanics of traumatic brain injury: predicting axonal strains from head loads. Biomech. Model. Mechanobiol. 2013;12:137–150. doi: 10.1007/s10237-012-0387-6. [DOI] [PubMed] [Google Scholar]
- 4.Smith D.H., Meaney D.F. Axonal damage in traumatic brain injury. Neuroscience. 2000;6:483–495. [Google Scholar]
- 5.Tang-Schomer M.D., Patel A.R., Smith D.H. Mechanical breaking of microtubules in axons during dynamic stretch injury underlies delayed elasticity, microtubule disassembly, and axon degeneration. FASEB J. 2010;24:1401–1410. doi: 10.1096/fj.09-142844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith D.H., Wolf J.A., Meaney D.F. High tolerance and delayed elastic response of cultured axons to dynamic stretch injury. J. Neurosci. 1999;19:4263–4269. doi: 10.1523/JNEUROSCI.19-11-04263.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tang-Schomer M.D., Johnson V.E., Smith D.H. Partial interruption of axonal transport due to microtubule breakage accounts for the formation of periodic varicosities after traumatic axonal injury. Exp. Neurol. 2012;233:364–372. doi: 10.1016/j.expneurol.2011.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hirokawa N., Shiomura Y., Okabe S. Tau proteins: the molecular structure and mode of binding on microtubules. J. Cell Biol. 1988;107:1449–1459. doi: 10.1083/jcb.107.4.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolf J.A., Stys P.K., Smith D.H. Traumatic axonal injury induces calcium influx modulated by tetrodotoxin-sensitive sodium channels. J. Neurosci. 2001;21:1923–1930. doi: 10.1523/JNEUROSCI.21-06-01923.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Iwata A., Stys P.K., Smith D.H. Traumatic axonal injury induces proteolytic cleavage of the voltage-gated sodium channels modulated by tetrodotoxin and protease inhibitors. J. Neurosci. 2004;24:4605–4613. doi: 10.1523/JNEUROSCI.0515-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Singh A., Kallakuri S., Cavanaugh J.M. Structural and functional changes in nerve roots due to tension at various strains and strain rates: an in-vivo study. J. Neurotrauma. 2009;26:627–640. doi: 10.1089/neu.2008.0621. [DOI] [PubMed] [Google Scholar]
- 12.Skotak M., Wang F., Chandra N. An in vitro injury model for SH-SY5Y neuroblastoma cells: effect of strain and strain rate. J. Neurosci. Methods. 2012;205:159–168. doi: 10.1016/j.jneumeth.2012.01.001. [DOI] [PubMed] [Google Scholar]
- 13.Pfister B.J., Weihs T.P., Bao G. An in vitro uniaxial stretch model for axonal injury. Ann. Biomed. Eng. 2003;31:589–598. doi: 10.1114/1.1566445. [DOI] [PubMed] [Google Scholar]
- 14.Fletcher D.A., Mullins R.D. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Saif T., Rajagopalan J., Tofangchi A. MRS Proceedings. Cambridge University Press; Cambridge, UK: 2010. The role of mechanical tension in neurons. [Google Scholar]
- 16.Rajagopalan J., Tofangchi A., Saif M.T.A. Drosophila neurons actively regulate axonal tension in vivo. Biophys. J. 2010;99:3208–3215. doi: 10.1016/j.bpj.2010.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Burgoyne R.D. Wiley-Liss; New York: 1991. The Neuronal Cytoskeleton. [Google Scholar]
- 18.Wegmann S., Schöler J., Muller D.J. Competing interactions stabilize pro- and anti-aggregant conformations of human Tau. J. Biol. Chem. 2011;286:20512–20524. doi: 10.1074/jbc.M111.237875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Suresh S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007;3:413–438. doi: 10.1016/j.actbio.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rosenberg K.J., Ross J.L., Israelachvili J. Complementary dimerization of microtubule-associated tau protein: Implications for microtubule bundling and tau-mediated pathogenesis. Proc. Natl. Acad. Sci. USA. 2008;105:7445–7450. doi: 10.1073/pnas.0802036105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu W., Baas P.W. Changes in microtubule number and length during axon differentiation. J. Neurosci. 1994;14:2818–2829. doi: 10.1523/JNEUROSCI.14-05-02818.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brady S., Siegel G., Price D. Elsevier Science; New York: 2005. Basic Neurochemistry: Molecular, Cellular and Medical Aspects. [Google Scholar]
- 23.Hui O., Nauman E., Shi R. Micro/Nano Symposium (UGIM), 2010 18th Biennial University/Government/Industry [Proceedings] Curran Associates; Red Hook, NY: 2010. Contribution of cytoskeletal elements to the mechanical property of axons; pp. 1–5. [Google Scholar]
- 24.Peter S.J., Mofrad M.R.K. Computational modeling of axonal microtubule bundles under tension. Biophys. J. 2012;102:749–757. doi: 10.1016/j.bpj.2011.11.4024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ahmadzadeh H., Connizzo B.K., Shenoy V.B. Determining the contribution of glycosaminoglycans to tendon mechanical properties with a modified shear-lag model. J. Biomech. 2013;46:2497–2503. doi: 10.1016/j.jbiomech.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Janmey P.A., Euteneuer U., Schliwa M. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J. Cell Biol. 1991;113:155–160. doi: 10.1083/jcb.113.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wright R.M., Ramesh K.T. An axonal strain injury criterion for traumatic brain injury. Biomech. Model. Mechanobiol. 2012;11:245–260. doi: 10.1007/s10237-011-0307-1. [DOI] [PubMed] [Google Scholar]
- 28.Guo H., Xu C., Zhang D. Mechanism and dynamics of breakage of fluorescent microtubules. Biophys. J. 2006;90:2093–2098. doi: 10.1529/biophysj.105.071209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schaap I.A.T., Hoffmann B., Schmidt C.F. Tau protein binding forms a 1 nm thick layer along protofilaments without affecting the radial elasticity of microtubules. J. Struct. Biol. 2007;158:282–292. doi: 10.1016/j.jsb.2006.11.010. [DOI] [PubMed] [Google Scholar]
- 30.Bell G. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 31.Wang Y., Zocchi G. The folded protein as a viscoelastic solid. Europhys. Lett. 2011;96:18003. [Google Scholar]
- 32.Kawakami M., Byrne K., Smith D.A. Viscoelastic study of the mechanical unfolding of a protein by AFM. Biophys. J. 2006;91:L16–L18. doi: 10.1529/biophysj.106.085019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Makrides V., Massie M.R., Lew J. Evidence for two distinct binding sites for tau on microtubules. Proc. Natl. Acad. Sci. USA. 2004;101:6746–6751. doi: 10.1073/pnas.0400992101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hinrichs M.H., Jalal A., Scholz T. Tau protein diffuses along the microtubule lattice. J. Biol. Chem. 2012;287:38559–38568. doi: 10.1074/jbc.M112.369785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Conde C., Cáceres A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat. Rev. Neurosci. 2009;10:319–332. doi: 10.1038/nrn2631. [DOI] [PubMed] [Google Scholar]
- 36.Baas P.W., Ahmad F.J. Beyond taxol: microtubule-based treatment of disease and injury of the nervous system. Brain. 2013;136:2937–2951. doi: 10.1093/brain/awt153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Drechsel D.N., Hyman A.A., Kirschner M.W. Modulation of the dynamic instability of tubulin assembly by the microtubule-associated protein tau. Mol. Biol. Cell. 1992;3:1141–1154. doi: 10.1091/mbc.3.10.1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wright R.M., Post A., Ramesh K.T. A multiscale computational approach to estimating axonal damage under inertial loading of the head. J. Neurotrauma. 2013;30:102–118. doi: 10.1089/neu.2012.2418. [DOI] [PubMed] [Google Scholar]


