Molecular Analysis of the Interaction between Staphylococcal Virulence Factor Sbi-IV and Complement C3d

Abstract

Staphylococcus aureus expresses numerous virulence factors that aid in immune evasion. The four-domain staphylococcal immunoglobulin binding (Sbi) protein interacts with complement component 3 (C3) and its thioester domain (C3d)-containing fragments. Recent structural data suggested two possible modes of binding of Sbi domain IV (Sbi-IV) to C3d, but the physiological binding mode remains unclear. We used a computational approach to provide insight into the C3d-Sbi-IV interaction. Molecular dynamics (MD) simulations showed that the first binding mode (PDB code 2WY8) is more robust than the second (PDB code 2WY7), with more persistent polar and nonpolar interactions, as well as conserved interfacial solvent accessible surface area. Brownian dynamics and steered MD simulations revealed that the first binding mode has faster association kinetics and maintains more stable intermolecular interactions compared to the second binding mode. In light of available experimental and structural data, our data confirm that the first binding mode represents Sbi-IV interaction with C3d (and C3) in a physiological context. Although the second binding mode is inherently less stable, we suggest a possible physiological role. Both binding sites may serve as a template for structure-based design of novel complement therapeutics.

Introduction

Staphylococcus aureus (S. aureus) produces numerous toxins and virulence factors known to disrupt a wide array of biological functions (1,2). Recent work has identified secreted proteins that disrupt function of the complement system (3–8), a branch of innate immunity responsible for phagocytosis of pathogens in the bloodstream. Sbi, a four-domain protein associated with the cell wall of S. aureus (9), contains two domains (III and IV) that bind complement component 3 (C3) and its thioester domain (C3d)-containing fragments (6). C3 is the central component of complement activation cascades, which is cleaved to form C3a and C3b by convertase enzymes. C3b covalently attaches to bacterial surfaces via its thioester domain (C3d), which becomes solvent exposed after C3a is cleaved from C3. Functional studies indicate that an Sbi construct comprised only of domains III and IV (Sbi-III/IV) leads to rapid consumption of C3 in the bloodstream, preventing C3 from being activated to C3b and opsonizing the bacterial surface. Interestingly, domain IV of Sbi (Sbi-IV) on its own specifically inhibits activation of the complement alternative pathway (AP) by preventing active convertase formation, representing an entirely different mechanism of action (6).

The structures of Sbi-IV, both free and in complex with C3d, were recently reported (10). Dual binding modes were reported for Sbi-IV, with binding observed at the concave acidic region (Complex 1) and at the convex thioester-containing region (Complex 2). Mutagenesis studies of Sbi-IV binding and function, together with astounding similarity to binding modes of staphylococcal complement inhibitors Efb-C and Ecb at the concave acidic region (11,12), suggest that Complex 1 is responsible for AP inhibition (10,13). Nearly all known ligands of C3d bind at or near the concave acidic region (Fig. S1 in the Supporting Material). This region is suggested to be evolutionarily conserved, facilitating complement-mediated recruitment of B cells to bacterial surfaces via interaction with complement receptor 2 (CR2) (14). The second proposed binding site of Sbi-IV (Complex 2) represents a novel C3d interaction site (Fig. S1). If Sbi-IV indeed binds to the convex thioester-containing region, this binding mode could represent a previously uncharacterized complement evasion tactic by pathogens. However, both the physiological significance and existential probability of Complex 2 remain unclear.

Macromolecular crystallography provides invaluable insight into the structural basis of protein interactions and how these interactions translate into functional phenomena observed in vitro and in vivo. However, one major limitation involves capturing molecules of interest in static conformations. Crystallization of proteins with their binding partners may induce nonphysiological binding conformations due to crystallization conditions and crystal packing effects. Indeed, recent cocrystal structures involving complement proteins suggest binding arrangements that are somewhat contradictory (15–21). We describe herein the integration of a variety of computational tools to analyze two recently published crystallographic structures of C3d in complex with Sbi-IV. We seek to evaluate the binding of Complexes 1 and 2 under simulated physiological conditions, by examining their dynamic stability and associative and dissociative properties.

Methods

Structure preparation

Three-dimensional cocrystal structures of C3d-Sbi-IV Complexes 1 (Protein Data Bank (PDB) code 2WY8) and 2 (PDB code 2WY7) were obtained from the PDB (22). In cases where multiple crystallographic positions were reported for given residues, position A was selected as the residue position, since all positions had 50% occupancy in the original PDB files.

Analysis of electrostatic similarities of proteins

Analysis of electrostatic similarities of proteins (AESOP) (23–26) was used to quantify the effects of specific charged residues on C3d-Sbi-IV association in Complexes 1 and 2. First, PDB2PQR (27) was used to add hydrogen atoms, partial charges, and atomic radii to each complex PDB structure, using the PARSE force field (28). Theoretical alanine scan mutagenesis was performed for all charged residues of the protein complexes, one at a time. For each mutated protein and protein complex, electrostatic potential maps and free energies were calculated using APBS (29), as described previously (23,24,26,30). For electrostatics calculations, we used protein and solvent dielectric values of 20 and 78.54, respectively, and ionic strength values of 0 and 150 mM. The choice of the value of protein dielectric is justified in an earlier study (25). Electrostatic similarity clustering and calculation of electrostatic free energies of association and solvation were performed as described previously (23,26).

Explicit-solvent molecular dynamics simulations

Molecular dynamics (MD) simulations of Complexes 1 and 2 were performed using NAMD (31). PDB structures of each complex were prepared using the PSFGEN utility in VMD (32) and the CHARMM27 force field (33). Complexes 1 and 2 were solvated in TIP3P water boxes measuring 87 Å × 87 Å × 87 Å and 82 Å × 82 Å × 82 Å, respectively. Sodium and chloride counterions were added to neutralize the charge of each system, with an ionic strength of 150 mM. Each system was minimized using 25,000 steps of conjugate gradient energy minimization, followed by heating from 0 to 300 K (62 ps total), four equilibration stages (50 ps each) with all protein atoms harmonically constrained (using force constants of 10, 5, 2, and 1 kcal/mol/Ų, respectively) to their postminimization positions, and a final equilibration stage (50 ps) with protein backbone atoms harmonically constrained (using a force constant of 1 kcal/mol/Ų), followed by the production run. All simulations were performed using periodic boundary conditions and particle-mesh Ewald electrostatics with a nonbonded interaction cutoff and switching distance of 12 Å and 10 Å, respectively. The SHAKE algorithm was employed to fix the length of bonds involving hydrogen atoms, enabling the use of 2 fs integration time steps. Langevin temperature and pressure controls were used for all NPT ensemble simulations. For each system, one 100 ns trajectory and three 20 ns trajectories were performed, using the energy-minimized coordinates of each system as the starting point for all simulations, with different random-number-generated seeds.

Steered MD simulations

Steered MD (SMD) simulations were also performed using NAMD. For each system, the solvent accessible surface of C3d atoms within 8 Å of Sbi-IV and its normal vectors were calculated using the UCSF Chimera (34). The mean of the normal vectors was used as the direction of induced Sbi-IV dissociation from C3d. To facilitate SMD simulations and analysis, each complex was rotated such that the mean normal vector was aligned with the +z axis. Complexes 1 and 2 were solvated in TIP3P water boxes measuring 76 Å × 87 Å × 105 Å and 75 Å × 78 Å × 104 Å, respectively, which provided additional space for Sbi-IV dissociation in the +z direction. Each system was minimized and heated as described above, followed by a 500 ps equilibration stage with all protein atoms harmonically restrained using a force constant of 10 kcal/mol/Ų. Equilibrated structures were used as input for all SMD simulations. Five 1.6 ns SMD simulations were performed for each complex. Residues of C3d >12 Å from Sbi-IV were harmonically constrained to their equilibrated positions during the SMD simulations with a force constant of 10 kcal/mol/Ų. The center of mass of all Sbi-IV atoms was constrained (with a force constant of 10 kcal/mol/Ų) to a point moving at a constant velocity of 10 Å/ns in the +z direction.

Brownian dynamics simulations

Brownian dynamics (BD) simulations for Complexes 1 and 2 were performed using BrownDye (35). For each complex, PQR files and electrostatic potential maps were generated for C3d and Sbi-IV as described above. In all simulations, C3d was the stationary molecule and Sbi-IV was the diffusing molecule. Reaction criteria were selected based on a pilot comparative study using mutants of barnase-barstar and corresponding experimental k_on data (data not shown). Pairwise residue interactions were calculated from energy-minimized structures of each complex, using cutoff distances of either 3.5 Å or 5.0 Å. Successful reactions in BD simulations required formation of at least two (or three) interactions from the pairwise list, with interatomic distance <6.0 (or 6.5) Å. The program bd_top was used to generate all necessary input files for BD simulations, and 100,000 trajectories were performed for each system under each set of reaction conditions. Reaction probabilities and corresponding k_on rates were calculated by BrownDye.

MD simulation analysis

MD trajectories were analyzed using the Bio3D package (36) and additional custom scripts in R. Analysis of hydrogen bonds and visual PDB and MD trajectory analysis were performed with UCSF Chimera. Solvent accessible surface area (SASA) for proteins and protein complexes was determined using VMD, and interfacial SASA was calculated according to

$$\Delta \text{SASA}={\text{SASA}}_{\text{AB}}-{\text{SASA}}_{\text{A}}-{\text{SASA}}_{\text{B}},$$ (1)

where SASA_AB, SASA_A, and SASA_B are the SASAs of the protein complex and free proteins, respectively. All SASA calculations were performed on MD snapshots with all hydrogen atoms present. Association free energies were calculated using the molecular mechanics/generalized Born surface area (MM-GBSA) method, based on snapshots from one 100 ns and three 20 ns trajectories for each protein complex. The first 10 ns of each simulation were not used in calculating MM-GBSA free energies. Free-energy values were calculated according to

$$\Delta G=G_{\text{AB}}-G_{\text{A}}-G_{\text{B}},$$ (2)

where G_AB, G_A, and G_B are the free energies of the protein complex (C3d-Sbi-IV) and free components (C3d and Sbi-IV), respectively. Free energy (G) is calculated according to

$$G_i=E_{\text{MM}}-G_{\text{solv}}-T\Delta S,$$ (3)

where

$$E_{\text{MM}}=E_{\text{bonded}}+E_{\text{vdw}}+E_{\text{Coul}},$$ (4)

and

$$G_{\text{solv}}=G_{\text{elec}}+G_{\text{np}}.$$ (5)

All free energies were calculated based on MD trajectories of the complex only, so conformational changes between free and bound C3d and/or Sbi-IV are neglected. Thus, in calculating ΔG, E_bonded terms cancel, leaving

$$\Delta G=\Delta E_{\text{vdw}}+\Delta E_{\text{Coul}}+\Delta G_{\text{elec}}+\Delta G_{\text{np}}.$$ (6)

The first and second terms on the righthand side of Eq. 6 were obtained using CHARMM and the CHARMM27 force field. The third term represents the Generalized Born approximation of solvation free energy, and it was calculated using the GBSW module in CHARMM. The final term represents the nonpolar contribution to solvation energy, calculated according to

$$\Delta G_{\text{np}}=\gamma \times \Delta \text{SASA,}$$ (7)

where γ is the surface-tension parameter, set to 0.005 kcal/mol/Ų. Per-residue MM-GBSA free energies were calculated in the same manner, but using a residue-protein rather than protein-protein interaction. Reported values for electrostatic free energy are comprised of the sum of the second and third righthand terms in Eq. 6, and the nonpolar free-energy values are comprised of the sum of the first and fourth terms. Total energy refers to the ΔG quantity described in Eq. 6. Mean energies were calculated for snapshots within each trajectory. The reported energy values reflect the mean ± SD across the four trajectories for each complex.

Results

Electrostatic analysis

Sbi-IV is a three-helix bundle that exhibits binding to C3d via the acidic concave region (Complex 1) and the convex thioester-containing region (Complex 2) according to the crystallographic structures (10). Fig. 1 A shows a comparison of both binding modes, with the Sbi-IV molecule from Complexes 1 and 2 on the left and right sides, respectively, of C3d. The interfacial SASA is similar for the two complexes (1901 Å² and 1671 Å², respectively). There is electrostatic complementarity at both binding interfaces, but the complementarity is much more pronounced in Complex 1 (Fig. 1, B and C). To quantify the role of electrostatics in C3d-Sbi-IV association at each binding site, we performed AESOP analyses. Based on the magnitudes and perturbations of electrostatic free energies upon mutation of ionizable residues to alanine, it is clear that Complex 1 (Fig. 2 A and C) is much more electrostatically driven than Complex 2 (Fig. 2 B and D). There are six C3d mutations and seven Sbi-IV mutations that experience >5 kJ/mol gain in association free energy in Complex 1, whereas in Complex 2, no C3d mutations and only two Sbi-IV mutations result in considerable changes in energy. These data reflect that the Complex 1 interface is significantly more polar than the Complex 2 interface.

Figure 1.

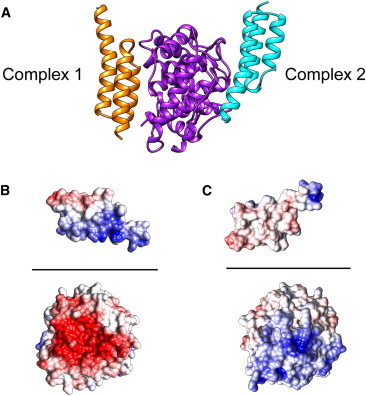
Molecular graphics representations of C3d-Sbi-IV complexes. (A) The two binding modes of Sbi-IV (orange and cyan) are shown bound to C3d (purple). (B and C) Open-book representations of C3d-Sbi-IV Complex 1 (B) and Complex 2 (C), illustrating electrostatic complementarity at each interface. C3d and Sbi-IV are rotated about the horizontal axis (black line) by −90° and +90°, respectively. Molecular surfaces are colored based on electrostatic potential values, with a gradient from −5 k_BT/e (red) to +5 k_BT/e (blue). To see this figure in color, go online.

Figure 2.

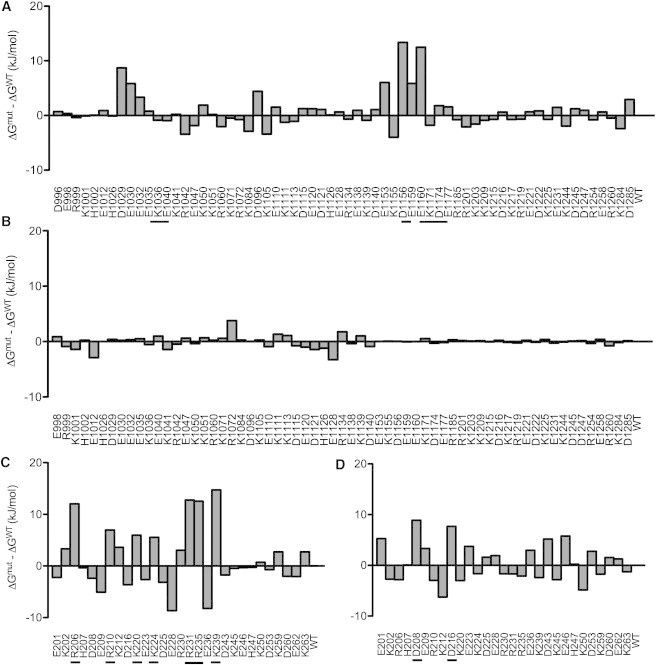
Electrostatic free energies of C3d-Sbi-IV association. Free energies were calculated using a thermodynamic cycle including protein association and solvation, and Poisson-Boltzmann electrostatics calculations, for C3d from Complex 1 (A), C3d from Complex 2 (B), Sbi-IV from Complex 1 (C), and Sbi-IV from Complex 2 (D). Residue labels refer to the corresponding alanine mutations, and magnitudes refer to calculated energies relative to the wild-type complex. Only ionizable residues are included. The underlined residues on the x axis indicate mutations that are most unfavorable to complex binding.

MD simulations

We used explicit-solvent MD simulations to examine the dynamic stability of Complex 1 and 2 binding modes (Movie S1). Data from a previous study suggest that Complex 1 is the primary binding mode for C3d-Sbi-IV (10). Fig. 3 shows the conformational changes of each complex over the course of 100 ns of MD simulation. Superposition of C3d at five representative snapshots (0, 25, 50, 75, and 100 ns) indicates a stable interaction between C3d and Sbi-IV in the Complex 1 binding mode (Fig. 3 A), with only slight fluctuations observed at the N- and C termini of Sbi-IV. In contrast, we observe larger fluctuations in the Sbi-IV structure when bound to C3d in the Complex 2 binding mode (Fig. 3 B), particularly at the N-terminus, which seems to remain only transiently bound to C3d. We quantified these dynamic fluctuations through root mean-square fluctuation (RMSF) calculations for Sbi-IV residues from Complex 1 and Complex 2 (Fig. S2). With the exception of a small number of residues in helix 3, the RMSF of Sbi-IV residues in Complex 2 is higher than that of Sbi-IV residues in Complex 1. Sbi-IV residues near the N- and C-termini in Complex 2 have significantly higher fluctuation, which suggests that these residues do not contribute significantly to C3d binding. Closer examination of the MD snapshots reveals that in Complex 1, C3d-Sbi-IV binding is dominated by a central core of interacting residues, supplemented by alternating peripheral interacting residues near the N- and C termini. In concordance with the AESOP electrostatic analysis, we observe that the interface is dominated by salt bridges and hydrogen bonds involving basic Sbi-IV residues (R206, R231, R235, K239, and K245), but is also reinforced by nonpolar residues present on all three helices (Fig. S3 A and Table S1). In Complex 2, the N-terminus of Sbi-IV helix 1 is only transiently bound to C3d, and thus the interface is stabilized primarily by a localized core of hydrogen bonds and nonpolar interactions at the C-terminus of helix 1 and the N-terminus of helix 3 (Fig. S3 B and Table S1).

Figure 3.

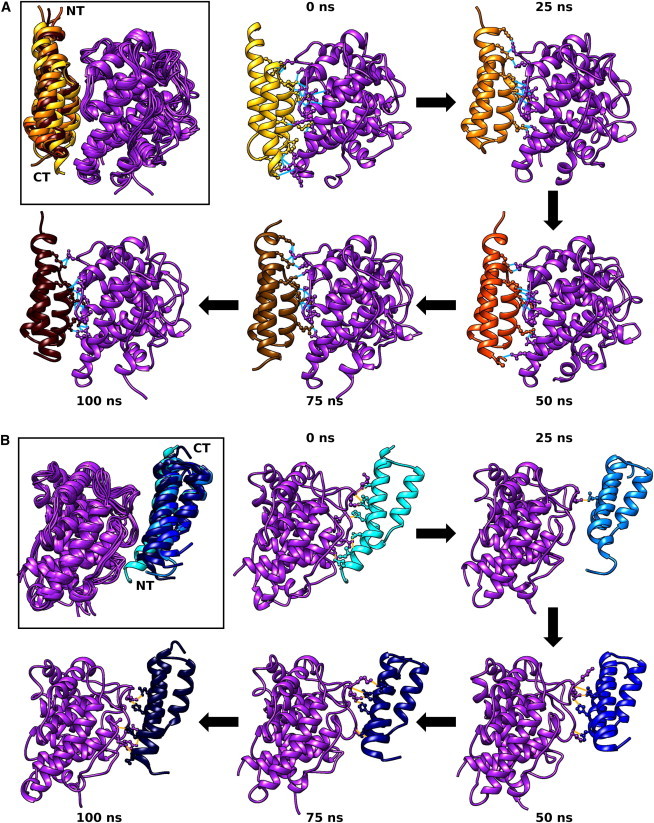
MD snapshots from 100 ns trajectories of C3d-Sbi-IV complexes. Upper left snapshots (black outline) show superpositions of C3d-Sbi-IV complexes of Complex 1 (A) and Complex 2 (B). The N- and C-termini of Sbi-IV are labeled NT and CT. Five snapshots at timepoints 0, 25, 50, 75, and 100 ns, as labeled in clockwise sequence (black arrows), are shown for each complex. Residues forming hydrogen bonds in each snapshot are shown (short blue lines). To see this figure in color, go online.

Since Complex 2 is largely stabilized by nonpolar interactions, we measured the interfacial SASA of both complexes over the course of all MD trajectories, to compare the stability of the observed crystallographic interfaces. We observe that in general, interfacial SASA of Complex 1 remains constant over time, whereas Complex 2 undergoes significant loss of interfacial SASA (Fig. 4). Despite these data, we did not observe complete dissociation of Complex 2 at any point, and the interfacial SASA tends to reach a steady state within ∼10 ns in all trajectories. In addition, observed losses in interfacial SASA were not always permanent. Near the end of the 100 ns MD trajectory for Complex 2, we observed a sudden increase in interfacial SASA (Fig. 4 B). Examination of this trajectory revealed unwinding of the N-terminus of Sbi-IV helix 1, which facilitated formation of charge-charge interactions that guided the N-terminus back to C3d (see Fig. 3 B).

Figure 4.

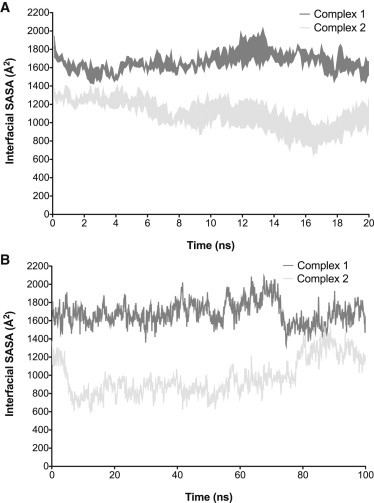
Change in interfacial SASA during MD trajectories of C3d-Sbi-IV complexes. Interfacial SASA versus time for three independent 20 ns (A) and 100 ns (B) MD trajectories of Complexes 1 (dark gray) and 2 (light gray). Data points in A represent the mean ± SE of interfacial SASA.

Weakening of Complex 2 (relative to the crystallographic structure) can be also observed through the number of nonpolar interactions, hydrogen bonds, and salt bridges throughout MD trajectories (Figs. S4–S6). Furthermore, although the two complexes are stabilized by comparable numbers of nonpolar interactions (Fig. 5, A and B), polar interactions are much more dominant at the Complex 1 interface (Fig. 5, C–F). In the initial configuration of Complex 2, there is a relative physicochemical mismatch between residues at the N-terminus of Sbi-IV and the N-terminal loops and helices of C3d. N-terminal Sbi-IV residues preferentially engage in intramolecular interactions, including salt bridges and a hydrophobic cluster. As a consequence, N-terminal residues 198–203 of Sbi-IV tend to move away from C3d, whereas nonpolar interactions in the C-terminal region of helix 1 and the N-terminal region of helix 3 hold the complex together (Fig. 5 B and Fig.S3 B). In contrast, intermolecular interactions are well conserved throughout the MD trajectories for Complex 1. The Sbi-IV N-terminus is less prone to dynamic instability; Arg and Lys residues (K202, R206, and R210) switch between stabilizing helix 1 of Sbi-IV and forming salt-bridging interactions with C3d residues. Notably, Sbi-IV residues responsible for interaction with C3d in Complex 1 are more dispersed, consisting of positively charged residues in the N-terminal region of helix 1, all of helix 2, and the N- and C-terminal regions of helix 3 (Fig. 5, A, C, and E, and Fig. S3 A).

Figure 5.

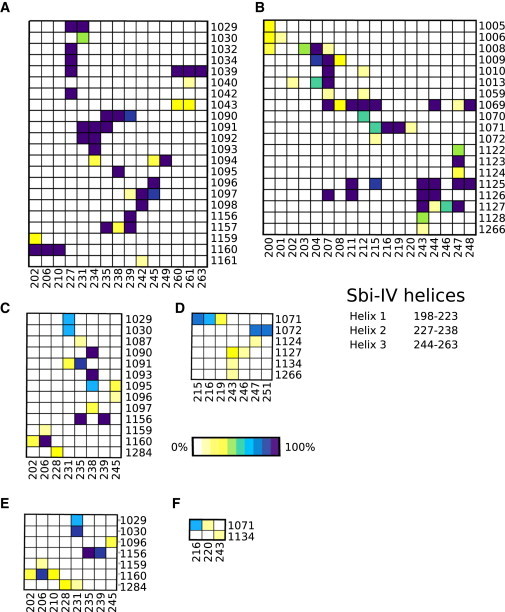
Interaction occupancy during MD trajectories of C3d-Sbi-IV complexes. Interactions were calculated at 100 ps intervals throughout one 100 ns and three 20 ns MD trajectories for Complexes 1 and 2. Occupancies represent the percentage of snapshots (across all trajectories) in which specific interactions were present. Residue numbers on the x and y axes represent residues of Sbi-IV and C3d, respectively. The legend shows the color scale from white (0% occupancy) to purple (100% occupancy). Interactions calculated include nonpolar interactions for Complex 1 (A) and Complex 2 (B), hydrogen bonds for Complex 1 (C) and Complex 2 (D), and salt bridges for Complex 1 (E) and Complex 2 (F). The residue ranges for Sbi-IV helices are indicated on the right. To see this figure in color, go online.

MM-GBSA calculations provide further quantitative insight into the energetic nature of Complexes 1 and 2. Overall, Complex 1 is enthalpically favored over Complex 2, in terms of both electrostatic and nonpolar interactions (Fig. 6 A). The importance of electrostatic interactions in Complex 1 is again evident here, as electrostatic interactions account for ∼33% of the total free energy (compared to ∼19% for Complex 2). Examination of per-residue free energy contributions reveals that the majority (14 of 20) of interacting residues in Complex 1 are charged (Fig. 6 B). Sbi-IV residues that contribute to the free energy of Complex 2 primarily interact via nonpolar interactions and hydrogen bonds (most charged Sbi-IV residues in Fig. 6 C interact via hydrogen bonds, not salt bridges). A large number of residues (from both C3d and Sbi-IV) contribute to binding of Complex 1. As discussed earlier, Complex 1 is stabilized by a central core of interactions, primarily involving electrostatic interactions between Sbi-IV helix 2 (residues 227–239) and acidic residues surrounding the concave surface of C3d. A number of residues from helix 1, and to a lesser extent from helix 3, form energetically favorable contacts as well, resulting in a dispersed network of interactions (Fig. S7 A). In Complex 2, fewer Sbi-IV residues make energetically favorable contacts with C3d, and these contribute less significantly to the free energy of C3d-Sbi-IV complex formation (Fig. 6 C). Furthermore, these residues are localized and not distributed well among Sbi-IV helices, compared to Complex 1 (Fig. S7 B).

Figure 6.

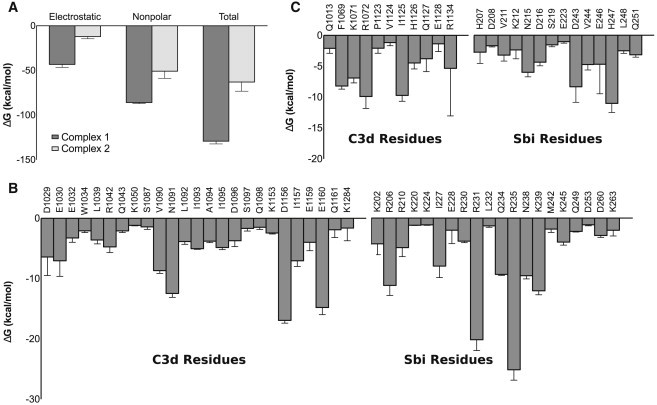
MM-GBSA free energies of C3d-Sbi-IV complexes. (A) Electrostatic, nonpolar, and total MM-GBSA association free energies for Complexes 1 and 2. (B and C) Per-residue MM-GBSA free energies for C3d and Sbi-IV are shown for Complexes 1 (B) and 2 (C).

BD simulations

Since equilibrium binding of protein complexes is comprised of association and dissociation phases, we used computational tools to probe each of these phases. BD simulations show that Complex 1 associates more than an order of magnitude faster than Complex 2 (Fig. 7). To verify that these data were not dependent on selected reaction criteria, we first calculated k_on values for mutants of barnase-barstar via BD simulations, using a diverse set of reaction criteria. We compared our results to experimental k_on data for barnase-barstar and identified reaction criteria that yielded the closest agreement between calculated and experimental data (37). Although BD simulations accurately depict electrostatically driven diffusion, there are inherent limitations in such simulations. BD simulations are necessarily rigid-body simulations, in which each binding partner remains in its static (bound) conformation. This assumption is adequate for long-range encounter complex formation. Once proteins encounter each other, in a near-native orientation, successful binding is almost inevitable, since residue side chains are locked in their binding configurations (Movie S2). Thus, the difference in association rates between Complexes 1 and 2 may be larger, especially since our MD data suggest that interactions observed from the crystal structure of Complex 2 may be inadvertently strengthened by crystal packing effects.

Figure 7.

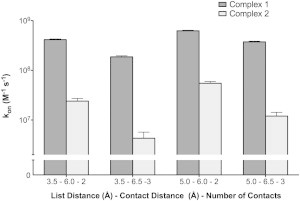
Comparison of association rates of C3d-Sbi-IV complexes. Rates were calculated by Brownian dynamics simulations under four conditions, with varied BD parameters including the cutoff distance for listing candidate atomic contact pairs (List Distance), the distance required for successful atomic contact (Contact Distance), and the number of atomic contacts (Number of Contacts). Dark gray and light gray bars represent calculated k_on values (with 95% confidence intervals) for Complexes 1 and 2, respectively.

SMD simulations

To examine the dissociation phase of C3d-Sbi-IV interactions, we induced unbinding using SMD simulations (38,39). In each simulation, the center of mass of Sbi-IV was pulled away from C3d at a constant velocity, and the force acting on Sbi-IV was calculated throughout the trajectories (Movie S3). The force required to pull Sbi-IV from C3d is approximately twofold larger for Complex 1 than for Complex 2, indicating that the latter interaction is less stable. This result is confirmed in multiple SMD trajectories (Fig. 8). In addition, by examining the number of intermolecular interactions over time, we observe that loss of interaction occurs gradually (Figs. S8–S10), which may explain the gentle slope of the force curves after the critical force is reached (see Movie S3, for example). It should be noted that Sbi-IV did not always dissociate from C3d in the same manner. Movie S3 shows the most representative trajectories for Complex 1 and 2 SMD simulations. In Complex 1, Sbi-IV dissociates nearly uniformly, with the N- and C-terminal regions dissociating first and helix 2 (with the strongest interacting residues) dissociating last (Fig. S11, A, B, and E). All of the force-time plots show a steady rise up to the critical force, followed by a gradual loss of force to near zero. The strength of C3d-Sbi-IV interactions is echoed in another SMD trajectory, in which Sbi-IV does not dissociate, but rather, helix 1 is pulled away from the rest of Sbi-IV (Fig. S11 D). Thus, intramolecular Sbi-IV interactions are preferentially disrupted over intermolecular C3d-Sbi-IV interactions. In Complex 2, on the other hand, dissociation was less uniform. In two SMD trajectories, Sbi-IV dissociated termini first, followed by helix 3, and finally by the C-terminus of helix 1 (Movie S3 and Fig. S11, F and H). In the remaining trajectories, the Sbi-IV N-terminus dissociated last, which may be influenced by the initial position of this region from the crystallographic structure (Fig. S11, G, I, and J). In contrast to the force-time plots for Complex 1 SMD trajectories, Complex 2 trajectories exhibit less well-defined force increase and decrease, likely due to less energetically favorable contacts (in both quantity and magnitude).

Figure 8.

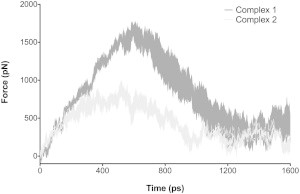
Unbinding forces for C3d-Sbi-IV complexes. Steered MD simulations were performed for each complex, in which the center of mass of Sbi was pulled away from C3d at a rate of 10 Å/ns, and exerted force was reported every 20 fs. The area of the curves represents the mean ± SE of the force on Sbi in Complex 1 (dark gray) and Complex 2 (light gray) for five SMD trajectories.

Discussion

We have implemented a computational framework comprised of electrostatic free energy calculations, MD simulations and MM-GBSA free energy calculations, and BD, and SMD simulations to shed light on the binding mode between staphylococcal virulence factor Sbi and complement fragment C3d. In accordance with extensive biophysical analyses for the C3d-Sbi-IV interaction (10), our data suggest that Sbi-IV likely binds via the mode observed in Complex 1. Complex 1 is stabilized by numerous polar and nonpolar interactions over a large area, most of which are conserved throughout MD trajectories and are energetically favorable. In addition, the interfacial SASA of Complex 1 remains constant. In contrast, there is significant loss of interfacial SASA for Complex 2; the N-terminus of Sbi-IV tends to move away from C3d, whereas the C-terminus of helix 1 and the N-terminus of helix 3 hold the complex together, primarily via nonpolar interactions. BD and SMD simulations illustrate that Complex 1 is a markedly more stable complex, as it is characterized by more favorable association and dissociation kinetics compared to Complex 2.

Although binding and mutagenesis studies have shown that Complex 1 is likely the physiologically relevant binding mode, NMR chemical-shift perturbation experiments identified interacting residues in both binding modes (10). Interestingly, none of the N-terminal residues (E201, V205, and E209) that in previous NMR experiments were shown to have large chemical shifts participated in persistent interactions with C3d in our analysis, although V244 and L248 (which also exhibited large chemical shifts) do indeed share persistent interactions with I1125 on C3d and contribute significantly to the association free energy of Complex 2. Other Sbi-IV residues deemed by our analysis to be most critical to C3d interaction in Complex 2 (Figs. 5, B, D, and F, and 6 C) did not show large chemical shifts. Despite inconsistencies between our MD data and previous NMR titration analysis data, there is better correlation between MM-GBSA energies and NMR titration data for Complex 1 compared with Complex 2 (data not shown).

Although Sbi-IV is an AP complement inhibitor on its own, full-length Sbi can inhibit all three pathways of complement. Previous studies have shown that domains I and II of Sbi bind immunoglobulin G molecules via their Fc region, conferring protection of S. aureus against antibody-mediated opsonization, whereas domains III and IV are involved in C3 binding (6). Recent structural analyses were unsuccessful in determining structure of Sbi-III/IV, and it was reported that Sbi-III has an inherently disordered structure (10,13). Since Sbi-III/IV (and full-length Sbi) exhibit a different mechanism of complement evasion compared to Sbi-IV alone, it is necessary to examine our results in light of this information.

Like Sbi-IV, Sbi-III/IV contains an interaction site on the thioester domain of C3 and exhibits similar binding preferences for thioester-domain-containing C3 fragments (C3d > C3 > C3b). Clark et al. suggest that the secondary binding site of Sbi-IV on C3d (Complex 2) may represent the binding mode when other domains of Sbi are also present (10). Based on the observation that the N-terminus of Sbi-IV (residues 198–205) makes strong contacts with C3d in the crystallographic structure, the authors suggest that the presence of Sbi-III may stabilize this weak binding site. We observed that the N-terminus of Sbi-IV moves away from C3d almost immediately in all MD simulations of Complex 2, indicating that interactions of these residues are not strong enough to keep the complex together.

In the context of structural information for C3 and C3b, it is unlikely that Sbi-III/IV binds to C3 via the Complex 2 binding mode, as there are extensive steric clashes. The thioester bond on C3d is intrinsically shielded from solvent in native C3, precluding binding of Sbi-IV at that site unless major conformational changes occur. In the Complex 1 site, Sbi-IV binds easily without clashes (Fig. S12 A). However, in C3b, the Complex 2 binding site appears to be the preferred mode, as Complex 1 shows clashes with C3b (Fig. S12 B). In addition, Sbi-III/IV binds to both C3d and C3a in native C3, which is likely simultaneous based on the slow biphasic association kinetics observed in surface plasmon resonance experiments (6). Although the Sbi-IV molecule in Complex 2 would be spatially closer to C3a than in Complex 1, steric clashes and Sbi-IV orientation likely preclude simultaneous binding. Through construction of a basic homology model of Sbi-E (domains I–IV), it is plausible that Sbi-III and Sbi-IV (in the Complex 1 binding mode) can simultaneously bind C3a and C3d, respectively (Fig. S12 C). Since Sbi-III/IV can form a covalent adduct to nascent C3b (6), binding of Sbi-III/IV in an arrangement bridging the region of C3 containing the thioester bond would facilitate rapid transacylation upon C3 cleavage.

Although our data demonstrate much higher stability for Complex 1 compared to Complex 2, and together with experimental data suggest that the structure of Complex 1 is physiological, Sbi-IV alone may be capable of binding to C3d via the Complex 2 binding mode. Despite weak interactions at the termini of Sbi-IV, there is a strong central core of polar and nonpolar interactions that remains bound during MD simulations. We suggest that Sbi-IV can provide a foundation for therapeutic development. C3b recognizes and covalently attaches to both host and pathogen cell surfaces, and host protection is reliant on tight regulation by other complement factors. Several autoimmune diseases are propagated by inadequate regulation and, in turn, deposition of complement on host cells. Rational structure-based design of Sbi-IV variants may lead to novel therapeutics targeting C3b deposition on host surfaces.