Coexistence of Twisted, Plectonemic, and Melted DNA in Small Topological Domains

Abstract

DNA responds to small changes in force and torque by over- or undertwisting, forming plectonemes, and/or melting bubbles. Although transitions between either twisted and plectonemic conformations or twisted and melted conformations have been described as first-order phase transitions, we report here a broadening of these transitions when the size of a topological domain spans several kilobasepairs. Magnetic tweezers measurements indicate the coexistence of three conformations at subpicoNewton force and linking number densities ∼−0.06. We present a statistical physics model for DNA domains of several kilobasepairs by calculating the full partition function that describes this three-state coexistence. Real-time analysis of short DNA tethers at constant force and torque shows discrete levels of extension, representing discontinuous changes in the size of the melting bubble, which should reflect the underlying DNA sequence. Our results provide a comprehensive picture of the structure of underwound DNA at low force and torque and could have important consequences for various biological processes, in particular those that depend on local DNA melting, such as the initiation of replication and transcription.

Introduction

In vivo, DNA is maintained in a negatively supercoiled state in small topological domains of several kilobasepairs (kbps) (1,2). This supercoiling forms the driving force for DNA compaction into chromosomes and has been implicated in regulating all processes involving DNA (3). Access to DNA by polymerases, for example, requires melting of a small amount of DNA and may be a rate-limiting step in the initiation of transcription and replication (4). The processive motion of these polymerases in topologically fixed domains can lead to accumulation of force and torque, which has been suggested to play an important role in DNA homeostasis (5–8). It is therefore important to understand how force and torque affect the conformation of DNA.

Using force spectroscopy techniques such as magnetic and optical tweezers, it is possible to control both the force and the torque on single DNA molecules (9–11). Seminal work by Strick et al. (12) showed that under- and overtwisting of DNA leads to plectonemic structures, i.e., supercoils, at stretching forces below 0.5 pN. Above 1.0 pN and negative torque, small dAdT-rich regions of double-stranded(ds)DNA melt and form single-stranded (ss)DNA bubbles (13,14). At higher force (F > 2.5 pN) and larger negative torque (Γ < −11 pN nm), a left-handed structure L-DNA (15) forms. Large positive torque and force, on the other hand, induces a highly overtwisted state called P-DNA (16). Thus, a rich variation of conformations accommodates physical stress and torque in DNA.

Statistical mechanics has been successfully employed to describe these remarkable features of DNA (17,18). In these reports, the DNA tether is assumed to be large enough for neglecting thermal fluctuations between different conformations. For a DNA tether with a finite number of basepairs (i.e., several kbps) held at low forces (F < 1.2 pN) and moderate linking number densities (|σ| < 0.06), representing physiologically relevant conditions (19), coexistence of three states has been suggested (20). However, detailed analysis of the extension of short DNA molecules in this low force and torque range is lacking.

In this article, we provide an extended experimental data set and introduce a numerical three-state model which shows the coexistence of three states in the same topological domain. We performed magnetic tweezers experiments on DNA molecules of several kilobasepairs and measured twist-extension curves in real time. This resolved simultaneously the rather large fluctuations in extension due to the presence of different states, and revealed a discontinuous change in the size of the melting bubbles that we attribute to differences in DNA sequence. Although we do not explicitly take the DNA sequence into account in our statistical physics model, there are indications that suggest that the phase-diagram can be affected by it. Together, these findings provide a quantitative understanding of DNA melting in small topological domains at forces and degrees of supercoiling that are representative for the conditions that occur in the living cell.

Materials and Methods

Magnetic tweezers

The home-build magnetic tweezers has been described by Kruithof et al. (21). During an experiment, a DNA molecule was constrained between the end of a superparamagnetic bead with diameter of 1 μm and the surface of a microscope coverslip. Twist was induced by rotating the magnetic field at 1 turn/s. The extension of DNA was measured in real time at a frame rate of 60 Hz with a charge-coupled device camera (Pulnix TM-6710CL; JAI, San Jose, CA).

DNA constructs

Two DNA constructs were studied based on Plasmid pGem-3Z (3 kb) and Puc18 with 25 repeats of the 601 sequence (8.5 kb) (a gift from D. Rhodes, Singapore). Both plasmids were digested with BsaI and BseYI yielding linear fragments of 2410- and 6960-bp, respectively, with corresponding sticky ends on either side. Digoxigenin and biotin-labeled handles were produced with PCR using biotin-dUTP and digoxigen-dUTP on the pGem-3Z template using the following primers: 5′ GAT AAA TCT GGA GCC GGT GA 3′ and 5′ CTC CAA GCT GGG CTG TGT 3′. After PCR amplification, these fragments were digested with BsaI and BseYI and ligated to the previously digested DNA backbone.

Sample preparation

A clean coverslip was coated with 1% polystyrene-toluene solution. The coverslip was then mounted on a poly-di-methysiloxane (PDMS, Dow Corning, Midland, MI) flow cell containing a 10 × 40 × 0.4 mm flow channel. The flow cell was incubated with 1 μg/mL anti-digoxigenin for 2 h and 2% BSA (w/v) solution overnight. A quantity of 20 ng/mL DNA in 10 mM HEPES pH 7.6, 100 mM KAc, and 10 mM NaN₃ was flushed into the flow cell and incubated for 10 min, followed by flushing in 1-μm streptavidin-coated superparamagnetic microspheres (MyOne; Invitrogen, Carlsbad, CA) in the same buffer after 10 min.

Results

We consider a DNA molecule consisting of N basepairs. When DNA is torsionally unconstrained, the linking number Lk₀ equals 1 helical turn per 10.4 bp (22). In the case of a torsionally constrained molecule, torque builds up as one end of the molecule is twisted ΔLk turns. This change in twist can be expressed in the linking number density, σ ≡ ΔLk/Lk₀. Here, we will examine the situation where three states, i.e., twisted (t), plectonemic (p), and melted (m) DNA occur simultaneously in the same molecule (Fig. 1). In this model, the basepairs in the molecule are divided into these three states,

$$N=n_t+n_p+n_m,$$ (1)

where n_i(i = t, p, m) is the number of basepairs in each state. The excess linking number is conserved and distributed between these three states:

$$\Delta Lk=\Delta L{k}_t+\Delta L{k}_p+\Delta L{k}_m.$$ (2)

The linking number density in the entire domain can thus be written as

$${\sigma }_{\text{tot}}=\frac{n_t}{N}{\sigma }_t+\frac{n_p}{N}{\sigma }_p+\frac{n_m}{N}{\sigma }_m$$ (3)

in which σ_i (i = t, p, m) is defined as the linking number density in each state (σ_i = ΔLk_i/(n_i/10.4)). The total free energy G equals the sum of the free energy in each state, following

$$G=n_t{G}_t+n_p{G}_p+n_m{G}_m,$$ (4)

in which G_i represents the free energy per basepair in state i. In general, G_i can depend on both the force and linking number density (15,17),

$$G_i\left(F,{\sigma }_i\right)=-g_i\left(F\right)+\frac{c_i\left(F\right)}{2}{\left({\sigma }_i-{\sigma }_{0,i}\right)}^2+{\epsilon }_i,$$ (5)

where g_i(F) is the stretching free energy and c_i(F) is the force-dependent twist modulus. For the twisted and melted state, the stretching free energy is described by a wormlike chain (17), whereas stretching of plectonemic DNA is force-independent because it has zero extension. The value σ_0,i is the degree of twist in each state in absence of torque. The value ε_i is the melting energy for basepair separation, which is zero for twisted and plectonemic DNA. Although the melting energy is sequence-dependent, we will assume an average value of 1.6 k_BT (23) per basepair. All parameters in Eq. 5 are summarized in Table S1 in the Supporting Material.

Figure 1.

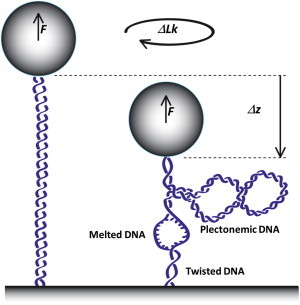
Schematic illustration of the conformational changes of a DNA molecule in a magnetic tweezers setup (not to scale). A DNA molecule is tethered between a superparamagnetic bead and a glass surface. Force and torque on the DNA molecule are applied by an external pair of magnets (not shown) to the bead. Here, we consider the coexistence of three states: twisted, plectonemic, and melted DNA. To see this figure in color, go online.

Previous work by Marko (17) reported an analytical solution for the distribution of states based on equating the torque in each state. In analogy with other phase transitions, only a single point in the phase diagram was reported to represent a three-phase coexistence. However, thermal fluctuations are not negligible in finite systems, such as a single topological domain of several kilobasepairs, allowing for a population of additional states that would remain unobserved in the thermodynamic limit. An analytical solution for such a three-state system has not been reported. Because of the finite number of states, we can numerically calculate the full partition function, using Eqs. 1, 3, and 4. The probability to be in a conformation defined by n_t, n_p, σ_t, and σ_p equals

$$P\left(F,{\sigma }_{\text{tot}}\right)=Z^{-1}\text{exp}\left(\frac{-G\left(F,{\sigma }_{\text{tot}},{\sigma }_t,{\sigma }_p,n_t,n_p\right)}{k_{\text{B}}T}\right),$$ (6)

with the partition function

$$Z=\sum _{{\sigma }_p=-\infty }^{\infty }\sum _{{\sigma }_t=-\infty }^{\infty }\sum _{n_p=N-n_s}^N\sum _{n_s=0}^N\text{exp}\left(\frac{-G\left(F,{\sigma }_{\text{tot}},{\sigma }_t,{\sigma }_p,n_t,n_p\right)}{k_{\text{B}}T}\right).$$ (7)

Using Eq. 4, the extension z of a DNA molecule with contour length L in a state comprising n_t stretched basepairs and n_m melted basepairs becomes

$$\frac{z\left(F,{\sigma }_{\text{tot}}\right)}{L}=\frac{n_t}{N}\left(-\frac{\partial G_t}{\partial F}\right)+\frac{n_m}{N}\left(-\frac{\partial G_m}{\partial F}\right).$$ (8)

Combining Eqs. 6 and 8 yields for the expected extension

$$\langle \frac{z\left(F,{\sigma }_{\text{tot}}\right)}{L}\rangle =Z^{-1}\sum _{{\sigma }_p=-\infty }^{\infty }\sum _{{\sigma }_t=-\infty }^{\infty }\sum _{n_p=N-n_s}^N\sum _{n_s=0}^N\frac{z\left(F,{\sigma }_{\text{tot}}\right)}{L}\text{exp}\left(\frac{-G\left(F,{\sigma }_{\text{tot}},{\sigma }_t,{\sigma }_p,n_t,n_p\right)}{k_{\text{B}}T}\right).$$ (9)

The mean value and variance of all other parameters that describe the conformation of the molecule are calculated likewise.

Three-state coexistence

We used magnetic tweezers to control the force and twist exerted on a single DNA molecule (Fig. 1). Briefly, the experimental setup consists of a DNA molecule that is anchored between a glass surface and a superparamagnetic bead. The position and the rotation of a pair of external magnets determines the force and twist applied to the bead. The height of the bead, corresponding to the extension of the DNA molecule, is measured in real time using video microscopy and image processing (21). Unlike previous reports (14,24,25), we do not average the extension over a given time interval, so changes in extension are directly revealed. The bandwidth to detect these changes is limited by the viscous drag of the bead, the stiffness of the DNA tether, and the frame rate of the camera (see Fig. S7 in the Supporting Material). Typically, for the conditions of the measurements reported here, fluctuations in extension can be detected at 20–60 Hz. Because each state has a different extension (see Eq. 8), the distribution of states can only be determined indirectly from the total extension of the molecule.

We carried out twisting experiments on 7.0- and 2.4-kbps DNA molecules at forces up to 1.0 pN and linking number densities up to |σ_tot| < 0.07 (Fig. 2 and see Fig. S1 A for 7.0 and 2.4 kbps, respectively). Over- and undertwisting the DNA molecule at 0.3 pN resulted in a symmetric decrease in end-to-end distance (Fig. 2, red circles). At this force, DNA buckles at both negative and positive torque. The resulting supercoils reduce the end-to-end distance of the DNA molecule. Increasing the force to 1.0 pN results in an asymmetric extension-twist curve (Fig. 2, blue circles). The extension remains constant for undertwisting due to DNA melting (13,16,17,26). Overtwisting the DNA creates plectonemes at all forces. The extension at these two conditions can be fully captured by considering the equilibrium between two states: a twisted-melted state or a twisted-plectonemic state (17).

Figure 2.

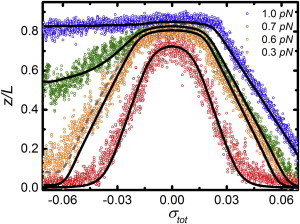
Experimental data of the relative extension of a 7.0 kbps DNA molecule as a function of the total linking number density at various forces (circles). The relative extension as calculated by Eq. 9 is shown (lines). Calculations are based on the parameters summarized in Table S1 in the Supporting Material. (Solid lines) Constant melting energy of 1.6 k_BT/bp. (Dashed line) Force-dependent melting energy (see Fig. S3B), resulting in a better match with the experimental data at 0.6 pN. To see this figure in color, go online.

The twist-extension curves at 0.6 and 0.7 pN fall in between these two regimes (Fig. 2, orange and green circles). We therefore consider the coexistence of twisted, plectonemic, and melted DNA to describe these data. The black lines superimposed on the experimental data in Fig. 2 are the calculations using Eq. 9. The used parameters for the mechanical properties of DNA are summarized in Table S1, using the same values as reported before (17) except for the twist modulus of melted DNA. We could only obtain a good agreement between experimental and simulated data using a twist modulus of melted DNA of 28 nm instead of 1 nm (27). Thus, it appears that small bubbles of melted DNA are more difficult to twist than previously reported.

Note that the model appears to underestimate the extension of the DNA at very small extensions. This is caused by excluded volume forces that originate from the impossibility for the DNA and the bead to penetrate the glass surface (21). We did not correct for this, leading to an underestimation of the effective force for short flexible tethers. Barring these deviations at very small extensions, we conclude that under conditions that resemble physiological salt concentrations, the three-state model quantitatively captures experimental twist-extension curves of small topological domains at moderate forces and linking number densities.

Phase diagram

To summarize the distribution of basepairs in the three-state model, we computed a phase diagram of the 7.0-kbps DNA as a function of the linking number density and force (Fig. 3). The fractions of basepairs in each state are color-coded, resulting in separate regions of twisted (blue) and plectonemic (green) DNA. Several regions show a mixed distribution of two states: twisted and plectonemic DNA (cyan), twisted and melted DNA (pink), and plectonemic and melted DNA (yellow). These features, representing two-state conformations, follow previously reported phase diagrams (9,15,17).

Figure 3.

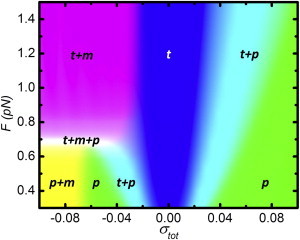
The force-linking number density phase diagram of a 7.0-kbps DNA molecule. Gradual transitions occur between twisted (t), plectonemic (p), and melted (m) DNA. (Blue, green, and red) The fraction of basepairs in t, p, and m, respectively. The fraction of melted bps was multiplied by 10 in all regions to optimize the contrast. (White region) Three-state coexistence phase. To see this figure in color, go online.

The phase diagram also shows a phase, rather than a single triple point (28), where the three states coexist (white). This phase is a direct consequence of the small size of the topological domain, which invalidates the thermodynamic limit assumption and exposes states that are usually obscured in large systems. The phase diagrams for 2.4 and 24.0 kbps DNA (see Fig. S2) reproduce the same trend, but the three-state coexistence regime shrinks when the tether length increases. For 24.0 kbps, we observe only a narrow line at F = 0.69 pN. Because of the large difference in linking number between melted DNA and dsDNA, a small melting bubble is more efficient in relieving torsional stress than twisted or plectonemic DNA. In larger tethers, such a small bubble represents a smaller fraction of the total DNA size, reducing the size of the coexistence phase.

To better understand the three-state coexistence, we looked into more details that can be calculated with the statistical mechanics model. Fig. 4 A shows the number of basepairs in the three states for 7.0 kbps DNA at F = 0.7 pN. The majority of the DNA is in the twisted state for |σ_tot| < 0.04. For |σ_tot| > 0.01, plectonemic DNA starts to form, whereas at σ_tot < −0.02, melted DNA is formed. A small fraction of the DNA contributes to this melting bubble, though it grows to 250 bps for σ_tot = −0.07.

Figure 4.

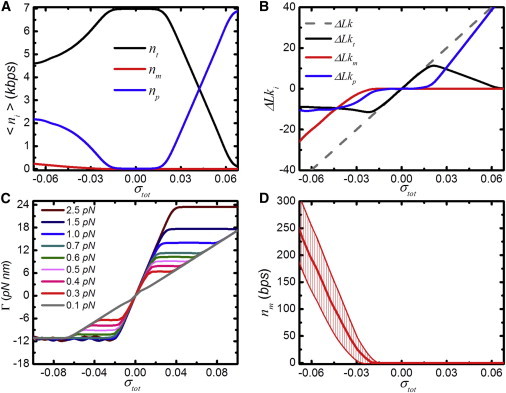
Calculations of the three-state coexistence in a 7.0-kbps DNA molecule at 0.7 pN and different linking number densities. (A) The distribution of basepairs in each state. (B) The distribution of linking numbers in each state. The sum of linking numbers converges to the total linking number ΔLk (shaded). (C) The torque present in the DNA molecule calculated between 0.1 and 2.5 pN. (D) The distribution of melted basepairs. (Error bars) Standard deviation. To see this figure in color, go online.

Although only a small fraction of the DNA molecule melts, these basepairs contribute to a large part of the total twist that is present in the DNA tether. Fig. 4 B shows the distribution of excess linking number among the three states. At small linking number densities, all the twist is absorbed in twisted DNA. When σ_tot in the DNA molecule exceeds 0.02, the molecule buckles, and the additional twist is stored in plectonemes. For negative torque, however, at σ_tot < −0.04 most of the twist is stored in melted DNA. The large difference in helicity and free energy between dsDNA and melted DNA makes melted DNA a good buffer for torsional stress.

We extended our analysis to the quantification of torque within a 7.0-kbps DNA molecule for different forces and linking number densities (see the Fig. S4, and Fig. 4 C). Fig. 4 C shows that the torque increases linearly with twist when DNA exists in a single state. For example, the plectonemic state dominates at F = 0.1 pN and σ_tot > −0.05 (with a small interruption at σ_tot = 0). Under these conditions, the slope represents the twist stiffness of plectonemic DNA. At larger forces and small twist densities, DNA is predominantly twisted, yielding a larger slope because of the larger twist persistence length of twisted DNA. When multiple states coexist, an increase of torsional stress is accommodated by a redistribution of the states rather than increasing the twist in either of the states. Thus, for mixed conformations, the torque stays constant but the distribution of basepairs between states is shifted (Fig. 4 A). Remarkably, the negative torque reaches a minimum value of −11 pN nm for all forces probed. This torque corresponds to a free energy of 2.6 k_BT, which is just sufficient to melt and twist an additional basepair. Thus, the maximum torque for negatively twisted DNA is limited. As a consequence, the linking number density in the plectonemic state, which comprises most of the DNA, is constrained, i.e., 〈σ_p〉 = −0.065, in excellent agreement with the natural linking number density observed in vivo (19,29).

The model presented here differs from previous work in two aspects (17):

• 1.We consider the distribution of all states, rather than only the lowest energy state. In small tethers, there is a large number of states with a comparable free energy contributing to the average extension of the molecule. Fig. 4 D shows the expected value and standard deviation of n_m as a function of the applied linking number density calculated. It is clear from these calculations that the bubble size is not well defined, with variations ranging up to 50 bps, emphasizing the extent of the statistical fluctuations in a small DNA tether.
• 2.The torque is not fixed within the molecule. As shown in Fig. S4, the mean values of the torque in each phase follow the mean torque of the entire molecule, but significant variations in torque occur when phases coexist. Imposing a constant torque throughout the entire molecule still results in the coexistence of three states (see Fig. S5). Fluctuations in torque between the different parts of the molecule therefore only contribute a small part of the states that define the average extension.

Fluctuations in extension

The relatively broad distribution of basepairs in each of the three states results in increased fluctuations in the extension of the molecule, due to the large differences in extension between the three states. Indeed, closer inspection of the extension-twist curves as shown in Fig. 2 reveals increased fluctuations in the extension in the three-state coexistence region. In these experiments, the data were not time-averaged, revealing independent extension measurements while twisting the DNA molecule. The magnitude of these fluctuations can be calculated using Eqs. 6 and 8. Fig. 5 A shows twist-extension measurements of a 2.4- and a 7.0-kbps DNA molecule along with the calculated median and variation in extension at F = 0.7 pN. The latter was calculated as the range that includes 68% of the extension distribution. Due to the variations among the three states, the extension is not Gaussian-distributed for undertwisting as opposed to overtwisting (Fig. 5 B and see Fig. S6 B), but displays an asymmetric distribution. The fluctuations caused by transitions between different states dominate over thermal fluctuations in extension that are always present in flexible polymers, as discussed in the Supporting Material. Overall, we obtain a fair agreement between the calculated magnitude of the fluctuations in extension and experimental data. This shows that the increased fluctuations in extension at undertwisting conditions can be attributed to transitions between different conformations of the molecule.

Figure 5.

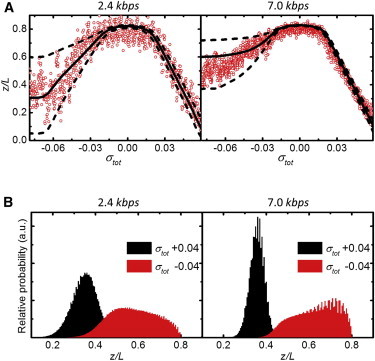
(A) Experimental data of the relative extension versus linking number density (red circles) at 0.7 pN for 2.4 kbps (left) and 7.0 kbps DNA (right). (Solid black line) Calculated median extension value. (Dashed lines) 68% range in extension. (B) Calculated extension distribution for 2.4 kbps (left) and 7.0 kbps DNA (right) at σ_tot = −0.04 (red) and σ_tot = +0.04 (black). Note the broad and asymmetric extension distribution compared to the Gaussian profile for negative and positive twist, respectively. To see this figure in color, go online.

Fluctuations in extension at constant force and linking number measured in real time (Fig. 6) uniquely reveal the kinetics of the transitions between different states in the molecule. Such kinetics cannot be obtained from the statistical mechanics model presented here, which only describes the equilibrium situation. Remarkably, we observed distinct transitions between discrete levels (∼110 nm) of extension of the molecule in the three-state coexistence regime. Because the twisted and melted DNA have a comparable extension in this force regime, the discrete extension levels can only be explained by changes in the size of the plectoneme. Our model suggests the extension levels correspond to changes of ∼400 bps of plectonemic DNA transferring back and forth into 380-bps twisted and 20-bps melted DNA. The transitions occur at intervals of several seconds. We attribute the discrete levels in extension to barriers originating from differences in the sequence of the DNA. Small stretches of GC basepairs, having one more hydrogen bond than AT basepairs, present a kinetic barrier for extension of the melting bubble. Such inhomogeneities will severely change the distribution and kinetics of the molecule’s extension. For bubbles spanning several tens of basepairs, this results in a limited number of favored states, depending on the local DNA sequence.

Figure 6.

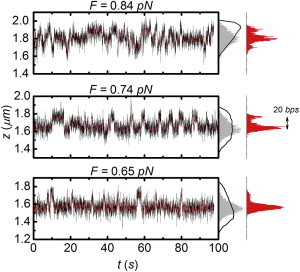
Constant force measurements at a linking number density σ_tot = −0.03. Three different forces are shown (top to bottom): 0.84, 0.74, and 0.65 pN. (Red) The 20 points of median filtered data, emphasizing the discrete transitions in extension. Histograms of the extension are shown on the right side of the time traces (black and red bars). The calculated extension distribution is superimposed on the histogram (solid black lines). The discrete levels are attributed to ∼400 bps of plectonemic DNA transferring back and forth into 380-bps twisted and 20-bps melted DNA. To see this figure in color, go online.

We noted that the shape of the twist-extension curves is salt-dependent (see Fig. S1). Increasing the ionic strength from 100 to 300 mM KAc shifts the twist-extension curves to smaller extensions for undertwisting. This is consistent with the well-known increase of the melting energy for DNA at higher salt concentrations (23), as also observed for force-induced melting without twist (30). Increasing the melting energy from 1.6 to 2.0 k_BT per basepair recovered a good agreement between experimental and calculated data.

Although in principle it should be straightforward to extend the current three-state model with a sequence-dependent melting energy, such calculations will require large computational effects, even for small molecules. It is important to note that this sequence heterogeneity can have a significant effect on the phase diagram. We expect that small melting bubbles will preferably be formed in AT-rich regions, but as the force increases, such AT-rich regions will expand into GC-rich parts at their boundaries. We modeled this increased contribution of GC basepairs by increasing the melting energy in a linear fashion from 1.5 to 2.1 k_BT for forces between 0.6 and 1.2 pN. For F = 0.6 pN, the adjusted twist extension curves show a small increase in extension at negative twist (Fig. 2, gray dashed line), yielding a better agreement with the experimental data (see Fig. S1 A; dashed lines = 2.4 kbps DNA). The resulting phase diagram is globally similar to that presented in Fig. 3, but displays a larger area in which the three states coexist (see Fig. S3). Thus, although the sequence dependence of melting bubbles is not included explicitly in our model, the data give clear indications that there is a significant effect of sequence heterogeneity, resulting in both discrete, 20-bp steps in the size of the melting bubble and in a larger area in which the three states coexist.

Discussion and Conclusions

We described the coexistence of twisted, plectonemic, and melted DNA in small topological domains. Using a numerical three-state model, we computed a force-twist phase diagram that reproduces earlier descriptions of supercoiled DNA. However, we observe gradual transitions and a region of three-state coexistence rather than a sharp first-order phase transition and a single triple point. DNA melting induced by large forces is well studied in recent works (31–34), including the effect of torque (9,15). Here we studied these effects at low forces and moderate linking number densities. This situation is particularly relevant in vivo, where topological domains are likely to be several kilobasepairs, forces are not likely to exceed several picoNewtons, and linking number densities are generally close to −0.06. Moreover, we computed that melting bubbles of several tens of basepairs appear in such a domain. The continuous presence and the large dynamics of such bubbles may have important consequences for processes involving ssDNA.

Sheinin et al. (15) showed that long stretches of melted DNA are organized in a L-DNA structure with 〈σ_m〉 = −1.8, corresponding with a helical repeat of ∼13 bp/turn, and a twist modulus of 20 nm. They also observed that the torque in undertwisted DNA is limited to −11 pN nm under extreme twist densities of σ_tot down to −2.0 and F > 5 pN. We show here that also under less extreme conditions, this torque limit applies. Strick et al. (13,14) reported that melted DNA remains in a disordered conformation resembling two strands of ssDNA with 〈σ_m〉 = −1. The twist modulus of a DNA bubble was considered very small, ∼1 nm. We obtained the best agreement between experimental and simulated data for 〈σ_m〉 = −1.05 and a twist modulus of 28 nm. This may indicate that small melting bubbles are more difficult to twist than long ssDNA molecules and may point to alternative interactions between the melted bases that are not present in larger stretches of melted DNA. Further studies are required to reveal possible structure in small melting bubbles.

It is clear that the finite size of the melting bubble and the large impact of sequence inhomogeneities have a significant effect on the twist-extension curves of DNA. From our studies, we cannot resolve the position of the bubble. A melting bubble could for example be positioned at the tip of the plectoneme, rather than in the twisted section of the DNA. Such a melting bubble in the plectonemic region would not lead to an increase of the extension, relative to plectonemic DNA, but would reduce the torsional stress. DNA sequence may also result in highly curved DNA stretches that could localize the plectoneme at specific locations. The good agreement of the experimental data with a simple three-state statistical physics model that does not include sequence effects suggests that such dependencies only play a minor role.

One of the most remarkable findings is that distinct steps in extension of the DNA molecule are clearly visible under small force and negative torque. Such steps can easily be confused with protein-induced changes in extension when studying protein-DNA interactions. Because long DNA substrates, such as λ-DNA with a contour length of 48 kbps, are generally replaced by shorter DNA molecules in more recent studies, the presence of bubble-plectoneme transitions may be relevant for many force-spectroscopy studies.

The lifetime of the distinct levels of DNA extension (Fig. 6) that we attribute to DNA melting are much longer than the lifetime of melting bubbles obtained from fluorescence correlation spectroscopy (FCS) measurements, i.e., ∼50 μs (35). This may be due to the force that is applied in the magnetic tweezers, which is absent in FCS. Moreover, the melting bubbles described here may be larger than those captured in the FCS experiments. We cannot exclude the presence of very short-lived states, because of the limited response time of the bead-tether mechanics.

The simulations are amendable for further refinements. In addition to introducing a sequence-dependent melting energy, which may resolve the discrete levels of extension, one can include an entropic penalty for the formation of a melting bubble (26). Similarly, a penalty may be included for the formation of a DNA buckle (36–38). Without such penalties, we do not discriminate between single or multiple domains within one DNA molecule. More advanced modeling of overtwisted DNA, which includes electrostatic interactions between DNA segments, suggests that the formation of multiple plectonemes or melting bubbles in the same topological domain may have a significant effect on twist-extension curves (18). However, experiments show that small molecules at moderate force and torque only feature single domains of bubbles and plectonemes (39,40). Although this indicates that the free energy for formation of a new domain exceeds that of the free energy increase per basepair, it may be relatively small compared to the total free energy of the entire domain. Therefore, Eq. 4 will be adequate for describing the different conformations of a small DNA tether.

In summary, our work resolved and quantitatively described the coexistence of three different states in DNA. This fresh insight may have implications for the interaction mechanism of proteins that interact with DNA in torsionally constraint domains, such as topoisomerases, transcription factors, histones, and DNA-based molecular motors such as DNA and RNA polymerases and chromatin remodelers.