Abstract
Background
A systems engineering approach is presented for describing the kinetics and dynamics that are elicited upon arsenic exposure of human hepatocytes. The mathematical model proposed here tracks the cellular reaction network of inorganic and organic arsenic compounds present in the hepatocyte and analyzes the production of toxicologically potent by-products and the signaling they induce in hepatocytes.
Methods and results
The present modeling effort integrates for the first time a cellular-level semi-mechanistic toxicokinetic (TK) model of arsenic in human hepatocytes with a cellular-level toxicodynamic (TD) model describing the arsenic-induced reactive oxygen species (ROS) burst, the antioxidant response, and the oxidative DNA damage repair process. The antioxidant response mechanism is described based on the Keap1-independent Nuclear Factor-erythroid 2-related factor 2 (Nrf2) signaling cascade and accounts for the upregulation of detoxifying enzymes. The ROS-induced DNA damage is simulated by coupling the TK/TD formulation with a model describing the multistep pathway of oxidative DNA repair. The predictions of the model are assessed against experimental data of arsenite-induced genotoxic damage to human hepatocytes; thereby capturing in silico the mode of the experimental dose–response curve.
Conclusions
The integrated cellular-level TK/TD model presented here provides significant insight into the underlying regulatory mechanism of Nrf2-regulated antioxidant response due to arsenic exposure. While computational simulations are in a fair good agreement with relevant experimental data, further analysis of the system unravels the role of a dynamic interplay among the feedback loops of the system in controlling the ROS upregulation and DNA damage response. This TK/TD framework that uses arsenic as an example can be further extended to other toxic or pharmaceutical agents.
Keywords: Arsenic, Nrf2, Anti-oxidant response, Human hepatocytes, Indirect response modeling
1. Background
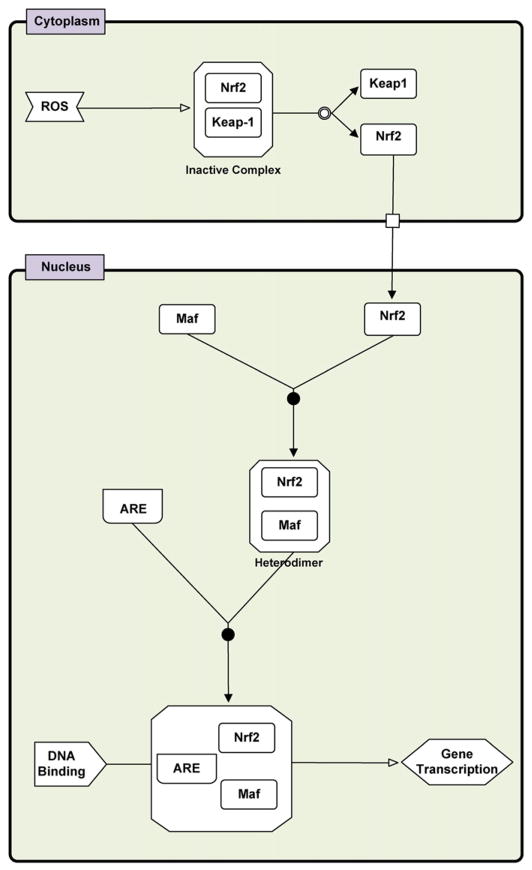
Arsenic is one of the most common environmental contaminants and carcinogens (IARC, 1987; IARC, 2003). In vitro exposure to arsenicals leads to oxidative stress, chromosomal aberrations, and inhibition of DNA repair (Kligerman and Tennant, 2007; Qin et al., 2008a, 2008b; Soriano et al., 2008), which are phenomena tightly linked to oxidative DNA damage and cancer phenotype (Kojima et al., 2009). Trivalent arsenicals bind to sulfhydryl groups (–SH) of proteins and interfere with a spectrum of signaling pathways regulating cell growth, proliferation, apoptosis and survival (Kitchin and Wallace, 2008). The cellular adaptive response to oxidative stress agents such as arsenic typically leads to the activation of the redox sensitive transcription factor Nuclear Factor-erythroid 2-related factor 2 (Nrf2) (Bloom et al., 2002; Kumagai and Sumi, 2007). This transcription factor is considered to be the orchestrator of the cellular antioxidant defense system (Kong et al., 2001b; Wu et al., 2011). Under homeostatic conditions Nrf2 predominantly localizes in the cytoplasm bound to an inactive complex with the Kelch-like ECH-associated protein 1 (Keap-1). This is a cysteine rich protein which facilitates Nrf2 ubiquitination and degradation (Kobayashi et al., 2006; Kobayashi and Yamamoto, 2005). The challenge of oxidative stress triggers Nrf2 nuclear translocation; in the nucleus it heterodimerizes with a Maf protein and binds to the antioxidant response element (ARE) or the electrophile response element (EpRE), commencing upregulation of various cytoprotective genes (Fig. 1) (Kensler et al., 2007).
Fig. 1.
General scheme of the induction of gene expression through the Keap-1/Nrf2/ARE signaling pathway. ROS increase induces the dissociation of Nrf2 with Keap-1, leading to translocation of Nrf2 to the nucleus. Heterodimerization of Nrf2 with Maf and its binding to ARE leads to transactivation of ARE-inducible genes (adapted from Kensler et al., 2007). The network of biochemical interactions is represented using the Systems Biology Graphical Notation (SBGN) (www.sbgn.org) (Le Novere et al., 2009).
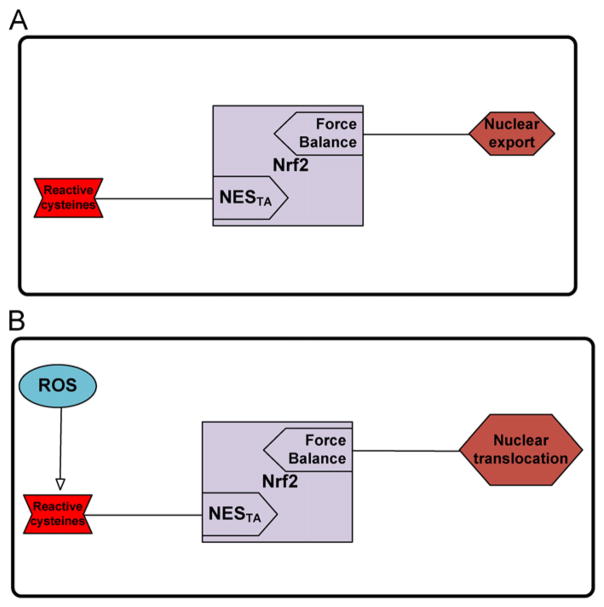
Two mechanisms have been proposed to describe the Nrf2 activation: (a) Keap-1 is the redox sensor and therefore the Nrf2 release is Keap-1 dependent, and (b) Nrf2 itself is the redox sensor. The former scenario relies on Keap-1 high cysteine content, and on the fact that experimental evidence supports the hypothesis that the cellular redox sensor is endowed with highly reactive –SH groups present on protein domains (Dinkova-Kostova et al., 2002, 2005). Although it is well known that trivalent arsenicals react with vicinal thiols, it has been experimentally demonstrated that arsenic does not disrupt Keap-1/Nrf2 association in the cytoplasm (He et al., 2006; Wang et al., 2008), posing an argument against the Keap-1 dependent pathway interpretation. Recently, Kong and co-workers proposed a novel mechanism of Nrf2 activation, in which a specific motif of the transcription factor NESTA itself is redox sensitive and its inactivation constitutes the driving force for nuclear retention and localization of Nrf2 (Li et al., 2006). Specifically, under oxidative stress conditions, the reactive cysteines embedded in this motif react with electrophiles and disable its function (Fig. 2). Upregulation of the antioxidant mechanism, leading to increased cellular GSH levels, may favor the restoration of NESTA motif activity and the inhibition of the Nrf2 nucleus translocation (Li and Kong, 2009). Therefore there is a “Force Balance” between ROS and GSH that dictates the localization of Nrf2 transcription factor.
Fig. 2.
A new Keap-1 independent model for Nrf2 activation by ROS. The identified NESTA motif contains reactive cysteines and when challenged by oxidative stress is inactivated, leading to Nrf2 nuclear translocation (adapted from Li et al. (Li and Kong, 2009)). Upregulation of the antioxidant mechanism via GSH increase alters the “Force Balance” leading to inhibition of Nrf2 nuclear translocation. The network of biochemical interactions is represented using SBGN formalism (www.sbgn.org) (Le Novere et al., 2009).
In this study, the recently proposed cellular-level TK model for arsenic exposure in human hepatocytes (Stamatelos et al., 2011) is integrated with a TD model focusing on oxidative stress and concomitant DNA damage. This mathematical formulation involves the description of the basic steps of reactive oxygen species (ROS) generation, antioxidant response via the recruitment of Nrf2, a transcription factor that regulates many cytoprotective genes (Kong et al., 2001a), the oxidative genotoxic damage, and subsequent repair. The present work incorporates a theoretical analysis of the contribution of various feedback loop mechanisms in the creation and modulation of dynamic response in network components. This behavior influences in a nonlinear manner the DNA damage across doses of arsenite (iAsIII).
2. Approach and methods
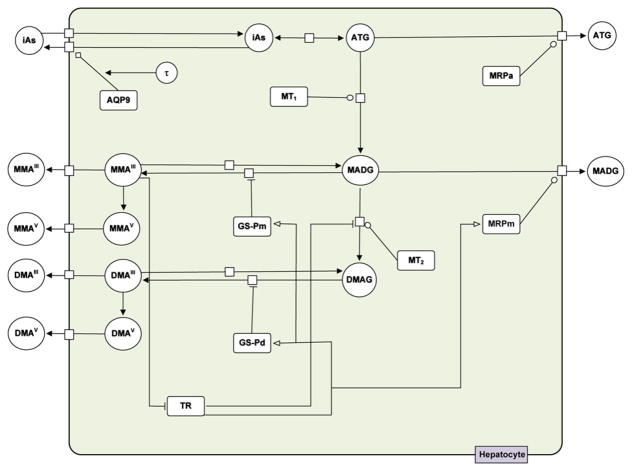
The semi-mechanistic cellular-level toxicokinetic (TK) model presented in Stamatelos et al. (2011) applies mass action kinetics describing uptake, biotransformation and efflux of arsenicals in human hepatocytes (Fig. 3). Novel concepts in this model included the incorporation of the pathway of arsenic-GSH adduct formation as described by (Hayakawa et al., 2005), and the description of the methylation reactions by arsenic methyltrasferase (AS3MT) (El-Masri and Kenyon, 2008) using a hybrid approach of Hill and Michaelis–Menten kinetics. Furthermore a “switch-like” formulation was introduced in the TK model in order to describe the antioxidant response of hepatocytes to arsenic exposure.
Fig. 3.
Schematic of the cellular-level TK model for arsenic in human hepatocytes showing the biochemical components. The variables depict extracellular and intracellular amounts of arsenicals, activities of macromolecules (AQP9, TR, MT1, MT2, MRPa, MRPm) and GSH (GS-Pm, GS-Pd). The network of biochemical interactions is represented using SBGN formalism (www.sbgn.org) (Le Novere et al., 2009) (adapted from Stamatelos et al., 2011).
The TD model that is presented here describes a more explicit biological mechanism for arsenic-induced protective response of cells applying principles of indirect response model theory; a theoretical framework commonly used to describe dynamic coupling of extracellular stimuli to intracellular signaling (Abraham et al., 2009a, 2009b; Foteinou et al., 2009; Ramakrishnan et al., 2002; Vodovotz et al., 2009). So, it addresses the arsenic-induced ROS production, the Nrf2-mediated mammalian antioxidant response, and the concomitant DNA damage in hepatocytes. The mathematical model of the underlying gene regulatory network is integrated with the TK model for arsenic and refines the previously formulated “switch-like” cellular response to toxicity, introducing a more mechanistic perspective. Moreover, a kinetic model of DNA damage repair (Sokhansanj and Wilson, 2004, 2006; Sokhansanj et al., 2002) is linked to the TK/TD model for arsenic. This allows the theoretical estimation of human DNA damage repair and the prediction of dose–response curves of arsenic-induced genotoxic damage in human hepatocytes.
2.1. Model development
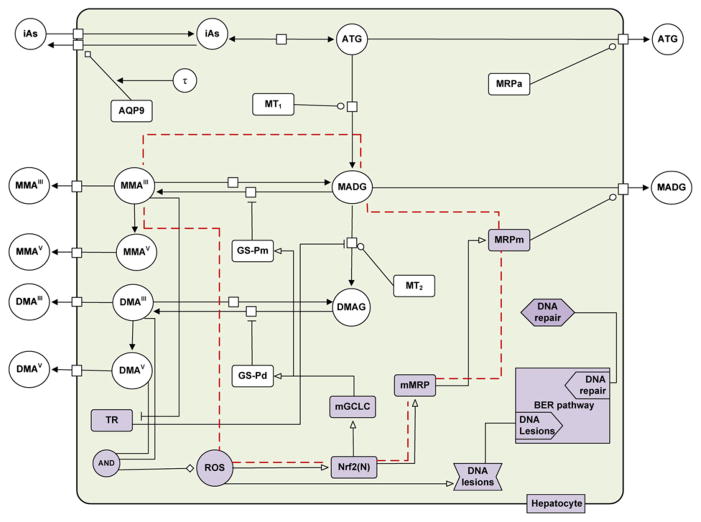
The proposed TD formulation illustrates an Nrf2-mediated antioxidant homeostatic mechanism that hepatocytes employ in order to scavenge ROS and efflux arsenicals. This mechanism is modeled as being controlled primarily via antioxidant enzyme-mediated coupled negative and positive feedback loops. The integrated TK/TD model components and the interactions among them are presented schematically in Fig. 4. This approach takes into account the assumptions made for the TK model and considers the following additional assumptions:
Fig. 4.
Schematic of the cellular-level TK/TD model for arsenic in hepatocytes showing the biochemical components. The variables depict extracellular and intracellular amounts of arsenicals, ROS, Nrf2 nuclear signaling (Nrf2(N)), activities of macromolecules (AQP9, BER, TR, mGCLC, MT1, MT2, MRPa, MRPm, mMRP) and GSH (GS-Pm, GS-Pd). The network of biochemical interactions is represented using SBGN formalism (www.sbgn.org) (Le Novere et al., 2009). The red dashed line represents a characteristic negative feedback loop mechanism for MMAIII (also in Table 2, second row).
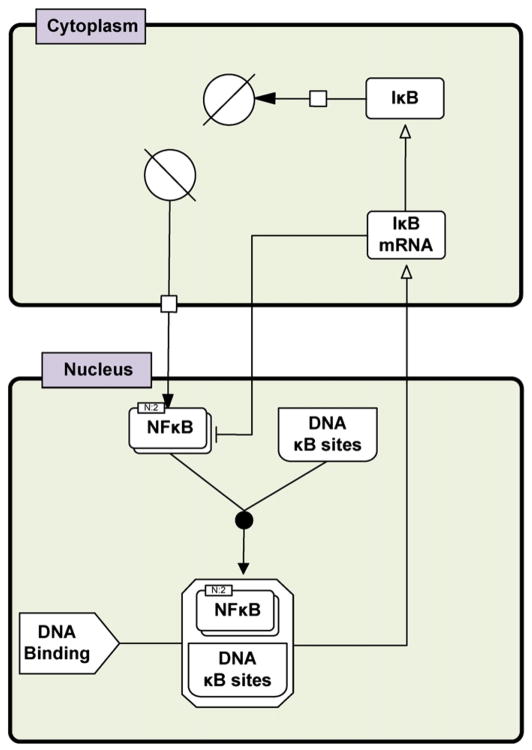
The ROS-induced Nrf2 signaling cascade is described by the Keap1-independent Nrf2 signaling, and can be modeled using a reduced dimensionality structure similar to a previously proposed model of NFκB dynamics.
The Nrf2-triggered upregulation of GSH levels stimulates nuclear export of Nrf2.
The DNA lesions caused by arsenic-induced ROS increase are modeled via a first order process and the base excision repair (BER) pathway is considered to be the major pathway for oxidative DNA damage repair.
Compared to the cellular-level TK model for human hepatocytes, where the critical signal for the threshold-dependent antioxidant response was the activity of thioredoxin reductase (TR) (Fig. 3), the present formulation introduces a more explicit mechanistic approach for the signaling cascade. That is to say, our prior modeling work included an indirect response formulation where TR is the signal for antioxidant response upregulation (GSH and MRP increase) and decreased methylation capacity of AS3MT enzyme. Therefore, the Nrf2 nuclear receptor pathway was not explicitly included in a step by step basis. In this model this single signal of TR inactivation is substituted with a toxicodynamic model characterized by a cascade of signaling events for the antioxidant mechanism (ROS increase, Nrf2 nuclear translocation, increased transcription of GCLC and MRP mRNA). Therefore, TR inactivation is presumed to affect only AS3MT activity. Based on the newly proposed model of Keap1-independent Nrf2 signaling, the transcription factor per se functions as a redox sensitive probe, upregulating GSH levels in cells and initiating nuclear export of Nrf2 (Fig. 2) (Li and Kong, 2009). In this case, Nrf2 signaling is regulated via a direct negative feedback interaction with GSH. Similarly, the NFκB core feedback mechanism involves the inhibition of transcription factor activity by NFκB-triggered expression of IκB proteins (Basak et al., 2007; Kearns et al., 2006; Shiha et al., 2009). The NFκB signaling module has been mathematically described as consisting of a very large number of interactions among the participating proteins, leading to negative feedback to control expression of proinflammatory genes (Hoffmann et al., 2002). Krishna et al. have shown that this huge network of interactions can be decomposed to a small set of variables describing the activity of signaling molecules that primarily affect the cascade’s output (Fig. 5) (Krishna et al., 2006). Based on this study, a conceptual analog is attempted in the present work, based on the Nrf2 signaling cascade; the variables chosen to describe the core pathway are: ROS activity (source signal), Nrf2 nuclear translocation (transcription factor activity in the nucleus), mRNA, and protein levels of an enzyme (GCLC) that controls GSH biosynthesis (transcription factor inhibitor).
Fig. 5.
Schematic diagram of key interactions in the NF-κB signaling system (three variable model). The variables represent the concentration of nuclear NF-κB homodimer, mRNA of IκB, and cytoplasmic IκB (adapted from Krishna et al., 2006). The network of biochemical interactions is represented using SBGN formalism (www.sbgn.org) (Le Novere et al., 2009).
The threshold-dependent elevation of ROS levels is described by the nonlinear Hill-type formula HTR that was used to describe oxidative stress in the TK model (Stamatelos et al., 2011) (Eqs. 1a–1c). The amplification factor for the Hill equation is assumed to be DMAIII, since trivalent DMAs are the most potent oxidative stress inducers (Kligerman et al., 2003). Degradation of ROS excess levels is modeled employing a saturation function introducing a time delay in the feedback loops of the system (Igoshin et al., 2004; Jacquet et al., 2003; Krishna et al., 2006; Tiana et al., 2002, 2007; Tyson et al., 2003). In the proposed formulation the anti-electrophilic response is expressed as a function of effluxed DMA, since this quantity has been suggested to have a positive correlation with the induction of antioxidant proteins in human hepatocytes (MRPs) and in rat liver (heme oxygenase—HO) following arsenite exposure (Drobna et al., 2010; Kitchin et al., 1999)
| (1a) |
| (1b) |
| (1c) |
where kinROS and kdecROS are the rate constants for ROS increase and decay respectively; ICTR is the inhibition constant (IC50) for TR by MMAIII in hepatocytes estimated in Lin et al. (2001); N is the Hill coefficient for enzyme inactivation from MMAIII.
The ROS-induced Nrf2 nuclear translocation (Nrf2(N)) (Eqs. 2a–2b) and its subsequent binding to the ARE that leads to upregulation of detoxifying enzymes and transporters is described via indirect response models. Specifically, the increase in GSH levels is assumed to be adequately described via the induction of GCLC (glutamate cysteine ligase catalytic subunit) (Eqs. 3–4c). This enzyme is used as a biomarker since it is the catalytic subunit of the GCL holoenzyme, contributing all its enzymatic activity and containing all the substrate-binding sites (Franklin et al., 2009). GCL is a heterodimeric enzyme that catalyzes the rate limiting reaction for GSH biosynthesis (Griffith and Mulcahy, 1999). The phase III transporters acting in cohort are modeled via the induction of MRP signaling processes that transport the GSH-bound arsenicals ATG and MADG out of the cells (Eqs. 5 and 6). These equations substitute the equations for GSH and MRPs for the antioxidant response of the initial cellular-level TK model for arsenic (Stamatelos et al., 2011)
| (2a) |
| (2b) |
| (3) |
| (4a) |
| (4b) |
| (4c) |
| (5) |
| (6) |
where ksynNF and kdegNF are the rate constants controlling Nrf2 translocation to the nucleus; [iAsIII]init is the initial exposure concentration of iAsIII and the threshold variable is the concentration defined in (Stamatelos et al., 2011); kmGC and ksynG are the rate constants governing the mRNA activity of GCLC; ksynGC and kdegGC are the synthesis and decay rate constants for GCLC protein synthesis; n4 and Kd4 are the Hill coefficient and dissociation constant for GCLC induction; kmMRP and ksynP are the rate constants controlling the mRNA activity of MRP; kMRP is the rate constant controlling MRP protein activity.
The oxidative stress-induced DNA damage (8-oxoG site formation) is modeled via a first-order process (Eq. 7) while the oxidative DNA damage repair is described via a previously developed kinetic model of the BER pathway (Sokhansanj and Wilson, 2004). This formulation describes the reaction cascade for DNA repair via Michaelis–Menten kinetics, an approach that is justified by the high concentration of repair proteins in the nucleus (Sokhansanj et al., 2002). In order to reduce the dimensionality of the model, the DNA repair process is assumed to take place through the BER subpathways B and C (Fig. 6) (short- and long-patch) which are primarily involved in the reaction cascade (Caldecott, 2003; Liu et al., 2007)
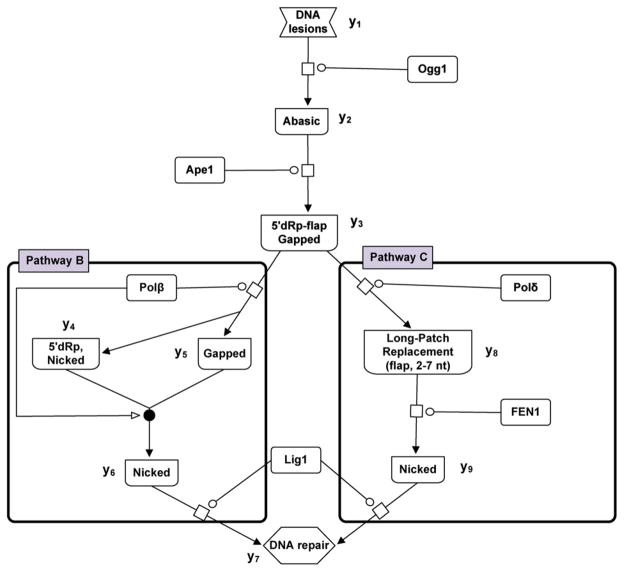
Fig. 6.
Schematic of the kinetic model for base excision repair (BER) pathway. The diagram depicts pathways B and C of base excision oxidative DNA damage repair. The variables represent activities of DNA parts being repaired, and proteins catalyzing this process (Ogg1 glycosylase, Ape1 AP endonuclease, Polβ gap-filling, Polβ dRp lyase, Lig1 ligation, Polδ gap-filling, Fen1 5′-endo) (adapted from Sokhansanj et al. (Sokhansanj and Wilson, 2004)). The network of biochemical interactions is represented using SBGN formalism (www.sbgn.org) (Le Novere et al., 2009).
| (7) |
where kDNA is the reaction constant for DNA lesions formation. The value of this constant is calculated based on estimates of the maximum rate of 8-oxoG sites formation in cells under basal conditions (Lindahl, 1993). Eq. (7) substitutes the term f0 in the BER model (Sokhansanj and Wilson, 2004) (Table 1).
Table 1.
Equations of the BER pathway model.
|
|
|
||
|
|
|
||
|
|
|
||
|
|
v4 = k4 × y4 | ||
|
|
|
||
|
|
v6 = k3 × y6 | ||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
The TK/TD model has been implemented in MATLAB; the system of ODEs comprising the TK/TD model is solved numerically using the stiff solver ode15s. The TK/TD model involves 39 variables depicting the different arsenical species and the various chemical processes involved in the signaling cascade, and 74 parameters (Supplementary Table S1). The parameters representing uptake and biotransformation of arsenicals are adopted from our published mathematical model for the kinetics of iAsIII in human hepatocytes (Stamatelos et al., 2011). The derivation of the parameters involved in the human BER pathway model is fully documented in the literature (Sokhansanj and Wilson, 2004, 2006; Sokhansanj et al., 2002). The deterministic optimization function fmincon was used for estimation of 13 model parameters. These parameters describing the Nrf2-mediated antioxidant cascade and the genetic damage are estimated using time course in vitro measurements of fold increase of mRNA and protein levels of GCLC enzyme in murine hepatocytes exposed to 10 μM of iAsIII (Thompson et al., 2009). Finally, the integrated TK/TD model predictions are tested with dose-response data of arsenite-induced DNA damage formation in human hepatocytes (5–100 μM) (Dopp et al., 2008) in order to computationally assess the validity of the fitted values.
2.2. Global sensitivity analysis and robustness to parameter perturbation
This study provides estimates of how variation in the outputs of the model can be apportioned to different sources of variation in model inputs and parameters, in a manner similar to that used previously for the TK model (Stamatelos et al., 2011). The TK/TD model parameters were assumed to be normally distributed with a coefficient of variation up to 30%. Ten thousand (10,000) samples were generated and the normal distributions for all parameters were truncated at 1% and 99% (approximately three standard deviations from the mean value). The model output selected for the sensitivity analysis was the area under the curve (AUC) of unrepaired DNA damage, MMAIII and DMAIII. The SIMLAB modeling platform (SIMLAB, 2009) was used to perform the global sensitivity analysis. Furthermore, we explored the robustness in the dynamic behavior of specific state variables due to stochastic perturbation of model parameters (Mirsky et al., 2009). We created 10,000 parameter sets by randomly sampling from normal distributions with a mean equal to the nominal value of each parameter. The standard deviation spanned from 5 to 50% of the nominal value. The cost function used for both analyses is the mean of the sum of squares of the difference between model predictions and experimental data.
3. Results
The semi-mechanistic TD model was parameterized using time course data of arsenic-induced GCLC expression in hepatocytes (Thompson et al., 2009). The estimated parameters are presented in Supplementary Table S1. The TK/TD model is able to predict the modes of both mRNA transcription (Fig. 7—left panel) and protein translation (Fig. 7—right panel) of GCLC. The TK/TD model captures the fast (within 1 h) upregulation of GCLC mRNA and the late and gradual increase in GCLC protein translation. From a biological standpoint this can be attributed to the multitude of signaling processes involved in oxidative stress sensing and antioxidant mechanism upregulation (Droge, 2002); this phenomenon introduces a time delay in the cellular adaptive response. During the next 3 h there is a sharp increase in mRNA transcripts of GCLC while at the same time the increase of protein levels is infinitesimal. The GCLC protein levels follow an increasing pattern, which subsequently coincides with the decrease in mRNA transcripts.
Fig. 7.
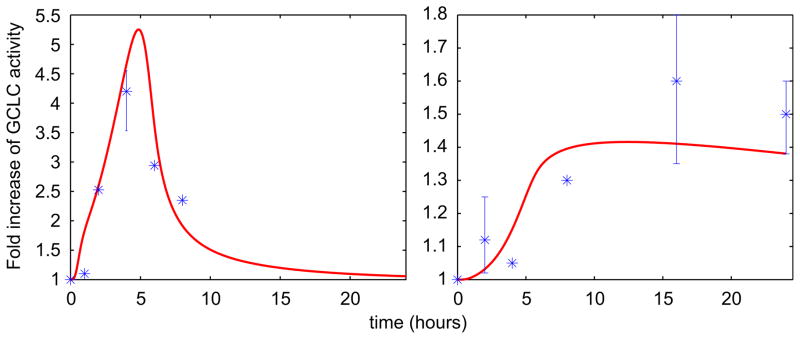
Predicted time course profiles of GCLC in hepatocytes using the cellular-level TK/TD model. The left panel shows mRNA and right panel shows protein levels fold increase of GCLC. Experimental data are from Thompson et al. (2009) for murine hepatocytes after exposure to 10 μM of iAsIII for 24 h. The data are averages plus/minus the standard error of the mean of at least three experiments and the p-values compared to untreated control are really low (<0.05).
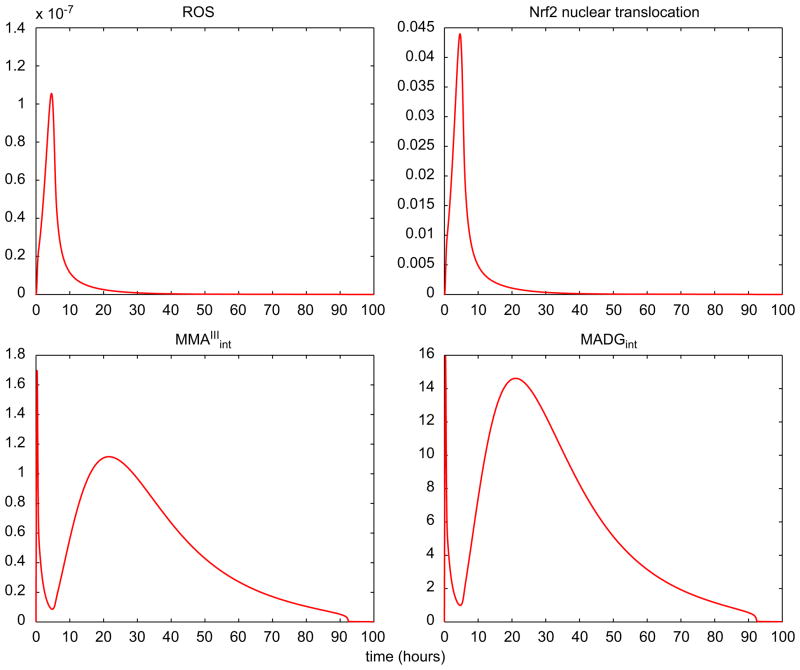
Fig. 8 presents the dynamics of selected state variables of the TK/TD system; ROS levels and Nrf2 nuclear translocation activity (upper row) follow a similar pattern and return to baseline at approximately 20 h. Intracellular concentration of MMAIII and MADG (bottom row) follow a multiphasic (“two-wave”) pattern and are cleared from the hepatocytes in a much later stage (~80 h). Thus, the cellular antioxidant mechanism scavenges the ROS; however the system does not quite return to homeostasis since MMAIII, a major inhibitor of thioredoxin reductase (TR), is not effluxed and remains in hepatocytes for much longer.
Fig. 8.
Predicted time course profiles of a number of cellular-level TK/TD model variables. The top row shows estimates for ROS (left panel) and Nrf2(N) activity (right panel). The bottom row shows intracellular concentration (μM) of MMAIII (left panel) and MADG (right panel). The exposure dose is assumed to be 10 μM of iAsIII.
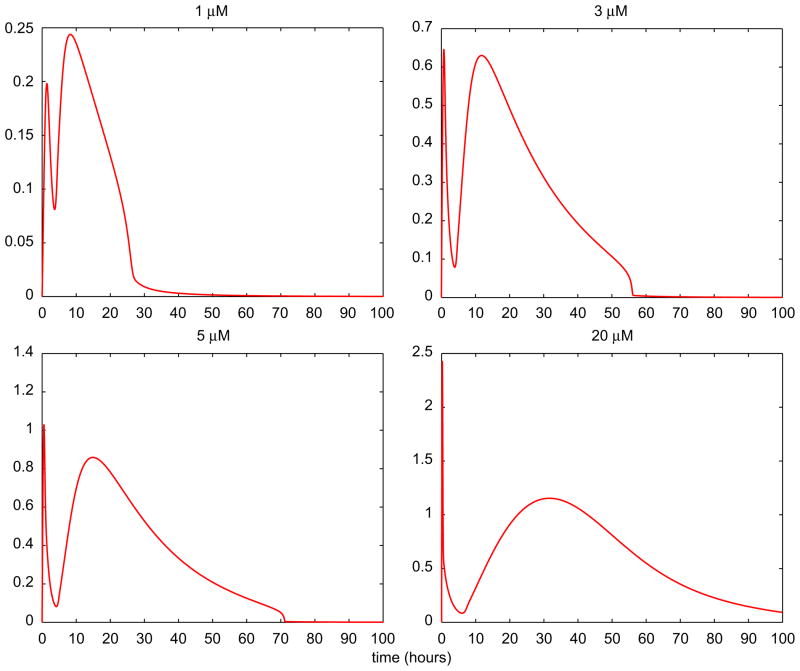
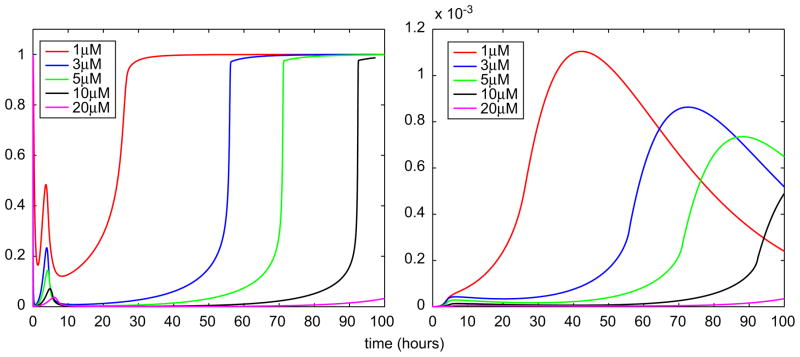
Because of the multiphasic behavior of intracellular MMAIII concentration, various in silico experiments were performed in order to explore this phenomenon for various doses of arsenite. As shown in Fig. 9, the nonlinear patterns vary both in frequency and in amplitude; the first “wave” becomes spikier and peaks earlier, while the second “wave” is clearly dampened and delayed with increasing arsenite doses. On the other hand, the reduction of the arsenic methyltransferase (AS3MT) methylation efficiency is higher and its restoration is delayed with increasing exposures/doses (Fig. 10—left panel). This pattern of AS3MT signal affects the cellular accumulation of DMAIII, a critical oxidative stress agent, which becomes extremely low while MMAIII concentration peaks (Fig. 9). In contrast, as shown in the right panel of Fig. 10, the sharp rise of DMAIII concentration takes place when eventually MMAIII is entirely effluxed after the second “wave”.
Fig. 9.
Predicted time course profiles of MMAIII in hepatocytes using the cellular-level TK/TD model. The figure shows estimates of the intracellular concentration (μM) of MMAIII for four initial doses (μM) of iAsIII.
Fig. 10.
Predicted time course profiles of AS3MT activity and DMAIII in hepatocytes using the cellular-level TK/TD model. The left panel shows estimates of AS3MT activity across doses (μM) of iAsIII. The right panel shows intracellular concentration (μM) of DMAIII across doses (μM) of iAsIII.
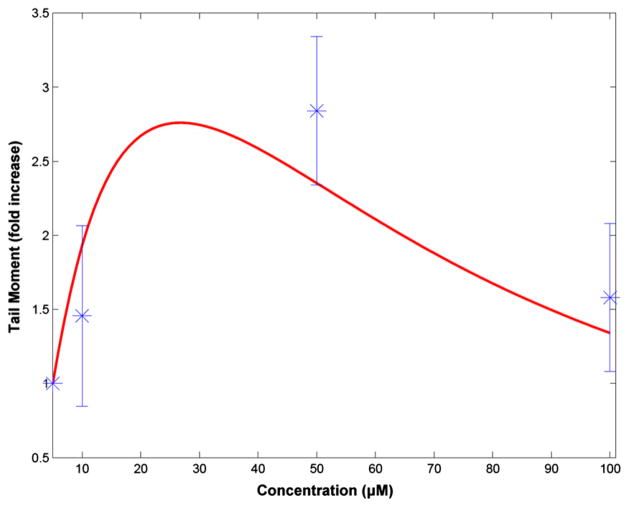
Fig. 11 presents an evaluation of the predictions of the TK/TD model against normalized data of arsenic-induced DNA damage formation (tail moment) in human hepatocytes after exposure to various concentrations of arsenite (5–100 μM) for 1 h (Dopp et al., 2008). Unrepaired DNA damage is calculated by adding the amounts of DNA lesions and repair pathway intermediates that are formed over the time course of the simulation. The results presented are normalized against the model output of the 5 μM exposure scenario. The model estimates are in good agreement with the experimental data of the relative change of DNA damage accumulation across doses, which follow an increasing pattern up to 20 μM and then decrease.
Fig. 11.
Predicted dose–response profiles of DNA damage in hepatocytes using the cellular-level TK/TD model. Estimates of unrepaired DNA damage after exposure to various doses of iAsIII (5–100 μM). Experimental data are adapted from Dopp et al. (2008) for human hepatocytes. The model predictions and experimental measurements are normalized against the DNA damage formation at 5 μM dose of iAsIII.
The TK/TD model predictions have been extended across doses and time (up to 24 h) with respect to DNA damage accumulation. The 3-D graph of Fig. 12 illustrates that the time course estimates of DNA damage follow a consistent “Gaussian-like” pattern across doses that resolves before 24 h, and take their maximum value at approximately 10 h. Moreover, the TK/TD model predicts a dose threshold (~10 μM) of arsenite above which the maximum values of DNA damage is reduced.
Fig. 12.
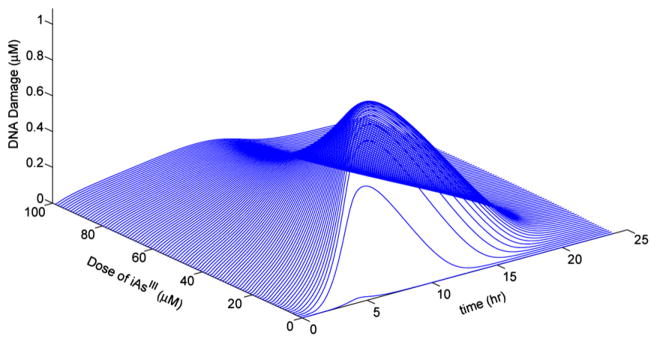
A three-dimensional representation of the cellular-level TK/TD model predictions for DNA damage in hepatocytes. Estimates of unrepaired DNA damage concentration (μM) across time (up to 24 h) and doses of iAsIII (0.1–100 μM).
The sensitivity analysis results for the parameters contributing to variance of unrepaired DNA damage vary depending on the time scale of exposure, as presented in Fig. 13. For 1 h exposure to iAsIII, the parameter of highest impact is the coefficient of DMAG hydrolysis fGSHd (Table S1, parameter 13). This parameter influences the activity of GSH-mediated hydrolysis of DMAG to DMAIII in an inhibitory fashion (Stamatelos et al., 2011) (Eq. (A.10a), see Supplementary Text), indicating the significance of the negative feedback loop controlling DMA production (Table 2, fourth row) during the early antioxidant response. It appears that the variation of fGSHd parameter modifies the ROS output, which is linked to MMAIII production via the corresponding negative feedback loop (Table 2, first row). This result also highlights the tight link between the two negative feedback loops involved in GSH upregulation (Table 2, first and fourth rows).
Fig. 13.

Sensitivity analysis of unrepaired DNA damage estimation. Total sensitivity indices (TSI) of the cellular-level TK/TD model parameters for various exposure times (1–10–24 h) to iAsIII; the parameters are listed in Table S1.
Table 2.
Feedback loops contained in the cellular-level TK/TD model.
| Stimulus | Elements of feedback | Type of feedback |
|---|---|---|
| MMAIII | MMAIII→ROS→Nrf2(N)→mGCLC→GS-Pm ⊣ MMAIII | Negative |
| MMAIII | MMAIII→ROS→Nrf2(N)→mMRP→MRPm ⊣ MMAIII | Negative |
| MMAIII | MMAIII ⊣ TR ⊣ AS3MT→MADG→MMAIII | Positive |
| DMAIII | DMAIII→ROS→Nrf2(N)→mGCLC→GS-Pd ⊣ DMAIII | Negative |
As shown in Fig. 13, for longer time intervals (10 and 24 h) of exposure the number of parameters that contribute to unrepaired DNA damage variation increases, since the cellular antioxidant response and DNA repair process are fully active. The parameter fGSHd continues to be of great importance, but almost equally important is the parameter fGSHm (Table S1, parameter 10) which is the coefficient of MADG hydrolysis. The latter coefficient of variation influences the response signal traveling in two MMAIII-driven feedback loops; one negative (Table 2, first row) and one positive (Table 2, third row). Finally, among the DNA repair enzymes, the one that appears to be the most influential is DNA Ligase I. Specifically, the turnover number kcat (Table S1, parameter 59) and the enzyme concentration (Table S1, parameter 67) of Ligase I, which accounts significantly for the enzyme’s activity, are the most crucial parameters among all those describing the BER pathway. The second sensitivity analysis study considering the model outputs MMAIII and DMAIII which are the state variables that drive ROS increase/decrease has resulted in 24 parameters that significantly contribute to their variance (see Supplementary Fig. S1). The multiphasic behavior of MMAIII due to stochastic changes in this parameter set is robustly sustained for all parameter perturbations that lead to similar optimization cost function values. We present the results for standard deviations 5%, 10% and 20% of nominal values (Supplementary Fig. S2), but we have seen the same results for even larger deviations (50%–results not shown). Interestingly, this profile is sustained even for cost function values that depart from the optimized result.
4. Conclusions and discussion
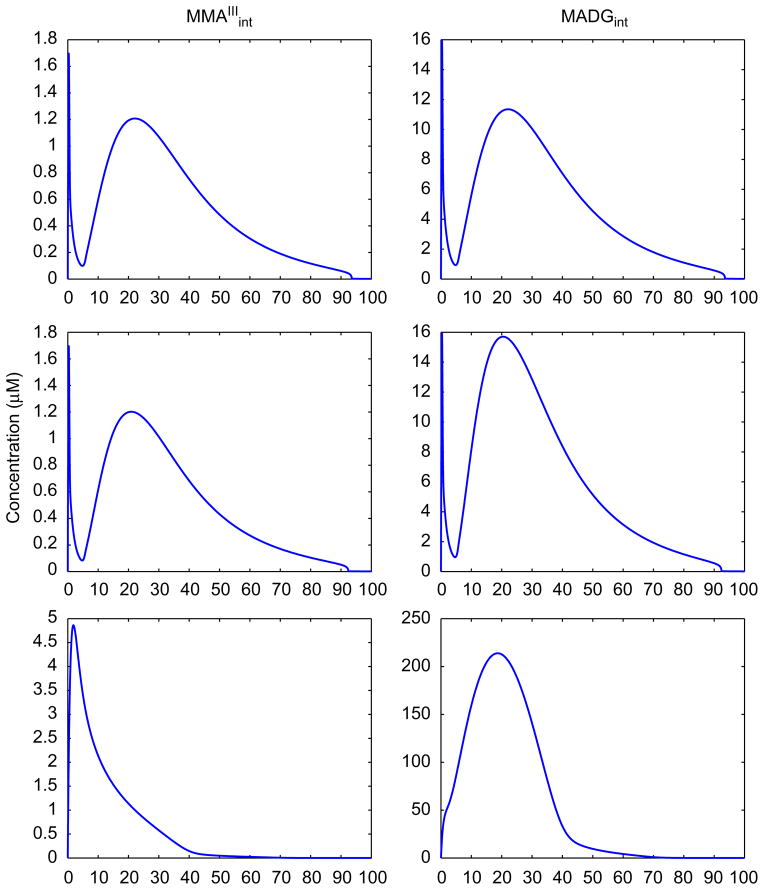
The present study illustrates in mathematical terms the biological control system of arsenic-induced anti-electrophilic/oxidative response in hepatocytes, based on a recently proposed model of Keap-1 independent Nrf2 transcription factor regulation (Li and Kong, 2009). The new cellular-level TD model has been integrated with the TK model presented in Stamatelos et al. (2011), incorporating uptake, biotransformation, efflux and threshold-dependent adaptive response to oxidative stress in human hepatocytes. This mathematical formalism describes a theoretical nonlinear mechanism of antioxidant action consisting of multiple nested feedback loops (three negative and one positive feedback: Table 2) leading to time-delayed responses, which are critical for the occurrence of multiphasic dynamics in the TK/TD model. Biologically, the time delays can be explained by the fact that processes such as transcription and translation are composed of a large number of intermediate Poisson-type “steps”, adding to the total delayed cellular response. Various formalisms have been used to introduce this time delay in mathematical models (Tiana et al., 2007). In the present case, in silico experiments that were conducted excluding specific feedback loops or combinations of them (Fig. 14) revealed that the negative feedback loop, that is necessary for the multiphasic behavior, is the one leading to the upregulation of phase III transport system (Table 2, second row and Fig. 4, red dashed line). This is a multicomponent negative feedback loop that appears to delay the propagation of the signal in the system in a way similar to the effect of the repressilator (Elowitz and Leibler, 2000). It should be stated that the multiphasic behavior has not been reported experimentally, and therefore their presence in actual cellular systems is currently a working hypothesis based on a basis of a theoretical framework regarding the time-delay introduced in cellular-systems. Nevertheless, based on the results of the robustness analysis (see Supplementary Fig. S2) these dynamics are preserved for a range of parameter sets; this highlights that this nonlinear behavior is not an “artifact” (e.g. local minimum) of the steepest descent multivariable optimization method.
Fig. 14.
Predicted time course profiles of MMAIII and MADG in hepatocytes using the cellular-level TK/TD model. Estimates of intracellular MMAIII and MADG in hepatocytes after exposure to 10 μM of iAsIII, excluding each of the negative feedback loops of the system presented in Table 2. First row: Exclusion of negative feedback related to upregulation of GSH and inhibition of MMAIII. Second row: Exclusion of negative feedback related to upregulation of GSH and inhibition of DMAIII. Third row: Exclusion of negative feedback related to upregulation of MRPs and clearance of arsenicals.
The prediction of prolonged elevation of ROS signal as presented in Fig. 7 is consistent with the results of a number of experimental studies that explore how oxidative stress contributes to genomic instability and tumorigenesis. Zhang et al. (Zhang and Zhou, 2012) have reported prolonged activation of ROS-regulated Wnt/β-catenin pathway (up to 24 h) due to arsenic exposure in similar dose ranges as the Dopp et al. (2008) study, which employed a human colorectal cell line. Furthermore, chronic oxidative stress is implicated to metabolic reprogramming of cancer cells (Haigis et al., 2012). Hypoxia in the tumor microenvironment induces deregulation of ROS homeostasis, stabilizing HIF1α leading to increased cellular aerobic glycolysis (Bell et al., 2011; Finley et al., 2011), and high proliferation rate in various cancer cell lines including hepatic ones (Zhang and Zhou, 2012). These types of experimental settings along with in vivo animal cancer xenografts can be employed in order to develop an arsenic-induced multiscale model of cancer initiation and progression. Such a modular model could involve an agent-based formulation for the cellular decision process (division, quiescence, apoptosis) along with the integrated TK/TD model of arsenic exposure, which will dictate this decision based on the ROS levels in each cell.
The combination of positive and negative feedback loops has been reported to generate oscillations in various biological networks, such as the levels of Ca2+-induced Ca2+ release (Goldbeter, 2002) and the mitotic oscillator in Xenopus embryos (Ferrell et al., 2009). On the other hand, while negative feedback is considered necessary for the creation of oscillations in components of the model, positive feedback has been suggested to be the primary mechanism tuning the amplitude and frequency of these oscillations (Tsai et al., 2008). Positive feedback appears to modulate the “two-wave” response of MMAIII, leading to higher and sharper spikes of the first “wave”, and influencing the dampening and the delayed appearance of the second “wave” (Fig. 9). The positive feedback acts via the persistent inactivation of TR in increasing arsenite doses (especially above 10 μM), leading to the inhibition of the second methylation reaction of arsenic (Fig. 10). This sensitivity testing revealed that the levels of MMAIII and DMAIII follow reciprocal but tightly related patterns and that the positive feedback loop appears to be the major factor modulating this phenomenon.
Dopp and coworkers have reported that primary human hepatocytes (which do not proliferate in culture) have almost the same viability after 1 h exposure to arsenite from 5 to 50 μM (Dopp et al., 2008). Moreover, for 24 h exposure to arsenic the increase of the percentage of cell death is much higher from 0.5 to 5 μM concentration than from 5 to 50 μM. A possible explanation of this non-linear phenomenon could be given from our modeling study via the predicted dose-dependent reduction of DNA damage. The proposed biological mechanisms highlight the crucial role the positive feedback loop for MMAIII plays in the system leading to the computational prediction about the dose threshold (Fig. 12). This result points to the potential critical role of the positive feedback loop in a faster-than-linear antioxidant response. Specifically, since it regulates in a nonlinear fashion the “spikiness” of the first phase of MMAIII increase. The importance of the shape of these phases in cellular response networks has already been reported in other systems, such as the p53-Mdm2 and NFκB module (Krishna et al., 2006; Tiana et al., 2002). The shape of this “wave” influences the contribution of the DMAIII-driven negative feedback loop to the antioxidant response mechanism which, according to the sensitivity analysis performed here, is the dominant loop for DNA damage formation.
Improvement and expansion of the existing modeling structure and its parameterization, in order to involve more signals and to account for phenomena such as arsenic-induced inhibition of DNA repair, hormesis or tolerance phenomena (Liu et al., 2001; Snow et al., 2005), demand additional experimental data. We have already demonstrated the parametric differences of cellular-level models for arsenic based on measurements from human hepatocytes compared to other species such as rats (Easterling et al., 2002; Stamatelos et al., 2011). The chemical speciation analysis of valent arsenicals and arsenic-GSH adducts is possible via liquid chromatography and mass spectrometry (Naranmandura et al., 2006, 2008; Watanabe et al.). There is a need to collect data to discern the levels of valent arsenical species in human hepatocytes across time for various exposure scenarios. The Nrf2 transcription factor control system consists of a multitude of enzymes and feedback loops that work in coordination in order to scavenge ROS and mediate the return to cellular homeostasis (Zhang and Andersen, 2007; Zhang et al., 2009). In order to properly evaluate and calibrate a model that would describe such a vast network of interactions there is a need for targeted arsenic- and cell-specific (Dahl and Mulcahy, 2001) experimental designs that would provide expression measurements of participating drug metabolizing and antioxidant enzymes across both time and dose ranges.
Supplementary Material
HIGHLIGHTS.
We present a theoretical model coupling kinetics/dynamics of arsenic in hepatocytes.
The modeled antioxidant mechanism is based on a novel pathway of Nrf2 activation.
The model estimations are assessed with data of DNA damage in human hepatocytes.
The analysis highlights the importance of feedback loops to antioxidant response
Acknowledgments
This work was primarily supported by the USEPA-funded Environmental Bioinformatics and Computational Toxicology Center (ebCTC), Grant GAD R 832721-010. Additional support was provided by the NIEHS sponsored UMDNJ Center for Environmental Exposures and Disease, Grant #. NIEHS P30ES005022.
Appendix A. Supporting Information
Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jtbi.2012.09.019.
Footnotes
Authors’ Contributions
S.K.S. conceived the study, developed and implemented the mathematical model, analyzed the results and drafted the manuscript. I.P.A. and A.N.K. contributed to the analysis of the results and manuscript drafting. P.G.G. conceived the study, contributed to manuscript drafting and supervised the work. All authors read and approved the manuscript.
Contributor Information
Spyros K. Stamatelos, Email: spyros@jhu.edu.
Ioannis P. Androulakis, Email: yannis@rci.rutgers.edu.
Ah-Ng Tony Kong, Email: kongt@pharmacy.rutgers.edu.
Panos G. Georgopoulos, Email: panosg@ccl.rutgers.edu.
References
- Abraham AK, Ramanathan M, Weinstock-Guttman B, Mager DE. Mechanisms of interferon-beta effects on bone homeostasis. Biochem Pharmacol. 2009a;77:1757–1762. doi: 10.1016/j.bcp.2009.01.007. [DOI] [PubMed] [Google Scholar]
- Abraham AK, Mager DE, Gao X, Li M, Healy DR, Maurer TS. Mechanism-based pharmacokinetic/pharmacodynamic model of parathyroid hormone-calcium homeostasis in rats and humans. J Pharmacol Exp Ther. 2009b;330:169–178. doi: 10.1124/jpet.109.152033. [DOI] [PubMed] [Google Scholar]
- Basak S, Kim H, Kearns JD, Tergaonkar V, O’Dea E, Werner SL, Benedict CA, Ware CF, Ghosh G, Verma IM, Hoffmann A. A fourth I kappa B protein within the NF-kappa B signaling module. Cell. 2007;128:369–381. doi: 10.1016/j.cell.2006.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell EL, Emerling BM, Ricoult SJ, Guarente L. SirT3 suppresses hypoxia inducible factor 1alpha and tumor growth by inhibiting mitochondrial ROS production. Oncogene. 2011;30:2986–2996. doi: 10.1038/onc.2011.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom D, Dhakshinamoorthy S, Jaiswal AK. Site-directed mutagenesis of cysteine to serine in the DNA binding region of Nrf2 decreases its capacity to upregulate antioxidant response element-mediated expression and antioxidant induction of NAD(P)H: quinone oxidoreductase1 gene. Oncogene. 2002;21:2191–2200. doi: 10.1038/sj.onc.1205288. [DOI] [PubMed] [Google Scholar]
- Caldecott KW. XRCC1 and DNA strand break repair. DNA Repair (Amst) 2003;2:955–969. doi: 10.1016/s1568-7864(03)00118-6. [DOI] [PubMed] [Google Scholar]
- Dahl EL, Mulcahy RT. Cell-type specific differences in glutamate cysteine ligase transcriptional regulation demonstrate independent subunit control. Toxicol Sci. 2001;61:265–272. doi: 10.1093/toxsci/61.2.265. [DOI] [PubMed] [Google Scholar]
- Dinkova-Kostova AT, Holtzclaw WD, Kensler TW. The role of Keap1 in cellular protective responses. Chem Res Toxicol. 2005;18:1779–1791. doi: 10.1021/tx050217c. [DOI] [PubMed] [Google Scholar]
- Dinkova-Kostova AT, Holtzclaw WD, Cole RN, Itoh K, Wakabayashi N, Katoh Y, Yamamoto M, Talalay P. Direct evidence that sulfhydryl groups of Keap1 are the sensors regulating induction of phase 2 enzymes that protect against carcinogens and oxidants. Proc Natl Acad Sci USA. 2002;99:11908–11913. doi: 10.1073/pnas.172398899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dopp E, von Recklinghausen U, Hartmann LM, Stueckradt I, Pollok I, Rabieh S, Hao L, Nussler A, Katier C, Hirner AV, Rettenmeier AW. Subcellular distribution of inorganic and methylated arsenic compounds in human urothelial cells and human hepatocytes. Drug Metab Disposition. 2008;36:971–979. doi: 10.1124/dmd.107.019034. [DOI] [PubMed] [Google Scholar]
- Drobna Z, Walton FS, Paul DS, Xing WB, Thomas DJ, Styblo M. Metabolism of arsenic in human liver: the role of membrane transporters. Arch Toxicol. 2010;84:3–16. doi: 10.1007/s00204-009-0499-7. [DOI] [PubMed] [Google Scholar]
- Droge W. Free radicals in the physiological control of cell function. Physiol Rev. 2002;82:47–95. doi: 10.1152/physrev.00018.2001. [DOI] [PubMed] [Google Scholar]
- Easterling MR, Styblo M, Evans MV, Kenyon EM. Pharmacokinetic modeling of arsenite uptake and metabolism in hepatocytes—mechanistic insights and implications for further experiments. J Pharmacokinet Pharmacodyn. 2002;29:207–234. doi: 10.1023/a:1020248922689. [DOI] [PubMed] [Google Scholar]
- El-Masri HA, Kenyon EM. Development of a human physiologically based pharmacokinetic (PBPK) model for inorganic arsenic and its mono- and di-methylated metabolites. J Pharmacokinet Pharmacodyn. 2008;35:31–68. doi: 10.1007/s10928-007-9075-z. [DOI] [PubMed] [Google Scholar]
- Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Ferrell JE, Pomerening JR, Kim SY, Trunnell NB, Xiong W, Huang CYF, Machleder EM. Simple, realistic models of complex biological processes: positive feedback and bistability in a cell fate switch and a cell cycle oscillator. FEBS Lett. 2009;583:3999–4005. doi: 10.1016/j.febslet.2009.10.068. [DOI] [PubMed] [Google Scholar]
- Finley LW, Carracedo A, Lee J, Souza A, Egia A, Zhang J, Teruya-Feldstein J, Moreira PI, Cardoso SM, Clish CB, Pandolfi PP, Haigis MC. SIRT3 opposes reprogramming of cancer cell metabolism through HIF1alpha destabilization. Cancer Cell. 2011;19:416–428. doi: 10.1016/j.ccr.2011.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foteinou PT, Yang E, Androulakis IP. Networks, biology and systems engineering: a case study in inflammation. Comput Chem Eng. 2009;33:2028–2041. doi: 10.1016/j.compchemeng.2009.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin CC, Backos DS, Mohar I, White CC, Forman HJ, Kavanagh TJ. Structure, function, and post-translational regulation of the catalytic and modifier subunits of glutamate cysteine ligase. Mol Aspects Med. 2009;30:86–98. doi: 10.1016/j.mam.2008.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter A. Computational approaches to cellular rhythms. Nature. 2002;420:238–245. doi: 10.1038/nature01259. [DOI] [PubMed] [Google Scholar]
- Griffith OW, Mulcahy RT. The enzymes of glutathione synthesis: gamma-glutamylcysteine synthetase. Adv Enzymol. 1999;73:209–267. doi: 10.1002/9780470123195.ch7. [DOI] [PubMed] [Google Scholar]
- Haigis MC, Deng CX, Finley LW, Kim HS, Gius D. SIRT3 is a mitochondrial tumor suppressor: a scientific tale that connects aberrant cellular ROS, the Warburg effect, and carcinogenesis. Cancer Res. 2012;72:2468–2472. doi: 10.1158/0008-5472.CAN-11-3633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayakawa T, Kobayashi Y, Cui X, Hirano S. A new metabolic pathway of arsenite: arsenic-glutathione complexes are substrates for human arsenic methyltransferase Cyt19. Arch Toxicol. 2005;79:183–191. doi: 10.1007/s00204-004-0620-x. [DOI] [PubMed] [Google Scholar]
- He XQ, Chen MG, Lin GX, Ma Q. Arsenic induces NAD(P)H-quinone oxidoreductase I by disrupting the Nrf2 center dot Keap1 center dot CuI3 complex and recruiting Nrf2 center dot Maf to the antioxidant response element enhancer. J Biol Chem. 2006;281:23620–23631. doi: 10.1074/jbc.M604120200. [DOI] [PubMed] [Google Scholar]
- Hoffmann A, Levchenko A, Scott ML, Baltimore D. The IkappaB-NF-kappaB signaling module: temporal control and selective gene activation. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- IARC. An Updating of IARC Monographs 1 to 42. International Agency for Research on Cancer; Lyon, France: 1987. Arsenic. Overall Evaluations of Carcinogenicity. [Google Scholar]
- IARC. Some Drinking-Water Disinfectants and Contaminants, Including Arsenic. International Agency for Research on Cancer; Lyon, France: 2003. IARC Monographs on the Evaluation of Carcinogenic Risks to Humans. [PMC free article] [PubMed] [Google Scholar]
- Igoshin OA, Goldbeter A, Kaiser D, Oster G. A biochemical oscillator explains several aspects of Myxococcus xanthus behavior during development. Proc Natl Acad Sci USA. 2004;101:15760–15765. doi: 10.1073/pnas.0407111101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquet M, Renault G, Lallet S, De Mey J, Goldbeter A. Oscillatory nucleocytoplasmic shuttling of the general stress response transcriptional activators Msn2 and Msn4 in Saccharomyces cerevisiae. J Cell Biol. 2003;161:497–505. doi: 10.1083/jcb.200303030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearns JD, Basak S, Werner SL, Huang CS, Hoffmann A. I kappa B epsilon provides negative feedback to control NF-kappa B oscillations, signaling dynamics, and inflammatory gene expression. J Cell Biol. 2006;173:659–664. doi: 10.1083/jcb.200510155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kensler TW, Wakabayashi N, Biswal S. Cell survival responses to environmental stresses via the Keap1-Nrf2-ARE pathway. Annu Rev Pharmacol Toxicol. 2007;47:89–116. doi: 10.1146/annurev.pharmtox.46.120604.141046. [DOI] [PubMed] [Google Scholar]
- Kitchin KT, Wallace K. The role of protein binding of trivalent arsenicals in arsenic carcinogenesis and toxicity. J Inorg Biochem. 2008;102:532–539. doi: 10.1016/j.jinorgbio.2007.10.021. [DOI] [PubMed] [Google Scholar]
- Kitchin KT, Del Razo LM, Brown JL, Anderson WL, Kenyon EM. An integrated pharmacokinetic and pharmacodynamic study of arsenite action. 1. Heme oxygenase induction in rats. Teratogen Carcin Mut. 1999;19:385–402. [PubMed] [Google Scholar]
- Kligerman AD, Tennant AH. Insights into the carcinogenic mode of action of arsenic. Toxicol Appl Pharmacol. 2007;222:281–288. doi: 10.1016/j.taap.2006.10.006. [DOI] [PubMed] [Google Scholar]
- Kligerman AD, Doerr CL, Tennant AH, Harrrington-Brock K, Allen JW, Winkfield E, Poorman-Allen P, Kundu B, Funasaka K, Roop BC, Mass MJ, DeMarini DM. Methylated trivalent arsenicals as candidate ultimate genotoxic forms of arsenic: induction of chromosomal mutations but not gene mutations. Environ Mol Mutagen. 2003;42:192–205. doi: 10.1002/em.10192. [DOI] [PubMed] [Google Scholar]
- Kobayashi A, Kang MI, Watai Y, Tong KI, Shibata T, Uchida K, Yamamoto M. Oxidative and electophilic stresses activate Nrf2 through inhibition of ubiquitination activity if Keap1. Mol Cell Biol. 2006;26:221–229. doi: 10.1128/MCB.26.1.221-229.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi M, Yamamoto M. Molecular mechanisms activating the Nrf2-Keap1 pathway of antioxidant gene regulation. Antioxid Redox Signal. 2005;7:385–394. doi: 10.1089/ars.2005.7.385. [DOI] [PubMed] [Google Scholar]
- Kojima C, Ramirez DC, Tokar EJ, Himeno S, Drobna Z, Styblo M, Mason RP, Waalkes MP. Requirement of arsenic biomethylation for oxidative DNA damage. J Natl Cancer Inst. 2009;101:1670–1681. doi: 10.1093/jnci/djp414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong ANT, Owuor E, Yu R, Hebbar V, Chen C, Hu R, Mandlekar S. Induction of xenobiotic enzymes by the map kinase pathway and the antioxidant or electrophile response element (ARE/EpRE) Drug Metab Rev. 2001a;33:255–271. doi: 10.1081/dmr-120000652. [DOI] [PubMed] [Google Scholar]
- Kong ANT, Yu R, Hebbar V, Chen C, Owuor E, Hu R, Ee R, Mandlekar S. Signal transduction events elicited by cancer prevention compounds. Mutat Res: Fundam Mol Mech Mut. 2001b;480:231–241. doi: 10.1016/s0027-5107(01)00182-8. [DOI] [PubMed] [Google Scholar]
- Krishna S, Jensen MH, Sneppen K. Minimal model of spiky oscillations in NF-kappa B signaling. Proc Natl Acad Sci USA. 2006;103:10840–10845. doi: 10.1073/pnas.0604085103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumagai Y, Sumi D. Arsenic: signal transduction, transcription factor, and biotransformation involved in cellular response and toxicity. Annu Rev Pharmacol Toxicol. 2007;47:243–262. doi: 10.1146/annurev.pharmtox.47.120505.105144. [DOI] [PubMed] [Google Scholar]
- Le Novere N, Hucka M, Mi HY, Moodie S, Schreiber F, Sorokin A, Demir E, Wegner K, Aladjem MI, Wimalaratne SM, Bergman FT, Gauges R, Ghazal P, Kawaji H, Li L, Matsuoka Y, Villeger A, Boyd SE, Calzone L, Courtot M, Dogrusoz U, Freeman TC, Funahashi A, Ghosh S, Jouraku A, Kim S, Kolpakov F, Luna A, Sahle S, Schmidt E, Watterson S, Wu GM, Goryanin I, Kell DB, Sander C, Sauro H, Snoep JL, Kohn K, Kitano H. The systems biology graphical notation. Nat Biotechnol. 2009;27:735–741. doi: 10.1038/nbt.1558. [DOI] [PubMed] [Google Scholar]
- Li WG, Kong AN. Molecular mechanisms of Nrf2-mediated antioxidant response. Mol Carcinog. 2009;48:91–104. doi: 10.1002/mc.20465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li WG, Yu SW, Kong ANT. Nrf2 possesses a redox-sensitive nuclear exporting signal in the Neh5 transactivation domain. J Biol Chem. 2006;281:27251–27263. doi: 10.1074/jbc.M602746200. [DOI] [PubMed] [Google Scholar]
- Lin S, Del Razo LM, Styblo M, Wang CQ, Cullen WR, Thomas DJ. Arsenicals inhibit thioredoxin reductase in cultured rat hepatocytes. Chem Res Toxicol. 2001;14:305–311. doi: 10.1021/tx0001878. [DOI] [PubMed] [Google Scholar]
- Lindahl T. Instability and decay of the primary structure of DNA. Nature. 1993;362:709–715. doi: 10.1038/362709a0. [DOI] [PubMed] [Google Scholar]
- Liu J, Chen H, Miller DS, Saavedra JE, Keefer LK, Johnson DR, Klaassen CD, Waalkes MP. Overexpression of glutathione S-transferase II and multidrug resistance transport proteins is associated with acquired tolerance to inorganic arsenic. Mol Pharmacol. 2001;60:302–309. doi: 10.1124/mol.60.2.302. [DOI] [PubMed] [Google Scholar]
- Liu YA, Prasad R, Beard WA, Kedar PS, Hou EW, Shock DD, Wilson SH. Coordination of steps in single-nucleotide base excision repair mediated by apurinic/apyrimidinic endonuclease 1 and DNA polymerase beta. J Biol Chem. 2007;282:13532–13541. doi: 10.1074/jbc.M611295200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirsky HP, Liu AC, Welsh DK, Kay SA, Doyle FJ., 3rd A model of the cell-autonomous mammalian circadian clock. Proc Natl Acad Sci USA. 2009;106:11107–11112. doi: 10.1073/pnas.0904837106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naranmandura H, Suzuki N, Suzuki KT. Trivalent arsenicals are bound to proteins during reductive methylation. Chem Res Toxicol. 2006;19:1010–1018. doi: 10.1021/tx060053f. [DOI] [PubMed] [Google Scholar]
- Naranmandura H, Suzuki N, Suzuki KT. Reaction mechanism underlying the in vitro transformation of thioarsenicals. Toxicol Appl Pharmacol. 2008;231:328–335. doi: 10.1016/j.taap.2008.05.005. [DOI] [PubMed] [Google Scholar]
- Qin XJ, Hudson LG, Liu W, Timmins GS, Liu KJ. Low concentration of arsenite exacerbates UVR-induced DNA strand breaks by inhibiting PARP-1 activity. Toxicol Appl Pharmacol. 2008a;232:41–50. doi: 10.1016/j.taap.2008.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin XJ, Hudson LG, Liu WL, Ding W, Cooper KL, Liu KH. Dual actions involved in arsenite-induced oxidative DNA damage. Chem Res Toxicol. 2008b;21:1806–1813. doi: 10.1021/tx8001548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramakrishnan R, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Fifth-generation model for corticosteroid pharmacodynamics: application to steady-state receptor down-regulation and enzyme induction patterns during seven-day continuous infusion of methylprednisolone in rats. J Pharmacokinet Pharmacodyn. 2002;29:1–24. doi: 10.1023/a:1015765201129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiha VFS, Kearns JD, Basak S, Savinova OV, Ghosh G, Hoffmann A. Kinetic control of negative feedback regulators of NF-kappa B/RelA determines their pathogen- and cytokine-receptor signaling specificity. Proc Natl Acad Sci USA. 2009;106:9619–9624. doi: 10.1073/pnas.0812367106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SIMLAB. Simulation Environment for Uncertainty and Sensitivity Analysis, Developed by the Joint Research Centre of the European Commission. 2009. Version 3.2. [Google Scholar]
- Snow ET, Sykora P, Durham TR, Klein CB. Arsenic, mode of action at biologically plausible low doses: what are the implications for low dose cancer risk? Toxicol. Appl Pharmacol. 2005;207:557–564. doi: 10.1016/j.taap.2005.01.048. [DOI] [PubMed] [Google Scholar]
- Sokhansanj BA, Wilson DM. Oxidative DNA damage background estimated by a system model of base excision repair. Free Radic Biol Med. 2004;37:422–427. doi: 10.1016/j.freeradbiomed.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Sokhansanj BA, Wilson DM. Estimating the effect of human base excision repair protein variants on the repair of oxidative DNA base damage. Cancer Epidem Biomarker Prev. 2006;15:1000–1008. doi: 10.1158/1055-9965.EPI-05-0817. [DOI] [PubMed] [Google Scholar]
- Sokhansanj BA, Rodrigue GR, Fitch JP, Wilson DM. A quantitative model of human DNA base excision repair. I. Mechanistic insights. Nucleic Acids Res. 2002;30:1817–1825. doi: 10.1093/nar/30.8.1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soriano C, Creus A, Marcos R. Arsenic trioxide mutational spectrum analysis in the mouse lymphoma assay. Mutat Res: Fundam Mol Mech Mut. 2008;646:1–7. doi: 10.1016/j.mrfmmm.2008.08.014. [DOI] [PubMed] [Google Scholar]
- Stamatelos SK, Brinkerhoff CJ, Isukapalli SS, Georgopoulos PG. Mathematical model of uptake and metabolism of arsenicals in human hepatocytes—incorporation of cellular antioxidant response and threshold-dependent behavior. BMC Syst Biol. 2011;5:16. doi: 10.1186/1752-0509-5-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JA, White CC, Cox DP, Chan JY, Kavanagh TJ, Fausto N, Franklin CC. Distinct Nrf1/2-independent mechanisms mediate As3+-induced glutamate-cysteine ligase subunit gene expression in murine hepatocytes. Free Radic Biol Med. 2009;46:1614–1625. doi: 10.1016/j.freeradbiomed.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiana G, Jensen MH, Sneppen K. Time delay as a key to apoptosis induction in the p53 network. Eur Phys J B. 2002;29:135–140. [Google Scholar]
- Tiana G, Krishna S, Pigolotti S, Jensen MH, Sneppen K. Oscillations and temporal signalling in cells. Phys Biol. 2007;4:R1–R17. doi: 10.1088/1478-3975/4/2/R01. [DOI] [PubMed] [Google Scholar]
- Tsai TYC, Choi YS, Ma WZ, Pomerening JR, Tang C, Ferrell JE. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson JJ, Chen KC, Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- Vodovotz Y, Constantine G, Rubin J, Csete M, Voit EO, An G. Mechanistic simulations of inflammation: current state and future prospects. Math Biosci. 2009;217:1–10. doi: 10.1016/j.mbs.2008.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Sun Z, Chen WM, Li YJ, Villeneuve NF, Zhang DD. Activation of Nrf2 by arsenite and monomethylarsonous acid is independent of Keap1-C151: enhanced Keap1-Cul3 interaction. Toxicol Appl Pharmacol. 2008;230:383–389. doi: 10.1016/j.taap.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe T, Ohta Y, Mizumura A, Kobayashi Y, Hirano S. Analysis of arsenic metabolites in HepG2 and AS3MT-transfected cells. Arch Toxicol. 2011;85:577–588. doi: 10.1007/s00204-011-0710-5. [DOI] [PubMed] [Google Scholar]
- Wu TY, Khor TO, Saw CLL, Loh SC, Chen AI, Lim SS, Park JHY, Cai L, Kong ANT. Anti-inflammatory/anti-oxidative stress activities and differential regulation of Nrf2-mediated genes by non-polar fractions of tea chrysanthemum zawadskii and licorice glycyrrhiza uralensis. AAPS J. 2011;13:1–13. doi: 10.1208/s12248-010-9239-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Andersen ME. Dose response relationship in anti-stress gene regulatory networks. Plos Comput Biol. 2007;3:345–363. doi: 10.1371/journal.pcbi.0030024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Pi J, Woods CG, Andersen ME. A systems biology perspective on Nrf2-mediated antioxidant response. Toxicol Appl Pharmacol. 2009;244:84–97. doi: 10.1016/j.taap.2009.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang YY, Zhou LM. Sirt3 inhibits hepatocellular carcinoma cell growth through reducing Mdm2-mediated p53 degradation. Biochem Biophys Res Commun. 2012;423:26–31. doi: 10.1016/j.bbrc.2012.05.053. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.