The use of interatomic contact areas to quantify discrepancies between RNA 3D models and reference structures

Abstract

Growing interest in computational prediction of ribonucleic acid (RNA) three-dimensional structure has highlighted the need for reliable and meaningful methods to compare models and experimental structures. We present a structure superposition-free method to quantify both the local and global accuracy of RNA structural models with respect to the reference structure. The method, initially developed for proteins and here extended to RNA, closely reflects physical interactions, has a simple definition, a fixed range of values and no arbitrary parameters. It is based on the correspondence of respective contact areas between nucleotides or their components (base or backbone). The better is the agreement between respective contact areas in a model and the reference structure, the more accurate the model is considered to be. Since RNA bases account for the largest contact areas, we further distinguish stacking and non-stacking contacts. We have extensively tested the contact area-based evaluation method and found it effective in both revealing local discrepancies and ranking models by their overall quality. Compared to other reference-based RNA model evaluation methods, the new method shows a stronger emphasis on stereochemical quality of models. In addition, it takes into account model completeness, enabling a meaningful evaluation of full models and those missing some residues.

INTRODUCTION

In recent years, the repertoire of known biological functions that ribonucleic acid (RNA) performs in the cell has greatly expanded (1). Many of these different functions are performed by RNA molecules or their regions adopting complex three-dimensional (3D) structures. Not surprisingly, the interest in RNA 3D structure has also increased considerably. However, the determination of RNA 3D structure using experimental approaches such as X-ray crystallography or nuclear magnetic resonance remains a formidable challenge. Therefore, computational RNA structure prediction methods are rapidly gaining importance (2). A critical component in both the development and comparison of such methods is the ability to evaluate computational models against the experimentally determined reference structure. Only through the effective reference-based model evaluation, one can hope to obtain useful comparison of the performance by different methods. Moreover, the quantitative data regarding discrepancies between models and corresponding reference RNA structures can provide much-needed guidance to methods developers. Therefore, the progress in RNA 3D structure prediction is tightly coupled with the availability of both informative and objective scores that quantify discrepancies between modeled and experimental structures.

The best-known score for measuring the differences between two 3D structures is root-mean-square deviation (RMSD), which reports the average distance between corresponding pairs of atoms after their optimal superposition. However, as an average measure, RMSD is overly sensitive to large local errors. One or two poorly modeled residues may give a misleading impression about the accuracy of the entire model. The recognition of RMSD shortcomings has recently led to introduction of several alternative scores. Global Distance Test (GDT) (3) is one of the scores in the protein field adopted for RNA (4–6). GDT Total Score (GDT-TS) calculates the fraction of residues that are within 1, 2, 4 and 8 Å of the correct position in four independent superpositions and reports the average (7). In contrast to RMSD, GDT-TS focuses on the most accurate parts of the model and is not influenced by outliers. However, the representation of a residue by a single atom (Cα for proteins and C3’ for RNA), while appropriate for proteins, seems to be too coarse-grained for RNA. Moreover, GDT-TS distance cutoffs selected to be meaningful for protein models may not be optimal for RNA. Several new scores, including Interaction Network Fidelity (INF) (8), Deformation Index (DI) (8), Deformation Profile (DP) (8) and RNAlyzer (9), have been developed specifically for RNA 3D structure. INF compares how closely base pairing and base stacking interactions within the reference RNA 3D structure are reproduced in a model (8). DI is RMSD adjusted by INF and has been introduced as an attempt to improve RMSD properties on RNA models. The other two new scores, DP and RNAlyzer, are also based on RMSD. DP highlights dissimilarities between a model and the reference structure at the nucleotide resolution. RNAlyzer works by comparing how well corresponding local neighborhoods in the reference structure and a model agree with each other (9). These new RNA-specific scores significantly expand the list of available model evaluation methods. However, it should be noted that they all, except INF, are based on RMSD and, therefore, inherit at least some of its drawbacks.

In addition to various distance-based approaches, contacts may also be used to compare models with reference structures. Contacts reflect physical interactions in 3D structure and even the simplest representation of contacts (presence/absence) may be quite informative. Checking not only the presence of a contact but also its strength, which reflects the relative interaction intensity, should be even more informative. One way to account for the strength of a contact is to consider its area size (10,11). Recently, applying this idea we developed Contact Area Difference score (CAD-score), a new method for reference-based protein model evaluation (11). CAD-score measures the agreement of contact areas for corresponding residues in the reference structure and a model. Since interatomic contacts reflect physical interactions (e.g. van der Waals (VDW) interactions, hydrogen bonds) independently of macromolecule type, we decided to explore the feasibility of contact area-based approach for RNA. In this study, we report a comparison of contacts in RNA with those in proteins, the adaptation of CAD-score for RNA and tests showing the performance of CAD-score on RNA.

MATERIALS AND METHODS

Definition of CAD-score

CAD-score for RNA can be defined in the same way as for proteins (11). Let (i,j) denote a contact between nucleotides i and j and T_(i,j) their contact area in the reference (target) structure T. Likewise, let M_(i,j) denote contact area between corresponding nucleotides in model M. Now, let G denote all the nucleotide–nucleotide contacts in the reference structure T. CAD-score quantifying the similarity between reference structure T and model M can then be expressed as follows:

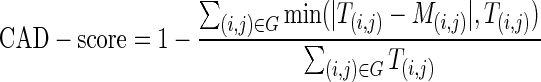(1)

The summation in the numerator is performed over contact area differences with their upper bound equal to the contact area T_(i,j) in the reference structure. In other words, the contact area difference exceeding T_(i,j) is equivalent to the missed contact (M_(i,j) = 0). If the nucleotides, present in the reference structure, are absent in the model, they are treated as if all of their contacts were incorrect. CAD-score values are always within the [0, 1] range, with CAD-score = 1 indicating identical structures. The equation for CAD-score defines global similarity between a model and the reference structure. By fixing i the same equation can be used to compute a local score for an individual nucleotide.

Definition and computation of contact areas

Interatomic contact areas in RNA 3D structure are defined and computed in the same way as described previously for proteins (11). To derive interatomic contacts within the input structure, we use the Voronoi tessellation of 3D balls, where balls correspond to the heavy atoms of VDW radii (12). Two atoms are considered to be in contact with each other if they are neighbors in the Voronoi tessellation and the water molecule cannot fit between them. For each atom, we define a sphere of the radius equal to the sum of VDW radius of the atom and the standard radius of the water molecule (1.4 Å). The entire surface of this sphere (we term it ‘contact sphere') is then partitioned into either interatomic contact areas or solvent accessible areas according to the Voronoi tessellation.

Contact areas between nucleotides are defined by simply grouping their interatomic contact areas. The interatomic contact areas corresponding to covalent bonds between nucleotides are not considered. Atomic resolution of contact areas makes it possible to define contact areas not only for entire nucleotides but also for subsets of nucleotide atoms. We use two standard subsets: the sugar-phosphate backbone and the base. This parallels the definition for proteins where the main chain and the side chain are considered as standard subsets of amino acid residue (11).

Partitioning of base–base contacts into stacking and non-stacking contacts

To partition base–base contacts into stacking and non-stacking ones, we introduced the following definition. Let us consider base i, which is in contact with base j, i≠j. If all atoms (represented as spheres of VDW radii) of base j are entirely on one side of the plane of base i, the base–base contact is defined as the stacking contact. Conversely, if one or more atoms (or part of their VDW spheres) of base j appear on the other side of the plane of base i than the remaining atoms of base j, the contact is defined as non-stacking. The illustration of this simple definition is provided in Figure 1.

Figure 1.

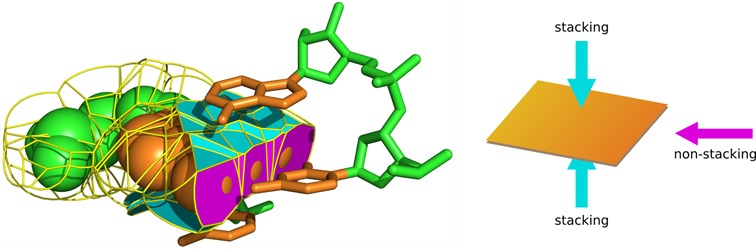
Illustration of the definition of stacking/non-stacking base–base contacts. On the left, a nucleotide in the space-filling representation is shown in contact with the three neighbors. Contacts are represented as faces of the Voronoi cells constrained by the contact spheres. Cyan and magenta indicate stacking and non-stacking contacts, respectively. On the right, the same contacts are shown in schematic representation. Molecular structures in this and other figures were rendered using Pymol.

CAD-score variants

In addition to all-atom CAD-score, it is possible to compute partial CAD-scores. The consideration of two standard subsets of nucleotide atoms, the sugar-phosphate backbone (main chain) and the base (side chain), results in nine CAD-score variants, six of them non-redundant (Figure 2). Further partitioning of base–base contacts into stacking and non-stacking ones results in two additional CAD-score variants.

Figure 2.

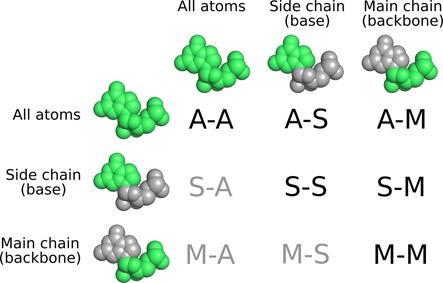
CAD-score variants based on standard subsets of nucleotide atoms. ‘A’ denotes all atoms, 'S', side chain (base), 'M', main chain (backbone). A non-redundant set is indicated in black color.

PDB structure set

For comparative analysis of contacts in RNA and proteins, we used experimentally determined 3D structures that were selected from Protein Data Bank (PDB) (as of 1 June 2013). The selection included only X-ray structures solved at the resolution of 3.0 Å or better. In addition, 30% sequence identity cutoff was applied to the initial selection to make the set non-redundant.

RNA model test set

As a test set we used RNA models and corresponding experimental structures available as part of RNA-puzzles (13), a collective experiment for blind RNA structure prediction. We used the data of all the challenges completed to date, namely 1, 2, 3, 4 and 6. Prior to the analysis, residue numbering and chain identities of raw models were set to match the naming of corresponding nucleotides in experimental structures. No coordinates of any model were modified.

RESULTS

Physical basis of interatomic contacts is the same in both protein and RNA 3D structures. We considered that therefore the contact area-based model evaluation score as defined in its general form (see Materials and Methods) should be also feasible for RNA. On the other hand, considerably different roles of main chain (backbone) and side chain (base) atoms in defining secondary and tertiary structures in proteins and RNA compelled us to perform a more thorough investigation of corresponding contacts.

Base–base contacts dominate RNA 3D structures

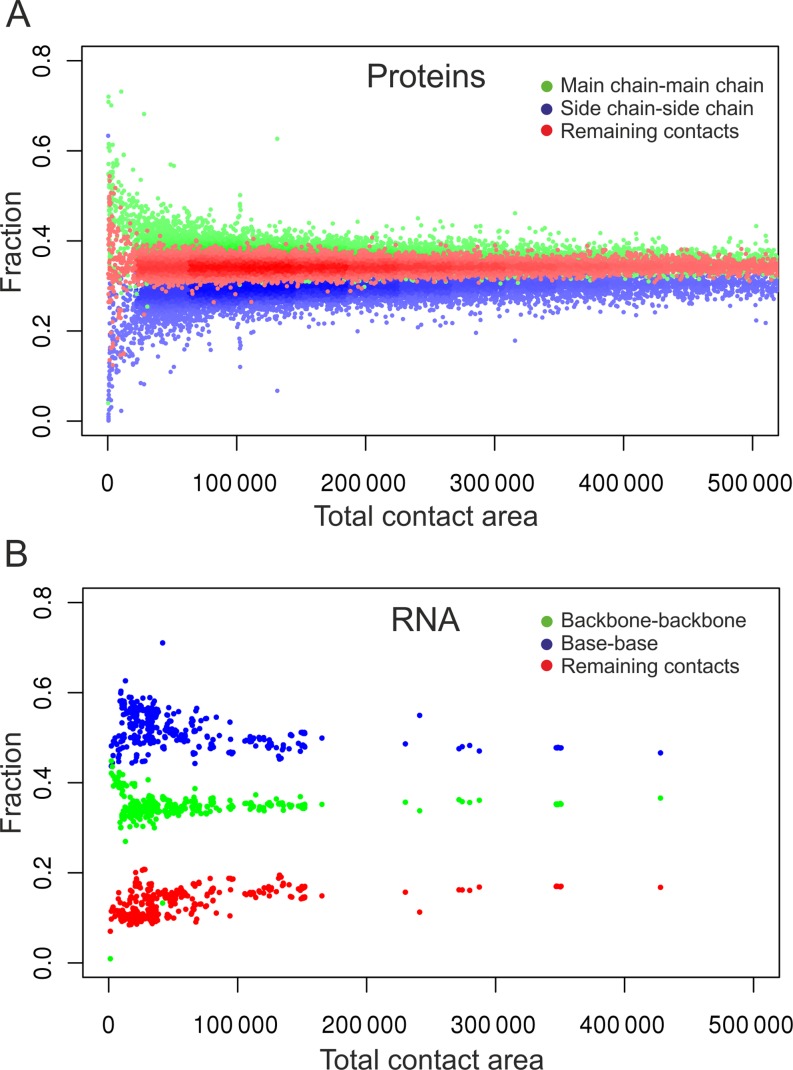
To investigate the contribution of different types of contacts in proteins and RNA, we performed the following analysis. We selected well-resolved non-redundant protein and RNA structures from PDB (see Materials and Methods for details). For every structure, we computed the total area of all contacts as well as fractions of contact area contributed by three types of contacts: (i) main chain-main chain (backbone–backbone), (ii) side chain-side chain (base–base) and (iii) the remaining contacts that consist of side chain-main chain (base-backbone) and main chain-side chain (backbone-base) contacts. The results (Figure 3) show that, except for the smallest structures, the individual contributions to the total contact area by the three contact types are largely independent of the structure size in both proteins and RNA. However, these contributions differ significantly in proteins and RNA. In the case of proteins the contributions by the three types of contacts are well-balanced. Although the share of the main chain-main chain contacts is the largest (36% on average), the fractions of both side chain-side chain and the remaining contacts are comparable (correspondingly 30% and 34% on average). In the case of RNA the picture is dramatically different. Base–base contacts strongly dominate, on average making up about half (49%) of all contact areas. These results indicate that base–base interactions in RNA make a significantly larger impact than side chain-side chain interactions in proteins and therefore merit a more detailed analysis.

Figure 3.

Contribution of the three components of all atom–all atom contacts to the total contact areas in 13336 protein (A) and 445 RNA (B) structures from PDB.

Contact area is an effective means for describing base–base interactions

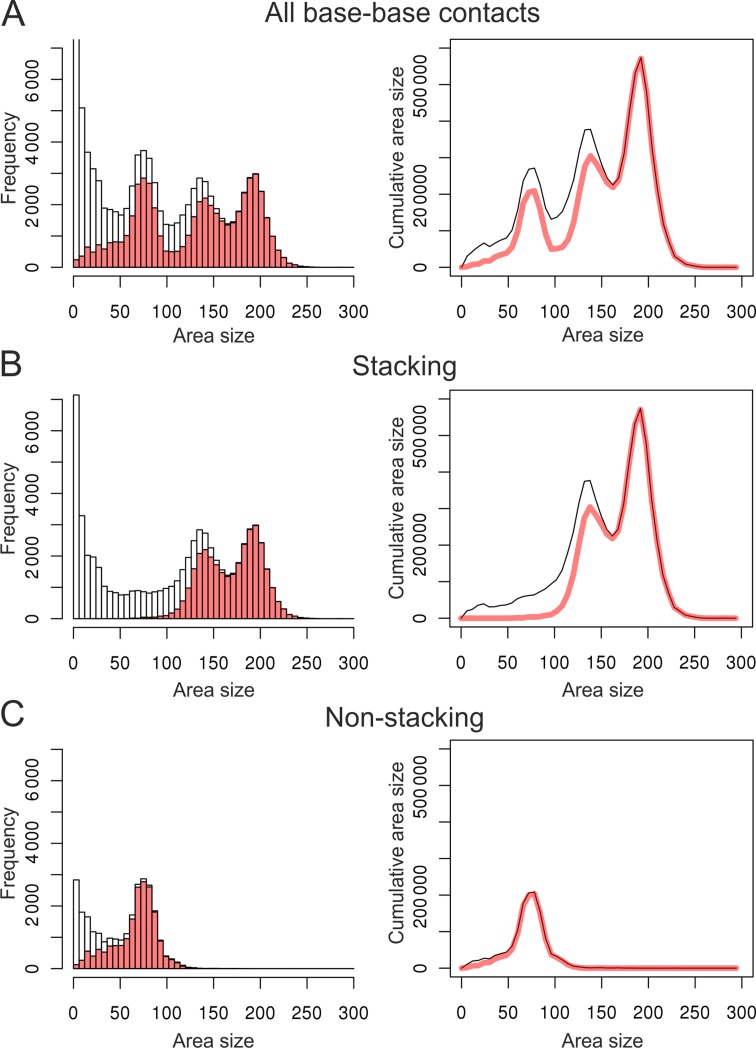
To perform a more detailed analysis of RNA base–base contacts, we divided them into bins according to the size of contact area. The area size corresponds to the physical impact of a contact; therefore, we also looked at the cumulative impact of contacts (frequency multiplied by the area size) for each bin. To compare our results with established approaches, for the same set of RNA structures we identified base–base interactions using MC-Annotate, a widely used RNA annotation method (14). MC-Annotate detects and annotates base–base interactions using a procedure involving both geometric and probabilistic considerations (14,15). Figure 4 shows the comparison of base–base contact data derived using our approach and MC-Annotate. Since MC-Annotate does not compute contact areas, its contact data was generated by our approach according to the MC-Annotate annotations. If the contact frequency is considered (Figure 4A, left), the two approaches show a reasonably close agreement, except for the contacts characterized by small area sizes. Apparently, MC-Annotate does not annotate bases as interacting if they barely contact each other. If the cumulative area size is considered (Figure 4A, right), the agreement is significantly better, since contacts with the negligible area size, despite their abundance, contribute almost nothing to the cumulative impact. One of the conclusions that can be made from this comparison is that the definition of contacts only as binary information (present/absent) may be misleading. A more appropriate way is to also consider contact strength, expressed here as the contact area size.

Figure 4.

Dependence of the base–base contact frequency (left) and cumulative contact areas (right) on the contact area size. The data on all base–base contacts (A), base stacking (B) and non-stacking (pairing) (C) are shown. Gray bars and lines correspond to contacts determined by the approach reported here; red bars and lines correspond to definitions by MC-annotate.

Simple contact-based definition provides a useful approximation of base stacking and base pairing

There are two major types of base–base interactions: base stacking and base pairing. Therefore, it would be desirable to assign at least approximately base–base contacts to one of these two interaction types. We devised an extremely simple definition to partition base–base contacts into the two types (see Materials and Methods; Figure 1) and applied it to the base–base contact data (Figure 4A). If we consider undivided base–base contacts, there are three peaks common to both the frequency plot (Figure 4A, left) and cumulative area plot (Figure 4A, right). According to our definition, the two rightmost peaks correspond to base stacking (Figure 4B) while the leftmost of the three peaks corresponds to non-stacking contacts (Figure 4C). To see how well this partitioning works, we compared it with the classification provided by MC-Annotate. Again, the agreement with MC-Annotate improves if the total cumulative contact area instead of the contact frequency is considered. In particular, stacking interactions characterized by the largest contact areas agree almost ideally. At the same time even for relatively large contact areas there is a visible gap between cumulative values of base stacking curves (Figure 4B). According to our visual analysis at least some of these cases can be assigned to either adjacent or non-adjacent base stacking interactions (examples are provided in Supplementary Figure S1). Many other differences represent inter-strand base–base overlaps. Although these overlaps are not identified as base stacking by MC-Annotate, many of them feature fairly large contact areas indicating important contribution to the interaction network. Quite unexpectedly, although non-stacking contacts (Figure 4C) do not involve special considerations for hydrogen bonding, they very closely recapitulate base pairing interactions defined by MC-Annotate.

In the case of unambiguously classified contacts (there was an agreement between our approach and MC-Annotate), we also looked into the nature of stacked bases and the number of hydrogen bonds in base pairs (Supplementary Figure S2). As might be expected, purine–purine stacking dominates the largest contact areas, while pyrimidine–pyrimidine stacking is at the lower end of stacking contact area size. Purine–pyrimidine stacking shows bimodal distribution. As for base pairs, most of them have two or three hydrogen bonds. Only a small fraction of contacts, both in numbers and in the cumulative area size, correspond to other base pairings.

Since our approach considers all base–base contacts, their division into stacking and non-stacking is, of course, oversimplification. However, even this extremely simple classification is able to provide a useful distinction between most stacking and pairing interactions and thus to reveal model errors specific to each interaction type.

CAD-score combines local contact area differences into the global score

By its nature CAD-score is a local score, as it analyzes discrepancies only within the immediate 3D neighborhood. The most inclusive CAD-score variant quantifies discrepancies that involve entire nucleotides by taking into account all atom–all atom contacts. Additionally defined partial CAD-scores measure other types of discrepancies by considering contacts between various sets of nucleotide atoms (all atoms, backbone or base) or even different types of base–base contacts (stacking, non-stacking). A simple combination of the local discrepancies of each kind produces a global score that summarizes the overall accuracy of a model with respect to the reference structure.

Different CAD-score variants allow addressing different questions. However, for practical applications the variants that consider either all atom–all atom or base–base contacts appear to be the most useful. The usefulness of all atom–all atom CAD-score is understandable, since contacts between all atoms represent the most complete description of the structure. On the other hand, as we have shown, base–base contacts represent the dominant contact fraction in the RNA and are largely responsible for its specific 3D shape. Therefore, the base–base CAD-score and its partial (stacking and non-stacking) scores can be particularly useful in figuring out the cause of discrepancies between the two structures.

Figure 5 shows an example of the evaluation of both local and global accuracy of two RNA-puzzles models (Challenge 3) using major variants of CAD-score. The two models are of different accuracy, appropriately reflected by the ‘summarizing' CAD-score values. Furthermore, both the local discrepancies and the global accuracy values reveal that one of the major reasons of the second model being inferior to the first one is poorly modeled non-stacking (base pairing) interactions. Often, base stacking and non-stacking CAD-score values alone may reveal the source of error and indicate whether the errors are confined to specific regions or dispersed throughout the modeled structure (Supplementary Figure S3).

Figure 5.

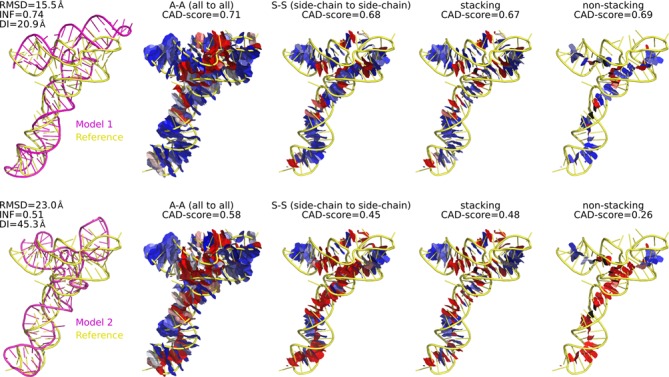
Example of CAD-score evaluation of two models of different accuracy at both global and local levels. Different panels show the contact areas considered by the indicated CAD-score variants. Contacts are represented as faces of the Voronoi cells constrained by the contact spheres. Blue–white–red color gradient represents the accuracy of reproduced contacts (blue—accurate, red—inaccurate).

CAD-score is an effective model ranking index

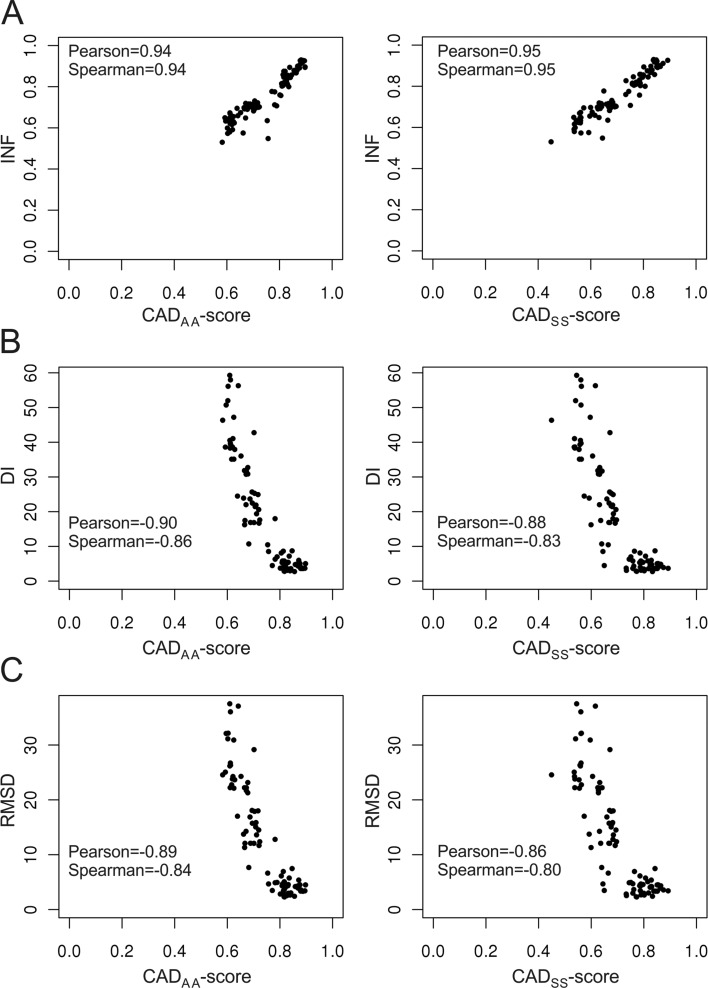
CAD-score efficiently accounts for all the local discrepancies between a model and the reference structure. The question is whether the global score, expressed as a simple combination of local errors, is also effective in ranking models by their overall accuracy. Model ranking is inherently subjective, because of the multiple features that have to be assessed simultaneously. On the other hand, to be considered effective, a new evaluation score should at least roughly agree with the currently used scores. To analyze model ranking by CAD-score, we compared it with the scores used in the RNA-puzzles experiment (13), namely, INF, DI and RMSD. We took all the models generated as part of the RNA-puzzles experiment, scored them against corresponding reference structures and analyzed how well CAD-score correlates with each of the other three scores. It turned out that CAD-score correlates best with INF, less well with DI and least with RMSD. This order does not depend on whether we use Pearson's correlation coefficient, which assumes the linear relationship between scores, or Spearman's ranking correlation coefficient, which makes no such assumption. Figure 6 shows the relationship between two representative CAD-score variants (all atom–all atom and base–base) and INF, DI and RMSD. The correlation between CAD-score and INF reaches as high as 0.95 indicating a good agreement between the two scores. The agreement with DI and RMSD is worse, but correlation values are still fairly high. Diverse models available as part of the RNA-puzzles experiment represent an excellent test set, but their number is relatively small (104 models for 5 reference structures). To make the test more rigorous, we performed the same analysis using over 30 000 models (for 67 reference structures) of the randstr decoy set (6). Although correlation coefficients calculated using the randstr decoy set are slightly smaller, we obtained the same correlation trend: INF > DI > RMSD (Supplementary Table S1, Supplementary Figure S4). Thus, overall results of the correlation analysis indicate that CAD-score model ranking properties are closest to those of INF, reflecting their common focus on the similarity of interactions.

Figure 6.

Relationship between CAD-score and INF (A), DI (B) and RMSD (C). Data is shown for CAD_AA-score (left) and CAD_SS-score (right). For each plot Pearson's correlation coefficients and Spearman's ranking correlation coefficients are indicated.

CAD-score favors physical realism of structural models

Correlation analysis revealed that CAD-score shows a fairly close agreement with other scores, INF in particular. However, inevitably there are cases when the scores disagree. For example, it may be that according to CAD-score, model A is more accurate than model B, but according to another score it is the opposite. An important question is which score to trust in such cases. One way to address this question is to consider physical realism of models, the feature that does not depend on how closely a model agrees with the reference structure (11). The idea is that if we take two scores, the score that shows stronger tendency to select physically more realistic models as the more accurate ones is likely to be more objective.

We asked how CAD-score compares to the other three scores (INF, DI and RMSD) in the light of physical realism of models. For the assessment of physical realism, we used the ‘clash score', ‘bad angles' and ‘bad bonds' as reported by Molprobity (16), a well-known structure validation software suite. We considered one of the two models to be more physically realistic if the model was better according to at least one of the three Molprobity scores and the other two scores did not contradict that (for example, the ‘clash score' was lower, while the values of ‘bad bonds' and ‘bad angles' were identical). To perform this analysis, we used the RNA-puzzles data set. For every reference structure, we compiled all the possible model pairs and identified those in which the relative ranking of models was in conflict according to CAD-score and either INF, DI or RMSD. We then analyzed the same model pairs with Molprobity. It turned out that CAD-score agreed with Molprobity more often than did any of the other three scores (Table 1). As could be expected by the highest correlation values, the smallest number of conflicting rankings was between CAD-score and INF. Nevertheless, the support of CAD-score by Molprobity was stronger than that of INF. In particular, the CAD_SS-score (evaluating base–base contacts) most closely corresponding to INF was supported in about two out of three cases. These results show that CAD-score favors physical realism of models more strongly than either INF, DI or RMSD.

Table 1. Molprobity's ‘judgment' on model pairs with the conflicting assignment of accuracy by CAD-score and either INF, DI or RMSD.

Model pairs with conflicting ranking	Supported by Molprobity
	First score	Model pairs	Second score	Model pairs
	CADAA-score (all atom–all atom contacts)
94	CADAA-score	54 (57%)	INF	40 (43%)
133	CADAA-score	109 (82%)	DI	24 (18%)
145	CADAA-score	122 (84%)	RMSD	23 (16%)
	CADSS-score (base–base contacts)
80	CADSS-score	54 (67.5%)	INF	26 (32.5%)
143	CADSS-score	121 (85%)	DI	22 (15%)
167	CADSS-score	140 (84%)	RMSD	27 (16%)

CAD-score accounts for model completeness

Structural models may not necessarily include all the residues. Most often, difficult-to-predict structural regions are omitted. A reference-based model evaluation score should be able to take this into account properly in order to make a fair comparison.

We asked how well CAD-score, INF, DI and RMSD cope with structural models that are heterogeneous as to their completeness. To this end, we performed the following analysis using RNA-puzzles models. We iteratively truncated each model by 20% (removing the equal number of residues from both 5′ and 3′ ends) and recalculated the scores at every step. We monitored the number of models for which the score has improved after each truncation step. The idea behind this test was that if the removed fragment had at least some correct features, its removal should make the score worse. Even if the removed fragment was completely incorrect, the score of the truncated model should be the same at best.

The results of this test are presented in Table 2. CAD-score (both all atom–all atom and base–base contacts) did not improve even once upon iterative truncation of models. INF has improved seven times, DI—90 times and RMSD—315 times. Thus, it may be concluded that CAD-score is suitable for evaluation of a mixture of complete/incomplete models. INF is not as good as CAD-score, while DI and RMSD could be applied only to models consisting of exactly the same residues.

Table 2. The effect of model truncation on evaluation scores.

Model completeness	80%	60%	40%	20%
	Number of models with the increased score				Total
CADAA-score	0	0	0	0	0
CADSS-score	0	0	0	0	0
INF	0	5	1	1	7
DI	18	19	17	36	90
RMSD	56	88	69	102	315

RNA CAD-score on the web

To make the RNA CAD-score easily accessible, we implemented it as part of the standalone open-source CAD-score software and the corresponding web server (http://www.ibt.lt/bioinformatics/CAD-score/) developed previously for proteins (11). RNA CAD-score is not limited to the analysis and comparison of RNA 3D structures. It can be used for DNA structures as well. The output of the CAD-score calculation for nucleic acids provides both the global similarity score and local errors in a similar manner as for proteins. One of the important differences is that for nucleic acids, base–base contacts are further subdivided into stacking and non-stacking contacts.

DISCUSSION

Our results show that contact area-based approach can be highly effective in quantifying discrepancies between modeled and reference structures not only for proteins but also for RNA. The same general definition of CAD-score can be applied to the both types of macromolecules despite their significant differences.

A number of features make CAD-score attractive as a similarity measure. First of all, since CAD-score is based on comparing contact areas, it does not require structure superposition. Moreover, contact areas not only define physical contacts in the structure, but also indicate their relative strength. Therefore, CAD-score reflects physical interactions that are relevant to the formation and stability of 3D structure. The global CAD-score is constructed by accounting for all the local discrepancies, thereby providing a transparent relationship between local errors and the overall model accuracy. Unlike some other scores such as RMSD or DI, CAD-score has a fixed value range, simplifying the comparison of different models. One other attractive feature of CAD-score is that its definition does not involve any arbitrary parameters. In fact, the only adjustable parameter used in computing CAD-score is VDW radii of heavy atoms.

In addition to CAD-score based on all atoms, a number of partial CAD-score variants can be defined based on subsets of residue atoms. Since RNA and proteins differ considerably, we explored the relative impact of contacts contributed by either main chain (sugar-phosphate backbone) or side chain (base). Given the importance of base–base interactions in the formation and maintenance of both the secondary and the tertiary RNA structures it came as no surprise that base–base contact areas represent by far the largest fraction of all contact areas. Typically, base–base interactions are classified into only two types: base stacking and base pairing. Therefore, we reasoned that it would be useful for CAD-score also to have the ability to consider these two types of interactions individually. We devised an extremely simple partitioning of all base–base contacts into two types (stacking and non-stacking). Our intention was not to substitute RNA annotation algorithms but rather to provide a useful approximation of the two interaction modes. RNA annotation algorithms are selective in defining base stacking and base pairing, while our approach takes into consideration all physical contacts. Thus, it was surprising to see that our approach and the annotation by MC-Annotate show fairly close agreement. It should be emphasized, however, that the agreement is good only when the cumulative contact area and not the contact count is considered. Perhaps most surprising observation was that non-stacking contact areas very closely correspond to base pairings defined by MC-Annotate. Since our definition of stacking/non-stacking contacts does not involve any special treatment of hydrogen bonds, such close agreement suggests that the absolute majority of significant non-stacking contacts originate from base pairs. Disagreement between the contact area approach and MC-Annotate largely coincides with smaller areas of stacking contacts. Many of these cases represent either tiny overlaps of base planes or bases contacting at an angle and therefore do not represent canonical base stacking. However, some large base overlaps ignored by MC-Annotate appear to represent typical base stacking, suggesting that the definition of stacking in current annotation algorithms could be improved. The contact area approach may help to increase the sensitivity of detecting candidate stacking interactions that subsequently could be refined using additional criteria. Overall, the analysis of base–base interactions suggested that our contact-based definition is specific enough to enable CAD-score to focus onto discrepancies related to base stacking and base pairing separately.

No matter how a score is defined, its usefulness depends entirely on the performance. To make a thorough analysis of CAD-score performance, we compared it with the three other scores, INF, DI and RMSD, used for the model assessment during the first round of the RNA-puzzles experiment (13). We made a comparison of scores according to their model ranking properties, the preference of physical realism and the ability to take into account model completeness. These tests revealed that, according to the overall behavior, CAD-score is most similar to INF, less so to DI and least similar to RMSD. Taking into account that DI was designed as an attempt to improve RMSD properties (8), the trend of CAD-score agreement with other scores is exactly what should be expected from an effective score. The similar behavior of CAD-score and INF should not be surprising, since both are assessing local interactions. However, despite the strong correlation between these two scores, CAD-score appears to be superior.

Firstly, CAD-score shows a stronger preference towards more physically realistic models than INF. We believe that this is an important property since the improvement according some reference-dependent score should not come at the expense of stereochemical quality, which is the reference-independent property. The stronger emphasis on physical reality by CAD-score might be due to the fact that CAD-score takes into account all physical contacts, while INF uses only selected set of interactions defined by the structure annotation. Furthermore, CAD-score takes into account contact strength. The penalty for missed contact depends on its area size. Missing important contacts (large contact area) is penalized strongly, while missing contacts with negligible contact area has almost no effect on the score. In contrast, INF considers only the presence or absence of interactions, without taking into account how important they are.

Secondly, CAD-score is able to properly account for the absence of nucleotides or their parts in a model. Although INF, unlike DI or RMSD, shows similar trend, it is not entirely consistent. When all the evaluated models are complete this feature has no bearing on model comparison. However, if models generated by different methods are compared, some heterogeneity of model completeness might be expected. In such cases the ability to account for missing regions would be important.

In summary, we believe that the attractive properties of CAD-score relevant to the RNA 3D structure make CAD-score an important addition to the reference-based RNA structure evaluation methods. Moreover, taking into account the applicability of the method to both nucleic acids and protein 3D structures, CAD-score offers new capabilities for the assessment of 3D structural models of protein–nucleic acid complexes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Research Council of Lithuania [PRO-02/2012].

Conflict of interest statement None declared.