Abstract
To initiate an adaptive immune response, T cells need to interact with dendritic cells (DCs), and the duration of these interactions plays an important role. In vitro and in vivo experiments have generally tried to estimate the required period of opportunity for T cell stimulation rather than the duration of individual T cell-DC interactions. Since the application of multi-photon microscopy (MPM) to living lymphoid tissues, the interactions between immune cells, as well as the duration thereof, can directly be observed in vivo. Indeed, long-lasting interactions between T cells and DCs were shown to be important for the onset of immune responses. However, because MPM imaging is typically restricted to experiments lasting one hour, and because T cell-DC conjugates frequently move into and out of the imaged volume, it is difficult to estimate the true duration of interactions from MPM contact data. Here, we present a method to properly make such an estimate of (the average of) the distribution of contact durations. We validate the method by applying it to spatially explicit computer simulations where the true distribution of contact duration is known. Finally, we apply our analysis to a large experimental data set of T-DC contacts. We identify a mismatch between these data and the model predictions, and investigate possible causes of the mismatch, including small tissue drift during imaging experiments. We discuss in detail how future experiments can be optimized such that MPM contact data will be minimally affected by these factors.
Keywords: Cellular Potts Model, censored data, Immunological Synapse, T cell-DC interactions, T cell motility, multi-photon microscopy
Introduction
Adaptive immune responses start with the activation of T cells of appropriate antigen specificity in secondary lymphoid tissues. Multi-photon microscopy (MPM) experiments applied to living mice or explanted organs have recently begun to visualize the dynamic processes underlying the development of such immune repsonses (Miller et al., 2002; Bousso et al., 2002; Miller et al., 2003, 2004b; Mempel et al., 2004; Hugues et al., 2004; Shakhar et al., 2005; Witt et al., 2005; Celli et al., 2005; Zinselmeyer et al., 2005; Bajénoff et al., 2006a,b; Castellino et al., 2006). This novel technique is becoming more and more influential in immunology. Despite the great technical advances in imaging, the development of techniques to analyse this new type of experimental data on cellular motility and interactions is lagging behind. Taking this analysis to a higher level is essential for quantification of the experiments.
One of the important observations by the MPM research field is that the activation of T cells occurs in several phases (Mempel et al., 2004; Miller et al., 2004a). In the absence of relevant antigen, T cells scan lymph nodes (LNs) for dendritic cells (DCs) presenting cognate antigen. The lymphocytes do this by crawling around at high mean velocities of 9 to 12 μm/min (Miller et al., 2002, 2003; Mempel et al., 2004), and by interacting briefly with DCs. Upon detection of the presence of cognate antigen, the motility of T cells decreases slightly, yet the duration of interactions with DCs remains on the order of minutes (Miller et al., 2004a; Mempel et al., 2004) (generally referred to as “phase one”). A much more pronounced change in the behaviour of T cells takes place after several hours (referred to as “phase two”): Most T cells are then organized in clusters around DCs, and have long-lived interactions with these antigen-presenting cells (APCs) (Mempel et al., 2004; Miller et al., 2004a). It is thought that immunological synapses (IS), i.e., a specific ordering of molecules of similar size in the opposing membranes of T cells and DCs, form during these long-lasting interactions (Monks et al., 1998; Grakoui et al., 1999; Stoll et al., 2002). The exact timing of progressing from phase one to phase two depends on experimental circumstances (Mempel et al., 2004; Miller et al., 2004a; Hugues et al., 2004; Shakhar et al., 2005; Celli et al., 2007). The requirements for the transition are becoming more and more evident lately. It was recently shown that expression of Intercellular Adhesion Molecule-1 (ICAM-1) by mature DCs is needed to establish a population-wide transition to phase two-like interactions (Scholer et al., 2008) (i.e., there are still some long-lasting T-DC interactions in the absence of ICAM-1). Further, the timing of the onset of “phase two” appears to depend on both the antigen dose and the number of DCs that present cognate antigen (Henrickson et al., 2008). Approximately one day after initial T cell transfer, the lymphocytes regain their high motility and start proliferating (“phase three”).
From in vitro and in vivo experiments it is known that the window of opportunity for T cell receptor (TCR) stimulation is a strong determinant for the ensuing T cell differentiation program (Gett et al., 2003; van Stipdonk et al., 2003; Prlic et al., 2006; Celli et al., 2007). Therefore, an important question related to T cell activation is how long the interactions between T cells and DCs last during phase two. Unfortunately, this question is difficult to answer because imaging experiments typically last only 30 to 60 minutes due to current technical constraints of MPM (Germain et al., 2006; Breart and Bousso, 2006) whereas T-DC interactions can be on the order of hours. As a result, a substantial fraction of the observed interactions lasts the entire imaging period. It is thus not possible to directly infer their exact duration, but only that the contact lasted at least as long as the imaging period. Further, the limited observation time entails that in many of the cases either the initiation or the termination of a contact is not observed. For these interactions, we again do not know the exact duration, but only that they must have lasted at least the time that the contact was truly observed. An additional problem is that the size of the imaged volume is relatively limited (Germain et al., 2006), especially with regard to the z-direction which is usually only approximately 50 μm thick (7 T cell diameters). Because even bound cells exhibit some (possibly passive) movement, T-DC conjugates drift in and out of the field of view. When this occurs, this again means that we know only the minimal, rather than the exact, duration of the observed interaction.
There is no clear consensus on how experimental observations on interaction times are presented. One common way is to plot the percentage of remaining contacts as a function of contact duration (e.g., Mempel et al., 2004; Miller et al., 2004a; Garcia et al., 2007). Another frequently used presentation method to compare different experimental settings is by plotting the individual contact durations against the experimental conditions (e.g., Hugues et al., 2007; Scholer et al., 2008). It is often not reported whether only interactions whose exact duration is known are included in these graphs, or whether they also comprise contacts of which only a minimal duration is known. So far, no “complete” data set has been presented in the literature, i.e., a data set containing contact duration information for all interactions, whether their beginning or end was observed, and whether it was the spatial or temporal constraints of imaging that prevented knowing the exact duration of the contact. One can certainly get qualitative insights without making a distinction between all these differently observed interactions. However, lumping these data into a single category fails to deliver an estimate for the average duration of T-DC contacts, possibly leading to severe misjudgements of the contact duration. Indeed, we will show that in order to arrive at a reasonable, quantitative estimate for the contact duration directly from such contact data, it is required to distinguish between the possible observation categories.
In this paper, we take a first step in trying to obtain a quantitative estimate of the true duration of contacts between T cells and DCs. We develop a method to estimate the true distribution of contact times, using as much of the available contact time information available as possible. Our analysis emphasizes that it is important to realize that the total number of observed events depends on both the imaging time and on the size of the imaged volume. Interactions that last longer than the time window of imaging (e.g., one hour) are over-represented in the observed events. For instance, a 2-hour contact that started 1 hour before imaging would be observed, but a 0.5-hour contact that started at the same time would not be observed, i.e., there is technically speaking a left truncation of the data. This gives the impression of a higher average contact time than is in reality the case. In Box 1 the “recipe” for our estimation method is summarized to give an impression of how such a procedure works in practice (this recipe may help to establish future collaborations between theoreticians and experimentalists). We further present a “shortcut approach” that can be used to estimate only the average true contact time rather than the entire distribution of true contact times. We test the analysis using artificial contact data generated by a simplified version of our previously published spatial model of T cell migration (Beltman et al., 2007b,a), and by applying it to brief and long computer simulations (in the latter case the true distribution is known). Finally, we analyze the largest experimental data set on contact times that is currently available (Henrickson et al., 2008). From that analysis, we identify a mismatch between the data and the necessarily simplified scenario we consider in our estimation method. This mismatch seems at least partially due to the problem of drifting of the entire visualized tissue in imaging experiments, especially when the spatial distribution of conjugates is inhomogeneous. We discuss in detail how future experiments can be set up such that MPM contact data will be minimally affected by artifacts due to such tissue drift. Application of our novel method to analyze such data should improve future estimates of the contact duration between immune cells from imaging experiments.
Box 1. recipe to estimate true contact time distribution.
Perform the following steps to obtain an estimate for the true distribution of contact duration:
Acquire the experimental contact data according to a well-defined protocol. For each observed interaction, report the initiation and termination time of observation, as well as to which class the observation belongs (oo, ot, os, to, tt, ts, so, st, or ss). Also report the imaging duration for each observation (this could vary between experiments).
Combine the data from multiple experiments, keeping the event classes of the observations intact.
Examine the data for a time-dependence of the dynamics: Plot the number of conjugates present at each moment in time, and the number of entry, exit, initiation, and termination events versus experimental time. In the ideal case, all these graphs should approximate flat, horizontal lines (see Fig. S4). Furthermore, the number of events in class ot should be apprimately equal to the number of events in class to. If any of these checks is not conform the expectation, try to understand what causes it and if possible try to repair for the artifact.
Decide which event classes you want to use for estimating the true distribution. If you do not trust some of the event classes on the basis of the previous checks for artifacts, discard the data from these event classes altogether.
Choose distribution types (e.g., lognormal distribution) that are to be used in the maximum likelihood procedure. Try multiple distribution types to check whether results depend on it.
Given a certain parameter combination of the chosen underlying true distribution, calculate for each data point the probability density of its occurrence according to equations (2a) to (2f) corrected such that the total number of used events sums up to one. See the Supporting Material for an example calculation of a single contact data point.
Per parameter combination, calculate the likelihood (or log-likelihood) of the entire data set, by multiplying the probability densities for each individual observation (or by adding the logarithm of the probability densities).
Find the parameter combination that results in the maximum (log)-likelikood using an optimization algorithm. To achieve this, the algorithm repeats the previous two steps multiple times.
Plot the observed event distributions along with the expected event distributions according to the fitted parameter combination, and see whether this looks reasonable. Note that this is not very meaningful when there is a small number of data points.
Plot the predicted true distribution and calculate distribution parameters such as the mean contact duration.
Determine 95% CIs for the desired measures (e.g., mean contact time) using bootstrapping. That is, generate new, random data sets by drawing events from all used data points. Observations remain in their original event class, and can be sampled multiple times (i.e., with replacement). The new data sets contain an equal number of points as the original set, but for each event class the number can be different. Repeat the maximum likelihood procedure for each generated data set, and plot distributions of the calculated measures.
Model
The true distribution
Consider the hypothetical scenario that we would not be limited by current MPM technology in terms of a limited time window of observation and a limited field of view. Hence, we would be able to monitor all occurring interactions between cells, and plot the ensuing distribution of contact times. The end result of this thought experiment would approach what we will refer to as the “true distribution”, which is the hypothetical frequency distribution of contact times considering that circumstances are constant over time. Although in reality circumstances might change continuously, considering a constant true distribution of contact times is required to be able to do a quantitative analysis (see also the discussion). The goal of this paper is to make an estimate of the true distribution from a set of observed interactions. To do this, the contact durations of all conjugates are considered to be independent of each other, which seems reasonable given the generally low density of fluorescently labeled cells in imaging experiments. The probability distribution of contact durations (i.e., the true distribution), which is taken to be constant with time, is denoted by g(x). Here, x is the true duration of an interaction (for instance in hours), and g(x) gives the relative frequency of occurrence of new contacts of duration x (i.e., g(x) is a probability density function, and ). The total number of new contacts per hour is given by , where N is the rate of new contact formation (contacts initiated per hour). If required, N could additionally be scaled to represent the rate of new contacts per volume (contacts initiated per hour and per mm3).
Limited time window of imaging
What happens when imaging allows us to only see contacts within a limited time window, for instance one hour (assuming that we are able to image an infinitely large space)? In that case, the initiation of newly formed conjugates could or could not be observed; the same is true for the termination of contacts. Therefore, four event types can occur (Fig. 1a): initiation and termination observed (oo); initiation observed but termination not because imaging ended (ot); termination observed but initiation not because imaging had not yet started (to); and contact present during entire imaging period (tt). The abbreviation codes in brackets consist of two letters, where o stands for “observed” and t means “not observed due to limited time window”. The first letter concerns the initiation of the event, and the second its termination. Technically speaking, a limited time window leads to data that are both left- and right-censored, i.e., the value of an observation is only partially known. Further, the data are left-truncated, because when a contact is initiated before imaging, it could be that its termination also occurs before we start observing. As a consequence, the conjugate would be “missed” entirely, and this happens more often for small contact times than for large contact times. Hence, a limited time window results in a bias in favour of observing long-lasting interactions.
Figure 1. Relation between contact duration and type of observed event when imaging is time-limited.
(a) Cartoon of possible event types for contacts between T cells (red) and DCs (green). Abbreviation codes for these event types are oo, ot, to, or tt (see further explanation in text). (b, c) The event type that is observed depends on the time at which the contact truly started (horizontal axis) relative to the imaging period, which lasts from 0 to T hours. The possible event types also depend on whether the true contact time x is shorter than the imaging period, i.e., x < T (b), or longer than the imaging period, i.e., x > T (c). See text for examples.
Our final goal is to attempt to use the observed events to reconstruct the underlying true distribution. To be able to solve this problem, we first need to know how the time interval that we observe each event during the imaging period (which we will refer to as w) depends on the true interaction time period x. For instance, a contact that was initiated one hour before imaging and that was terminated half an hour after we started imaging (i.e., we would observe it as a to event), has a true contact time of x = 1.5 hours, and an observed contact time of w = 0.5 hours. Note that w is always between 0 and T (where T is the length of the time window of observation, which is typically one hour), because observation time can never exceed the imaging period, whereas the true contact time x can vary from 0 to infinity.
For events of type oo (initiation and termination observed) the relationship between x and w is straightforward: the observation time w is equal to the true contact time x. To observe both the beginning and the end of an interaction, it should fall completely within our window of observation. For instance, when considering a 1-hour observation period, a 45-minute contact (duration x = 0.75) should start somewhere during the first 15 minutes (between time 0 and 0.25), otherwise its termination would not be observed (Fig. 1b). The longer an interaction truly takes, the smaller the probability of observing its beginning and end (i.e., this is proportional to T − x). The expected distribution of these “completely” observed events, referred to as foo(w), therefore becomes (T − w)g(w) (Fig. 2b).
Figure 2. Distributions of different event types.
(a) An example of a true distribution. Contact time (x) is on the horizontal axis, where imaging time is scaled to T hours. (b–d) Accompanying distributions of expected oo, tt, ot, and to events (see explanation in text). The observed contact time (w) is on the horizontal axis. (d) The distribution of events whose initiation or termination is not observed (ot or to) is built up out of two parts, contributed by interactions lasting shorter (denoted by “A”) or longer (denoted by “B”) than the imaging period.
The observed duration of events of type tt (neither beginning nor end observed) is always equal to the length of the imaged time window, i.e., length T. Hence, the “distribution” ftt(w) is 0 for every w except w = T. We need to take into account that only interactions that last at least the duration of imaging (i.e., T) will contribute to tt events (for instance, an event that is observed for 1 hour cannot last 45 minutes in reality). Further, an interaction should start between time T − x and time 0 to observe neither the initiation nor the termination (Fig. 1b). Therefore, the frequency of tt contacts is proportional to (0 − (T − x))g(x) (latest time of start minus earliest time of start to become observed as a tt event), that is, (x − T)g(x). The probability density of tt events at w = T thus equals (Fig. 2c). Importantly, this means that a limited time window leads to tt events becoming over-represented in the observed data. For example, suppose that g(2) = g(10), that is, the probability density in the true distribution is equal for 2-hour and 10-hour interactions. In that case, an interaction of 10 hours will occur as a tt event within the imaging period with a (10 − T)/(2 − T) times higher frequency than a 2-hour interaction (which equals 9 for the frequently used T = 1 hour in experiments). This further entails that the higher the average true contact duration, the larger the fraction of observed tt events will be. This could erroneously give the impression of a higher average contact duration than is in reality the case. Our method of analysis will automatically take this phenomenon into account (i.e., will correct for it).
For events of type ot and to (either initiation or termination observed), we know how long they have lasted minimally (i.e., w). Thus, we should take into account that only contacts lasting longer than w contribute to ot and to events of length w. To derive the distribution of ot events, consider the separate contributions of interactions lasting shorter (x < T) or longer (x > T) than the imaging duration separately: When x < T the frequency of ot interactions (of length x) is proportional to xg(x) (namely, events that start between time T − x and time T, Fig. 1a). The observation time w of these interactions must lie somewhere between 0 and x. Each of these observations is equally likely because for every particular duration new interactions start with an equal probability at any point in time (from the perspective of the entire population of cells that we consider here; it need not be true from the perspective of individual cells as this may depend on the history of a cell). Therefore, the contribution of contacts of length x to ot events of length w is xg(x) divided by x, or simply g(x). Taking only interactions of length x < T into account would thus contribute to the distribution of ot events. Note that this means that this part of the fot distribution will decline with w (Fig. 2d, denoted by “A”), irrespective of the shape of the true distribution. What will be the contribution to fot of interactions lasting longer than the imaging duration (x > T)? In that case, the contribution to ot events is proportional to Tg(x) because for any event that starts in the observation window the end will not be observed (Fig. 1b). These interactions will spread out evenly between observations of length 0 < w < T. Thus, the contribution of contacts of length x to ot events of length w now becomes Tg(x) divided by T, or simply g(x) as before. This predicts that the contribution to the distribution of ot events by interactions of length x > T equals . Note that this part of the ot distribution is equal for different w values (Fig. 2d, denoted by “B”). Summing up the two contributions, the predicted distribution for ot events becomes . The distribution for to events, fto(w), can be derived in a similar fashion, and is equal to fot(w). This symmetry automatically follows from considering a true distribution that does not change over time.
Summarizing, if we would know the true distribution of contact durations (e.g., Fig. 2a), we could predict the distributions of different event types to be (Fig. 2b–d):
| (1a) |
| (1b) |
| (1c) |
| (1d) |
The latter equation gives the total number of events one expects to observe during imaging normalized to the total number of contacts initiated per hour (i.e., it does not count up to one). This equation can alternatively be derived in a more direct manner (see Supporting Material). Further, from equation (1d), one can see that the higher the frequency of contacts longer than the observation window (of length T), the more events will be observed (per hour).
We have so far derived how the expected event distributions depend on the true distribution for the case of imaging limited in time. Before considering how we can solve the reverse problem, i.e., estimate the true distribution from observed distributions, we need to consider the expected event distributions when imaging is not only limited in time, but also limited in space.
Imaging limited in both time and space
Imaging of a limited field of view means that conjugates can enter or leave the imaged volume during observation. Hence, there are now three instead of two possible manners for observing initiation and termination of events, resulting in nine possible event types in total. Apart from the previously discussed oo, ot, to, and tt events, there are now also os, ts, so, st, and ss events (Fig. 3). Here, s means “not observed due to entering or leaving the imaged space” (the meaning of o and t is as before).
Figure 3. Possible event types when imaging is limited in both space and time.
Cartoon of all possible event types for contacts between T cells (red) and DCs (green). Abbreviation codes for these event types are oo, ot, os, to, tt, ts, so, st, and ss (see further explanation in text). Dashed arrows denote movement of conjugates into or out of the imaged volume, and solid arrows denote the initiation or termination of an interaction.
To derive how the distributions for each of these event types depends on the true distribution, we need to describe the dynamics causing conjugates to leave and enter the imaged volume. The most basic way to do this is to define a constant rate (per hour), δ, of leaving and entry of conjugates. Note that this parameter is distinct from the rate of leaving and entry of individual cells that are not in contact: cells will generally leave and enter at a much higher rate than conjugates, but this is irrelevant for our approach. Considering a constant δ will enable us to analytically derive the expected event distributions, thus giving us a baseline prediction to compare with. Note that the simplification does not take into account that δ may in reality depend on the observed contact time and on time itself (i.e., δ is a function of w and of time), as discussed in more detail later. We further need to introduce another time variable, w′, to distinguish from w used in the previous section. The time variable w is the time that a conjugate would have been visible if it had not walked out of view prematurely. Instead, w′ denotes the time interval that a conjugate is observed, taking entry and exit into account, i.e., for each event w′ ≤ w. Because we consider a constant rate of leaving and entry of conjugates, the fraction of conjugates that have not left the imaged volume in a time interval of w′ hours is proportional to e−δw′. Furthermore, the probability density of conjugate leaving at time w′ is to δe−δw′ (i.e., an exponential probability distribution). Using these equations we can derive each of the nine event distributions.
For the derivation of the nine distributions, it helps to look back to the event distributions derived above. For oo, ot, to, and tt events this is most straightforward. Because in these cases conjugates do not walk into or out of view, the time that conjugates are observed, w′, is equal to w. Therefore, the distributions found previously are simply multiplied by the probability that the conjugates have not left during a time interval of w′ hours, i.e., by e−δw′ for oo, ot, and to events, and by e−δT for tt events (because in the latter case w′ = T).
Next consider events of type os (initiation observed, then conjugate walked out of view). These occur when events whose initiation is observed (i.e., the oo and ot events for the case of imaging only limited in time) leave the imaged space after exactly w′ hours. The interactions giving rise to these events must last at least w′ hours. Using equations (1a) and (1b), the expected distribution for os events becomes , which can be simplified to .
The expected distribution of ts events (contact was present when imaging started, then conjugate moved out) can be derived analogously. Interactions that would have been to or tt events when imaging were not limited in space contribute to this distribution. Again, the interactions must last at least w′ hours. Using equations (1b) and (1c), the distribution for ts events becomes ,which simplifies to .
Thus, to derive the distributions for oo, ot, os, to, ts, and tt events, we used the previous derivations for the case when imaging is limited in time but not in space (equations (1a) to (1c)). The distributions for events that are initiated by a conjugate moving into the field of view (so, st, and ss events), however, need to be derived “from scratch” which is much more complicated (shown in the Supporting Material for ss events, which is the most complicated of the derivations). However, note that the distributions for so and st events should be equal to those for os and ts events, respectively. This symmetry is a consequence of our simplification that conjugates enter and leave with a constant rate (irrespective of their spatial position), and that g(x) does not change over time. In summary, the different event types depend on the true distribution as follows:
| (2a) |
| (2b) |
| (2c) |
| (2d) |
| (2e) |
| (2f) |
| (2g) |
As before, the latter equation gives the total number of events one expects to observe during imaging normalized to the total number of contacts initiated per hour (see Supporting Material for the derivation). From this equation one can see that the expected number of events depends on the size of the imaged volume: a small field of view implies a high rate of entering and leaving because conjugates are generally close to one of the borders.
As mentioned previously, the rate of leaving and entry of conjugates (δ) is in reality not constant. One effect playing a role is that conjugates that are close to one of the borders of the field of view are more likely to enter or leave than those far away from it. Thus, conjugates that walk into view are likely to leave again soon afterwards (because they are located close to one of the borders), making δ dependent on observation time w. Below, we will investigate how strongly this phenomenon affects the event distributions, and we will show that the best strategy is to exclude the entry event distributions from the fitting procedure. Finally, the rate of leaving could depend on time itself (which appears to be the case in the experimental data set we analyze below). We later discuss how such a time-dependent δ would affect the expected event distributions.
Maximum Likelihood Estimate for the contact time distribution
Knowing how we can go from true distribution to event distributions, we next need to consider how the inverse problem of reconstructing the true distribution from the event distributions can be approached. A partly non-parametric reconstruction method is discussed in the Supporting Material. However, this approach becomes very complex and observations contribute as entire event classes rather than individually to the reconstructed true distribution (for details, see the Supporting Material). Therefore, we here discuss a maximum likelihood approach where we begin by choosing a particular, parametric form for the true distribution. Because we do not know what form the true distribution has, we will try several options (for the probability density functions that describe the distributions used in the entire paper see the Supporting Material). One natural choice that is often used in biology is the lognormal distribution, which describes a more or less skewed distribution with a long tail (Fig. S1a). We further use a gamma distribution which can describe a similar shape, but is more versatile because depending on its “shape” parameter it can additionally take an exponential-like form (Fig. S1c). By using the gamma distribution we can thus have the fitting algorithm choose which of the two possible forms fits best. Finally, we use a distribution that is the sum of two lognormal distributions (Fig. S1b), because this can describe a peak of brief and a peak of long interactions (which could be the case in reality). For every parameter combination of the chosen distribution g(x), equations (2a) – (2f) can be used to calculate the expected frequency of occurrence of each event type of certain observed length w′. Note that the event distributions need to be rescaled to sum up to one, which is achieved by dividing by the total number of events (equation (2g)). In case only a subset of event classes is being used, equation (2g) is replaced by the sum of the used classes. Hence, for each event that was actually recorded in an experiment, we can calculate the probability density of this specific event, which will depend on the parameter values of the chosen distribution g(x). Multiplying the probability densities for all observed events gives the likelihood for the occurrence of an entire data set of observed events (or analogously adding the logarithm of the probabilities gives the loglikelihood). The parameter values that maximize the likelihood then determine the distribution that fits the data best (given that particular type of distribution). Box 1 shows a summary of the recipe for reconstructing the true distribution. We performed the likelihood maximization procedure in R using the package bbmle (both R and bbmle are available at http://www.r-project.org).
Calculating the average contact duration
After having used the above maximum likelihood approach to estimate the true distribution that underlies a specific data set of event distributions, one can also calculate the accompanying average contact time for the predicted distribution (as we will do below for simulated as well as for experimental data). However, the considerations behind the developed model imply that there also exists an alternative, simple way to estimate the average contact duration (we refer to this as the “shortcut approach”). As explained in the Supporting Information (section “Expected number of observed events”), the number of conjugates one expects to observe at any point in time equals (where N is the number of contacts initiated per hour; because of the symmetry of the considered system this also equals the number of conjugates terminated per hour). Note that the integral is in fact the same as the definition of the average of a probability distribution. Thus, dividing the number of conjugates observed at a specific time point by the number of conjugates one sees initiating (or terminating) per hour provides an estimate for the average contact time. For instance, one could use the number of conjugates at the start of imaging (note that this is equal to the number of events in classes tt, to and ts as is explained in the Supporting Information). However, because the number of conjugates will fluctuate over time even if it remains approximately constant, it is better to use the average number of conjugates over all time points. Furthermore, the estimate can be refined by dividing by the average of the number of conjugates one sees initiating and those that one sees terminating.
As is the case for the event-based approach to estimate the true distribution, the shortcut approach relies on a true distribution that does not change over time, and on a constant rate of leaving and entry of conjugates. It has the advantage that we do not need to choose a particular form for the underlying true distribution. However, one cannot directly visualize how good the estimate is (which is possible in the event-based estimate because one can plot the observed versus fitted event distributions). Furthermore, having an estimate for the entire distribution of contact times is more informative than of only the average contact time, which is especially true when both brief and long interactions occur.
Results
Testing on simulated data
To assess whether the method to estimate the true distribution of contact time gives appropriate results, we need a way to generate artificial contact data for which the true distribution is known. We take two approaches to generate artificial data. First, we use a Monte Carlo approach to generate contact data from a known distribution and split these in the various event classes according to the scenario we consider (see Supporting Information). This ensures that the equations for each of the event distributions we derived are correct (see Supporting Fig. S2).
We next generate artificial contact data using a spatially explicit model of T cell-DC interactions, which allows us to validate our event-based approach in a more realistic setting. For this we use a simplified version of our previously published computer simulations of T cell-DC interactions in lymph nodes using the Cellular Potts Model (CPM) formalism to describe cell motion and cell-cell interactions (Beltman et al., 2007b,a) (for details see the Supporting Information). Briefly, in silico T cells perform a random walk on long time scales yet move persistently in the short term. During their journey they come into contact with in silico DCs that do not move persistently but displace themselves passively, randomly, and slowly, by stochastic membrane fluctuations. Depending on adhesive preferences between T cells and DCs, and on membrane fluctuations, cellular interactions are broken after a variable (i.e., not predetermined) duration. Because the simulations are meant to validate our method to estimate the true distribution of contact times only, we combine multiple simulations with 10 T cells that interact with a single DC in a two-dimensional space that is devoid of other cells (see Fig. S3 and Video S1). In order to approach the true distribution of contact times for a particular parameter setting in such simulations, we need to be able to follow contacts for a long time. Therefore, we first perform very long (100-hour) simulations where we consider a wrapped space that cells cannot leave (note that the latter is required to follow contacts for their entire duration). This strategy allows us to circumvent the time window and spatial window problems. Subsequently, we analyze exactly the same simulations a second time taking both problems into account: The time window problem is reproduced by splitting the 100-hour simulations in 100 simulations of one hour. The spatial window problem is introduced by counting a conjugate that crosses one of the borders as one that is leaving, whereas we consider that conjugate to enter as a “new” one at the other side at the same time. Thus, we have established a system that provides us with artificial contact data (events) that we can apply the proposed method to in order to predict the true contact time distribution. At the same time, performing sufficiently long simulations of contacts between cells in a wrapped space allows us to approach the true distribution, and thus to test the validity of the method.
Using the simulated contact data we first investigate how strongly the entry event distributions are affected by the relatively high probability of leaving for conjugates that have just moved into view. Artificial contact data from representative simulations (at one particular parameter setting for the CPM simulations) are shown in Fig. S4a (histograms).
We fitted all observed events (i.e., including entry events) to a true distribution described by the sum of two lognormal distributions. The resulting fit appears to be very poor for most event distributions (compare solid lines with histograms in Fig. S4a). This is because including the entry events in the fitting procedure leads to an overestimate of δ. Note that despite the poor fit, the prediction of the average contact duration is very accurate (Fig. S4b).
When we use all observed events minus those in which conjugates moved into view to perform the fitting procedure, it is clear that the method gives much more appropriate results than when all event classes are used (Fig. 4a). Furthermore, we are not introducing a bias by leaving out these entry events, as confirmed using the Monte Carlo simulations (see Supporting Information). Therefore, when using the presented model to predict the true contact time distribution, the best strategy is to leave out the entry event data (which is what we will do in the rest of this paper). Note that in that case deviations between observations and fit are still present for os and ts events (Fig. 4a). This is again a consequence of not taking into account that conjugates that are close to the border of the field of view are more likely to leave or enter than those far away from it. Although this phenomenon affects mainly the entry event distributions, the simplification also has a, less pronounced, effect on the os and ts distributions. Newly formed contacts and contacts that were already present at the onset of imaging are equally likely to occur close to, or far away from, the border of the field. Still, those conjugates that have not left after a long time are more likely to be positioned in the centre of the imaged volume than close to the border. Therefore, os and ts events with long observation times occur less often than expected from our analysis, and consequently those with brief observation times more often.
Figure 4. Estimating the contact duration of simulated data.
The sum of two lognormal distributions was fitted to cellular interaction data (excluding entry event data) from spatial simulations using our estimation method (1-hour observation window). (a) The observed distributions (types oo, ot, to, tt, os and ts; see explanation in text) are shown in histograms, along with the maximum likelihood fit (solid lines; filled square in lower rightmost panel). The observed contact time (w′) is on the horizontal axis. (b) The estimated fit (solid line) for the true contact time distribution plotted through a histogram of data from a 100-hour simulation, which approaches the true distribution. The true contact time (x) is on the horizontal axis. The inset shows the fitted distribution (black line) along with fits for 50 random permutations of the simulated data (grey lines). Note the logarithmic scale of the vertical axis. (c) The average contact duration estimated for 1000 random permutations of the simulated data (bootstrap analysis; median of this distribution is 1.45 hours, and the 95% CI is 1.38–1.52 hours) (d) A comparison of the estimated average contact duration (using the event-based approach in upper panel; using the shortcut approach in lower panel) with the true average contact duration. The latter is calculated from the distribution of oo events in 100-hour simulations in which entry and exit is not taken into account. Note that, because the probability of observing these events declines with the duration of the event, to calculate the true average we assign different weights to each event (see main text). Error bars denote 95% CIs (determined with a bootstrap analysis).
The distribution for the true contact time (for one particular parameter setting of the CPM simulations) that is predicted from the observed events in 1-hour simulations using our method is shown in Fig. 4b (solid line). It approximately follows the observed data from the 100-hour simulation (which approaches the true distribution for the particular CPM parameters used), thus demonstrating the validity of our estimation method. Indeed, the estimated average contact duration for the fitted distribution (1.45 hours) is close to the true average observed in the 100-hour simulation (1.47 hours). To find confidence intervals (CIs) for the estimated average contact duration we performed bootstrapping (for details see Box 1). That is, we randomly sample “new” data sets from the simulated data and applied the estimation method to these data sets (inset in Fig. 4b). The result gives an indication for the distribution of the predicted mean contact duration (Fig. 4c).
To see how the estimation method behaves depending on the relative length of the observation window we performed simulations with different average contact times, which was achieved by modifying the adhesion preference between DCs and T cells in the simulations. In simulations with long average contact times, the true distribution (approached by the 100-hour simulation data) becomes clearly bimodal (Fig. S5a), containing both a peak of brief interactions and one of long interactions. Using a distribution that can describe two separate peaks, such as the sum of two lognormal distributions, therefore indeed seems an appropriate choice. Using the event-based method we can very accurately predict the average contact duration (Fig. 4d, upper panel). Note that the shortcut approach to estimate the average contact duration (based on number of conjugates present and number of initiating and terminating conjugates) also results in a very good estimate (Fig. 4d, lower panel). These estimates are clearly much better than the underestimate one would obtain by calculating the average of all observed contact durations (i.e., lumping all events). That procedure is often used in papers investigating contact times, but this generally fails to deliver a good estimate. For instance, for the simulation with a true average contact duration of 5.50 hours, the minimal prediction from the lumped data would give 47.1 minutes, while applying our method gives 5.51 hours. Note that, for the calculation of the true average, even in simulations that are as long as 100 hours, small deviations from the true distribution will occur because the longer an oo event takes, the lower is the probability of observing it (equation (1a)). Therefore, in the calculation of the true average in Fig. 4d we assigned weights to correct for this declining probability, i.e., each oo observation gets weight 1/(1 − w). For instance, in 100-hour simulations an oo event of 10 hours gets a weight of 1/(1 − 10/100) ≈ 1.11. For our 100-hour simulations this gives a small, but non-neglible correction (e.g., without applying the correction we would find an average of 3.69 hours instead of 3.82 hours for one of our simulation settings).
Despite the accurate results for estimation of the average contact time, it appears that the method is not necessarily able to provide a good reconstruction of the location of the peak of long interactions (Fig. S5b). Related to this, estimating the median contact time depends very much on the distribution that is used as a basis for the fit, whereas the average contact time does not. The prediction for that average is very robust because, apart from finding an estimate for g(x), any fit also needs to estimate the integral . This term, which is in fact the definition of the average of a distribution, is part of each event distribution equation because it is present in the total number of events one expects to observe during imaging (see equations (1d) and (2g)). It is intuitive that especially tt events will play an important role in the calculation of the average: These events provide us with no information about the shape (and as a consequence about the median) of the true distribution, yet it is clear that a large number of tt events entails a long average contact duration. From the equation for tt events one can indeed see that it contains the factor (representing a certain fraction of the definition of the average of a probability distribution). Hence, these considerations explain why any good fit of the event distributions of a data set entail an accurate and robust average of that fit. Another consequence of this is that there may be multiple parameter settings that result in a similar likelihood (i.e., the likelihood landscape may contain multiple maxima of similar height). Nevertheless, the average contact times resulting from these different maxima are very similar (Fig. S5b).
Towards estimating the length of in vivo T-DC interactions
Having developed and validated our novel method for the estimation of the average contact duration directly from imaging data, we next wish to make a first step towards estimating the duration of interactions between T cells and DCs in living mice during phase two. We need a large data set in order to be able to meaningfully compare between observed and fitted event distributions. We therefore used the largest MPM data set on cellular interactions that is currently available (Henrickson et al., 2008). The data contains observed T-DC interaction lengths for conditions that vary in the antigen dose presented to T cells. All experiments lasted one hour, and the timing of interactions between cells was judged by studying maximum intensity projection (MIP) movies with the naked eye. Because MIPs rather than 3D projections were used, it was required to define interactions rather stringently: only when T cells show a deviation towards a DC, or when a DC extends towards a T cell, this was counted as an interaction.
To perform our analysis we need to know both the duration of observed interactions and to which event class each interaction belongs. The paper in which these data were originally published (Henrickson et al., 2008) focussed only on the length of the interactions, which was reliably determined in terms of the number of video frames. It was further registered whether the initiation and termination of each event was observed or not, but it was not recorded for what reason an initiation or termination was not observed (due to the limited temporal or to the limited spatial window of observation). Nevertheless, we inferred this from the available time information, because an estimation of the initiation time of each event was also recorded. Our reconstruction of the reason for not observing the termination of an event was therefore imprecise. This demonstrates that it is more efficient to classify the observed events immediately during the analysis of the videos.
Henrickson et al. (2008) defined the immune response to be in phase two during an experiment when the average duration of observed events was at least 30 minutes (half of the imaging time). Note that this average involves observed rather than true interaction lengths, i.e., all nine event classes are lumped together. We combined data (excluding so, st, and ss events for reasons as explained above) from all experiments where the immune response was in phase two according to this definition, and applied our method in order to estimate the true distribution of contact times in phase two.
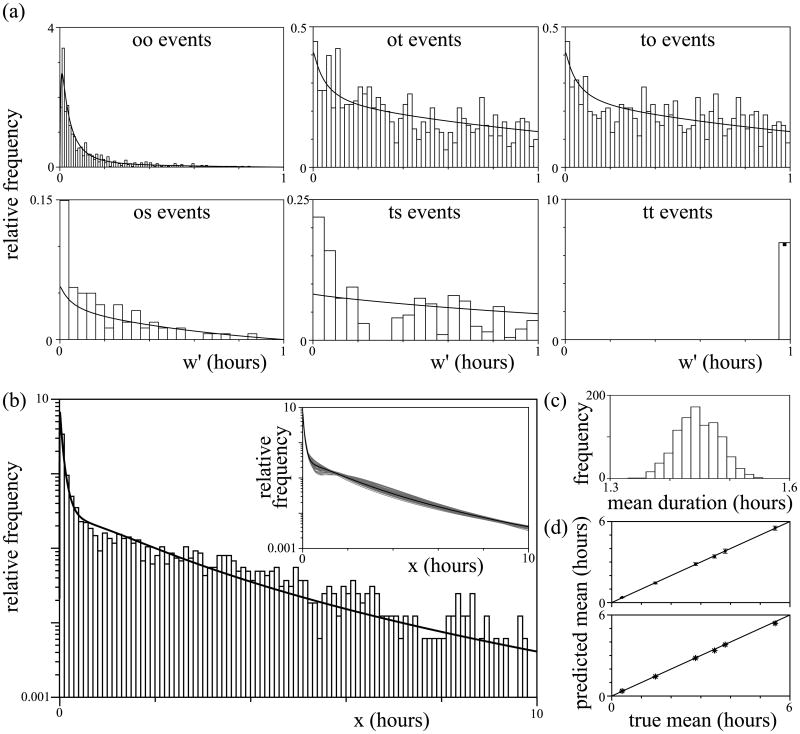
In order to reconstruct the true distribution from the experimental data, we need to choose an underlying distribution for the analysis. As explained before, we tried several distribution types to see whether results depend on this choice (gamma distribution, lognormal distribution, and the sum of two lognormal distributions). Thus, for each of these choices, we found the best fitting true distribution (Fig. 5a). For all three cases the integrals in equations (2a) to (2g) can be solved analytically (not shown, though one example is shown in the Supporting Material). Our analysis predicted an average contact duration of, respectively, 3.26 hours (95% CI of the mean 2.84–3.78), 3.27 hours (95% CI of the mean 2.84–3.78), and 3.28 hours (95% CI of the mean 2.31–3.78) given these three distribution types. Although the CIs of the mean are relatively narrow, the true distribution is predicted to be rather broad (independent of the underlying distribution g(x), Fig. 5a). Further, as expected from our analysis of artificial contact data, the estimated average contact duration hardly depends on the chosen distribution type g(x), i.e., is very robust. The shortcut approach to estimate the average contact duration (based on the number of conjugates present and on the number of initiations and terminations observed per hour) gives a consistent, approximately equal result of 3.42 hours. Although the estimated average appears robust, the observed and fitted event distributions exhibit some clear mismatches (Fig. 5b). According to our derivation of the event distributions, the to, ot, os, and ts distributions should all decline with the observed contact duration, independent of the underlying distribution g(x) (see for instance Fig. 2d). However, this is not the case in the experimental data.
Figure 5. Estimating the duration of contacts between T cells and DCs.
(a) The estimated distribution of contact duration in the “phase two” data from Henrickson et al. (2008). Fits were made using a gamma distribution (solid line), a lognormal distribution (dotted line), and the sum of two lognormal distributions (dashed line). Note the logarithmic scale of the vertical axis. (b) The experimentally observed distributions (types oo, ot, to, tt, os and ts; see explanation in text) are shown in histograms along with the maximum likelihood fit using the sum of two lognormal distributions (solid lines; filled square in lower rightmost panel). The observed contact time (w′) is on the horizontal axis. (c) Each MPM experiment was categorized according to the observed average of all interactions (0–15 min, 15–30 min, 30–45 min, or 45–60 min). The data points from experiments in each category were combined, and the average true contact duration was estimated by applying our analysis (using a lognormal distribution as a basis). Note that the vertical axis has a logarithmic scale, suggesting an exponential relationship between observed and true contact time.
To build up further understanding into what causes these deviations between the experimentally observed and the expected event distributions, we plotted the number of conjugates for which initiation, termination, entry, or leaving was observed over the experimental time course of one hour (Fig. 6; compare Fig. S6 for simulation results). These are all expected to be flat distributions (considering a homogeneous distribution of conjugates and circumstances that remain constant over time). However, initiation events (Fig. 6a) and entry events (Fig. 6c) are observed more often at the beginning than at the end of an experiment. Another deviation is present in the exit events, whose observation becomes more likely over the course of an experiment (Fig. 6d). Note that near the end of the experiments a sudden, large increase in observed exit events occurs. We suspect that part of these events has been classified as a conjugate moving out of view, while in reality the end was not observed due to the limited time window (see classification procedure described above). Although we cannot correct for this potential caveat completely, we investigated what would be the effect on the predicted average contact time when the late-occurring exit events are assumed to have ended due to the limited time window instead. This “correction” did not affect the predicted average contact duration (3.26 hours (95% CI of the mean 2.80–3.79 hours), 3.27 hours (95% CI of the mean 2.83–3.84 hours), and 3.28 hours (95% CI of the mean 1.79–3.80 hours) for gamma distribution, lognormal distribution, and the sum of two lognormal distributions, respectively). Finally, other evidence for a time dependence of the dynamics comes from studying the total number of conjugates observed at each time point (Fig. 6e). This is expected to remain constant over time, yet most conjugates are observed in the middle of the experiments (around the time point 20 minutes).
Figure 6. Deviations between experimental contact data and expectation.
(a–d) The frequency of observed initiation (a), termination (b), entry (c), and leaving (d) events combined per time interval of 6 minutes. (e) The number of observed conjugates present at each moment of experimental time. In all panels data from multiple experiments exhibiting phase two behaviour according to the definition by Henrickson et al. (2008) (see main text) are combined.
How can the presence of these deviations from expectation be explained? Most likely, multiple factors play a role. One obvious issue that may contribute to the found deviations are observation biases. It may for instance be difficult to pick up certain events in the beginning or by the end of an experiment. Furthermore, the stringent definition of interactions that is required because of the use of MIPs rather than 3D projections (i.e., the requirement for deviation of T cell trajectories towards DCs, or DCs extending towards T cells), could lead to biases. In particular, one might miss interactions of up to a few minutes because T cells could walk along a DC in a relatively straight manner for some time before the contact terminates. Hence, this could explain why in the experimental data the ot, to, os, and ts event distributions have lower numbers of observed events for observation times (w′) of up to several minutes than expected on the basis of our derivations.
Probably one of the most important factors giving rise to the found deviations is related to well-known, but rarely mentioned, technical imaging issues such as small tissue drift and tissue swelling as these both change the part of the lymph node that is being imaged. We considered a spatially homogeneous distribution of (cells and) conjugates leading to a constant rate of entry and leaving of contacting cells. We needed to consider that scenario to be able to derive the complex relationship between true contact time distribution and expected event distributions at all. In reality, the cellular distribution in lymph nodes is quite heterogeneous (e.g., newly arrived, adoptively transferred DCs gather around high endothelial venules (Bajénoff et al., 2003; Katakai et al., 2004)). In imaging experiments, one usually searches for a region of interest, i.e., where an appropriate number of T cells and DCs are present (neither too many nor too few). When such relatively dense areas are initially located in the middle of the imaged volume, then small tissue drift will entail a non-constant rate of leaving and entry of conjugates. This could explain the change in the number of exit and entry events (Fig. 6c and 6d) in the course of the experiment (i.e., the observation that the rate of leaving, δ, is time dependent). As a consequence, this can also explain that the frequency of experimentally observed os and ts events does not decline with w′ according to the expectation, but contains a peak at high w′ values. Considering that a significant part of the os and ts events would have been oo, ot, to or tt events if tissue drift were absent from the experiments, the model prediction may not be as bad as it seems at first sight.
To evaluate whether tissue drift is indeed an important factor leading to a poor fit of these experimental contact data, we selected a subset of the experiments that had relatively limited tissue drift. We visually inspected the videos of all phase two experiments, and classified them into five categories varying from low to high tissue drift. We further quantified the amount of tissue drift for each of these experiments by studying the drift of DCs that appeared to be relatively stable (e.g., because of attachment to the network of Fibroblastic Reticular Cells (Lindquist et al., 2004; Sixt et al., 2005)). Out of 33 phase two experiments, a subset of 9 experiments appeared to have low tissue drift in terms of each of those measures (for further details see the legend of Fig. S7). The majority of experiments in this subset also ranked among the phase two experiments that had the most stable number of conjugates over time (in terms of their coefficient of variation, not shown). This correspondence implies that tissue drift is an important factor causing a non-constant rate of leaving/entry. Applying our method to estimate the contact time distribution to this small subset resulted in an estimated average contact time of 4.95 hours (95% CI of the mean 1.72–6.74). Note that the confidence interval is now quite broad because the estimate is based on a limited number of data points, and that the estimate for the entire phase two data set lies within this confidence interval. Importantly, the quality of the fit of the experimental subset improved markedly in comparison with that of the entire data set of phase two experiments (compare Fig. S7 with Fig. 5b). In particular, the peaks that were previously present in the os and ts event distributions (Fig. 5b) are absent in the subset of experiments with limited tissue drift (Fig. S7). Hence, tissue drift is an important factor leading to the mismatches between model prediction and these experimental data. In the discussion we propose ways to minimize the problems associated with tissue drift for analyzing contact data in future experiments.
Another mismatch between model and reality is that in the model we needed to consider a true distribution that does not change over time. This is obviously not true in reality, and one may indeed argue that over time more and more cells will transit to phase two. However, the data suggest that this effect remains relatively limited in comparison to the discrepancy caused by tissue drift: The observed event distributions for ot and to events are not dramatically different which would otherwise be the case (Fig. 5b). Furthermore, more and more cells transiting to phase two would entail a steady increase in the total number of observed conjugates over time. Although there is indeed an initial increase in the total number of observed conjugates at each time point (Fig. 6e), at later times this number drops again, most likely as a consequence of the increase in the number of exit events due to tissue drift. However, note that in the experimental subset that has limited tissue drift, there is a clear difference between to and ot event distributions (Fig. S7), i.e., some cells may not yet have entered phase two in that subset. Thus, in order to estimate the true contact time distribution, future experiments that minimize the effect of tissue drift should also be timed more “in the middle” of phase two (see Discussion).
Considering the deviations between expected and observed event distributions, the average contact duration predicted by our analysis should be viewed as a first attempt of refining our knowledge of contact times during phase two. To also give a first impression of how observed contact duration translates into true contact duration, for each experiment in the entire data set we classified the data in one of four possible categories (according to the average observed duration, 0–15 min, 15–30 min, 30–45 min, or 45–60 minutes). For each category we subsequently determined the predicted average duration by applying the presented method. These averages are, respectively, 8.3 minutes, 46.7 minutes, 3.03 hours, 20.41 hours (Fig. 5c). It should be noted that the latter estimate is unreliable due to its very large 95% confidence interval (8.38 – ∞ hours). Indeed, this wide confidence interval does contain the time period that phase two was estimated to last in total (approximately 12 hours) by imaging at different time points (Mempel et al., 2004; Miller et al., 2004a) (though this was done at only one particular antigen concentration). Again, these estimates should be viewed only as an initial attempt to investigate the relationship between observed and true contact time. Nevertheless, a qualitative, important conclusion from this analysis is that a small increase in observed average contact time leads to a dramatic, approximately exponential, increase in the true average contact time. This implies that there could be a lot of variation between experiments that are currently designated as being in “phase two”.
Discussion
We presented a method to directly estimate from MPM contact data how long interactions between immune cells really last. The analysis uses as much information as possible, i.e., takes into account that conjugates can drift out of the field of view during imaging, and that initiation and termination is often not observed because the experiment had not yet started or ended already. We also presented a “shortcut approach” which can be used to estimate only the average contact time rather than the entire true contact time distribution. Both approaches were validated on contact data generated by in silico simulations (Beltman et al., 2007b,a) (for which the true contact time distribution can be derived from long simulations). The shortcut approach is straightforward to perform and is a significant improvement over the lumped average observed contact time that is often calculated for experimental contact data. Still, care should be taken because one cannot demonstrate that the fit of the data, and thus the estimate, is good. Using the analyses subsequently on a large MPM experimental data set (Henrickson et al., 2008), we here take a first step towards determining a more quantitative estimate on the duration of T cell-DC interactions in living tissues during phase two.
Importantly, our analysis revealed clear deviations between expected and observed event distributions that are at least partially due to experimental tissue drift. This leads to a time-dependent rate of leaving, distinct from the constant rate of leaving we needed to consider in our model (this was required to be able to determine the complex relationship between observed and true contact time at all). Therefore, in order to improve the fit between model and experimental data, the impact of tissue drift on cellular interaction data needs to be minimized in future experiments.
The most important step in preventing tissue drift from making the rate of leaving time-dependent is to increase the size of the imaged volume: The field of view is usually rather large in the x and y direction, but is only a relatively thin slice in the z direction (usually approximately 50 μm or less). When conjugates are clustered in space, small tissue drift thus easily leads to the relatively sudden disappearance of entire clusters via the z dimension. We expect that increasing the imaged volume in this dimension would significantly diminish the effect of tissue drift. A volume with a thickness of just over 100 μm has been imaged before (Allen et al., 2007; Gardner et al., 2008), and would be a great improvement. Another way to assist in circumventing the effect of tissue drift is to choose the exact region of imaging in a more varied manner than is generally done. In particular, we expect that it would help to choose the initial location of the regions where conjugates are clustered in some experiments in the centre, and in others more at the border of the imaged volume. As a result, the time point around which most conjugates drift away would differ for each experiment, and combining all data points would lead to a leaving rate that is approximately constant over time. Note that our method can also be applied to estimate the duration of interactions between other immune cell types. When cellular interactions are quite motile, such as those between B and T cells (Okada et al., 2005; Allen et al., 2007; Mempel et al., 2006), we expect the active movement of conjugates to be a more important factor in determining when a conjugate leaves than the apparent movement due to small tissue drift. Thus, the rate of leaving is likely to be approximately constant over time in this case.
The concept of a true distribution of contact times we considered in this paper is a simplification of T cell-DC interactions occurring during an immune response. Because the contact time distribution in vivo changes over time (due to the different phases), each estimated true distribution should be viewed as an approximation of reality comparable to the concept of a “running average”. Hence, performing future experiments as much as possible “in the middle of” phase two seems the best approach to get a good approximation of the true contact time in this phase. For instance, if phase two at a particular antigen concentration and experimental setting lasts approximately from 8 until 20 hours after antigen administration, then it is best to image around 14 hours. In the data set we analyzed in this paper, an alternative approach was taken (due to the originally different goal of the experiments by Henrickson et al. (2008), which was to assess the time to transition from phase one to phase two for various doses of peptide): An experiment was considered to be in phase two when the average observed interaction time was at least half of the imaging time, i.e., 30 minutes (Henrickson et al., 2008). One might argue that, despite the synchronization of cells at the beginning of the experiment by the administration of an antibody to L-selectin (which prevents further entry of T cells into LNs), at this point many cells might effectively still be in phase one. Indeed, a difficulty in studying phase two is that one tends to think about it in terms of individual cells, but the measurement takes place on the population level. This is a fundamental problem that will persist until imaging techniques are able to follow individual cells for their entire journey through the LN. Our method of analyzing contact durations is also fundamentally unable to solve this problem: it can estimate the distribution of the entire population of cells, but it cannot reconstruct the history or “future” of individual cells.
Another inherent limitation of the method we developed is that, although it can provide us with a rigorous estimate of the average duration of cellular interactions, the prediction of the entire distribution of interactions is not necessarily accurate. The latter is particularly the case when the tail of the distribution is long with respect to the time of observation (for instance, the true distribution peaks at three hours but imaging occurs for only one hour). Because no additional information on the contacts lasting longer than the imaging period is available, multiple combinations of distribution parameters could render a fit with comparable likelihood. Therefore, the distribution fitted in such a scenario should be interpreted as indicative rather than exact. An overall measure of the distribution, such as the average contact duration in this case, is much more robust than the fit of the entire distribution or than the fitted parameter combination (De Boer et al., 2003; Gutenkunst et al., 2007). In order to get a more detailed impression of the entire distribution of T-DC interaction times in phase two, imaging experiments lasting longer than one hour will be essential. Note that a “too long” period of imaging could also lead to wrong estimates because the immune system could again be changing its behaviour (that is, move on to “phase three”). Therefore, if current technical limitations can be overcome, two to four hours of imaging probably would represent a golden mean. Although technical limitations may not allow for huge steps in terms of for instance increased imaging time, it is important to realize that every bit of improvement will help to obtain better estimates of the true contact time distribution.
Obtaining more detailed and more quantitative knowledge about the true distribution of interaction times distribution and/or the average contact time during phase two is important for several reasons. First, the various molecular steps that are involved in the activation of T cells during their interactions with antigen-presenting cells, for instance with respect to the formation of the immunological synapse, are a subject of intense investigation. Having good knowledge of something as elementary as the duration of cellular contacts can be viewed as a prerequisite for the interpretation of such lower-level processes. Furthermore, the longer the average true contact duration between cells, the more difficult it is to observe differences between experiments based on the average observed contact time. This is because the discriminating ability of this lumped average decreases for high true contact times (Fig. 5c). Finally, a comparison between experiments that are performed in different settings (e.g., size of imaged volume, duration of experiment), is impossible if one does not apply a quantitative analysis. In order to improve the potential for comparison between experiments from different laboratories, and for instance of the behaviour of CD4+ and CD8+ T cells, it is further of paramount importance to clearly present the precise protocol used to measure contact duration in the methods section of papers investigating individual cellular contacts, which is currently not the case (see e.g. Mempel et al., 2004; Miller et al., 2004a,b; Hugues et al., 2004; Mempel et al., 2006; Mrass et al., 2006; Tadokoro et al., 2006; Garcia et al., 2007; Celli et al., 2007; Allen et al., 2007; Schwickert et al., 2007; Hugues et al., 2007; Guarda et al., 2007; Henrickson et al., 2008; Scholer et al., 2008; Gardner et al., 2008). It would also be very useful if the analysis of contact data would be (partly) automatized in the future, as is already the case for the tracking of cell movement. Note however that automatic detection methods may also introduce biases.
MPM imaging is increasing our understanding of the development of immune responses. Videos of travelling and interacting immune cells give an intuitive idea about the functioning of our immune system. A wealth of cellular motility and interaction data results from the analysis of these videos. MPM imaging is at its most powerful when these variables can be correlated with functional readouts of immune responses. However, it is of vital importance that the motility and interaction data are analysed thoroughly. As much information as possible should be extracted from the experimental data, and a comparison with theoretical expectations is required to pinpoint, understand, and repair or circumvent potential biases in the data. This calls for the further development of novel techniques of analysis. Experimental work that goes hand in hand with rigorous analysis and modelling represents the most efficient way to proceed in the field of MPM imaging.
Acknowledgments
We thank Veronica Grieneisen, Marianne Jonker, and Vitaly Ganusov for commenting extensively on a previous version of the paper and/or statistical advice. This work was supported by the Netherlands Organisation for Scientific Research (NWO), grants 916.86.080 (JBB) and 016.048.603 (JBB, RJDB), by the National Institutes of Health (NIH), grants AI069259 (UHvA), AI072252 (UHvA), HL07623 (SEH) and a Medical Scientist Training Program (SEH), and by the Osaka University Immunology Frontier Research Center (SEH).
Footnotes
Abbreviations used: MPM, multi-photon microscopy; APC, antigen presenting cell; DC, dendritic cell; LN, lymph node; TCR, T cell receptor.
The authors have no conflicting financial interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allen CD, Okada T, Tang HL, Cyster JG. Imaging of germinal center selection events during affinity maturation. Science. 2007;315(5811):528–31. doi: 10.1126/science.1136736. [DOI] [PubMed] [Google Scholar]
- Bajénoff M, Breart B, Huang AYC, Qi H, Cazareth J, Braud VM, Germain RN, Glaichenhaus N. Natural killer cell behavior in lymph nodes revealed by static and real-time imaging. J Exp Med. 2006a;203(3):619–631. doi: 10.1084/jem.20051474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajénoff M, Egen JG, Koo LY, Laugier JP, Brau F, Glaichenhaus N, Germain RN. Stromal cell networks regulate lymphocyte entry, migration, and territoriality in lymph nodes. Immunity. 2006b;25(6):989–1001. doi: 10.1016/j.immuni.2006.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajénoff M, Granjeaud S, Guerder S. The strategy of T cell antigen-presenting cell encounter in antigen-draining lymph nodes revealed by imaging of initial T cell activation. J Exp Med. 2003;198(5):715–724. doi: 10.1084/jem.20030167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beltman JB, Marée AFM, De Boer RJ. Spatial modelling of brief and long interactions between T cells and dendritic cells. Imm Cell Biol. 2007a;85(4):306–314. doi: 10.1038/sj.icb.7100054. [DOI] [PubMed] [Google Scholar]
- Beltman JB, Marée AFM, Lynch JN, Miller MJ, De Boer RJ. Lymph node topology dictates T cell migration behaviour. J Exp Med. 2007b;204(4):771–780. doi: 10.1084/jem.20061278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bousso P, Bhakta NR, Lewis RS, Robey E. Dynamics of thymocyte-stromal cell interactions visualized by two-photon microscopy. Science. 2002;296:1876–1880. doi: 10.1126/science.1070945. [DOI] [PubMed] [Google Scholar]
- Breart B, Bousso P. Cellular orchestration of T cell priming in lymph nodes. Curr Opin Immunol. 2006;18(4):483–90. doi: 10.1016/j.coi.2006.05.006. [DOI] [PubMed] [Google Scholar]
- Castellino F, Huang AY, Altan-Bonnet G, Stoll S, Scheinecker C, Germain RN. Chemokines enhance immunity by guiding naive CD8+ T cells to sites of CD4+ T cell-dendritic cell interaction. Nature. 2006;440:890–895. doi: 10.1038/nature04651. [DOI] [PubMed] [Google Scholar]
- Celli S, Garcia Z, Bousso P. CD4 T cells integrate signals delivered during successive DC encounters in vivo. J Exp Med. 2005;202(9):1271–1278. doi: 10.1084/jem.20051018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celli S, Lemaitre F, Bousso P. Real-time manipulation of T cell-dendritic cell interactions in vivo reveals the importance of prolonged contacts for CD4+ T cell activation. Immunity. 2007;27(4):625–34. doi: 10.1016/j.immuni.2007.08.018. [DOI] [PubMed] [Google Scholar]
- De Boer RJ, Mohri H, Ho DD, Perelson AS. Estimating average cellular turnover from 5-bromo-2′-deoxyuridine (BrdU) measurements. Proc Biol Sci. 2003;270(1517):849–58. doi: 10.1098/rspb.2002.2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia Z, Pradelli E, Celli S, Beuneu H, Simon A, Bousso P. Competition for antigen determines the stability of T cell-dendritic cell interactions during clonal expansion. Proc Natl Acad Sci USA. 2007;104(11):4553–8. doi: 10.1073/pnas.0610019104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner JM, Devoss JJ, Friedman RS, Wong DJ, Tan YX, Zhou X, Johannes KP, Su MA, Chang HY, Krummel MF, Anderson MS. Deletional tolerance mediated by extrathymic Aire-expressing cells. Science. 2008;321(5890):843–7. doi: 10.1126/science.1159407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Germain RN, Miller MJ, Dustin ML, Nussenzweig MC. Dynamic imaging of the immune system: progress, pitfalls and promise. Nat Rev Immunol. 2006;6(7):497–507. doi: 10.1038/nri1884. [DOI] [PubMed] [Google Scholar]
- Gett AV, Sallusto F, Lanzavecchia A, Geginat J. T cell fitness determined by signal strength. Nat Immunol. 2003;4(4):355–60. doi: 10.1038/ni908. [DOI] [PubMed] [Google Scholar]
- Grakoui A, Bromley SK, Sumen C, Davis MM, Shaw AS, Allen PM, Dustin ML. The immunological synapse: a molecular machine controlling T cell activation. Science. 1999;285(5425):221–7. doi: 10.1126/science.285.5425.221. [DOI] [PubMed] [Google Scholar]
- Guarda G, Hons M, Soriano SF, Huang AY, Polley R, Martin-Fontecha A, Stein JV, Germain RN, Lanzavecchia A, Sallusto F. L-selectin-negative CCR7− effector and memory CD8+ T cells enter reactive lymph nodes and kill dendritic cells. Nat Immunol. 2007;8(7):743–52. doi: 10.1038/ni1469. [DOI] [PubMed] [Google Scholar]
- Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput Biol. 2007;3(10):1871–78. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henrickson S, Mempel T, Mazo I, Liu B, Artyomov M, Zheng H, Peixoto A, Flynn M, Senman B, Junt T, Wong H, Chakraborty A, von Andrian U. T cell sensing of antigen dose governs interactive behavior with dendritic cells and sets a threshold for T cell activation. Nat Immunol. 2008;9(3):282–91. doi: 10.1038/ni1559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hugues S, Fetler L, Bonifaz L, Helft J, Amblard F, Amigorena S. Distinct T cell dynamics in lymph nodes during the induction of tolerance and immunity. Nat Immunol. 2004;5(12):1235–1242. doi: 10.1038/ni1134. [DOI] [PubMed] [Google Scholar]
- Hugues S, Scholer A, Boissonnas A, Nussbaum A, Combadiere C, Amigorena S, Fetler L. Dynamic imaging of chemokine-dependent CD8+ T cell help for CD8+ T cell responses. Nat Immunol. 2007;8(9):921–30. doi: 10.1038/ni1495. [DOI] [PubMed] [Google Scholar]
- Katakai T, Hara T, Lee J, Gonda H, Sugai M, Shimizu A. A novel reticular stromal structure in lymph node cortex: an immuno-platform for interactions among dendritic cells, T cells and B cells. Int Immunol. 2004;16(8):1133–1142. doi: 10.1093/intimm/dxh113. [DOI] [PubMed] [Google Scholar]
- Lindquist RL, Shakhar G, Dudziak D, Wardemann H, Eisenreich T, Dustin ML, Nussenzweig MC. Visualizing dendritic cell networks in vivo. Nat Immunol. 2004;5(12):1243–50. doi: 10.1038/ni1139. [DOI] [PubMed] [Google Scholar]
- Mempel TR, Henrickson SE, von Andrian UH. T cell priming by dendritic cells in lymph nodes occurs in three distict phases. Nature. 2004;427:154–159. doi: 10.1038/nature02238. [DOI] [PubMed] [Google Scholar]
- Mempel TR, Pittet MJ, Khazaie K, Weninger W, Weissleder R, von Boehmer H, von Andrian UH. Regulatory T cells reversibly suppress cytotoxic T cell function independent of effector differentiation. Immunity. 2006;25(1):129–41. doi: 10.1016/j.immuni.2006.04.015. [DOI] [PubMed] [Google Scholar]
- Miller MJ, Safrina O, Parker I, Cahalan MD. Imaging the single cell dynamics of CD4+ T cell activation by dendritic cells in lymph nodes. J Exp Med. 2004a;200(7):847–856. doi: 10.1084/jem.20041236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MJ, Wei SH, Cahalan MD, Parker I. Autonomous T cell trafficking examined in vivo with intravital two-photon microscopy. Proc Natl Acad Sci USA. 2003;100(5):2604–2609. doi: 10.1073/pnas.2628040100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MJ, Wei SH, Cahalan MD, Parker I. T cell repertoire scanning is promoted by dynamics dendritic cell behavior and random T cell motility in the lymph node. Proc Natl Acad Sci USA. 2004b;101(4):998–1003. doi: 10.1073/pnas.0306407101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MJ, Wei SH, Parker I, Cahalan MD. Two-photon imaging of lymphocyte motility and antigen response in intact lymph node. Science. 2002;296:1869–1873. doi: 10.1126/science.1070051. [DOI] [PubMed] [Google Scholar]
- Monks CR, Freiberg BA, Kupfer H, Sciaky N, Kupfer A. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature. 1998;395(6697):82–6. doi: 10.1038/25764. [DOI] [PubMed] [Google Scholar]
- Mrass P, Takano H, Ng LG, Daxini S, Lasaro MO, Iparraguirre A, Cavanagh LL, von Andrian UH, Ertl HC, Haydon PG, Weninger W. Random migration precedes stable target cell interactions of tumor-infiltrating T cells. J Exp Med. 2006;203(12):2749–61. doi: 10.1084/jem.20060710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada T, Miller MJ, Parker I, Krummel MF, Neighbors M, Hartley SB, O'Garra A, Cahalan MD, Cyster JG. Antigen-engaged B cells undergo chemotaxis toward the T zone and form motile conjugates with helper T cells. PLOS Biol. 2005;3(6):1047–1061. doi: 10.1371/journal.pbio.0030150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prlic M, Hernandez-Hoyos G, Bevan MJ. Duration of the initial TCR stimulus controls the magnitude but not functionality of the CD8+ T cell response. J Exp Med. 2006;203(9):2135–43. doi: 10.1084/jem.20060928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholer A, Hugues S, Boissonnas A, Fetler L, Amigorena S. Intercellular adhesion molecule-1-dependent stable interactions between T cells and dendritic cells determine CD8+ T cell memory. Immunity. 2008;28(2):258–70. doi: 10.1016/j.immuni.2007.12.016. [DOI] [PubMed] [Google Scholar]
- Schwickert TA, Lindquist RL, Shakhar G, Livshits G, Skokos D, Kosco-Vilbois MH, Dustin ML, Nussenzweig MC. In vivo imaging of germinal centres reveals a dynamic open structure. Nature. 2007;446(7131):83–7. doi: 10.1038/nature05573. [DOI] [PubMed] [Google Scholar]
- Shakhar G, Lindquist RL, Skokos D, Dudziak D, Huang JH, Nussenzweig MC, Dustin ML. Stable T cell-dendritic cell interactions precede the development of both tolerance and immunity in vivo. Nat Immunol. 2005;6(7):707–714. doi: 10.1038/ni1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sixt M, Kanazawa N, Selg M, Samson T, Roos G, Reinhardt DP, Pabst R, Lutz MB, Sorokin L. The conduit system transports soluble antigens from the afferent lymph to resident dendritic cells in the T cell area of the lymph node. Immunity. 2005;22(1):19–29. doi: 10.1016/j.immuni.2004.11.013. [DOI] [PubMed] [Google Scholar]
- Stoll S, Delon J, Brotz TN, Germain RN. Dynamic imaging of T cell-dendritic cell interactions in lymph nodes. Science. 2002;296:1873–1876. doi: 10.1126/science.1071065. [DOI] [PubMed] [Google Scholar]
- Tadokoro CE, Shakhar G, Shen S, Ding Y, Lino AC, Maraver A, Lafaille JJ, Dustin ML. Regulatory T cells inhibit stable contacts between CD4+ T cells and dendritic cells in vivo. J Exp Med. 2006;203(3):505–11. doi: 10.1084/jem.20050783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Stipdonk MJ, Hardenberg G, Bijker MS, Lemmens EE, Droin NM, Green DR, Schoenberger SP. Dynamic programming of CD8+ T lymphocyte responses. Nat Immunol. 2003;4(4):361–5. doi: 10.1038/ni912. [DOI] [PubMed] [Google Scholar]
- Witt CM, Raychaudhuri S, Schaefer B, Chakraborty AK, Robey EA. Directed migration of positively selected thymocytes visualized in real time. PLOS Biol. 2005;3(6):1062–1069. doi: 10.1371/journal.pbio.0030160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zinselmeyer BH, Dempster J, Gurney AM, Wokosin D, Miller M, Ho H, Millington OR, Smith KM, Rush CM, Parker I, Cahalan M, Brewer JM, Garside P. In situ characterization of CD4+ T cell behavior in mucosal and systemic lymphoid tissues during the induction of oral priming and tolerance. J Exp Med. 2005;201(11):1815–1823. doi: 10.1084/jem.20050203. [DOI] [PMC free article] [PubMed] [Google Scholar]