High-resolution X-ray spectroscopy of rare events: a different look at local structure and chemistry

Abstract

The combination of large-acceptance high-resolution X-ray optics with bright synchrotron sources permits quantitative analysis of rare events such as X-ray fluorescence from very dilute systems, weak fluorescence transitions or X-ray Raman scattering. Transition-metal Kβ fluorescence contains information about spin and oxidation state; examples of the characterization of the Mn oxidation states in the oxygen-evolving complex of photosystem II and Mn-consuming spores from the marine bacillus SG-1 are presented. Weaker features of the Kβ spectrum resulting from valence-level and ‘interatomic’ ligand to metal transitions contain detailed information on the ligand-atom type, distance and orientation. Applications of this spectral region to characterize the local structure of model compounds are presented. X-ray Raman scattering (XRS) is an extremely rare event, but also represents a unique technique to obtain bulk-sensitive low-energy (<600 eV) X-ray absorption fine structure (XAFS) spectra using hard (~10 keV) X-rays. A photon is inelastically scattered, losing part of its energy to promote an electron into an unoccupied level. In many cases, the cross section is proportional to that of the corresponding absorption process yielding the same X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) features. XRS finds application for systems that defy XAFS analysis at low energies, e.g. liquids or highly concentrated complex systems, reactive compounds and samples under extreme conditions (pressure, temperature). Recent results are discussed.

1. Introduction

The interaction of X-rays with matter forms the basis for many techniques to study local structure and chemistry of condensed matter. In this paper, some less established cases are presented, all concerning rare events. Two examples with quite different origin are discussed, namely X-ray fluorescence spectroscopy (XFS) and X-ray Raman scattering (XRS). Despite their fundamental differences, they require almost identical instrumentation and yield similar information. Both phenomena have a quasi-isotropic signal (4π sr) and, besides an intense X-ray source, they demand X-ray optics covering a large solid angle. The required energy resolution depends on the particular problem. The work described here has been performed with a ~1 eV multi-crystal analyzer, covering a total solid angle of up to 0.5% of 4π sr (Bergmann & Cramer, 1998). The experiments were carried out at beamline 10-2 at the Stanford Synchrotron Radiation Laboratory (SSRL) and beamline X-25 at the National Synchrotron Light Source (NSLS). The energy resolution of the incident beam was ~2 eV using Si (1,1,1) monochromators, and the flux was ~10¹¹–10¹² photons s⁻¹.

2. X-ray fluorescence spectroscopy

The X-ray spectrum resulting from atomic fluorescence transitions has been a subject of study for more than a century. Substantial work has focused on identifying lines for elemental analysis and particle characterization, and to serve as detection channels for X-ray absorption spectroscopy (XAS) of dilute systems (Jaklevic et al., 1977). Chemical effects on X-ray spectra have also been studied for a long time; an excellent overview can be found in a book by Meisel et al. (1989). Intense X-ray sources and efficient high-resolution analyzer devices now enable researchers to use XFS for quantitative physical, chemical and structural analysis, including the study of very dilute biological systems with weak fluorescence lines. Transition metals are of particular interest, because they occur in a variety of different chemical states and play an important role in catalytic processes.

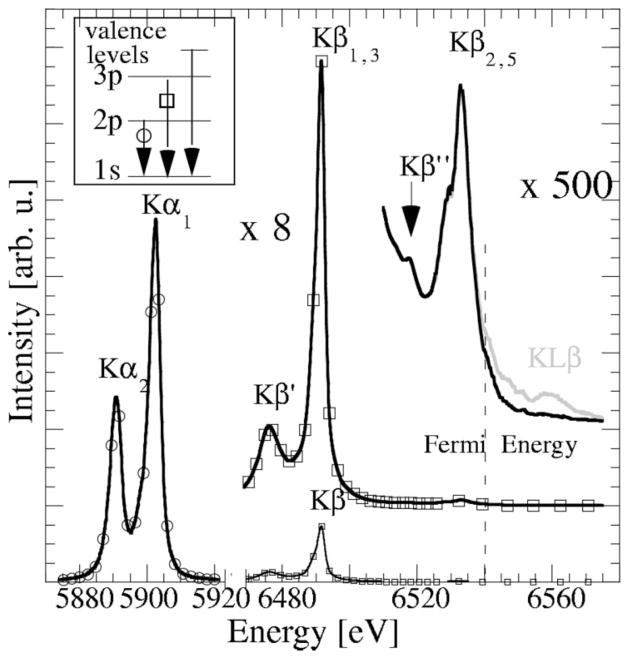
Fig. 1 shows the total Mn K fluorescence spectrum for Mn^IIO, in which the 1s electron is excited well above its binding energy. The spin-orbit split Kα₁/Kα₂ doublet (2p → 1s; circles in Fig. 1) is at the lowest energy, while the eight-times-weaker Kβ main region (3p → 1s; squares in Fig. 1) is at 600 eV higher, split into Kβ_1,3 and Kβ′ through a 3p–3d exchange interaction. At even higher energies, much weaker transitions from valence levels are apparent after magnifying the spectrum by a factor of 500 (black solid line in Fig. 1). The Kβ_2,5 region results from a transition with ligand 2p as well as metal 4p and 3d character. The Kβ″ peak corresponds to ‘interatomic’ or ‘cross-over’ transitions from ligand valence levels. At excitation energies sufficient to create Mn 1s and 2p holes simultaneously, spectral features (grey line in Fig. 1) can be observed, even above the Fermi level indicated by the dashed line in Fig. 1. These lines, referred to as KLβ or Kβ‴, are 3p → 1s transitions with a 2p spectator hole.

Figure 1.

Mn K fluorescence spectrum of Mn^IIO. Inset: schematic transition scheme.

For Mn systems, pioneering work on Kβ_1,3 and Kβ′ lines was performed by Tsutsumi (1959), who used an X-ray tube for excitation and a film to record the spectra. Studies of the weaker spectral regions have been reported by, among others, Koster & Mendel (1970), Tsutsumi et al. (1976), Urch (1979), Mukoyama et al. (1986, 1990), Peng et al. (1994) and very recently by Bergmann et al. (1999). KLβ lines have been extensively studied by, for example, Deutsch et al. (1996), and will not be discussed further in the following.

Using the example of a series of Mn oxides, it will now be discussed how different parts of the spectrum are affected by changes in the local Mn environment.

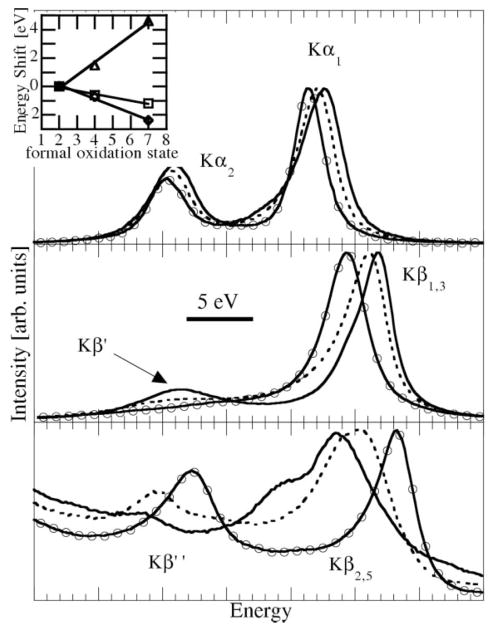
Fig. 2 shows the effects of the oxidation state of Mn on the different K emission features for Mn^IIO (solid lines), Mn^IVO₂ (dashed lines) and KMn^VIIO₄ (circles). Both Kα₁ and Kβ_1,3 shift to lower energies with increasing oxidation state, whereas the Kβ_2,5 and Kβ″ peaks shift in the opposite direction. There are also changes in the shape and relative intensities of all features. The origin of the shifts of Kα₁ and Kβ_1,3 lies in the respective exchange interaction between the 2p and 3p hole with the unpaired 3d electrons. The Slater integrals for 2p–3d are smaller by a factor of 2 to 3 than those for 3p–3d. Consequently, Kα₁ shifts less than Kβ_1,3. The strongest shifts are observed for Kβ_2,5 and Kβ″ where, similar to the K-absorption edge, the shifts are to higher energy with higher oxidation state, reflecting an increase of the 1s binding energy when 3d electrons are removed. This difference indicates how Kβ_1,3 complements the K edge.

Figure 2.

K fluorescence features for Mn^IIO (solid lines), Mn^IVO₂ (dashed lines) and KMn^VIIO₄ (circles) and corresponding shifts of Kα₁ (squares), Kβ_1,3 (diamond) and Kβ_2,5 (triangles).

Kβ_1,3 XFS has been applied to characterize the oxidation states of the Mn cluster in photosystem II, the protein complex responsible for photosynthetic splitting of water and oxygen release (Bergmann et al., 1998; Cinco et al., 1998; Messinger et al., 1998, 2000). In the catalytic Kok cycle, the Mn₄ cluster goes through a series of five S states (S₀–S₄), where a photon is absorbed at each of the first four steps and oxygen is released in the last one (Kok et al., 1970). There is consensus that in each of the first two steps (S₀ → S₁ and S₁ → S₂) one of the four Mn atoms is oxidized (Yachandra et al., 1996). Whether there is a Mn- or ligand-centered oxidation in the third step, S₂→S₃, is a disputed question (Ono et al., 1992; Roelofs et al., 1996; Iuzzolino et al., 1998). Its answer has important consequences with regard to the mechanism of photosynthetic water splitting.

Fig. 3 shows the result of the first-moment analysis^† of samples flashed through the Kok cycle, where zero flash (0F) corresponds to ~95% S₁, 1F to 80% S₂, 2F to 65% S₃, and 3F to 60% S₀, with the remaining populations in each sample in other S states. As seen in the left graph of Fig. 3, the shift between 1F (mostly S₂) and 2F (mostly S₃) is much smaller than in the other cases. For comparison, the inflection-point energies of XANES spectra from the same samples are shown (right side of Fig. 3), yielding a similar result. Both data sets independently suggest a ligand rather than direct Mn oxidation at S₂ → S₃.

Figure 3.

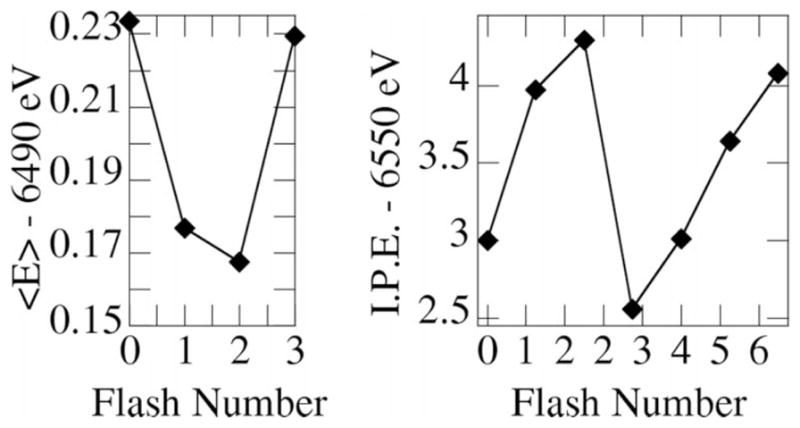
First moment of the Mn Kβ_1,3 peak (left) and the XANES inflection-point energy (right) of photosystem II as a function of flash number. The S₁ state corresponds to zero flashes.

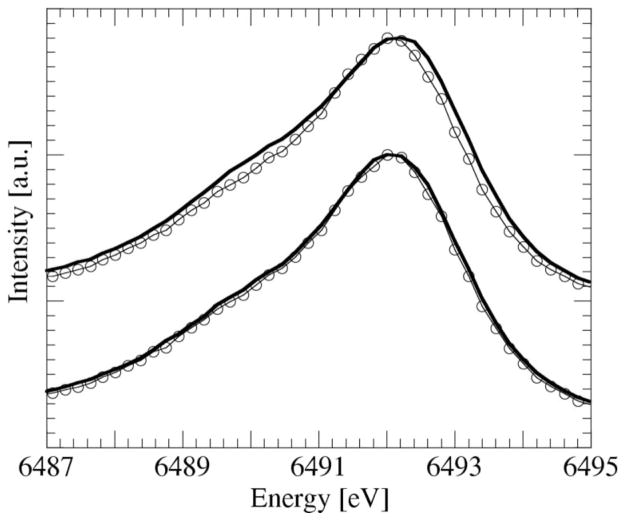
Another biocatalytic mechanism, which is not understood, is the Mn oxidation by bacteria. Manganese is an essential element for all living organisms. Transformations between soluble Mn^II and solid Mn^IV oxides catalyzed by bacteria are tightly coupled to changes in O₂ concentration. Because Mn oxide mineral surfaces are important sites for adsorption of inorganic and organic chemical species, these transformations can have a significant impact on the bio-availability of toxic wastes. Also, there is a scientific need to understand the processes and rates of manganese oxidation in order to interpret anomalous concentrations of manganese oxides in geological rock strata. Mn oxidation catalyzed by bacteria may have some unique mineralogical and chemical biosignatures, which could be used in studies of early life. It may lead to a different sequence of oxidation states, minerals and rates when compared to non-biological manganese oxidation under the same conditions of temperature, Mn^II concentration and time. There has been considerable discussion in the scientific literature over the question of whether the oxidation is a one-electron or two-electron process (Mandernack et al., 1995; Nealson & Tebo, 1988; Tebo et al., 1997). Fig. 4 shows preliminary results of Kβ_1,3 XFS on Bacillus SG-1 spores, isolated from Mn-coated sand grains from marine sediments (Rosson & Nealson, 1982).

Figure 4.

Kβ_1,3 spectrum of crystallites from SG-1 spores after 11.5 h in 10 mM Mn^IICl₂ solution (circles). Top: best fit using only Mn^II and Mn^IV. Bottom: best fit allowing for Mn^II, Mn^III and Mn^IV.

The top spectrum in Fig. 4 shows the Mn Kβ_1,3 peak from minerals precipitated by SG-1 spores after spending 11.5 h in a 10 mM Mn^IICl₂ solution (circles), compared with the best Mn^IIMn^IV simulation, namely a mixture of 78% Mn^IICl₂ and 22% birnessite (solid line). Birnessite is one of the known Mn^IVend products of the reaction. The Mn^IIMn^IV spectrum is clearly too broad. Also allowing for Mn^III yields a much better result (bottom solid line in Fig. 4), where a mixture of 61.5% Mn^IICl₂ and 38.5% (Mn^III)₂O₃ gives the best fit. This result, which still has to be reproduced, indicates that despite its generally high reactivity, Mn^III seems to form as an intermediate in a one-electron two-step catalytic Mn oxidation by SG-1 spores.

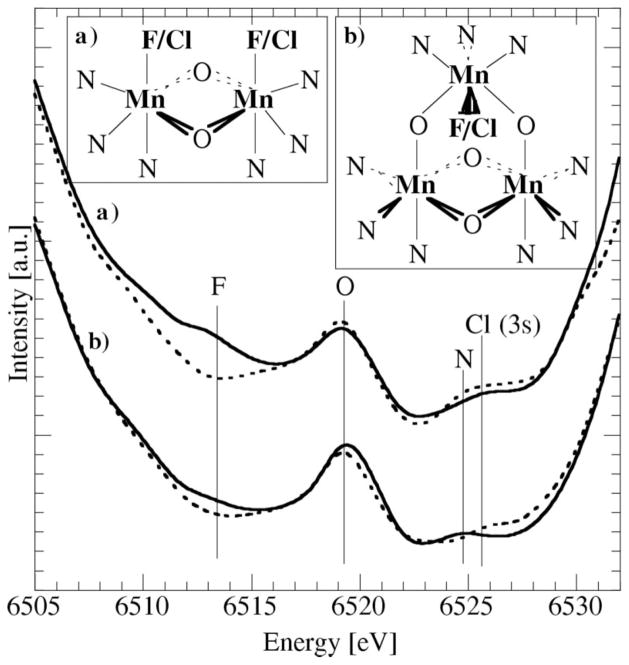
As shown in Fig. 1, the spectral region above Kβ_1,3 contains several features, and in the following, the potential of using Kβ″ to gain detailed structural information is discussed. A recent study of Kβ″ ‘interatomic’ ligand (N, O, F) 2s to Mn 1s transitions (Bergmann et al., 1999) showed that the energy of Kβ″ is very distinct for each ligand (shifting by ~5 eV, respectively) and the intensity of Kβ″ decreases exponentially with the ligand distance. It is estimated that the method can be used to determine distances to ~0.1 Å accuracy if the number of ligands is known. Besides transitions from F, O and N 2s levels, we have observed the ‘interatomic’ transition from the Cl 3s level, which has a binding energy very close to that of the N 2s level. Fig. 5 shows results for model compounds relevant to photosystem II.

Figure 5.

Kβ″ region of two sets of models, where F (solid lines) is interchanged with Cl (dashed lines). Top insets: local Mn structure for each set.

Two sets of models, in which F is interchanged with Cl, are compared: set (a) tacnMn₂O₂F₂/Cl₂-tacn (Fig. 5a), and set (b) [Mn₃O₄(F/Cl)(bpea)₃](ClO₄)₃ (Fig. 5b). The vertical lines in Fig. 5 indicate the energy positions of expected Kβ″ peaks from different ligands. Spectra of compounds containing F and Cl are plotted with solid and dashed lines, respectively. The compounds in the top spectra have one F/Cl per Mn and a clear difference can be seen when comparing the F regions. In the bottom spectra this difference is still apparent but smaller, since only one F/Cl per three Mn atoms is present. Not surprisingly, the O peaks are strongest in all cases. In the top spectra, they result from two short O bonds at each of the di-μ-oxo bridged Mn atoms, and in the bottom spectra from di-μ-oxo and mono-μ-oxo bridges. The spectral region where a Cl feature is expected overlaps with that of the N ligands. The strength of the N peaks is weak, despite the large number of N ligands, since their distances are much longer. It appears that, in both Cl-containing systems, the signal in this region is somewhat stronger, which may be accounted for by a Cl peak. A more quantitative analysis, considering the exact ligand distances, is in progress.

These results demonstrate that with appropriate models and good data quality, Kβ″ features yield detailed structural information. Unlike EXAFS, Kβ″ XFS clearly discriminates between F, O and N, and it can be a useful tool for systems which defy structural analysis using other techniques. Because of the low intensity of Kβ″ (~10⁻⁴ of Kα), work on metalloproteins is difficult. We are currently trying to obtain Kβ″ spectra relevant to the binding of O and Cl to the Mn cluster of photosystem II. Kβ″ studies to determine the nature of the Fe–Ni bridging ligand in hydrogenase enzymes are also underway.

3. X-ray Raman scattering

X-ray absorption spectroscopy (XAS) at edges well below 1 keV encounters experimental difficulties, such as the need for ultra-high vacuum, small probe depth and related problems. Consequently, complex systems, liquids, reactive specimens, or samples under extreme conditions (temperature, pressure) often defy low-energy XAS analysis. Using hard X-rays as a probe avoids these difficulties; inelastic X-ray Raman scattering (XRS) is such a technique, having its largest cross section at low energy transfers (<500 eV).

The phenomenon was first noted in the early 20th century (Smekal, 1923; DuMond, 1933; Sommerfeld, 1936), but because of its weakness and the lack of an appropriate X-ray source, it took more than 20 years before first results were published. Starting with the work on polystyrene by Das Gupta (1959), several experimenters reported the observation of this effect, which was then sometimes called Smekal–Raman scattering (e.g. Das Gupta, 1962; Faessler & Mühle, 1966). However, to indicate how difficult the experiment was, others, including Weiss (1965), were not successful. Finally, the works by Mizuno & Ohmura (1967) and Suzuki (1967) started a series of papers based on experimental and theoretical results, which clearly established the close connection between XRS and XAS. Even until now this technique has not been widely used, and besides some demonstration experiments, there have been very few applications (Watanabe et al., 1996; Bergmann et al., 2000). The reason is mainly the extremely small cross section. From our measurements, we estimate that, for concentrated Li and C compounds, only ~10⁻⁸ of the incident photons contribute to the edge jump in a 1 eV energy slice integrated over 4π sr (this number includes the analyzer and detector efficiency). Even large-acceptance high-resolution analyzers collect only a small fraction of 4π sr (0.5% at our device). Nevertheless, a flux density of 10¹³–10¹⁴ photons s⁻¹ eV⁻¹ (as provided by the most intense undulator beamlines) is sufficient to obtain a good spectrum in a matter of minutes in the most favorable cases, and X-ray Raman spectroscopy may become a routinely used tool in coming years. Besides its bulk sensitivity, X-ray Raman scattering, unlike conventional XAS, is not restricted by the dipole selection rule and has a q dependence, which can reveal the symmetry of unoccupied states (Schülke et al., 1988; Krisch et al., 1997).

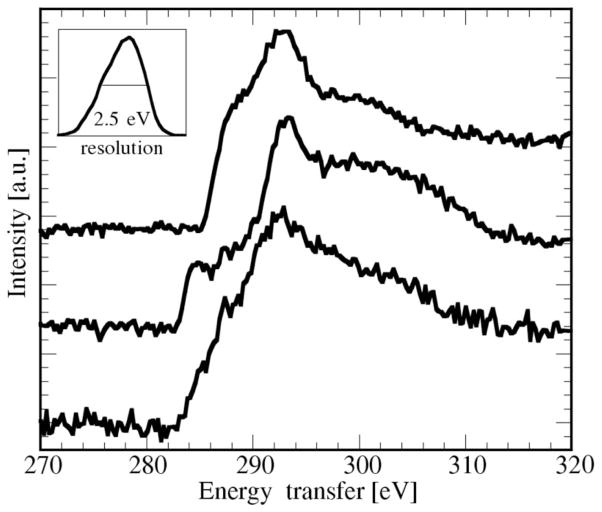
Fig. 6 shows X-ray Raman results on the C edge of asphaltene, compared with coronene and paraffin, representing models of unsaturated and saturated carbon (Bergmann et. al., 2000). Asphaltenes are complex mixtures of hetero-rich aromatic hydrocarbons that are present in solid suspension in crude oils. They dramatically affect the chemical and physical properties of crude oils, limiting the range of processes that can be utilized. Conventional C XANES analysis on these materials suffers from saturation effects when using fluorescence detection and from surface oxidation when using photocurrent or electron yield detection.

Figure 6.

X-ray Raman spectra of (top to bottom): paraffin, coronene and asphaltene. Inset: measured energy resolution of the elastic peak, resulting from convolution of the incident-beam resolution and the analyzer resolution.

The spectrum of paraffin (Fig. 6 top) shows a sharp edge with a shoulder at ~288 eV and the main 1s → σ* resonance at about 293 eV. By contrast, coronene (Fig. 6 middle) shows a 1s → π* resonance at about the same energy, as well as a feature at ~285 eV corresponding to a 1s → π* transition. The asphaltene (Fig. 6 bottom) exhibits a more diffuse edge spectrum, which is not surprising considering the complex mixture of molecules involved in this sample. Nevertheless, low-energy structure can be distinguished that clearly represents 1s → π* intensity, and a fit to the entire XANES region (282–320 eV) suggests a mixture of 50% aromatic and 50% saturated carbon. More qualitative analysis with a large set of models is in progress. Carbon is a prime candidate for XRS, and we are currently also studying Li compounds (batteries) and the oxygen K edge of aqueous systems.

4. Conclusions and outlook

The large increase in brightness provided by new synchrotron radiation facilities makes the rare interaction events of X-rays with matter attractive as a spectroscopic tool. Examples of X-ray fluorescence spectroscopy and X-ray Raman scattering have been discussed. There are countless potential applications of XRS as a bulk-sensitive hard X-ray probe to obtain XAS-type information for low-Z compounds. Both the X-ray sources and the X-ray optics are now available to perform such experiments on a routine basis and we are very optimistic with regard to the future development of this field of research.

Finally, a technique based on XFS, the so-called site-selective XAS, should also be mentioned. Here an XANES or EXAFS spectrum is recorded on a distinct feature of the X-ray fluorescence spectrum. If this feature is unique to a particular site in the system under study (e.g. its spin or oxidation state), the absorption spectrum will reflect the local structure or chemistry of this site. This additional discrimination can largely facilitate the XAS analysis of complex systems. We have obtained excellent Kβ_1,3-detected EXAFS spectra for Fe₄[Fe(CN)₆]₃ (prussian blue), in which the low-spin and high-spin sites could be separated (Glatzel et. al., 2000). The obtained data quality indicates that such studies are also possible on very dilute systems.