Frequency preference in two-dimensional neural models: a linear analysis of the interaction between resonant and amplifying currents

Abstract

Many neuron types exhibit preferred frequency responses in their voltage amplitude (resonance) or phase shift to subthreshold oscillatory currents, but the effect of biophysical parameters on these properties is not well understood. We propose a general framework to analyze the role of different ionic currents and their interactions in shaping the properties of impedance amplitude and phase in linearized biophysical models and demonstrate this approach in a two-dimensional linear model with two effective conductances g_L and g₁. We compute the key attributes of impedance and phase (resonance frequency and amplitude, zero-phase-frequency, selectivity, etc.) in the g_L−g₁ parameter space. Using these attribute diagrams we identify two basic mechanisms for the generation of resonance: an increase in the resonance amplitude as g₁ increases while the overall impedance is decreased, and an increase in the maximal impedance, without any change in the input resistance, as the ionic current time constant increases. We use the attribute diagrams to analyze resonance and phase of the linearization of two biophysical models that include resonant (I_h or slow potassium) and amplifying currents (persistent sodium). In the absence of amplifying currents, the two models behave similarly as the conductances of the resonant currents is increased whereas, with the amplifying current present, the two models have qualitatively opposite responses. This work provides a general method for decoding the effect of biophysical parameters on linear membrane resonance and phase by tracking trajectories, parametrized by the relevant biophysical parameter, in pre-constructed attribute diagrams.

Introduction

A variety of rhythmic oscillations are observed in different areas of the central nervous system which are known to be critical in cognitive and motor behaviors and are thought to emerge from the coordinated activity of the neurons in the respective networks (Gray 1994; Marder and Calabrese 1996; Wang 2010). Recent work suggests that the frequency of the network oscillations may crucially depend on the intrinsic preferred frequencies of the constituent neurons (Lau and Zochowski 2011; Wu et al. 2001; Tohidi and Nadim 2009; Ledoux and N. 2011; Moca et al. 2012; Sciamanna and Wilson 2011). These preferred frequencies arise in different contexts: the ability of a neuron to generate subthreshold oscillations at a particular frequency, often in response to a DC current input (Dickson and Alonso 1997; Lampl and Yarom 1997; Schmitz et al. 1998; Reboreda et al. 2003); the tendency of a neuron to produce subthreshold membrane potential resonance, a peak in the impedance amplitude in response to an oscillatory input current at a non-zero (resonant) frequency (Hutcheon and Yarom 2000); or membrane potential oscillations with zero phase lag in response to an oscillatory current input at a specific frequency (zero-phase-frequency).

The properties of membrane resonance has been investigated in various systems (Gutfreund et al. 1995; Llinás and Yarom 1986; Reboreda et al. 2003; Schreiber et al. 2004; Hu et al. 2002; Reinker et al. 2004; Tohidi and Nadim 2009; Dembrow et al. 2010; Narayanan and Johnston 2007) but the biophysical mechanisms underlying the generation of membrane resonance and its relationship to suprathreshold oscillations are not well understood (Richardson et al. 2003). Membrane resonance results from a combination of low- and high-pass filter mechanisms that also require a negative feedback effect (Hutcheon and Yarom 2000). The passive membrane currents typically act as a low-pass filter, and the so-called resonant voltage-gated currents oppose voltage changes at low frequencies and act as a high-pass filter, thus creating a preferred frequency band. Other voltage-gated ionic currents, labeled amplifying currents, do not produce resonance but generate a positive feedback effect that amplifies voltage changes and hence make existing resonance more pronounced (Hutcheon and Yarom 2000).

Although many studies have examined the impedance amplitude, much less attention has been paid to the phase of impedance which determines the phase of the subthreshold voltage response to oscillatory input currents (Richardson et al. 2003). In a linear approximation, as the amplitude of the oscillatory input increases, the phase of the output determines the phase at which the neuron first reaches threshold. This provides a first-order measure of the spiking phase of the neuron with respect to the input. For linear RLC circuits in series, this phase is zero at the resonant frequency. On the other hand, for RLC circuits in parallel, such as neural circuits, the zero-phase and the resonant frequencies do not necessarily coincide. We refer to the phase corresponding to the resonant frequency as the resonant phase, to the occurrence of a zero-phase voltage output at a positive input frequency as the zero-phase-frequency (f_phase). Although f_phase is often measured experimentally (Gutfreund et al. 1995) and its importance for synchronization has been explored (Fuhrmann et al. 2002), the mechanisms underlying the occurrence of the zero-phase-frequency in biophysical neuronal systems have not been carefully investigated.

It is clear that the parameters of resonant and amplifying ionic currents shape the impedance and phase profiles but the relationship between these factors is far from intuitive. For instance, as we show in this study, increasing the maximal conductance of a so-called resonant current may lead to an increase or decrease of the maximal impedance value depending on the properties of this ionic current. As such, the characterization of the impedance and phase profiles (and the corresponding membrane resonance frequency and zero-phase-frequency) in terms of the properties of the ionic current parameters can provide valuable information on how interactions among biophysical properties of neurons may lead to emergent preferred frequencies.

The existence of subthreshold oscillations implies the presence of an intrinsic time scale in the neuron that is comparable in magnitude to the subthreshold oscillation period. The resonant frequency, on the other hand, reflects an emergent time scale which is a property of the interaction between the neuron and the input it receives. Intrinsic subthreshold oscillations and subthreshold resonance are related (Lampl and Yarom 1997) but are not equivalent phenomena. Linear models, for instance, may exhibit one but not the other (Richardson et al. 2003). Similarly, emergent time scales may be different from the neuron's intrinsic time scale, and are expected to be more relevant in the communication of subthreshold activity to the spiking and network activity. For instance, with large enough DC current, spikes are more likely to occur at the subthreshold oscillation peaks, whereas, with increased amplitude levels of an oscillatory input, spikes are more likely to occur at the resonant phase and inherit the resonant frequency.

In this paper we investigate the biophysical mechanisms underlying the emergence of the resonance and zero-phase-frequencies in two-dimensional models. In particular, we examine the role that different ionic currents and their associated time constants play in determining the resonant and zero-phase-frequencies and in shaping other relevant properties of a neuron's voltage response to oscillatory inputs. Our study consists of two parts. First we investigate the basic mechanisms of generation of resonance and zero-phase-frequency in a reduced two-dimensional linear model with two effective dimensionless conductances, a leak conductance g_L and a “resonant” conductance g₁ (Richardson et al. 2003). This reduced system represents a linearization of a non-dimensionalized two-variable conductance-based model. We construct diagrams of the basic attributes (resonant and zero-phase-frequencies, amplitude, etc.) of the impedance and phase profiles in the g_L − g₁ parameter space. We then investigate the effect of g_L and g₁ on these attributes by exploring changes in their properties along horizontal (constant g₁) and vertical (constant g_L) lines in the corresponding attribute diagrams. In these reduced linear models, the kinetics of the resonant gating variable is not explicit but included in the effective conductances (Richardson et al. 2003). Additionally, we show that the effect of the corresponding time constants can be examined in the attribute diagrams along oblique lines in the g_L − g₁ parameter space.

In the second part of the study we use the attribute diagrams mentioned above to investigate the mechanisms of generation of resonance and zero-phase-frequency in two-dimensional linearized conductance-based models. We consider two types of models, each with a resonant current. In the first model, the resonant current is a hyperpolarization-activated inward current I_h (Haas and White 2002; Hutcheon et al. 1996; Schreiber et al. 2004). In the second model, the resonant current is a slow potassium current I_Ks activated by depolarization (Gutfreund et al. 1995). In each model we also examine the effect of a fast amplifying current I_P (Haas and White 2002; Hutcheon et al. 1996; Schreiber et al. 2004; Gutfreund et al. 1995) considered here with instantaneous kinetics. The study of the interaction between two distinct resonant currents with slow dynamics leads to models with at least three variables and is outside the scope of this paper. Changes in the biophysical conductances associated with these currents are reflected in changes in the effective conductances g_L and g₁. The model nonlinearities are captured by nonlinear trajectories in the g_L − g₁ parameter space as one of the biophysical conductances change. We show that, although both I_h and I_Ks are resonant currents, the dependence of the resonance attributes on the biophysical conductances, in particular, the mechanisms underlying the amplification of the voltage responses are qualitatively different.

Methods

Conductance-based models

In this paper we consider biophysical (conductance-based) models of Hodgkin-Huxley type (Hodgkin and Huxley 1952). The current-balance equation is given by

$$C\frac{dV}{dt}=-I_L-\sum _k{I}_{x_k}+I_{\mathit{\text{app}}}+I_{\mathit{\text{in}}}(t)$$ (1)

where V is the membrane potential (mV), t is time (msec), C is the membrane capacitance (μF/cm²), I_app is the applied DC current (μA/cm²), I_L = G_L(V−E_L) is the leak current, and I_xk are generic expressions for ionic currents of the form

$$I_x=G_{x}x(V-E_x)$$ (2)

with maximal conductance G_x (mS/cm²) and reversal potentials E_x (mV). All gating variables x follow a first order differential equation of the form

$$\frac{dx}{dt}=\frac{x_{\infty }(V)-x}{{\tau }_x(V)}$$ (3)

where x_∞(V) and τ_x(V) are, respectively, the voltage-dependent activation/inactivation curves and time constants. The function I_in(t) is a time-dependent input current (in μA/cm²). For sinusoidal input currents, we use the following notation

$$I_{\mathit{\text{in}}}(t)=A_{\mathit{\text{in}}}\text{sin}(\omega t)\text{with}\omega =\frac{2\pi f}{T}$$ (4)

Where T = 1000 msec and f is in Hz.

The generic ionic currents (Eq. (2)) we consider here are restricted to have a single gating variable x and are linear in x. This choice is motivated by the persistent sodium current I_P, hyperpolarization-activated inward current I_h and slow M-type potassium current I_Ks found in a variety of neurons that exhibit subthreshold resonance (Schreiber et al. 2004; Acker et al. 2003; Rotstein et al. 2006). Ionic currents of this form have been used in a variety of other models (Morris and Lecar 1981; Rinzel and Ermentrout 1998). The methods we use in this paper can be easily adapted for currents with two gating variables and gating variables raised to powers higher than 1.

We focus on two-dimensional models that describe the dynamics of voltage V and a gating variable x₁, respectively. Additional currents whose gating variables evolve on a fast time scale (faster than all other variables), such as persistent sodium currents, can be included by using the adiabatic approximation, x_k = x_k,∞(V). Here we consider one such additional (generic) current I_x2 with x₂ = x_2,∞(V). Additional fast currents can be considered without significantly changing the formalism used here.

Linearized conductance-based models

Linearization of conductance-based models around a stable fixed-point (V̅, x̅₁) with V̅ below threshold for spike generation is a standard procedure (Ermentrout and Terman 2010). In its simplest form, it consists of substituting the right hand side of Eqs. (1) and (3) by their first order Taylor expansions calculated at the fixed point.

Here we follow Richardson et al. (Richardson et al. 2003) and linearize the autonomous part of system (1)–(3) around the fixed-point (V̅, x̅₁) for the isolated system (I_in(t) = 0) by defining

$$\nu =V-\mathrm{V̅},w_1=\frac{x_1-{\mathrm{x̅}}_1}{x_{1,\infty }^{\text{'}}(\mathrm{V̅})}$$ (5)

where x̅₁ = x_1,∞(V̅). The linearized equations are given by (Richardson et al. 2003)

$$C\frac{d\nu }{dt}=-g_L\nu -g_1{w}_1+I_{\mathit{\text{in}}}(t){\mathrm{\tau ̅}}_1\frac{d{w}_1}{dt}=\nu -w_1$$ (6)

where the effective leak and ionic conductances and time constants are defined by

$$g_L=G_L+G_1+G_2+g_2{G}_1=G_{x_1}{x}_{1,\infty }(\mathrm{V̅})G_2=G_{x_2}{x}_{2,\infty }(\mathrm{V̅})g_2=G_{x_2}{x\text{'}}_{2,\infty }(\mathrm{V̅})(\mathrm{V̅}-E_{x_2})$$ (7)

$$g_1=G_{x_1}{x\text{'}}_{1,\infty }(\mathrm{V̅})(\mathrm{V̅}-E_{x_1}),{\mathrm{\tau ̅}}_1={\tau }_{x_1}(\mathrm{V̅})$$ (8)

respectively. Note that the effective leak conductance g_L includes components from both the biophysical leak conductance G_L and the voltage-dependent ionic conductances: the slow ionic currents contributes a single term G₁ whereas the fast current I_x2 contributes two terms, G₂ and g₂.

The effective ionic conductance g₁ can be either positive or negative. The sign of g₁ determines whether the associated gating variable is resonant (g₁ > 0) or amplifying (g₁ < 0) (Richardson et al. 2003; Hutcheon and Yarom 2000). In our discussion, we will limit the values of g₁ to the positive range which produces resonance. Note that g₂, the last term of g_L, may also be positive or negative, depending on whether V̅ > E_x2, and is of the same form as g₁. Thus, if g₂ is negative, the fast current is amplifying.

Note that the gating variable w₁ in (5) has units of voltage. Note also that the linearization process described above is not restricted to ionic currents of the form (2) and can be applied to models with an arbitrary number of ionic currents and any voltage-dependent time constant (Richardson et al. 2003).

System (6) can be rescaled in order to reduce the number of parameters (from four to two) that effectively govern its dynamics with no loss of information. We follow (Richardson et al. 2003) and define the following dimensionless time and parameters

$$\mathrm{t̂}=\frac{t}{{\mathrm{\tau ̅}}_1},{\gamma }_L=\frac{g_L{\mathrm{\tau ̅}}_1}{C},{\gamma }_1=\frac{g_1{\mathrm{\tau ̅}}_1}{C}.$$ (9)

Substituting into (6) we obtain

$$\frac{d\nu }{d\mathrm{t̂}}=-{\gamma }_L\nu -{\gamma }_1{w}_1+{Î}_{\mathit{\text{in}}}(\mathrm{t̂})\frac{d{w}_1}{d\mathrm{t̂}}=\nu -w_1$$ (10)

where

$${Î}_{\mathit{\text{in}}}(t)={Â}_{\mathit{\text{in}}}\mathit{\text{sin}}(2\pi f\mathrm{t̂}/\mathrm{T̂})\text{with}{Â}_{\mathit{\text{in}}}=\frac{A_{\mathit{\text{in}}}{\mathrm{\tau ̅}}_1}{C}$$ (11)

with T̂ = T/τ̅₁ = 1000/τ̅₁. Note that [f] = Hz, and [ν] = [w₁] = V. We refer to γ_L and γ₁ as the dimensionless effective conductances. We will use dimensionless variables and parameters in Figs. 1–6.

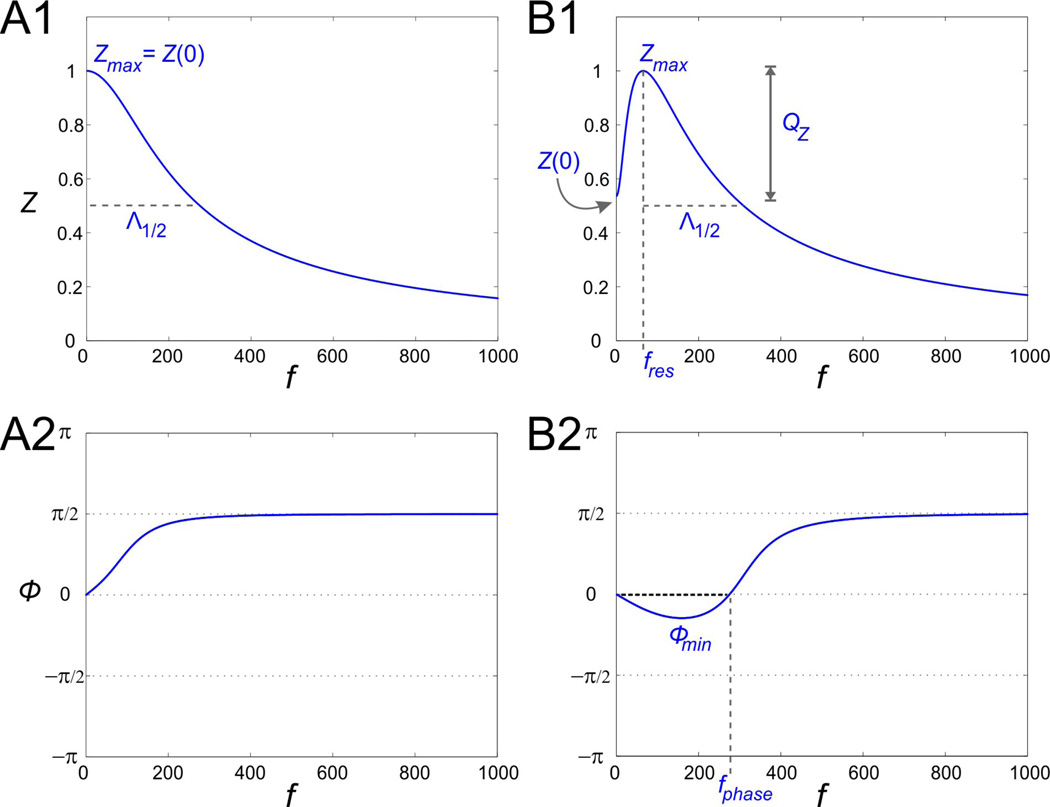
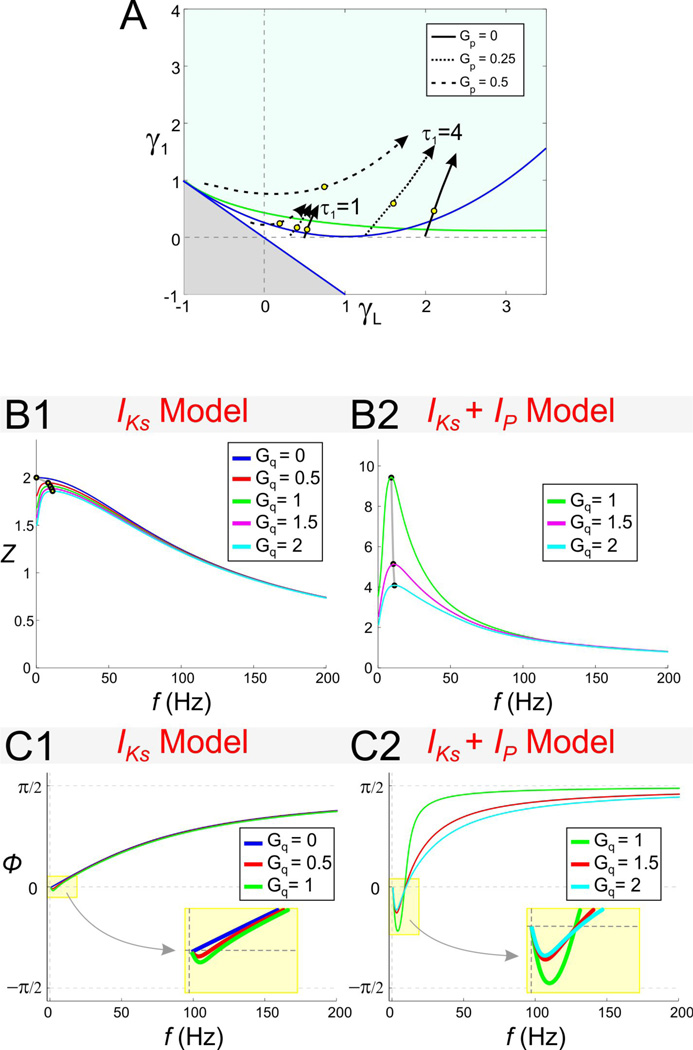
Figure 1.

Impedance (Z) and phase (□) profile diagrams. A1. The impedance profile of a low-pass filter RC cell. A2. The RC cell in A1 only shows a positive response phase. B1. The impedance profile of a band-pass filter resonant cell. The resonant frequency f_res is the frequency at which the impedance function reaches its maximum Z_max. The parameter Q_Z is defined as the difference between Z_max and Z₀. The characteristic frequency range Λ_1/2 measures the length of the frequency interval for which Z(f) is above ½ of its maximum value. B2. The phase of the resonant cell shown in B1 includes both a negative and a positive region. Φ_min is the minimum phase and f_phase represents the zero-phase-frequency and is equal to the length of the frequency band for which the voltage response leads the input signal (negative phase).

Figure 6.

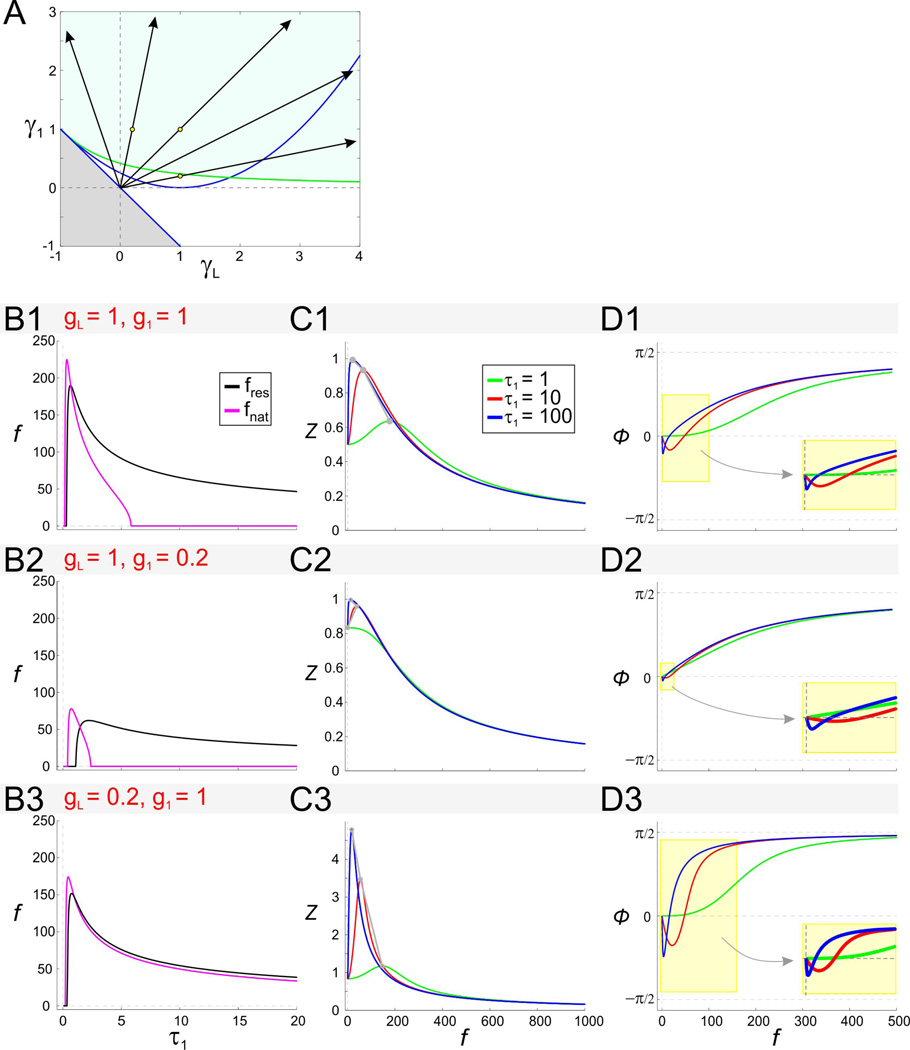
The effect of the time constant τ₁ on impedance and phase in the linear model. A. The effect of τ₁ on the rescaled conductances γ_L and γ₁. The region shown is as in Fig. 2A2. For fixed values of the conductances g₁ and g_L, as τ₁ increases, the rescaled effective conductances γ₁ and γ_L increase along lines emanating from the origin. B. Resonant and natural frequencies of the 2D linear system as a function of τ₁ for representative values of g₁ and g_L. C. Impedance profiles for representative values of g₁ and g_L with different values of τ₁ (as shown in C1). D. Phase profiles for representative values of g₁ and g_L with different values of τ₁ (as shown in C1). Insets show expansions of the shaded box and demonstrate that increasing τ₁ moves the zero-phase-frequency to smaller values.

Impedance and impedance-like functions

The voltage response of a linear system receiving sinusoidal current inputs of the form (4) is given by

$$V_{\mathit{\text{out}}}(t;f)=A_{\mathit{\text{out}}}(f)\text{sin}(\omega t-\varphi (f))$$ (12)

where ϕ(f) is the phase offset (time difference between the peaks of the input current and the output voltage normalized by 2π) and ω is given by the second equation in (4). Linear systems exhibit membrane (amplitude) resonance, if there is a peak in ratio of the output voltage and input current amplitudes:

$$Z(f)=\frac{A_{\mathit{\text{out}}}(f)}{A_{\mathit{\text{in}}}}$$ (13)

at some positive (resonant) frequency f_res, and zero-phase-frequency, if the phase offset ϕ(f) vanishes at some positive frequency f_phase. We calculate the phase as the time difference between the output voltage and input current peaks normalized by the oscillation period. Henceforth, we will refer to the amplitude of impedance as impedance.

Figs. 1A and 1B show two representative graphs for the impedance profile of a low-pass filter RC model (panel A) and a band-pass filter model (panel B) exhibiting resonance at f = f_res. We will use four parameters to characterize impedance profiles:

1. the resonant frequency f_res,

2. the maximum impedance Z_max = Z(f_res),

3. the resonance amplitude or power Q_Z = Z_max − Z(0), and

4. the characteristic right-band-width Λ_1/2 defined as the range of values of f ≥ f_res such that Z(f) ≥ Z_max/2.

Λ_1/2provides information about the selectivity of the neuron to input frequencies. The smaller the value of Λ_1/2, the higher the selectivity, i.e., the impedance profile is peakier around the resonant frequency f_res. The choice of ½ is arbitrary and other values can be used. The restriction f ≥ f_res is useful for comparison between cases where Z(0) > Z_max/2 in one or more of the impedance profiles. In these cases, a “full” bandwidth will not be representative of the difference between impedance profiles. For a low-pass filter RC cell as in Fig. 1A, f_res = 0 and Q_Z = 0.

Figs. 1C and 1D show two representative graphs for the phase (ϕ). They both approach π/2 for large values of f. The phase in panel C is always increasing and positive; the voltage response is always delayed by at most one quarter of a cycle. The phase in panel D, on the other hand, is negative for f < f_phase and positive for larger values of f. The negative phase can be interpreted as the response leading the input. For f = f_phase, voltage response and input are in phase, so f_phase represents the zero-phase-frequency. We characterize the phase profile with an additional parameter ϕ_min measuring the minimum phase.

In this paper we consider sinusoidal current inputs of the form (4) where A_in is a non-negative constant and the frequency f is measured in number of oscillations per 1000 units of time. For dimensional consistency with most experimental measurements, in Figs. 8–12, time t is expressed in milliseconds and f is measured in Hz.

Figure 8.

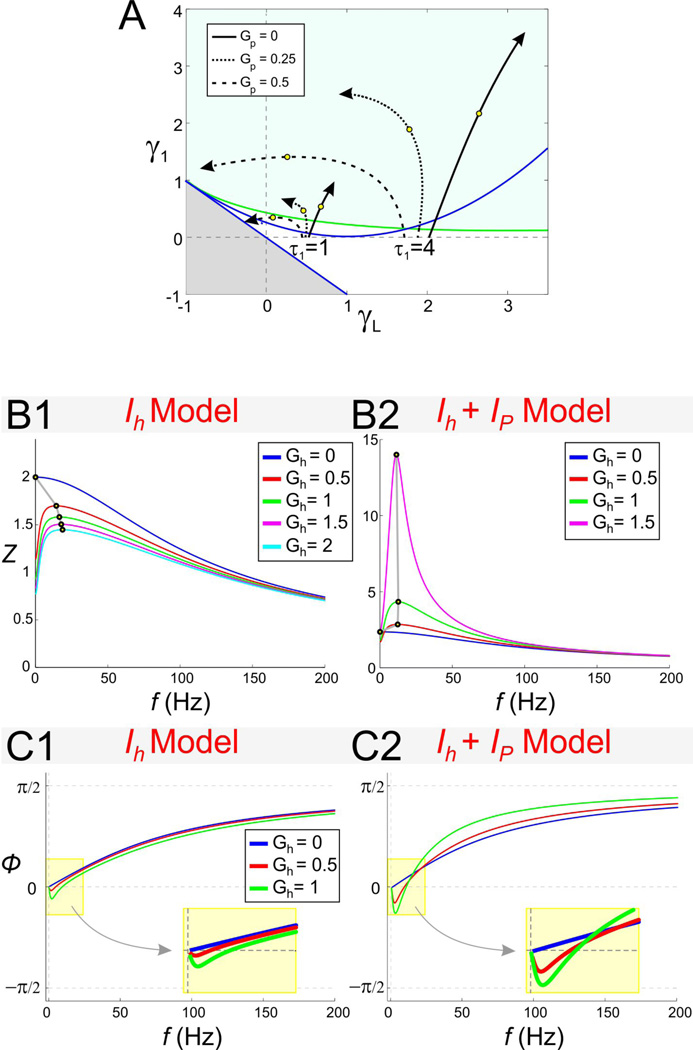
The effect of G_h on resonance and zero-phase-frequency in the I_h + I_p model. A. Trajectories in γ_L − γ₁ space parameterized by the resonant conductance G_h (arrows indicate increasing values of G_h). All trajectories start at G_h = 0 and the value G_h = 1.5 is marked by an open circle. Different trajectories correspond to different representative values of G_p and τ₁ (as indicated). The trajectories are computed until the fixed-point V̅ ceases to exist. Gray region and curves as in Fig. 2A2. B. Impedance profiles for the linearized I_h + I_p model with G_p = 0 (B1) and G_p = 0.5 (B2). C. Phase profiles for the linearized I_h + I_p model with G_p = 0 (C1) and G_p = 0.5 (C2). In B and C I_app = −2.5.

Results

1. Generation of resonance and zero-phase-frequency in two-dimensional linear models

In the first part of the Results we consider the 2D linear system (6) and sinusoidal current inputs I_in (t) of the form (4) with constant values of A_in. Because the system is linear, without loss of generality, we assume A_in = 1. For simplicity in the notation, we drop the “bar” from τ₁ and the “hat” from t and other parameters in (6) and (10). The eigenvalues, impedance, and resonant frequency for system (6) can be calculated from Eqs. (18), (21) and (22) in Appendix A by substituting $a=-g_L{C}^{-1},b=-g_1{C}^{-1},c={\tau }_1^{-1}$, and $d=-{\tau }_1^{-1}$. Alternatively, one can use the rescaled system (10) and compute the eigenvalues, impedance, and resonant frequency (r̂_1,2, Ẑ and ω̂_res respectively) by substituting a = −γ_L, b = −γ₁, c = 1 and d = −1 in Eqs. (18), (21) and (22) of Appendix A. This information can then be used in the two-dimensional parameter space of effective conductances to investigate the effects of the biophysical parameters g_L, g₁, τ₁, and C using

$$r_{1,2}=\frac{{\mathrm{r̂}}_{1,2}}{{\tau }_1},Z(\omega )=\frac{{\tau }_1}{C}Ẑ({\tau }_1\omega ),\text{and}{f}_{\mathit{\text{res}}}=\frac{{\mathrm{\omega ̂}}_{\mathit{\text{res}}}}{{\tau }_1}\frac{1000}{2\pi }.$$ (14)

For C = 1 and τ₁ = 1, g_L = γ_L and g₁ = γ₁ the two systems (6) and (10) are equivalent. Without loss of generality, we let C = 1 and only consider the effects of changing τ₁. Changes in τ₁ affect the magnitude of the eigenvalues but not their sign. These changes, therefore, do not affect the stability properties of the autonomous system but do affect, for instance, the natural frequency f_nat (when the autonomous system exhibits damped oscillations). Changes in τ₁ also affect the shape of the impedance function and the resonant frequency as will be discussed.

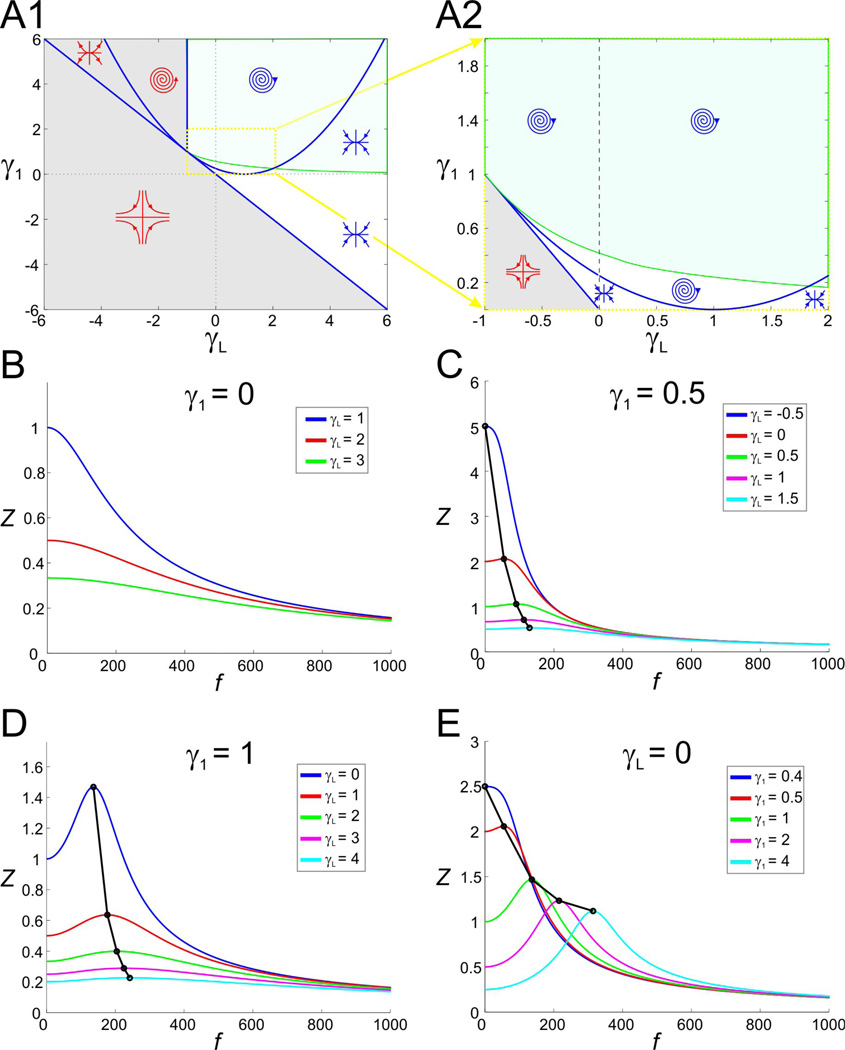
In Fig. 2A1 (magnified in 2A2) we show the stability diagram for the 2D linear system (6) with τ₁ = 1. This diagram is similar to that presented in (Richardson et al. 2003). The blue curves separate regions in parameter space with different stability properties or distinct fixed point types (focus, node or saddle). The system is stable in the regions marked with blue symbols and unstable in regions marked with red. The green curve, referred to as the resonance curve, separates the regions in parameter space for which the system exhibit resonance (shaded green) and exhibit no resonance. Note that the regions in parameter space where the system exhibits intrinsic (damped) oscillations and resonance do not coincide (Richardson et al. 2003). In particular, resonance can occur in the absence of intrinsic oscillations where the fixed point is a node.

Figure 2.

Stability, oscillatory, and resonant properties for the 2D linear system (6) With C = 1 and τ₁ = 1 in the g_L − g₁ space. (For these parameters values, g₁ = γ₁ and g_L = γ_L and the 2D linear (6) and the 2D rescaled system (10) are equivalent.) A1. Superimposed stability and resonance diagrams. The blue curves separate between regions in parameter space with different stability properties or fixed point types. Symbols indicate whether the fixed point is a focus, node or saddle (blue symbols stable; red symbols unstable). The green curve (resonance curve; obtained from Eq. (22); see Results) separates between regions in parameter space where the system exhibits resonance (green) or does not (other). A2. A magnification of A1 (yellow dotted box). All regions above the grey saddle region are stable. B. to D. Representative examples of impedance profiles for the rescaled system (10) with γ₁ and γ_L values denoted in the figure. Black dots and lines denote the resonant points.

Representative impedance profiles show a variety of possible resonant behaviors (Figs. 2B to 2E). For γ₁ = 0, the first equation in the 2D linear system is independent of w₁; the system has no resonance and simply describes a low-pass filter (Fig. 2B). As γ_L increases, Z_max(= Z(0)) decreases (and Λ_1/2increases linearly; not shown). In this case, the phase ϕ shows a delayed response for all values of γ_L but this delay decreases as γ_L increases (not shown). The expression of resonance in this system occurs when γ₁ > 0. For any fixed positive value of γ₁, increasing the value of γ_L results in an increase in the value of the resonance frequency f_res and a concomitant decrease in Z_max (Figs. 2C and 2D). Note, however, that resonance can occur with γ_L = 0 (Fig. 2E).

An increase in g₁ generates resonance by an unbalanced decrease in Z_max and Z(0)

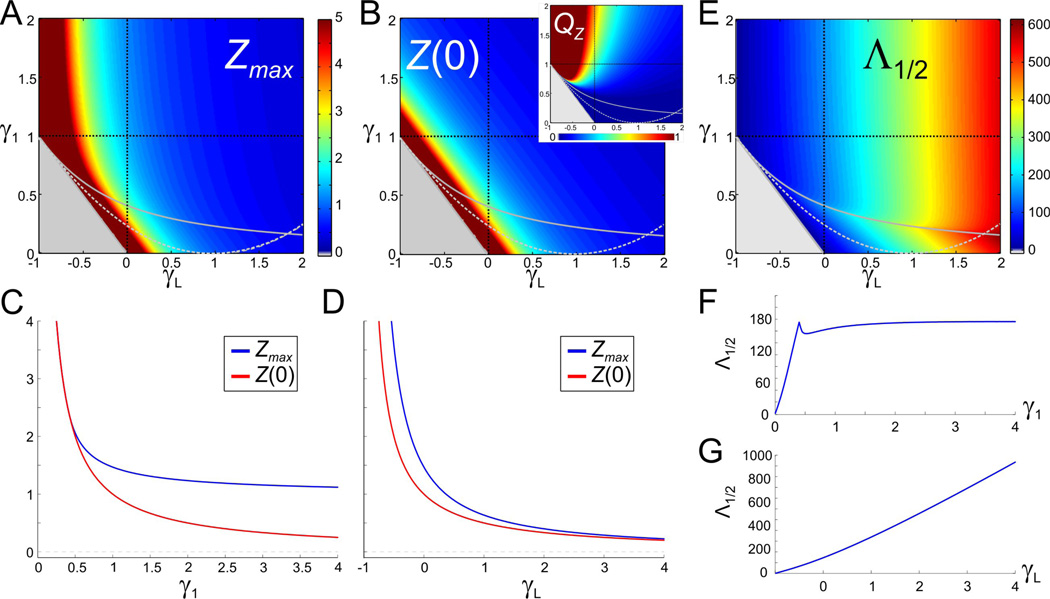
In order for the 2D linear system to exhibit resonance, the value of γ₁ has to be in the resonant region above the resonance curve in Fig. 2A. For small enough values of γ₁, the system acts as a low-pass filter similar to the γ₁ = 0 case described above. For resonance to emerge, a difference between Z_max and Z(0) (hence, a positive value of Q_Z = Z_max − Z(0)) has to be generated as γ₁ crosses the resonance curve. Figs. 3A and 3B show that, below the resonance curve, both the Z_max (and Z(0)) level curves are almost linear and parallel to the line γ₁ + γ_L = 1, and they also nearly coincide (e.g., see Fig. 3C for γ₁ < 0.5). Above the resonance curve, the Z_max level sets are no longer linear while the Z(0) level sets remain linear. Thus, as γ₁ increases along vertical lines in γ_L − γ₁ parameter space, resonance emerges because Z(0) decreases faster than Z_max (Figs. 3C and 3B inset). The difference (Q_Z) is more attenuated for larger values of γ_L (Fig. 3B inset).

Figure 3.

The attributes of resonance for the 2D linear system (6) (as in Fig. 2). A. The maximum impedance Z_max. B. The zero-frequency input resistance Z(0) (same scale as A). Dark red regions in A and B are outside the scale of the graph. Gray region and curves as in Fig. 2A2. Inset shows Q_Z (the difference between Z_max and Z(0)) in the same range of γ₁ and γ_L. C. Representative example of Z_max and Z(0) as a function of γ₁ for γ_L = 0 (vertical dashed black line in A and B). D. Representative example of Z_max and Z(0) as a function of γ_L for γ₁ = 1 (horizontal dashed black line in A and B). E. Half band-width Λ_1/2. F. Representative example of Λ_1/2 as a function of γ₁ for γ_L = 0 (vertical dashed black line in E). G. Representative example of Λ_1/2 as a function of γ_L for γ₁ = 1(horizontal dashed black line in E).

The resonance line is marked by a peak in the half-band-width Λ_1/2 in the γ_L − γ₁ parameter space as γ₁ increases (Figs. 3E and 3F). As γ₁ increases further, Λ_1/2 settles into an almost constant value. The selectivity of resonance is therefore independent of γ₁ for large enough values of γ₁ (Fig. 3F). In contrast, Λ_1/2 increases monotonically with γ_L (Fig. 3G).

An increase in g_Lgenerates low amplitude resonance

Resonance occurs for all values of γ_L within the stability region for the underlying autonomous system, provided γ₁ is large enough to be above the resonance curve (Fig. 2A, green region). For smaller values of γ₁ (as in Fig. 2C), resonance can be generated by decreasing γ_L along horizontal lines that cross the resonance curve (solid gray curve in Figs. 3A–B). Along these lines, both Z_max and Z(0) decrease (as 1/γ_L) but at a slightly different pace (Fig. 3D), thus generating resonance. The resonance generated by this mechanism is much weaker as compared to the one described above for increasing values of γ₁ in the sense that Q_Z is much smaller (Fig. 3B inset). This is because, as γ_L decreases, both Z_max and Z(0) change almost in parallel (e.g., Fig. 3D; also compare Figs. 3A and 3B).

A decrease in g_Lamplifies the voltage response and decreases f_res

A decrease in the effective leak conductance g_L (Eq. (7)) can be caused by a decrease in the biophysical leak conductance G_L, a decrease in the ionic conductances G₁ and G₂, or an increase in the fast ionic conductance g₂ when the associated gating variable is amplifying (g₂ < 0; see Methods). In the latter case there is a competition between the relative magnitudes of the last two terms in Eq. (7). In some cases, as with the biophysical model we discuss later in this paper, the effective leak conductance g_L can in fact be negative.

Figs. 3A and 3B show that, as γ_L decreases, both Z_max and Z(0) increase, and so does Q_Z due to the different rates at which Z_max and Z(0) change in parameter space (Fig. 3D; see also Fig. 2D). The amplification of the voltage response is more dramatic for values of γ_L close to the boundary between the stability and instability regions, and is more pronounced for larger values of γ₁. In addition to these changes, Λ_1/2 decreases with γ_L; i.e., as γ_L decreases, the impedance profile becomes narrower and the selectivity increases (Figs. 3E and 3G). For values of γ₁ close to the resonance curve, for which Z_max and Z(0) are not significantly different, resonance can be abolished for larger values of γ_L (see Fig. 2D).

Together, these results show that a decrease in γ_L (and therefore g_L) causes an amplification of resonance, marked by an increase in the resonance amplitude Q_Z and an increase in the selectivity (decrease in Λ_1/2), accompanied by a decrease in f_res. An increase in g_L, therefore, causes an attenuation of resonance accompanied by an increase in f_res.

Resonance and oscillations

To explore the distinction between membrane resonance and oscillations in the 2D linear model (i.e., the presence of a focus fixed point), we plotted the resonance and natural oscillation frequencies in the γ_L − γ₁ parameter space (Fig. 4). A frequency of 0 indicates lack of oscillation or resonance, as indicated. We found that both f_nat and f_res increase with γ₁ but do not generally coincide (see, for example, FIG. 4C). As γ_L is increased, both f_nat and f_res increase for small γ_L values but only f_res continues to increase with large γ_L values whereas f_nat decreases back to 0 in this range (Fig. 4D). Note that if γ₁ is large (e.g., γ₁ = 1 here), f_res and f_nat almost coincide during the increasing part of f_nat as γ_L increases (not shown).

Figure 4.

Natural and resonant frequency color bar diagrams for the 2D linear system (6) (as in Fig. 2). A. Natural frequency f_nat. B. Resonant frequency f_res (same scale as A). Gray region and curves as in Fig. 2A2. C. Representative example of f_res and f_nat as a function of γ₁ for γ_L = 1.5 (vertical dashed black lines in A and B). D. Representative example of f_res and f_nat as a function of γ_L for γ₁ = 0.5 (horizontal dashed black lines in A and B).

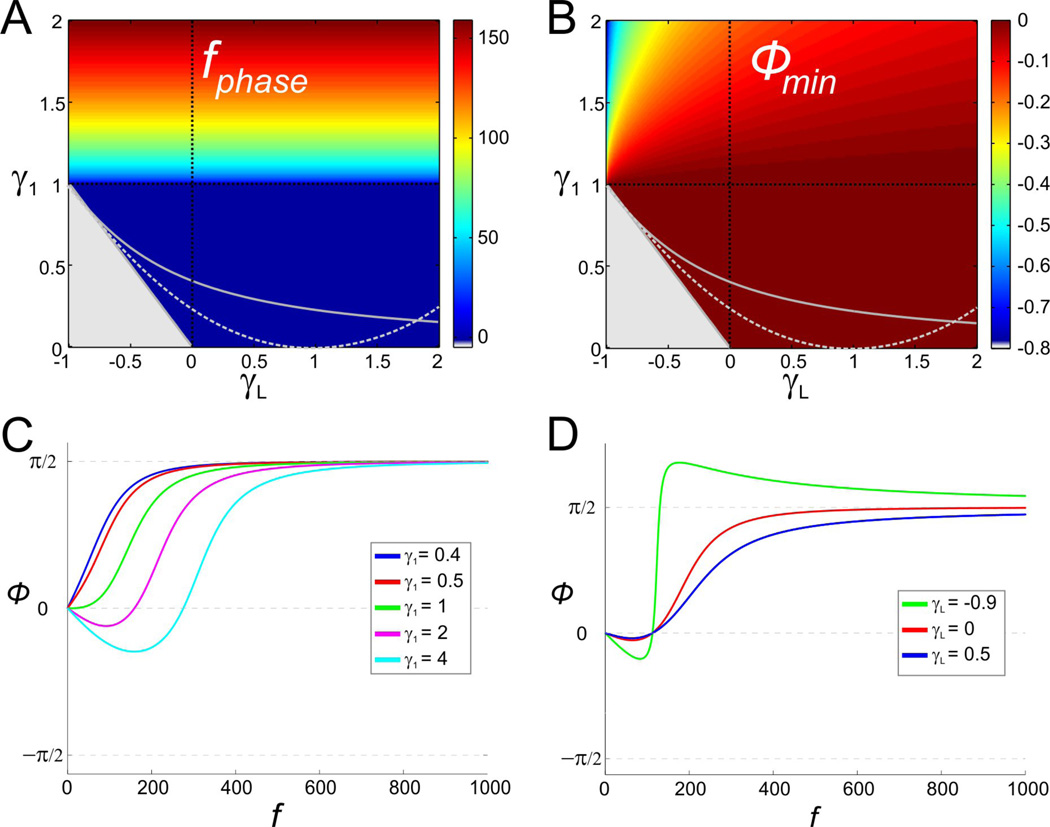
An increase in g₁ generates zero-phase-frequency with f_phase ≠ f_res

We examined how the response phase of the membrane potential shifts with respect to the sinusoidal input current for the 2D linear system (6) with τ₁ = 1 and under what conditions the system exhibits zero-phase-frequency. For γ₁ = 0 (low-pass filter), the phase ϕ is always positive with ϕ_min = ϕ(0) = 0 and the system does not exhibit zero-phase-frequency. Fig. 5A shows that this persists for values of γ₁ < 1 for which the 2D system exhibits resonance but not zero-phase-frequency. For γ₁ > 1, a negative frequency band of length f_phase emerges (see also Fig. 5C). This band starts at f just above zero and its width also determines the zero-phase-frequency (= f_phase). The value of f_phase increases with γ₁ but is independent of γ_L. It should be noted that f_phase is different from the resonant frequency f_res, and the two variables have different monotonic dependencies on γ₁. Note also that the minimum phase ϕ_min increases with γ₁, and therefore with f_phase, but decreases with γ_L (Fig. 5B).

Figure 5.

Negative-phase-frequency-band for the 2D linear system (6) (as in Fig. 2). A. The length of the negative-phase-frequency band (or, equivalently, the zero-phase-frequency f_phase). B. Minimum phase (ϕ_min) of the voltage response. Gray region and curves as in Fig. 2A2. C. Representative example of the phase profile as a function of γ₁ for γ_L = 0 (vertical dashed black line in A and B). D. Representative example of the phase profile as a function of γ_L for γ₁ = 1 (vertical dashed black line in A and B).

The effect of the time constant τ₁ on resonance

We now consider the effect of the time constant τ₁ of the gating variable w₁ (Eq. (6)). Although Figs. 2 to 5 were produced with τ₁ = 1, the effects of changes in τ₁ can be investigated using these figures and Eqs. (14). When τ₁ ≠ 1, the normalized parameters are changed and therefore γ_L ≠ g_L and γ₁ ≠ g₁. For fixed values of g_L and g₁, changes in τ₁ cause γ_L and γ₁ to move in parameter space along lines (parametrized by τ₁) with slopes γ₁/γ_L = g₁/g_L as shown in Fig. 6A. Each of these lines converges to the origin as τ₁ approaches zero, and its slope has the same sign as g_L (in the region of resonance for which g₁ > 0). Fig. 6A shows that, for small enough values of τ₁, the system exhibits neither intrinsic (damped) oscillations nor resonance, reflecting the fact that both phenomena depend upon a (relatively) slow negative feedback.

As τ₁ increases, the system exhibits first intrinsic oscillations with no resonance for small τ₁ and then, for larger values of τ₁, both intrinsic oscillations and resonance (Figs. 6B1–B3; most clearly seen in 6B2). Depending on the slope γ₁/γ_L, intrinsic oscillations may disappear as τ₁ increases further. Note that for g_L < 0, relatively small increases in τ₁ causes the system to reach the instability region in parameter space.

An increase in τ₁ amplifies the voltage response and this amplification is marked by an increase in Q_z and Z_max (while Z(0) remains constant; Fig. 6C1–C3) and a decrease in Λ_1/2 (i.e., increase in selectivity; not shown). The mechanism of generation of resonance as τ₁ increases is different from the mechanism described above for increasing values of g₁ (with constant τ₁). Direct substitution of the model parameters (g_L, g₁ and τ₁) into Eq. (21) in Appendix A yields Z(0) = (g_L + g₁)⁻¹. In other words, changes in τ₁ do not affect the value of Z(0) and hence Q_Z = Z_max for all values of τ₁. As such, an increase in the time constant τ₁ generates resonance by an increase in Z_max with no changes in Z(0)(Fig. 6C1–3).

Increasing the time constant τ₁ causes the natural and resonant frequencies to increase for small values of τ₁ and to decrease for larger values. Information about the effect of τ₁ on the resonant and natural frequencies can, in principle, be extracted from Figs. 6B and 6C and the expressions for r_1,2 and f_res in Eqs. (14). However, in most cases, especially when f_nat or f_res increase along lines in parameter space, the net effect of increasing values of τ₁ is not readily apparent from the graphs because both the numerator and denominator are increasing functions of τ₁. In these cases, it is more useful to analyze the expressions f_nat and f_res given by Eqs. (19) and (22) in Appendix A. Substituting $a=-g_L,b=-g_1,c={\tau }_1^{-1}$, and $d=-{\tau }_1^{-1}$ yields

$$f_{\mathit{\text{nat}}}=\frac{1000}{2\pi }\frac{\sqrt{4g_1{\tau }_1-{(1-g_L{\tau }_1)}^2}}{2{\tau }_1}{f}_{\mathit{\text{res}}}=\frac{1000}{2\pi }\frac{\sqrt{-1+\sqrt{g_1^2{\tau }_1^2+2g_L{g}_1{\tau }_1^2+2g_1{\tau }_1}}}{{\tau }_1}.$$ (15)

Equation (15) gives the imaginary part of the eigenvalues (18) and is valid for calculating f_nat so long as the eigenvalues are complex. As such, f_nat is zero for the minimum value of τ₁ for which it is defined, reaches a maximum at τ₁ = (2g₁ + g_L)⁻¹ (provided this value is positive) and is zero again for large enough τ₁ when the right hand side of (15) fails to be a real number. f_res is zero for the minimum value of τ₁ for which it is defined $({\tau }_1=(-g_1+\sqrt{2g_1^2+2g_L{g}_1)/(g_1^2+2g_L{g}_1)})$, it is positive for larger values of τ₁ (e.g., ${\tau }_1=g_1^{-1}$), and approaches zero as τ₁ approaches infinity (Figs. 6B1–3).

The non-monotonic effect of τ₁ on f_res is particularly clear in the impedance profile shown in Fig. 6C2. Note, however, that increasing τ₁ always results in an increase of the peak impedance value as seen in Fig. 6C1–3.

We now examine the effect of the time constant τ₁ on phase. Increasing τ₁ generates zero-phase-frequency with f_phase ≠ f_res. As before, it is useful to examine the expression for ϕ given by Eq. (23) in Appendix A. The zero-phase-frequency is obtained when the denominator in Eq. (23)vanishes. Substituting $a=-g_L,b=-g_1,c={\tau }_1^{-1}$, and $d=-{\tau }_1^{-1}$ yields

$$f_{\mathit{\text{phase}}}=\frac{1000}{2\pi }\frac{\sqrt{g_1{\tau }_1-1}}{{\tau }_1}.$$ (16)

Zero-phase-frequency occurs for values of time constant τ₁ above $g_1^{-1}$ as illustrated in Fig. 6D. Figs. 6D and 6C also illustrate that the critical value of τ₁ above which zero-phase-frequency occurs is different from the critical value above which resonance occurs. From Eq. (16), the zero-phase-frequency f_phase increases with τ₁ for ${\tau }_1<2g_1^{-1}$ and decreases for larger values of τ₁. A comparison between Eq. (16) and the second equation in (15) shows that in general f_phase ≠ f_res.

2. Generation of resonance and zero-phase-frequency in linearized biophysical two-dimensional models

The study of the roles of the effective conductances g₁ and g_L (or their dimensionless versions γ₁ and γ_L) on the generation of both resonance and zero-phase-frequency using the diagrams in Figs. 2 to 7 provides a mechanistic insight into these phenomena. However, it does not produce a useful explanation of the mechanisms underlying resonance and zero-phase-frequency in realistic biophysical models. In this section we will use the description of the dependence of resonance and zero-phase-frequency in the 2D linear system, developed thus far, to explain how linear approximations to biophysical models can be mapped onto our framework of the linear systems and how biophysical ionic currents shape preferred frequencies for impedance and phase.

Figure 7.

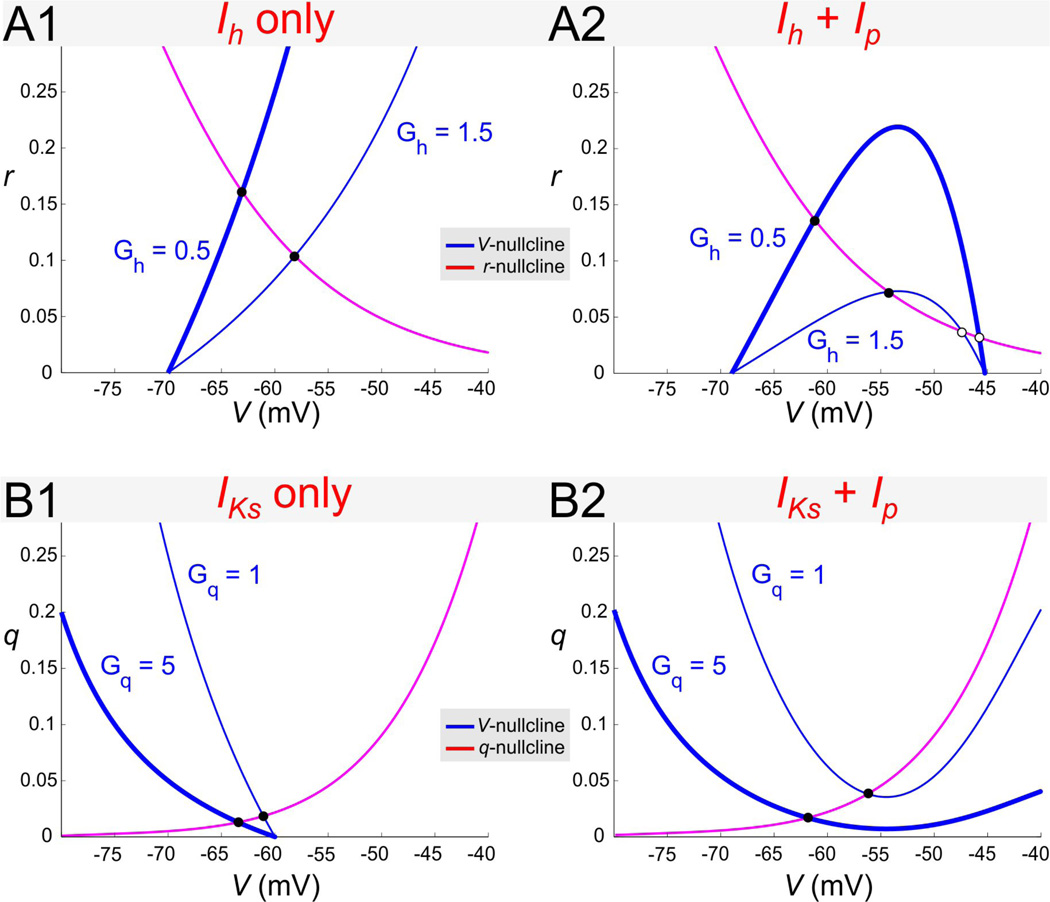
Nullclines for different 2D biophysical models. A. In the I_h + I_p model with G_p = 0 (A1) different values of G_h lead to nullclines that are close to linear near the fixed point. In contrast, when G_p > 0 (A2; G_p = 0.5) the V-nullcline can show quadratic nonlinearities near the fixed point. B. Similarly in the I_M + I_p model with G_p = 0 (B1) the nullclines are close to linear whereas when G_p > 0 (B2; G_p = 0.5) the V-nullcline shows quadratic nonlinearities. Note that the individual nullclines are qualitatively mirror images of those of the I_h + I_p model. In all panels filled circles denote stable fixed points and open circles denote saddle points.

In the previous sections we kept one parameter fixed and varied another. Changes in either g_L or g₁ resulted in trajectories in the g_L − g₁ parameter space that moved along horizontal and vertical lines (Figs. 3–5). Additionally, changes in τ₁ generated oblique linear trajectories (Fig. 6). In contrast to these parameters, changes in the biophysical conductances may lead to nonlinear trajectories in the g_L − g₁ parameter space. While changes in the biophysical leak (G_L) and fast conductance (G_x2) directly affect only the effective leak conductance g_L (Eq. (7)), changes in the biophysical conductances with slower time scales (G_x1) affect both g_L and g₁. It is important to note, however, that changing G_L (or the fast conductances) may change the value of g₁ indirectly, by changing the position of the fixed point.

In this section we investigate the effects of changes in the resonant and amplifying currents on the mechanisms of generation of resonance and zero-phase-frequency in two prototypical biophysical models I_h + I_p and I_Ks + I_p. The governing equations are given in Appendix B. The nonspecific cation h current I_h is a hyperpolarization-activated inward current whereas the slow non-inactivating potassium current (e.g., the M current) I_Ks is a depolarization-activated outward current and, as such, both I_h and I_Ks are resonant currents (Hutcheon and Yarom 2000). The depolarization-activated persistent sodium current I_P is an amplifying current (Hutcheon and Yarom 2000). The fact that I_h and I_Ks activate by moving the membrane potential in different directions (hyper- or depolarizing) results in qualitatively different effects on resonance and zero-phase-frequency properties, and their dependence on the biophysical conductances. These two models were chosen as representative models that are known to produce resonance but the effects of these ionic currents can be replaced by other currents with similar biophysical properties. The inward rectifying potassium currents can also act as amplifying currents; however, these currents are typically active in ranges of voltage below values where subthreshold resonance is observed and we do not examine their effect.

An increase in the maximal conductance of I_p generates strong nonlinearities in the I_h + I_p and I_Ks + I_p models as seen in the nullclines (Fig. 7). In the absence of I_p the nullclines are only weakly nonlinear; i.e., the linearized nullclines around the fixed-point V̅ (the intersection between nullclines) provide a good approximation to the nonlinear nullclines. This is true in both models for a large range of values of V̅. An increase in the amount of I_p generates a strong nonlinearity (of parabolic type) in both models (Figs. 7A2 and 7B2). If the fixed-point V̅ is near the “knee” of the V -nullcline, the linearized nullclines do not provide a good approximation to the nonlinear ones, and cannot be expected to capture the dynamics of the nonlinear system. For values of G_h and G_q for which V̅ lies further away from the knee, however, along the left branch of the corresponding parabolic-like V -nullclines, the nullclines are only weakly nonlinear (not shown). Qualitatively, the phase plane diagrams for the two models are almost mirror images of each other (Fig. 7A vs. 7B). Although an increase in G_h causes V̅ to increase while an increase in G_q causes V̅ to decrease, both phase planes respond in a similar way to changes in G_p.

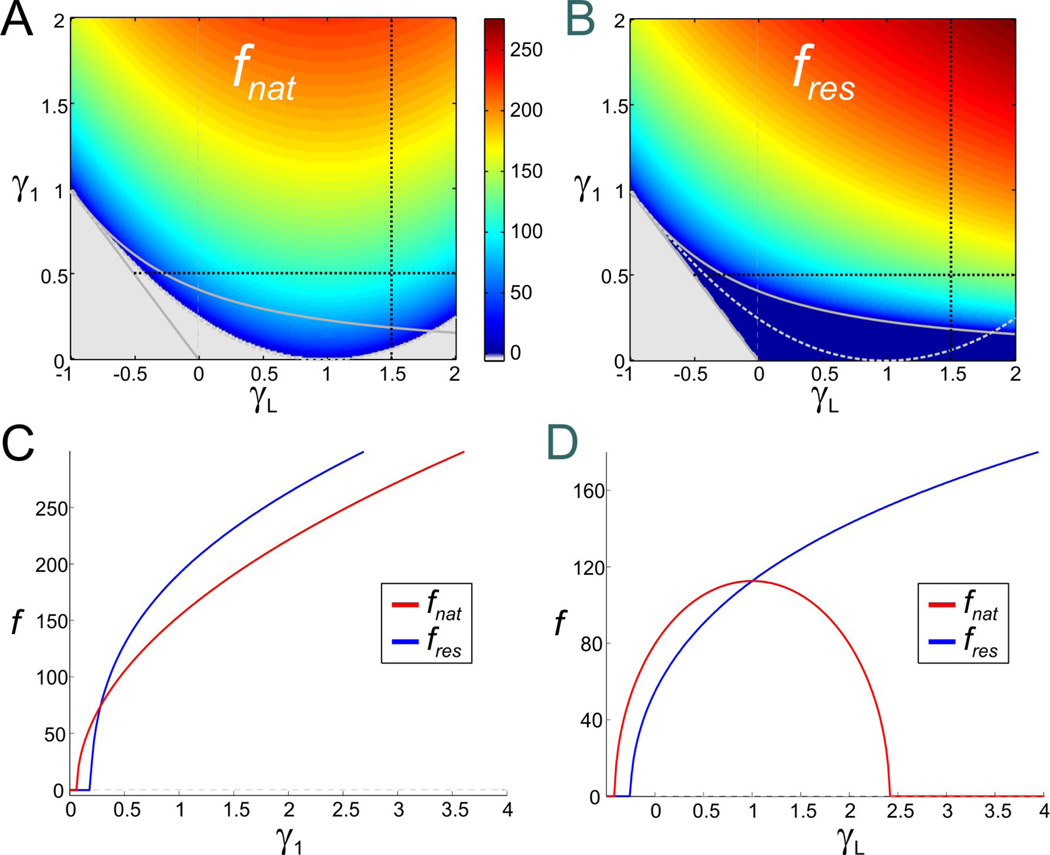
Nonlinear effects generated by increases in the maximal conductance of I_p are captured by the impedance profiles

Changes in the biophysical ionic conductances (G_h, G_q, and G_p) cause changes in the effective conductances g_L and g₁ through Eqs. (7) and (8), and generate trajectories in γ_L − γ₁ parameter space (Figs. 8A and 9A). The shapes of the trajectories in γ_L − γ₁ parameter space depend not only on the biophysical conductances but also on the value of the fixed-point V̅ which, in turn, depends on the shape of the V -nullclines. Note that, for linear systems, the location of the fixed-point has no effect on the resonance and zero-phase-frequency properties. The nonlinearities of the V -nullclines are translated to the nonlinear trajectories in γ_L − γ₁ parameter space through V̅. If changes in G_h, G_p and G_q had no effect on the location of V̅, then an increase in G_p would still cause a decrease in the effective conductance g_L, and an increase in either G_h or G_q would cause an increase in both effective conductances g_L and g₁. In this case, changes in G_h and G_q would have generated oblique linear trajectories in γ_L − γ₁ parameter space. If the changes in V̅ (as a result of changes in the biophysical conductances) are small, as it occurs when the nullclines are weakly nonlinear, then one would expect trajectories in parameter space to be weakly nonlinear as well, as is the case for the solid trajectories for to G_p = 0 (Figs. 8A and 9A). For larger values of G_p for which the nullclines are strongly nonlinear, the corresponding trajectories are also strongly nonlinear (dashed trajectories for G_p = 0.5 in Figs. 8A and 9A).

Figure 9.

The effect of G_q on resonance frequency in the I_Ks + I_p model. A. Trajectories in γ_L − γ₁ space parameterized by the resonant conductance G_q (arrows indicate decreasing values of G_q). Each trajectory starts at the value of G_q at which the two nullclines first intersect and V̅ emerges. The end of each trajectory marks G_q = 3 in all cases and open circles mark G_q = 1. Different trajectories correspond to different representative values of G_p and τ₁ (as indicated). Gray region and curves as in Fig. 2A2. B. Impedance profiles for the linearized I_Ks + I_p model with G_p = 0 (B1) and G_p = 0.5 (B2). C. Phase profiles for the linearized I_Ks + I_p model with G_p = 0 (C1) and G_p = 0.5 (C2). In B and C I_app = 2.5.

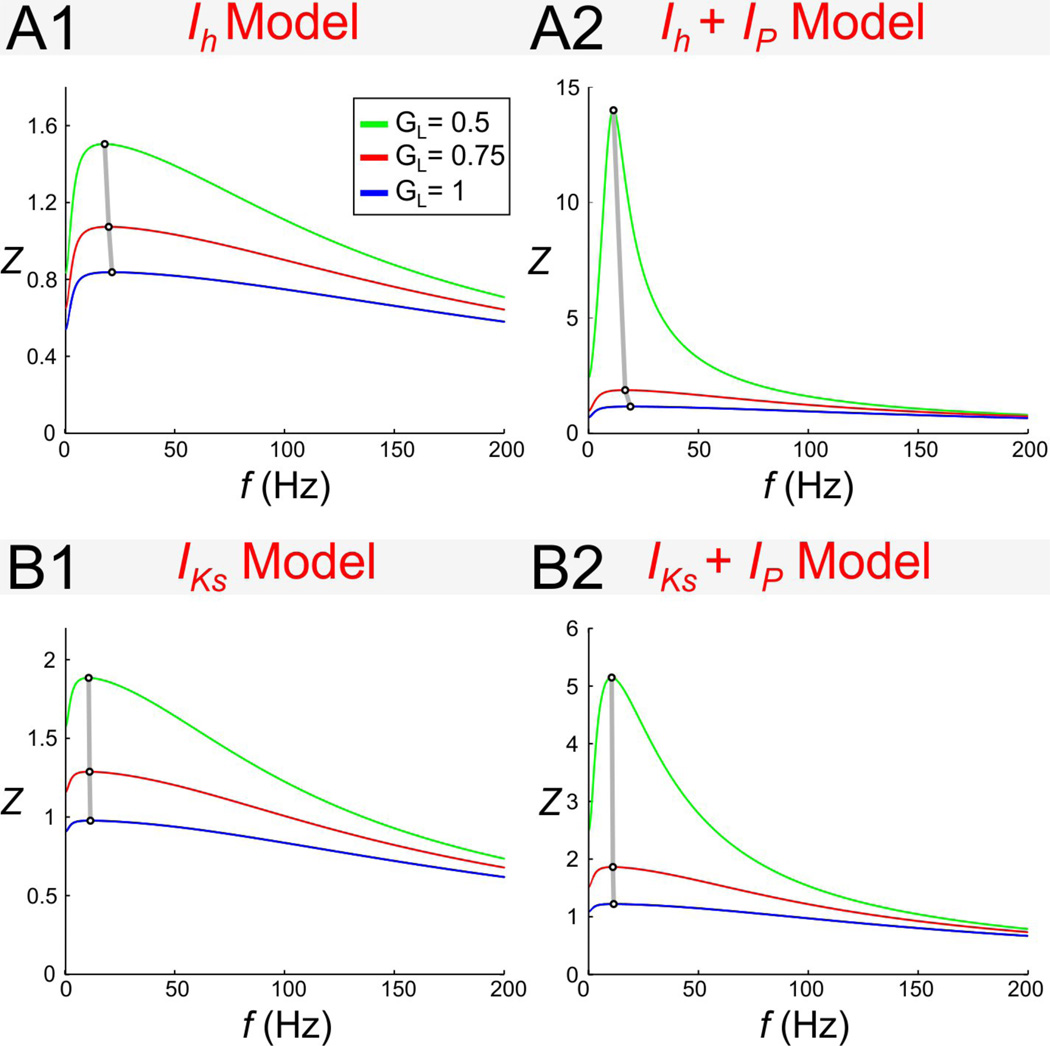
The effect of changing G_L in the biophysical models

Our results in the dimensionless model indicated that increasing γ_L (and therefore g_L) led to an increase in f_res (Fig. 4D). This raises the question of whether an increase in G_L in the biophysical models would also lead to a similar change in f_res. To examine this question, we varied the level of G_L in both the I_h + I_p and I_Ks + I_p models (Fig. 10). We found that, in both models, an increase in G_L led to a relatively small but noticeable increase in f_res (Figs. 10A1 and 10B1). The effect of G_L on f_res was not influenced much by the presence of I_p (i.e. 0.5 G_P = 0.5; Figs. 10A2 and 10B2).

Changes in the maximal conductances of the resonant currents I_h and I_Ks in the presence of I_p have qualitatively different effects on the resonance and zero-phase-frequency

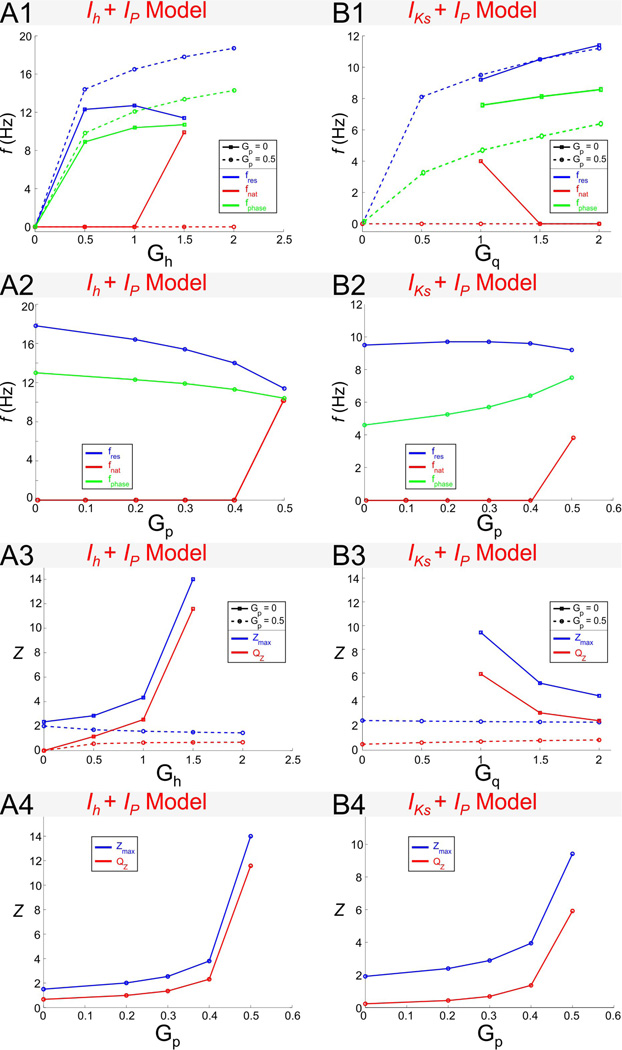
Resonant currents, or resonant gating variables, are usually classified into one single group (Richardson et al. 2003; Hutcheon and Yarom 2000). In the absence of I_p, changes in G_h and G_q generate weakly linear, almost oblique trajectories with positive slope in the corresponding γ_L − γ₁ parameter spaces (solid arrowed curves in Figs. 8A and 9A). In this case, changes in G_h and G_q have similar effect on the resonance and zero-phase-frequency properties of the corresponding models.

In contrast, when I_p is present, changes in G_h and G_q affect the shape of the corresponding trajectories in almost opposite ways (Figs. 8A and 9A, dashed curves for G_p = 0.5) reflecting the different biophysical roles these two currents play. In the I_h + I_p model, in particular, the direction of motion of the trajectories for G_p = 0.5 and G_p = 0 are opposite as G_h increases and, for large enough values of τ₁, trajectories cross the line γ_L = 0 leading to a strong amplification of the voltage response (Fig. 8B2). This is in contrast to the I_Ks + I_p model where an increase in G_q leads to a strong de-amplification of the voltage response (Fig. 9B2). The differences between the trajectories in parameter space for the two models indicates that the dependence of their resonant properties on G_h or G_q are different. In particular,

1. the voltage response is amplified for the I_h + I_p model and attenuated for the I_Ks + I_p model,

2. the selectivity increases (Λ_1/2 decreases) for the I_h + I_p model and decreases (Λ_1/2 increases) for the I_Ks + I_p model, and

3. ϕ_min increases in absolute value for the I_h + I_p model and decreases for the I_Ks + I_p model.

An increase in G_h reduces the voltage response for G_p = 0 (Fig. 8B1) but amplifies the voltage response for G_p = 0.5 (Fig. 8B2). This amplification is much stronger for larger values of I_app (not shown). In contrast, an increase in G_q reduces the voltage response for all values of G_p (Figs. 9B1 and 9B2). The amplification of the voltage response is still larger for larger values of I_app but this amplification is stronger for lower values of G_q (not shown).

In the I_h + I_p model both f_res and f_phase increase with increasing values of G_h but f_res decreases for high values of both G_h and G_p. For G_p = 0, both f_res and f_phase increase as G_h increases (Fig. 11A1; also see Figs. 8B1and 8C1), and they do so almost linearly once resonance has been generated. In contrast, for G_p = 0.5, while f_phase increases with increasing values of G_h, f_res first increases and then decreases (Fig. 11A1). These values of G_h and G_p correspond to a fixed-point located near the knee of the V -nullcline (Fig. 7A2). The switch in the monotonic behavior of f_res can therefore be attributed to a nonlinear effect.

In the I_Ks + I_p model f_res and f_phase increase with increasing values of G_q (Fig 10B1; also see Figs. 9B1 and 9C1). This is similar to the increase of f_res and f_phase with G_h in the I_h + I_p model (Fig. 11A1). Note however that, in contrast to the I_h + I_p model, f_phase is larger for G_p = 0.5 than for G_p = 0, and f_res is almost insensitive to changes in G_p (Fig. 11B1). For G_p = 0 neither model show intrinsic oscillatory activity,but oscillatory activity can emerge for G_p > 0 and with G_h above a certain threshold (Fig. 11A1) or G_q below a certain threshold (Fig. 11B1; also see Figs. 11A2 and 11B2). Interestingly, as G_h increases, f_res decreases and f_nat increases and these frequencies approach the same value (Fig. 11A1). Similarly, the values of f_res and f_nat approach the same value but, in contrast to the I_h + I_p model, as G_q decreases (I_Ks + I_p model; Fig. 11B1). The fact that the nullclines of the two models are qualitatively mirror images of each other suggests that for these parameter values both models might have a common underlying mechanism for the generation of both intrinsic oscillations and resonance.

Similarly, in the I_h + I_p and I_Ks + I_p models Z_max and Q_Z show opposite monotonic behaviors as G_h and G_q increase for G_p > 0. Even though, in both models, when G_p = 0, Z_max and Q_Z are small and almost insensitive to changes in G_h and G_q (Figs. 11A3 and 11B3), when G_p > 0, these models exhibit opposite behaviors as the corresponding resonant conductance increases : in the I_h + I_p model resonance is amplified by increasing G_h while in the I_Ks + I_p model resonance is attenuated by increasing G_q (Figs. 11A3 and 11B3). Note that the largest values of both Z_max and Q_Z occur in the strongly nonlinear regions in parameter space referred to above. The increase in Q_Z and decrease in Z_max as G_h and G_q demonstrate that, in both models, resonance is created by a combined decrease in both Z_max and Z(0) as explained in the previous section for the reduced models.

We now turn to the effect of G_p in the two models. f_res has a similar monotonic behavior as G_p changes in the two models but f_phase has a different monotonic behavior as G_p changes in the two models. Figs. 11A2 and 11B2 show the behavior of both f_res and f_phase as G_p increases. In both models, f_res decreases with increasing values of G_p. This change is more pronounced in the I_h + I_p model than in the I_Ks + I_p model. The dependence of f_phase with G_p is different in the two models: f_phase slightly decreases in the former and increases in the latter. Interestingly, in spite of the different monotonic behavior between the two models, the difference between f_res and f_phase decreases as G_p increases, and both characteristic frequencies become closer in the nonlinear region in parameter space with a high amplifying effect (Figs. 11A2 and 11B2). As mentioned above, neither model shows intrinsic oscillations for low values of G_p but oscillations arise as G_p increases (Figs. 11A2 and 11B2).

The amplification of the voltage response due to increasing values of G_p dramatically increases in the nonlinear region in parameter space in the two models. This is seen in Figs. 11A4 and 11B4 (see also Figs. 8 and 9) where both Z_max and Q_Z increase for large values of G_p as either G_h increases) or G_q decreases. This amplification does not occur for G_p = 0 or with G_p = 0.5 together with lower values of G_h or larger values of G_q, suggesting that it results from the strong nonlinearities present in both models for large values of G_p.

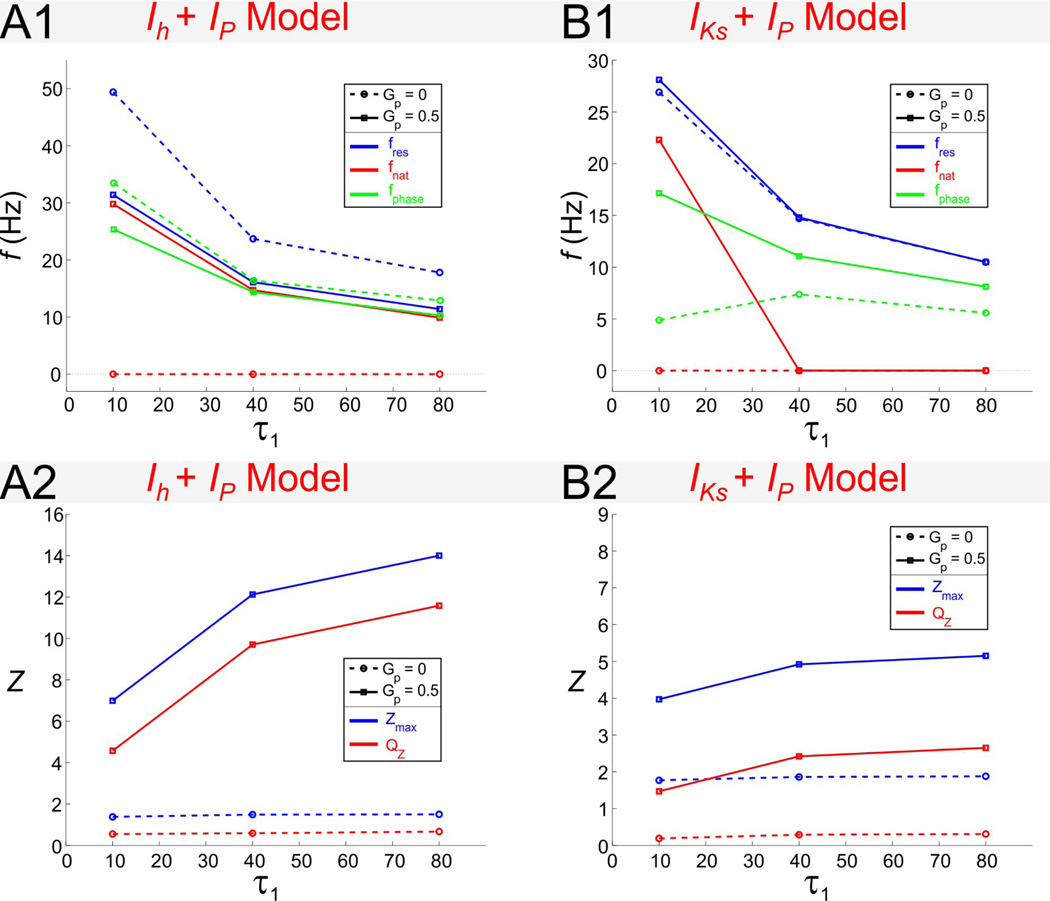
f_res and f_phase decrease with increasing values of the time constant τ₁ in the two models

For the I_h + I_p model (Fig. 12A1), f_res and f_phase are both decreasing functions of τ₁, and are both larger for G_p = 0 than for G_p > 0. For G_p > 0, the difference between f_res and f_phase decreases and they approach identical values. For the I_Ks + I_p model (Fig. 12B2), f_phase first increases with τ₁ for G_p = 0 and then decreases. For G_p = 0.5, both f_res and f_phase are decreasing functions of τ₁. In contrast to the I_h + I_p model, in the I_Ks + I_p model, f_res and f_phase are larger for G_p > 0 than for G_p = 0, although the difference between f_res for these two values of G_p is very small.

The two models show also similarities and differences in their natural frequencies as a function of τ₁. As mentioned above, neither model shows intrinsic oscillations for G_p = 0. For G_p > 0, in both models f_res is always larger than f_nat (Figs. 12A1 and 12B1). For the I_h + I_p model (Fig. 12A1), f_res and f_nat are almost identical for all values of τ₁ (and G_p > 0), while the value of f_res is significantly different than for G_p = 0. In contrast, for the I_Ks + I_p model (Fig. 12B1), intrinsic oscillations (for G_p > 0) disappear as τ₁ increases and f_res is not significantly different for different values of G_p.

Resonance is amplified as τ₁ increases in the presence of I_p in the two models. In the absence of I_p (G_p = 0) both Z_max and Q_Z are insensitive to changes in the time constant τ₁ (Figs. 12A2 and 12B2). However, for G_p = 0.5, both Z_max and Q_Z increase as τ₁ increases. Their difference remains constant since changes in τ₁ have no effect on Z(0). Note that changes in Z_max and Q_Z with τ₁ are more pronounced for the I_h + I_p model (Fig. 12A2) than for the I_Ks + I_p model (Fig. 12B2).

Finally, although for the sake of brevity we do not show these data, f_res and f_phase are almost insensitive to changes in I_app in the two models whereas resonance (Z_max and Q_Z) is significantly amplified by increasing values of I_app in the presence of I_p in both models.

Discussion

A large number of studies in recent years has focused on subthreshold membrane resonance in neurons, its dependence on ionic currents and its influence on neuronal and network oscillations (Richardson et al. 2003; Ledoux and N. 2011; Castro-Alamancos et al. 2007; Tohidi and Nadim 2009; Izhikevich et al. 2003; Engel et al. 2008; Reinker et al. 2004; Kispersky et al. 2012; Moca et al. 2012; Thevenin et al. 2011). Subthreshold membrane resonance is primarily described on the basis of a linear RLC circuit where R is equated with the membrane resistance, C with the membrane capacitance and the inductance L, more abstractly, with voltage-gated ionic conductance properties (Erchova et al. 2004). Membrane resonance is defined by a peak in the impedance amplitude plotted as a function of input frequency (the impedance profile) and can be characterized by a few attributes describing this impedance profile (Fig. 1B1). The frequency and quality (“peakiness”) of membrane resonance is captured by these attributes. A number of voltage-gated ionic currents are known to result in membrane resonance. Yet, even in a simple model neuron that is based on biophysical currents, the dependence of the attributes of the impedance profile on biophysical parameters such as the maximal conductances of the leak and voltage-gated currents is neither well-described nor intuitive.

In the first part of this paper we used a linear 2D model (Richardson et al. 2003) to show how the attributes of the resonance and phase profiles depend on three model parameters, the two effective conductances and the time constant. This analysis resulted in graphs that show how resonance and phase depend on the model parameters (Figs. 2–5). We also compared the resonance frequency in this model with the frequency of subthreshold oscillations, when present (Fig. 4). In the second part, we used this description to understand the emergence and properties of resonance and phase-frequency relationships in two representative conductance-based biophysical models. We began by exploring how changing a biophysical parameter affected the linearization (about an equilibrium point) of the conductance-based model. We then mapped the resulting trajectories (parameterized by the biophysical parameter) in the effective-conductance parameter space described in part one. These trajectories provided us with information on the dependence of resonance and phase attributes on the biophysical parameter. Together, these two parts provide a framework to study linear impedance and to analyze how changing biophysical parameters affects linear resonance and phase profiles in nonlinear conductance-based models. We limited our analysis to 2D models where the linear system is effectively described by two parameters and could be readily illustrated graphically. The framework we presented can be readily generalized to higher-dimensional models by projecting to lower-dimensional parameter spaces or in the form of look-up tables.

We identified two qualitatively different mechanisms for the generation of resonance in 2D systems. The first mechanism depends on the effective conductance γ₁: as γ₁ increases, there is a decrease in both Z_max and Z(0) but the latter decreases at a higher rate (Fig. 3C) which results in an increase in Q_Z. The second mechanism is due to changing τ₁. For very small values of τ₁ the 2D system does not exhibit resonance (Fig. 6A). As τ₁ increases, the system first transitions through a region of the parameter space which shows intrinsic (damped) oscillations with no resonance and for larger values of τ₁ resonance emerges (Fig. 6A–B). Increasing τ₁ further can allow the system to resonance without subthreshold oscillations (Fig 6B1–B2). As such, factors such as temperature that modulate time constants can allow a neuron to transition to resonance without changing the maximal conductances of expressed ionic currents.

The phenomenon of subthreshold resonance is often related to the presence of subthreshold oscillations (Lampl and Yarom 1997) although it is known that these are separate phenomena even in linear models (Richardson et al. 2003). The analysis of the linear 2D model shows that in certain parameter ranges these two frequencies can show similar parameter dependence but that they are also clearly distinct (Fig. 4).

Typically the voltage response of a neuron is studied by focusing on the amplitude of the impedance profile (Hutcheon and Yarom 2000). Yet, just as the impedance amplitude describes the scaling of the membrane potential, the impedance phase as a function of frequency (the phase profile) describes the membrane potential phase shift in response to an oscillatory current. The zero-phase-frequency f_phase—the frequency at which the input current and the membrane potential are synchronous in phase—provides information complementary to the resonance frequency f_max (Richardson et al. 2003). Although in an RLC circuit in series the values of f_phase and f_max are equal, in parallel circuits, such as membrane equivalent circuits, the two values remain distinct (Fig. 1B). Here we examined the dependence of f_phase in a 2D system and found that this frequency remains independent of the effective leak conductance, although the extent to which negative phase shifts occur (ϕ_min) does change with both effective leak and voltage-gated conductances (Fig. 5).

The zero-phase-frequency f_phase has been measured experimentally for the subthreshold response (Gutfreund et al. 1995) or the spike phase response (Fuhrmann et al. 2002; Smith et al. 2000; Carandini et al. 1996). In the latter case, f_phase was used in network models of spiking neurons in determining population synchrony (Fuhrmann et al. 2002). Our analysis provides a description of the dependence of f_phase of the subthreshold linear response on model parameters. As the amplitude of the response approaches threshold, this dependence can be used as a first-order approximation for the neuron’s spike phase and therefore provides a mechanistic understanding of how model ionic currents can affect spike phase.

Voltage-gated ionic conductances have been classified into resonant and amplifying (Hutcheon and Yarom 2000; Richardson et al. 2003) with the underlying implication that all currents in each group behave similarly with respect to changes in parameters. Here we explored two representative conductance-based models with distinct resonant currents, one hyperpolarization-activated (I_h) and the other depolarization-activated (I_Ks). We found that, in the absence of an amplifying current (I_p), the resonant attributes in both models exhibit a similar dependence on the conductance of the two respective resonant currents. This is most easily seen by comparing the solid trajectories in Figs. 8A, B1 and C1 with the corresponding panels of Fig. 9. In contrast, in the presence of the amplifying current I_p, changing the conductance of the resonant current in the two models has opposite effects on the attributes of resonance. For instance, whereas increasing G_h can amplify the voltage response, a similar increase in G_q does the opposite (Figs. 8B2 and 9B2). Similarly, increasing these two conductances in the respective models can have opposite effects on the properties of the phase profile (Figs. 8C2 and 9C2). The difference in the effects of G_h and G_q are again readily observed by examining the corresponding trajectories in the effective-conductance parameter space (compare dashed curves in Figs. 8A and 9A). Although these differences are expected, they have been previously overlooked in the analysis of membrane resonance in neural models.

One of the interesting results of the analysis of the dimensionless model is that an increase in the effective leak conductance g_L leads to an increase in the resonance frequency (Fig. 4D). Recent experimental results have indicated that manipulating the leak conductance does not change f_res significantly (Fernandez et al. 2013; Fernandez and White 2008). For comparison, we varied the levels of G_L in our 2D biophysical models and found that the changes in f_res were much smaller than those seen in Fig. 4D and, in some cases, almost unnoticeable (Fig. 10). This difference is due to two factors. First, a change in G_L in the biophysical model does not result in a linear (vertical) trajectory in the γ_L − γ₁ parameter space. Second, the changes in the parameter values using the linear approximation cannot account for the nonlinear effects of the biological neurons or the biophysical models. A proper exploration of the effects of the leak conductance requires tracking the nonlinear properties of the neurons which is beyond the scope of the current study.

It is important to note that the effect of subthreshold preferred frequencies on the spiking activity of neurons is not straightforward. Although there is experimental evidence of the correlations between subthreshold resonance and spiking activity and, in some cases, this is supported by modeling (Richardson et al. 2003), the spike frequency of neurons is shaped by factors, such as refractoriness, that are nonlinear and are not restricted to the subthreshold regime (Broicher et al. 2012). In particular, the ability of a neuron or network to produce spiking or oscillations cannot be simply equated with how the neuron or network responds to inputs of different frequencies (Fernandez and White 2008; Stark et al. 2013).

In this study we have explored the properties of resonance and phase profiles in a linear system and used this information to examine similar properties for linearizations of simple conductance-based models. Interestingly, some effects of the nonlinearities in the models are captured by the nonlinear trajectories in the effective-conductance parameter space. Yet, it is important to note that the linearizations do not capture other effects that may arise due to nonlinearities that are present even in these simplified conductance-based models. Such effects include, but are not limited to, nonlinear amplifications of the voltage response with input current and the emergence of voltage responses that do not match the input frequency. We will address these issues in future work.

Figure 10.

The effect of G_L on resonance frequency in the I_h + I_p and I_Ks + I_p models. B. Impedance profiles for the linearized I_h + I_p model with G_p = 0 (B1) and G_p = 0.5 (B2) and G_h = 1.5. C. Impedance profiles for the linearized I_Ks + I_p model with G_p = 0 (C1) and G_p = 0.5 (C2) and G_q = 1.5. In all panels I_app = 2.5. Figure legend in A1 applies to all panels.

Figure 11.

Dependence of resonance and phase properties for the I_h + I_p (column A) and I_Ks + I_p (column B) models on the maximal conductances. Panels A1 and B1 show f_res, f_nat and f_phase as a function of G_h (A1) or G_q (B1) with G_p = 0 or G_p = 0.5. Panels A2 and B2 show f_res, f_nat and f_phase as a function of G_p. Panels A3 and B3 show Z_max and Q_Z as a function of G_h (A3) or G_q (B3). f_res and f_nat as a function of G_q. Panels A4 and B4 show Z_max and Q_Z as a function of G_p. I_app = −2.5 for the I_h + I_p model and I_app = 2.5 for the I_Ks + I_p model. The time constant τ₁ = 80 for both models.

Figure 12.

Dependence of resonance and phase properties for the I_h + I_p (column A) and I_Ks + I_p (column B) models on the time constant τ₁. Panels A1 and B1 show f_res, f_nat and f_phase as a function of τ₁. Panels A2 and B2 show Z_max and Q_Z as a function of τ₁. I_app = −2.5 for the I_h + I_p model and I_app = 2.5 for the I_Ks + I_p model. The time constant τ₁ = 80 for both models.

Appendix A. Two-dimensional linear systems: eigenvalues, natural frequency and impedance

Consider the following two-dimensional linear system

$$\{\begin{array}{c}X\prime =aX+bY+A_{\mathit{\text{in}}}{e}^{i\omega t}\hfill \\ Y\prime =cX+dY\hfill \end{array}$$ (17)

a, b, c and d are constant, ω > 0 and A_in ≥ 0.

Intrinsic oscillations and natural frequency

The Jacobian of the corresponding homogeneous system (A_in = 0) is given by

$$J=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right).$$

The roots of the characteristic polynomial are given by

$$r_{1,2}=\frac{(a+d)\pm \sqrt{{(a-d)}^2+4bc}}{2}.$$ (18)

From Eq. (18), the homogeneous system displays stable oscillatory solutions (focus points) for values of the parameters satisfying

$${(a-d)}^2+4bc<0a+d\le 0.$$

The natural frequency is given by

$$\mu =\frac{\sqrt{4bc+{(a-d)}^2}}{2}.$$ (19)

Impedance function

The particular solutions to system (17) have the form

$$X_p(t)=A_{\mathit{\text{out}}}{e}^{i\omega t}{Y}_p(t)=B_{\mathit{\text{out}}}{e}^{i\omega t}$$

Substituting into system (17) and rearranging terms we obtain

$$\left(\begin{array}{cc}\hfill (i\omega -a)\hfill & \hfill -b\hfill \\ \hfill -c\hfill & \hfill (i\omega -d)\hfill \end{array}\right)\left(\begin{array}{c}\hfill A_{\mathit{\text{out}}}\hfill \\ \hfill B_{\mathit{\text{out}}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill A_{\mathit{\text{in}}}\hfill \\ \hfill 0\hfill \end{array}\right).$$ (20)

By solving the algebraic system (20) we obtain

$$Z(\omega )=\frac{A_{\mathit{\text{out}}}}{A_{\mathit{\text{in}}}}=\frac{-d+i\omega }{(ad-bc-{\omega }^2)-i\omega (a+d)},{|Z(\omega )|}^2=\frac{A_{\mathit{\text{out}}}^2}{A_{\mathit{\text{in}}}^2}=\frac{d^2+{\omega }^2}{{(ad-bc-{\omega }^2)}^2+{(a+d)}^2{\omega }^2}.$$ (21)

The impedance Z peaks at the resonant frequency

$${\omega }_{\mathit{\text{res}}}=\sqrt{-d^2+\sqrt{b^2{c}^2-2abcd-2d^{2}bc}}.$$ (22)

The impedance phase is given by

$$\text{tan}(\varphi )=\frac{(ad-bc-{\omega }^2)\omega -(a+d)\omega d}{(ad-bc-{\omega }^2)d+(a+d){\omega }^2}=-\frac{bc+d^2+{\omega }^2}{(ad-bc)d+a{\omega }^2}\omega .$$ (23)

Appendix B. The 2D Biophysical Models

The voltage-dependent activation/inactivation curves x_∞(V) and voltage-dependent time scales τ_x(V) used in the kinetic Eq. (3) for the gating variables x are frequently expressed in terms of

$$x_{\infty }(V)=\frac{{\alpha }_x(V)}{{\alpha }_x(V)+{\beta }_x(V)}{\tau }_x(V)=\frac{1}{{\alpha }_x(V)+{\beta }_x(V)}.$$ (24)

Below we present the functions and parameters corresponding to the various models we use in this paper.

I_h + I_p model

This model has been proposed in (Acker et al. 2003). It has a persistent sodium current and a two-component (fast and slow) h-current given by I_p =G_pp(V−E_Na) = G_pp_∞(V)(V−E_Na) and I_h = G_hr(V−E_h) = G_h(c_fr_f + c_sr_s)(V−E_h) respectively with E_h = −20 mV, E_Na = 55 mV, c_f = 0.65 and c_s = 0.35. The voltage-dependent activation/inactivation and time constants are given by

$$p_{\infty }(V)=1/(1+e^{-(V+38)/6.5}){\tau }_p(V)=0.15r_{f,\infty }(V)=1/(1+e^{(V+79.2)/9.78}){\tau }_{r_f}(V)=0.51/(e^{(V-1.7)/10}+e^{-(V+340)/52})+1r_{s,\infty }=1/(1+e^{(V+71.3)/7.9}){\tau }_{r_s}(V)=5.6/(e^{(V-1.7)/14}+e^{-(V+260)/43})+1.$$

I_Ks + I_p model

This model has been proposed in (Acker et al. 2003). It has a persistent sodium current and a slow potassium (M-type) current given by I_p = G_pp(V−E_Na) = G_pp_∞(V)(V−E_Na) and I_Ks = G_qq(V−E_K) with E_Na = 55 mV and E_K = −90 mV. The voltage-dependent activation/inactivation and time constants are given by

$$p_{\infty }(V)=1/(1+e^{-(V+38)/6.5}){\tau }_p(V)=0.15q_{\infty }(V)=1/(1+e^{-(V+35)/6.5})q_{\tau }(V)=90$$