Smoothness of In vivo Spectral Baseline Determined by Mean Squared Error

Abstract

Purpose

A nonparametric smooth line is usually added to spectral model to account for background signals in vivo magnetic resonance spectroscopy (MRS). The assumed smoothness of the baseline significantly influences quantitative spectral fitting. In this paper, a method is proposed to minimize baseline influences on estimated spectral parameters.

Methods

In this paper, the non-parametric baseline function with a given smoothness was treated as a function of spectral parameters. Its uncertainty was measured by root-mean-squared error (RMSE). The proposed method was demonstrated with a simulated spectrum and in vivo spectra of both short echo time (TE) and averaged echo times. The estimated in vivo baselines were compared with the metabolite-nulled spectra, and the LCModel-estimated baselines. The accuracies of estimated baseline and metabolite concentrations were further verified by cross-validation.

Results

An optimal smoothness condition was found that led to the minimal baseline RMSE. In this condition, the best fit was balanced against minimal baseline influences on metabolite concentration estimates.

Conclusion

Baseline RMSE can be used to indicate estimated baseline uncertainties and serve as the criterion for determining the baseline smoothness of in vivo MRS.

INTRODUCTION

Metabolite quantification is generally achieved by non-linear spectral fitting that estimates the signal intensities of metabolite components (1, 2). Various global or iterative nonlinear least squares algorithms have been used to estimate an optimal fit to magnetic resonance spectroscopic (MRS) data (3–10). The background signals —in addition to signal to noise ratio (SNR), spectral resolution, and lineshapes—also influence metabolite concentration estimates. These background signals arise from residual water, lipids, and macromolecules. They typically have broad line widths and overlap with metabolite signals, thus complicating the estimation of metabolite concentrations, particularly for short echo time (TE) spectroscopy.

Macromolecular signals can be identified and then partially removed from spectral data (11–13). However, these methods require additional data and assume very large differences in relaxation properties between macromolecules and metabolites. In addition to prolonged scan time, heterogeneous in vivo distribution of relaxation properties and poor SNR also lead to errors in determining macromolecule baselines. For example, the heterogeneity of metabolite T₁ leads to an imperfect metabolite null, complicating the often-used T₁ null method. Modeling specific macromolecular signals (14, 15) could result in a much larger and more complex spectral model and increase the difficulty of spectral fitting. Because the linewidths of background signals are significantly broader than metabolite peaks, in more commonly used approaches, a non-parametric smooth line is added to the fitting model to account for background signals (4, 5, 16, 17).

Incorporating a baseline into the fitting model certainly improves goodness of fit. However, a good fit of the spectral model—as indicated by a minimized least squares difference between the model and data—does not necessarily indicate that metabolite and baseline signal contributions are correctly estimated. An under-smoothed baseline can lead to large errors even when fitting residuals are minimized. Conversely, an over-smoothed baseline often results in poor fitting characterized by large fit residuals because background signals are not well represented. The LCModel bundles baseline smoothness with the regularization parameter of lineshape (4). As a result, with the LCModel, a broadened linewidth is often associated with a smoother baseline and, conversely, a less smoothed baseline is usually observed in conjunction with a narrowed linewidth.

Generally, the lowest possible variance for an unbiased estimated parameter can be derived from Cramér-Rao lower bound (CRLB) (18). CRLB gives quantitative insight into uncertainties of statistical inference. The baseline complicates the computation and interpretation of the CRLBs of metabolite concentrations. One time domain semi-parametric estimation approach accommodated the baseline contribution to the CRLBs by adding a separate term to the Fisher matrix (19). This term arose from the baseline characterized by nuisance parameters. Another study adopted a Bayesian point of view to derive the CRLBs that included the baseline contributions (20). The resulting CRLBs reduce to the conventional form in the case of a vanishing baseline.

In this paper, the 3 Tesla in vivo proton MRS baseline was modeled with B-splines and described by a function of spectral parameters. Its contribution to the CRLBs was directly derived from the Fisher matrix. The baseline root-mean-squared error (RMSE) was suggested to quantify the estimation errors of the baseline, and its minimum was used to determine baseline smoothness. The proposed method was verified by both simulated data and in vivo spectroscopy of human brains.

THEORY

Spectral fitting can be performed in either frequency or time domain (1, 2). Frequency domain fitting was adopted in this study because it has the flexibility for choosing any region of interest. Both real and imaginary parts of the spectrum were used after the time domain data were transferred into frequency domain by Fourier transform (FT). For simplicity, only the real part was notated in the following theory.

Baseline Model

Frequency domain data are denoted by a column vector y = (y₁, y₂, …, y_i, …, y_N)^T with index i corresponding to frequency v_i. The values of the model are given by f = (f₁, f₂, …, f_i, …, f_N)^T. The model is a function of spectral parameters represented by a vector p = (p₁, p₂, …, p_l, …, p_M)^T, with l standing for the lth parameter and M for the total number of the parameters. The background signals are represented by cubic B-splines:

$$b(v)=\sum _{i=1}^N{Q}_i(v)c_i,$$ [1]

where Q_i (v) and c_i are the ith cubic B-splines basis and the ith control point, respectively, and v₁ ≤ v ≤ v_N. The vector c = (c₁, c₂, …, c_i, …, c_N)^T is determined by minimizing

$$\sum _{i=1}^N{[y_i-f_i-b_i]}^2+\beta {\int }_{v_1}^{v_N}{[b^{″}(v)]}^{2}dv$$ [2]

with respect to c after substituting Eq. 1 into Eq. 2. b_i stands for b(v_i) and is the ith element of the vector b = (b₁, b₂, …, b_i, …, b_N)^T. b″(v) is the second order derivative with respect to v. The parameter β in Eq. 2 is the regularization term that controls the smoothness of the baseline. For instance, b(v) becomes a straight line when β → ∞. In Eq. 2, the spectral model f is a function of spectral parameters. Given the smoothness parameter β, the baseline b is determined by spectral parameters. Therefore, the baseline model is a function of β and spectral parameters, and can be denoted by b(β, p).

Spectral fitting is conducted by minimizing

$${\Vert \mathbf{y}-\mathbf{f}(\mathbf{p})-\mathbf{b}(\beta ,\mathbf{p})\Vert }^2+\eta (\mathbf{p})$$ [3]

with respect to p. η(p) represents the additional constraints based on a priori knowledge of spectral parameters (4, 21).

Incorporation of Baseline Contribution into the Fisher Matrix

CRLB evaluation uses the Fisher information matrix F, which essentially describes the correlations between spectral parameters. Given the spectral model, the Fisher matrix can be expressed as (18):

$${\mathbf{F}}_{m,n}=\frac{1}{{\sigma }^2}\sum _{i=1}^{N}Re(\frac{\partial x_i^{\ast }}{\partial p_m}\frac{\partial x_i}{\partial p_n}).$$ [4]

Re stands for taking the real part. The superscript * denotes complex conjugation, and σ² is the noise variance in frequency domain. The vector x = [x₁, x₂, …, x_i, …, x_N] usually represents the values of the spectral model at each discrete point. Because the baseline is taken as a part of the model, we extend x to encompass the baseline, i.e., x = f + b. Therefore,

$$\frac{\partial \mathbf{x}}{\partial p_l}=\frac{\partial \mathbf{f}}{\partial p_l}+\frac{\partial \mathbf{b}}{\partial p_l}.$$ [5]

Baseline Mean Squared Error (MSE) and Determination of Baseline Smoothness

The mean-squared-error (MSE) of an estimator θ̂ and the variance (Var) satisfy the following equation (22):

$$\text{MSE}(\widehat{\theta })={[\text{Bias}(\widehat{\theta })]}^2+\text{Var}(\widehat{\theta }).$$ [6]

CRLB is defined as the lower bound of the root of the variance, which is the second term on the right side of Eq. 6.

Provided the spectral model is accurate, all biases are attributable to the baseline when the baseline cannot sufficiently describe the background signals due to enforced baseline smoothness. Determining spectral parameters requires incorporating a baseline. Baseline biases can then propagate into spectral parameters through the process of fitting. As a result, spectral parameter estimates can also be biased. However, those biases are difficult to estimate for in vivo data, because the true spectral parameters per se are unknown. In this study, we treated spectral parameters as unbiased estimators when calculating their CRLBs. An unbiased CRLB for the variances of spectral parameters p gives the inequality (18):

$$\text{Var}(p_l)\ge {({\mathbf{F}}^{-1})}_{l,l}.$$ [7]

In the discrete frequency domain, the baseline is considered as a vector b that consists of an array of estimators (b₁, …, b_N). The baseline variance and the square of the bias can thus be defined as the sum of the variances and the sum of the squares of bias over all points (i = 1, …, N), respectively. Because the non-parametric baseline is a function of the spectral parameters, its variance can be conveniently derived from the variances of the spectral parameters p:

$$\text{Var}[\mathbf{b}(\beta ,\mathbf{p})]=\sum _{i=1}^N\sum _{l=1}^M{\left(\frac{\partial b_i}{\partial p_l}\right)}^2\text{Var}(p_l).$$ [8]

Substituting Var(p_l) with Eq. 7, we have

$$\text{Var}[\mathbf{b}(\beta ,\mathbf{p})]\ge \sum _{i=1}^N\sum _{l=1}^M{\left(\frac{\partial b_i}{\partial p_l}\right)}^2{({\mathbf{F}}^{-1})}_{l,l}.$$ [9]

According to Eq. 6, the baseline MSE can be written as:

$$\begin{array}{l}\text{MSE}(\mathbf{b}(\beta ,\mathbf{p}))=\sum _{\mathrm{i}=1}^N{e}_i^2+\text{Var}[\mathbf{b}(\beta ,\mathbf{p})]\\ \ge \sum _{i=1}^N\left\{e_{\mathrm{i}}^2+\sum _l^M{\left(\frac{\partial b_i}{\partial p_l}\right)}^2{({\mathbf{F}}^{-1})}_{l,l}\right\},\end{array}$$ [10]

where e_i is the bias of the baseline at ith point (i = 1, …, N). Ideally the fit residuals are simply noise in the absence of bias and, as such, the bias e_i can be estimated by

$$e_i^2=r_i^2-{\sigma }^2,$$ [11]

where r_i is the fit residual at ith point, and σ² is the variance of noise. Equation 11 attributed biases to the baseline as described above. The baseline RMSE is the square root of the right hand side of Eq. 10.

Note that the baseline smoothness parameter β cannot be determined by the non-linear least square given by Eq. 3 because the minimum least square always requires β → 0. The baseline b(β, p) interacts with the spectral model f(p) when minimizing Eq. 3, leading to estimation errors for both b(β, p) and f(p). Optimal β should lead to minimal baseline RMSE to minimize the influence of the baseline.

METHODS

Fitting Procedure

The Levenberg-Marquardt algorithm was used to minimize the non-linear least square Eq. 3. The fitting procedure was outlined in our previous article (21). Briefly, it was carried out sequentially by two steps; the step of hard constraints (step 1) was followed by the step of soft constraints (step 2). Hard constraints reduced the number of degrees of freedom, while soft constraints allowed the fitting parameters to vary in a certain degree (4, 21, 23, 24). Step 1 was more robust than step 2 if the starting parameter values differed significantly from the real values, due to the reduced number of degrees of freedom. It was used to provide a starting point for step 2. For each of the inner iterations of the Levenberg-Marquardt procedure, a new set of spectral parameters and a new baseline were used to search for the minimum of the fit residuals. The first baseline originated from the difference residuals at the starting point. A new baseline was created after 20 inner iterations.

All derivatives were numerically computed. The program was written in-house in interactive data language (IDL; Research Systems, Inc., Boulder, CO) and executed using a personal computer.

Simulation

The influence of baseline smoothness was investigated using a simulated spectrum that had three singlet Lorentzian peaks, representing metabolite resonance signals, and an uneven baseline. No constraints were applied to the simulated spectrum. The spectral parameters consisted of individual area, linewidth, and frequency for each peak, and a zero order phase for all three peaks. Results were averaged from the Monte Carlo simulations. Gaussian noise was generated by computer with different random seeds (n = 20). Results were further averaged from the fittings with different starting points (n = 5).

Fitting of In vivo Short TE and TE-averaged Spectroscopy Data

The short TE spectral model consisted of basis spectra of N-acetyl-aspartate (NAA), N-acetyl-aspartyl-glutamate (NAAG), total creatine (tCr), total choline (tCho), glutamate (Glu), glutamine (Gln), myo-inositol (mI), aspartate (Asp), γ-aminobutyric acid (GABA), taurine (Tau), and glutathione (GSH) spanning the region of 1.2–4.0 ppm. The model basis spectra were generated by spin density calculation, with the coupling constants obtained from the literature (25). The linewidths of individual metabolite components were constrained in a soft manner, allowing a certain degree of adjustment to compensate for potential T₂ inaccuracies in basis spectra (21). The assumed values of T₂ in basis spectra were based on literature values (26, 27). Asp, GABA, Tau, and GSH were represented by weaker resonance signals than the rest of the metabolites in the model. The reliability of detecting those weak signals in typical clinical short TE studies is generally poor. Their linewidths and resonance frequencies were soft-constrained to a set of reasonable values (relative to NAA) as described in (21). The lineshape was described using the Voigt model (28), in which the Gaussian decay factor was a common parameter shared by all peaks in the spectral model.

Compared to short TE spectroscopy, TE-averaged echo time spectroscopy has simplified spectral structures (29, 30). The basis spectra consisted of NAA, NAAG, tCr, tCho, and Glu. The lineshape and constraints were implemented in a manner similar to that described above for short TE spectroscopy.

The number of data points (4096) was expanded to 8192 by zero-filling in the time domain. The spectral data were scaled by the reference water intensity, which had an assumed concentration of 35880 mM (31). The starting values of the metabolite concentrations were (mM): [NAA] = 10.0, [NAAG] = 1.0, [tCr] = 7.0, [tCho] = 1.5, [Glu] = 7.0, [Gln] = 2.0, and [mI] = 10.0. All other weakly represented components had a starting value of 1.5 mM. The spectral phase was corrected using the reference water signal. The frequency was adjusted by referencing the position of the NAA peak at 2.0 ppm. The starting Lorentz and Gaussian decay factors were 2.0 Hz and 2.5 Hz, respectively.

Comparison and Cross-validation

Metabolite-nulled spectra were acquired with the inversion recovery (IR) method (11,12) and served as the IR-generated baselines. The estimated baselines of short TE spectra were compared with the IR-generated baselines and with the baselines yielded by the LCModel (4). The IR-generated baselines assume that the metabolite protons have identical T₁s and that all macromolecule or lipid protons are fully recovered after the IR time. For the comparison with the LCModel, the basis spectra of macromolecule MM20 and lipid Lip20 defined by the LCModel were removed from the basis set. As such, the LCModel baseline was defined the same as in this study.

The cross-validation was designed to test the accuracy of the estimated baselines. The IR-generated baseline served as the known baseline. First, the estimated baseline and the fit residuals of a short TE in vivo spectrum were removed from the original data, yielding a baseline-free spectrum. Then, a metabolite-nulled spectrum, the known baseline, was added to the baseline-free spectrum to create a synthetic spectrum. The same fitting procedure was performed on the synthetic data. The resulting baseline was compared with the known baseline, i.e., the added metabolite-nulled spectrum.

Data Acquisition

In vivo data were collected from healthy volunteers using the GE 3 T Excite scanner (GE Medical Systems, Waukesha, WI) with a standard head coil. Written informed consent was obtained from all participants. In vivo spectra were acquired from voxels in three regions: frontal lobe (n = 10), anterior cingulate cortex (ACC) (n = 10), and occipital (OCC) lobe (n =10). All voxels measured 2.0×2.0×4.5 cm³. The short echo time spectra used 30 ms TE and 32 averages. TE-averaged spectra were acquired with 32 different echo times (four averages for each echo time). The echo times of TE-averaged spectra started at 35 ms (8.5 ms from the excitation pulse to the first refocusing pulse, and 17.5 ms from the first refocusing pulse to the second refocusing pulse), and were incremented in 6 ms steps for each of the 31 following echoes. The reference data of unsuppressed water were collected immediately after spectral data acquisition. Short TE and TE-averaged spectra were acquired with a repetition time (TR) of 2 s. Metabolite-nulled data were acquired with an inversion flip-angle of 170° (bandwidth 1500 Hz), TR 5.0 s, and an IR time in the range of 680–900 ms. All spectra had 5 kHz bandwidth, and 4096 data points.

RESULTS

Figure 1 illustrates three simulated peaks (in black) with areas of 60.0 (peak 1), 60.0 (peak 2), and 100 (peak 3), respectively. All had a linewidth of 7.0 Hz. The true baseline and estimated baseline are displayed on the bottom in black and red, respectively. The top traces are the fit residuals. Three different degrees of baseline smoothness are shown, with β = 1.70×10⁴ (a), 0.02×10⁴ (b), and 0.17×10⁴ (c), respectively.

Fig. 1.

Fits of the simulated spectra (black) with different degrees of baseline smoothness. The fitted spectra are in red. The true and estimated baselines are displayed on the bottom in black and red, respectively. The top traces are the fit residuals. The estimated baselines were obtained with β = 1.70×10⁴ (a), 0.02×10⁴ (b), and 0.17×10⁴ (c), respectively.

Table 1 gives the averages from the Monte Carlo simulations (n = 20). The actual baseline errors were derived from the differences between the true baseline and the fitted baseline. The error was defined as the root of the sum of squared errors. The smoothness condition with β = 0.17×10⁴ yielded the smallest baseline RMSE (31.2) and the smallest baseline error (27.8). It also yielded the best overall estimate of the peak areas. In Table 1, the uncertainties given in the brackets are the CRLBs of the estimated peak areas, derived from Eq.7. The other two cases—β = 1.7 ×10⁴ and β = 0.02×10⁴—yielded larger baseline RMSEs than β = 0.17×10⁴. The mean standard deviations of estimated peak areas (averaged from the three peaks) were 1.35, 4.38, and 1.56 for β = 1.70 ×10⁴, 0.02×10⁴, and 0.17×10⁴, respectively. Those values are comparable to the uncertainties predicted by the CRLBs (the values within the brackets in Table 1). β = 1.70 ×10⁴ yielded the large biases (peak 2 area was 8% larger than its true value), though the corresponding standard deviations were relatively small. For β = 0.02×10⁴ (the under-smoothed baseline), the fitted peak areas were found to be sensitive to the starting values and, as a result, the largest estimate uncertainties were observed for this case.

Table 1.

Effects of baseline smoothness on estimated peak areas¹.

β(×104)	CRLBbaseline	2 Errorbaseline	Peak 1	Peak 2	Peak 3
1.70	44.4	62.1	59.3(0.83)	65.6(0.85)	97.3(0.78)
0.02	60.1	185	58.6(3.05)	57.4(3.85)	98.1(3.04)
0.17	31.2	27.8	61.2(1.37)	59.7(1.48)	98.5(1.30)

¹The true areas are 60.0, 60.0, and 100, for peaks 1, 2, and 3, respectively; the area uncertainties in brackets are the CRLBs calculated using Eq. [7]

²The actual baseline error was the square root of the sum of the squared differences between the fitted baseline and the true baseline. The reported values (baseline CRLBs, baseline errors, and estimated areas) were averaged from the Monte Carlo simulations and from the fittings with different starting peak areas. Gaussian noise was generated by computer with different seeds (n = 20, σ² = 2.2).

CRLB: Cramér-Rao lower bound.

β = 1.7 ×10⁴ (Fig. 1a) led to an over-smoothed baseline with the largest fitting residuals, while β = 0.02 ×10⁴ (Fig. 1b) yielded an under-smoothed baseline that significantly differed from the true baseline. For the latter, although the fitting residuals (top trace of Fig. 1b) showed no significant fitting errors, the large errors in baseline were actually absorbed by the metabolite peaks because of the strong correlation between the baseline and the spectral peaks in this case. If the baseline contributions were not included in the Fisher matrix, the peak area CRLBs for all three peaks in Table 1 would have similar values, which were smaller than 0.3 (not listed in Table 1).

The effects of baseline smoothness and spectral linewidth were analyzed using the simulated data in Fig. 1. The baseline RMSE versus log β and linewidth are shown in Fig 2a. The effects of five different linewidths (5, 7, 8, 9, and 11Hz) are displayed. The curves were generated by repeated spectral fitting with different β values. Each curve shows a region with a minimal baseline RMSE, and the minimal RMSE varies with the peak linewidth. As expected, the optimal β values increased with greater linewidth.

Fig. 2.

(a): Baseline root-mean-squared error (RMSE) versus the logarithm of the smoothness parameter β and metabolite linewidth. The minimal baseline RMSE and the required smoothness increased with metabolite linewidth. (b): The errors of the estimated peak areas versus metabolite linewidth.

Figure 2b shows the RMSE of the three estimated peak areas as a function of linewidth. The peak areas were estimated with the optimal baseline smoothness, as determined by Fig. 2a. The RMSE of the peak areas was less than 0.2 (the three peak areas are 60.0, 60.0, and 100, respectively) when the linewidth was below 5 Hz. It increased dramatically to ~10 after 9 Hz and then plateaued. The baseline spectral features at 220 and 320 Hz shown in Fig. 1 could not be reliably determined when the overlapping spectral signal was of similar width.

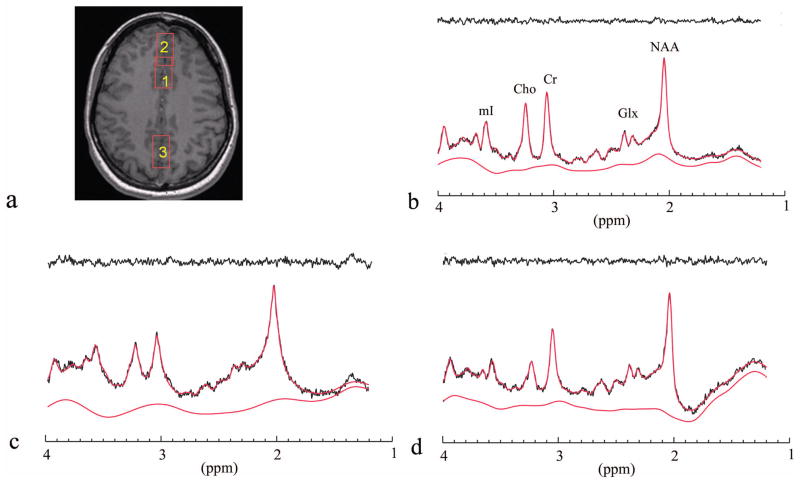
Figure 3 provides three examples for the fitting of short TE spectra (TE = 30 ms). The data were acquired from the frontal lobe (Fig. 3b), ACC (Fig. 3c), and OCC (Fig. 3d), respectively. Fig. 3a is the axial image showing the positions of the voxels in this study. β = 0.2×10⁴ resulted in the minimal baseline RMSE in the fit for the spectra in the ACC and OCC. The spectrum in the frontal lobe had a much wider linewidth and required β = 10.0×10⁴ to yield the minimal baseline RMSE. Table 2 reports the estimated metabolite concentrations relative to tCr.

Fig. 3.

(a): Scout anatomical image showing the location of all the magnetic resonance spectroscopy (MRS) voxels used in this study. Voxels 1–3 were in the anterior cingulate cortex (ACC), frontal lobe, and occipital (OCC) lobe, respectively. (b): ACC short echo time (TE) spectrum (voxel 1) and the fit. (c): frontal lobe short TE spectrum (voxel 2) and the fit. (d): OCC lobe short TE spectrum (voxel 3) and the fit. The ACC and OCC lobe short TE spectra were fitted with the optimized baseline smoothness of β = 0.20×10⁴; the frontal lobe short TE spectrum was fitted with β = 5.0×10⁴. The traces on the top are the fit residuals. The fitted baselines are displayed on the bottom. The resulting metabolite concentrations are listed in Table 2.

Table 2.

^*In vivo metabolite concentrations (relative to tCr) and uncertainties estimated by CRLB.

Region	tCr	NAA	NAAG	Glu	Gln	tCho	mI
Voxel1	1.00(3.0%)	1.21(3.0%)	0.14(19%)	1.24(8.3%)	0.28(28%)	0.28(3.2%)	1.03(4.4%)
Voxel2	1.00(4.7%)	1.51(5.1%)	0.12(52%)	1.27(13%)	0.22(77%)	0.25(6.3%)	1.20(6.3%)
Voxel3	1.00(4.9%)	1.60(4.8%)	0.26(13%)	1.20(10%)	0.26(46%)	0.19(6.7%)	0.76(8.0%)

^*The metabolite concentrations of aspartate, γ-aminobutyric acid, taurine, and gluthinone are not listed. Their CRLBs are generally larger than 50%.

CRLB: Cramér-Rao lower bound; tCR: total creatine; NAA: N-acetyl-aspartate; NAAG: N-acetyl-aspartyl-glutamate; Glu: glutamate; Gln: glutamine; tCho: total choline; mI: myo-inositol.

Figure 4 compares the estimated baseline with the metabolite-nulled spectrum and with the LCModel-estimated baseline. The data (TE = 30 ms) were collected from an ACC voxel of a healthy female (age 21, IR time 720 ms) that comprised mostly gray matter. The spectral fit in Figure 4a used the method of the current study. The fitted baseline is displayed in red under the spectrum. The bottom trace of Fig. 4a is the metabolite-nulled spectrum. The LCModel fit is depicted in Fig. 4b. Estimated metabolite concentrations are shown in Table 3.

Fig. 4.

Comparisons of an estimated baseline with the metabolite-nulled spectrum and with the LCModel-estimated baseline. The data (echo time (TE) = 30ms) were collected from an anterior cingulated cortex (ACC) voxel dominated by gray matter. (a): fit using the method outlined in the current study. The fitted baseline and the inversion recovery (IR)-generated baseline are displayed under the spectrum in red and black, respectively. (b): the LCModel fit. The basis spectra of macromolecule MM20 and lipid Lip20, defined by the LCModel, were removed from the basis set.

Table 3.

Metabolite concentrations (relative to tCr) and CRLBs estimated by the current method versus the LCModel analysis.

Method	tCr	NAA	NAAG	Glu	Gln	tCho	mI
This Study	1.00(4.6%)	1.39(4.3%)	0.04(52%)	1.30(10%)	0.19(50%)	0.23(5.5%)	0.73(7.2%)
LCModel	1.00(3.0%)	1.33(2.0%)	0.09(40%)	1.56(8.0%)	0.49(23%)	0.23(3.2%)	0.73(6.0%)

CRLB: Cramér-Rao lower bound; tCR: total creatine; NAA: N-acetyl-aspartate; NAAG: N-acetyl-aspartyl-glutamate; Glu: glutamate; Gln: glutamine; tCho: total choline; mI: myo-inositol.

Cross-validation is illustrated in Fig. 5. The synthetic spectrum originated from the ACC spectrum shown in Fig. 3c. The fitted baseline and the fit residuals were removed from the original spectrum, yielding a metabolite spectrum without the baseline. A metabolite-nulled spectrum, which served as the known baseline, was then added to this spectrum to create the synthetic spectrum. The estimated baseline and the known baseline are displayed under the spectrum in black and red, respectively. The optimal baseline smoothness was 0.25×10⁴. Figure 5b shows a series of baselines estimated with different degrees of smoothness. The baseline RMSE versus the degrees of smoothness is shown in Fig. 5c. The minimal baseline RMSE led to the estimated baseline in Fig. 5a.

Fig. 5.

Demonstration of cross-validation. (a): fit of the synthetic spectrum. The estimated baseline (red line) and the known baseline (black line) are displayed under the spectrum. (b): the estimated baselines (red lines) versus degrees of baseline smoothness. (c): the baseline root-mean-squared error (RMSE) versus degrees of baseline smoothness. The minimal baseline RMSE led to the best overall fit in (b).

TE-averaged spectroscopy has smoother baselines than short TE spectroscopy due to TE averaging (29, 30). Figure 6 shows the fit of an in vivo TE-averaged spectrum, acquired from voxel 5 in Fig. 3a, with three cases of baseline smoothness: β = 10.0×10⁵, 0.01×10⁵, and 0.20×10⁵, respectively. In β = 10.0×10⁵, the baseline was over-smoothed (a), thereby giving the largest fitting residuals. For β = 0.01×10⁵ (b), however, the baseline was under-smoothed, most likely leading to large errors because the correlation between the baseline and the metabolite peaks was considerably increased, although the residual (top trace) showed an overall excellent fit. The third case, β = 0.20×10⁵(c), yielded the minimal baseline RMSE and, based on our numerical simulations above, would be expected to have the fewest estimation errors for both the metabolites and the baseline.

Fig. 6.

An in vivo echo time (TE)-averaged spectrum, acquired from voxel 3 in Fig. 3a, was fitted with different degrees of baseline smoothness. (a): β = 10.0×10⁵. (b): β = 0.01×10⁵. (c): β = 0.20×10⁵. β = 0.20×10⁵ (c) yielded the minimal baseline root-mean-squared error (RMSE). The traces on the top are the fitting residuals. The estimated baselines are depicted at the bottom of each panel.

DISCUSSION

Spectral fitting in conjunction with the non-parametric baseline falls into the category of semi-parametric regression (32). The model has two parts: the parametric spectral model and the non-parametric baseline. In this study, the non-parametric baseline was considered as a function of the spectral parameters. Its contribution to the CRLBs was directly derived from the Fisher matrix. The baseline is used to account for the background signals that are not included in the spectral model. An over-smoothed baseline cannot sufficiently represent the background signals, resulting in estimate biases that are reflected by the fitting residuals, while an under-smoothed baseline leads to strong correlations between the baseline and metabolite peaks and estimate uncertainties as revealed by the Fisher matrix. The data contained herein illustrates that there exists an optimal degree of smoothness that represents a trade-off between the two requirements.

An extreme case is β = 0, namely, there is no smoothing regularization, and then, b = y − f, and ∂b/∂p_l = −∂f/∂p_l, and consequently, RMSE = ∞ according to Eqs. [4], [5], and [7] (note that σ² > 0). Both estimated spectral parameters and the baseline are completely uncertain because of the correlation between them. In direct contrast, β = ∞ gives a straight baseline and, thus, the correlation between estimated baseline and spectral peaks vanishes. However, a straight line is usually not an ideal baseline model for in vivo spectra and would mostly yield a poor fit.

The minimal baseline RMSE increased with larger linewdith (Fig. 2a). A larger linewidth requires a smoother baseline to prevent the baseline from intruding into spectral peaks, while a smaller linewidth allows for a less smoothed baseline to achieve a better fit to background signals. The first term (i.e., the bias term) in the baseline RMSE (Eq. 10) is unrelated to the noise level, while the second term is proportional to the noise level. Therefore, an elevated noise level leads to an increased degree of smoothness. Conversely, a reduced noise level gives a less smoothed baseline.

Estimation uncertainties can be significantly underestimated when the baseline contribution to the CRLBs is not considered (19, 20). Our simulated data showed that the baseline contribution accounted for more than half of the peak intensities of CRLBs. Neglecting biases can also lead to underestimated CRLBs. If fit residuals contain model errors, the bias term in the baseline RMSE (Eq. 10) will be overestimated, and the baseline RMSE would then suggest a less smoothed baseline to offset the residuals. However, the non-parametric baseline is not aimed at correcting the errors in parameterized model; the errors will be concealed by the baseline instead of being reflected by fit residuals.

Baseline bias occurs when the baseline cannot sufficiently describe the background signals due to inappropriate smoothness. Presently, those biases are not included in the CRLBs for peak areas or in metabolite concentrations; thus, the CRLBs are likely to be underestimated. This is why β = 1.70×10⁴ in Table 1 yielded the smaller peak area CRLBs than β = 0.17×10⁴, i.e., the optimal baseline smoothness; with a very large β, the correlation errors arising from the baseline were substantially reduced while the fitting generated large residuals as a result of the over-smoothed baseline, resulting in biased estimation.

In Fig. 4, the estimated baseline is similar to the IR-generated baseline and the baseline yielded by the LCModel. Nevertheless, the differences are noticeable and not surprising. First, one would expect a certain number of differences between an IR-generated baseline and the true baseline due to the well-known T₁ heterogeneity (e.g., freely rotating methyl protons generally have a longer T₁ than other protons). Second, the estimated baseline had errors, as indicated by the baseline RMSE. The estimated metabolite concentrations were mostly in line with those given by the LCModel, as shown in Table 3. The large variations in NAAG, Glu, and Gln are not surprising, given that separation of NAAG from NAA and Gln from Glu is generally not reliable at 3 Tesla using short TE MRS. In addition, Glu and Gln have no singlet resonance lines to be differentiated from the baseline; estimated concentrations are more likely to be influenced by the baseline. The CRLBs are sensitive to the method used to accommodate the baseline in uncertainty estimates. In Table 3, the CRLBs are mostly larger than those yielded by the LCModel. In two previously reported methods (19, 20), the estimate uncertainties of metabolite concentrations attributed to the baseline were taken into account by the “nuisance” parameters associated with the baseline. In the current study, they were directly derived from the Fisher matrix.

Constraints also affect the computation of the CRLBs. Constraints are necessary for the weakly represented spectral components such as NAAG, GABA, and GSH. The variables to be determined by spectral fitting are thus kept within a reasonable scope. In the current study, the fitted linewidths showed only slight differences between individual metabolite components. Therefore, a single linewidth variable was used to compute the CRLBs. The resonance frequencies of Gln and NAAG (relative to Glu and NAA) changed little and were also not used to compute the CRLBs.

The designated cross-validation (Fig. 5) used a synthetic spectrum that ruled out the potential differences between the IR-generated baseline and the true baseline. It also eliminated possible model errors, because the metabolite signals were generated by the previous fitting. Thus, the estimate uncertainties observed here are only attributable to noise and to the interactions between the baseline and metabolite peaks. Cross-validation revealed that the minimal baseline RMSE led to the best overall fit of estimated baseline to the true baseline. Because the baseline RMSE includes the uncertainties arising from the baseline in addition to fit residuals, it is a more reliable indicator of the fit confidence than fit residuals.

In the current study, a single degree of smoothness was applied to the cubic B-splines over the entire region of spectral fit. Usually, the spectral region toward upfield beyond 1.5 ppm contains stronger macromolecule or lipid signals than the downfield. In Fig. 3b, the fit residuals at ~1.3 ppm were clearly stronger than the rest of the spectrum. Although those residuals could be easily reduced by using a less smoothed baseline, the overall minimal baseline RMSE pointed to a smoother baseline. A locally specified or varying smoothing could be a better approach to handling the baseline over a wide spectral range, leading to a more accurate calculation of the baseline RMSE. As an alternative, the regions containing unexpected signals could be excluded from the baseline RMSE; thus, baseline smoothness would only be determined by uncontaminated spectral regions.

The convergence of a non-linear fitting procedure is often sensitive to the starting point of fitting parameters (33). In this study, the values of the starting point were randomly changed by ~30% in order to test the variability of estimated metabolite concentrations. Estimated concentrations depended only weakly on the starting concentration values with optimally determined baseline smoothness. However, the starting lineshape variables, i.e., the starting Lorentz and Gaussian decay factors, noticeably influenced the resulting metabolite concentrations. Nonetheless, the resulting variations were generally close to the uncertainties predicted by the CRLBs. The interactions between the baseline and the lineshapes of metabolite peaks (8) not only increase the CRLBs, but also influence the convergence of the spectral fitting. As expected, this effect increased with degree of reduced baseline smoothness.

CONCLUSION

Baseline RMSE can be used to determine the smoothness of the baseline and to indicate the uncertainties of estimated parameters and the baseline. The non-parametric baseline can be treated as a function of the spectral parameters. Its contribution to the CRLBs can be directly derived from the Fisher matrix. An optimal baseline condition was found to exist that corresponded to the minimal baseline RMSE and the best fit for both metabolites and the baseline.