Midline Frontal Cortex Low-Frequency Activity Drives Subthalamic Nucleus Oscillations during Conflict

Abstract

Making the right decision from conflicting information takes time. Recent computational, electrophysiological, and clinical studies have implicated two brain areas as being crucial in assuring sufficient time is taken for decision-making under conditions of conflict: the medial prefrontal cortex and the subthalamic nucleus (STN). Both structures exhibit an elevation of activity at low frequencies (<10 Hz) during conflict that correlates with the amount of time taken to respond. This suggests that the two sites could become functionally coupled during conflict. To establish the nature of this interaction we recorded from deep-brain stimulation electrodes implanted bilaterally in the STN of 13 Parkinson's disease patients while they performed a sensory integration task involving randomly moving dots. By gradually increasing the number of dots moving coherently in one direction, we were able to determine changes in the STN associated with response execution. Furthermore, by occasionally having 10% of the dots move in the opposite direction as the majority, we were able to identify an independent increase in STN theta-delta activity triggered by conflict. Crucially, simultaneous midline frontal electroencephalographic recordings revealed an increase in the theta-delta band coherence between the two structures that was specific to high-conflict trials. Activity over the midline frontal cortex was Granger causal to that in STN. These results establish the cortico-subcortical circuit enabling successful choices to be made under conditions of conflict and provide support for the hypothesis that the brain uses frequency-specific channels of communication to convey behaviorally relevant information.

Introduction

The ability to avoid automatic responses during conflict is crucial to successful decision-making. Classically, one area of the brain that has been implicated in influencing behavior during conflict is the medial prefrontal cortex (mPFC; Botvinick et al., 2004). Accordingly, mPFC theta frequency band (4–8 Hz) activity increases during conflict and correlates with conflict-induced fluctuations in reaction time (Cavanagh et al., 2011, 2012; Cohen and Cavanagh, 2011). However, there is increasing awareness that subcortical processes may also play a critical role in inhibiting impulsive responses during conflict (Aron et al., 2007; Frank et al., 2007; Cavanagh et al., 2011). One key structure in this regard is the subthalamic nucleus (STN; Frank, 2006; Bogacz and Gurney, 2007; Weintraub and Zaghloul, 2013). This nucleus has come to the fore as a major target for deep-brain stimulation (DBS) in the treatment of Parkinson's disease. The STN is thought to inhibit movement via its excitatory input to the inhibitory internal globus pallidus (Albin et al., 1989; DeLong, 1990). Accordingly, an intact STN has been shown to be crucial for response inhibition (Baunez and Robbins, 1997; Frank et al., 2007; Eagle et al., 2008), and one of the side effects associated with STN DBS can be impulsivity (Hälbig et al., 2009). With DBS on, patients have faster response times during high-conflict scenarios and are more likely to commit impulsive errors (Frank et al., 2007; Cavanagh et al., 2011; Coulthard et al., 2012; Green et al., 2013). These results, together with the computational models that predicted them (Frank, 2006; Bogacz and Gurney, 2007), have led to the hypothesis that the STN may serve a “hold your horses” function during conflict. According to this hypothesis, the STN inhibits responses, effectively raising the “evidence threshold” and buying more time for corticostriatal pathways to determine the correct response (Cavanagh et al., 2011; Ratcliff and Frank, 2012).

Both neuroanatomical and imaging studies have demonstrated connectivity between the mPFC and the STN (Smith et al., 1998; Nambu et al., 2002; Aron et al., 2007). A functional homology is further suggested by reports showing, as with the mPFC, increased STN theta-band activity during conflict (Cavanagh et al., 2011; Brittain et al., 2012; Zavala et al., 2013). These observations have led to the hypothesis that mPFC theta activity drives similar activity in the STN, which then adjusts the threshold of evidence necessary for a response to be made during conflict. Strong support for this comes from the ability of STN DBS to disrupt the correlation between mPFC theta power and response time slowing during conflict (Cavanagh et al., 2011). Yet to date there has been no proof of a dynamic theta drive from the mPFC to the STN that is explicitly conflict related and dissociable from motor processing related to the selected response. Here we show that this is the case by simultaneously recording STN local field potential (LFP) activity and midline electroencephalographic activity (EEG) while patients performed a sensory integration task that separates conflict and motor responses in time.

Materials and Methods

Subjects and task.

Thirteen subjects (seven males, mean disease duration 10 years, mean age 56 years, range 42–66 years) underwent bilateral implantation of DBS electrodes into the STN, as a prelude to high-frequency stimulation for the treatment of advanced PD. Techniques to target and implant electrodes in the STN were previously described (Foltynie and Hariz, 2010). At University College London Hospital, patients were operated on under general anesthesia, and lead location was confirmed with intraoperative stereotactic magnetic resonance imaging (MRI). At the John Radcliffe Hospital and King's College Hospital, where implantation was performed with patients awake, effective stimulation was confirmed intraoperatively, and lead location was further confirmed with immediate postoperative stereotactic computerized tomography. The permanent quadripolar electrode used was model 3389 (Medtronic Neurologic Division) featuring four platinum-iridium cylindrical surfaces. Electrode extension cables were externalized through the scalp to enable recordings before connection to a subcutaneous DBS pacemaker, implanted in a second operation up to 7 d later.

Patients participated in a decision-making task while on their regular medication 3–6 d after electrode implantation. All subjects gave their written informed consent to take part in the study, which was approved by the appropriate local ethical committees. Clinical details of the patients are provided in Table 1. The mean percentage improvement in the motor section of the Unified Parkinson's Disease Rating Scale (UPDRS) on treatment with levodopa was 63 ± 4% across subjects (p < 0.001, permutation testing between ON and OFF levodopa scores for the 12 subjects with UPDRS scores; Case 3's scores were unavailable; mean UPDRS score difference was compared with 1000 surrogate differences generated by randomly permuting each subject's On and OFF scores before calculating the mean score difference across subjects). The improvement in all subjects' scores with medication indicated a good responsiveness to levodopa in our study participants. Only Cases 10 and 13 had been diagnosed as having an impulse control disorder, however, neither showed behavior that deviated significantly from the other subjects. The mean response time for the two patients with impulse control disorders was 3.182 and 4.594 s, which fell well within the range of the other 11 patients (1.828–4.817 s).

Table 1.

Clinical details

Case	Age	Disease duration	UPDRS Off (III)	UPDRS On (III)	First symptom	Reasons for surgery	Medication (mg/d)
1	49	10	42	6	Tremor	Tremor	Levodopa 300; Trihexyphenidyl 2
2	50	9	58	23	Shoulder stiffness	Motor fluctuations, tremor	Levadopa 1050
3	50	4	N/A	N/A	Right arm tremor	Tremor	Levadopa 400; Rotigotine 16; Entacapone 600
4	66	16	32	13	Loss of dexterity	Bradykinesia	Levodopa 600; Amantadine 200; Ropinerole 24; Rasagiline 1
5	51	7	58	13	Loss sense of smell	Tremor, gait difficulties	Levodopa 1300
6	64	12	70	20	Tremor	Dyskinesias	Levodopa 1200; Apomorphine 7 mg/h
7	47	14	34	11	Left arm bradykinesia	Dyskinesias, motor fluctuations	Levodopa 350; Pramipexole 1.05; Amantadine 300
8	66	14	63	24	Shoulder pain, stiffness	Motor fluctuations	Levodopa 650; Pergolide 9
9	57	7	43	17	Left hand tremor	Tremor	Levodopa 600; Rotigotine 8; Ropinerole 8; Rasagiline 1; Entacapone 1200
10	57	6	21	7	Left side bradykinesia	Dyskinesias, motor fluctuations	Levodopa 750; Entacapone 1000
11	61	4	37	15	Left side tremor	Tremor	Amantadine 200; Levodopa 750; Entacapone 1000
12	65	15	51	21	Left hand tremor	Freezing	Amantadine 200; Levodopa 400; Ropinirole 12
13	42	9	60	42	Loss of dexterity	Bradykinesia, dystonia, freezing	Amantadine 400; Levodopa 600

UPDRS, Part III motor score of the United Parkinson's Disease Rating Scale.

A schematic of the task is shown in Figure 1A. Subjects were asked to stare at a target circle containing 200 randomly moving white dots presented on a black background. The task was generated using the program Psychopy (Peirce, 2007) and presented on a 33 cm Macintosh laptop (60 Hz screen refresh rate). The target circle was 14 cm in diameter and the white dots were 10 pixels large (visual angle ≈0.25°). Before the beginning of the experiment, the subjects were asked to indicate the overall direction the dots were moving whenever they noticed that the dots were coherently moving either left or right. Left direction choices were indicated with a left forefinger press of the “z” key on the keyboard, and right direction choices were indicated with a right forefinger press of the “/” key. Each randomly moving dot moved in a straight line at a rate of 0.14 mm per frame for 20 frames (333 ms) before moving to another part of the target circle and moving in a new direction chosen pseudorandomly between −180 and 180°. This was done to prevent the subjects from focusing on any individual dot and using it to identify coherent motion of the dots.

Figure 1.

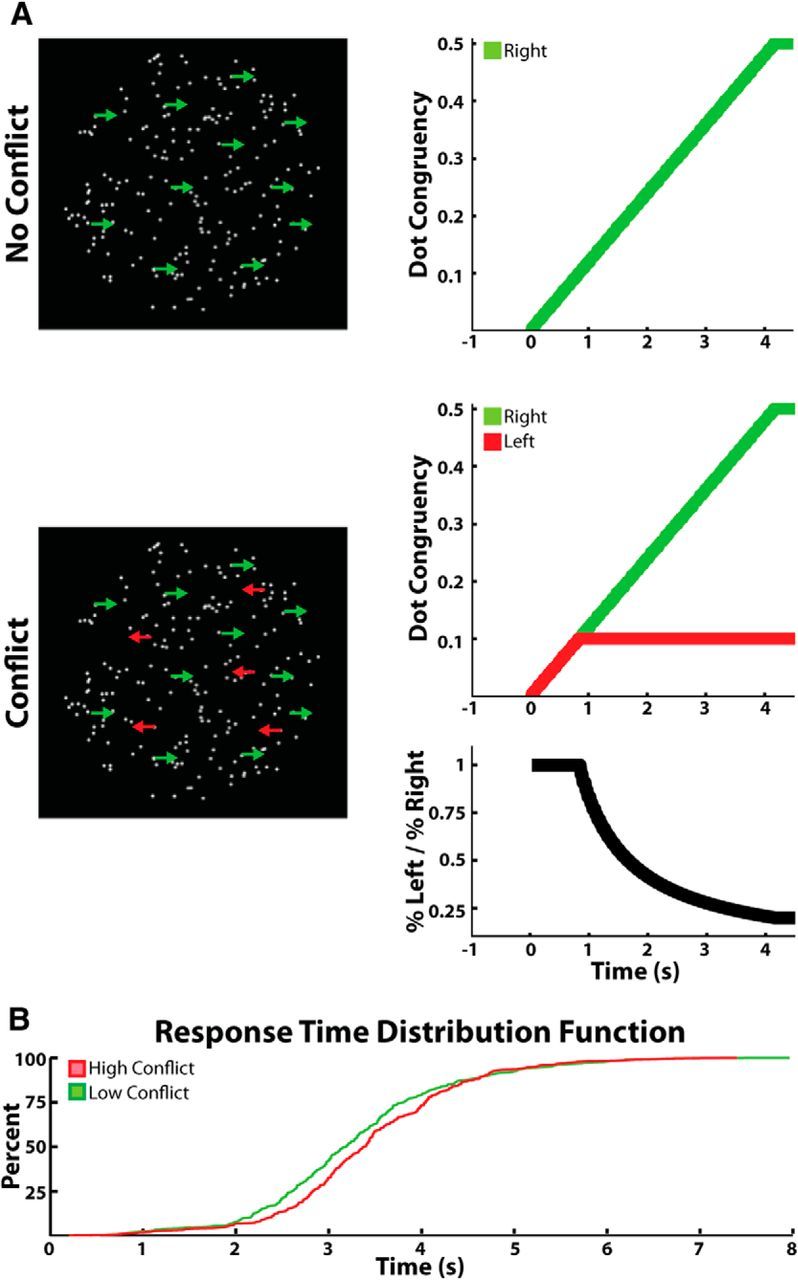
Task and behavior. Randomly moving dots were displayed continuously on screen. During low-conflict trials (A, top), dots began moving coherently in one horizontal direction until either 50% of the dots moved coherently, the subject indicated the direction he or she perceived the dots were moving in, or the trial timed out after 14 s. During high-conflict trials (A, bottom), up to 10% of the dots gradually moved in the opposite direction to the above population. Conflict was highest during the first 833 ms of the trial and then gradually decreased over time as the number of dots moving in the correct direction exceeded the number of dots moving in the conflicting direction (bottom, black trace). Low- and high-conflict trials were randomly interleaved throughout the experiment without the subject knowing what the current trial type was. B, Cumulative distribution function of the response times for all of the low- and high-conflict trials (collapsed across all subjects) used in the analysis.

Two types of trials were randomly shown throughout the experiment. Half of the trials (40 trials) were what we will refer to as “low-conflict trials.” At the beginning of all low-conflict trials, some of the dots started moving horizontally to either the right (0°) or the left (180°) of the screen. The number of dots moving coherently in one direction increased linearly from 0 to 50% at a rate of 0.002% per frame. By 4.16 s, the maximum number of dots moving coherently had been reached (100 dots, 50% of all 200 dots). The second half of the trials (40 trials) were what we will refer to as “high-conflict trials.” The high-conflict trials were identical to the low-conflict trials with the exception that at the same time that some of the dots started moving coherently in one direction, a second group of dots started moving coherently in the opposite direction. Though the percentage of dots moving coherently in either direction increased at the same rate, the maximum number of dots moving in the “conflicting” direction was capped at 20 (10% of all 200 dots; Fig. 1A, bottom). By 0.833 s, the maximum number of dots moving coherently in the “conflict” direction had been reached. Regardless of trial type, subjects were instructed to indicate the direction of the majority of the dots. If the subject answered incorrectly or took longer than 14 s to indicate a response, the word “incorrect” was briefly displayed in the center of the screen for 0.75 s. Incorrect trials were excluded from all analysis. Subjects were allowed to practice the task as long as they wished before the electrophysiological recordings were made. The practice sessions were generally quite short (<10 trials) as the task was designed to be as simple as possible.

It is important to note here that at no point were the subjects given a “cue” indicating that a trial had begun. In other words, there was never a defined stimulus onset and all increases in coherent dot movement were gradual. After the subject pressed a keyboard key to indicate his or her response for a given trial, all dots immediately began to move in random directions. They continued to do so for a pseudorandomly chosen time period of no less than 2 s and no more than 4 s before slowly starting to move coherently again for the next trial. Only when the subject noticed that the dots were moving coherently to the left or the right did the subject become aware that the trial had begun. These gradual changes were designed to suppress neuronal activity caused by abrupt stimulus changes and to increase the separation in time of neuronal activity associated with conflict processing from activity associated with movement (O'Connell et al., 2012).

For the comparison of correct low- and high-conflict trials, all incorrect responses (11 ± 3% of all trials) as well as any trials with reaction time >8 s or <150 ms were discarded (6%). From the remaining trials, any trial with a response time that was greater than two SDs above the mean latency of the other trials was discarded. To determine whether there was a significant difference in reaction time between the two trial types on an individual subject level, the difference of the mean high-conflict trial reaction time and the mean low-conflict trial reaction time was compared with 1000 surrogate differences generated by randomly permuting the low- and high-conflict trials. To determine significance across subjects, the mean difference across subjects between the two trial types was compared with the distribution of 1000 surrogate mean differences generated by randomly permuting the low- and high-conflict trials of each subject before calculating the mean difference across subjects. To determine whether there was a significant across-subject difference in error rates between low- and high-conflict trials, the mean error rate difference across subjects was compared with 1000 surrogate mean error rate differences generated by randomly permuting each subject's error rate for the high- and low-conflict condition before calculating the mean error rate difference across subjects.

Electrophysiological data recording and analysis of power.

STN LFPs were recorded from the DBS electrodes. Simultaneously, continuous scalp EEG was recorded from frontocentral, central and parietal electrodes at the midline (FCz, Cz and Pz; International 10-20 System). More lateral electrodes were prohibited by surgical wounds and dressings in this patient group. All signals were sampled at 2048 Hz, bandpass filtered between 0.5 and 500 Hz, and amplified using a TMSi porti and its respective software (TMS International). Data were analyzed using custom written MATLAB (MathWorks) scripts. Before any analysis, monopolar recordings were down-sampled to 1000 Hz, notch filtered at 50 Hz, and converted to a bipolar montage between contacts (three bipolar channels per STN side and two bipolar channels for the EEG recordings: FCz-Cz and Pz-Cz). Re-referencing was done so as to limit the effects of volume conduction from distant sources. Any trial with a clear artifact in either the EEG or LFP bipolar traces was discarded (mean final trial count after removing artifact trials, incorrect response trials, and behavioral outliers = 56 ± 3.8 trials per subject). For one subject (Case 2), the entire recording had to be discarded due to artifacts. One subject (Case 1) was only implanted in one STN, therefore the total number of STNs studied was 23. In two of the STNs, only one bipolar channel was available because one of the electrode's middle two contacts was not active.

The power and phase of the bipolar channels in each trial were calculated from 4.5 s before to 1.5 s after the response using the Morlet wavelet at 8 scales/octave from 2 to 107 Hz. To assess the differences in induced power between low- and high-conflict trials, the following approach was used. First, the mean power in each of the three STN bipolar recordings and both of the EEG bipolar recordings was calculated by averaging the power spectrum across trials separately for low- and high-conflict trials in each recording channel. The mean evoked response was also calculated by averaging the raw bipolar signal across trials in each recording channel and calculating the power spectrum of the resulting event-related potential. The difference between the mean power spectrum and the evoked power spectrum activity was then calculated to find the induced power spectrum. This method produced a time–frequency image for low- and high-conflict trials for each of the three bipolar contacts on each STN electrode and each of the two EEG bipolar contacts. Each channel's time–frequency pixels were then normalized to the overall mean power of that frequency across all time points in all trials for that channel. The normalized induced power was then averaged across the three bipolar contacts in each STN, and the difference between the low- and high-conflict trials was calculated for each STN and for the two EEG bipolar channels. Averaging across all the contact pairs in a given STN electrode was performed so as to avoid selection bias, although this procedure might serve to underestimate spectral changes in the STN as not all contact pairs were necessarily within or bridging this nucleus.

To assess the statistical significance of the mean induced power difference between low- and high-conflict trials, the same procedure was repeated 1000 times with the low- and high-conflict labels of each trial randomly assigned during each permutation. The p value of each time–frequency pixel was found by comparing the actual mean difference to the distribution of the 1000 permutations for that time–frequency pixel. The p values were then corrected for multiple comparisons using exceedance mass testing (Maris and Oostenveld, 2007). Exceedance mass testing involves integrating the excess mass of suprathreshold clusters in the spectrogram and recording the largest per iteration. The top 5% of this distribution then determined the corrected threshold for imagewise significance.

Because we have previously shown significant correlations between conflict-related changes in theta power and reaction time (Zavala et al., 2013), we also tested whether the low-frequency power we observed during conflict could be correlated to each subject's error rate or to the reaction time on a single-trial level using Spearman's correlation. Unfortunately, this analysis failed to reveal any significant correlations and, for simplicity, these data are not presented. There are several reasons why no correlation was apparent. First, a low number of trials were used to prevent patient fatigue during the task. Second, the low number of trials combined with the ease of the task resulted in a low number of errors being recorded for each subject. Finally, the variability in reaction time across and within subjects made it difficult to pick a particular window for establishing within trial correlations.

Granger causality analysis.

One of the primary interests of this experiment was to explore cortico-STN electrical coupling during conflict. To do so, we used multivariate autoregressive (MVAR) modeling to estimate the coherence (Gardner, 1992; Pesaran, 2008) and Granger causality (Granger, 1969; Kamiński and Blinowska, 1991; Ding et al., 2006; Seth, 2010) between LFP signals recorded from the STN and EEG signals recorded over the frontal and posterior cortices. We use the term coherence to refer to the correlation coefficient of two signals in the frequency domain (Gardner, 1992; Lachaux et al., 2002; Pesaran, 2008). When we say that one signal is “Granger-causal” to a second signal, we mean that the inclusion of past observations of the first signal reduces the prediction error of the second signal in a linear regression model (relative to a model that only includes past observations of the second signal; (Granger, 1969; Seth, 2010). To preprocess the data and calculate the MVAR estimated coherence and Granger causality, the Granger causality connectivity analysis (GCCA) toolbox (Seth, 2010) was used to analyze the raw, bipolar EEG and LFP signals.

Before any analysis, 50 Hz mains artifact was removed by notch filtering, and the data were downsampled to 250 Hz. This was done so as to improve frequency resolution while maintaining the time scale of the interactions (Schlögl and Supp, 2006; Ruiz et al., 2013). Because our recordings took place over multiple trial iterations (as opposed to one long recording) each trial was treated as an independent realization of a statistically stationary process. To minimize nonstationarities across trials, each bipolar channel was normalized horizontally and vertically as follows (Ding et al., 2000; Seth, 2010). First, each trial was zero-meaned across time (horizontal normalization) by subtracting the mean voltage amplitude of that trial from each time point in the trial and dividing the resulting values by the SD of the voltage amplitude of that trial (Ding et al., 2000). Next, the mean and SD of the evoked response (averaged across all trials) was calculated and each corresponding time point in each trial was z-scored (vertical normalization) by the appropriate values corresponding to that time point in the evoked response (Ding et al., 2000; Seth, 2010). The vertical normalization step was done separately for the low- and high-conflict trials. Though vertical normalization is consistently used in the literature (Brovelli et al., 2004; Ruiz et al., 2013) to “(1) remove the first-order nonstationarity from the data and (2) make the ensemple mean equal to zero”(Ding et al., 2000), we found nearly identical results when the vertical normalization step was omitted (data not shown). This is most likely due to our use of gradual changes in the dot coherence that never resulted in a stimulus-onset triggered evoked response. After the data were preprocessed, each 6 s trial was windowed into thirteen 1000 ms blocks with a 500 ms overlap between blocks.

The appropriate model order (i.e., the number of time lags to include when generating the MVAR model matrix) was then found for each STN:EEG electrode pair as follows. First, the best model order of each bipolar LFP:EEG pair was found for each of the conflict trial time windows using the Bayesian information criterion (Schwarz, 1978). This resulted in 39 model orders for each STN:EEG pair (13 time windows by 3 bipolar LFP channels); these 39 model orders were then condensed into one number by averaging across the 13 time windows and the three LFP contacts in that STN. Therefore, each STN finished with two model orders: one for the STN:FCz-Cz interaction and one for the STN:Pz-Cz interaction. There were no significant differences between the STN:FCz-Cz and STN:Pz-Cz model orders across subjects (8.74 vs 8.79; p > 0.05, permutation testing between FCz and Pz model orders; mean model order difference was compared with 1000 surrogate differences generated by randomly permuting each subject's FCz and Pz model orders before calculating the mean model order difference across subjects). The average difference in model order between the STN:FCz-Cz analysis and the STN:Pz-Cz analysis was 0.05 orders, which is approximately equal to 0.2 ms for a 250 Hz sampling rate. Given our 250 Hz sampling rate, our model order of ≈9 steps corresponds to “looking into the past” for ∼36 ms. This model order is consistent with the model orders others have used to resolve frequencies in the delta and beta bands (Brovelli et al., 2004; Schlögl and Supp, 2006; Ruiz et al., 2013). For example, Ruiz et al. (2013) use a model order of 7 with a sample rate of 250 Hz to analyze Granger connectivity in frequencies as low as 4 Hz. Once the appropriate model order had been found for each STN:EEG pair, the coherence (Gardner, 1992) between each LFP:EEG bipolar pair was found by calculating the MVAR model matrix for each trial, averaging the MVAR matrixes across trials and converting the matrix into the spectral domain using the “‘cca_pwcausal” function of the GCCA toolbox (Geweke, 1982; Kamiński and Blinowska, 1991; Ding et al., 2000; Seth, 2010). The formulas used by the GCCA toolbox to convert from the MVAR matrix to the spectral coherence are outlined by Ding et al. (2006). Low- and high-conflict trials were analyzed separately for each electrode pair using the same model order determined for that pair. To determine the directionality of each STN–EEG interaction, the directed transfer function (DTF) provided in the Neurophysiological Biomarker Toolbox (http://www.nbtwiki.net/) was used to find the directed coherence for each LFP: EEG pair (Kamiński and Blinowska, 1991). The frequency range used for the coherence and DTF analysis was the same as the logarithmic range used for the power analysis described above (2–107 Hz, 8 scales per octave).

To verify that the model order we used was indeed capable of analyzing the frequencies we analyzed (2–100 Hz), we also used the GCCA toolbox to analyze two pairs of simulated signals with known connectivity (Fig. 2). The sampling rate was the same sampling rate we used in the analysis of our real data (250 Hz), and the model order was the same as the average model order used in our analysis (9 points). The left column of Figure 2 shows the results for two signals in which signal A Granger caused 30 and 70 Hz oscillations in signal B. Signal B did not cause any oscillations in signal A. Accordingly, there is high coherence at 30 and 70 Hz, and this coherence is due to signal A Granger causing 30 and 70 Hz oscillations in signal B. The right column shows the results for the same signals modified in the following ways: (1) SignalB_filt was produced by bandpass filtering signal B between 1 and 5 Hz. (2) SignalB_filt was then shifted by 40 ms. (3) The time-shifted, filtered signal was then added to signal A. (4) Signal B was left unchanged. Due to the time-shifted filtered signal that was added to signal A, one would expect to see an increase in the Granger causality of signal B to signal A, but not an increase in the Granger causality of signal A to signal B. Accordingly, the analysis on the right column shows an increase in delta band coherence and Granger causality from signal B to signal A. The Granger causality from signal A to signal B remained unchanged, as did the coherence in the higher frequencies. Further validation of our methods stems from that fact that very similar results (higher 2–8 Hz STN:FCz-Cz coherence during conflict) were obtained when we used the fast Fourier transform (Pesaran, 2008) or the wavelet transform (Lachaux et al., 2002) to calculate the coherence between the cortex and the STN (data not shown).

Figure 2.

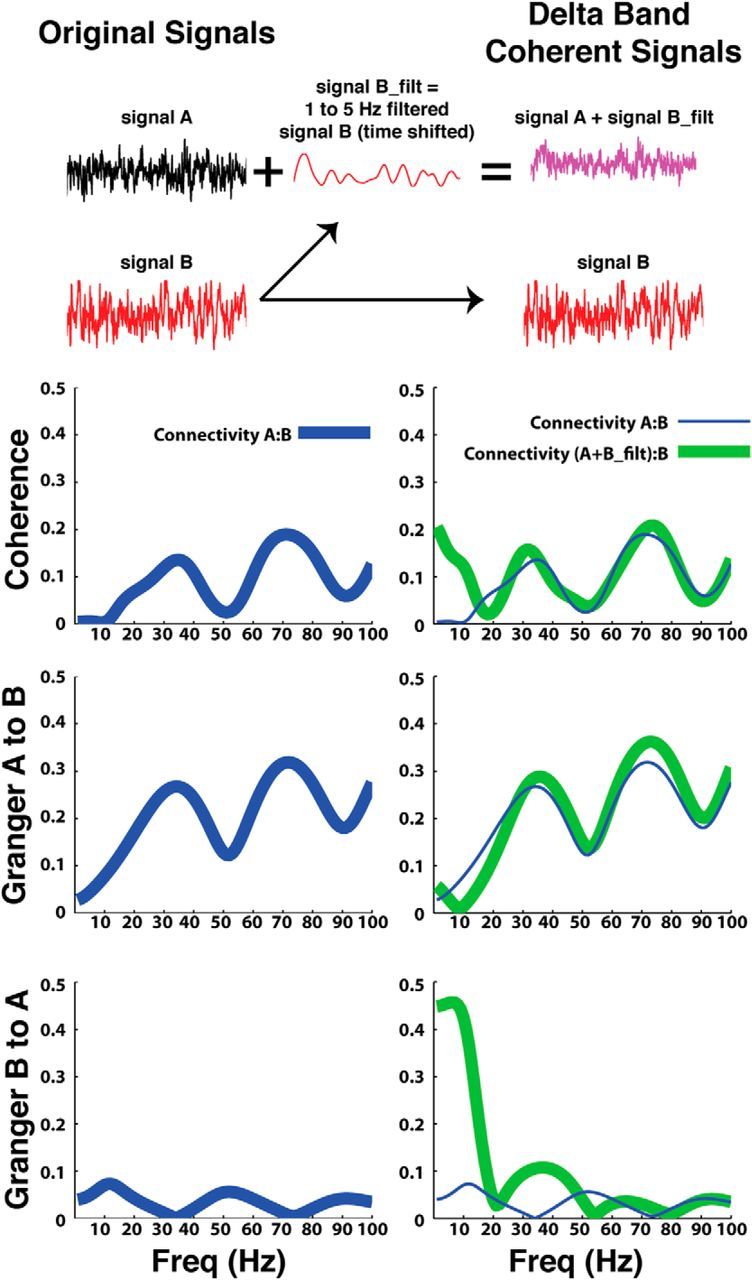
Granger connectivity analysis. The GCCA toolbox (Seth, 2010) was used to analyze the LFP and EEG recordings made while patients performed a decision making task. Along with the analysis of the real data, the toolbox was also used to analyze two simulated signals of known connectivity where one signal (signal A) Granger caused 30 and 70 Hz oscillations in signal B. The left column, which shows the coherence and Granger causality analysis of signals A and B, shows high coherence and A to B Granger causality for these two signals in the 30 and 70 Hz bands. The right column shows the results for the same analysis when signal A was manipulated in a way that resulted in signal B Granger causing 1–5 Hz oscillations in signal A (to this end signal B was filtered, time shifted by 40 ms and then added to signal A, whereas signal B was left unchanged). In line with these manipulations to signal A, the right column shows elevated coherence in the lower frequencies (<10 Hz) and a corresponding elevation in Granger causality from signal B to A. The Granger causality from signal A to B remained unchanged. The results from the left column are replotted in the right column for ease of comparison.

Granger causality differences between low- and high-conflict trials.

To test for time evolving differences in STN:cortical coupling between low- and high-conflict trials, the following procedure was done for each STN:EEG pair (STN:FCz-Cz, STN:Pz-Cz). First, the MVAR matrix was used to estimate the coherence between each LFP–EEG bipolar pair as outlined above. The LFP–EEG coherence was found for each of the three bipolar contacts for each STN. The coherence values at each time-frequency window for each STN contact:EEG electrode pair was then normalized to the “baseline” coherence value for that frequency in that STN contact:EEG electrode pair. Low- and high-conflict trials were normalized separately using the same baseline. The baseline at each frequency was determined by calculating the mean coherence value (averaged across all 13 time blocks) for a set of trials randomly chosen from all of the correct trials. The number of trials used to generate this baseline for each subject was equal to the number of correct low-conflict trials for that subject. Once the LFP:EEG coherence had been normalized for each of the three contacts in each STN, it was averaged across all three STN contacts giving a mean STN:EEG coherence spectrogram. The mean difference across all STNs was then found by subtracting the normalized STN:EEG coherence spectrogram for the low-conflict trials from the normalized STN:EEG coherence spectrogram of the high-conflict trials and averaging across all 23 STNs. This mean difference was then compared with 1000 permuted differences found by randomly permuting the low- and high-conflict trials before calculating the MVAR matrixes. Aside from the shuffling of trials, the 1000 permutations were analyzed in the exact same way as the real data; they were normalized to the same baseline, and the model order used to analyze the permutated data were the same as that used to analyze the real data. To correct for multiple comparisons across time-frequency points, exceedance mass testing was used as detailed above (Maris and Oostenveld, 2007). When testing for a conflict related difference in DTF coupling, the same normalization and permutation analysis used to test for differences in coherence was applied to the DTF values for the STN-to-cortex direction and for the cortex-to-STN direction.

Hilbert coherence analysis.

To further validate our results, the cortico:STN coherence was also calculated using the continuous time evolving methods outlined by Lachaux et al. (2002). Traditionally, the coherence between two signals is the cross-correlation of the two signals in the frequency domain. It is essentially an estimate of the consistency of the phase difference between the two signals and the correlation of the two signal's power. Coherence is estimated by calculating the average cross spectrum of the two signals and dividing by the product of each signal's auto-spectrum:

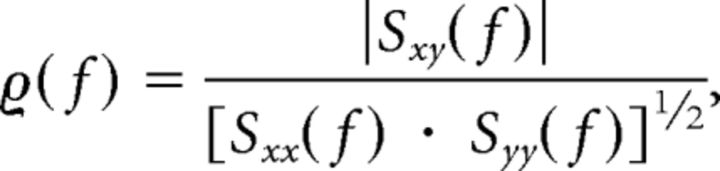where

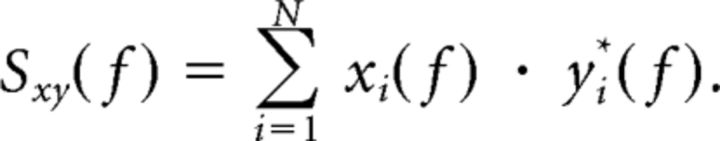x_i(f) and y_i(f) are the discrete Fourier coefficients at frequency f of the finite time series x(t) and y(t), and N are different time windows from which x_i and y_i are estimated. The N time windows can be calculated by dividing a continuous time segment into N windows or by calculating x_i(f) across N trials for the same time window in event locked data. Analyzing our dataset using this traditional Fourier-based method for calculating coherence produced results very similar to those shown in Figure 4 (data not shown). In contrast, for the continuous, time-evolving coherence (Lachaux et al., 2002) the averaging over the window N is replaced by an integration across time over a window that is proportional to the frequency being analyzed:

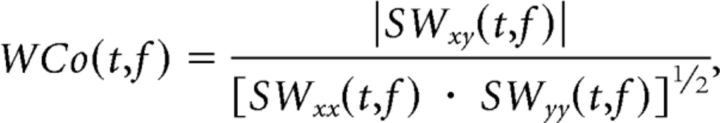where

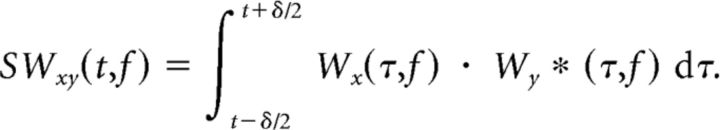W_x and W_y are the wavelet transform (or Hilbert transform in this case) of the signals x(t) and y(t), and δ is a scaler that depends on frequency. By integrating across time and across trials for our response locked data, we were able to generate a time evolving estimate of the coherence between the STN and the frontal cortex.

Figure 4.

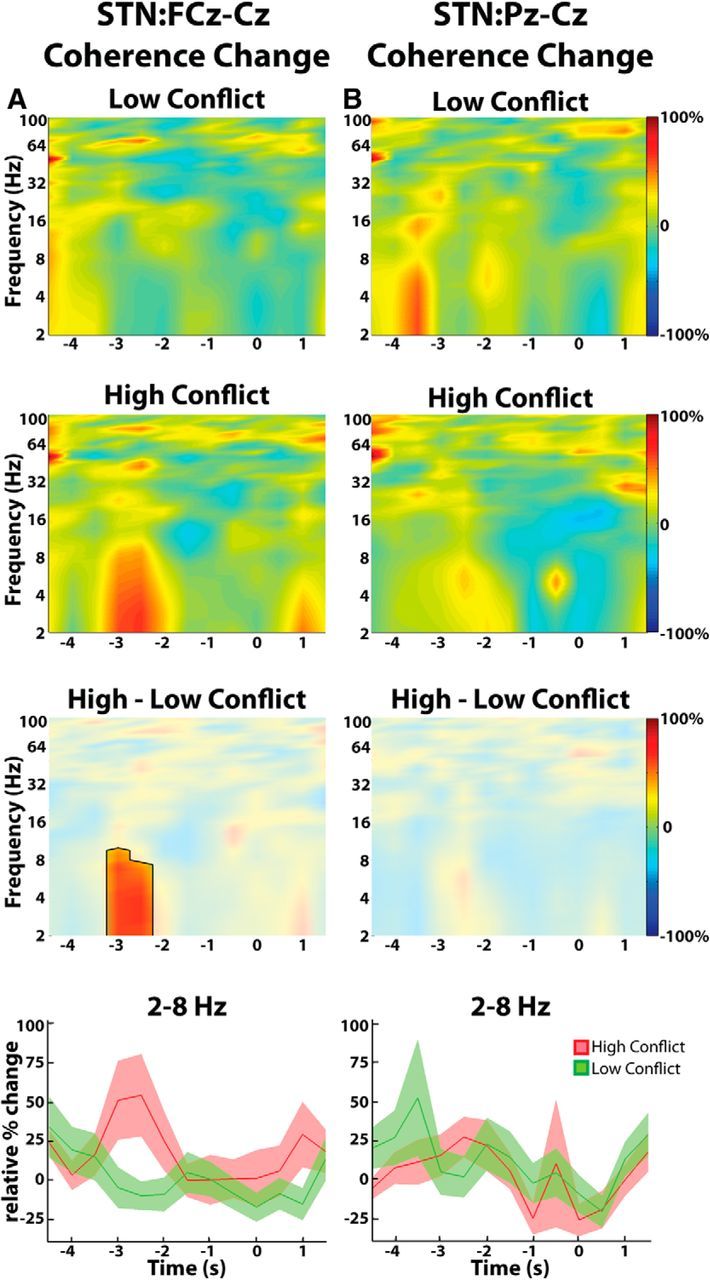
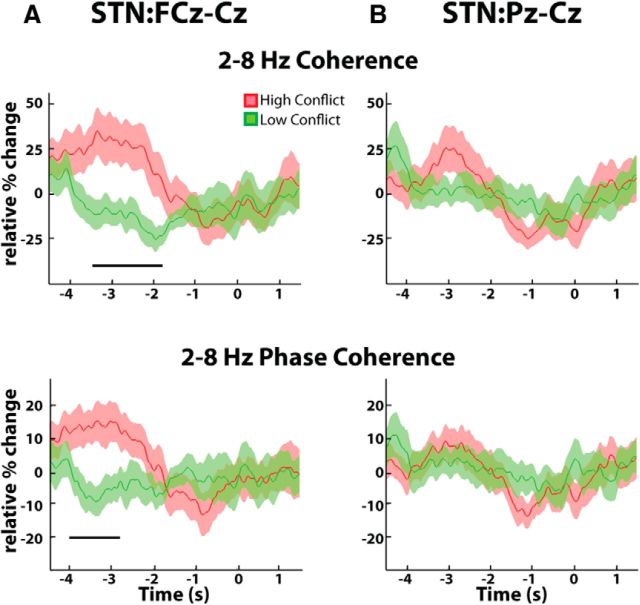
Group average normalized changes in EEG-STN LFP coherence estimated from the Granger causality MVAR matrix. A, High-conflict trials showed a relative increase in response locked STN-frontal (FCz-Cz) cortex coherence compared with low-conflict trials. Differences were significant (p < 0.05, unmasked area, third row). B, There were no conflict-related changes in STN-parietal (Pz-Cz) cortex coupling. Bottom, Mean ± SEM theta-delta coherence changes over time. T = 0 corresponds to response onset.

Low- and high-conflict trials were analyzed separately. Before any analysis, the raw data were bandpass filtered between 2 and 8 Hz and the Hilbert transform was used to extract the power and phase of each LFP bipolar channel and the FCz-Cz bipolar channel. The cross spectrum at each time point was then found by multiplying the LFP's complex Hilbert value at each time point in each trial by the conjugate of the EEG's complex Hilbert value for the corresponding time point. The complex cross-spectrum values were then averaged across trials and a sliding window was used to integrate across time. The width of the window (δ) was chosen to be 1.6 s, according to the recommendations outlined by Lachaux et al. (2002)(8 cycles per frequency × 5 Hz). The absolute value of the resulting average cross spectrum was then divided by the product the two signals' auto-spectrum to produce the Hilbert coherence. The Hilbert coherence between the LFP bipolar channels and the FCz-Cz bipolar channel was found for each LFP channel separately. The time evolving coherence signal was then normalized by each channel's baseline coherence. The baseline was chosen in the same way as it was chosen for the Granger analysis: calculating the mean coherence value (averaged across the entire time series) for a set of trials randomly chosen from all of the correct trials. The three resulting normalized time series generated for each of the three contacts in each STN were then averaged within each STN before averaging across all 23 STNs. Statistical significance was determined using permutation testing as outlined above. To calculate the Hilbert parietal cortex:STN coherence, the same analysis was done using the Pz-Cz bipolar electrode instead of the FCz-Cz electrode.

As a final validation of our results, the same analysis outlined above for the Hilbert coherence was redone using only the phase values; i.e., the phase coherence or intersite phase clustering (Cohen and Gulbinaite, 2014). In other words, instead of finding the magnitude of the average cross-spectrum and dividing by the average auto-spectrum at each time point, the magnitude of the average phase difference between the LFP and the EEG signals was calculated at each time point.

Calculation of power and coherence distributions across STN bipolar contacts.

Here we assumed that the bipolar contact pair with the highest beta band power in each electrode was in or nearest to the dorsolateral motor territory of the subthalamic nucleus (for review, see Brown, 2013). Nineteen of the STNs contained at least one bipolar contact that was ventral to the contact with the highest beta. Comparing the changes in power observed over the highest beta contact with the changes in power observed over the remaining ventral contacts revealed that the higher theta power observed during high-conflict trials was independent of beta power localization (ANOVA, within-subject repeated-measures, conflict × channel: conflict, F = 8.02, df = 1, p = 0.006; channel, F = 0.02, df = 1, p = 0.91; interaction, F = 0.01, df = 1 p = 0.92). Similarly, we were unable to show any localization of the higher delta power observed during high-conflict trials (ANOVA, within-subject repeated-measures, conflict × channel: conflict, F = 5.13, df = 1, p = 0.03; channel, F = 0.62, df = 1, p = 0.43; interaction, F = 0.13, df = 1 p = 0.71) or the higher frontal cortex:STN coherence observed during high-conflict trials (ANOVA, within-subject repeated-measures, conflict × channel: conflict, F = 5.7, df = 1, p = 0.02; channel, F = 0.05, df = 1, p = 0.83; interaction, F = 0.1, df = 1 p = 0.77).

Results

Behavioral results

A schematic of the task is shown in Figure 1A. During the low-conflict trials, dots that were randomly moving in all directions of the screen gradually increased their coherent horizontal motion to either the left or the right. Dot coherence was increased linearly at a rate of 0.002% per frame (60 Hz refresh rate) until the subject indicated the overall direction of movement or the dots reached a 50% coherent movement limit (Fig. 1A, top). During the high-conflict trials, the above population of coherent moving dots behaved in the exact same way as they did during low-conflict trials. Additionally though, a subpopulation of the remaining dots gradually increased their coherent motion in the opposite direction to the majority, inducing conflict (Fig. 1A, bottom). Dots moving in the conflicting direction never exceeded those moving in the preferred direction and were capped early in the trial (after 0.83 s) at 10% of the total number of dots on screen.

On average, subjects required 3.29 ± 0.23 s (SD) to respond on low-conflict trials and 3.43 ± 0.23 s to respond on high-conflict trials (p < 0.05, permutation testing; Fig. 1B). Reaction time differences were therefore small but significant at the group level. Three of the 13 subjects showed a within-subject conflict induced slowing (p < 0.05, permutation testing), and none of the subjects showed conflict induced speeding. High-conflict trials were also associated with a significant increase in error rate (14 ± 3 vs 8 ± 3%, p < 0.01, permutation testing). Due to the low number of errors committed by each subject (4.3 ± 1.2 errors for high-conflict and 2.5 ± 1.0 errors for low-conflict trials), the remaining analyses relate only to correct trials. It is important to note that all changes were gradual and that at no point in the task were subjects informed that a trial had commenced (i.e., there was no cue). Therefore, all data presented below are aligned to the response.

Power changes during low- and high-conflict correct trials

Beginning before the response, low-conflict trials demonstrated a decrease in beta (16–32 Hz) power and an increase in delta (2–4 Hz) power in the STN LFP (Fig. 3A). High-conflict trials also demonstrated a decrease in beta power and an increase in delta power in the STN LFP beginning before the response (Fig. 3B). However, the delta power began increasing earlier than it did in the low-conflict trials and was associated with a significant increase in theta (4–8 Hz) power that was not present in the low-conflict trials. Figure 3C denotes time-frequency points where LFP power was significantly different between the two trial types. Over the time window from − 3 to −1 s, the mean theta power was 10.9 ± 4.3% for high-conflict trials and −1.5 ± 1.5% for low-conflict trials. In the delta band, these values were 5.0 ± 1.8% for high-conflict trials and −3.8 ± 1.4% for low-conflict trials (ANOVA, within-subject repeated-measures, conflict × frequency: conflict, F = 16.96, df = 1, p = 0.0001; frequency, F = 2.55, df = 1, p = 0.11; interaction, F = 0.48, df = 1, p = 0.48). As further reinforced in Figure 3D, the changes in theta and delta power in the high-conflict trials began at least 2 s before the response, when the number of dots moving coherently in one direction was similar to the number of dots moving coherently in the opposite direction. There was no difference in the localization of conflict-triggered delta and theta power increases with respect to beta power across STN contacts (see last paragraph of Materials and Methods).

Figure 3.

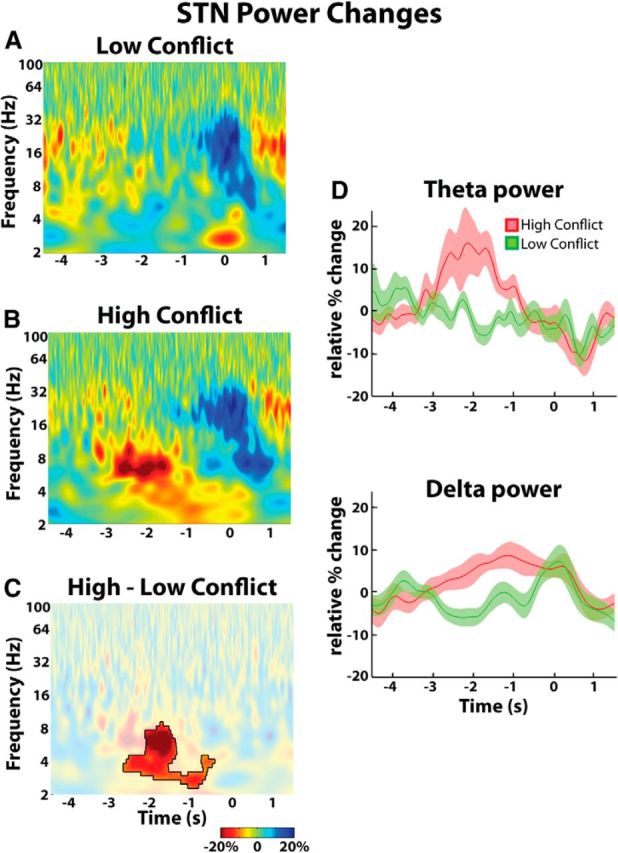
Group average percentage power changes in STN LFP. A, Low-conflict trials showed a decrease in beta power and an increase in delta power beginning just before response onset. B, High-conflict trials showed a response locked theta-delta power increase that began even earlier. The beta power decrease was unchanged. C, Differences were significant (p < 0.05, unmasked area). D, Delta and theta power change over time. Mean ± SEM are shown. T = 0 corresponds to response onset.

Bipolar EEG was simultaneously recorded over midline frontal cortex (FCz-Cz) and parietal cortex (Pz-Cz) during the experiment. The only consistent finding was a decrease in beta power that began before the response; however, there was no significant conflict-related difference in induced power (data not shown). Conducting the same analysis using the FCz-Pz bipolar configuration also failed to show any significant conflict-related differences in induced power (data not shown).

Coherence differences between EEG and STN in low- and high-conflict trials

Given the lack of any difference in the theta and delta bands in pre-response reactivity or localization across STN contacts, we collapsed across these two bands for further analysis of functional connectivity. High-conflict trials demonstrated significantly higher coherence in the theta-delta band between the STN LFP and frontal EEG relative to the low-conflict trials (Fig. 4A). This coherence difference between trial types was not observed over the parietal cortex (Fig. 4B). Although response locked, the coherence increase peaked ∼2–3 s before the response. As power analyses revealed no difference in the behavior or localization of subthalamic theta and delta activities over the key time window of −3 to −2 s before the response, and changes in coherence failed to distinguish between these two bands, we will hereafter consider the theta-delta band as one. During this key time window, the mean change in theta-delta coherence relative to the average coherence observed throughout the entire experiment was 43.3 ± 20.6% for high-conflict trials and −8.4 ± 8.9% for low-conflict trials (p < 0.01, permutation testing). The corresponding values for the STN parietal cortex coherence were 21.3 ± 11.8% for the high-conflict trials and 9.5 ± 12.3% for the low-conflict trials, confirming that there was no significant STN parietal coherence increase during conflict (p > 0.05, permutation testing). Finally, a continuous, time-evolving estimate of the cortical:STN coherence further confirmed that the conflict related increases in the theta-delta band coherence were specific to the frontal cortex (Fig. 5). Even when only the consistent nature of the phase difference (intersite phase clustering; Cohen and Gulbinaite, 2014) between the cortex and the STN was considered, similar results were obtained (Fig. 5B). There was no difference between localization of theta-delta frequency band coherence with frontal EEG across STN contacts (see last paragraph of Materials and Methods).

Figure 5.

Group averaged normalized changes in continuous EEG:STN LFP theta-delta band coherence estimated using the Hilbert transform. A, top, High-conflict trials showed a relative increase in response locked STN-frontal (FCz-Cz) cortex coherence compared with low-conflict trials. Differences were significant (p < 0.05, horizontal bar). A, Bottom, Similar results were obtained when only the consistency of the intersite phase difference was considered. B, There were no conflict related changes in STN-parietal (Pz-Cz) cortex coupling. All mean ± SEM theta-delta coherence changes over time. T = 0 corresponds to response onset.

We then tested whether this increase in theta-delta STN-frontal coherence in high-conflict trials was symmetrical or biased in one or other direction. Only the frontal cortex-to-STN direction revealed any significant conflict related differences, peaking again at ∼2–3 s before the response (Fig. 6). During this time window, the mean change in frontal cortex to STN Granger causality relative to the average Granger causality observed throughout the entire experiment was 17.9 ± 9.7% for high-conflict trials and −10.0 ± 5.2% for low-conflict trials (p < 0.001, permutation testing). The corresponding values for the STN-to-frontal cortex direction were 5.7 ± 6.3% for the high-conflict trials and −7.7 ± 8.2% for the low-conflict trials confirming that there was no significant STN-to-frontal cortex coherence increase during conflict (p > 0.05, permutation testing). In accordance with Figure 4B, repeating the Granger causality analysis for the posterior cortex recordings (Pz-Cz) did not reveal any significant differences in cortex-to-STN and STN-to-cortex Granger causality (data not shown).

Figure 6.

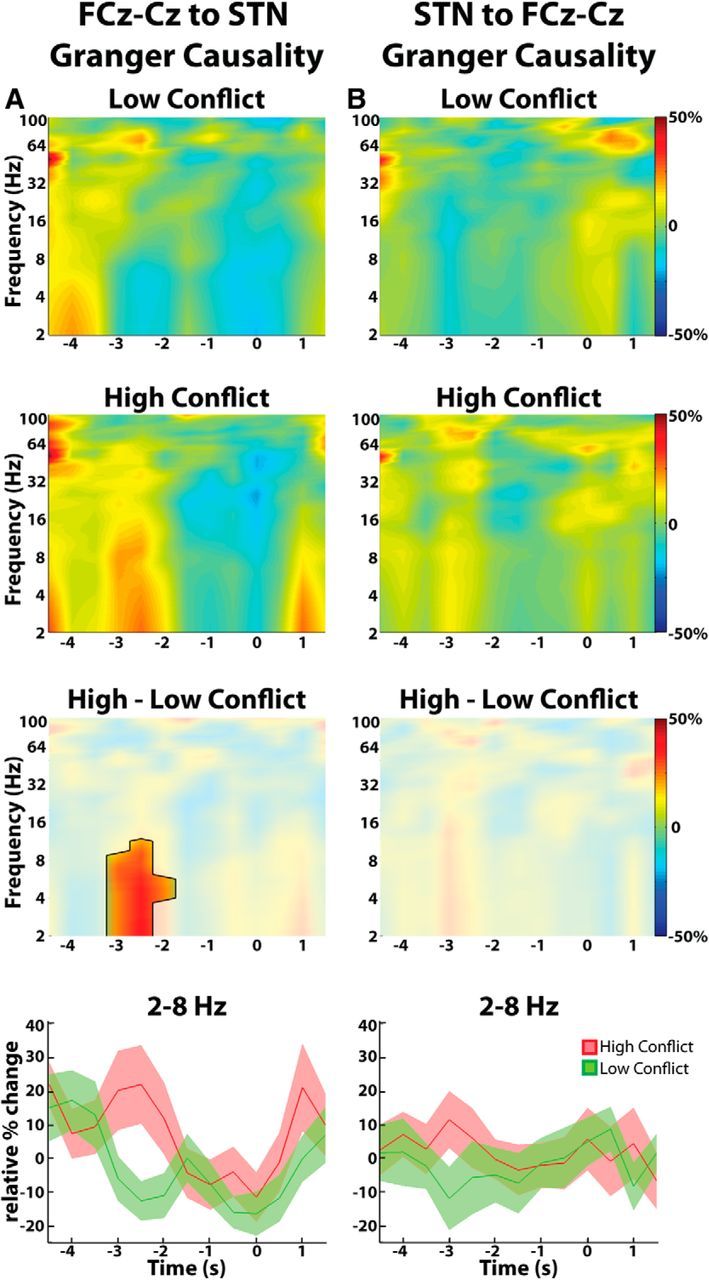
Group average directed coherence between FCz-Cz and STN LFP. A, DTF analysis shows a conflict related increase in response aligned directed coherence in the frontal cortex-to-STN direction. Differences between low- and high-conflict trials were significant (p < 0.05, unmasked area, third row). B, There were no conflict-related changes in response aligned directed coherence in the STN-to-frontal cortex direction. Bottom, Mean ± SEM theta-delta directed coherence changes over time. T = 0 is response onset.

Discussion

This is the first study to demonstrate dynamic coupling of neuronal activity between two key brain areas during conflict, the midline frontal cortex and the STN, and to indicate that this coupling is dominated by information flow from cortex to STN. As such, our findings provide critical support for the hypothesis that the STN and the mPFC work together to raise the brain's decision threshold during times when individuals should “hold their horses” (Frank et al., 2007; Cavanagh et al., 2011; Green et al., 2013). Though prior studies have looked at the behavior of the STN during conflict (Cavanagh et al., 2011; Fumagalli et al., 2011; Brittain et al., 2012; Zaghloul et al., 2012; Zavala et al., 2013), this study is the first to isolate the STN activity due to conflict from that related either to the processing of stimulus onset or the execution of the response. This was achieved in two ways. First, by using gradual rather than discrete changes in stimuli we avoided a discrete stimulus onset (O'Connell et al., 2012). Second, we arranged for conflict to peak after ∼0.8 s, which was ∼2.5 s earlier than the typical response time (∼3.3 s). Theta-delta band activity in the STN and coherence between the STN and the mPFC increased in high-conflict trials during this early period of conflict, and it was not until the activity was no longer present that a response was actually executed. Thus, our study confirms that the elevated STN theta activity we and others have observed is indeed specific to conflict and not a signal of time-on-task as others have proposed (Nachev, 2011; Yeung et al., 2011; Cohen and Nigbur, 2013; Scherbaum and Dshemuchadse, 2013; Zavala et al., 2013).

In contrast, the spectral changes associated with response execution were a decrease in STN and cortical beta power and an increase in STN delta power. Movement related decreases in STN beta power have been repeatedly reported in the literature (for review, see (Hammond et al., 2007). Recently, Alegre et al. (2013) demonstrated an increase in STN delta power during a stop signal reaction time task. This increase in power was triggered by a go stimulus, but was not significantly different between go trials, stop trials, and failed stop trials. Likewise, our delta power increase at the time of the response was not affected by trial type, suggesting that it is a signal specifically associated with the STN′s role in movement execution, and not with the onset of an imperative “Go” stimulus (Alegre et al., 2013) or of a conflicting flanker or Stroop stimulus (Brittain et al., 2012; Zavala et al., 2013).

High-conflict trials were also associated with a higher delta power than in low-conflict trials, and this began concurrently with the theta increase and extended until ∼0.5 s before the response, when the periresponse delta increase seen in low-conflict trials set in. We posit that this early delta power increase during high-conflict trials is related physiologically to conflict, although we cannot exclude the possibility that some of it represents spectral leakage of the greater power in the theta band during this time period.

Role of theta-delta activity in conflict

The elevated theta-delta power associated with high conflict was accompanied by an increase in frontal cortical driven cortico-STN coherence. The mPFC, which sends projections directly to the STN (Smith et al., 1998; Nambu et al., 2002; Aron et al., 2007), has long been postulated to be the area of the brain associated with monitoring conflict (Botvinick et al., 2004). Recently, theta band oscillations have received attention as being the potential “language” the mPFC uses to communicate with other brain structures during conflict (Wang et al., 2005; Hanslmayr et al., 2008; Cohen and Cavanagh, 2011; Cavanagh et al., 2012). Crucially, it has been shown that disrupting STN function through high-frequency DBS dislocates the relationship between mPFC theta power and reaction time during high conflict scenarios (Cavanagh et al., 2011). Furthermore, STN DBS weakens the relationship between conflict and mPFC blood–oxygen level-dependent MRI signaling (Schroeder et al., 2002; Ballanger et al., 2009). In one of the most recent computational models of decision-making, Wiecki and Frank (2013) propose a simple model in which the anterior cingulate cortex, which is widely believed to be the structure in the mPFC that generates theta oscillations (Gevins et al., 1997; Pizzagalli et al., 2003; Wang et al., 2005) and detects conflict (Botvinick et al., 2004), activates the STN when it perceives that conflicting responses have been triggered by sensory input. Here, we have shown a theta-delta frequency band increase in midline frontal cortical-STN coupling specific to high-conflict trials. In the context of the above, this provides compelling evidence of a direct functional link between these two structures and conflict-related processing.

Much of the literature implicating the STN as a crucial player in conflict resolution does so in the context of the drift diffusion model of decision-making (Ratcliff and McKoon, 2008; Cavanagh et al., 2011; Green et al., 2013). In this model, a noisy neuronal process accumulates information supporting one of two alternatives until there is enough neurophysiological evidence to cross a “decision threshold” and execute the winning response (Ratcliff and McKoon, 2008). The STN, with its ability to inhibit movement via activation of the internal globus pallidus and with its numerous connections to various sensory and conflict detecting areas of the cortex (Smith et al., 1998; Aron et al., 2007), is hypothesized to adjust the decision threshold during high conflict decisions by inhibiting movement whenever it (or a structure that activates it) detects conflict (Frank, 2006; Bogacz and Gurney, 2007; Cavanagh et al., 2011). Several studies have shown that when STN function is disrupted by DBS, impulsive mistakes are made during conflict presumably because the STN can no longer adjust the threshold according to the amount of conflict present in a trial (Frank et al., 2007; Wylie et al., 2010; Cavanagh et al., 2011; Green et al., 2013). From the point of view of the drift diffusion model, it is tempting to relate the increased theta-delta band drive from the mPFC and correspondingly increased activity in STN seen during conflict with the evidence threshold adjuster of the model.

Potential limitations of the study

Nevertheless, the present study has several potential limitations. First, all recordings were made from the STN of patients with Parkinson's disease, which has been repeatedly shown to induce abnormal STN activity (for review, see Hammond et al., 2007). However, all recordings were made with patients on their dopaminergic medication in an attempt to approximate physiological functioning as closely as possible. Second, LFP and EEG recordings can be subject to volume conduction of electrical signals. To mitigate this effect, all channel comparisons were made using a bipolar configuration of adjacent channels. The success of this approach was supported by the asymmetry of information flow between the cortex and STN; volume conduction would result in symmetrical information flows. Third, we should consider the effects of any eye movements potentially not rejected through visual inspection of the raw data, particularly as the spectral changes of interest were at low-frequencies. The bipolar configurations adopted will also have served to militate the effects of eye-movement artifacts. Moreover, the asymmetry of information flow between the cortex and STN would again be against simple contamination by eye-movement artifacts. However, our use of bipolar electrodes does diminish spatial resolution within the LFP and may have contributed to the fourth limitation of the present study; that we were unable to localize the effects we observed to either dorsal or ventral STN. Finally, it should be noted that coherence and Granger causal drives can arise in connections between structures like the mPFC and STN, but also from common drives to both from a third area. However, this possibility would be at odds with studies that point to a functional dependency of STN activity on that in mPFC (Ballanger et al., 2009; Cavanagh et al., 2011; Wiecki and Frank, 2013).

Future perspectives

Taken as a whole, our results yield insight into the major role played by low-frequency STN oscillations during conflict processing. Most of the computational and animal models that focus on the STN′s role in decision-making, however, consider single-unit firing (Frank, 2006; Bogacz and Gurney, 2007; Wiecki and Frank, 2013). Therefore, one important future step will be to test how the oscillatory changes we have reported interact with the firing rate changes that have been observed in the STN during conflict and response inhibition (Isoda and Hikosaka, 2008; Zaghloul et al., 2012; Schmidt et al., 2013). This will not only shed light on the network wide mechanisms underlying decision making, it may also have implications for understanding the side effects associated with DBS (Hälbig et al., 2009), as well as the pathophysiology of impulse control disorders in Parkinson's disease, which have been associated with abnormal low-frequency activity in the STN (Rodriguez-Oroz et al., 2011).