Abstract
Background:
Gene expression data often contain missing expression values. Therefore, several imputation methods have been applied to solve the missing values, which include k-nearest neighbour (kNN), local least squares (LLS), and Bayesian principal component analysis (BPCA). However, the effects of these imputation methods on the modelling of gene regulatory networks from gene expression data have rarely been investigated and analysed using a dynamic Bayesian network (DBN).
Methods:
In the present study, we separately imputed datasets of the Escherichia coli S.O.S. DNA repair pathway and the Saccharomyces cerevisiae cell cycle pathway with kNN, LLS, and BPCA, and subsequently used these to generate gene regulatory networks (GRNs) using a discrete DBN. We made comparisons on the basis of previous studies in order to select the gene network with the least error.
Results:
We found that BPCA and LLS performed better on larger networks (based on the S. cerevisiae dataset), whereas kNN performed better on smaller networks (based on the E. coli dataset).
Conclusion:
The results suggest that the performance of each imputation method is dependent on the size of the dataset, and this subsequently affects the modelling of the resultant GRNs using a DBN. In addition, on the basis of these results, a DBN has the capacity to discover potential edges, as well as display interactions, between genes.
Keywords: Bayesian method, DNA microarrays, gene expression, gene regulatory networks, gene expression regulation
Introduction
Deoxyribonucleic acid (DNA) microarrays are extensively used to represent the genetic expression of tens of thousands of genes under a variety of conditions, as well as in the study of many biological processes, varying from human tumours (1) to yeast sporulation (2). Several statistical, mathematical and machine-learning algorithms exploit these data for diagnosis, drug discovery, and protein sequencing for example. The most commonly used methods include data dimension reduction techniques (1), class prediction techniques, and clustering methods. Consisting of hundreds, or even thousands, of gene-specific DNA sequences, gene expression microarrays produce massive gene expression data sets in the form of large matrices; however, some values may be absent. The missing values can be due to a variety of factors, such as insufficient resolution, image corruption or simply dust or scratches on the slide. Moreover, systematic data that are missing may also present themselves in the robotic method for the generation of gene expression profiles (2).
Repetition of identical experiments has been conducted to validate downstream microarray analysis algorithms addressing the issue of the missing values. However, this is costly and time-consuming. These methods are widely used by biologists, but their disadvantages are obvious: omission of the profile vector results in the loss of useful information; and padding with zeros and row averages does not provide accurate missing value estimation. However, some rather sophisticated alternative approaches have been proposed (2), and these are based on the k-nearest neighbour (kNN) algorithm (kNNimpute) and the singular value decomposition (SVD) algorithm (SVDimpute). The kNNimpute method aims to identify k genes that are very similar to the genes with missing values, where the similarity is estimated by the Euclidean distance measure, and the missing values are imputed with the values of weighted average from these neighbouring genes. The SVDimpute method obtains a set of mutually orthogonal expression patterns (eigengenes) from the gene expression matrix, and imputes the missing values by regressing the gene against the k eigengenes and then linearly combining the eigengenes.
Oba et al. (3) recently developed an optimisation method based on Bayesian principal component analysis (BPCA), which outperforms the kNNimpute and SVDimpute methods. One of the features of BPCA that allows it to provide a better performance than the latter two methods is its capacity to auto-select the parameters used in the estimation. This method also produces an improved estimation performance when the number of the samples is huge. Kim et al. (4) also proposed a method, based on local least squares (LLS; LLSimpute), which exploited the local similarity structures in the data, as well as the least squares optimisation process. However, some of these methods do not make the most use of missing values in one row of certain expression profiles (see Methods section), such that other missing values are just excluded, or padded with zeros or row averages in the estimation. Despite this, the effects of imputation methods on the modelling of gene regulatory networks (GRNs) from gene expression data have been rarely investigated and analysed using a dynamic Bayesian network (DBN). In this paper, we assessed gene expression data obtained from Escherichia coli and Saccharomyces cerevisiae with a variety of parameter settings. With regard to the performance outcome, we used the kNN, BPCA, and LLS impute methods and investigated their effects on the resultant GRNs, by comparing them with the results of previous studies.
Materials and Methods
Here, we describe the details of each method we used in this study. In essence, the gene network construction steps include missing values imputation, discretisation of the dataset, and modelling of GRNs using a DBN.
Missing Values Imputation and Discretisation of Dataset
This experimental study was based on E. coli SOS DNA repair network gene expression data (5) and S. cerevisiae cell cycle time-series gene expression data (6). The former include the expression kinetics of the primary eight genes of the SOS DNA repair network of E. coli (the dataset is available at http://www.weizmann.ac.il/mcb/UriAlon/), and this well-known gene network is responsible for repairing the DNA after damage. Initial measurements are taken after irradiation the DNA with ultraviolet (UV) light, and four experiments are conducted using various light intensities. Each experiment consists of 50 instants that are evenly spaced at 6 minutes intervals, and eight genes are monitored: uvrD, lexA, umuD, recA, uvrA, uvrY, ruvA and polB. Conversely, the S. cerevisiae cell cycle pathway gene expression data (the dataset is available at http://genome-www.stanford.edu/cellcycle/data/rawdata) consists of 6178 genes observed through three different condition-specific experiments, namely, factor arrest, elutriation, and temperature-induced arrest of mutant. The missing values found in gene expression data can influence a significant amount of genes, thereby negatively impacting subsequent downstream analysis and experiments (7). In this study, the E. coli S.O.S. DNA Repair network gene expression data contains 11.5% missing values (184 out of 1600 observations) while the S. cerevisiae gene expression data contains 5.9% missing values (28127 out of 475706 observations). To tackle this problem, we imputed the experimental data before discretisation using three different imputation methods; kNN (natively available in MATLAB Bioinformatics Toolbox), LLS (available at http://www.cc.gatech.edu/~hpark/software), and BPCA (available at http://hawaii.sys.i.kyoto-u.ac.jp/~oba/tools).
kNN-based methods tend to select genes with expression profiles similar to the gene of interest to impute missing values (2). Consider that gene A has one missing value in experiment 1; this method would find other k genes, which have a value present in experiment 1, with expression most similar to A in experiments 2–N (where N is the total number of experiments). A weighted average of values in experiment 1 from the closest k genes is then used as an estimate for the missing value in gene A. In the weighted average, the contribution of each gene is weighted by similarity of its expression to that of gene A. Conversely, BPCA uses a Bayesian estimation algorithm to predict missing values (8), and suggests using the number of samples minus 1 as the number of principal axes. The missing values estimation, or imputation method, based on BPCA consists of three processes: principal component regression, Bayesian estimation, and an expectationmaximisation-like repetitive algorithm. In the LLS method, a target gene that has missing values is represented as a linear combination of similar genes. Rather than using all available genes in the data, only similar genes, based on a similarity measure, are used. There are basically two steps in LLS imputation; the first of these is to select k genes by the L2 -norm or by Pearson’s correlation coefficients, and the second is regression and estimation to impute missing values, regardless of how the k genes are selected (8).
Discretisation is applied to the experimental data, as it offers robustness and simplicity of learning (9). In the present study, we discretised the experimental data into three classes (upregulation, down-regulation, and normal), on the basis of the expression rate, and determined the threshold value for discretisation by using the baseline cut-off of gene expression values (10).
A Dynamic Bayesian Network
A DBN is essentially an extension of a Bayesian network; it extends the latter’s capacity to address the temporal aspect of a stochastic network. In general, a DBN represents sequences of variables. These sequences are often timeseries (i.e. in speech recognition) or sequences of symbols (i.e. protein sequences). A DBN is defined as a pair (B0, B→), where B0 defines the prior P (Z1), and is a two-slice temporal Bayes net, which defines P (Zt | Zt-1) by means of a directed acyclic graph, as follows:
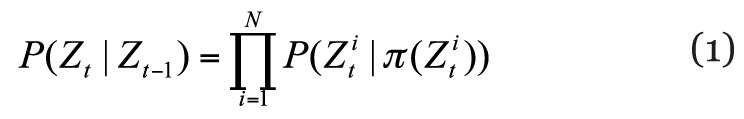
However, a discrete DBN (dDBN) is a DBN specialisation that models temporal processes. Its graphical topology is divided into columns of nodes, such that each column represents a time frame. Each random variable is represented by one node in each of the columns. Links are allowed to connect nodes between columns, provided the link points forward in time. Ideally, there would be one column for every time frame and links could connect nodes separated by arbitrary time steps (including nodes in the same time frame). However, such dDBNs are intractably large, and require far more data and computational resources to learn than are likely to be available.
Results
We compared the resultant GRNs for the E. coli dataset with the well-known E. coli SOS DNA repair network (11), and compared the inferred GRNs for the S. cerevisiae dataset with the established S. cerevisiae cell cycle pathway at Kyoto Encyclopedia of Genes and Genomes (KEGG) (http://www.kegg.jp), as well as the results obtained by Dejori (12). The S. cerevisiae cell cycle sub-networks that we chose for comparison were the YOR263C and the YPL256C sub-networks. An edge signifies the existence of a relationship between the two connected genes, a cross attached to the edge represents an incorrect inference and an edge without any addon is a correct inference. Sensitivity relates to the capacity of the test to identify positive results, and specificity indicates the test’s capacity to identify negative results.
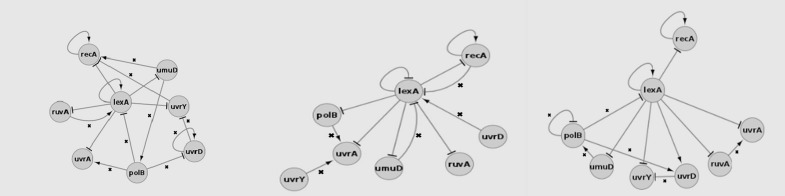
Table 1 shows the sensitivity and specificity of the E. coli SOS DNA repair network constructed by using a DBN with different imputation methods. We calculated sensitivity and specificity by comparing the established E. coli SOS DNA repair network (Figure 1) and the resultant GRNs from the E. coli SOS DNA repair network gene expression data (Figure 2). The imputation method with the highest sensitivity and specificity was kNN, which had a sensitivity of 70% and a specificity of 88.89%. The BPCA method produced the lowest sensitivity value, as well as the lowest specificity value, these being 63.64% and 78.05%, respectively. With 63.64% sensitivity and 83.72% specificity, LLS performed better than BPCA, but worse than kNN.
Table 1.
The sensitivity and specificity of the E. coli SOS DNA Repair network constructed by using DBN with different imputation methods
| Imputation Methods | Sensitivity | Specificity |
|---|---|---|
| kNN | 70.00% | 88.89% |
| BPCA | 63.64% | 78.05% |
| LLS | 63.64% | 83.72% |
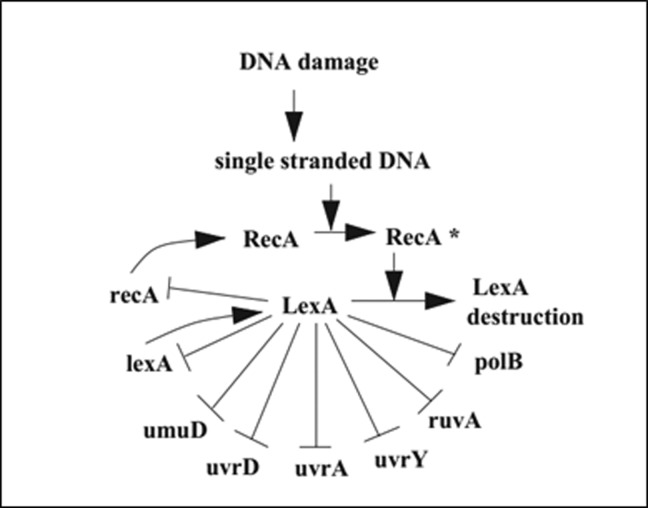
Figure 1:
SOS DNA Repair network (11).
Figure 2:
SOS DNA Repair network constructed with: left – BPCA, middle – kNN, right – LLS imputation method.
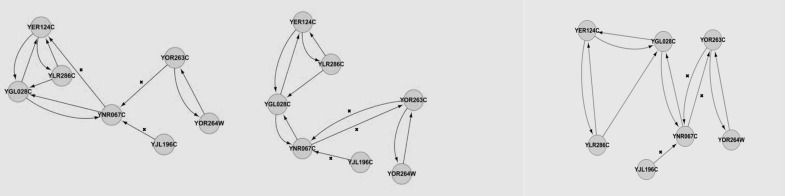
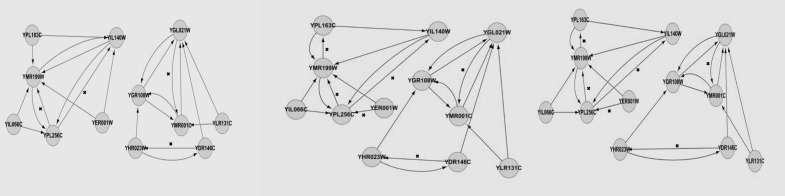
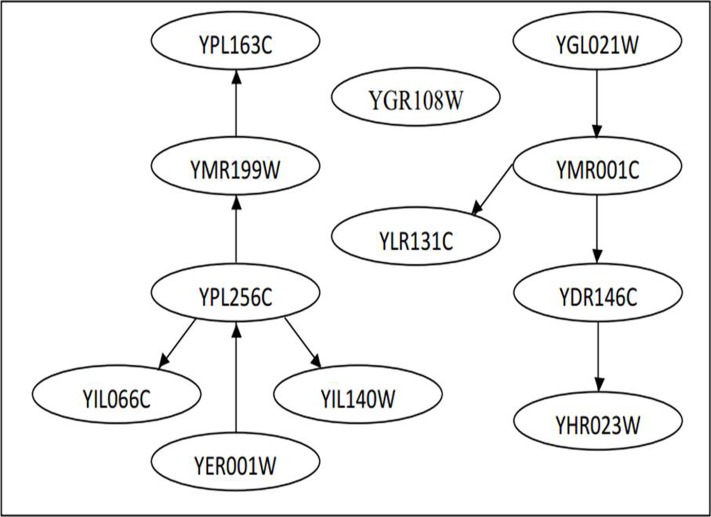
Table 2 summarises the sensitivity and specificity of the S. cerevisiae YOR263C subnetwork inferred by using DBN with different imputation methods. We calculated the sensitivity and specificity by comparing the S. cerevisiae cell cycle pathway at KEGG, and the results obtained by Dejori (12) (Figure 3), with the resultant GRNs from the S. cerevisiae cell cycle pathway gene expression data (Figure 4). Again, kNN registered the highest sensitivity and specificity, at 83.33% and 92.86%, respectively. LLS performed relatively competitively against kNN, it recorded a sensitivity of 83.33% and specificity of 80.00%, while BPCA produced the lowest sensitivity at 71.42%, but achieved a specificity of 92.86%. Table 3 shows the sensitivity and specificity of the S. cerevisiae YPL256C sub-network constructed by using DBN with different imputation methods. Again, the resultant GRNs (Figure 6) were compared with the pathway at KEGG and the results obtained by Dejori (12) (Figure 5). With regard to kNN, the sensitivity was 44.44% while the specificity was 84.96%. Both BPCA and LLS achieved the same sensitivity and specificity of 66.67% and 82.18%, respectively.
Table 2.
The sensitivity and specificity of S. cerevisiae YOR263C sub-network constructed by using DBN with different imputation methods
| Imputation Methods | Sensitivity | Specificity |
|---|---|---|
| kNN | 83.33% | 92.86% |
| BPCA | 71.42% | 92.86% |
| LLS | 83.33% | 80.00% |
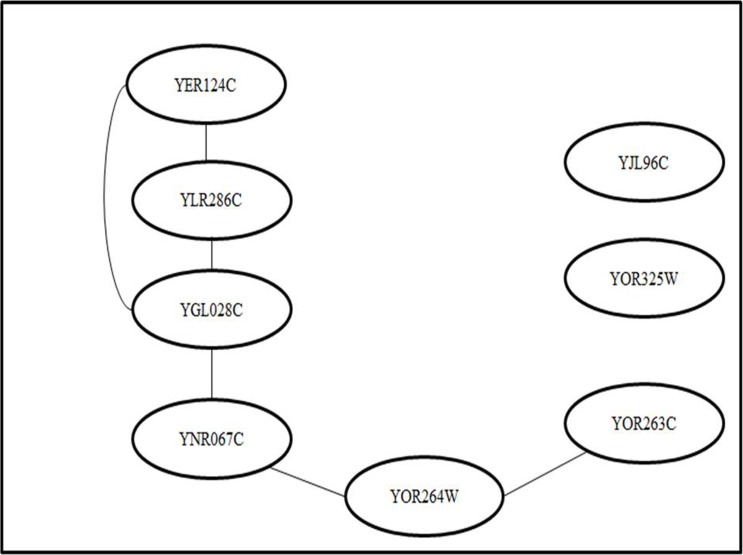
Figure 3:
YOR263C sub-network (12).
Figure 4:
YOR263C sub-network constructed with: left – kNN, middle – BPCA, right–LLS imputation method.
Table 3.
The sensitivity and specificity of S. cerevisiae YPL256C sub-network constructed by using DBN with different imputation methods
| Imputation Methods | Sensitivity | Specificity |
|---|---|---|
| kNN | 44.44% | 84.96% |
| BPCA | 66.67% | 82.18% |
| LLS | 66.67% | 82.18% |
Figure 6:
YPL256C sub-network constructed with: left – BPCA, middle – kNN, right–LLS imputation method.
Figure 5:
YPL256C sub-network (12).
Discussion
Escherichia coli S.O.S. DNA repair network
The entire system is composed of approximately 30 genes regulated at the transcriptional level. Usually, when no DNA damage occurs, a master transcription factor, LexA, binds sites in the promoter regions of these genes, repressing all genes in the network. One of the SOS proteins, RecA, acts as a sensor to DNA damage: by binding to single-stranded DNA; it becomes activated and mediates LexA destruction. The drop in LexA levels causes the de-repression of SOS genes. Once damage has been repaired or bypassed, the level of activated RecA drops, LexA then accumulates and represses the SOS genes, and cells return to their initial state (13).
The method that produces the highest sensitivity and specificity was the most suitable for our experiment, and Table 1 shows that this was kNN. kNN produces a lower error rate than BPCA and LLS; with high sensitivity, kNN results in a low number of type II errors, or false negatives, while high specificity means a low number of type I errors, or false positives. We used a relatively small E. coli dataset, and this favoured the kNN method in imputing the missing values. However, if the datasets are too large or too small, kNN method will perform poorly. BPCA did not perform well in this experiment, because of the size of the dataset; it is a global method that favours large datasets (3). Conversely, LLS is a very simple method to apply because it does not produce any computational burdens, unlike BPCA.
Saccharomyces cerevisiae YOR263C Sub-network
The edges between YOR263C and YOR264W were the most conspicuous features in the subnetwork. This is primarily because both genes are located adjacent to one another on the DNA strand of chromosome XV. However, the biological and molecular functions of both genes are unknown. Another feature with a high confidence level is the edges between YNR067C and YGL028C. The function of YNR067C is currently unknown, while YGL028C is known to function as a soluble cell wall protein. It has a connection with YER124C, but the function of YER124C is unknown. YGL028C is also related to YLR286C, an endochitinase that is involved in cell wall biogenesis. These two nodes (genes) are again connected by edges of high confidence. Since YER124C has directed edges with two nodes (YLR286C and YGL028C) and both nodes are functionally related to cell wall biogenesis, it can be assumed that it is also involved in cell wall biogenesis. Therefore, this gene network, which we constructed using a DBN, has provided a testable prediction of an unknown gene function.
The main difference between the subnetworks constructed by Dejori (12) and those used our research is that the edges in the network we constructed were directed, and they more clearly show the interactions between genes. For example, the edge formed between YOR263C and YOR264W in a sub-network constructed by Dejori (12) could not show which gene is regulating which other. However, the network we formed clearly showed that YOR263C was regulating YOR264W and vice versa. This means that the expression level of YOR264W depends on YOR263C, as well as on YNR067C.
Saccharomyces cerevisiae YPL256C Sub-network
Both BPCA and LLS produced a higher sensitivity and specificity rate than did kNN, proving that, in this sub-network dataset, BPCA and LLS outperformed kNN, producing more accurate gene networks with lower error rates. The performance of kNN was mainly influenced by the size of the YPL256C sub-network, which is relatively large compared to the YOR263C sub-network. On the basis of our results, BPCA and LLS would be preferable in handling larger datasets.
There was one directed edge from gene YIL066C to gene YPL256C. This means that there is a causal dependency between these two genes. YPL256C encodes for G1-cyclin, which is involved in the regulation of the cell cycle, while YIL066C is involved in DNA replication, which occurs in the S-phase. Therefore, a causal dependence with regard to YIL066C and YPL256C is biologically logical, since their functions are correlated. YDR146C encodes for a transcription factor that activates transcription of genes expressed at the M/G1 boundary and in the G1 phase of the cell cycle. YDR146C regulates YHR023W, which encodes a protein that plays a non-essential role in cytokinesis in the M phase. An unexpected finding is that gene YGR108W did not form any edges with other nodes, which is in direct contrast to the results of a study conducted by Spellman et al. (6). The number of edges we found is almost three times higher than was observed by Dejori (12). In addition, all the edges in the network we developed through our research had at least one directed edge with other nodes. However, Dejori (12) failed to find or construct any edge for one node; YGR108W. This suggests that the DBN we implemented is capable of predicting and forming a greater number of potential edges between genes in a sub-network.
We captured 20 new edges between nodes that Dejori (12) was unable to capture. The new edges are shown in Figure 6, and they are edges without any attachment. One of the new edges that we discovered is from gene YLR131C to gene YMR001C. YLR131C encodes the transcription factor that activates transcription of genes expressed in the G1 phase of the cell cycle. Conversely, YMR001C encodes a protein that is involved in the regulation of DNA replication. Therefore, YLR131C is likely to regulate YMR001C.
Conclusion
In this study, we probed the effects of imputation methods for GRNs modelling using a DBN based on two different gene expression datasets, namely the E. coli SOS DNA repair network and the S. cerevisiae cell cycle pathway. We observed and analysed the effects and influence of the BPCA, kNN and LLS imputation methods on the resultant GRNs, and found that kNN outperforms BPCA and LLS with relatively small size datasets, as it produced the highest sensitivity and specificity for both the E. coli SOS DNA repair network and the S. cerevisiae YOR263C sub-network. However, its performance dropped drastically when the size of the dataset increased. In contrast, BPCA was outperformed by kNN and LLS on smaller networks, but maintained its performance on the larger YPL256C sub-network. In addition, LLS produced the most consistent performance on all three datasets. Although it did not particularly excel in any of the three experiments, it did produce relatively competitive results compared with the other imputation methods. Our results also suggest that the performance of imputation methods is influenced by the characteristics of the dataset, that is, its size and complexity, which in turn influences the resultant GRNs. Moreover, based on the resultant GRNs, it is shown that a DBN is capable of uncovering potential edges or interactions between genes, for example, twoway interactions. Further research must also be conducted with regard to the effects of imputation methods on modelling GRNs using a DBN. For example, expanding the selection of imputation methods and using other gene expression data, such as Arabidopsis thaliana.
Acknowledgments
We would like to thank the Malaysian Ministry of Science, Technology and Innovation for supporting this research by an e-science research grant (Grant number: 01-01-06-SF1234). This research is also funded by an Exploratory Research Grant Scheme (Grant number:R. J130000.7807.4L096) and a Fundamental Research Grant Scheme (Grant number: R.J130000.7807.4F190) from the Malaysian Ministry of Higher Education.
Footnotes
Conflict of interest
None.
Funds
Grant number: 01-01-06-SF1234, grant number: R.J130000.7807.4L096 and grant number: R.J130000.7807.4F190.
Authors’ contributions
Conception and design: LEC, MSM
Analysis and interpretation of the data and drafting of the article: LEC, CKL, CKC, YWC
Critical revision of the article for the important intellectual content and final approval of the article: SD, RMI, MSM
Obtaining of funding: MSM
Collection and assembly of data: LEC, CKL
References
- 1.Sehgal MSB, Gondal I, Dooley LS. Collateral missing value imputation: a new robust missing value estimation algorithm for microarray data. Bioinformatics. 2005;21(10):2417–2423. doi: 10.1093/bioinformatics/bti345. [DOI] [PubMed] [Google Scholar]
- 2.Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, et al. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17(6):520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- 3.Oba S, Sato M, Takemasa I, Monden M, Matsubara K, Ishii S. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics. 2003;19(16):2088–2096. doi: 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- 4.Kim H, Golub G, Park H. Missing value estimation for DNA microarray gene expression data: local least squares imputation. Bioinformatics. 2005;21(2):187–198. doi: 10.1093/bioinformatics/bth499. [DOI] [PubMed] [Google Scholar]
- 5.Ronen M, Rosenberg R, Shraiman B, Alon U. Assigning numbers to the arrows: Parameterizing a gene regulation network by using accurate expression kinetics. Proc Natl Acad Sci U S A. 2002;99(16):10555–10560. doi: 10.1073/pnas.152046799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, et al. Comprehensive Identification of Cell Cycle–regulated Genes of the Yeast Saccharomyces cerevisiae by Microarray Hybridization. Mol Biol Cell. 1998;9(12):3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ouyang M, Welsh WJ, Geogopoulos P. Gaussian mixture clustering and imputation of microarray data. Bioinformatics. 2004;20(6):917–923. doi: 10.1093/bioinformatics/bth007. [DOI] [PubMed] [Google Scholar]
- 8.Yoon D, Lee Ek, Park T. Robust imputation method for missing values in microarray data. BMC Bioinformatics. 2007;8(2 Suppl):S6. doi: 10.1186/1471-2105-8-S2-S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kim SY, Imoto S, Miyano S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief Bioinform. 2003;4(3):228–235. doi: 10.1093/bib/4.3.228. [DOI] [PubMed] [Google Scholar]
- 10.Zou M, Conzen SD. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics. 2005;21(1):71–79. doi: 10.1093/bioinformatics/bth463. [DOI] [PubMed] [Google Scholar]
- 11.Radman M. Phenomenology of an inducible mutagenic DNA repair pathway in Escherichia coli. Basic Life Scie. 1975;5A:255–367. doi: 10.1007/978-1-4684-2895-7_48. [DOI] [PubMed] [Google Scholar]
- 12.Dejori M. Austria (AT): Graz University of Technology; 2002. Analyzing Gene Expression Data with Bayesian Networks. [Google Scholar]
- 13.Perrin BE, Ralaivola L, Mazurie A, Bottani S, Mallet J, D’alche-Buc F. Gene networks inference using dynamic Bayesian networks. Bioinformatics. 2003;19(2 Suppl):138–148. doi: 10.1093/bioinformatics/btg1071. [DOI] [PubMed] [Google Scholar]