Abstract
Scale score measures are ubiquitous in the psychological literature and can be used as both dependent and independent variables in data analysis. Poor reliability of scale score measures leads to inflated standard errors and/or biased estimates, particularly in multivariate analysis. To assess data quality, reliability estimation is usually an integral step in the analysis of scale score data. Cronbach’s α is a widely used indicator of reliability but, due to its rather strong assumptions, can be a poor estimator (Cronbach, 1951). For longitudinal data, an alternative approach is the simplex method; however, it too requires assumptions that may not hold in practice. One effective approach is an alternative estimator of reliability that relaxes the assumptions of both Cronbach’s α and the simplex estimator and, thus, generalizes both estimators. Using data from a large-scale panel survey, the benefits of the statistical properties of this estimator are investigated and its use is illustrated and compared with the more traditional estimators of reliability.
Keywords: reliability, Cronbach’s alpha, simplex, scale scores, longitudinal
Scale score (also known as composite score) measures (SSMs) are very common in psychological and social science research. As an example, the Child Behavior Checklist (CBCL) is a common SSM for measuring behavior problems in children (see Achenbach, 1991 for the version of the CBCL used in this paper). It consists of 118 items on behavior problems, each scored on a 3-point scale (1 = not true, 2 = sometimes true, and 3 = often true). The CBCL Total Behavior Problem Score is an empirical measure of child behavior computed as a sum of the responses to the 118 items. The usefulness of any SSM in data analysis depends in large part on its reliability. An SSM with poor reliability is infected with random errors that obscure the underlying true score values. SSMs with good reliability are relatively free from random error, which increases the statistical power of the variable for analysis. As an example, Biemer and Trewin (1977) show that as reliability (ρ) decreases, the standard errors of estimates of means, totals, and proportions increase by the factor . In the same paper, the authors show that, for simple linear regression, the estimator of slope coefficient, , estimates βρ rather than the true parameter, β; i.e., is biased toward 0 if the explanatory variable is not reliable. Estimates of quantiles, goodness-of-fit tests, and measures of association in categorical data analysis are also biased. Thus, assessing scale score reliability is typically an integral and critical step in the use of SSMs in data analysis.
A common method for assessing scale score reliability is Cronbach’s α (Hogan, Benjamin, & Brezinsky, 2000), which is based upon the internal consistency of the items comprising the SSM. It can be shown that, under certain assumptions (specified below) the reliability of an SSM is proportional to the item consistency. Many authors in numerous disciplines have used α to assess the reliability of scale scores (see, for example, Burney & Kromrey, 2001; Sapin et al., 2005; Yoshizumi, Murakami, & Takai, 2006). For example, Hogan, Benjamin, and Brezinski (2000) found that α was used in about 75% of reported reliability estimates in publications by the American Psychological Association. One reason for its ubiquity is that data analysis software packages (for example, SAS, SPSS, and STATA) provide subroutines for computing α with relative ease. In addition, few alternatives exist for assessing reliability in cross-sectional studies. Yet, Cronbach’s α and other so-called internal consistency indictors of ρ have been criticized in the literature due to the rather strong assumptions underlying their development (see, for example, Bollen, 1989, p. 217; Cortina, 1993; Green & Hershberger, 2000; Lucke, 2005; Raykov, 2001; Shevlin, Miles, Davies, & Walker, 2000; Zimmerman & Zumbo, 1993).
For longitudinal data, an alternative to α is the (quasi-) simplex estimator that operates on the repeated measurements of the same SSM over multiple waves of a panel survey. While the simplex estimator relaxes some of α’s assumptions, it imposes others that can be overly restrictive in some situations. A more general estimator extends the simplex model by incorporating equivalent forms of the SSMs using the method of split halves (see, for example, Bollen, 1989, p. 213). This method, referred to as the generalized simplex (GS) method, relaxes many of the parameter constraints imposed by the traditional simplex method.
The GS model also provides a framework based upon formal tests of significance for identifying the most parsimonious model for estimating reliability. By imposing parameter constraints on the GS model, estimators that are equivalent to α, the simplex estimator, and several other related estimators can be compared for a particular set of data. As an example, in situations where its assumptions hold, α may be preferred over the more complex, longitudinal estimators that typically have larger standard errors. However, for large sample sizes, bias may be the determining factor and researchers may prefer to compute the estimators of reliability from the unrestricted GS model. Even in these situations, it is instructive to identify situations where the assumptions underlying α and the traditional simplex model do not hold to inform future uses of the simpler models.
The next section briefly reviews the concept of reliability, particularly scale score reliability, and introduces the notation and models needed for describing the methods. We examine the assumptions underlying Cronbach’s α and consider the biases that result when assumptions are violated, as often occurs in survey work. Section 3 considers some alternatives to Cronbach’s α for longitudinal data such as the simplex approach and a generalization of that approach that relaxes a critical and restrictive assumption of the simplex model. This section also develops the methodology for testing the assumptions underlying several alternative estimates of reliability. In Section 4, we apply this methodology to a number of scale score measures from the National Survey of Child and Adolescent Well-being (NSCAW) to illustrate the concepts and the performance of the estimators. Finally, Section 5 summarizes the findings and provides conclusions and recommendations.
The Need for Alternatives to Cronbach’s α
To establish the notation used in this discussion, let Si denote the SSM for the ith person in the population consisting of J items yij, j = 1,…,J; Si = Σj yij. Let E(·|i) and var(·|i) denote expectation and variance holding the person fixed as well as all essential (i.e., stable/repeatable) survey conditions that obtain at the time of the interview. Let Ei(·) and Vari(·) (either with or without the subscript i) denote the corresponding operators over all persons in the population and other sources of variation. The variance of Si can be written as the sum of between and within subject variance components as follows:
| (1) |
(see, for example, Lord & Novick, 1968, p. 38). Thus, the reliability of S can be defined generically as the ratio of the between subject component to the total variance; i.e.,
| (2) |
(Lord & Novick, 1968, p. 208). The term E(Si|i) is referred to as the true score of Si and thus VariE(Si|i) is the true score variance. Thus, the reliability of Si is the ratio of true score variance to the total variance of the SSM. The specific forms of ViE(Si|i) and Var(Si) depend upon the assumed model for yij and/or Si. The goal of reliability analysis is to obtain unbiased estimates (1) under the specified model.
One of the simplest models is the so-called classical test theory (CTT) model that assumes an observation is equal to a true score, τij and a random measurement error, εij
| (3) |
where τij = E(yij|i), εij = yij − τij, and Cov(τij, εij|j) = 0. The CTT model further assumes that the J measurements are parallel (Lord & Novick, 1968, p. 58); i.e., (a) Cov(εij, εij’|i) = 0 for j ≠ j ≠ j’, (b) τij = τi, for all j (identical true scores), and (c) for all j (equal error variance). Under this model, (2) can be rewritten as
| (4) |
where which implies that reliability improves as J increases. It can be further shown that for a simple random sample of size n, Cronbach’s α given by
| (5) |
is unbiased for ρ(S) where
| (6) |
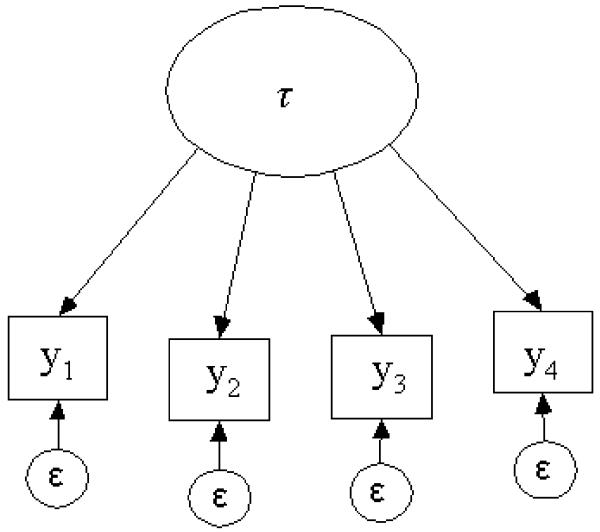
and var (S) is identical to (6) after replacing yij by Si and by (Lord & Novick, p. 92).1 We use the symbol to denote the estimator of . If the assumption of tau-equivalence relaxes assumption (c) above to (c’) , or, in words, error variances differ by item. Even in this more general situation, is still unbiased for ρ(S) after replacing in (4) by . As will be discussed subsequently, Cronbach’s α may also be estimated within a structural equation modeling (SEM) framework. (See Figure 1 for the four-item path model corresponding to α).
Figure 1.
Cronbach’s Alpha Model for a Four-Item Scale Score.
It is well-known that when the uncorrelated measurement error assumption is violated; i.e., when Cov(εij, εij’,|i) ≠ 0 for some j ≠ j’, is no longer an unbiased estimator of reliability (see, for example, Lord & Novick, 1968; Green & Hershberger, 2000; Lucke, 2005; Raykov, 2001; Rae, 2006; Vehkalahti et al., 2006; Zimmerman et al., 1993; Komaroff, 1997; Shevlin, 2000). Correlated measurement errors occur, for example, when respondents try to recall their answers to previous items so that they may respond consistently to later items rather than answering later items independently. Interviewers and the general interview setting can also induce positive correlations. As an example, the mere presence of an interviewer can cause respondents to provide more socially acceptable rather than truthful responses to sensitive questions. Random conditions such as the presence of family members, ambient noise and other distractions during the interview, the respondent’s current physical/emotional health, interview time constraints and so on can lead to inter-item correlated errors. These are transient effects due to conditions that obtain at the time of the interview that may change or vanish should the interview process be independently replicated. For survey designers and data analysts, these influences are not considered part of the true score variance component (i.e., reliable variance). (For a comprehensive a review of the effects of survey design on survey error, see Biemer and Lyberg, 2003).
Denote the cumulative effects of these error sources by δij where it is assumed that E(δij|i) = 0, Cov(δij, δij’,|i) ≠ 0 for some j, j’. Under this model, it is straightforward to show that ρ(S) is given by
| (7) |
while
| (8) |
where σδδ’ = ΣiΣj≠j’, EiCov(δij,δij’,|i) and (see Raykov, 2001). Thus, the relative bias in is
| (9) |
implying that positive error covariances (i.e., σδδ’ > 0) will induce positive biases in . As we shall see, the bias in can be considerable.
As Shevlin et al. (2000) note, researchers and analysts do not universally agree on the interpretation of δij and its effects on α. Some researchers (Shevlin et al. cite Bollen, 1989) believe that the correlations between the errors across items represent “consistent and reliable” variance that should increase reliability as shown in (8). Under this argument, δij is assumed to be constant conditional upon the ith unit. Hence, E(δij|i) = δij and, thus, should be counted in the true score variance component, VariE(Si|i), rather than the error component, EiVar(Si|i). This view of reliability holds that the expectation operator, E(g|i), should be conditional not only on the respondent i and essential (i.e., stable/repeatable) survey conditions, but also on all other extraneous variables that are operating during the survey interview, including the transient survey conditions noted above. Shevlin et al. suggest that this line of reasoning is inconsistent with the psychometric definition of reliability, which is based on a specific trait being measured, not the trait plus all extraneous error components.
For example, if S is intended to measure some aspect of child behavior, the estimator of ρ(S) should reflect the variation of the child behavior factor (or true score), excluding the many unknown and uncontrollable factors that may be simultaneously measured during a particular interview. Using this interpretation of ρ(S), an interviewer’s influence on the ith child’s responses should be counted as part of the error variance component rather than the child’s true score. This is the approach espoused in the present paper and, as such, correlations from fleeting, unstable error sources will lead to biased ’s.
Cronbach’s α will also underestimate ρ(S) if assumption (b) does not hold (Alwin, 2007; Raykov, 1998; Raykov & Shrout, 2002; Komaroff, 1997). For example, Raykov (2001) considers the simple case where the true score for the jth item is a multiple (say, bj) of a single common factor. He shows that the bias in is proportional to the variation in the bj. A similar result holds if the items comprising S are multi-dimensional (i.e., they measure two or more correlated factors). For example, an SSM that is intended to measure depression may include some items that measure anger or pain. Or, the questions may be worded so that respondents interpret the questions erroneously and report behaviors or attitudes inconsistent with the construct of interest. This situation may be depicted by the following model for the true score:
| (10) |
where the vij are specific factors uncorrelated with the common factor, τi. Unlike the measurement error variables defined previously as δij, specific factors are stable influences on yij in the sense that E(vij|i) = vij and Var(vij|i) = 0. Thus, their variance contributes to the reliable variance rather than to error variance. Unfortunately, as Alwin and Jackson (1979) show, α does not recognize this distinction and, consequently, will overestimate measurement error variance and underestimate true score variance. As shown in the Appendix, the relative bias of under this model is
| (11) |
indicating that the bias is negatively proportional to the average variance of the specific factors denoted by . Thus, will underestimate scale score reliability under model (10) and considerably so whenever the specific factor variance is large.
When both specific factors and correlated random errors are operating together, the bias in α is unpredictable. For example, suppose
| (12) |
where the terms in the model are defined as above; i.e., the observation is combination of the true score, a specific factor, a correlated error component and a random error component. In that case, reliability of the SSM is given by
| (13) |
while, combining the previous results, α estimates
| (14) |
with relative bias given by
| (15) |
Thus, the direction and magnitude of the bias is a trade-off between the error covariance and specific factor variance: can either overestimate or underestimate SSM reliability.
For longitudinal data, alternatives to α will provide unbiased estimators of ρ(S) when the assumptions of independent errors (assumption a) and unidimensionality (assumption b) are violated. One of these is the simplex (or quasi-simplex) estimator of reliability (Wiley & Wiley, 1970). Unlike , the simplex estimator does not rely on internal consistency because it is a function of the scores Si rather than the items yij. Thus, the systematic errors (δij) and the vij in (12) will not necessarily bias the simplex estimates of ρ(S). This is not to say that simplex estimates are always more accurate than Cronbach’s α because the simplex model assumptions can also be violated.
Analysts using different methods to estimate ρ(S) may face a dilemma when the estimates vary considerably. Which estimate of ρ(S) should be believed? This question needs to be addressed for each application because the model assumptions are satisfied to varying degrees depending on the SSM and the study design. In the next section, we attempt to answer this question for many practical applications.
Estimating Reliability with Longitudinal Data
In a panel study,2 the SSM (S) and its reliability can be computed at each wave using cross-sectional survey methods such as . Let Sw denote the SSM and the corresponding estimate of α at wave w. In practice, α is estimated separately and independently for each wave. By contrast, the method of estimating reliability discussed next uses information both within and across waves to assess reliability at each wave.
For longitudinal data, scale score reliability can also be estimated using the so-called simplex (or quasi-simplex) model (Heise, 1969; Heise, 1970; Wiley & Wiley, 1970; Jöreskog, 1979; Alwin, 2007). The simplex method uses a longitudinal SEM to estimate scale score reliability at each wave using the scale scores themselves (i.e., the Si’s) rather than the responses to the individual items comprising the scale. This is a key advantage of the simplex model over Cronbach’s α. Because it operates on the aggregate scale scores, correlations between the items within the scale do not bias the estimates of reliability.
To use this method, the same scale must be available from at least three waves of a panel study, and the scores must be computed identically at each wave. The covariation of individual scores both within and between the waves provides the basis for an estimate of the reliability of the measurement process. In this sense, the simplex model is akin to a test-retest reliability assessment where the correlation between values of the same variable measured at two or more time points estimates the reliability of those values. An important difference is that while test-retest reliability assumes no change in true score, true score variance, or error variance across repeated measurements, the simplex model can accommodate changes in these parameters across time (i.e., panel waves).
To achieve an identified model, the original simplex model (Wiley & Wiley, 1970) assumes that error variances are equal across all waves (referred to as the stationary error variance assumption). It is also possible to obtain an identifiable model by equating the true score variances across waves and allowing the error variances to vary (referred to as the stationary true score variance assumption). Unfortunately, allowing both true score and error variances to vary by wave leads to a non-identified model (i.e., insufficient number of degrees of freedom to obtain a unique solution to the SEM). In the present work, both types of assumptions (stationary true score variance and stationary error variance) will be considered although the stationary error variance assumption seems plausible for most practical situations.
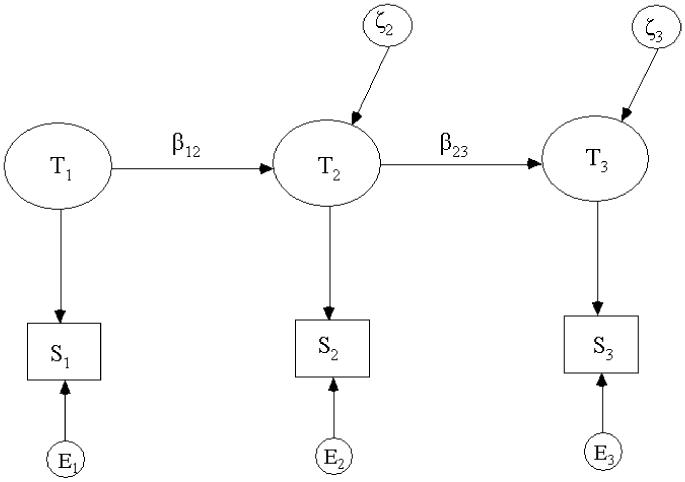
The original simplex model for three repeated measurements is illustrated in Figure 2. This model is composed of a set of measurement equations and structural equations. The measurement equations relate the unobserved true scores to the observed scores as follows:
| (16) |
for w = 1,2,3 where Sw is the observed score (i.e., the sum of the yij), Tw is the unobserved true score (i.e., the sum of the J item true scores, τj) and the Ew is measurement error (i.e., sum of the J item error terms, εij) at wave w. Consistent with the item-level models, assume E(Ew|i|i) = 0 and variance, . We further assume Cov(Ew,Ew’,|i) = 0 for any two waves, w and w’. Following the usual notational conventions, in this model and for the remainder of the paper, we have dropped the index i denoting the individual or population unit.
Figure 2.
Simplex Model for Three Repeated Scores.
The structural equations define the relationships among true scores. From Figure 2, we can write the system
| (17) |
where β12 is the effect of the true score at time 1 on the true score at time 2 and β23 is the effect of true score at time 2 on true score at time 3. The βw,w+1 (often referred to as stability coefficients) are the parameters that measure change in true score from wave w to wave w+1. The terms ξ2 and ξ3 are random disturbance (or shock) terms representing the deviations in the change in true scores from wave to wave.3 Because E(ξw|i) = ξw, it follows that the true score variance at time w is
| (18) |
Further, by back substitution for τw in (17) we can write
| (19) |
where for w=1,2,3. Assumptions of the simplex model include, for all w ≠ w’ E(Ew) = 0, Cov(Ew, Ew’) = 0, Cov(Ew, Ew’) = 0, Cov(Ew, Tw’) = 0, and Cov(ξw, Tw’) = 0. For identifiabity, the original simplex model assumed stationary error variance, that is,
| (20) |
for all w and w’ (see Wiley & Wiley, 1970). The assumption of stationary true score variance can be substituted for (20) as will be discussed subsequently.
The reliability of Sw is given by
| (21) |
for w=1,2,3 where . Estimates of β12, β23, , , w = 1,2,3 can be obtained using standard SEM estimation approaches. Then ρw can be estimated by replacing the parameters in (21) and (19) by their SEM estimates.
It is straightforward to show that, if the SSM items conform to the model in (12), then
| (22) |
where the components , , , are analogous to , , , , respectively, at each wave w. If we assume that , for all w (i.e., error variances are stationary), the simplex model is identified and its estimator of ρ(S) is unbiased under model (12).
In some situations the error variances are nonstationary because, as Alwin (2007, p. 107) states, “measurement error variance is a property both of the measuring device as well as the population to which it is applied.” As an example, the information collected on children for the CBCL may be less (or more) subject to measurement error as the children age. To the extent that measurement is related to comprehension error and older children have a greater understanding of the concepts, measurement error may decrease over a child’s time in the panel. On the other hand, older children may be more subject to the influences of parents or siblings present during the interview, which could increase measurement variance over time. As previously noted, allowing both true score and measurement error variances to change over time will yield a non-identified model. Thus, if nonstationary measurement error variances are specified, then score variances () must be held constant or otherwise constrained to achieve an identified model.4
To illustrate, Table 1 provides estimates of reliability for the Youth Self-Report for three waves of the NSCAW. Cronbach’s α and the simplex reliability estimates are provided under both the assumptions of stationary error variances and stationary true score variances. The sample sizes varied somewhat for each estimate from 1,200 to 1,800 cases. Differences as small as 0.05 can be interpreted as statistically significant. Note that the simplex estimates vary considerably within wave: from 0.57 to 0.77 in Wave 1. The simplex estimates tend to be smaller than α, substantially so in some cases, which may be evidence that inter-item correlations are inflating the α estimates of reliability. These results also illustrate the degree to which estimates ρ(S) can vary depending upon the method used.
Table 1. Youth Self Report (YSR) Scale Score Reliability Estimates Using the Simplex Model and Cronbach’s α.
| Model | Wave 1 | Wave 2 | Wave 3 |
|---|---|---|---|
| Simplex Model | |||
| Stationary Error Variance | 0.77 | 0.71 | 0.67 |
| Stationary True Score Variance | 0.57 | 0.71 | 0.81 |
| Cronbach’s α | 0.96 | 0.95 | 0.95 |
Although the simplex model is unaffected by inter-item correlated error, it can still be biased due to the failure of other assumptions made in its derivation. If both measurement error and true score variances change at each wave, the simplex estimates of reliability will be biased regardless of which is assumed to be stationary. As an example, suppose that measurement error variance increases monotonically over time while true score variance remains constant. In this situation, ρ(Sw) decreases with each wave. However, the simplex model under the stationary error variance assumption will attribute the increase in total variance across time to increasing true score variances. This means that reliability will appear to increase over time—just the opposite of reality.
On the other hand, if stationary true score and nonstationary measurement error variances are assumed, the opposite effect can occur. For example, if true score variances are actually decreasing and error variances are constant, ρ(Sw) decreases but the simplex estimate of ρ(Sw) will show reliability to be increasing at each wave.
In the worst case, both the true score and error variances may change nonmonotonically over time. Thus, the simplex model with the stationary variances assumption is misspecified and the estimate of ρ(S) will be biased. However, if the relationship of the variances over time is known or can be supported theoretically, it can be specified as part of the model in order to obtain unbiased estimates of ρ(S).
The simplex model can also be contaminated to some extent by correlated errors between waves because it assumes that the score-level errors are independent across time, or more precisely, Cov(Ew,Ew’|i) = 0 for any two waves, w and w’. As an example, if the waves are spaced only a few weeks apart, subjects may remember their answers from the last interview and repeat them rather than providing independently derived responses. On the other hand, if the time interval between waves is a few months or more, the risk of recall and, consequently, between-wave correlated error is much reduced. In the NSCAW, the time interval between waves is at least 18 months, which should obviate any concern about memory induced correlations between waves.
The next section introduces a more general model that subsumes the models used to generate the estimates in Table 1 as special cases. An important additional feature of the model is that it is identified even if true score and error variances are not stationary; that is, when both are allowed to vary across waves. We also provide an approach for testing which set of model restrictions are satisfied in order to choose the best estimates of reliability for a given SSM and population.
The Generalized Simplex (GS) Model for Estimating Scale Score Reliability
Using the method of split halves (Brown, 1910; Spearman, 1910), a more general model for estimating scale score reliability can be formulated that relaxes many, but not all, of the assumptions associated with the α and simplex models. For the split halves method, two SSMs are constructed for the same wave by dividing the J items into two half-scales consisting of J/2 items (assuming, for simplicity, J is even). One approach might assign odd-numbered items to one half and even-numbered items the other half. However, any method for dividing the items that satisfies the subsequent model assumptions is acceptable. Denote the SSMs constructed from the two half-scales by Sw1 and Sw2. Under very general assumptions, the GS model will provide estimates of reliability for each half of a scale for each wave of data collection. The half-scale reliability estimates for each wave can then be combined to produce a full-scale estimate of ρ(Sw) using a generalization of the Spearman-Brown prophecy formula (Carmines & Zeller, 1979) that is applicable when the errors of the two half-scales are correlated. To simplify the exposition of the model, we assume three panel waves are available; however, extending the model to more than three waves is straightforward.
This split-halves sample approach that we advocate is similar in some respects to item parceling (see, for example, Bandalos, 2008 or Nasser & Wisenbaker, 2006) which also partitions the SSM into subscales. The key difference is that, with our approach, the split-half samples are used merely as a device for creating degrees of freedom for estimating an otherwise unidentifiable model. Our analysis is still focused on the reliability of the full SSM which is obtained through a Spearman-Brown-like transformation of the half-sample reliabilities. By contrast, item parceling does not seek to uncover the true reliability of the full-scale; rather in that literature, interest is focused on the psychometric properties of the subscales (or testlets) themselves.
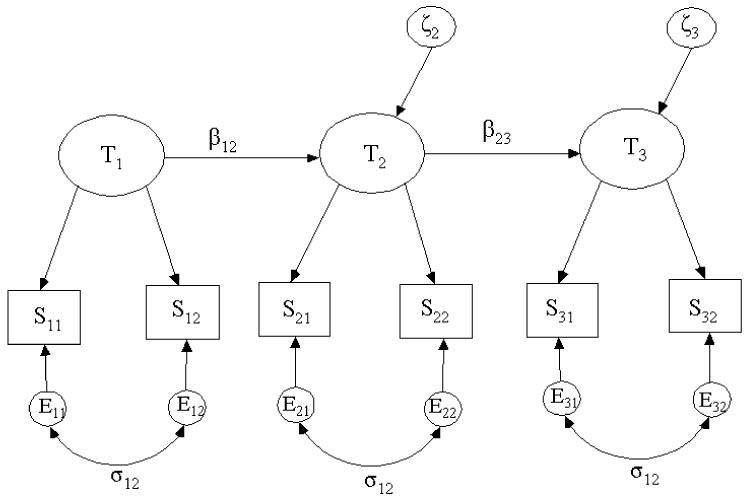
The path model representation of the split halves model is shown in Figure 3. Note its resemblance to the model in Figure 2; the only difference is that the single score Sw has been replaced by Sw1 and Sw2 corresponding to the split halves. The GS model assumptions regarding means, variances, and covariances of true scores and errors are the same as the simplex model assumptions. Between split halves, it assumes the following:
| (23) |
and Cov(Ews, Tw’s’) = 0 for all w, w’, s, s’. Note that (23) accounts for any within wave, between split-half correlated measurement error from the δij-terms in (12). However, for identifiability, we must assume the covariance between the split halves within a wave, σ12, is constant over time. Because the composition of the halves is arbitrary, this is equivalent to assuming that σδδ’, defined for (8) is the same at each wave.
Figure 3.
Generalized Simplex Model for Three Repeated Scores.
Thus, although the sources of correlated measurement error may change at each wave, the magnitude of the correlation between the errors does not. In Section 5 we show that this restriction, which is made for all GS models, tends to slightly attenuate the differences between the GS models. The zero between wave covariance assumption in (23) is not required for identifiability; however, this constraint produced better results in our application. Models without this constraint performed poorly and produced negative error variances for some SSMs (which is evidence of an over-parameterized model). However, in some applications, removing this assumption may be warranted. Finally, we assume that the true score variances are equal across the split halves; that is, , say. This assumption is dependent upon the method for forming the two halves. If at random (as it is in the illustrative example below), then the assumption holds when expectation is taken over all possible random splits of the J items. An additional assumption is that the measurement of the construct is invariant over time, that is, the coefficient for the linear relationship between Swj and Twj is the same for all w. Although the invariance assumption is not necessary for the GS model, invariance was tested and confirmed for the SSMs presented in this paper. All the aforementioned assumptions are summarized in the path diagram in Figure 3.
Let , and denote the estimates corresponding variance components. Then an estimator of the reliability of the score, Sw, is
| (24) |
Except for the covariance term in the denominator, this formula is equivalent to the well-known Spearman-Brown prophecy formula (Carmines & Zeller, 1979).
This model can be viewed as a generalization of both α and the simplex models. To see this, note that the model underlying Cronbach’s α at any wave, w, can be summarized by the path diagram in Figure 3 for wave w when the split halve errors are uncorrelated (i.e., a two-item version of Figure 1). Further, imposing the restriction σ12 =0 will produce estimates of ρ(Sw) that are consistent with Cronbach’s α at wave w. The GS model is also equivalent to the simplex model in Figure 2 if constraints on the appropriate variance components (either stationary true score or measurement error variances) are imposed. Thus, the GS model provides a general structure for testing the fit of Cronbach’s α as well as the simplex models. It can also be used to test some of the key assumptions of a number of alternative simplex-like models. An advantage of the GS model is that it can be used in situations where the assumptions underlying Cronbach’s α and the simplex models do not hold. In those situations, GS model can provide better estimates of ρ(Sw) than either the or the simplex models with the stationary variance assumptions.
Application: Measures of Child Well-being
This section considers the various alternative estimators of scale score reliability for a number of SSMs in the National Survey of Child Adolescent Well-being (NSCAW). The NSCAW is a panel survey of about 5,100 children who were investigated for child abuse or neglect in 87 randomly selected U.S. counties (Dowd et al., 2004). An important component of the data quality evaluation for this survey was the assessment of reliability for all the key SSMs. Biemer et al. (2006) provided estimates for more than 40 SSMs using both Cronbach’s α and the simplex model assuming stationary true score variances, stationary error variances, or both. A representative subset of these scores will be considered here including: the CBCL, Teacher Report Form (TRF), and the Youth Self-Report (YSR) (Achenbach, 1991). Each of these SSMs has three versions: a total score, an internalizing behavior score, and an externalizing behavior score resulting in nine scores assessed.
First, the wide range of estimates of ρ(Sw) that can be produced by varying the method and the model assumptions will be illustrated. We shall consider an approach for determining which estimate of ρ(Sw) is preferred. Working within the GS modeling structure, the effects of three sets of assumptions will also be evaluated. These assumptions are: (a) stationary error variances, (b) stationary true score variances, and (c) inter-item correlated errors. As discussed above, the GS model under assumption (a) should produce estimates of ρ(Sw) that are consistent with the original simplex model proposed by Wiley and Wiley, 1970. The GS model under assumption (b) should produce estimates consistent with the alternative simplex model discussed above. The GS model under assumption (c) should produce estimates that are consistent with Cronbach’s α.
For each wave, w, seven of estimates of ρ(Sw) were computed at each NSCAW wave corresponding to:
simplex model with stationary error variance and nonstationary true score variance (SSEV),
simplex model with stationary true score variance and nonstationary error variance (SSTV),
Cronbach’s α (ALPHA)
the unconstrained GS model (GS),
GS model with stationary true score variance and nonstationary error variance (GSSTV),
GS model with stationary error variance and nonstationary true score variance (GSSEV), and
GS model with α-like constraints; i.e., both nonstationary true score and error variances with uncorrelated measurement errors (GSAL).
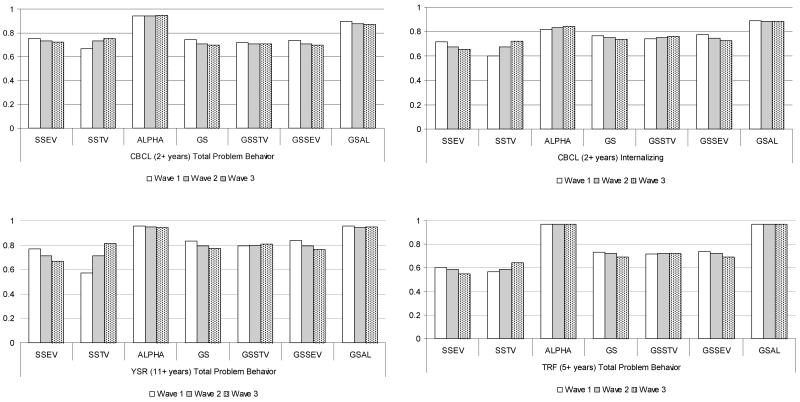
Figure 4 presents a histogram of these estimates for four SSMs to represent the range of results that were obtained for all nine SSMs. As a simple metric for interpreting these graphs, differences of about 3, 7, and 10 percentage points for waves 1, 2, and 3, respectively, should be considered statistically significant. One striking feature of the SSMs in this figure as well as the other SSMs considered is that ALPHA and the GSAL estimates are always higher than the other estimates. In many cases, the differences are highly statistically significant. For the GSAL model, the higher estimates are due primarily to the constraint σ12 =0, i.e., uncorrelated measurement errors. Removing this constraint always improved model fit while producing estimates that were lower and at the level of the other estimates. As shown below, empirical testing confirmed that both the GSAL and ALPHA are positively biased for all SSMs considered in our analysis due to the assumption σ12 =0.
Figure 4.
Estimates of Reliability by Wave for Four Scale Score Measures Under Seven Model Assumptions.
The stationary variance assumptions of the simplex models can also change the estimates of ρ(Sw) dramatically. As an example, the SSEV model produces estimates that tend to decrease as w increases. However, the SSTV model produces the opposite pattern. To understand why, recall that total variance is the sum of true score and error variance. Therefore, if true score variance is held constant, the model will attribute change in true score variance over time to changing error variances. Conversely, under the stationary error variance assumption, the model will attribute change in the error variances over time to changing true score variances. For these scales, total variance in the SSMs seems to be decreasing, resulting in changes in reliability estimates when either true score variance or error variance are constrained to be constant over time. Thus, depending upon which stationarity assumption is chosen, reliability can appear to either increase or decrease over time.
The GS models with either stationary true score or stationary error variance constraints (i.e., GSSEV and GSSTV) have similar, though less dramatic, stairstep patterns across waves as the simplex models with these same constraints (i.e., SSEV and SSTV, respectively). This attenuated effect is likely due to the constant error covariance constraint—viz., Cov(Ew1, Ew2) = Cov(Ew’1, Ew’2) = σ12 for all w, w’ – imposed on all GS models as a requirement for model identifiability. The constraint tends to dampen changes in the variances across waves. The extent to which the stationary covariance assumption holds is not known and cannot be evaluated with these data. Despite this additional assumption, the three GS models (except the GSAL) produced very similar estimates by wave in all the cases we examined. In addition, the GSEV and GSTV produced estimates comparable to the SSEV and SSTV models, respectively, as expected.
For the next analysis, we tested assumptions (a)-(c) above within the GS model framework. We began by fitting the most general form of the GS model and then imposed parameter constraints on this model corresponding to each assumption. Because in each case, the restricted model is nested within the unrestricted GS model, a test of each assumption can be obtained by the nested Wald test (Bollen, p. 293). This process also yielded the most parsimonious GS model which, except for a few cases, was the unrestricted GS model. The results of the significance testing are reported in Table 2. Note that the assumption of uncorrelated errors is rejected for all nine SSMs considered. The assumption of stationary error variance was rejected for seven SSMs and the assumption of stationary true score variance was also rejected for seven SSMs. For six of these SSMs, the GS model was the most parsimonious model for estimating ρ(Sw).
Table 2. Nested Wald Tests for Nine Scale Score Measures.
| Measure | n | Uncorrelated errors | Stationary error variance | Stationary true score variance | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ( vs. ) | ( vs. ) | ( vs. ) | ||||||||
| Chi-square | DF | p-value | Chi-square | DF | p-value | Chi-square | DF | p-value | ||
| CBCL (2+ years) Total Problem Behavior | 5330 | 122.786 | 1 | 0.000 | 7.613 | 2 | 0.0222 | 16.692 | 2 | 0.0002 |
| CBCL (2+ years) Externalizing | 5330 | 78.244 | 1 | 0.000 | 3.650 | 2 | 0.1612 | 18.660 | 2 | 0.0001 |
| CBCL (2+ years) Internalizing | 5330 | 65.005 | 1 | 0.000 | 28.805 | 2 | 0.0000 | 15.411 | 2 | 0.0005 |
| YSR (11+ years) Total Problem Behavior | 1825 | 21.031 | 1 | 0.000 | 18.360 | 2 | 0.0001 | 23.782 | 2 | 0.000 |
| YSR (11+ years) Externalizing | 1825 | 10.681 | 1 | 0.0011 | 10.629 | 2 | 0.0049 | 18.613 | 2 | 0.0001 |
| YSR (11+ years) Internalizing | 1825 | 9.583 | 1 | 0.0020 | 7.307 | 2 | 0.0259 | 25.084 | 2 | 0.000 |
| TRF (5+ years) Total Problem Behavior | 2643 | 25.338 | 1 | 0.000 | 2.135 | 2 | 0.3438 | 4.688 | 2 | 0.0959 |
| TRF (5+ years) Externalizing | 2642 | 24.243 | 1 | 0.000 | 6.415 | 2 | 0.0405 | 6.042 | 2 | 0.0488 |
| TRF (5+ years) Internalizing | 2642 | 31.154 | 1 | 0.000 | 15.481 | 2 | 0.0004 | 5.494 | 2 | 0.0641 |
Note: Constraints that could not be rejected are underscored.
Table 3 presents average standard errors for all seven models across the nine SSMs in the study. Because the GS estimates are based upon method of random split halves, the variation due to scale splitting step must also be represented in the standard error. This was accomplished by fitting each GS model five times for five difference random splits, producing five sets of estimates for each SSM by wave by GS model combination. The random split variance component was computed as
| (25) |
where is the estimate of ρ(Sw) for the rth random split and is the average of these estimates over the five splits. This variance component was added to the estimate of obtained from a single pair of split halves. Table 3 shows that Cronbach’s α (ALPHA) has the smallest standard error by a large margin. The worst standard errors are produced by the GS model and its constrained versions (GSEV and GSTV), primarily because of the random split variance component in (25) which accounts for about two thirds, on average, of the total standard error of the GS estimates.
Table 3. Standard Errors (×100) Averaged Over Nine Scale Score Measures.
| Model | Wave 1 | Wave 2 | Wave 3 |
|---|---|---|---|
| SSEV | 4.60 | 4.71 | 5.54 |
| SSTV | 4.99 | 10.32 | 18.57 |
| ALPHA | 0.54 | 0.49 | 0.46 |
| GS | 8.54 | 9.34 | 10.10 |
| GSSTV | 8.82 | 9.17 | 9.92 |
| GSSEV | 8.70 | 9.27 | 10.13 |
| GSAL | 6.50 | 7.20 | 7.98 |
The significance tests in Table 2 suggest that the GSAL, GSEV, and GSTV model constraints are often violated by these data and, by implication, the key assumptions underpinning ALPHA, the SSEV, and the SSTV methods are also violated. However, these results do not indicate the magnitude of the bias in these estimates due to model misspecification. To address this question, the estimates of ρ(Sw) from the six constrained models were compared to those of unconstrained models for each SSM. In this comparison, the GS model estimates have the least bias because the GS model fit the data best in almost all cases. In the few instances when the model did not fit, GS model estimates were still very close to the estimates of the best model. In addition, as an essentially unconstrained model, it provides the best benchmark available for evaluating the bias in the constrained models when those constraints are violated.
Table 4 provides the key results from this analysis. In this table, RSEw is the average relative standard error for the nine SSMs given by
| (26) |
where is the estimator of ρ(Sw) using the method corresponding to the row of the table, is its standard error, and is the estimator of ρ(Sw) from the GS model. Likewise, the relative bias of is estimated by
| (27) |
As measure of the total error of an estimator, we use relative root mean squared error (RRMSE) defined as the square root of the relative bias squared plus the relative standard error squared. It is estimated by RRMSE = |RBIAS| + RSE.
Table 4. Comparisons of Relative Standard Error (RSE), Relative Bias (RBIAS) and Relative Root Mean Squared Error (RRMSE) for Seven Models and Three Time Points Averaged Over the Nine Scale Score Measures.
| Model | Time 1 | Time 2 | Time 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RSE | RBIAS | RRMSE | RSE | RBIAS | RRMSE | RSE | RBIAS | RRMSE | |
| SSEV | 6.03 | −1.80 | 19.00 | 7.69 | −1.80 | 15.59 | 9.37 | −1.72 | 17.30 |
| SSTV | 6.52 | −2.35 | 27.30 | 16.43 | −2.35 | 24.87 | 30.09 | −0.57 | 36.53 |
| ALPHA | 0.70 | 21.52 | 14.57 | 0.85 | 21.52 | 22.37 | 0.83 | 23.36 | 24.20 |
| GS | 11.07 | n/a | 11.07 | 17.99 | n/a | 17.99 | 19.71 | n/a | 19.71 |
| GSSTV | 11.43 | −0.02 | 24.74 | 17.75 | −0.02 | 18.39 | 19.47 | 2.04 | 22.47 |
| GSSEV | 11.28 | −0.01 | 23.09 | 17.87 | −0.01 | 18.02 | 19.73 | −0.30 | 20.23 |
| GSAL | 8.46 | 21.08 | 21.73 | 13.44 | 21.08 | 34.52 | 15.04 | 23.01 | 38.05 |
As expected from the previous results, ALPHA and GSAL exhibit the greatest biases, which exceed 20% for all three waves. ALPHA has a smaller RRMSE than GSAL because, as noted previously, GSAL’s variance is inflated by the split sample component. Regarding the two simplex estimators, SSEV (i.e., the original simplex model) has slightly smaller variance and considerably smaller RRMSE than SSTV. On the other hand, there is little to choose between GS versions of these estimators. Both GSEV and GSTV exhibit very similar variance and bias properties. The overall best performer in terms of RRMSE (apart from the unconstrained GS estimator whose biased was assumed to be 0) appears to be the SSEV estimator.
Conclusions
For longitudinal surveys, a wide choice of estimators of scale score reliability is available. The illustration in the last section clearly shows that choosing an estimator is a critical decision in the estimation of reliability. Blind use of Cronbach’s α can and often does lead to a biased assessment of the reliability of SSMs. In our study, the assumption of inter-item uncorrelated error, upon which α relies, was rejected for all the SSMs we considered. Consequently, was positively biased – often substantially so – compared to estimators that do not require that assumption. When longitudinal data are available, the simplex model with either the stationary error or true score variance assumption can be employed and will permit a more valid assessment of reliability. However, as we have shown in Table 2, the assumptions underlying the simplex approach also do not hold for many SSMs. In such cases, more valid estimates of reliability can be obtained using the GS model, which requires neither the variance stationarity nor uncorrelated inter-item error assumptions to provide valid estimates of reliability.
One limitation of the GS model is its reliance on split half scores. The standard errors due to split halves increased by at least two thirds for the SSMs evaluated in this study. For smaller scale lengths (say, 10 or fewer items), the contribution to variance was even greater. In such cases, we recommend the SSEV (original simplex) estimator when three or more waves of panel data are available. In general, the SSEV method performed quite well in this study and, based upon other results from the literature (see, for example, Alwin, 2007), it is recommended as a general purpose estimator of ρ(Sw) whenever the GS model cannot be used.
Placing restrictions on the GS models is often worthwhile when possible, without sacrificing model fit or increasing model bias. As an example, in the few cases where the stationary variance assumptions were not rejected by the model selection process, the precision of the restricted model was somewhat better than the unrestricted model with no increase in bias. Overall, the RMSE improved as much as 20%. Therefore, we recommend the model fitting strategy described for Table 2; i.e., begin with the unrestricted GS model and use the nested Wald statistic to determine whether the model can be further reduced. We further recommend that the total variance of the GS estimators, including the split sample contribution in equation (25), be routinely assessed and reported.
Finally, we hope this paper will encourage further investigations of the methodologies used in scale score reliability estimation. To the extent that SSMs perform similarly across a range of study settings and designs, testing the assumptions underlying reliability estimation and reporting the results can be quite useful to other analysts who are contemplating the SSM and reliability estimation methods in other studies. It would be informative to accumulate experiences with various methods for estimating ρ(S) across many studies and SSMs. As an example, if either assumption (a), (b), or (c) in the previous section is rejected for an SSM in one study, then that assumption should be questionable for assessing the reliability of this SSM in other similar studies. At a minimum, it can serve as a forewarning to other researchers that the assumption is suspect for the SSM and to look for alternative methods for estimating its reliability.
Appendix
Derivation of Bias in under Model (10)
First note that and where . Therefore, while . Turning to , it can be shown that and . Using these results, after some algebraic calculations, leads to the result in (11). The relative bias in α is given by .
Footnotes
Other equivalent forms of appear in the literature. For example, Henson (2001) expresses as a function of the covariances between two measurements.
A panel study collects data from the same subjects (i.e., a panel) at different points in time, usually at regular intervals.
Note that a minimum of three waves is necessary for identifiability. With only two waves, as in a test-retest design, the stability coefficients are confounded with shock terms and it must be assumed that the stability coefficient, β12, is 1; i.e., measures are tau-equivalent.
It is also possible to obtain an identified model assuming the reliability ratio is constant over waves (i.e., stationary reliability). The case was considered in our work but not reported here to save space. This produced reliability estimates that were constant across waves and approximately equal to the average reliability obtained by the alternative stationarity assumptions.
An earlier version of this paper was presented at the American Association for Public Opinion Research Meetings in May, 2007 in Anaheim, California.
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/met
Contributor Information
Paul P. Biemer, Odum Institute for Research in Social Science, The University of North Carolina at Chapel Hill
Sharon L. Christ, Odum Institute for Research in Social Science, The University of North Carolina at Chapel Hill; Center for Developmental Science, The University of North Carolina
Christopher A. Wiesen, Odum Institute for Research in Social Science, The University of North Carolina at Chapel Hill
References
- Achenbach TM. Manuals for the Child Behavior Checklist, Youth Self-Report, Teacher’s Report Form, and 1991 Profile. Department of Psychiatry, University of Vermont; Burlington, VT: 1991. [Google Scholar]
- Alwin DF. Margins of error: A study of reliability in survey measurement. John Wiley & Sons; Hoboken, NJ: 2007. [Google Scholar]
- Alwin DF, Jackson DJ. Measurement models for response errors in surveys. In: Schuessler KF, editor. Sociological methodology 1980. Jossey-Bass; San Francisco: 1979. pp. 68–119. [Google Scholar]
- Bandalos DL. Is parceling really necessary? A comparison of results from item parceling and categorical variable methodology. Structural Equation Modeling. 2008;15:211–240. [Google Scholar]
- Biemer PP, Christ SL, Wiesen CA. Scale score reliability in the National Survey of Child and Adolescent Well-being. RTI International; Research Triangle Park, NC: 2006. Internal report. [Google Scholar]
- Biemer PP, Lyberg LE. Introduction to survey quality. John Wiley & Sons, Inc.; Hoboken, NJ: 2003. Wiley Series in Survey Methodology. [Google Scholar]
- Biemer PP, Trewin D. A review of measurement error effects on the analysis of survey data. In: Lyberg L, et al., editors. Survey measurement and process quality. John Wiley & Sons; New York: 1997. pp. 603–632. [Google Scholar]
- Bollen KA. Structural equations with latent variables. John Wiley & Sons; New York: 1989. [Google Scholar]
- Brown W. Some experimental results in the correlation of mental abilities. British Journal of Psychology. 1910;3:296–322. [Google Scholar]
- Burney DM, Kromrey J. Initial development and score validation of the adolescent anger rating scale. Educational and Psychological Measurement. 2001;61:446–460. [Google Scholar]
- Carmines EG, Zeller RA. Reliability and validity assessment. In: Carmines EG, editor. Sage university papers series on quantitative applications in the social sciences. Sage; Newbury Park, CA: 1979. pp. 107–117. [Google Scholar]
- Cortina JM. What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology. 1993;78:98–104. [Google Scholar]
- Cronbach LJ. Coefficient alpha and the internal structure of tests. Psychometrika. 1951;16:297–334. [Google Scholar]
- Dowd K, Kinsey S, Wheeless S, Suresh S, the NSCAW Research Group . National Survey of Child and Adolescent Well-being: Combined waves 1-4 data file user’s manual. RTI International; Research Triangle Park, NC: 2004. [Google Scholar]
- Green SB, Hershberger SL. Correlated errors in true score models and their effect on coefficient alpha. Structural Equation Modeling. 2000;7:251–270. [Google Scholar]
- Heise DR. Separating reliability and stability in test-retest correlation. American Sociological Review. 1970;34:93–101. [Google Scholar]
- Heise DR. Comment on “The estimation of measurement error in panel data.”. American Sociological Review. 1969;35:117. [Google Scholar]
- Henson RK. Understanding internal consistency reliability estimates: A conceptual primer on coefficient alpha. Measurement and Evaluation in Counseling and Development. 2001;34:177–189. [Google Scholar]
- Hogan TP, Benjamin A, Brezinski KL. Reliability methods: A note on the frequency of use of various types. Educational and Psychological Measurement. 2000;60:523–531. [Google Scholar]
- Jöreskog KG. Statistical models and methods for analysis of longitudinal data. In: Jöreskog, Sörbom, editors. Advances in factor analysis and structural equation models. Abt Books; Cambridge, MA: 1979. [Google Scholar]
- Komaroff E. Effect of simultaneous violations of essential τ-equivalence and uncorrelated error on coefficient α. Applied Psychological Measurement. 1997;21:337–348. [Google Scholar]
- Lord FM, Novick MR. Statistical theories of mental test scores. Addison-Wesley; Reading, MA: 1968. [Google Scholar]
- Lucke JE. Rassling the gog. The influence of correlated item error on internal consistency, classical reliability, and congeneric reliability. Applied Psychological Measurement. 2005;29:106–125. [Google Scholar]
- Nasser F, Wisenbaker J. A Monte Carlo study investigating the impact of item parceling strategies on parameter Eetimates and their standard errors in CFA. Structural Equation Modeling. 2006;13:204–228. [Google Scholar]
- Rae G. Correcting coefficient alpha for correlated errors: Is αK a lower bound to reliability? Applied Psychological Measurement. 2006;30:56–59. [Google Scholar]
- Raykov T. Coefficient alpha and composite reliability with interrelated nonhomogeneous items. Applied Psychological Measurement. 1998;22:375–385. [Google Scholar]
- Raykov T. Bias of coefficient alpha for fixed congeneric measures with correlated errors. Applied Psychological Measurement. 2001;25:69–76. [Google Scholar]
- Raykov T, Shrout PE. Reliability of scales with general structure: Point and interval estimation using a structural equation modeling approach. Structural Equation Modeling. 2002;9(2):195–212. [Google Scholar]
- Sapin C, Simeoni MC, El Khammar M, Antoniotti S, Auquier P. Reliability and validity of the VSP-A, a health-related quality of life instrument for ill and healthy adolescents. Journal of Adolescent Health. 2005;36:327–336. doi: 10.1016/j.jadohealth.2004.01.016. [DOI] [PubMed] [Google Scholar]
- Shevlin M, Miles JNV, Davies MNO, Walker S. Coefficient alpha: A useful measure of reliability? Personality and Individual Differences. 2000;28:229–237. [Google Scholar]
- Spearman C. Correlation calculated from faulty data. British Journal of Psychology. 1910;3:271–295. [Google Scholar]
- Vehkalahti K, Puntanen S, Tarkkonen L. Estimation of reliability: A better alternative for Cronbach’s alpha. Department of Mathematics and Statistics; Finland: 2006. Reports on Mathematics, Preprint 430, University of Helsinki. [Google Scholar]
- Wiley DE, Wiley JA. The estimation of measurement error in panel data. American Sociological Review. 1970;35:112–117. [Google Scholar]
- Yoshizumi T, Murase S, Murakami T, Takai J. Reliability and validity of the parenting scale of inconsistency. Psychological Reports. 2006;99:74–84. doi: 10.2466/pr0.99.1.74-84. [DOI] [PubMed] [Google Scholar]
- Zimmerman DW, Zumbo BD. Coefficient alpha as an estimate of test reliability under violation of two assumptions. Educational & Psychological Measurement. 1993;53:33–50. [Google Scholar]