Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2014 Feb 3;30(11):1569–1578. doi: 10.1093/bioinformatics/btu021

Complete enumeration of elementary flux modes through scalable demand-based subnetwork definition

Kristopher A Hunt 1,2,*, James P Folsom 1,2, Reed L Taffs 1,2, Ross P Carlson 1,2,*
PMCID: PMC4029027  PMID: 24497502

Abstract

Motivation: Elementary flux mode analysis (EFMA) decomposes complex metabolic network models into tractable biochemical pathways, which have been used for rational design and analysis of metabolic and regulatory networks. However, application of EFMA has often been limited to targeted or simplified metabolic network representations due to computational demands of the method.

Results: Division of biological networks into subnetworks enables the complete enumeration of elementary flux modes (EFMs) for metabolic models of a broad range of complexities, including genome-scale. Here, subnetworks are defined using serial dichotomous suppression and enforcement of flux through model reactions. Rules for selecting appropriate reactions to generate subnetworks are proposed and tested; three test cases, including both prokaryotic and eukaryotic network models, verify the efficacy of these rules and demonstrate completeness and reproducibility of EFM enumeration. Division of models into subnetworks is demand-based and automated; computationally intractable subnetworks are further divided until the entire solution space is enumerated. To demonstrate the strategy’s scalability, the splitting algorithm was implemented using an EFMA software package (EFMTool) and Windows PowerShell on a 50 node Microsoft high performance computing cluster. Enumeration of the EFMs in a genome-scale metabolic model of a diatom, Phaeodactylum tricornutum, identified ∼2 billion EFMs. The output represents an order of magnitude increase in EFMs computed compared with other published algorithms and demonstrates a scalable framework for EFMA of most systems.

Availability and implementation: http://www.chbe.montana.edu/RossC.

Contact: rossc@erc.montana.edu or kristopher.hunt@erc.montana.edu

Supplementary Information: Supplemental materials are available at Bioinformatics online.

1 INTRODUCTION

Extracting biologically meaningful information from the continuously expanding ‘omics’ databases is often limited by bioinformatics tools. Stoichiometric modeling is one approach making advances in the quantification of metabolic phenotypes reflected by fluxomic data and inferred from metabolomic, proteomic, transcriptomic and genomic data (Reed and Palsson, 2003). Stoichiometric modeling assumes that during appropriate time scales, cellular biochemistry can be approximated as a steady state process with respect to intracellular enzyme and metabolite concentrations. This assumption simplifies the differential equations describing cellular mass balances, and when coupled with reaction directionality and flux magnitude constraints, permits the calculation of physiologically reasonable flux distributions. There are two major stoichiometric modeling approaches with numerous subvariations (Klamt and Stelling, 2003; Orth et al., 2010; Reed and Palsson, 2003; Trinh et al., 2009). One stoichiometric modeling approach, elementary flux mode analysis (EFMA), enumerates all genetically distinct indecomposable flux distributions in a metabolic network (Schuster and Hilgetag, 1994). These elementary flux modes (EFMs) are the minimal set of stoichiometrically balanced flux distributions representable as unique binary vectors based on participation of every model reaction. This set must also represent every steady state flux distribution in a given network through non-negative combinations without cancellation (Klamt and Stelling, 2003; Llaneras and Picó, 2010; Schilling et al., 2000). Cancellation refers to removal of reaction participation through combination of fluxes with equal but opposite magnitudes (i.e. genetic distinction). Another stoichiometric modeling approach, flux balance analysis (FBA), uses linear programing to identify optimal flux distributions through a metabolic network. Various objective functions are possible, including the maximization of biomass yield from a substrate (e.g. Varma et al., 1993). These two stoichiometric modeling methods have been used for decades to direct metabolic engineering efforts and predict physiological and ecological behaviors (Carlson, 2009; Carlson et al., 2002; Feist et al., 2006; Liao et al., 1996; Reed and Palsson, 2003; Taffs et al., 2009; Trinh et al., 2009; Varma and Palsson, 1994).

Both stoichiometric modeling approaches have strengths and limitations. A major strength of EFMA is enumeration of the entire solution space in an unbiased manner. FBA generates only a limited number of distinct solutions using a directed objective function (Orth et al., 2010; Reed and Palsson, 2003; Trinh et al., 2009). However, the directed FBA approach reduces computational costs relative to EFMA, permitting examination of complex metabolic reconstructions, commonly referred to as genome-scale models. Complex (e.g. genome scale and microbial community) metabolic networks have often been intractable using EFMA (Klamt and Stelling, 2002; Terzer et al., 2009), despite algorithmic advances (Klamt et al., 2005; Schuster and Hilgetag, 1994; Schuster et al., 2000; Terzer and Stelling, 2008; Urbanczik and Wagner, 2005a).

Approaches that circumvent the problem of enumerating all EFMs have been explored. One such approach, convex basis analysis [i.e. extreme pathway analysis (Schilling et al., 2000)] identifies a subset of EFMs that still reproduce any feasible steady state flux distribution but lack the biological interpretability of the complete EFM set (Klamt and Stelling, 2003; Llaneras and Picó, 2010). Efforts have also been made to enumerate subsets or patterns of elementary flux vectors that allow genome-scale investigations. These efforts include generating the conversion cone (a simpler projection of the solution space considering external fluxes only) (Urbanczik, 2007; Urbanczik and Wagner, 2005b), enumerating only EFMs containing the largest number of zero fluxes (de Figueiredo et al., 2009), enumerating a set of EFMs that can explain a given flux distribution (Ip et al., 2011), applying regulation to minimize computation (Jungreuthmayer et al., 2013) and identifying elementary flux patterns, which are EFMs for subsystems that consider the constraints imposed by the parent network (Kaleta et al., 2009; Schuster et al., 2010). Finally, computationally intractable networks have been divided into manageable pieces based on biochemical knowledge (Schilling and Palsson, 2000; Verwoerd, 2011), metabolite connectivity (i.e. the number of reactions involving a particular metabolite) (Schuster et al., 2002; Verwoerd, 2011), path length between reactions (Ma et al., 2004), examination of the nullspace of the stoichiometric matrix (Poolman et al., 2007) and random sampling of the solution space to calculate eigenvectors that can be rotated to produce distinct reaction sets (Barrett et al., 2009).

For many applications, the ideal approach is an unbiased investigation of the entire solution space, although this scenario was previously out of computational reach for complex networks (Klamt and Stelling, 2002; Llaneras and Picó, 2010). It has been proposed that otherwise infeasible EFM enumerations can be performed through the dissection of metabolic networks into simpler subnetworks via suppression or enforcement of reaction fluxes, a technique referred to as splitting (Klamt et al., 2005). Suppression of a reaction defines a subnetwork that does not contain the reaction, whereas enforcement of a reaction defines a subnetwork that excludes EFMs that do not use the reaction, both of which reduce the computational burden (e.g. Fig. 1). Complete coverage of a metabolic network’s solution space without overlap is ensured at each split by paired suppression and enforcement of a single reaction. An additional example of suppressing and enforcing can be found in Jevremović et al. (2011b), which used the EFMA algorithm, Elmo-Comp. Unfortunately, Elmo-Comp lacked enumeration completeness, as shown through a disagreement between the presented and published EFM counts (Jevremović and Boley, 2012; Jevremović et al., 2011a). The primary objective of the current study is to successfully implement a scalable demand-based splitting technique for complete enumeration of all network EFMs. The objective is achieved through (i) the development of rational rules for effectively splitting networks, (ii) the successful use of a network splitting algorithm that continuously divides networks until they are computationally tractable and (iii) the use of a workstation-based computational cluster to distribute EFM enumeration of genome-scale models. The presented work demonstrates efficacy across network models containing EFM counts spanning four orders of magnitude. This algorithm is the first successful implementation of the splitting technique and establishes a scalable framework for EFMA of most metabolic models.

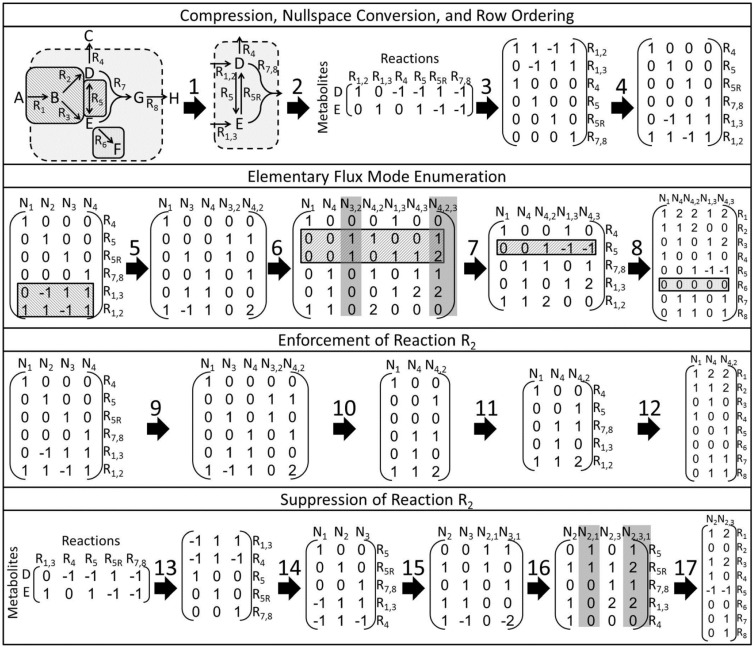
Fig. 1.

Fig. 1.

Open in a new tab

Overview of EFM enumeration using EFMTool and the splitting approach. Step 1) The model is compressed removing dead-end reactions (R6), separating reversible reactions into forward and reverse reactions (R5 becomes R5 and R5R), and combining reaction sets that always occur together into a single reaction (R7 and R8 combined into R7,8, removing metabolite G). Step 2–3) The compressed network, represented by a stoichiometric matrix with reactions in columns and metabolites in rows, is solved for the nullspace basis vectors (i.e. the nullspace kernel). External metabolites are not constrained by conservation relationships and are therefore not considered in the stoichiometric matrix. Step 4) The kernel rows are reordered to minimize memory usage and computational runtime. Steps 5–6) The EFMTool algorithm then applies directionality constraints to each reaction sequentially; vectors containing negative fluxes in the reaction being constrained are replaced by all non-negative linear combinations resulting in a zero flux through the reaction. The negative flux in reaction R1,3 at N2 is replaced by N3,2 (N3 + N2) and N4,2 (N4 + N2), whereas the negative flux in reaction R1,2 at N3 is replaced by N1,3 (N1 + N3), N4,3 (N4 + N3) and N4,2,3 (N4,2 + N3). EFMTool bit-masks each row of values after the directionality constraint is applied, improving memory usage (not shown). Step 7) N3,2 is removed during recompilation of reversible reactions, and N4,2,3 is removed because at least q-m-1 zeros per flux vector are required by the degrees of freedom constraint, where q and m are the number of reactions and metabolites, respectively (Gagneur and Klamt, 2004). Step 8) The remaining vectors are EFMs and decompressed. This procedure can be modified to enforce (Steps 9–12) or suppress (Steps 13–17) reactions as needed. Enforced reactions are moved to the end of the algorithm and directionality constraints are applied as described earlier; however, when the enforced reaction is reached, all positive flux vectors have already been enumerated (Step 9), therefore flux vectors that violate the directionality constraint or do not use the reaction are discarded (Step 10). Suppressed reactions result in a new stoichiometric matrix that is then processed as described earlier. The highlighted examples of a combined reaction in the backslash patterned box Inline graphic, reversible reaction in the forward slash patterned box Inline graphic and dead-end reaction in the gray box Inline graphic are to be avoided for use in splitting

2 METHODS

2.1 Experimental and computational systems

Development and analysis of the presented splitting techniques was performed using three previously published metabolic models described in Table 1 with additional detail available in Supplementary Table S1. The test models, chosen to demonstrate efficacy over a range of model complexity, included a prokaryotic (ECOLI), a simplified eukaryotic (YEAST1) and a multicompartment eukaryotic model (YEAST2) (Supplementary Material). These test models were calculated as both unsplit and split networks to validate the compiled subnetwork results. Unsplit networks were computed using the software package EFMTool on a Windows 7 machine with a maximum configuration of 120 GB of RAM and 2 Intel Xeon processors (X5690). Implementation of EFMTool (Terzer and Stelling, 2008) version 4.7.1 (www.csb.ethz.ch/tools/efmtool) used documented options described in Supplementary Table S2. The basic splitting and iterative splitting algorithms were written in Windows PowerShell v2.0 for implementation with Microsoft high performance computing (HPC), clustering software which supports workstation-based clusters. The computational cluster included 50 workstation nodes, which ranged from 4–120 GB of RAM per node. Result compilations and analyses were performed using MATLAB on machines with 32 GB of RAM.

Table 1.

Metabolic models used in the presented study

Organism Model Reactions/ Metabolites EFMs
Saccharomyces cerevisiae YEAST1a 78/62 1 515 315d
S. cerevisiae YEAST2a 83/63 68 868 602d
Escherichia coli ECOLIb 95/94 226 269 020d
P. tricornutum DIATOMc 318/335 1 934 729 551e
Open in a new tab

aJevremović and Boley, 2012. bJungreuthmayer et al., 2013. cThis work. dEFMs validated by comparing split and unsplit network results. eFourteen reactions used for iterative splitting. Some subnetworks were recalculated varying the number of reactions for splitting to validate results.

2.2 EFM concatenation and comparison

Subnetwork results produced by the splitting algorithm were screened for consistency with subnetwork definitions and concatenated into a single output set (as in Fig. 2). EFMTool identifies futile cycles based on the number of non-zero fluxes in a flux vector, removes them from processing and adds them back at the end of processing regardless of subnetwork definition. This necessitated screening all EFMs to verify that they did not violate the definition of their subnetwork. The screening process required minimal computational effort. For example, the CONCATENATOR script checked and compiled 2 billion EFMs in ∼1 day; most of the elapsed time involved reading, decompressing, compressing and writing the results, which occupy ∼1 TB of hard drive space.

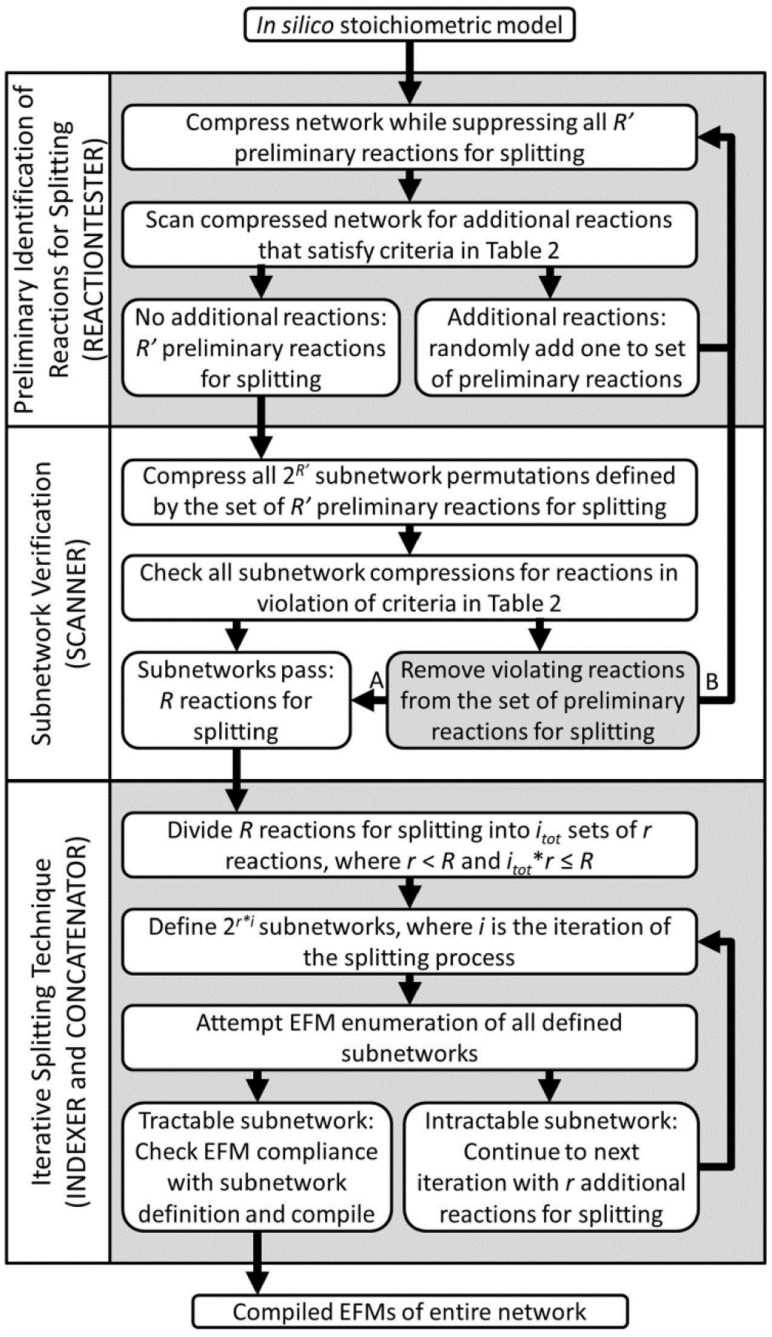
Fig. 2.

Fig. 2.

Open in a new tab

Work flow of reaction identification and iterative splitting approaches. Initially, the list of identified preliminary reactions for splitting is empty but increases by one reaction per loop through preliminary reaction identification. The final quantity of reactions for splitting was adjusted at the gray box by choosing route A if a predefined R was achieved or route B if more reactions for splitting were required. Depicted processes describe the pseudo-code or MATLAB functions listed in parentheses. See the Symbols Section for additional variable definitions

Network results were compared across different algorithms and splitting configurations by converting all EFMs to a binary representation based on reaction participation and identifying EFMs not shared by both result sets being compared. This comparison was done using standard MATLAB functions. Binary representation removed rounding effects associated with normalization and allowed for comparison of all test models presented.

2.3 Optimizing EFMTool performance

EFMTool’s use of RAM was inspected and optimized using the management application, Jconsole, and Java options. Briefly, Java 1.6.× uses a generational memory construct that assigns new objects to one memory space while moving older objects to a separate predefined memory space. This is usually an efficient use of RAM, as most Java applications do not produce many old objects, and memory management is easier when newer objects are kept together. However, EFMTool stores each EFM as an object that stays in RAM for the duration of the calculation, eventually becoming an old object. EFMTool filled the memory allocated for older objects that resulted in ‘out of RAM’ errors, despite having only used 25–33% of the RAM assigned to Java. Thus, the default Java options limit EFMTool execution to smaller networks. This practice was corrected and performance optimized using command line switches described in Supplementary Table S2.

2.4 k-1 EFM correction

During early attempts at EFM enumeration using the EFMTool functionality to enforce reactions, EFMs were absent from the resulting solution set. The missing EFMs contained k-1 enforced reactions, where k is the number of non-zero fluxes in the EFM. This issue was corrected through a modification in EFMTool code to consider enforced reactions during the subroutine that removes futile cycles (Supplementary Material).

3 RESULTS

3.1 Selecting reactions for defining subnetworks

Appropriate reaction selection for subnetwork definition is essential for effective splitting. Selected reactions must permit complete enumeration of EFMs while distributing calculations over subnetworks. Initially, random reactions for splitting were screened using a brute force method to confirm functionality for splitting; analysis of the results identified four major categories of reactions to avoid. First, reactions for splitting should not produce or consume metabolites that are not consumed or produced by other reactions (i.e. dead-end reactions, R6 in Fig. 1). Dead-end reactions result in empty subnetworks when enforced and do not reduce computations when suppressed.

Second, reactions for splitting should not include reversible reactions. EFMTool divides reversible reactions into two separate irreversible reactions, a forward and reverse reaction, during EFM enumeration and then recombines the fluxes before reporting the final EFMs (R5 in Fig. 1). If used for splitting, the forward and reverse reactions are enforced or suppressed concurrently; EFMs with flux in only one of these reactions would be lost. This property makes reversible reactions unacceptable for splitting.

Network compression improves memory efficiency by combining reactions, which must operate together into a single compressed reaction (e.g. R1 and R2 are combined into R1,2 in Fig. 1; Gagneur and Klamt, 2004); however, compression can cause problems during splitting, resulting in a third category of reactions to avoid for splitting. Two adverse scenarios can result from compression. In a branching series, a single reaction can be combined separately with multiple reactions to form multiple compressed reactions. Using that single reaction as a reaction for splitting prevents certain subnetwork permutations because multiple independent compressed reactions are enforced or suppressed simultaneously (e.g. R1 in Figs. 1 and 3 and Supplementary Fig. S1). In a linear series, a set of reactions that must occur together combine to form a single compressed reaction (e.g. R7 and R8 in Fig. 1 and Supplementary Fig. S1). Using multiple reactions that define a compressed linear series is ineffective for the same reason as enforcing dead-end reactions (R7 and R8 in Fig. 1 and Supplementary Fig. S1). However, one reaction from a linear series or the branch reactions in a branched series may be effective for splitting (e.g. R2, R3 and R7 or R8 in Figs 1 and 3 and Supplementary Fig. S1). Although more reactions may be available for subnetwork definition when compression is not used, compression greatly reduces computational burden during the enumeration process, vastly outweighing the benefit of additional potential reactions for splitting (data not shown; Klamt et al., 2005).

Fig. 3.

Fig. 3.

Open in a new tab

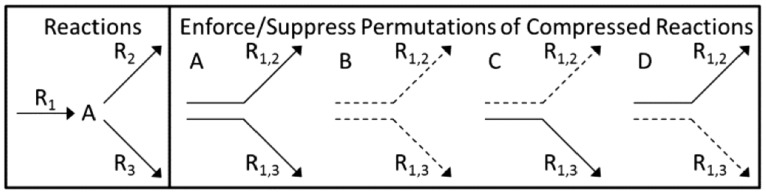
Network compression effect on reactions. Network compression results in two reactions: R1,2 is R1 + R2 and R1,3 is R1 + R3. Enforcing (solid lines)/suppressing (dotted lines) reaction R1 generates only two (A and B) of the four reaction combinations needed to fully describe possible reaction participation (A, B, C and D)

A fourth type of reaction to avoid has poorly scaled coefficients that can lead to numerical instability. This often occurs with biomass synthesis associated reactions. For instance, accounting for the synthesis of a low abundance vitamin (e.g. B12) and a common amino acid (e.g. glycine) can lead to a >103-fold difference between the reaction’s largest and smallest coefficients. Such a model could not be analyzed with EFMTool due to numerical instabilities in the stoichiometric matrix. This issue can be exacerbated during the network splitting process when potential EFMs with small, but nonzero, fluxes in enforced reactions are removed based on the software’s computational definition of zero. The removed EFMs are not present when the reaction is suppressed by definition and are therefore missed in the results. One method explored to circumvent this problem used the higher accuracy arithmetic of fixed-point notation instead of the default floating-point notation (double to fractional arithmetic in EFMTool nomenclature). The use of fixed-point notation permitted complete enumeration of EFMs for some test networks but introduced a substantial computational cost with a minimal increase in the number of usable reactions for splitting (data not shown). Increasing the precision of the zero definition for floating-point notation was also examined but not found to consistently improve EFM enumeration. Although there are multiple methods to circumvent this problem, this study avoided using reactions containing poorly scaled coefficients for splitting, defined as coefficients with a difference >10 within a single reaction. This approach was sufficient for the three test models.

A list of effective reactions for splitting was identified through application of the rules summarized in Table 2 and confirmed through additional checks (i.e. REACTIONTESTER and SCANNER, respectively, in Fig. 2). The rules were applied iteratively as follows: (i) reactions were identified that did not violate the rules in Table 2, given the current network compression, (ii) one such reaction was selected randomly and added to a list with R′ preliminary reactions for splitting and (iii) the subnetwork was defined by suppressing all R′ preliminary reactions for splitting, providing the basis for the next iteration of reaction selection. This was repeated until all remaining reactions violated the rules. Repeatedly adjusting the compression basis was necessary because as reactions are suppressed, they change the model compression through production of dead-ends and new sets of combined reactions. Then, to ensure effective splitting, all 2R′ subnetwork permutations defined using enforce/suppress combinations of the preliminary reactions for splitting were compressed and examined for rule violations. Any reactions that violated the rules under any enforce/suppress permutation were removed, resulting in a final list of R usable reactions for splitting. Reaction validation for all subnetworks also allowed for screening of reactions that create incompatibility issues with EFMTool. These processes for preliminary reaction identification and subnetwork permutation checking, depicted in Figure 2, are described in the pseudo-code found in the Supplementary Material (REACTIONTESTER function and SCANNER subroutine, respectively).

Table 2.

Criteria for removal of reactions from enforce/suppress sets

Rule Reaction type Issue
1 Dead-end Subnetworks cannot evenly distribute EFMs
2 Reversible Misses EFMs containing flux in either but not both directions
3 Combineda May not allow for all reaction combinations
4 Poorly scaled coefficients Poorly conditioned matrix and zero definition may miss EFMs (threshold difference of 10)
Open in a new tab

Note: All reaction combinations must be tested to confirm that an EFM is not represented in the enforce/suppress set and that the subnetwork definition and compression does not rearrange reactions causing violation of the stated rules. aSee Section 3.1 for detailed description of combined reactions to avoid.

3.2 Efficacy of splitting

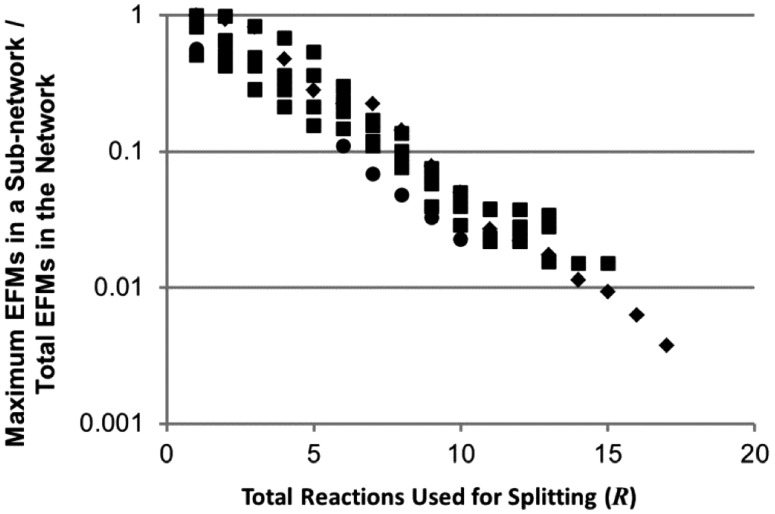
The number and choice of reactions used to define subnetworks are important control points for splitting. To quantify splitting effectiveness based on these considerations, subnetworks were defined using a set of R reactions, EFMs for all subnetworks were enumerated and the largest number of EFMs in any subnetwork was used as a basis to assess splitting efficacy. A single set of reactions for splitting was identified for each of the ECOLI and YEAST2 models, whereas four distinct sets were identified for the YEAST1 model using the procedure detailed in the preceding section (pseudo-code presented in Supplementary Material). The four distinct sets of reactions for splitting exist due to the sequential random identification of reactions for splitting (e.g. most reactions could work in isolation, but only some sets of reactions work together). R was varied within each set of reactions for splitting by removing reactions without replacement to form smaller sets. The linear trend on a semi-log plot (Fig. 4) suggests an exponential decay of maximum EFMs per subnetwork with increasing R. There were no deviations in the number or identity of the EFMs enumerated between the 77 splitting-based enumerations and the respective unsplit enumerations. This analysis also demonstrates that the reaction selection rules are functional over a broad range of R.

Fig. 4.

Fig. 4.

Open in a new tab

Subnetwork EFM count reduction with increasing number of reactions for splitting (R). The test models YEAST1 (squares), YEAST2 (diamonds) and ECOLI (circles) were analyzed in 77 separate configurations; every configuration resulted in complete enumeration of the solution space

3.3 Iterative splitting

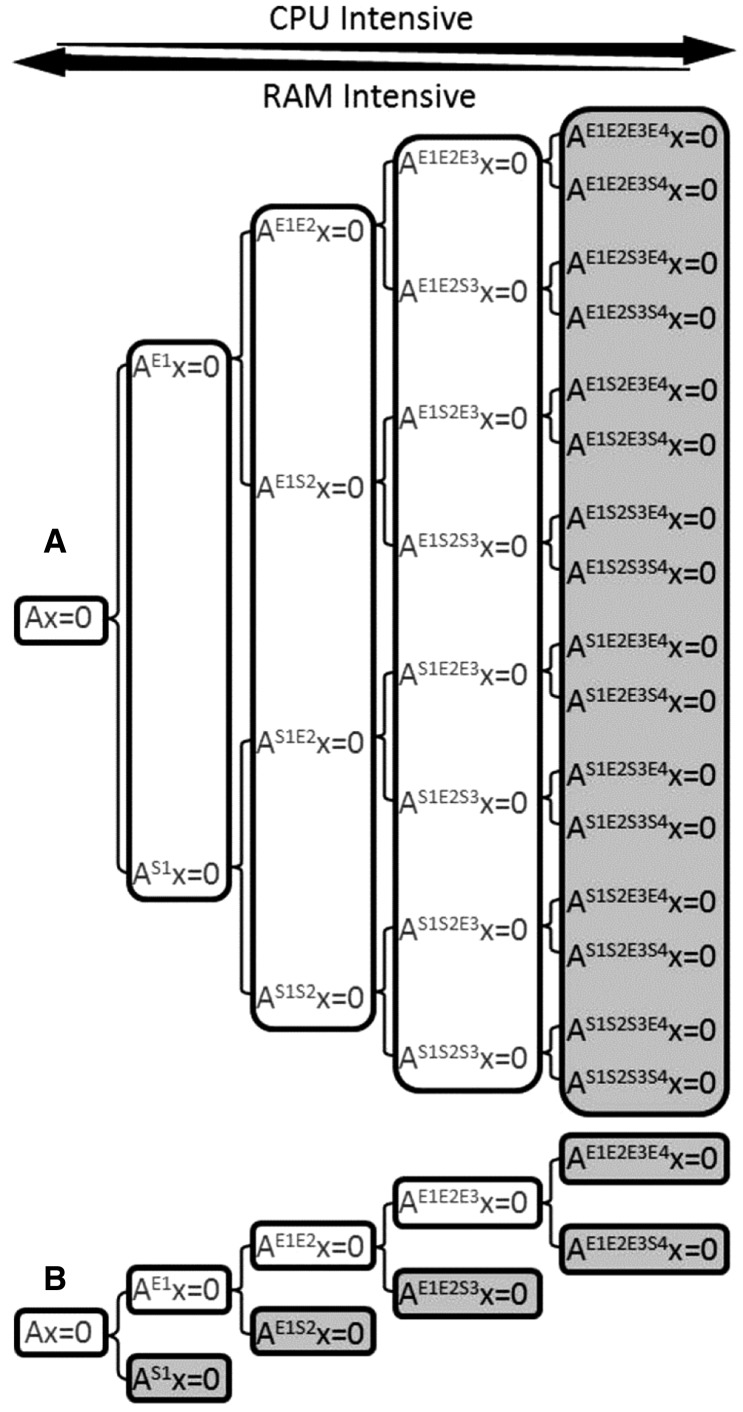
Identifying the optimal number of reactions for splitting a model is a major theoretical and practical challenge. There are two competing effects with increasing magnitude of R that are (i) the rate of new subnetwork definition and (ii) the rate of reduction in subnetwork complexity. Splitting shifts the computational burden from memory limitation to CPU limitation (Fig. 5A and B). The number of subnetworks grows with 2R when using basic splitting, resulting in a prohibitive number of files for larger values of R. Figure 5A demonstrates a case of basic splitting in gray where R is 4.

Fig. 5.

Fig. 5.

Open in a new tab

Comparison of two network splitting approaches. The basic splitting approach (A) uses combinations of enforced/suppressed reactions to create calculable subnetworks where the number of subnetworks increases exponentially with the number of reactions for splitting (Klamt et al., 2005). The iterative splitting approach (B) only generates subnetworks when the previous ones are intractable (white) until all EFMs for all subnetworks in the branch can be enumerated (gray) (Klamt et al., 2005). Both approaches shift the burden of computation from a RAM-limited problem to a CPU-limited problem as the subnetworks become smaller but greater in number. The example uses R = 4 reactions for splitting with each iteration considering one additional reaction (i.e. r = 1) for a total of i = 4 iterations. Superscripts refer to the enforced (E) or suppressed (S) reactions in the labeled subnetworks

A demand-based network splitting algorithm can be implemented, which minimizes the total number of analyzed subnetworks without sacrificing complete coverage of the solution. This strategy is referred to as iterative splitting (Fig. 5B). The procedure initially uses a set of r reactions to define subnetworks, where r is less than the total number of reactions needed to complete the network (Rmin). EFMs of calculable subnetworks are enumerated and subnetworks that are assessed to be intractable (e.g. EFM enumeration fails due to memory limitation or terminates via the algorithm discussed in Section 3.5) form branches that are further divided using an additional set of r reactions. The process continues until each branch completes or the list of reactions for splitting is exhausted. Computational savings are realized when branches complete at intermediate iterations instead of the final iteration. Figure 5B illustrates a case where r is 1, Rmin is 4 and the total number of iterations, itot, is 4. In this example, one branch completes per iteration resulting in a 2-fold decrease in total subnetworks attempted compared with basic splitting (Fig. 5A and B). The YEAST2 model in Table 1 demonstrated a 76-fold decrease in number of subnetworks calculated using iterative splitting (r = 2, Rmin = 14 and itot = 7) as compared with basic splitting with the same 14 reactions (reactions for splitting: R4, R5, R9, R12, R14, R21, R27, R33, R37, R40, R46, R53, R58 and R61). Rmin is a function of computational resources and was increased by decreasing available memory for computation (e.g. 6718 MB heap size for the YEAST2 example).

3.4 Optimizing the number of reactions for splitting per iteration (r)

Iterative splitting has substantial computational benefits when branches complete before the final iteration; however, the computational costs of intractable subnetworks may overwhelm this benefit. This tradeoff provides a basis for optimization, the number of reactions for splitting (r) applied per iteration, i. Increasing r defines a larger number of more constrained subnetworks per iteration, which have an increased likelihood of completion compared with subnetworks defined using smaller r. This approach decreases failed enumeration attempts but increases the number of attempted subnetworks per iteration. Two scenarios bound the total possible number of subnetworks analyzed during iterative splitting. The upper limit occurs when all subnetworks are intractable until the last iteration at which point they all complete (Fig. 5A, r = 1). This scenario represents basic splitting when r equals R. The lower limit occurs when each step of iterative splitting produces only one intractable subnetwork until R reactions are used, at which point all subnetworks complete and the entire solution space for the whole network is covered (Fig. 5B, r = 1).

Optimization based on limiting the number of intractable subnetworks enables prediction of a generalized ideal r without a priori network-specific information. The equation for the total number of subnetworks (N) is:

graphic file with name btu021m1.jpg (1)

where f is the number of intractable subnetworks. Equation (1) does not include the original unsplit network. As r→Rmin, f→0, therefore, basic splitting with at least the number of reactions required (Rmin) eliminates time spent on intractable subnetworks. However, this neglects the benefit of early branch completion, reducing the total number of attempted subnetworks and therefore the total CPU time (Fig. 5A and B).

Assigning a theoretical relative CPU time for tractable and intractable subnetworks permits evaluation of effective values of r with respect to CPU time. For this analysis, a theoretical model is considered that requires one hour of CPU time to enumerate the EFMs from the unsplit network, tunsplit. An approximate relation between tunsplit and the average CPU time to enumerate the EFMs of a subnetwork of the same network was determined empirically using the test models in Table 1. For the subnetwork defined by r*i reactions, the CPU time for EFM enumeration (tr,i) follows the relationship:

graphic file with name btu021m2.jpg (2)

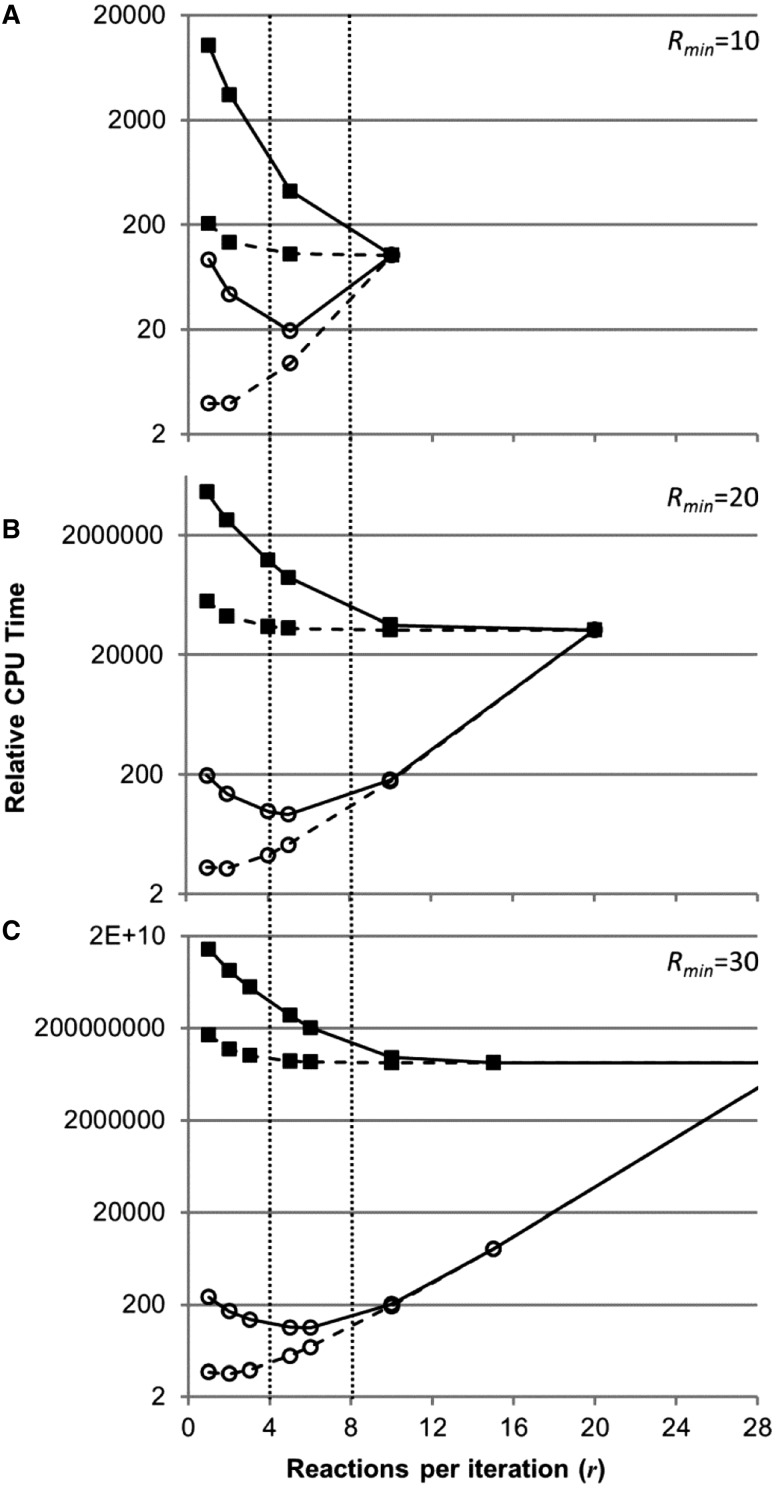
(data not shown). For analysis purposes, the CPU time for subnetworks with failed EFM enumeration attempts, tfail, was bracketed between 10-fold longer and 10-fold shorter than tunsplit. A 10-fold longer run time was used as an upper limit because Java garbage collection will run until it uses 90% of the total CPU time before crashing, inflating the run time ∼10-fold. A 10-fold shorter run time was used for the lower limit because networks with an explosion in the number of potential EFMs may quickly fill available memory with objects that cannot be cleared (data not shown). Combining Equation (2) and the bounds for tfail with the number of subnetworks defined by Equation (1), total CPU time boundaries were estimated as a function of r and normalized by tunsplit (Fig. 6). Simulations considered three theoretical models with Rmin = 10, 20 and 30 and all combinations of itot and r producing a respective Rmin. Increasing r reduces the maximum potential CPU time investment independent of R; however, the time minimum increases significantly with r after ∼5 reactions (Fig. 6). The minimum time increases due to the large number of subnetworks and the associated redundant calculations during reaction enforcement. Considering both the minimum relative CPU time for the lower tfail limit scenario and the exponential decrease in relative CPU time for the upper tfail limit scenario, an r in the range of 4–8 reactions appears optimal without a priori knowledge (Fig. 6). The analysis considers total relative CPU time; implementation on computational clusters would reduce real-world time because of parallel computations.

Fig. 6.

Fig. 6.

Open in a new tab

Optimization of reactions for splitting applied per iteration (r). Relative CPU time for theoretical networks requiring 10 (A), 20 (B) and 30 (C) total reactions for splitting to complete, assuming that one subnetwork is intractable per iteration (open circles) or all subnetworks are intractable until the last iteration (closed squares). Time for intractable subnetworks was varied between 10-fold increase (solid lines) and 10-fold decrease (dashed lines) relative to an unsplit model. Relative CPU time is the summation of time to complete all subnetworks normalized by time to complete the whole unsplit network. Vertical dotted lines designate the optimal working range based on the minimum (open circles with solid lines) and the exponential decrease (closed squares), given no prior knowledge of network splitting behavior

3.5 Minimizing intractable subnetwork runtime

Intractable subnetworks can have a high CPU time cost; therefore, large run time savings can be obtained by minimizing CPU time spent on intractable subnetworks. An empirical detection strategy was applied to identify EFM enumeration attempts that were not likely to complete; those attempts were then terminated before failure and the subnetwork was further divided. Applying the intractable subnetwork detection strategy resulted in substantial time savings for the models in this study (data not shown). Details of the prediction algorithm and used time thresholds can be found in the Supplementary Material.

3.6 Application of the iterative splitting algorithm to a genome-scale diatom model

EFMA of a genome-scale metabolic model for the diatom Phaeodactylum tricornutum Pt1 was conducted to demonstrate the iterative splitting algorithm. This model was reconstructed using the extensive knowledge base for P. tricornutum Pt1, including a finished genome (Markowitz et al., 2012) and literature-based manual analyses (e.g. Fabris et al., 2012; Kroth et al., 2008). The DIATOM model considers 680 genes that were manually compressed into 318 reactions with 335 metabolites. Reactions and metabolites were partitioned into five distinct physical compartments based on analysis of organelle signal peptides (Emanuelsson et al., 2007) and biochemical studies (e.g. Tachibana et al., 2011). The metabolic model with genomic information, stoichiometries, biomass requirements and a graphical representation can be found in the Supplementary Material.

The workflow for successful application of the iterative splitting algorithm (i.e. Fig. 2) to the DIATOM model can be described as follows: a set of 14 reactions for splitting (R = 14) was identified by calling the REACTIONTESTER function (Supplementary Material). The reactions were divided into two sets of seven reactions (r = 7 and itot = 2) based on the theoretical optimal values of r (Fig. 6) and the complete use of the set of reactions for splitting. The INDEXER function submitted EFM enumeration jobs to the HPC cluster and on completion of the first iteration, scanned the results for intractable subnetworks to further divide with the next seven reactions in the second iteration. The PowerShell script used is available in the Supplementary Material. EFMA of the DIATOM model resulted in 1 934 729 551 EFMs; this count was validated by reanalyzing random model subnetworks using different sets of reactions for splitting. The output exceeds the largest reported for EFMA to date by ∼1 order of magnitude (Jungreuthmayer et al., 2013).

4 DISCUSSION

The complete and reproducible EFMA of metabolic networks that were previously computationally intractable was demonstrated here through the definition of subnetworks based on serial enforcement and suppression of reaction fluxes. This is in contrast to other recent attempts to parallelize EFM enumeration by splitting, which were found to be incomplete at times (Jevremović and Boley, 2012; Jevremović et al., 2011a). The presented basic and iterative splitting algorithms are expected to be fully compatible with that group’s recent efforts to implement distributed EFMA computing with shared memory (Jevremović et al., 2011b), offering additional computing power for recalcitrant subnetworks.

When using EFMTool, the reactions for splitting cannot contain a subset representing all non-zero flux reactions in an EFM; enforcing such a subset causes an error. The ability to identify the error by examining all subnetworks at the level of compression indicates the error is caused during preprocessing. Additionally, manual application of the nullspace algorithm did not yield an explanation for the error. The error was reproducibly avoided by identifying the subnetworks with the error and eliminating at least one of the reactions in the EFM from the set of reactions for splitting. This solution is algorithmically inconvenient, as one of these reactions must be removed from the set of reactions for splitting and the new combination of reactions reanalyzed (Fig. 2). However, subnetworks enforcing an EFM cannot contain more than the defined EFM, as an EFM cannot be represented within another EFM (due to the decomposability constraint). The EFM in an enforced reaction set can be identified through EFMA of the problematic reaction set, a negligible computational investment. By confirming enforcement of an EFM to be the problem, rechecking of reactions and empty subnetworks may be avoidable through early completion of the branch enforcing a complete EFM and addition of the identified EFM to the solution set.

Selection criteria were established for identifying effective reactions for splitting (Table 2). Some of these criteria could be incorporated into a new EFMA algorithm. Examples include (i) changing the representation of reversible reactions and (ii) changing when the algorithm networks are compressed. Recording reversible reactions in the original network model as separate forward and reverse reactions would allow the algorithm to define enforce/suppress combinations involving currently unusable reactions thereby eliminating the need for the reversibility rule. Compressing networks before applying the enforce/suppress subroutine would prevent the network from reconfiguring with subnetwork definition, removing the need for subnetwork verification. However, this operational order may reduce effectiveness of subnetwork definition, as some suppressed reactions result in additional combinable reactions, as shown by the creation of a dead-end reaction when suppressing R8 in Figure 1 and Supplementary Figure S1 (Klamt et al., 2005). Although the likelihood of reaction rearrangement as a function of network complexity should be examined, the costs of accounting for network compression effects were not prohibitive to the analysis for presented models.

The presented splitting approaches are subject to the availability of reactions for splitting. For instance, a hypothetical model composed exclusively of reversible reactions or a model where every reaction had poorly scaled coefficients could not be analyzed with the presented approach. Fortunately, such models are not typically biologically relevant. Although all chemical reactions are theoretically reversible, many are effectively irreversible under physiologically relevant concentrations and temperatures. Additionally, the scaling of reaction coefficients for a metabolic model is dictated by product/substrate stoichiometries of the enzymes, which are often in a range that do not cause numerical instability. A more practical limit would be a model that does not have enough reactions satisfying the rules in Table 2 to sufficiently divide the network into tractable subnetworks. Although such a model is theoretically possible, it is hypothesized that with computational resource improvements, most models will be tractable.

The basic splitting and iterative splitting algorithms allow for distributed computation of models through division into subnetworks. Microsoft HPC software permitted enumeration of the nearly 2 billion EFMs in the DIATOM model in <1 month using academic computer laboratories during idle hours. Although the total CPU time is unavoidable, the real time required to run large models can be reduced substantially based on the number and computational power of nodes. For instance, the most complex subnetwork in the DIATOM model took ∼2 days of run time; therefore, given appropriate resources, the EFMA could have been completed in 2 days if the other subnetworks were concurrently run on additional nodes. This highlights the lower limits of computational time for EFMA of genome-scale models, given current computer capabilities. Using the splitting algorithm and sufficient computational resources, the presented study substantially expands the applicability of EFMA.

SYMBOLS

f Number of intractable subnetworks
i Iteration in the iterative splitting process
itot Number of iterations in the iterative splitting process
k Number of reactions with non-zero coefficients within an EFM
m Number of metabolites in the compressed model
N Number of subnetworks attempted
q Number of reactions in the compressed model
R Number of reactions used for subnetwork definition during the splitting process
Rmin Minimum number of reactions needed for complete subnetwork enumeration during the splitting process
R′ Number of preliminary reactions for splitting (reactions that have not been verified at the subnetwork level)
R# Reaction #, where # identifies a specific reaction from Figures 1 or 3
r Number of reactions used for subnetwork definition at each iteration
tfail Average CPU time spent on intractable subnetworks
tr,i Average completion time for subnetwork defined by r*i reactions
tunsplit Time for unsplit network to complete
Open in a new tab

Supplementary Material

Supplementary Data
supp_30_11_1569__index.html (843B, html)

ACKNOWLEDGEMENT

The authors would like to thank Jeffrey J. Heys, Marco Terzer, and Austin Jacobs for helpful discussions.

Funding: Centers of Biomedical Research Excellence (COBRE) Center for Analysis of Cellular Mechanisms and Systems Biology, National Institute of Health (P20RR024237 to J.P.F. and R.L.T.), Integrative Graduate Education and Research Traineeship (IGERT) in Geobiological Systems, National Science Foundation (DGE 0654336 to K.A.H. and R.L.T.) and the Emerging Frontiers in Research and Innovation (EFRI), National Science Foundation (0937613 to K.A.H.). The diatom reconstruction was supported by the Air Force Office of Scientific Research (FA9550-09-1-0243 to R.P.C.).

Conflict of interest: none declared.

REFERENCES

  1. Barrett CL, et al. Decomposing complex reaction networks using random sampling, principal component analysis and basis rotation. BMC Syst. Biol. 2009;3:30. doi: 10.1186/1752-0509-3-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Carlson RP. Decomposition of complex microbial behaviors into resource-based stress responses. Bioinformatics. 2009;25:90–97. doi: 10.1093/bioinformatics/btn589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Carlson RP, et al. Metabolic pathway analysis of a recombinant yeast for rational strain development. Biotechnol. Bioeng. 2002;79:121–134. doi: 10.1002/bit.10305. [DOI] [PubMed] [Google Scholar]
  4. de Figueiredo LF, et al. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics. 2009;25:3158–3165. doi: 10.1093/bioinformatics/btp564. [DOI] [PubMed] [Google Scholar]
  5. Emanuelsson O, et al. Locating proteins in the cell using TargetP, SignalP and related tools. Nat. Protoc. 2007;2:953–971. doi: 10.1038/nprot.2007.131. [DOI] [PubMed] [Google Scholar]
  6. Fabris M, et al. The metabolic blueprint of Phaeodactylum tricornutum reveals a eukaryotic Entner-Doudoroff glycolytic pathway. Plant J. 2012;70:1004–1014. doi: 10.1111/j.1365-313X.2012.04941.x. [DOI] [PubMed] [Google Scholar]
  7. Feist AM, et al. Modeling methanogenesis with a genome-scale metabolic reconstruction of Methanosarcina barkeri. Mol. Syst. Biol. 2006;2:2006.0004. doi: 10.1038/msb4100046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gagneur J, Klamt S. Computation of elementary modes: a unifying framework and the new binary approach. BMC Bioinformatics. 2004;5:175. doi: 10.1186/1471-2105-5-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ip K, et al. Analysis of complex metabolic behavior through pathway decomposition. BMC Syst. Biol. 2011;5:91. doi: 10.1186/1752-0509-5-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Jevremović D, et al. 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum. Anchorage, AK: IEEE; 2011a. Divide-and-conquer approach to the parallel computation of elementary flux modes in metabolic networks; pp. 502–511. [Google Scholar]
  11. Jevremović D, et al. Parallelization of nullspace algorithm for the computation of metabolic pathways. Parallel Comput. 2011b;37:261–278. doi: 10.1016/j.parco.2011.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jevremović D, Boley D. The 6th Conference on Partitioned Global Address Space Programming Models. CA: Santa Barbara; 2012. Parallel computation of elementary flux modes in metabolic networks using global arrays. [Google Scholar]
  13. Jungreuthmayer C, et al. regEfmtool: Speeding up elementary flux mode calculation using transcriptional regulatory rules in the form of three-state logic. Biosystems. 2013;113:37–39. doi: 10.1016/j.biosystems.2013.04.002. [DOI] [PubMed] [Google Scholar]
  14. Kaleta C, et al. Can the whole be less than the sum of its parts? Pathway analysis in genome-scale metabolic networks using elementary flux patterns. Genome Res. 2009;19:1872–1883. doi: 10.1101/gr.090639.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Klamt S, et al. Algorithmic approaches for computing elementary modes in large biochemical reaction networks. IEE Proc. Syst. Biol. 2005;152:249–255. doi: 10.1049/ip-syb:20050035. [DOI] [PubMed] [Google Scholar]
  16. Klamt S, Stelling J. Combinatorial complexity of pathway analysis in metabolic networks. Mol. Biol. Rep. 2002;29:233–236. doi: 10.1023/a:1020390132244. [DOI] [PubMed] [Google Scholar]
  17. Klamt S, Stelling J. Two approaches for metabolic pathway analysis? Trends Biotechnol. 2003;21:64–69. doi: 10.1016/s0167-7799(02)00034-3. [DOI] [PubMed] [Google Scholar]
  18. Kroth PG, et al. A model for carbohydrate metabolism in the diatom Phaeodactylum tricornutum deduced from comparative whole genome analysis. PLoS One. 2008;3:e1426. doi: 10.1371/journal.pone.0001426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Liao JC, et al. Pathway analysis, engineering, and physiological considerations for redirecting central metabolism. Biotechnol. Bioeng. 1996;52:129–140. doi: 10.1002/(SICI)1097-0290(19961005)52:1<129::AID-BIT13>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
  20. Llaneras F, Picó J. Which metabolic pathways generate and characterize the flux space? A comparison among elementary modes, extreme pathways and minimal generators. J. Biomed. Biotechnol. 2010;2010:753904. doi: 10.1155/2010/753904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ma H-W, et al. Decomposition of metabolic network into functional modules based on the global connectivity structure of reaction graph. Bioinformatics. 2004;20:1870–1876. doi: 10.1093/bioinformatics/bth167. [DOI] [PubMed] [Google Scholar]
  22. Markowitz VM, et al. IMG: the integrated microbial genomes database and comparative analysis system. Nucleic Acids Res. 2012;40:D115–D122. doi: 10.1093/nar/gkr1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Orth JD, et al. What is flux balance analysis? Nat. Biotechnol. 2010;28: 245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Poolman MG, et al. Modular decomposition of metabolic systems via null-space analysis. J. Theor. Biol. 2007;249:691–705. doi: 10.1016/j.jtbi.2007.08.005. [DOI] [PubMed] [Google Scholar]
  25. Reed JL, Palsson BO. Thirteen years of building constraint-based in silico models of Escherichia coli. J. Bacteriol. 2003;185:2692–2699. doi: 10.1128/JB.185.9.2692-2699.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schilling CH, et al. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 2000;203:229–248. doi: 10.1006/jtbi.2000.1073. [DOI] [PubMed] [Google Scholar]
  27. Schilling CH, Palsson BØ. Assessment of the metabolic capabilities of Haemophilus influenzae Rd through a genome-scale pathway analysis. J. Theor. Biol. 2000;203:249–283. doi: 10.1006/jtbi.2000.1088. [DOI] [PubMed] [Google Scholar]
  28. Schuster S, et al. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000;18:326–332. doi: 10.1038/73786. [DOI] [PubMed] [Google Scholar]
  29. Schuster S, et al. Exploring the pathway structure of metabolism: decomposition into subnetworks and application to Mycoplasma pneumoniae. Bioinformatics. 2002;18:351–361. doi: 10.1093/bioinformatics/18.2.351. [DOI] [PubMed] [Google Scholar]
  30. Schuster S, et al. Predicting novel pathways in genome-scale metabolic networks. Biochem. Soc. Trans. 2010;38:1202–1205. doi: 10.1042/BST0381202. [DOI] [PubMed] [Google Scholar]
  31. Schuster S, Hilgetag C. On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Syst. 1994;02:165–182. [Google Scholar]
  32. Tachibana M, et al. Localization of putative carbonic anhydrases in two marine diatoms, Phaeodactylum tricornutum and Thalassiosira pseudonana. Photosynth. Res. 2011;109:205–221. doi: 10.1007/s11120-011-9634-4. [DOI] [PubMed] [Google Scholar]
  33. Taffs R, et al. In silico approaches to study mass and energy flows in microbial consortia: a syntrophic case study. BMC Syst. Biol. 2009;3:114. doi: 10.1186/1752-0509-3-114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Terzer M, et al. Genome-scale metabolic networks. Wiley Interdiscip. Rev. Syst. Biol. Med. 2009;1: 285–297. doi: 10.1002/wsbm.37. [DOI] [PubMed] [Google Scholar]
  35. Terzer M, Stelling J. Large-scale computation of elementary flux modes with bit pattern trees. Bioinformatics. 2008;24:2229–2235. doi: 10.1093/bioinformatics/btn401. [DOI] [PubMed] [Google Scholar]
  36. Trinh CT, et al. Elementary mode analysis: a useful metabolic pathway analysis tool for characterizing cellular metabolism. Appl. Microbiol. Biotechnol. 2009;81:813–826. doi: 10.1007/s00253-008-1770-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Urbanczik R. Enumerating constrained elementary flux vectors of metabolic networks. IET Syst. Biol. 2007;1:274–279. doi: 10.1049/iet-syb:20060073. [DOI] [PubMed] [Google Scholar]
  38. Urbanczik R, Wagner C. An improved algorithm for stoichiometric network analysis: theory and applications. Bioinformatics. 2005a;21:1203–1210. doi: 10.1093/bioinformatics/bti127. [DOI] [PubMed] [Google Scholar]
  39. Urbanczik R, Wagner C. Functional stoichiometric analysis of metabolic networks. Bioinformatics. 2005b;21:4176–4180. doi: 10.1093/bioinformatics/bti674. [DOI] [PubMed] [Google Scholar]
  40. Varma A, et al. Stoichiometric interpretation of Escherichia coli glucose catabolism under various oxygenation rates. Appl. Environ. Microbiol. 1993;59:2465–2473. doi: 10.1128/aem.59.8.2465-2473.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Varma A, Palsson BØ. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl. Environ. Microbiol. 1994;60:3724–3731. doi: 10.1128/aem.60.10.3724-3731.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Verwoerd WS. A new computational method to split large biochemical networks into coherent subnets. BMC Syst. Biol. 2011;5:25. doi: 10.1186/1752-0509-5-25. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_30_11_1569__index.html (843B, html)
supp_btu021_20140116Supplemental_Materials.zip (1.4MB, zip)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES