Abstract
Motivation: Gene set analysis is a popular method for large-scale genomic studies. Because genes that have common biological features are analyzed jointly, gene set analysis often achieves better power and generates more biologically informative results. With the advancement of technologies, genomic studies with multi-platform data have become increasingly common. Several strategies have been proposed that integrate genomic data from multiple platforms to perform gene set analysis. To evaluate the performances of existing integrative gene set methods under various scenarios, we conduct a comparative simulation analysis based on The Cancer Genome Atlas breast cancer dataset.
Results: We find that existing methods for gene set analysis are less effective when sample heterogeneity exists. To address this issue, we develop three methods for multi-platform genomic data with heterogeneity: two non-parametric methods, multi-platform Mann–Whitney statistics and multi-platform outlier robust T-statistics, and a parametric method, multi-platform likelihood ratio statistics. Using simulations, we show that the proposed multi-platform Mann–Whitney statistics method has higher power for heterogeneous samples and comparable performance for homogeneous samples when compared with the existing methods. Our real data applications to two datasets of The Cancer Genome Atlas also suggest that the proposed methods are able to identify novel pathways that are missed by other strategies.
Availability and implementation: http://www4.stat.ncsu.edu/∼jytzeng/Software/Multiplatform_gene_set_analysis/
Contact: john.hu@omicsoft.com, jhu7@ncsu.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
High-throughput genome-wide assays, such as microarray and next-generation sequencing, have become more reliable and affordable. With the ever-increasing throughput and the scale of omics studies, more and more projects choose to measure multiple genomic features (e.g. gene expression, methylation, gene mutation, copy number, promoter binding and protein expression) on the same samples. Evaluating multiple genome features can lead to a better examination of functional responses and provide a comprehensive understanding of the underlying biological mechanisms. In recent years, well-known large-scale projects, such as The Cancer Genome Atlas (TCGA) (2012), the Cancer Cell Line Encyclopedia and the Encyclopedia of DNA Elements, have generated genomic profiles across multiple platforms. In addition, more and more recent projects in the Gene Expression Omnibus contain multi-platform data. With diverse data types from different platforms, it becomes challenging to properly integrate, analyze and interpret the results to obtain biological insights. Gene set analysis is a powerful strategy developed to analyze large-scale profiling data. Instead of studying one gene at a time, gene set analysis focuses on a set of related genes, such as genes in one Kyoto Encyclopedia of Genes and Genomes pathway (Kanehisa and Goto, 2000) or those related to the same Gene Ontology (Ashburner et al., 2000) term. Joint analysis of genes in a set often improves power, especially when the signals of individual genes are moderate. Because the set itself often has biological meanings, gene set analysis also facilitates the interpretation of experiment results and helps to identify important biological findings (Ramanan et al., 2012). Many methods have been developed to perform gene set analysis in a single platform, for example, Gene Set Enrichment Analysis (GSEA) (Subramanian et al., 2005), GSA (Efron and Tibshirani, 2007) and Globaltest (Goeman et al., 2004). Several review articles have been published that discuss the performances of different gene set methods (Ackermann and Strimmer, 2009; Goeman and Buhlmann, 2007; Hung et al., 2012; Maciejewski, 2013).
Gene set analysis on multi-platform genomic data is gaining momentum. Approaches can be roughly classified into three different categories, characterized by how the multi-platform information is integrated. The first type performs a gene set analysis on each platform and then combines the single platform information, such as P-values (e.g. Jia et al., 2012). Such a strategy is commonly used when the multi-platform data are from similar, but not identical, samples. The second strategy, such as that used in the SumZ approach of Xiong et al. (2012), first sums the gene-specific association score of each platform to compute a multi-platform score for each gene and then uses the gene scores to perform gene set analysis. The third strategy is similar to the second except that it directly derives the multi-platform gene scores using data from all platforms simultaneously. One representative approach is the integrative (INT) approach proposed by Tyekucheva et al. (2011), which uses a logistic regression with all multi-platform values of a gene as predictors and takes the model deviances as the gene scores for downstream gene set analysis (Tyekucheva et al., 2011). Bayesian methods have also been developed to analyze multi-platform genomic data, e.g. iBAG (Wang et al., 2013) and PARADIGM (Vaske et al., 2010). Compared with traditional gene set methods, Bayesian methods often use extensive knowledge of the biological relationships among different data platforms and/or the interactions between studied genes.
Sample heterogeneity refers to molecular and cellular differences among biological samples. Such differences are commonly encountered in complex diseases like cancer, where cases with different genotypes, genomic copy numbers or expression patterns often lead to different disease progressions and treatment strategies (Fisher et al., 2013; Russnes et al., 2011). Several methods have been developed to address sample heterogeneity, e.g. cancer outlier profile analysis (MacDonald and Ghosh, 2006), outlier sum (Tibshirani and Hastie, 2007), outlier robust t-statistics (ORT) (Wu, 2007), cancer likelihood ratio statistics (LRS) (Hu, 2008) and non-parametric change-point statistics (Wang et al., 2011). Although the superiority of these methods over ordinary analysis has been demonstrated with heterogeneous data in a single platform, to the best of our knowledge, there are no corresponding gene set approaches for multi-platform heterogeneous data. The impact of sample heterogeneity on multi-platform analyses can be more substantial than on single platform analyses. First, the level of heterogeneity can be different from platform to platform, e.g. platforms such as somatic mutations and DNA methylation have much higher diversity (heterogeneity) among individuals and samples than DNA copy number (Aryee et al., 2013; Chin et al., 2011). In addition, the heterogeneous subsets can be different from one platform to another, e.g. some samples might have changes on platform A but no changes on platform B, whereas different subsets of samples have changes on platform B but not on platform A. Such a scenario may lead to power loss due to the attenuation of signals when the association is evaluated across platforms. In contrast, a multi-platform method that can tackle platform-specific heterogeneous data would be able to identify the signals when integrating information across platforms.
In this study, we perform simulation studies to systematically evaluate different integrative methods under a range of scenarios. We observe that the true-positive rates (TPR) and the true-negative rates of existing multi-platform gene set methods decrease dramatically when heterogeneity exists. These results motivated us to construct three methods to account for sample heterogeneity in multi-platform gene set analysis: multi-platform Mann–Whitney statistics (MPMWS), multi-platform outlier robust T-statistics (MPORT) and multi-platform likelihood ratio statistics (MPLRS). We use simulations and real data analyses to demonstrate the utility of these methods under various conditions.
2 METHODS
2.1 TCGA datasets
We downloaded the TCGA breast cancer data from the National Cancer Institute ftp site in January 2013. We focused on the level 3 gene summary data from RNA sequencing (RNA-Seq), methylation and copy number variation (CNV) and extracted 530 common samples (480 case samples and 50 control samples) and 10 371 common genes shared among the three platforms. For RNA-Seq data, the log2 reads per kilo base per million were used as gene expression values. Before the log2 transformation, a minimal value (0.0001) was added to prevent infinite values. For methylation, the mean beta values of all of the probes mapped to a gene were first computed and then converted into an M value for each gene (Du et al., 2010). The CNV values were provided in log2 format. Within each platform, the data were standardized to have mean 0 and standard deviation 1. The TCGA breast cancer data were used to perform simulations and a real data analysis. We also performed a data analysis on the TCGA Kidney Renal Clear Cell Carcinoma (KIRC) dataset, for which we applied the same procedures of data processing and obtained 486 common samples (463 case samples and 23 control samples) and 11 182 common genes shared among the three platforms of methylation, CNV and RNA-Seq data.
2.2 Simulations design
We generated simulated data based on the TCGA breast cancer dataset, which contains 480 cancer samples and 50 control samples (i.e. the case proportion η = 91%). First, we created 207 non-overlapping gene sets by randomly drawing genes from the 10 371 genes without replacement. The sizes of the 207 gene sets were randomly determined based on the size distribution of the MSigDB canonical pathways (Subramanian et al., 2005). The genomic data for cases and controls were simulated using the scheme described in the Tyekucheva study (Tyekucheva et al., 2011). In short, we first shuffled the case–control labels to remove any association that may exist in the original data. Then, we randomly selected 10 gene sets as causal gene sets and ‘spiked in’ signals into the causal gene sets as detailed below. We performed 300 replicates for each simulation scenario.
(A) Simulation with homogenous samples. Given a causal gene set, we randomly selected  % (25, 50 or 75%) of the genes as causal genes. For each causal gene, one platform was randomly selected as causal and Δk was added to the genomic values of the causal platform for cases. The value of Δk was derived such that the two-sample t-test between cases and controls had power
% (25, 50 or 75%) of the genes as causal genes. For each causal gene, one platform was randomly selected as causal and Δk was added to the genomic values of the causal platform for cases. The value of Δk was derived such that the two-sample t-test between cases and controls had power  (0.2, 0.4, 0.6, 0.8 or 0.9).
(0.2, 0.4, 0.6, 0.8 or 0.9).
(B) Simulation with heterogeneous samples. We considered two scenarios (referred to as Scenarios B1 and B2) to simulate datasets with sample heterogeneity. In Scenario B1, we followed the simulation scheme for Scenario A, except we randomly selected  % (20, 40, 60, 80, 90 or 100%) of the case samples as ‘true’ cases for each causal gene. In other words, we only ‘spiked in’ Δk signals into the (randomly selected) causal platform of the causal gene for the ‘true’ cases. Because the causal platform of a causal gene was randomly selected, the causal genes in a platform are different from each other (although there may be some overlaps).
% (20, 40, 60, 80, 90 or 100%) of the case samples as ‘true’ cases for each causal gene. In other words, we only ‘spiked in’ Δk signals into the (randomly selected) causal platform of the causal gene for the ‘true’ cases. Because the causal platform of a causal gene was randomly selected, the causal genes in a platform are different from each other (although there may be some overlaps).
In Scenario B1, there is only a single causal platform for each causal gene for the ‘true’ cases. In real biological situations, we often see genes that have changes in multiple platforms. To account for these scenarios, we considered Scenario B2, in which each causal gene is allowed to have changes in more than one platform. Specifically, let 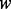 be the number of causal platforms of a casual gene; then, the probability of
be the number of causal platforms of a casual gene; then, the probability of 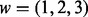 is (
is (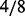 ,
, 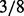 ,
, 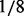 ), respectively. That is, we first determined the number of causal platforms from binomial (3, ½) and then converted
), respectively. That is, we first determined the number of causal platforms from binomial (3, ½) and then converted 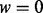 to
to 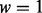 . We then added Δk values to the genomic data of the causal platform(s) of a causal gene for the ‘true’ cases.
. We then added Δk values to the genomic data of the causal platform(s) of a causal gene for the ‘true’ cases.
2.3 Multi-platform methods for gene set analysis without sample heterogeneity
The general steps of integrative gene set analysis start with computing gene-specific association scores (gene scores in short) of multi-platform data and then using these scores to perform gene set analysis. For the gene set analysis, we conducted the gene set tests using R function ‘geneSetTest’ from the R/Bioconductor package ‘limma’ (Smyth, 2005) and obtained P-values for each gene set. The ranks of the gene scores were used instead of the actual scores (Michaud et al., 2008). We selected different thresholds of P-value cutoff and computed the TPR, i.e. the percentage of the causal gene sets truly identified, and the false-positive rate, i.e. the percentage of non-causal gene sets falsely identified as causal gene sets. We plotted the receiver operating characteristic (ROC) curves to compare the performances of the different methods using R. Below; we describe how different methods obtain the multi-platform gene scores considered in the simulation study.
Integrative (INT) analysis (Tyekucheva et al., 2011): For each gene, regress the disease status on the genomic variables from all platforms using a logistic regression model. The multi-platform gene scores are computed by taking the differences of the deviances between the null models (excluding genomic predictors) and the full models (including all genomic predictors).
Hotelling’s T2 (HT2): For each gene, perform the Hotelling’s T2 test to conduct a case–control comparison using the genomic variables from all platforms (Xiong et al., 2002). The multi-platform gene scores are the Hotelling’s T2 statistics.
SumZ (Xiong et al., 2012): For each gene at each platform, calculate the association score (t-statistics). Next, use permutations to obtain the null distribution of the t-statistics within each platform. Then, standardize the t-statistics of each gene based on the null distributions. Finally, for each gene, obtain the gene scores by taking the sum of the standardized values across different platforms.
Deviance summarization: For each gene at each platform, fit the logistic regression under the null model (i.e. excluding the genomic variable) and under the full model (i.e. including the genomic variable). Next, obtain the deviance difference between the two models. Finally, for each gene, take the average of the deviance difference across platforms as the multi-platform gene scores (referred to as AveD). The method of MaxD is obtained in the same manner except that the maximum is used rather than the average.
Single platform method (benchmark): For each gene at each platform, perform the same analysis as described in ‘deviance summarization’. Then, obtain the single-platform gene scores by taking the deviance difference between the null model and the full model. We applied this strategy on methylation, CNV and RNA-Seq expression platforms and referred to the corresponding methods as Methy, CNV and Exp, respectively.
2.4 Multi-platform methods for gene set analysis accounting for sample heterogeneity
We constructed three multi-platform methods to address sample heterogeneity. Specifically, we extended two current methods designed for single platform analysis to the multi-platform setting, i.e. MPORT [based on ORT of Wu (2007)] and MPLRS [based on LRS of Hu (2008)]. We also developed a non-parametric method, MPMWS, which obtains the gene scores based on the Mann–Whitney statistics and does not assume symmetric distributions for the genomic variables.
The general procedure of multi-platform heterogeneous methods is as follows. Assume that there are 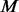 genes and
genes and 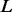 platforms measured from
platforms measured from 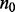 control samples and
control samples and 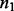 case samples (i.e. in total,
case samples (i.e. in total, 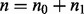 samples). Let
samples). Let 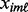 be the observed value of the genomic variable for gene
be the observed value of the genomic variable for gene  and platform
and platform 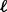 of sample
of sample  . For each gene, use the single platform method to compute association statistic
. For each gene, use the single platform method to compute association statistic 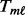 for platform
for platform 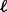 . Next, similar to the SumZ method, use permutations to obtain a null distribution of the statistics for platform
. Next, similar to the SumZ method, use permutations to obtain a null distribution of the statistics for platform 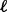 . Finally, calculate the standardized gene statistics within platform
. Finally, calculate the standardized gene statistics within platform 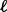 , denoted by
, denoted by 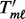 , using the mean and standard deviation (denoted by
, using the mean and standard deviation (denoted by 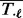 and
and 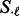 , respectively) obtained from the permuted null distribution, i.e.
, respectively) obtained from the permuted null distribution, i.e.
| (1) |
As is done in the SumZ implementation, these scores are made positive by adding a constant, 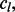 that is the absolute value of the most negative score across the platform. This translation makes all of the
that is the absolute value of the most negative score across the platform. This translation makes all of the 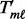 values positive but does not change the shape of their distribution. Then, the sum of the standardized gene statistics from each platform defines the multi-platform gene scores:
values positive but does not change the shape of their distribution. Then, the sum of the standardized gene statistics from each platform defines the multi-platform gene scores:
| (2) |
The MPORT, MPLRS and MPMWS methods differ only in how 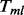 is obtained. We show the formula for computing
is obtained. We show the formula for computing 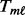 when detecting ‘upregulated’ genes. (Here, the term ‘upregulated’ indicates the increase of numerical values rather than the biological ‘turning on’ of the gene.) The approaches can be extended to detecting downregulated genes by reversing the signs of the observed values.
when detecting ‘upregulated’ genes. (Here, the term ‘upregulated’ indicates the increase of numerical values rather than the biological ‘turning on’ of the gene.) The approaches can be extended to detecting downregulated genes by reversing the signs of the observed values.
- MPORT:
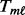 is computed using the ORT method (Wu, 2007). For each gene at each platform, calculate the mean absolute deviance (MAD) by
is computed using the ORT method (Wu, 2007). For each gene at each platform, calculate the mean absolute deviance (MAD) by 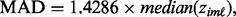 where
where
For upregulated genes,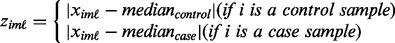
(3) 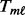 is computed from the case samples using the ORT method:
is computed from the case samples using the ORT method:
where
(4) 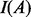 is an indicator function of event
is an indicator function of event 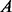 ,
, 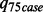 is the 75th percentile of
is the 75th percentile of 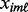 for the case samples and
for the case samples and 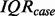 is the interquartile range of the case samples.
is the interquartile range of the case samples. - MPLRS:
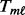 is computed using the LRS method (Hu, 2008). For upregulated genes, the genomic data are sorted from the smallest to the largest under the constraint that all controls are ranked lower than cases.
is computed using the LRS method (Hu, 2008). For upregulated genes, the genomic data are sorted from the smallest to the largest under the constraint that all controls are ranked lower than cases.
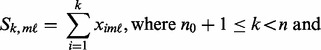
(5) 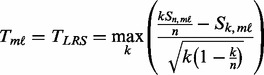
(6) - MPMWS:
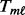 is computed using the non-parametric Mann–Whitney change point detection method implemented in R package CPM (Ross, 2013; Ross et al., 2011). The genomic data are sorted from the smallest to the largest under the constraint that all controls are ranked lower than cases; the Mann–Whitney U statistic,
is computed using the non-parametric Mann–Whitney change point detection method implemented in R package CPM (Ross, 2013; Ross et al., 2011). The genomic data are sorted from the smallest to the largest under the constraint that all controls are ranked lower than cases; the Mann–Whitney U statistic, 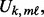 for each case sample is computed; and
for each case sample is computed; and 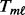 is selected as the largest
is selected as the largest 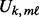 .
.
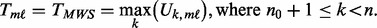
(7)
2.5 Real data analysis
We performed real data analysis using the methods that have the best performances in the simulation studies (i.e. MPMWS and INT). The 1452 pathways in MSigDB were tested using both the breast cancer and the KIRC datasets, which comprised genomic data from methylation, CNV and RNA-Seq platforms.
3 RESULTS
3.1 Multi-platform methods for gene set analysis with homogenous samples (scenario A)
We evaluated the abilities of AveD, MaxD, INT, SumZ and Hotelling’s T2 (HT2) to correctly identify causal gene sets under various parameter settings. Single platform methods Methy, CNV and Exp were used to benchmark the performances of the multi-platform methods. Figure 1 shows the ROC plots under different proportions of causal genes in a causal set, i.e. 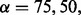 and
and 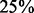 for Figure 1A–C, respectively, while fixing
for Figure 1A–C, respectively, while fixing 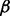 (power) at 0.8 and η (percentage of case samples) at 0.91. The corresponding areas under the curves (AUCs) are summarized in Supplementary Table S1A. From Figure 1A, it is clear that multi-platform methods outperformed single platform methods. Among the multi-platform methods, Hotelling’s T2 and INT had similar performances, and these methods had the best performances among all methods. AveD and MaxD had slightly lower TPRs than INT, and SumZ followed closely. In Figure 1B and C, the relative performance among different methods stayed the same as in Figure 1A, except that the TPRs decreased when α decreased. The same patterns were observed for β = 0.6 (Supplementary Fig. S1; Supplementary Table S1A).
(power) at 0.8 and η (percentage of case samples) at 0.91. The corresponding areas under the curves (AUCs) are summarized in Supplementary Table S1A. From Figure 1A, it is clear that multi-platform methods outperformed single platform methods. Among the multi-platform methods, Hotelling’s T2 and INT had similar performances, and these methods had the best performances among all methods. AveD and MaxD had slightly lower TPRs than INT, and SumZ followed closely. In Figure 1B and C, the relative performance among different methods stayed the same as in Figure 1A, except that the TPRs decreased when α decreased. The same patterns were observed for β = 0.6 (Supplementary Fig. S1; Supplementary Table S1A).
Fig. 1.
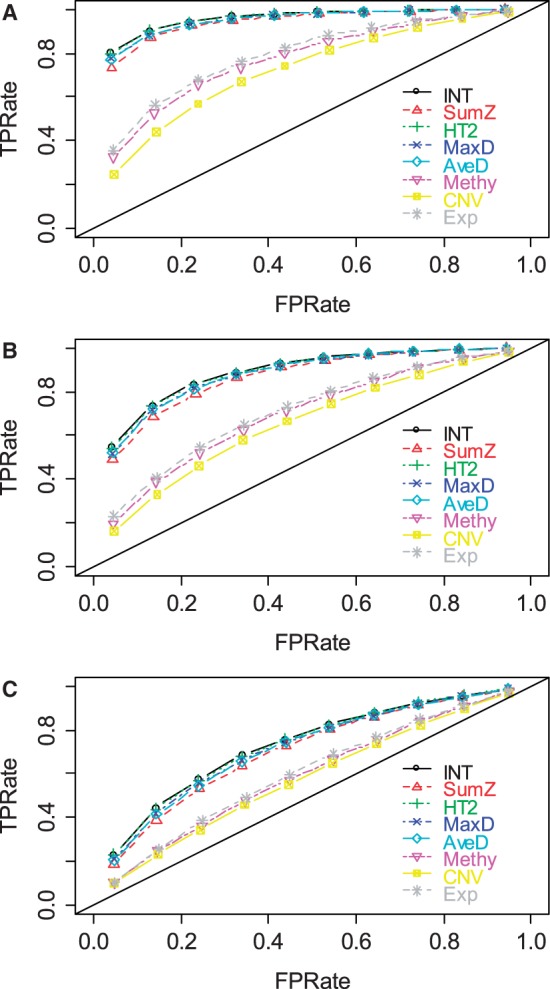
ROC plots for gene set methods at different α levels [(A) α = 75%; (B) α = 50%; and (C): α = 25%]. The simulated data were generated with β = 0.8 and η = 0.91
Figure 2 shows the ROC plots under different β levels, i.e. 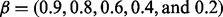 when α = 75% and η = 0.91. (The AUC values are shown in Supplementary Table S1A). The patterns for the relative performances of different methods were observed to be similar to those of Figure 1. As expected, all methods performed better when the difference between case and control became larger (i.e. larger β).
when α = 75% and η = 0.91. (The AUC values are shown in Supplementary Table S1A). The patterns for the relative performances of different methods were observed to be similar to those of Figure 1. As expected, all methods performed better when the difference between case and control became larger (i.e. larger β).
Fig. 2.
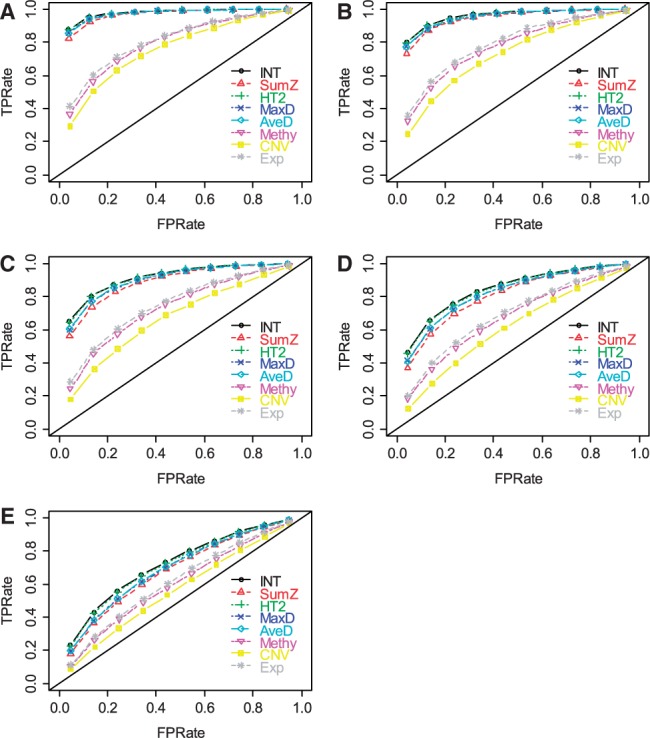
ROC plots for gene set methods at different β levels [(A) β = 0.9; (B) β = 0.8; (C) β = 0.6; (D) β = 0.4; and (E) β = 0.2]. The simulated data were generated with α = 75% and η = 0.91
The case proportion, η, is known to affect the power of statistical methods (Evans and Purcell, 2012). We repeated the studies for η = 0.5 (Supplementary Fig. S2) and 0.1 (Supplementary Fig. S3); similar results were observed under these scenarios.
3.2 Multi-platform methods for gene set analysis with heterogeneous samples (Scenarios B1 and B2)
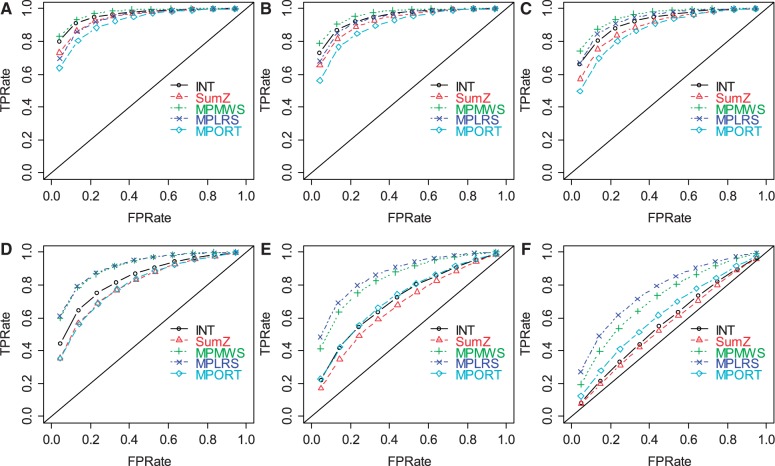
To evaluate the performance under sample heterogeneity, we simulated datasets by randomly selecting 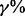 of case samples to be ‘true’ cases. We focused our comparisons on the two represented approaches from Section 3.1 (i.e. INT and SumZ) and the three proposed methods for sample heterogeneity, i.e. MPLRS, MPORT and MPMWS. The results of Scenario B1 are shown in Figure 3, where α = 75%, β = 0.8 and η = 0.91, and the percentage of ‘true’ cases among all cases varies, i.e. γ = (100, 90, 80, 60, 40 and 20%). The corresponding AUC values are presented in Supplementary Table S1B. We see that INT and SumZ, which are designed for multi-platform homogeneous data, quickly lost power as γ decreased. In contrast, MPLRS and MPMWS retained good power when
of case samples to be ‘true’ cases. We focused our comparisons on the two represented approaches from Section 3.1 (i.e. INT and SumZ) and the three proposed methods for sample heterogeneity, i.e. MPLRS, MPORT and MPMWS. The results of Scenario B1 are shown in Figure 3, where α = 75%, β = 0.8 and η = 0.91, and the percentage of ‘true’ cases among all cases varies, i.e. γ = (100, 90, 80, 60, 40 and 20%). The corresponding AUC values are presented in Supplementary Table S1B. We see that INT and SumZ, which are designed for multi-platform homogeneous data, quickly lost power as γ decreased. In contrast, MPLRS and MPMWS retained good power when 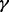 decreased. However, the relative performance between MPLRS and MPMWS depended on
decreased. However, the relative performance between MPLRS and MPMWS depended on 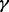 . When
. When 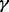 was low (e.g.
was low (e.g.  40%), MPLRS performed the best; when
40%), MPLRS performed the best; when 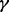 was
was 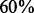 , MPLRS and MPMWS had similar power. However, when
, MPLRS and MPMWS had similar power. However, when 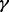 was high (e.g.
was high (e.g. 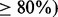 , MPLRS had less TPRs than MPMWS, sometimes even less than INT. MPORT performed inferior to MPLRS and MPMWS, and its power advantages over INT and SumZ did not show until
, MPLRS had less TPRs than MPMWS, sometimes even less than INT. MPORT performed inferior to MPLRS and MPMWS, and its power advantages over INT and SumZ did not show until 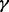 became small, i.e. ∼20–40%. Because
became small, i.e. ∼20–40%. Because 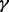 is unknown in practice, MPMWS appears to be the most robust choice; it yielded the highest or the second highest TPRs regardless of the γ values. Although the method is designed to account for sample heterogeneity, it had similar power to INT when samples were homogeneous (γ = 100%). This behavior is likely attributable to the fact that the genomic variables of certain platforms tended to deviate away from normal distributions, e.g. methylation values, and the non-parametric MPMWS is robust against non-normality. Finally, the improved TPR obtained using MPLRS and MPMWS with heterogeneous samples was observed when we repeated the analysis for α = 50% and η = 0.5 (Supplementary Fig. S4) and 0.1 (Supplementary Fig. S5).
is unknown in practice, MPMWS appears to be the most robust choice; it yielded the highest or the second highest TPRs regardless of the γ values. Although the method is designed to account for sample heterogeneity, it had similar power to INT when samples were homogeneous (γ = 100%). This behavior is likely attributable to the fact that the genomic variables of certain platforms tended to deviate away from normal distributions, e.g. methylation values, and the non-parametric MPMWS is robust against non-normality. Finally, the improved TPR obtained using MPLRS and MPMWS with heterogeneous samples was observed when we repeated the analysis for α = 50% and η = 0.5 (Supplementary Fig. S4) and 0.1 (Supplementary Fig. S5).
Fig. 3.
ROC plots for gene set methods at different sample heterogeneity levels [(A) γ = 100%; (B) γ = 90%; (C) γ = 80%; (D) γ = 60%; (E) γ = 40%; and (F) γ = 20%)]. The simulated data were generated with α = 75%, β = 0.8 and η = 0.91
By design, INT is good at identifying pathways with systematic changes, whereas MPMWS has robust power to detect pathways involving sample heterogeneity. In Table 1, we show the number of significant pathways and the number of true-positive (TP) pathways identified by INT and MPMWS. We observe that both methods identified many common significant/TP pathways. In addition, there was a high percentage of TPs among the common significant pathways, especially when the heterogeneity level was not extremely high. The results also show that each method identified some unique significant/TP pathways that were missed by the other method. For INT, the proportion of TPs among the unique pathways became smaller as the heterogeneity increased. For MPMWS, the corresponding TP proportion stayed roughly constant until severe heterogeneity (e.g. 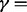 20%).
20%).
Table 1.
The average number of significant gene sets identified by INT and MPMWS at different heterogeneity levels
| Significant gene set | Both INT and MPMWS |
INT only |
MPMWS only |
||||||
|---|---|---|---|---|---|---|---|---|---|
| γ values (%) | Positive | TP | TP (%) | Positive | TP | TP (%) | Positive | TP | TP (%) |
| 100 | 7.33 | 6.92 | 94.41 | 8.52 | 1.08 | 12.68 | 9.04 | 1.37 | 15.15 |
| 90 | 6.59 | 6.17 | 93.63 | 8.75 | 1.13 | 12.91 | 9.51 | 1.72 | 18.09 |
| 80 | 5.79 | 5.36 | 92.57 | 9.09 | 1.24 | 13.64 | 9.94 | 2.05 | 20.62 |
| 60 | 3.61 | 3.14 | 86.98 | 9.54 | 1.28 | 13.42 | 11.06 | 2.86 | 25.86 |
| 40 | 1.7 | 1.17 | 68.82 | 9.78 | 1.04 | 10.63 | 11.5 | 2.96 | 25.74 |
| 20 | 0.76 | 0.19 | 25.00 | 9.72 | 0.63 | 6.48 | 10.66 | 1.77 | 16.60 |
Ten of 207 gene sets were selected as causal, and the results were averaged over 300 repeats.
The analyses above were performed under Scenario B1, where each causal gene only had one causal platform. We repeated the same analyses under Scenario B2, where each causal gene had at least 1 causal platform. We obtained similar results as observed in Scenario B1 (Supplementary Fig. S6).
3.3 Real data application
We first considered the TCGA breast cancer dataset containing methylation, CNV and RNA-Seq measurements. We performed multi-platform gene set analyses on the 1452 MSigDB pathways using MPMWS and INT (i.e. the top two methods from Scenarios B1 and B2). Unlike the simulated gene sets, pathways in MSigDB often share common genes and can have significant overlaps. Figure 4 shows the number of pathways identified by each method and their overlaps at false discovery rate (FDR) 0.05 using the Benjamini and Hochberg’s FDR procedure (Benjamini and Hochberg, 1995). The numbers of significant pathways identified by INT and MPMWS were 116 and 78, respectively. Comparing the significant findings from MPMWS and INT, we found that a majority (58 and 74%) of the pathways were shared between the two methods (Supplementary Table S2). This includes many well-known pathways related to breast cancer, e.g. PKL1 (King et al., 2012; Wierer et al., 2013) and the cell cycle pathway (Caldon et al., 2006). As was observed in the simulation study, there were quite a few overlaps between MPMWS and INT. However, some significant pathways that were identified by one method had large P-values in the other method. For example, the pathways of DNA replication and DNA strand elongation are important for breast cancer (Lomonosov et al., 2003; Thomassen et al., 2009); they were identified by INT but missed by MPMWS (Supplementary Table S3A). In contrast, the BRG1-associated factor complex (Hargreaves and Crabtree, 2011; Kadoch et al., 2013), the well-known tumor suppressors and the G1 pathway (Thomassen et al., 2008), a known breast cancer-related pathway, were found to be significant by MPMWS but not by INT (Supplementary Table S3B). These results agree with the observations in the simulation study: INT and MPMWS appear to identify different types of signals and can be used together in real practice.
Fig. 4.
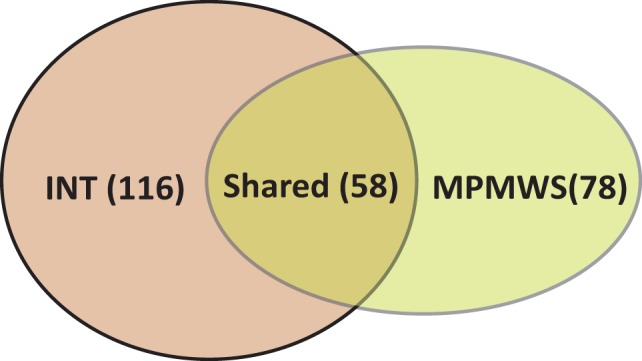
Significant pathways identified by MPMWS and INT. The numbers of significant pathways are listed in parentheses
We applied multi-platform gene set analyses on a second TCGA dataset, i.e. the KIRC dataset. We observed similar results as for the breast cancer data and reported the detailed results in Supplementary Table S4.
4 DISCUSSION
In the presented work, we compared different multi-platform methods for gene set analysis using extensive simulated studies. First, when there is no sample heterogeneity, we found that INT and Hotelling’s T2 method had the best performances compared with other methods. INT might have wider applicability compared with Hotelling’s T2 because it can accommodate covariates. Second, to account for sample heterogeneity, we proposed and tested three different strategies, MPMWS, MPORT and MPLRS, for multi-platform gene set analysis. We found that the non-parametric MPMWS method had satisfactory TPRs and robust performance regardless of the degree of heterogeneity. Finally, based on the results of the simulations and the real data applications, we recommend using both MPMWS and INT: the significant gene sets identified by both methods are more likely to be true positives, while each approach is able to identify orthogonal, yet relevant, biological gene sets. It might be worth following up with these orthogonal findings combining with additional biological information so to minimize the false positives.
We performed the tests assuming that genes are uncorrelated within and across platforms. This assumption may not be valid in real practice, especially for genes within the same gene sets. Inter-gene correlation is known to inflate the FDR of single-platform gene set analysis, and several methods have been proposed to address this issue (Gatti et al., 2010; Wu and Smyth, 2012). In addition, the genomic variables of a gene from different platforms can also be highly correlated with each other. For example, copy number change can lead to a change of transcript level, and a high methylation level of the gene promoter region often leads to downregulation of transcription. It is worth future studies to evaluate how inter-gene and inter-platform correlations will affect multi-platform gene set analysis.
In our analysis, we ignored the issues of missing values by focusing on genes with complete observations in all platforms. In reality, missing data are commonly observed in large-scale studies because of the experimental conditions, individual sample differences or platform constraints. When a considerable amount of data are missing, removing all the samples or genes with missing data could lead to substantial loss of information. To address this issue, imputing can be used to fill in the missing values. Performing self-contained gene set analysis tests is another strategy (Tyekucheva et al., 2011). Further research is needed to characterize the patterns of missing data on different platforms, understand their impact on the gene set analysis and develop the proper statistical methods for missing data.
The R code for all of the methods and test datasets are available on the Web site: http://www4.stat.ncsu.edu/∼jytzeng/Software/Multiplatform_gene_set_analysis/
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Dr Kejun Liu at Omicsoft Inc. and Dr Shannon Holloway at North Carolina State University for helpful discussion and invaluable suggestions.
Funding: This work is partially supported by NIH grants (R01 MH084022 and P01 CA142538).
Conflict of Interest: none declared.
REFERENCES
- Ackermann M, Strimmer K. A general modular framework for gene set enrichment analysis. BMC Bioinformatics. 2009;10:47. doi: 10.1186/1471-2105-10-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aryee MJ, et al. DNA methylation alterations exhibit intraindividual stability and interindividual heterogeneity in prostate cancer metastases. Sci. Transl. Med. 2013;5:169ra110. doi: 10.1126/scitranslmed.3005211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M, et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Method. 1995;57:289–300. [Google Scholar]
- Caldon CE, et al. Cell cycle control in breast cancer cells. J. Cell Biochem. 2006;97:261–274. doi: 10.1002/jcb.20690. [DOI] [PubMed] [Google Scholar]
- Chin L, et al. Making sense of cancer genomic data. Genes Dev. 2011;25:534–555. doi: 10.1101/gad.2017311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du P, et al. Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC Bioinformatics. 2010;11:587. doi: 10.1186/1471-2105-11-587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. On testing the significance of sets of genes. Ann. Appl. Stat. 2007;1:18. [Google Scholar]
- Evans DM, Purcell S. Power calculations in genetic studies. Cold Spring Harb. Protoc. 2012;2012 doi: 10.1101/pdb.top069559. pdb.top069559. [DOI] [PubMed] [Google Scholar]
- Fisher R, et al. Cancer heterogeneity: implications for targeted therapeutics. Br. J. Cancer. 2013;108:479–485. doi: 10.1038/bjc.2012.581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatti DM, et al. Heading down the wrong pathway: on the influence of correlation within gene sets. BMC Genomics. 2010;11:574. doi: 10.1186/1471-2164-11-574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goeman JJ, Buhlmann P. Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics. 2007;23:980–987. doi: 10.1093/bioinformatics/btm051. [DOI] [PubMed] [Google Scholar]
- Goeman JJ, et al. A global test for groups of genes: testing association with a clinical outcome. Bioinformatics. 2004;20:93–99. doi: 10.1093/bioinformatics/btg382. [DOI] [PubMed] [Google Scholar]
- Hargreaves DC, Crabtree GR. ATP-dependent chromatin remodeling: genetics, genomics and mechanisms. Cell Res. 2011;21:396–420. doi: 10.1038/cr.2011.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J. Cancer outlier detection based on likelihood ratio test. Bioinformatics. 2008;24:2193–2199. doi: 10.1093/bioinformatics/btn372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung JH, et al. Gene set enrichment analysis: performance evaluation and usage guidelines. Brief. Bioinform. 2012;13:281–291. doi: 10.1093/bib/bbr049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia P, et al. Integrative pathway analysis of genome-wide association studies and gene expression data in prostate cancer. BMC Syst. Biol. 2012;6(Suppl. 3):S13. doi: 10.1186/1752-0509-6-S3-S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadoch C, et al. Proteomic and bioinformatic analysis of mammalian SWI/SNF complexes identifies extensive roles in human malignancy. Nat. Genet. 2013;45:592–601. doi: 10.1038/ng.2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Goto S. KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King SI, et al. Immunohistochemical detection of Polo-like kinase-1 (PLK1) in primary breast cancer is associated with TP53 mutation and poor clinical outcom. Breast Cancer Res. 2012;14:R40. doi: 10.1186/bcr3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomonosov M, et al. Stabilization of stalled DNA replication forks by the BRCA2 breast cancer susceptibility protein. Genes Dev. 2003;17:3017–3022. doi: 10.1101/gad.279003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald JW, Ghosh D. COPA—cancer outlier profile analysis. Bioinformatics. 2006;22:2950–2951. doi: 10.1093/bioinformatics/btl433. [DOI] [PubMed] [Google Scholar]
- Maciejewski H. Gene set analysis methods: statistical models and methodological differences. Brief. Bioinform. 2013 doi: 10.1093/bib/bbt002. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaud J, et al. Integrative analysis of RUNX1 downstream pathways and target genes. BMC Genomics. 2008;9:363. doi: 10.1186/1471-2164-9-363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramanan VK, et al. Pathway analysis of genomic data: concepts, methods, and prospects for future development. Trends Genet. 2012;28:323–332. doi: 10.1016/j.tig.2012.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross GJ. cpm: Sequential Parametric and Nonparametric Change Detection. R package version 1.1. 2013 http://CRAN.R-project.org/package=cpm. [Google Scholar]
- Ross GJ, et al. Nonparametric monitoring of data streams for changes in location and scale. Technometrics. 2011;53:379–389. [Google Scholar]
- Russnes HG, et al. Insight into the heterogeneity of breast cancer through next-generation sequencing. J. Clin. Invest. 2011;121:3810–3818. doi: 10.1172/JCI57088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth GK. Bioinformatics and Computational Biology Solutions Using {R} and Bioconductor. 2005. Limma: linear models for microarray data. Springer, New York, pp. 397–420. [Google Scholar]
- Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl Acad. Sci. USA. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature. 2012;490:61–70. doi: 10.1038/nature11412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomassen M, et al. Gene expression meta-analysis identifies metastatic pathways and transcription factors in breast cancer. BMC Cancer. 2008;8:394. doi: 10.1186/1471-2407-8-394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomassen M, et al. Gene expression meta-analysis identifies chromosomal regions and candidate genes involved in breast cancer metastasis. Breast Cancer Res. Treat. 2009;113:239–249. doi: 10.1007/s10549-008-9927-2. [DOI] [PubMed] [Google Scholar]
- Tibshirani R, Hastie T. Outlier sums for differential gene expression analysis. Biostatistics. 2007;8:2–8. doi: 10.1093/biostatistics/kxl005. [DOI] [PubMed] [Google Scholar]
- Tyekucheva S, et al. Integrating diverse genomic data using gene sets. Genome Biol. 2011;12:R105. doi: 10.1186/gb-2011-12-10-r105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaske CJ, et al. Inference of patient-specific pathway activities from multi-dimensional cancer genomics data using PARADIGM. Bioinformatics. 2010;26:i237–i245. doi: 10.1093/bioinformatics/btq182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, et al. iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics. 2013;29:149–159. doi: 10.1093/bioinformatics/bts655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, et al. Non-parametric change-point method for differential gene expression detection. PloS One. 2011;6:e20060. doi: 10.1371/journal.pone.0020060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wierer M, et al. PLK1 signaling in breast cancer cells cooperates with estrogen receptor-dependent gene transcription. Cell Rep. 2013;3:2021–2032. doi: 10.1016/j.celrep.2013.05.024. [DOI] [PubMed] [Google Scholar]
- Wu B. Cancer outlier differential gene expression detection. Biostatistics. 2007;8:566–575. doi: 10.1093/biostatistics/kxl029. [DOI] [PubMed] [Google Scholar]
- Wu D, Smyth GK. Camera: a competitive gene set test accounting for inter-gene correlation. Nucleic Acids Res. 2012;40:e133. doi: 10.1093/nar/gks461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong M, et al. Generalized T2 test for genome association studies. Am. J. Hum. Genet. 2002;70:1257–1268. doi: 10.1086/340392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong Q, et al. Integrating genetic and gene expression evidence into genome-wide association analysis of gene sets. Genome Res. 2012;22:386–397. doi: 10.1101/gr.124370.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.