ARTS: automated randomization of multiple traits for study design

Abstract

Summary: Collecting data from large studies on high-throughput platforms, such as microarray or next-generation sequencing, typically requires processing samples in batches. There are often systematic but unpredictable biases from batch-to-batch, so proper randomization of biologically relevant traits across batches is crucial for distinguishing true biological differences from experimental artifacts. When a large number of traits are biologically relevant, as is common for clinical studies of patients with varying sex, age, genotype and medical background, proper randomization can be extremely difficult to prepare by hand, especially because traits may affect biological inferences, such as differential expression, in a combinatorial manner. Here we present ARTS (automated randomization of multiple traits for study design), which aids researchers in study design by automatically optimizing batch assignment for any number of samples, any number of traits and any batch size.

Availability and implementation: ARTS is implemented in Perl and is available at github.com/mmaiensc/ARTS. ARTS is also available in the Galaxy Tool Shed, and can be used at the Galaxy installation hosted by the UIC Center for Research Informatics (CRI) at galaxy.cri.uic.edu.

Contact: mmaiensc@uic.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Data collected on high-throughput biological platforms, such as microarray and next-generation sequencing (NGS), can often be processed in parallel in batches, greatly lowering the cost and time for collection. However, details in the personnel, protocol or instrument setting/calibration often vary slightly from batch-to-batch. When large studies with hundreds or thousands of samples are conducted, these variations may result in statistically significant, but biologically irrelevant, anomalies between batches (Leek et al., 2010), confounding efforts to determine true biological differences between sample conditions.

Such batch effects can be mitigated by proper randomization of samples across batches (Hu et al., 2005): sample traits, such as diseased or control, should be evenly distributed across batches. A number of methods exist that attempt to remove batch effects after data are already collected (Johnson et al., 2007; Leek and Storey, 2007; Scherer, 2009). However, these approaches should be considered a last resort to salvage data collected after poorly randomized studies, as they must make assertions about the type of bias introduced by batches, for example using linear models to quantify distortions (Leek et al., 2010). Also, these methods cannot correct for batch effect in completely unrandomized studies, for instance if all diseased samples are put into the same batch.

When one or two traits are pertinent for a large study, randomization can be done manually with moderate effort. However, patients in large clinical studies often have many relevant traits, such as sex, age, genotype, medical background and multiple measures of disease state. In such cases, proper randomization cannot reasonably be prepared by hand, and will be confounded by the likely combinatorial interaction between traits (e.g. the combined effect of age and gender may be different than the sum of age and gender effects independently).

Here, we present the ARTS (automated randomization of multiple traits for study design) tool for automated study randomization. ARTS uses a genetic algorithm to optimize an objective function based on a rigorous statistic from information theory, the mutual information. We validate ARTS using several objective functions to illustrate the versatility of the one chosen, and by showing that the genetic algorithm we use for optimization obtains a good balance between computational speed and optimization quality.

2 METHODS AND RESULTS

2.1 Objective function

We start with a motivation of our objective function. In a properly randomized study, the distribution of traits in each batch will equal the distribution of traits across all samples. As we show in Supplementary Section S1, this definition directly motivates the use of mutual information (MI) between sample traits and batch. The MI quantifies the extent to which the batch assignment can predict the traits of a sample. If the MI is large, then the distribution of the traits depends strongly on the batch, and the study is not randomized; the MI of an ideally randomized study is 0.

As we discuss in more detail in Supplementary Section S2, we should quantify the MI between both combinations of traits and the batch assignment, and individual traits and the batch assignment. Combinations are important when the affect of traits on biological outcomes cannot be considered independent; this is usually the case. However, in studies with a large number of traits and a smaller number of samples, particular combinations of traits may occur only a few times in the sample set; randomization of the combined traits becomes a trivial but useless exercise, but individual traits should still be randomized. Thus, we introduce the mixed mutual information (MMI), an average of the combined and individual MIs; the definition of the MMI is given in Supplementary Equation (7). The MMI allows greater flexibility to accommodate studies of any size and with any number of traits, as it appropriately distributes both individual traits (e.g. age) and combined traits (e.g. age + sex) over all batches. For comparison, we also define the combined mutual information (CMI) [Supplementary Equation (4)] and individual mutual information (IMI) [Supplementary Equation (8)].

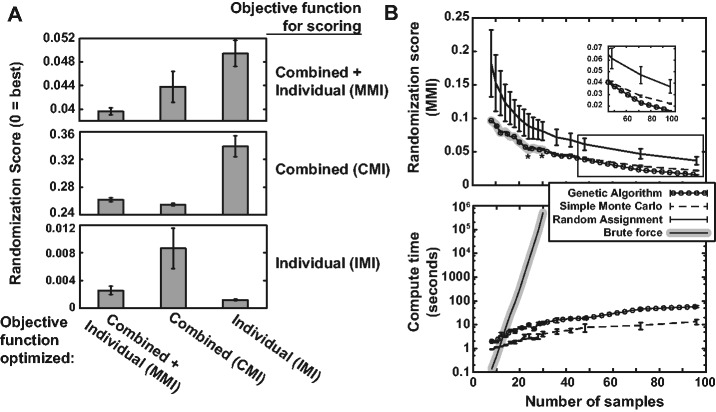
To illustrate the versatility of MMI optimization, we compare it to consideration of the combinations of traits only (the CMI), and of individual traits only (the IMI). We optimized randomizations for each objective function on a simulated set of 100 samples with six binary traits and batches of size 25. We then re-scored each randomization using each of the three objective functions. The results are shown in Figure 1A: each panel gives the score for all three randomizations under a particular objective function.

Fig. 1.

Comparing objective functions and optimization algorithms. (A) The MMI, CMI and the IMI objective functions were optimized on the same sample set (all using the genetic algorithm; recall that the ideal randomization score is 0). We then re-scored each randomization using each objective function; the top panel was scored using the MMI, the middle panel using the CMI and the bottom panel using the IMI. Note that y-axis ranges are different for each panel. (B) Comparison of optimized randomization score (for the MMI) and computing time using: (i) the genetic algorithm, (ii) a simple Monte Carlo procedure, (iii) random assignment and (iv) a brute force enumeration approach, using two evenly sized batches for each sample size. Times are essentially zero for the random assignment, and so are not given. In the top panel, asterisk symbols represent sample sets where the MC algorithm did not achieve the same optimized score as brute force. For (A) and (B), error bars are standard deviations over repeated randomizations. No error bars are plotted for brute force (which is deterministic), and for randomization scores with zero standard deviation (in (B), <96 samples for GA, <24 for MC)

Importantly, optimizing the MMI randomizes combined traits about as well as the CMI, and individual traits about as well as the IMI (i.e. left-hand bars are always low). However, optimizing the CMI sacrifices individual traits’ randomization (IMI score), and vice-versa. Thus, MMI optimization appropriately randomizes both individual and combined traits, making it appropriate for any situation regardless of the number of samples and traits. We refer the reader to Supplementary Sections S2 and S3 for further discussion about the motivation and testing of the MMI. In particular, Supplementary Figure S1 extends the results in Figure 1A over a range of batch sizes and different numbers of traits.

2.2 Optimization algorithm

ARTS optimizes the MMI using a genetic algorithm (GA), which iteratively refines a population of candidate batch assignments through immigration, mutation and crossover, and selects the most optimal (lowest MMI) batch assignments for subsequent generations; it is described in more detail in Supplementary Section S4. We compare the GA to three other optimization methods, briefly described below.

First, a simple Monte Carlo (MC) procedure generates batch assignments randomly and independently, testing each and saving the best; it continues until 1000 assignments have been tested without an improvement. Second, a random assignment procedure simply generates a single random batching. Third, a brute force procedure exhaustively enumerates all possible batch assignments and chooses the global minimum. We compare each method in Figure 1B, giving MMI scores for randomizing a varying number of samples into two equal-sized batches in the top panel, and the computational time on a 2.4-GHz processor in the bottom panel.

The random assignment and brute force methods are unfavorable, for different reasons: scores from random assignment are highly variable, as indicated by the larger error bars in the top panel of Figure 1B, and brute force because compute time grows exponentially and quickly becomes intractable ∼25–30 samples (it would be intractable earlier for more than two batches). For small sample sizes the MC and GA algorithms obtain equally optimal results to brute force, except for two sample sizes (24 and 30 samples, indicated by asterisk in Fig. 1B) where MC was sub-optimal. However, as sample size increases the score from MC is consistently worse and more variable than the GA, highlighted in the inset plot. The small increase in compute time, still less than a minute for the GA with the largest sample set, is a minor trade-off for consistently better, highly reproducible optimizations.

2.3 Using ARTS

Users have several options for downloading and using ARTS, including command-line and graphical user interfaces. More details are given in Supplementary Section S5. Additionally, Supplementary Section S6 presents two case studies describing randomization of clinical sample sets by ARTS.

Funding: National Institutes of Health (grants UL1TR000050, in part) (University of Illinois CTSA); University of Illinois Cancer Center.

Conflict of interest: none declared.