A benchmark for comparison of cell tracking algorithms

Abstract

Motivation: Automatic tracking of cells in multidimensional time-lapse fluorescence microscopy is an important task in many biomedical applications. A novel framework for objective evaluation of cell tracking algorithms has been established under the auspices of the IEEE International Symposium on Biomedical Imaging 2013 Cell Tracking Challenge. In this article, we present the logistics, datasets, methods and results of the challenge and lay down the principles for future uses of this benchmark.

Results: The main contributions of the challenge include the creation of a comprehensive video dataset repository and the definition of objective measures for comparison and ranking of the algorithms. With this benchmark, six algorithms covering a variety of segmentation and tracking paradigms have been compared and ranked based on their performance on both synthetic and real datasets. Given the diversity of the datasets, we do not declare a single winner of the challenge. Instead, we present and discuss the results for each individual dataset separately.

Availability and implementation: The challenge Web site (http://www.codesolorzano.com/celltrackingchallenge) provides access to the training and competition datasets, along with the ground truth of the training videos. It also provides access to Windows and Linux executable files of the evaluation software and most of the algorithms that competed in the challenge.

Contact: codesolorzano@unav.es

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Cell migration is an essential process in normal tissue development, tissue repair and disease (Friedl and Gilmour, 2009). The dynamics of cell movement (e.g. speed, directionality) and migration type (i.e. the morphological changes that the cell undergoes during the movement) are closely related to the biomechanical properties of the surrounding environment (Friedl and Alexander, 2011). Therefore, accurate quantification of both is the key to understanding the complex mechanobiology of cell migration.

Traditionally, cell migration experiments have been performed in two dimensions (2D) using phase or differential interference contrast microscopy. Nowadays, it is increasingly acknowledged that proper evaluation of the cellular movement, as well as related forces, requires looking at the cells in their three-dimensional (3D) tissue environment (Legant et al., 2010). This can be done by taking advantage of the versatility of fluorescence labeling and the optical sectioning capability of multidimensional fluorescence in vivo microscopy (Fernandez-Gonzalez et al., 2006). Fluorescence microscopy has several advantages (e.g. multidimensionality, specificity). However, tracking fluorescent cells poses specific challenges compared with more traditional phase contrast enhancing techniques: non-homogenous staining, low signal-to-noise ratio, uneven background illumination, photobleaching, phototoxicity, etc. Moreover, an important challenge, specific to the use of green fluorescent protein (GFP) transfection-based staining, is the cell-to-cell intensity variability caused by differential transfection efficiency. Therefore, tracking of fluorescent cells requires specialized tools.

Several methods have been described for the segmentation of cells in static 3D fluorescence microscopy images (Indhumathi et al., 2011; Lin et al., 2005; Long et al., 2007; Ortiz-de-Solorzano et al., 1999). These methods have been extended to account for the temporal variable in multidimensional time-lapse microscopy, combining accurate segmentation of the cells with proper tracking of their movements and lineage events (e.g. apoptosis, mitosis, cell merging and overlapping). They can be classified into two broad categories: tracking by detection and tracking by model evolution (Meijering et al., 2009; Rohr et al., 2010; Zimmer et al., 2006). In the former paradigm, cells are first detected in all the frames of the video independently using gradient features (Al-Kofahi et al., 2006), intensity (Li et al., 2010) or wavelet decomposition (Padfield et al., 2011). Subsequently, an optimization strategy, such as multiple-hypothesis tracking (Chenouard et al., 2013), integer programming (Li et al., 2010), dynamic programming (Magnusson and Jaldén, 2012) or coupled minimum-cost flow tracking (Padfield et al., 2011), is used to determine the most likely cell correspondence between frames. In the latter paradigm, cells are segmented and tracked simultaneously, using the final result of each frame as the initial condition for the analysis of the following frame. This is mostly done by evolving the contours of the cells, represented either parametrically (Dufour et al., 2011; Zimmer et al., 2002) or implicitly (Dufour et al., 2005; Dzyubachyk et al., 2010; Li et al., 2008; Maška et al., 2013), using a velocity term defined by the content of the “target” frame (e.g. gradient features or intra- and inter-region heterogeneity) and by the internal properties of the evolved contours (e.g. mean curvature, shape or topology). The main benefit of the first paradigm is the mutual independence of detection and association steps, which allows straightforward tracking of new cells entering the field of view as well as forward-backward spatiotemporal data association (Bise et al., 2011). On the contrary, the tracking by model evolution approaches is popular for easy accommodation of morphological and behavioral clues into the model to inherently deal with the topologically flexible behavior of live cells. Bridging both paradigms together to take advantage of their benefits, Li et al. (2008) proposed a complex cell tracking system that combines a fast level set framework with a local spatiotemporal data association step.

The tracking methods described until this date have been tested in one or few private datasets using different metrics and have seldom been compared against other algorithms. A noteworthy attempt toward a formalization of the evaluation of cell tracking algorithms was described by Kan et al. (2011). They compared a novel cell tracking strategy to a publicly available probabilistic tracker using a customized tracking measurement and mostly publicly available data. Similarly, Rapoport et al. (2011) partly addressed this issue by providing a method for the validation of the accuracy of cell tracking results and a dataset composed of two manually annotated brightfield microscopy videos. Finally, two recent studies (Dima et al., 2011; Held et al., 2011) presented two rigorous comparisons of algorithms developed for the segmentation of fluorescently labeled cells from static 2D images, using their own image repositories and adapted accuracy measures.

The limitations of these studies, such as being monomodality, using 2D or static images, one or two cell types only, or comparing with none or few competing algorithms, highlight the need for common standards to evaluate new and existing algorithms. Bearing this in mind, we organized the first Cell Tracking Challenge (http://www.codesolorzano.com/celltrackingchallenge) hosted by the 2013 IEEE International Symposium on Biomedical Imaging (ISBI 2013, http://www.biomedicalimaging.org/2013/). In this article, we present the methods used in the challenge, briefly describe the competing algorithms and report on the results of the comparison, which was based on common accuracy measures and datasets covering a wide variety of scenarios of live cell imaging in fluorescence microscopy.

2 METHODS

2.1 Logistics

The challenge was organized by members of three research institutions: Center for Biomedical Image Analysis, Masaryk University, Brno, Czech Republic (CBIA-CZ); Center for Applied Medical Research, University of Navarra, Pamplona, Spain (CIMA-ES); and Erasmus University Medical Center, Rotterdam, The Netherlands (ERASMUS-NL). The challenge, announced via various media including targeted emails, mailing lists and the ISBI 2013 Web site, was opened for registration through the challenge Web site. Four weeks after opening the challenge for registration, all registered participants were given individual access to the challenge FTP server, where they could download the training datasets, along with the ground truth, and self-evaluation software. The registered participants worked on the training datasets during the 4 weeks before the competition datasets were released. The participants were then given six additional weeks to submit their results and the algorithms used to produce them. After the deadline, the consistency and the compliance of the submissions were verified by the organizers before the presentation of the preliminary results at ISBI 2013. After the ISBI 2013 workshop, the organizing committee confirmed the accuracy of the submitted results and compiled the final rankings presented in this article.

2.2 Datasets

Forty-eight time-lapse sequences used in the challenge were evenly distributed between the training and competition phases. Each group of 24 videos consisted of 12 real microscopy time-lapse sequences and 12 computer-simulated videos, 6 2D and 6 3D, with various cell densities and noise levels. The acquisition setup for each dataset is listed in Table 1, and representative regions of each dataset are displayed in Figure 1. Representative sample videos can also be found as Supplementary Videos S1–S8. The complete raw data are available at the challenge Web site. The datasets were named using the following convention: a four-letter prefix (LNDR) identifies the labeling (L) method -cytoplasmic (C) or nuclear (N); the dimensionality (ND) -2D or 3D; and the resolution (R) -low (L) or high (H). The suffix, separated by a hyphen from the prefix, describes the cell line.

Table 1.

Acquisition parameters and properties of the datasets

Name	Objective lens/Numerical aperture	Frame size (grid points)	Voxel size (µm)	Time step (min)	Number of frames	Difficulty
C2DL-MSC	20× Plan-apochromat/0.75	992 × 832 (1200 × 782)	0.397 × 0.397	20 (30)	48	High
C3DH-H157	63× Plan-apochromat/1.2 water	992 × 832 × 35 (80)	0.126 × 0.126 × 0.5	1 (2)	60	Low
C3DL-MDA231	20× Plan/0.7	512 × 512 × 30	1.242 × 1.242 × 6.0	80	12	Very High
N2DH-GOWT1	63× Plan-apochromat/1.4 oil	1024 × 1024	0.240 × 0.240	5	92	Medium
N2DL-HeLa	10× Plan/0.4	1100 × 700	0.644 × 0.644	30	92	High
N3DH-CHO	63× Plan-apochromat/1.4 oil	512 × 443 × 5	0.202 × 0.202 × 1.0	9.5	92	Medium
N2DH-SIM	40× Plan-apochromat/1.3 oil	505–755 × 535–775	0.125 × 0.125	28.8 (57.6)	56–100	Medium
N3DH-SIM	40× Plan-apochromat/1.3 oil	520–755 × 520–730 × 49 (60)	0.125 × 0.125 × 0.2	28.8 (57.6)	56–100	Medium

Note: The numbers in parentheses indicate particular values for the second half of a given dataset.

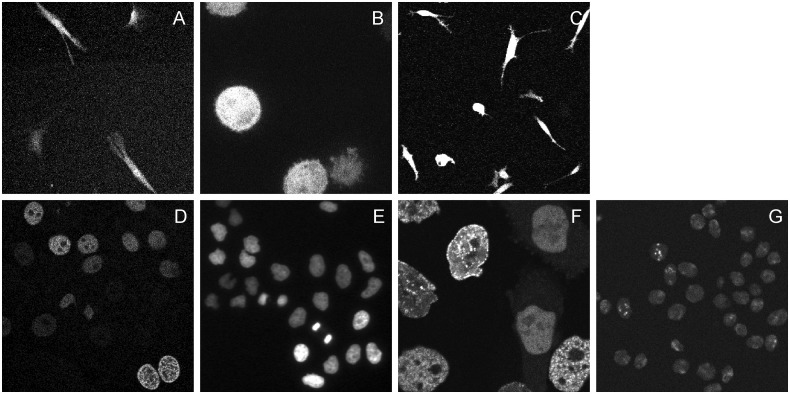
Fig. 1.

Representative regions from the video dataset repository. (A) C2DL-MSC; (B) C3DH-H157 (selected z-slice); (C) C3DL-MDA231 (selected z-slice); (D) N2DH-GOWT1; (E) N2DL-HeLa; (F) N3DH-CHO (selected z-slice); (G) N2DH-SIM (also representative of a selected z-slice of N3DH-SIM)

2.2.1 Real videos

The real video repository consists of six datasets.

C2DL-MSC (Fig. 1A and Supplementary Video S1). GFP transfected rat mesenchymal stems cells on a flat polyacrylamide substrate, acquired using a Perkin Elmer UltraVIEW ERS spinning disk confocal microscope (courtesy of Dr F. Prósper, CIMA-ES). The difficulty of the dataset is high because of the low signal-to-noise ratio and the presence of filament-like protruding areas caused by cell stretching, which sometimes appear as discontinuous extensions of the cells. Further complicating the analysis of the scenes, these protrusions often come in contact with other cells.

C3DH-H157 (Fig. 1B and Supplementary Video S2). GFP transfected H157 human squamous lung carcinoma cells embedded in a 3D matrigel matrix, acquired using a Perkin Elmer UltraVIEW ERS spinning disk confocal microscope (courtesy of Dr A. Rouzaut, CIMA-ES). The difficulty of the dataset is low because of low cell density and high resolution. However, the presence of cell blebbing and cells entering and leaving the field of view impose a certain degree of complexity for segmentation and tracking.

C3DL-MDA231 (Fig. 1C and Supplementary Video S3). MDA231 human breast carcinoma cells infected with a pure Murine Stem Cell Virus (pMSCV) vector including GFP. The cells were embedded in a 3D collagen matrix and acquired using an Olympus FluoView F1000 laser scanning confocal microscope (courtesy of Prof R. Kamm, Massachusetts Institute of Technology, Cambridge, MA, USA). The difficulty of the dataset is high because it was acquired under high-throughput conditions (i.e. low signal-to-noise ratio, low resolution, especially in the axial direction, and large time step). Moreover, there are a high number of colliding elongated cells as well as cells entering and leaving the field of view.

N2DH-GOWT1 (Fig. 1D and Supplementary Video S4). GFP transfected GOWT1 mouse embryonic stem cells on a flat substrate, acquired using a Leica TCS SP5 laser scanning confocal microscope (courtesy of Dr E. Bártová, Academy of Sciences of the Czech Republic, Brno, Czech Republic). The difficulty of the dataset is considered medium because of heterogeneous staining, prominent nucleoli, mitoses, cells entering and leaving the field of view and frequent cell collisions.

N2DL-HeLa (Fig. 1E and Supplementary Video S5). Histone 2B (H2B)-GFP expressing HeLa cells on a flat substrate, acquired using an Olympus IX81 inverted epifluorescence microscope. The videos were obtained with permission from the Mitocheck consortium video repository (http://www.mitocheck.org). The difficulty of the dataset is classified as high because of the high cell density and low resolution. In particular, the videos display frequent mitoses, both normal and abnormal, in addition to the presence of colliding, entering and leaving cells with low fluorescence intensity.

N3DH-CHO (Fig. 1F and Supplementary Video S6). Chinese hamster ovarian cells overexpressing proliferating cell nuclear antigen tagged with GFP, acquired using a Zeiss LSM 510 laser scanning confocal microscope (courtesy of Dr J. Essers, ERASMUS-NL). The dataset is considered of medium difficulty because of nuclei with heterogeneous staining, the presence of prominent nucleoli, mitotic cells with unstained nuclear periods, colliding cells and cells entering and leaving the field of view.

2.2.2 Simulated videos

The synthetic image data, along with the inherent ground truth, were generated using a simulation toolkit based on our previous work in CBIA-CZ (Svoboda and Ulman, 2012; Svoboda et al., 2009). As this challenge was dedicated to cell tracking, special attention was paid to the accuracy of cell movement during the cell cycle and to the mitotic events. The simulated videos displayed fluorescently labeled nuclei of the HL60 cell line migrating on a flat 2D surface (N2DH-SIM) and in a 3D matrix (N3DH-SIM) (Fig. 1G and Supplementary Videos S7 and S8). They differ in the level of noise, cell density of the initial population, the number of cells leaving and entering the field of view and the number of simulated mitotic events, yielding up to 70 cells in the field of view. Therefore, both datasets are considered of medium difficulty.

2.3 Ground truth generation for real datasets

One expert from CIMA-ES annotated all the real datasets used in the training phase. For the competition phase, all real videos were manually annotated by three experts from three sites (CBIA-CZ, CIMA-ES and ERASMUS-NL). Each expert created ground truth for tracking (TRA-GT) and ground truth for segmentation (SEG-GT) for each video. Each pair of SEG-GT and TRA-GT was manually revised by its creator to correct for automatically detected inconsistencies of two types: a segmentation mask either overlapping with multiple tracking markers or without any complete tracking marker. Finally, to account for inter-subject variability, two final ground truths (SEG-GT-F and TRA-GT-F) were created by combining the three existing ground truths, using a majority-voting scheme, as suggested, for instance, by Foggia et al. (2013). The way the majority voting was performed is described in detail in the Supplementary Note.

2.3.1 Field of interest

To simplify dealing with incomplete objects, entering or leaving the image frame, only objects that had substantially advanced into the image frame were analyzed. This is equivalent to defining a virtual inner field of interest (FoI) and analyzing only those objects that are at least partially inside the FoI. The distance in grid points (pixels or voxels) between the image frame border and the FoI border varied between datasets depending on the size of the objects of interest (50 grid points in C2DL-MSC, C3DH-H157, N2DH-GOWT1 and N3DH-CHO; 25 grid points in C3DL-MDA231 and N2DL-HeLa).

2.3.2 Ground truth for segmentation

The task for annotators was to mark grid points belonging to cells as accurately as possible. Therefore, each cell was segmented as a set of grid points with the same unique label. The length of the videos and the high number of cells per frame in some of the datasets prevented from having a complete manual annotation of all the cells. Therefore, we first randomly permutated all the frames of each video to unbiasedly select the cells that were used as ground truth. In the 3D videos, we also randomly selected at least one of its 2D z-slices, excluding empty slices. Then, the annotators were asked to segment all the cells within each frame in the given random order until at least 100 cells were segmented and two frames were fully segmented. The segmentation masks were drawn in the entire image frame and not just in the FoI. Cells visible only outside the FoI were not segmented at all. After reaching the limit of 100 cells and two full frames, the annotators inspected the remaining frames in the random order provided, and they were asked to identify and annotate cells that in their opinion were prone to causing segmentation problems, such as cells undergoing abnormal mitoses, dimly stained cells, oddly shaped cells and colliding pairs of cells. They segmented at least 20 instances of each problematic event.

2.3.3 Ground truth for tracking

The task for the annotators was to draw a quintessential “marker” (i.e. a set of grid points with the same unique label) inside each cell and in every frame where the cell consecutively appears entirely or partly within the limits of the FoI. These markers do not need to accurately follow the boundaries of the cells. Markers of a given label located in consecutive frames are called “tracks”. Tracks end when a cell entirely leaves the FoI, the video reaches the final frame or the cell divides into two, or abnormally more than two, daughter cells. When this happens, new tracks are created, one for each daughter cell, and the parental connection is stored in the TRA-GT file.

2.4 Evaluation

2.4.1 Segmentation measure

The main purpose of the segmentation (SEG) accuracy measurement is to understand how well the segmented cells match the actual cell regions. To quantify it, we used the Jaccard similarity index, defined as:

where R is a reference segmentation of a cell in SEG-GT-F and S is an automatic segmentation of the particular cell provided by a participant. A reference cell, R, and a segmented one, S, are considered matching if the following condition holds:

Note, for each reference cell, there can be one segmented object at most. If there is no significant overlap with any segmented object, the matching function is set to empty. The Jaccard index always falls in the [0, 1] interval, where 1 means perfect match and 0 means no match. The final SEG measure for a particular video is calculated as the mean of the Jaccard indices of all the reference objects in the video.

2.4.2 Tracking measure

The goal of the tracking (TRA) measurement is to evaluate the ability of the tracking algorithms to detect the cells and follow them in time. Although TRA does not evaluate the segmentation accuracy, reliable cell detection is the key to this measurement. To the best of our knowledge, there is no standardized, commonly used cell tracking accuracy measure currently available. Two popular approaches for measuring the performance of tracking algorithms are based on either the ratio of completely reconstructed tracks to the total number of ground-truth tracks (Li et al., 2008) or the ratio of correct temporal relations within reconstructed tracks to the total number of temporal relations within ground-truth tracks (Kan et al., 2011). Obviously, both approaches quantify, at different scales, how well the cell tracking algorithms are able to reconstruct a particular ground-truth reference. However, they neither penalize for spurious tracks nor account for division events, which are often evaluated separately (Kan et al., 2011; Li et al., 2008). Therefore, we developed a novel cell tracking accuracy measure that penalizes for all possible errors in tracking results and combines them with different weights, reflecting the manual effort needed to correct a particular error, into a single number.

Cell tracking results can be represented using an acyclic oriented graph. The nodes of such a graph correspond to the detected cells, whereas its edges coincide with temporal relations between them. They are of two kinds: track links (the cell continues with the same label in the consecutive frames) and parent links (the cell continues with a different label not necessarily in the consecutive frames). Non-dividing cells have one successor at most, whereas those that undergo division have two or even more successors in the case of abnormal division. The TRA measurement computes the difference between the acyclic oriented graph provided by a participant algorithm and the reference TRA-GT-F. To this end, we automatically quantify how difficult it is to transform the computed graph into the reference one as the least number of operations needed to make the graphs identical. The operations allowed (split/delete/add a node; delete/add or change the semantics of an edge) are penalized differently based on the effort that would be required if manually performed. The correspondence between operations and weights (w) is as follows: delete a node (w = 1, requires one mouse click); split a node (w = 5, requires drawing a divider); add a node (w = 10, requires adding a whole mask); delete an edge (w = 1, requires one mouse click); change an edge semantics (w = 1, requires one mouse click); add an edge (w = 1.5, it is slightly more difficult than deleting an edge, as it requires to determine both nodes of the edge). The TRA measure is defined as the weighted sum of graph operations, normalized by the number of markers (i.e. by the number of nodes in the reference graph) to facilitate the comparison between videos (datasets) with different numbers of cells. The best result, which requires no changes, has a TRA measure equal to zero.

To establish the optimal transformation of a participant graph into the reference graph, we have implemented the following automatic procedure. First, correspondences between the nodes of both graphs are determined using the same criterion that is used for finding matching segmentation masks. Then, the nodes are classified into four categories: false negatives (ground-truth nodes without any match to the participant nodes), false positives (participant nodes without any match to the ground-truth nodes), true positives (ground-truth nodes that match to some participant nodes) and non-split nodes (participant nodes that match to multiple ground-truth nodes). Knowing the category of each node, the procedure directly computes how many edges need to be removed from the participant graph. They are either connected to at least one false-positive node or they connect two correctly detected nodes, which are not linked in the ground-truth graph. Analogously, it counts the number of missing edges in the participant graph. These are the ground-truth edges without counterpart in the participant graph. Finally, the number of edges between matching nodes, which differ in semantics, is counted. The optimal transformation making the participant graph identical to the reference graph first involves separating all non-split nodes, adding false-negative nodes and removing all false-positive nodes. Having the sets of nodes of both graphs unified, redundant edges are removed, missing edges added and finally those with wrong semantics corrected. The whole procedure is fully automatic, requires no optimization and is easy to implement.

2.4.3 Time consumption

Time consumption (TIM) was evaluated on a common workstation (Intel Core i7-3770 3.40 GHz, 24 GB RAM) running the 64-bit Windows 7 or the Ubuntu 13.10 operating system. The total execution time needed to analyze each video of a given dataset was measured. The memory consumption was not considered for the performance evaluation, but the participants were asked to ensure that their algorithms would not require more than the given physical memory limit on that PC configuration.

2.4.4 Evaluation tools

Two command-line executable programs, one for segmentation and one for the tracking accuracy evaluation, were provided along with the training datasets to help the participants with the self-evaluation and refinement of their algorithms. These programs were also used by the organizers to evaluate SEG and TRA for the results submitted by the participating teams for the competition datasets. Both programs were written in C++ and are publicly available at the challenge Web site.

2.4.5 Compilation of rankings

First, for each method, the SEG, TRA and TIM measures were averaged over all the videos of a given dataset. For each dataset, all the methods were ranked (1 = best) and, subsequently, a final ranking was compiled based on the following formula:

where N is the number of ranked methods for a particular dataset. The reason for using different weights for accuracy (SEG and TRA) and speed (TIM) is to prefer more accurate, but possibly slower, methods to faster, but less accurate, ones.

The best performing method is that with the lowest Final rank for a particular dataset. Note that the methods having partial or empty submitted results for a particular dataset were not ranked for that dataset. Instead, their Final rank was established as NA (not applicable).

3 RESULTS AND DISCUSSION

3.1 Participants and algorithms

At the time the challenge was closed, six groups had uploaded consistent results to the challenge FTP server. The main principles of the competing algorithms are briefly described in Table 2 and are fully described in Supplementary Methods. Furthermore, executable versions of most of the competing algorithms, along with the instructions of use, are available through the challenge Web site.

Table 2.

Summarized description of the algorithms competing in the challenge

Methods	T	Preprocessing	Segmentation	Tracking	Post-processing
COM-US	D	Mean filtering	Iterative histogram analysis	Multiple-hypothesis tracking of extracted cell baricenters	Identification of parent links
HEID-GE	D	Gaussian and median filtering	Region adaptive thresholding followed by a watershed transform for splitting clusters	Local optimization using a cost function within spatially-limited search regions	Detection of mitotic events based on likelihood measurements
KTH-SE	D	Gaussian band-pass filtering	Global thresholding followed by a watershed transform for splitting clusters	State-space diagram optimization in a greedy fashion.	Seeded k-means clustering; Merging segments without tracks into adjacent segments with tracks
LEID-NL	M	Not used	Region-based contour evolution using the multi-phase level set framework. Radon transform for splitting clusters; Compensation for inter-frame cell motion		Improved handling of mitotic events (for cytoplasmic labeling) based on shape solidity measurements
PRAG-CZ	D	Gaussian filtering	Adaptive k-means thresholding followed by a watershed transform for splitting clusters	Nearest-neighbor tracking of extracted centers of mass	Not used
UPM-ES	D	Median filtering; Grayscale spatial area opening	Stochastic spatio-temporal morphological reconstruction combined with hierarchical clustering	Iterative spatio-temporal association based on three-dimensional connectivity for 2D data	Not used

Note: T, tracking paradigm (D: tracking by detection; M: tracking by model evolution).

3.2 Submissions and rankings

The percentage of submissions received for each dataset is listed in Supplementary Table S1. This table also displays the mean and standard deviation of the SEG, TRA and TIM measures obtained for each dataset, combining all the submissions received.

Table 3 presents a summary of the rankings obtained for each dataset, considering each measurement separately, and also combined, as described in Methods. The specific results for each dataset, including the values of the three performance measures for each video are listed in Supplementary Table 1. Sample results are presented as Supplementary Videos 9–16.

Table 3.

Summary of top-3 rankings per dataset and measure, along with the combined (FINAL) rankings

Rank	C2DL-MSC	C3DH-H157	C3DL-MDA231	N2DH-GOWT1	N2DL-HeLa	N3DH-CHO	N2DH-SIM	N3DH-SIM
FINAL
#1	KTH-SE	PRAG-CZ	KTH-SE	KTH-SE	KTH-SE	HEID-GE	LEID-NL	LEID-NL
#2	HEID-GE	KTH-SE	HEID-GE	PRAG-CZ	HEID-GE	KTH-SE	KTH-SE	KTH-SE
#3	UPM-ES	HEID-GE	COM-US	HEID-GE	PRAG-CZ	LEID-NL	HEID-GE	HEID-GE
SEG
#1	KTH-SE	HEID-GE	KTH-SE	PRAG-CZ	KTH-SE	HEID-GE	LEID-NL	LEID-NL
#2	HEID-GE	KTH-SE	COM-US	KTH-SE	HEID-GE	LEID-NL	HEID-GE	HEID-GE
#3	UPM-ES	PRAG-CZ	HEID-GE	HEID-GE	PRAG-CZ	COM-US	KTH-SE	KTH-SE
TRA
#1	KTH-SE	PRAG-CZ	KTH-SE	KTH-SE	HEID-GE	KTH-SE	KTH-SE	LEID-NL
#2	HEID-GE	KTH-SE	HEID-GE	PRAG-CZ	KTH-SE	PRAG-CZ	LEID-NL	KTH-SE
#3	UPM-ES	HEID-GE	PRAG-CZ	HEID-GE	PRAG-CZ	HEID-GE	HEID-GE	HEID-GE
TIM
#1	COM-US	PRAG-CZ	PRAG-CZ	COM-US	COM-US	COM-US	COM-US	PRAG-CZ
#2	KTH-SE	COM-US	COM-US	KTH-SE	KTH-SE	PRAG-CZ	KTH-SE	COM-US
#3	PRAG-CZ	KTH-SE	KTH-SE	PRAG-CZ	PRAG-CZ	KTH-SE	PRAG-CZ	KTH-SE

3.3 Discussion

In the next paragraphs, we will discuss the main contributions of the challenge.

Datasets. We have created a public data repository composed of 24 annotated time-lapse sequences obtained from conventional and confocal fluorescence microscopes, along with 24 realistic computer simulations of moving nuclei. The cell types selected are relevant in the context of cell migration, being cells with stem-like properties involved in embryonic and adult organ development and homeostasis, or cancer cell lines with metastatic properties. These videos cover a wide variety of cell types, microscopy and experimental setups, cell density and motility, resolution, image quality and dimensionality. There are 2D sequences of nuclearly stained cells, commonly used in cell population studies (e.g. N2DL-HeLa), and 3D sequences of cytoplasmically stained cells, more appropriate for single-cell studies that demand a realistic rendering of the cellular environment (e.g. C3DL-MDA231). The characteristics of the videos in terms of contrast, resolution and signal-to-noise ratio are also diverse, covering conditions ranging from those that could be considered “high quality” (i.e. high numerical aperture lens, homogeneous and bright fluorescent staining) to conditions that could be classified as “high-throughput” (i.e. low magnification, low numerical aperture lens, heterogeneous and dim fluorescent staining). All real videos used in the competition were manually annotated at three different sites, and a final ground truth per video was generated using a majority voting approach, to account for inter-subject variability. The two additional simulated datasets provide an absolute ground truth for the comparison of the algorithms, eliminating the possible bias introduced by the annotators of the real videos.

Measures and rankings. Key to the establishment of a credible benchmark is the use of common measures for algorithm evaluation and comparison. We have described and used measures that account for two aspects of the cell tracking problem: segmentation and tracking accuracy. The segmentation accuracy measure was based on the Jaccard similarity index, which evaluates how close the cell segmentations are to the ground truth. Tracking accuracy was evaluated using a novel measure, based on matching acyclic oriented graphs. This method automatically assesses the difficulty of transforming a computed graph into the ground-truth reference. The difficulty is measured as the weighted sum of the least number of operations needed to make the graphs identical. Therefore, the tracking accuracy was measured by one comprehensive scalar measure, whereas in most previous works it required evaluating multiple measures to characterize various cell tracking events (Kan et al., 2011; Li et al., 2008). The weights are not biologically motivated; therefore, the measure is application-independent. The highest weight is put on missing nodes in the weighted sum; therefore, the ability of the method to detect all the cells is important for achieving low score. Because both parameters (i.e. segmentation and tracking accuracy) are of similar importance, they were weighted equally in the final ranking function. Only when the algorithms achieved the same rank in terms of accuracy, the faster one was preferred, which was guaranteed by adding time performance with a smaller adaptive weight.

Results: Participants and algorithms. Six algorithms were submitted to the first Cell Tracking Challenge, covering a wide variety of methods, stemming from the two main tracking paradigms: tracking by detection and tracking by model evolution. Most of the existing state-of-the-art methods for filtering, enhancement, segmentation, particle analysis and track association are represented. Four of the six participating groups (COM-US, HEID-GE, KTH-SE and PRAG-CZ) provided results for all the datasets. This is a remarkable fact that emphasizes the generalization of the results.

Results: Global analysis. Based on the numbers provided in Supplementary Table S1, both SEG and TRA accuracy measures were higher for nuclear labeling than for cytoplasmic labeling. Furthermore, they both reflected the level of complexity provided in Table 1, along with the description of the datasets.

There were large differences in the segmentation accuracy, the lowest mean values being for C2DL-MSC and C3DL-MDA231 (both with cytoplasmic labeling), the highest mean value being for N3DH-CHO. This could be explained by the fact that the algorithms seem to be developed and tuned for the segmentation of nuclei, as they often incorporate cluster separation routines based on the circularity of segmented objects. Therefore, they are not appropriate for cellular shapes, which are seldom uniform, present protrusions and frequently establish contacts or overlaps.

The TRA measure generally provided more uniform results among datasets, with the exception of C2DL-MSC. Interestingly, the algorithms achieved significantly higher tracking accuracy on the simulated datasets than on the real ones. This is likely because of the fact that the computer-simulated nuclei are in general uniformly sized, and the simulated cell motility does not cover all possible random events that occur in real live-cell experiments.

Finally, the TIM measure strongly depended on the size of each video, being the lowest for C2DL-MSC and N2DH-SIM and the highest for N3DH-SIM and C3DH-H157. Another important factor influencing time consumption of the competing algorithms was the number of objects to be analyzed. Note that the standard deviations of the TIM measure indicate significant differences in the speed of competing algorithms for all the datasets.

Results: Rankings. The FINAL ranking in Table 3 shows that KTH-SE performed best in four real datasets (C2DL-MSC, C3DL-MDA231, N2DH-GOWT1 and N2DL-HeLa). HEID-GE and PRAG-CZ performed best in one real dataset (N3DH-CHO and C3DH-H157, respectively). LEID-NL performed best in the two simulated datasets (N2DH-SIM and N3DH-SIM). When we look at the number of appearances of each method among the top three best performing methods, both KTH-SE and HEID-GE appeared in all eight datasets, LEID-NL and PRAG-CZ appeared in three datasets and finally UPM-ES and COM-US appeared in one dataset.

It is also important to note that in the case of C3DH-H157, N2DH-GOWT1, N2DL-HeLa and N3DH-SIM, the decisive factor for establishing the final ranking was the speed of competing algorithms because multiple methods were evenly ranked based on the SEG and TRA accuracy measures only.

Looking at each accuracy measure separately, HEID-GE and KTH-SE ranked among the top three most accurate methods for all the datasets, with the exception of the segmentation accuracy for N3DH-CHO, where KTH-SE ranked fourth. However, one should note that in this specific case, the difference in SEG between the most accurate method, HEID-GE, and KTH-SE was small. The other two methods that often belonged to the top three most accurate methods were PRAG-CZ and LEID-NL. In terms of TIM measure, COM-US, PRAG-CZ and KTH-SE were consistently the top three fastest methods for all the datasets. It is remarkable that KTH-SE was, at worst, second fastest among the top three best performers in terms of SEG and TRA.

Results per dataset: We will now look at the results of each particular dataset in detail, trying to extract relevant conclusions about the best performing methods (see Table 3 and Supplementary Table S1):

C2DL-MSC (Supplementary Video S9). The accuracy measures were generally poor, especially because of problems with the segmentation of elongated protrusions, often incorrectly considered as whole cells. KTH-SE achieved significantly better accuracy than the other methods because of the optimized track-linking algorithm used, and an adaptive post-processing step, which merges segmented object portions into adjacent segments with tracks. Regardless of this additional post-processing step, the method was still fast, being the second fastest in terms of TIM and >2× faster than the other two top three best performing methods, HEID-GE and UPM-ES.

C3DH-H157 (Supplementary Video S10). All the algorithms that competed for this dataset achieved comparable segmentation accuracy, HEID-GE being the most accurate. Compared with the segmentation accuracy, the tracking accuracy was more spread out, PRAG-CZ being the most accurate. The decisive factor for establishing the final ranking of the top three best performing methods was TIM. Globally, PRAG-CZ was ranked first, having the lowest time consumption, namely, because the preprocessing step, involving Gaussian filtering, is applied only in 2D, slice-by-slice.

C3DL-MDA231 (Supplementary Video S11). The calculated accuracy measures were generally poor, because of the high-throughput acquisition conditions, making it difficult to properly separate tightly packed clusters as well as accurately segment elongated protrusions. Analogously to C2DL-MSC, KTH-SE significantly outperformed the other methods in terms of accuracy. This is due to the additional arcs included in the state space diagram, which allow the delayed creation of correct tracks originally blocked by incorrect preexisting tracks (Magnusson and Jaldén, 2012). Moreover, this is also a benefit of the track-free object merging used as an adaptive post-processing step.

N2DH-GOWT1 (Supplementary Video S12). Both accuracy measures were high, especially SEG. A decisive factor for achieving these good results was the use of a cluster separation routine (e.g. watershed or the Radon transform), and a hole-filling approach to remove small background components within segmented cells at places of prominent nucleoli. The top two best performing methods, KTH-SE and PRAG-CZ, performed similarly. Based on the SEG and TRA measures, they were assigned the same rank of 3, with PRAG-CZ the best in segmenting and KTH-SE the best in tracking. Globally, KTH-SE was ranked first because it was ∼5× faster than PRAG-CZ.

N2DL-HeLa (Supplementary Video S13). The accuracy measures were high, especially TRA. Analogously to N2DH-GOWT1, the use of a cluster separation routine resulted in more accurate results, although such routine sometimes led to over-segmentation, especially when multiple touching nuclei formed clusters of highly irregular shape. The top two best performing methods, KTH-SE and HEID-GE, produced results of comparable accuracy. Based on the SEG and TRA measures, they were assigned the same rank of 3, KTH-SE being the best in segmenting and HEID-GE being the best in tracking, mainly because of the specific mitosis detection phase implemented in their method. Globally, KTH-SE was ranked first as it was >2× faster than HEID-GE.

N3DH-CHO (Supplementary Video S14). The accuracy measures were the best among all the real datasets. This can be explained by the high magnification objective lens used and low cell density. Furthermore, these videos contain little of noise. Analogously to N2DH-GOWT1, a crucial factor for achieving more accurate results was to involve a hole-filling approach to deal with nucleoli. Globally, HEID-GE was ranked first, thanks to its ability to deal with the presence of cell invaginations and a morphology-based likelihood measure used to identify candidates for mitotic events.

N2DH-SIM and N3DH-SIM (Supplementary Videos S15 and S16). The obtained SEG measures were similar to those for the real datasets displaying stained nuclei. This indicates that our simulator generates images of realistic static content in terms of cell texture, noise level and image degradations. However, in terms of tracking accuracy, as mentioned before, the algorithms performed generally better than in the real datasets. Globally, LEID-NL was ranked first for both simulated datasets, fitting with the idea that the model behind this method highly conforms to computer-simulated nuclei of controlled cell motility. However, it needs further optimization to properly work in real scenarios. From the analysis of the submitted results, we can finally stress the importance of the mitosis detection phase implemented by HEID-GE, and the linking and adaptive track post-processing phases implemented by KTH-SE, especially in low signal-to-noise ratio conditions.

4 CONCLUSION

In this article, we have presented the implementation of a benchmark for objective comparison of cell tracking algorithms, based on the use of a common diverse video dataset repository and ground truth, specific measures for both the evaluation of the segmentation and tracking accuracy, and unified criteria for comparing and ranking the algorithms. This is something recently highlighted by Carpenter et al. (2012) as a requirement for the usability of biomedical imaging software. The logistics, datasets, methods and results of the challenge have been described herein. In the future, we expect this benchmark to serve as a reference for the development and evaluation of novel cell tracking algorithms. To this end, the training and competition datasets are available to the general public, along with the ground truth for the training datasets and the self-evaluation software. Moreover, executable versions of most of the competing algorithms will be available through the challenge Web site. We expect the challenge to remain open for online submissions, because there are open problems that need to be addressed and new algorithms that can be developed to improve the existing ones. Namely, accurately segmenting and tracking cytoplasmically labeled cells is still something far from being solved. Automated segmentation and tracking of other cell types, other modalities (e.g. brightfield time-lapse microscopy) and existing or new high-throughput modalities, such as selected plane illumination microscopy, may require further algorithmic developments, and therefore proper testing and validation that could be achieved through this benchmark.

Funding: The Spanish Ministry of Economy (DPI2012-38090-C03-02 to C.O.d.S. and M.M.); the Czech Science Foundation (302/12/G157 to M.K., P.M., P.M., D.S., G.M.H.); the European Social Fund and the Czech Ministry of Education (1.07/2.3.00/30.0009 to M.M.); the Swedish Research Council (VR) (621-2011-5884 to K.M. and J.J.); the National Institutes of Health (R01 HL096113 to H.B.) and California Institute for Regenerative Medicine (RT1-01001-1, to H.B.); the Grant Agency of the Czech Republic (P205/12/P392 to P.Křížek); the project UNCE 204022 from the Charles University (P.Křížek); the BMBF projects ENGINE (NGFN+) and FANCI (SysTec) (N.H., K.R.); Spain's Gov. projects (CDTI-AMIT, TEC2010-21619-C04-03, TEC2011-28972-C02-02) and European Development Funds (D.P-E, D.J-C and M.J.L-C.).

Conflict of Interest: none declared.