Abstract
We built three simulation models that can assist rail transit planners and operators to evaluate high and low probability rail-centered hazard events that could lead to serious consequences for rail-centered networks and their surrounding regions. Our key objective is to provide these models to users who, through planning with these models, can prevent events or more effectively react to them. The first of the three models is an industrial systems simulation tool that closely replicates rail passenger traffic flows between New York Penn Station and Trenton, New Jersey. Second, we built and used a line source plume model to trace chemical plumes released by a slow-moving freight train that could impact rail passengers, as well as people in surrounding areas. Third, we crafted an economic simulation model that estimates the regional economic consequences of a variety of rail-related hazard events through the year 2020. Each model can work independently of the others. However, used together they help provide a coherent story about what could happen and set the stage for planning that should make rail-centered transport systems more resistant and resilient to hazard events. We highlight the limitations and opportunities presented by using these models individually or in sequence.
Keywords: Passenger rail risk, resilience, simulation
1. INTRODUCTION
The purposes of this article are to describe and illustrate the use of three simulation models built to assist in rail security planning and risk analysis, and to provide examples of how to integrate the results across a passenger rail system. The work began with the announcement that the U.S. government was planning to substantially expand its passenger rail network, focusing on high speed corridors. Ten systems across the United States were in the planning stages and noted in President Obama’s year 2010 State of the Union speech.(1–3) The only existing high speed rail in the United States is the 450-mile-long Northeast Corridor (NEC) between Washington, DC and Boston, Massachusetts.
A fundamental challenge for risk analysis is to build models that replicate reality and will be used by managers in planning and operations. Here we describe and illustrate three that we believe can be used to test medium to low probability rail hazard or human exposure events that have medium to high public health and economic consequences. The illustration is in New Jersey, which contains 60 miles of the NEC, owned and operated by Amtrak and also used by New Jersey Transit (NJT), the third largest public-operated mass transit system in the nation. Major freight rail systems crisscross and parallel the NEC in this most densely populated and second most affluent state in the United States. New York City and Philadelphia, two of the largest metropolitan regions in the United States, are its immediate neighbors and the flow of people and goods through the state is among the highest in the nation, further increasing the intrinsic value of the New-Jersey-centered study region.
The article is divided into four parts. After placing this work in a risk analysis context, the article presents the three simulation models and summarizes the empirical results. The discussion emphasizes the limitations and opportunities of this approach.
2. RISK ANALYSIS CONTEXT
The first published article in Risk Analysis, An International Journal, described the first three stages of risk analysis as determining what can go wrong, the chances that something serious will go wrong, and the consequences of something going wrong.(4) Later authors have added risk management stages that focus on prevention/reduction of impact, resilience if an event occurs, and organizational capacity to respond.(5)
This article describes part of an effort to address these six risk analysis stages for passenger rail lines in the United States. It touches on all six but focuses on consequences and organizational capacity. With regard to risk assessment, the events start with signal and other equipment failures that cause delays of 15 minutes to several hours. We have historical data for these events, modeled them, and they served as part of the validation. The focus of this article is on two major events, a chemical release and a major bridge failure, for which there are no likelihood data. Consequences of the two major events include deaths, serious injuries, and regional economic consequences. This article concentrates on regional economic impacts. With regard to risk management, the chemical event can be prevented by a policy change, which is discussed, and the bridge failure can be made less consequential by a well-conceived resilience effort, which is illustrated. Organizational capacity is the sixth stage, and we think it is the most challenging aspect of using these tools in passenger rail planning and operations.
We are not aware of any similar effort to build this set of models for passenger rail systems. In the larger risk analysis context, we point to a number of papers that have used models and multidisciplinary frameworks to gain a better understanding of the consequences of events that would help guide risk management decisions.(6–11) It is in the spirit of these studies that we undertook this one.
3. THREE SIMULATION MODELS
Before building the models, we spoke on multiple occasions with representatives of NJT, Amtrak, and other responsible parties. Collectively, they told us that they wanted tools that they could use in routine planning, or paraphrasing what one senior staff member said: we would want to be able to use this for planning for the Super Bowl (U.S. professional football championship game) and for periodic outages of an hour or more. They advised us against a model that could only be applied to the worst events, which they said would not be incorporated into their operations. Also, the responsible parties wanted us to concentrate on those parts of the system that were sufficiently complicated that decision support tools were needed to replace existing spreadsheets and collective experience. These discussions with users substantially influenced our model designs.(12)
3.1. Rail Systems Model
We developed a rail simulation model with the ARENA simulation tool developed by Rockwell Software.(13,14) We deliberately chose ARENA because many engineers have been trained in its use, and it is not perceived as an indecipherable black box. It allows the user to build a systems model and generate statistics and accompanying animation that helps users follow the flow of information during operations. ARENA allowed us to incorporate multiple components of the operating rail network, including number of trains in service, number of cars per train, number of boarding/deboarding passengers, time spent at a station for boarding/deboarding operations during rush hour (AM and PM) and nonpeak hours, the tracks, the stations, bridges, and other physical elements.
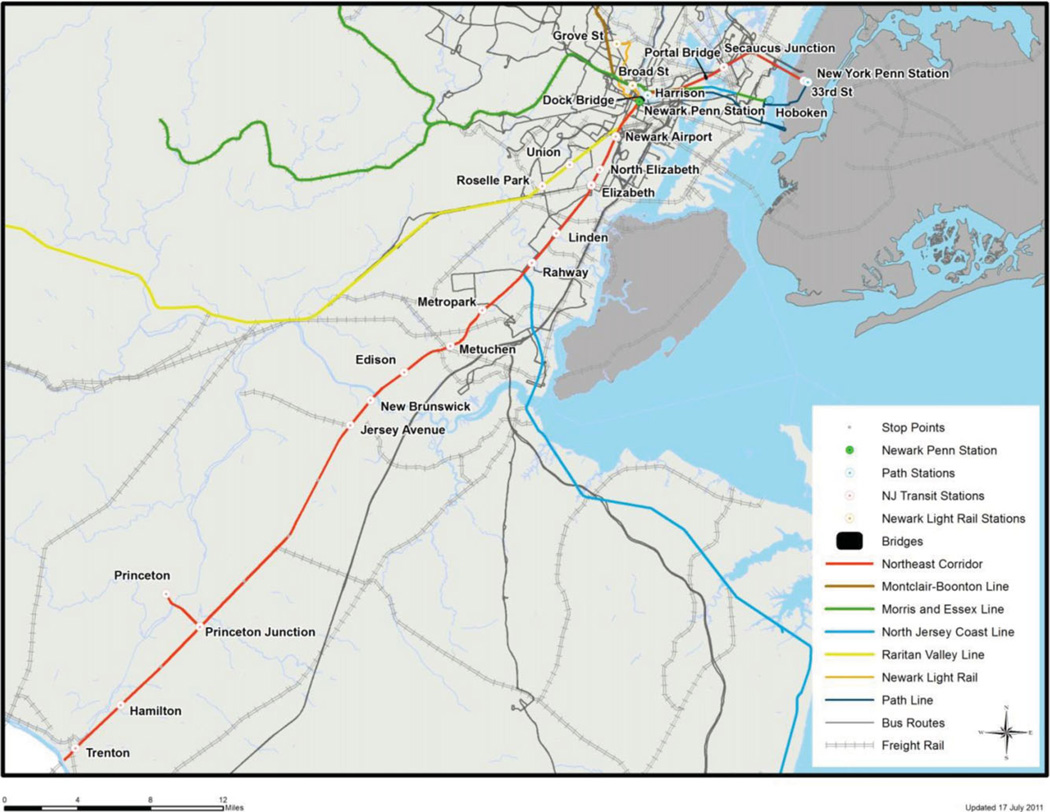
Our original intent was to model a major segment of the NEC, giving equal weight to all components. However, the users advised us to focus on the main rail line between Trenton, New Jersey and Penn Station, New York City, and specifically to concentrate on Newark Penn Station (NPS) in New Jersey, which is the most important asset in New Jersey for both Amtrak and NJT. Fig. 1 shows the system that we included in the model.
Fig. 1.
Rail simulation study area.
The simulation model includes 19 rail services that stop at NPS. Nine are Amtrak and five are NJT, including the Light Rail, and the PATH lines that run to Jersey City, Hoboken, and New York City (Table I). We also included three NJT trains that do not stop at NPS but could serve as alternative paths (work-around options for resilience) in the event of a serious problem at the Newark train station.
Table I.
Service Providers Included in the Model
| Service Provider, NJT | Color | Actual Terminuses |
|---|---|---|
| Northeast Corridor | Red | Trenton, NJ–New York Penn, NY |
| North Jersey Coast | Blue | Long Branch/Bay Head, NJ–New York Penn, NY or Hoboken, NJ |
| Raritan Valley | Yellow | Raritan or High Bridge Station, NJ–Newark Penn, NJ |
| Atlantic City Express Service | Red | Atlantic City, NJ–New York Penn, NY |
| Newark Light Rail | Orange | Grove Street, NJ–Newark Penn, NJ |
| Newark Light Rail Extension | Orange | Broad Street, NJ–Newark Penn, NJ |
| Montclair–Boonton | Brown | Hackettstown, NJ–New York Penn, NY or Hoboken, NJ |
| Morristown | Green | Hackettstown, NJ–New York Penn, NY or Hoboken, NJ |
| Gladstone | Green | Gladstone, NJ–New York Penn, NY or Hoboken, NJ |
| Amtrak | ||
| Acela Express | Red | Washington, DC–Boston, MA |
| Cardinal | Red | Chicago Union, IL– New York Penn, NY |
| Crescent | Red | New Orleans, LA–New York Penn, NY |
| Carolinian | Red | Charlotte, NC–New York Penn, NY |
| Keystone | Red | Harrisburg, PA–New York Penn, NY |
| Northeast Regional | Red | Washington, DC–Boston, MA |
| Pennsylvanian | Red | Philadelphia, PA–New York Penn, NY |
| Silver Service/Palmetto | Red | Georgia or Florida–New York Penn, NY |
| Vermonter | Red | Washington, DC–St. Albans, VT |
| Port Authority of NY and NJ | ||
| PATH | Dark blue | Newark Penn, NJ–Manhattan, NY |
When we began this work, the December 2010 timetables were in use, and we incorporated those into the model. Separate schedules were prepared for weekdays and weekends/holidays for both directions. NJT and Amtrak gave us the number of cars per train and number of passengers per car. For example, NJ Transit trains, with several exceptions for smaller lines, have 10 cars during rush hours and 8–10 cars the rest of the day (we randomized these). The maximum car capacity for NJ Transit trains is 140 people during rush hours and it is assumed that car capacity has a uniform distribution between 120 and 140 during nonrush hours (randomized). We incorporated similar data for Amtrak, PATH, Light Rail, and the others.
Train speed was estimated by dividing distance by travel time and comparing it to schedules. We also learned that the track structures between Trenton and Newark are different from those between Newark and New York City. Consequently, the model changes train speeds at Newark to reflect destination.
Assumptions were made about waiting time, boarding, and other operations for both peak and off-peak times. Based on expert advice, we also added upper and lower limits ±10% of the mode. Each train has its own deboarding and boarding proportions based on historical data. If there is a service disruption less than an hour, people are assumed to wait, if the service disruption is more than one hour, only 50% of people will continue to wait and in two hours everybody will leave. It is also assumed that the rescue time for passengers held on disrupted trains is 60 minutes.
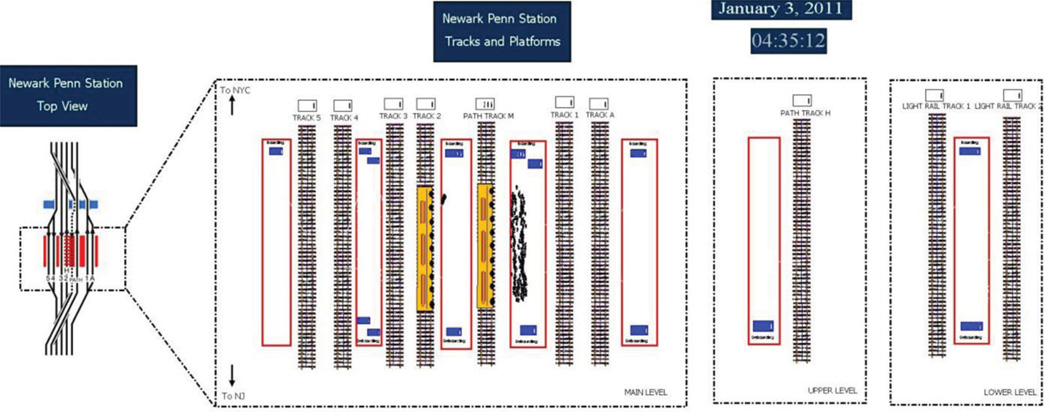
The NPS is the key node, and its track structure was modeled in detail. December 2010 data showed that over 1,000 trains per day stopped at NPS. The main part of the station has five platforms and seven tracks. Normally, each has a set of trains that stop, yet tracks are reassigned during rush hours and can change if the managers change the operational priorities. All of these platforms and tracks were incorporated into the model in order to test the validity of the model, and these details allowed us to show the operators how our model results compared to their routing and rerouting protocols and spreadsheets.
The model allows us to stop the trains and then operators can adjust the system, while the model keeps track of how many people are stranded at what locations in the system. When the system recovers, the model resumes and trains start running again. Assuming the model is valid (see below for validation), then we can figuratively stop the system at any time and watch what happens. The graphs allow the users to see trains (different colored dots for different train lines) and trains and people moving and stopped, and cumulative passenger totals on the screen.
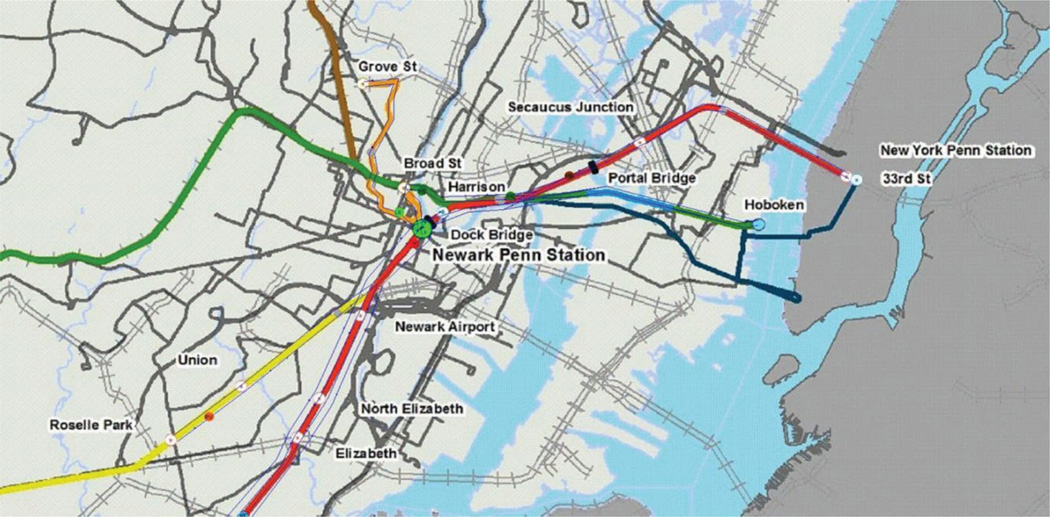
Fig. 2 shows a more detailed view of the network of rail around NPS. The different colors of the rail lines in Fig. 2 (colors visible in online version) represent the different lines, with red, for example, representing the NEC line. Fig. 3 shows a top view schematic of the NPS and the specific screen shows two trains in the station and passengers on the platform. While not visible in these shots, the model accumulates the number of people in each station and at platforms in NPS as trains come in and out.
Fig. 2.
The Newark Penn Station study area for the rail simulation model (screenshot of the study area).
Fig. 3.
General view of the Newark Penn Station building.
It was abundantly clear to the research team that the potential users were not interested in any model unless they could be shown that it closely replicated reality. Accordingly, we ran the model to simulate a 25-year timespan and compared the average results to the data provided to us by the rail system managers for number of trains, average travel time, and average number of passengers boarding and deboarding at NPS. (Please note that these simulations are based on the data provided by the managers in late 2010, and would no longer be considered appropriate without updating.)
We found very close agreement (see Tables II–IV). Tables II–IV show the validations for numbers of trains, times between stations, and boardings and deboardings at NPS. For example, the average daily number of NJT trains arriving at NPS was 290, and the simulated number was 289.62 ± 0.022. Running time between stations for the major rail lines was also very close. For instance, eastbound (toward New York City) NJT trains were simulated to take 28.28 minutes compared to an actual time of 28 minutes. The numbers of passenger boardings and deboardings were close to actual counts. For example, NJ Transit boardings at Newark were 26,525 ± 4.68 compared 26,449 in the actual data. Given these simulation results, we conclude that the model, assuming that is updated, can closely replicate reality and can be used to model disruptions.
Table II.
Validation Results, Number of Trains at Newark Penn Station, Daily Average
| Train | Simulation | Real Data | Relative Error |
|---|---|---|---|
| NJ Transit | 289.62 ± 0.0223 | 290 | −0.0028 |
| Amtrak | 103.57 ± 0.0052 | 104 | −0.0041 |
| Light Rail | 384.56 ± 0.0417 | 386 | −0.0037 |
| PATH | 247.63 ± 0.0228 | 250 | −0.0095 |
Table IV.
Validation: Boardings and Deboardings at Newark Penn Station, Average Daily Values
| Simulation | Real Data | Relative Error | |
|---|---|---|---|
| NJ Transit Boardings | 26,525 ± 4.6761 | 26,449 | 0.0029 |
| Amtrak Boardings | 1,800 ± 0.4107 | 1,800 | 0.0000 |
| Subway Boardings | 6,103 ± 0.8924 | 6,152 | −0.0079 |
| PATH Boardings | 29,805 ± 4.8177 | 29,923 | −0.0039 |
| NJ Transit Deboardings | 26,405 ± 5.9433 | 26,449 | −0.0017 |
| Amtrak Deboardings | 1,803 ± 0.4881 | 1,800 | 0.0021 |
| Subway Deboardings | 6,252 ± 1.1593 | 6,215 | 0.0061 |
| PATH Deboardings | 29,622 ± 4.1459 | 29,923 | −0.0101 |
3.2. Likely Events, and Major Bridge Closure and Air Pollution Events
Service disruptions can be caused by deliberate and nondeliberate events, from bombs to tornadoes, by derailing a train, failure of an electronic system, and by a long list of other precipitating events.
3.2.1. Routine Events
Before running the two major consequence events (bridge failure and air pollution), we obtained estimates of “routine” system failures that can occur once a week, and less likely events that occur about once every other week. We caused these events to occur in the rail model, calculated their impacts on passengers, and then showed the results to the user community. This validation test was successful.
3.2.2. Bridge Failure for an Extended Period
We figuratively disabled a major bridge for an extended period of time, and used buses, light rail, other rail, and PATH with delays in schedules to introduce a resilient solution that also involved some people driving to work (impacting travel time) and a small proportion telecommuting. The economic consequences of these delays were estimated (see below for more details).
3.2.3. Major Air Pollution Event
With regard to a major human health event, after much discussion, we made a choice of an event based on two principles. First, given the geographical and temporal precision of the location, we did not want to illustrate the capability with a terrorist event. Second, we wanted to directly connect the rail system model to the event model. Accordingly, we chose an industrial chemical leak from a slow moving freight train that necessitated building a plume model.
Plume models assess how gases and particles disperse from a source. Sources can be a single point (factory, power plant), a moving line (motor vehicles, trains), or a large area with many emitters (residential neighborhood). Emissions can be continuous, such as from a sulfur scrubber at a petroleum refinery, or they can be episodic, such as fires, explosions, and leaks from a stationary (e.g., factory) or mobile source (e.g., tank car on a moving train).
The scenario presented as an illustration here is more complicated with regard to modeling than others we have seen, which was verified by U.S. Department of Homeland Security (DHS) and U.S. Department of Defense (DOD) research staff who have been involved in rail and chemical risk assessments for their departments. It assumes a hypothetical leak of liquid chlorine from a rail car that is traveling from a major chlorine production facility located in northern New Jersey. We picked chlorine because it is a ubiquitous substance, widely used for purifying potable water and wastewater, and as an intermediate chemical in many other products. Chlorine and ammonia account for much of chemical shipments by rail in the United States. There have been incidents. In 2005, a train derailment near Graniteville, South Carolina ruptured a tank car with chlorine and nine people were killed, 75 injured, and over 5,000 people living within a 1-mile radius were evacuated for several days. The estimated cost of this event exceeded $100 million.(15) The plausibility of the event is discussed below, and we emphasize that it is meant to be an illustration.
Several dozen air dispersion models are available. We chose SCIPUFF (Second-Order Closure Integrated Puff), which has been validated both in the field and laboratory.(16,17) SCIPUFF is a Lagrangian model that uses a collection of Gaussian puffs to describe time-varying three-dimensional concentration profiles, and predicts both the average concentration and the concentration variance out to regional scales. For our purposes, the SCIPUFF model formulation allows for predicting short- and long-term concentration profiles from a moving source (a freight train), in conjunction with time-varying meteorological inputs. This model also uses adaptive multigrid and time-stepping schemes, and captures sharp changes in concentration fields over both space and time. Concentration estimates can be obtained either at specific locations, over a regular grid, or as contours of concentration profiles. Notably, the model permits adjustment for terrain, particle and gas movement, degradation, short and range transport, and direct input of meteorological information.
The SCIPUFF implementation used in this simulation was from the Hazard Prediction and Assessment Capability (HPAC) system,(18) which provides dispersion modeling in addition to chemical, biological, and nuclear databases for source definitions. The HPAC system can utilize user-specified weather data from National Weather Service (NWS) and military providers. Local topography is incorporated into the model via generation of an interpolated wind field with data from any number of surface and upper-air measurements, but the surface roughness is required to be constant over the entire domain. It uses a modification of the Dense Gas Dispersion Model (DEGADIS) when the source gas is heavier than air. HPAC has been tested in the URBAN 2000 field experiment(19) and in various other comparative evaluation studies.(20–22)
We ran four versions of the model that varied by point of origin, train path, and plume direction, and we illustrate one of the four in the article. The concentration profiles predicted by the plume model were examined within a context that was linked to the Acute Exposure Guideline Levels (AEGL) framework. It describes the dangers to humans in nonoccupational settings resulting from short-term exposure to airborne chemicals. The AEGL values are intended to serve as planning values for the safety layout of industrial plants for which the possibility of a hazardous incident is relevant. Additionally, measures for alert and emergency response planning as well as for disaster control can be projected more accurately on the basis of the AEGL framework.(23–25)
AEGL values represent toxicologically substantiated ceiling exposure levels for different relevant exposure periods (e.g., 10 minutes, 30 minutes, 1 hour, 8 hours, etc.). They are specified for three different degrees of severity of toxic effects. AEGL1 is the threshold for notable discomfort, AEGL2 is threshold for serious, long-lasting effects or an impaired ability to escape, and AEGL3 is the threshold for lethal effects (Table V). The actual percentage of people injured above each value depends upon the age, sex, infirmities, and susceptibility of the population placed at risk. Thus, each AEGL can be used to provide estimates of the impact on public health. It must be noted that in order for health effects to manifest, the concentrations at any location have to persist beyond a threat level over the corresponding time duration. Therefore, if we consider a specific location, such as a rail system, the risks associated with exposure will depend on when the trains arrive, who is inside and outside, and how long high levels of concentrations persist; all of these are stochastic elements that can be simulated. Table V shows the AEGLs for chlorine.
Table V.
AEGLs for Chlorine
| Ppm | 10 Minutes | 30 Minutes | 60 Minutes | 4 Hours | 8 Hours |
|---|---|---|---|---|---|
| AEGL1 | 0.5 | 0.4 | 0.5 | 0.5 | 0.5 |
| AEGL2 | 2.8 | 2.8 | 2 | 1 | 0.5 |
| AEGL3 | 50 | 28 | 20 | 10 | 7.1 |
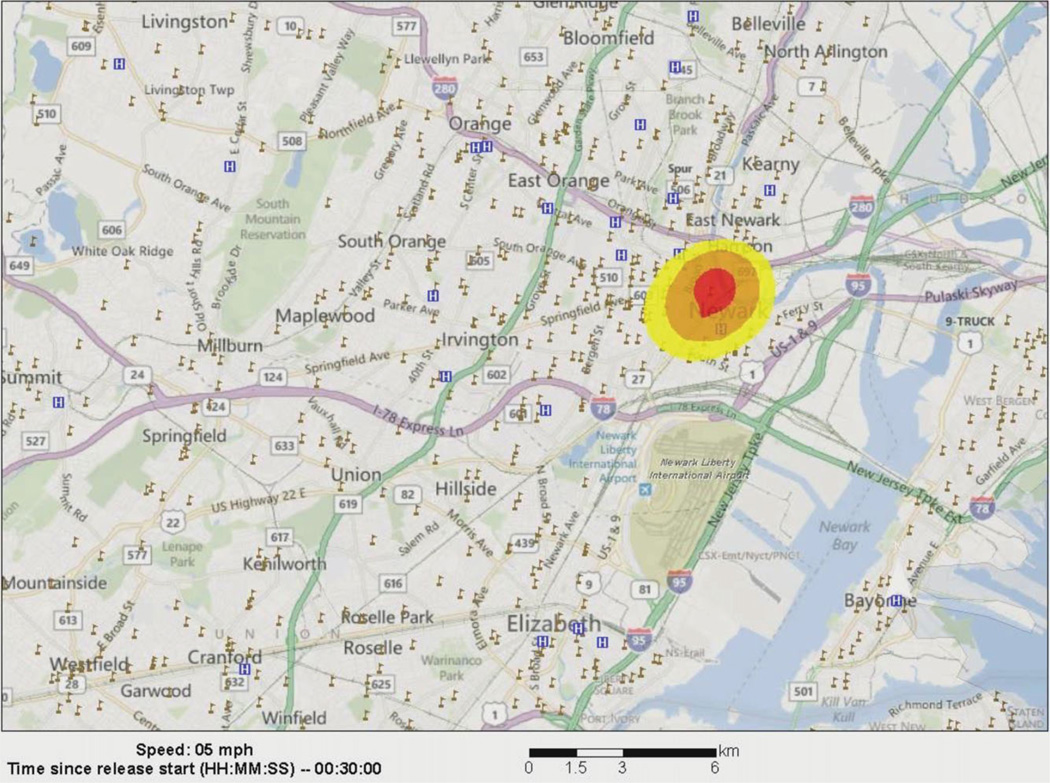
The chlorine release simulation starts near Kearny, New Jersey, where the train including chlorine tankers travels near the main NEC line. Traveling at 5 miles/hour with low wind speed, a rail car begins to leak chlorine at 10 kg per second. Stage 1 of the hazard events is a small plume at 10 minutes, with a high dose near the train. The results obtained for the next 90 minutes are described below. The simulation evolves in 194 stages of the plume’s movement into the air as the train heads southwest along the NEC with the lethal dose attenuating over time.
Several frames are shown below to illustrate the results.
3.3. Regional Economic Impact Simulation Model
Regional economic impact tools estimate the economic consequences of hazard events and follow the ripples of the events through the regional economy, that is, beyond the local area where the event originates.(26–34) People see the immediate impacts of a bridge collapse, an accident, and derailment. They may not see other impacts, at least not immediately. A serious prolonged rail-related disruption would lead some people to be late to work and/or lose sleep and time at home. Some would drive to work, increasing traffic congestion, and even potentially leading to local gasoline price increases. A prolonged event would add pressure on the capacity of other mass transit options and highways. Some people may not be able to get to work, and some freight may not be delivered or be shifted to other modes. If the flow of supplies is disrupted because the same rail network carries freight, then products in commerce will decrease. If the problem lingers, workers will be furloughed and reduce consumption, especially of items that they can defer. Government tax collections would drop because of business losses and consequent reductions in worker earnings. And most important, business owners could choose to relocate their businesses.
In this demonstration, we used an econometric model because we wanted to show the cumulative results annually over time beginning with an event date. We also built a computable general equilibrium model, but results are not presented here because the model was not yet sufficiently developed to model the scenarios we developed.
Econometric simulation models have a long history. Analysts gather data that link historical relationships among gross national product, consumer spending, labor, and other key elements of the economy. Our model links an updated econometric model of the State of New Jersey to an econometric model of the New York City region built for this application. The New York Region is comprised of 10 counties in southern New York State: the five counties (boroughs) in New York City and five other counties to the east and northeast of New York City. This area is within commuting distance of New Jersey and would be affected if, for some reason, a transportation hub in New Jersey were to suspend operations for a significant time period. Quarterly data are used in the model and extend, for the most part, from 1990 to 2010.
The heart of the model is the industry sector—particularly employment. Employment in an industry is modeled as depending on U.S. employment in the sector, output in the sector, the earnings rate, and other important factors (for example, the mortgage rate in the construction sector). Output in an industry depends on sector prices (deflators), and some indicator of demand (for example, U.S. output, or regional income or population). The earnings rate in an industry depends on U.S. wage rates in the sector as well as some indication of labor market conditions. Finally, sectoral prices depend on earnings rates, U.S. sectoral wholesale prices or deflators, or the ratio of the regional to the national CPI.
The New Jersey model includes 210 stochastic equations as well as 58 identities. (The New York Metro Model is smaller.) The sectors included in the model are: employment and gross state product for 40 industries, wage rates and price deflators for major industries, consumer price index (New Jersey), personal income and its components, population, labor force and unemployment, housing permits and construction contracts, energy prices and usage, motor vehicle registrations, and state tax revenues by type of tax, and current and capital expenditures.
We assume that the New Jersey and New York regions are primarily connected through a shared workforce for some particular industries as well as shared media, culture, and history. The specific industries we linked to employment are construction, finance, information, manufacturing, wholesale trade, and professional and business services. Generally rising employment in these industries in one region is related to rising employment in the other region. Further, rising total workplace employment in one is related to rising household employment in both. There is also a positive and direct link between the residence adjustment in New Jersey and that in New York as well as indirect links in the residence adjustments in the two areas through household employment. Finally, there is a direct link between the Consumer Price Index (CPI) for NY-NJ-CT with the CPI for New Jersey.
Given these connections, major disruptions to New Jersey’s economy should also have an impact on New York, although to a smaller extent. Thus, using this model we should be able to gauge the impact of a disruption in New Jersey and the larger region as well. The major limitation of econometric models is that the historical relationships may produce misleading results if the economy is rapidly changing.
Disruption of rail transit in the study area would increase usage of New Jersey’s road infrastructure, causing congestion on freeways, motorways, arterials, and surface streets between the homes and workplaces of former rail commuters. We would expect that all commuters’ travel times, not just those of rail commuters, would rise due to the increased demand on the roadway network.(35–37) This is because traffic slowdowns and accident frequencies rise as roads exceed their capacities. In the short run, this increase in travel time would leave commuters three possible options: work from home, reduce their leisure time, or reduce work hours. In the longer run, however, they can change jobs.
For the most part, however, heightened congestion is likely to have a negative impact on productivity. Individuals are likely to become increasingly fatigued at their workplace due to declines in leisure activities, or they will wind up spending less time in the workplace, essentially counting time in transit as work hours. Some companies would adjust work hours to accommodate the situation in ways that would minimize travel time.
4. RESULTS
4.1. Preliminary Results
Before illustrating the results for two low probability and high consequence events (bridge failure and air pollution), we summarize the preliminary results. The first runs made with the rail system and regional economic simulation models tested the system by creating a one-hour delay, once a week; then a one-hour delay twice a week; and then loss of service for a week. No health impacts were assumed as part of these. The first simulation was barely noticed by the economic models, the second two showed progressively larger results that nevertheless would be swallowed in this massive economic region.
Table VI shows the baseline econometric simulations. We show the actual data for 2001, 2005, and 2010, then simulations for 2012, 2016, and 2020. The reader will see that the New York part of the region suffered less during the recession and is expected to continue to perform slightly better than New Jersey through the year 2020. For some applications it is appropriate to review the simulation results of all of these indicators. However, we have concentrated on two key ones for this article: nonagricultural employment, and real gross domestic product. In other words, all of the comparisons that follow will compare these forecasted results and the postevent results.
Table VI.
Baseline Economic Simulation Results
| Area and Metric | Year 2001 | 2005 | 2010 | 2012 | 2016 | Year 2020 | Annual % Change, 2010–2020 |
|---|---|---|---|---|---|---|---|
| New Jersey | |||||||
| Nonagricultural Employment (000) | 3,996.9 | 4,038.9 | 3,854.1 | 3,923.7 | 4,088.5 | 4,181.3 | 0.8 |
| Unemployment Rate,% | 4.3 | 4.5 | 9.4 | 7.2 | 5.0 | 5.0 | −6.2 |
| Population (000) | 8,451.4 | 8,601.0 | 8,791.9 | 8,880.5 | 9,049.7 | 9,192.2 | 0.4 |
| Personal Income ($bill) | 336.6 | 379.7 | 450.4 | 482.0 | 565.3 | 672.8 | 4.1 |
| Wage Rate ($000) | 44.3 | 49.5 | 56.6 | 59.5 | 65.7 | 73.5 | 2.7 |
| Real Gross Domestic Product (2005 = 100,$bill) | 402.0 | 430.0 | 438.7 | 459.6 | 504.5 | 560.3 | 2.5 |
| Consumer Price Index NJ (1982 = 100) | 184.1 | 208.4 | 234.1 | 242.1 | 255.7 | 278.8 | 1.8 |
| New York Region (10 Counties)a | |||||||
| Nonagricultural Employment (000) | 5,160.8 | 5,114.3 | 5,169.5 | 5,265.7 | 5,658.8 | 5,951.7 | 1.4 |
| Unemployment Rate,% | 5.1 | 5.1 | 8.8 | 5.5 | 6.3 | 5.6 | −4.5 |
| Population (000) | 12,096.3 | 12,213.2 | 12,368.5 | 12,429.5 | 12,641.3 | 12,969.1 | 0.5 |
| Personal Income ($bill) | 486.6 | 555.2 | 668.4 | 716.7 | 823.5 | 966.5 | 3.8 |
| Wage Rate ($000) | 54.9 | 61.2 | 70.8 | 68.4 | 85.4 | 103.7 | 3.9 |
| Real Gross Domestic Product (2005 = 100,$bill) | 705.3 | 715.7 | 778.9 | 816.8 | 858.4 | 942.7 | 1.9 |
| Consumer Price Index NY (1982 = 100) | 187.1 | 212.7 | 240.9 | 250.8 | 268.5 | 296.8 | 2.1 |
New York City, Westchester, Rockland, Putnam, Nassau, Suffolk.
4.2. Major Event: Loss of Major Bridge for a Year
A major catastrophic event would be loss of one of the main bridges between NPS and New York City. Over 100 million passenger rides that pass through NPS would be disrupted by loss of a major asset that could not be replaced for a year. The Dock Bridge, lying just north of NPS, is a key rail asset that we figuratively disabled for this illustration.
The region and the United States as a whole could not afford to lose these kinds of major assets, even if there were no injuries or deaths. We ran multiple economic simulations to test plausible options. Of these, the last, we think, is most likely. Our first assumption is that there will be efforts to provide resilience to the system. It is inconceivable that Amtrak and NJT would not respond. Hence, the first set of analyses assume that the railroads and the local governments provide a shuttle service from the NPS to the PATH rail line in Harrison, New Jersey and to Broad Street station in Newark that goes around the Dock Street bridge failure. This plausible solution, however, is not without complications. The most obvious is the need to provide carefully supervised boarding and deboarding from NPS to buses (assuming their availability, which is not certain at all hours) that would travel to Harrison. Indeed, this is not a long distance. However, as riders of this system and other rail systems know, there will be substantial crowding, frustrated people, equipment limitations, aggravating weather conditions, and other circumstances that will slow down the transfer of the riders. It is reasonable to expect that the average trip would be delayed one hour in both directions, that is, a total of two hours a day. A much better result is that the delay would only be one-half hour in each direction—or a total delay of one hour. These were the first two simulations of this low probability and high consequence bridge failure. A key missing piece of this first scenario is our assumption that no one who runs a business or works in one decides to leave the region as a result of this disruption.
A more probable resilience option based on discussions with staff is that only 40% are willing to accept a one hour per day delay, another 40% drive in their autos or take buses, and the remaining 20% telecommute (aircraft are not considered in these simulations). Again, these simulations assume that no one who operates or works in a business leaves the region over this event. The issue is the impact on road congestion, which adds to the commute time and/or cuts into leisure time for those who drive.
The fourth and last result is by far the most painful and likely the most realistic behavioral response. It is the first option (two hour a day delay) with one-third of the job losses associated with the event not replaced in the region and the economic impact of those loses beginning to accumulate. That is, businesses in the area permanently relocate their activity outside of the study area.
No one knows how many jobs would permanently be lost. However, following the events on 9/11 at New York’s World Trade Center over 100,000 jobs were lost.(38) The Fiscal Policy Institute reported that most of these had relocated elsewhere in New York City, but that 22,000 relocated outside New York City, principally in New Jersey.
Before reviewing these simulation results, a context is in order. This is a large economic region with over 21 million people, 9million jobs, and a real gross domestic product of $1.3 trillion in 2005 dollars. Because this region is so massive and multifaceted, it has enormous capacity to adjust to negative events, whether they are natural hazards, human-initiated problems, financial miscalculations, and others. A region like NJ-NYMR has the ability to absorb major events, especially over time, unlike many others.(39) One of the strengths of econometric models is that they play out the event while at the same time continuing regional economic growth. Internally, as in this case, an initial economic blow is delivered but unless it is accompanied by decisions that permanently remove economic activity from the region, the region rebounds. In this set of simulations, we caused the event to occur in the year 2012. Gradually, the national and regional economies grow, and the impact is absorbed, unless there is a major permanent loss of jobs caused by decisions that the region is no longer viable. Readers will observe this in these results (Table VII).
Table VII.
Comparison of Baseline Economic Results and Impacted Results: Full Year Loss of Major Bridge Asset
| Region and Metric | 2010 | 2012 | 2020 | Difference Between Baseline and Impacted, 2010–2020 |
|---|---|---|---|---|
| Baseline | ||||
| New Jersey | ||||
| Nonagricultural employment (000) | 3,854.1 | 3,923.7 | 4,181.3 | – |
| Real gross domestic product (2005 = 100,$bill) | 438.7 | 459.6 | 560.3 | – |
| New York region | ||||
| Nonagricultural employment (000) | 5,169.5 | 5,265.7 | 5,951.7 | – |
| Real gross domestic product (2005 = 100,$bill) | 778.9 | 816.8 | 942.7 | – |
| Impacted, Limited Resilence, 2-Hour Delay per Day | ||||
| New Jersey | ||||
| Nonagricultural employment (000) | 3,854.1 | 3,899.0 | 4,175.6 | −5.7 |
| Real gross domestic product (2005 = 100,$bill) | 438.7 | 459.2 | 558.9 | −1.4 |
| New York | ||||
| Nonagricultural employment (000) | 5,169.5 | 5,257.0 | 5,947.7 | −4.0 |
| Real gross domestic product (2005 = 100,$bill) | 778.9 | 815.8 | 941.7 | −1.0 |
| Impacted, Resilience, 1-Hour Delay per Day | ||||
| New Jersey | ||||
| Nonagricultural employment (000) | 3,854.1 | 3,910.7 | 4,179.4 | −1.9 |
| Real gross domestic product (2005 = 100,$bill) | 438.7 | 459.2 | 559.1 | −1.2 |
| New York | ||||
| Nonagricultural employment (000) | 5,169.5 | 5,261.3 | 5,948.5 | −3.2 |
| Real gross domestic product (2005 = 100,$bill) | 778.9 | 816.2 | 941.9 | −0.8 |
| Impacted, Resilience, 1-Hour Delay (40%), Shift to Auto and Bus (40%), and Shift to Telecommute (20%) | ||||
| New Jersey | ||||
| Nonagricultural employment (000) | 3,854.1 | 3,903.7 | 4,177.1 | −6.2 |
| Real gross domestic product (2005 = 100,$bill) | 438.7 | 459.2 | 559.0 | −1.3 |
| New York | ||||
| Nonagricultural employment (000) | 5,169.5 | 5,258.7 | 5,948.0 | −3.7 |
| Real gross domestic product (2005 = 100,$bill) | 778.9 | 816.0 | 941.8 | −0.9 |
| Impacted, 2-Hour Delay, and Partial Replacement of Job Losses | ||||
| New Jersey | ||||
| Nonagricultural employment (000) | 3,854.1 | 3,899.0 | 4,151.7 | −29.6 |
| Real gross domestic product (2005 = 100,$bill) | 438.7 | 459.2 | 558.6 | −1.7 |
| New York | ||||
| Nonagricultural employment (000) | 5,169.5 | 5,257.0 | 5,940.6 | −11.1 |
| Real gross domestic product (2005 = 100,$bill) | 778.9 | 815.8 | 940.8 | −1.9 |
With this context, the two-hour delay with resilience shows job and GDP losses by 2013. By the year 2020, the economy has come back. But about 10,000 jobs are lost by 2020. New Jersey, where the event occurs, is disproportionately impacted. Assuming decision makers feel that the problem would be fixed and commuters could tolerate the loss of time for a year, the impact in a region of this size is relatively modest. It becomes even more modest if the time loss were cut from two hours to one hour. The job loss drops to 5,100 and the GDP loss is reduced.
Resilience is a positive attribute, but it is not without negative consequences. Our 40%-40%-20% resilient solution produces some predictable results. If 20% of the loss can be replaced by telecommuting, that results in no job loss for one-fifth of the commuters, which is perhaps an optimistic assumption. The one-hour loss of time because the rail system is able to transfer people to another rail option is a constructive response and as just discussed does cut the negative impact. The third “resilient” alternative is a problem, which is people get into their cars and a few take buses to work. The congestion impact is felt by everyone else on those already busy roads. Adding thousands more vehicles to the bridges and tunnels that link New York and New Jersey is a serious problem. The job loss, even taking into account the telecommuting and reducing the delay on rail to one hour, is higher than the two-hour delay scenario because so many people are delayed by road congestion.
The last scenario is the one we believe is the most likely for an event that lasted for a year without a clear ending date. Some decision makers would figure out ways to provide temporary housing for their employees and shuttles. But others would not have the patience or the budget. We assume for purposes of this simulation that among those who are losing productivity, one-third would choose to leave the area. The job loss estimate compared to the baseline is 41,000, of which three-fourths are in New Jersey.
4.3. Major Event 2: Chlorine Leak
One of the four chlorine leak scenarios was chosen as an illustration because it shows how the rail corridor and plume models can be used together to characterize a plausible situation. The chlorine leak starts near an actual chlorine manufacturing facility and the plume follows the train carrying the chlorine south and west. The plume covers NPS, the PATH station in Harrison, and then part of the New Jersey Turnpike and Interstate 78, touching the edge of Newark Liberty International Airport and approaching the city of Elizabeth 90 minutes later. We recognize that the scenario is very low probability, given leak detection systems; however, it is plausible and realistic (see discussion below).
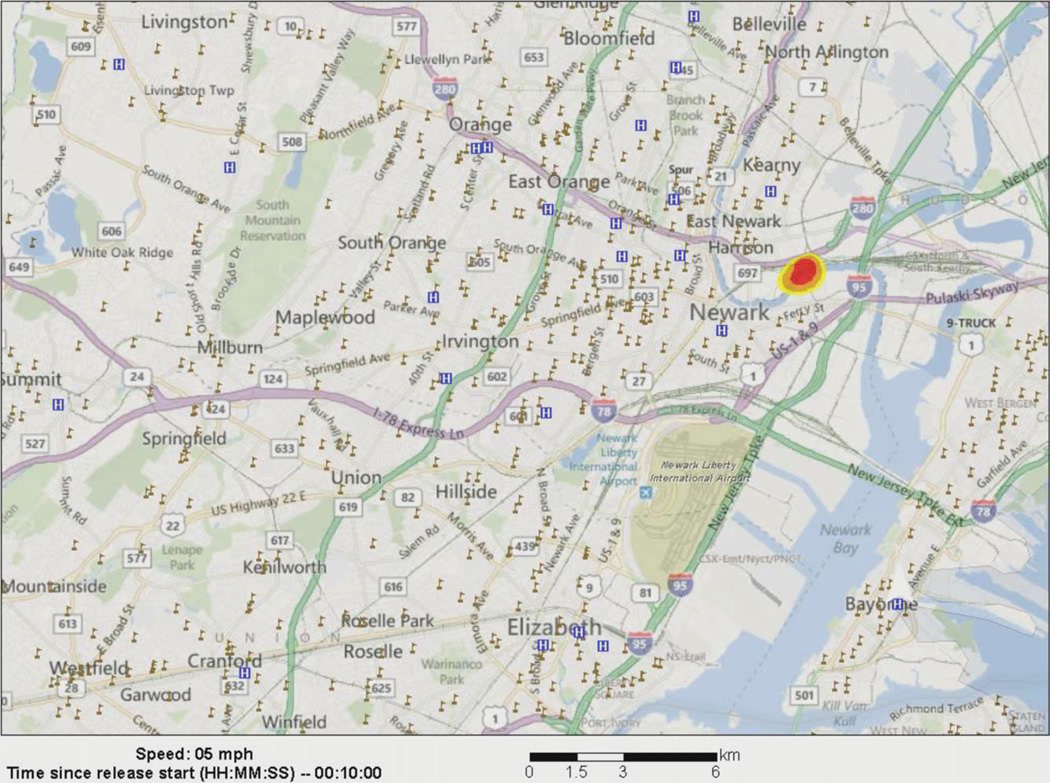
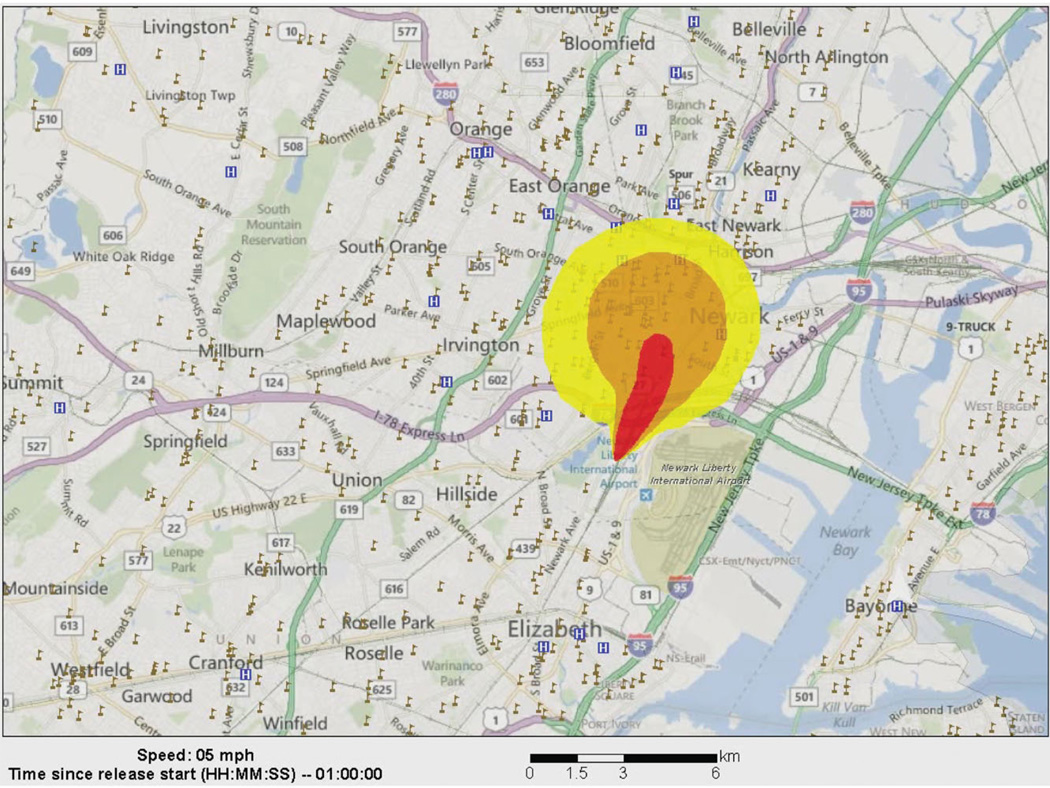
With that caveat in order, Fig. 4 shows three of the 194 exposure frames. The first occurs within 10 minutes of the event, and the lethal area occupies most of the small and growing plume. At 30 minutes, the plume has spread and is moving along with the train. The reader can see that the train is heading southwest and is over the Newark rail station and part of downtown Newark. The third frame is an estimate of the plume at one hour. Assuming no intervention, the plume is now dispersing and the lethal zone is following the rail line. Economic damage would be associated with deaths and injuries. Some might die, and others might be severely injured. The plume would temporarily disrupt rail service and the surrounding communities. Even after the event concluded and evacuees return to their homes and jobs, there likely would be some level of economic stigma for at least a short time.
Fig. 4.
Three frames from air pollution event simulation.
In order to portray some of the health and physical damage, we mapped all 194 frames over the 90-minute event that showed the distribution of the plume on top of the census areas below the plume. The census data are from the year 2010. We gathered resident population, population that is African American and Latino, persons employed in the units, housing units and their value, and individuals in trains and on train platforms covered by the plume estimated by the rail model. We also determined the number of schools and hospitals in the area.
Several important caveats are in order. The plume is created by the model, and the plume concentrations are a simulation. As noted above, the concentrations are based on emptying a single tank at 10 kilograms per second. The numbers must not be taken at face value. Location in the red zone is not a death sentence. The risk is higher at the beginning of the event and as the train and plume head southwest, the concentration of chlorine in the red zone decreases as does the likelihood of a chlorine-caused fatality. Being indoors with closed windows will help, and immediately alerting people not to run outside would reduce the risk.
For purposes of the demonstration, we focus on people in the red zone. We counted the number of people who live in the red zone and everyone who was as NPS, the Harrison PATH station, Grove Street, and Broad Street estimated by the rail model. This number is 13,000 people at the train stations, as the event evolves during morning rush hour, and another 36,000 people living in the surrounding residential areas. Notably, 75% of the residents are African American and Latino compared to 31% in the State of New Jersey as a whole (Table VIII).
Table VIII.
Demographic Characteristics of Most Exposed People (Red Zone)
| Group and Attributes | Red (High) Exposure Zone (%)a |
|---|---|
| Total Resident Population, 2010 | 36,079 |
| African-American Resident Population, 2010 | 13,991 (38.8%) |
| Hispanic Resident Population, 2010 | 13,602 (37.7%) |
| Commuters on Trains and at Stations, During First 30 Minutes of the Event, Newark Penn Station, PATH, Broad Street, Grove Street, Harrison (Estimated by Rail Simulation Model)a | 13,123 |
| Hospitals | 0 |
| Schools | 15 |
| Total Included in Red Zone Exposed Calculations | 49,202 |
Assumption is that security personnel stop access to the stations at 30 minutes, so that exposure of rail passengers does not continue for 90 minutes.
In order to understand the health impacts of the event, we spoke with three public health colleagues at our universities (two physicians and an epidemiologist); all have experience with these chemical events. We also spoke with researchers from the U.S. Army and U.S. DHS who have experience with chlorine and have worked on chlorine risk assessments.
Based on these discussions and our own research, we constructed two scenarios. The first, called “less impact,” assumes that 1%, or 500 people, would die as a result of the exposure and another 10% would be injured (5,000). Of those injured, half would return to work in three days (2,500), 25% in two weeks (1,250), and 25% would suffer permanent injury and not be able to return to work (1,250). The relatively low number of people who die and are injured is based on the assumption that the vast majority of people are inside buildings and cars. The second scenario, the “more impact” version, assumes that 5% would die (2,500), and that 20% would be injured (10,000). Of those injured, 25% would return to work in three days (2,500), another 50% would return to work in two weeks (5,000), and 25% would be permanently disabled (2,500). In reality, both scenarios probably underestimate what would happen. A major issue in this scenario is that a large number of people would be outdoors on platforms and while people often evacuate in an orderly fashion, the nature of this event is such that orderly evacuation will be a challenge because of the limited number of exits from the platforms and the likelihood that some individuals will panic causing the entrances to block and further injuries. Furthermore, access to individuals who have been injured in the street will be difficult, but will be much more difficult for those at the train station. These are crowded (this event assumes that we begin during rush hour at 7:30 AM) and it would be extremely difficult for rescue personnel to gain access to all of the people who have been exposed and to have a sufficient amount of equipment to prevent the injuries, even if they do have access. Also, while we would expect people to stay inside, many might not. In short, our two scenarios may understate the health consequences to the affected population.
There is one hospital in the red zone and 15 schools. In order to avoid double-counting children and school employees, we have not counted any of them in the red zone calculations. Nor have we included the people who do not live in the area who would be in buses or automobiles passing through. We have not included employees, and assumed that there are no recreational events at other local facilities. By starting the event at 7:30 AM and trying to avoid any double-counting, the 50,000 estimated to be in the red zone (actual simulation was 49,000) is likely an underestimate.
Being located in the orange and yellow exposure zones implies less exposure; however, it does not mean that some exposed individuals would not be injured. The outcomes would range from overstimulation of their cardiovascular system to mild irritation. Furthermore, there might be indirect health impacts caused by auto accidents, exhaustion on the part of medical teams, and other health-related consequences. Consequently, while we estimated the number of people in each of the three zones at over 1 million, with billions of dollars of property also in this area, the public health and economic results at this stage for the orange and yellow zones were not pursued (interested readers should review the larger report from which this article was constructed).
5. DISCUSSION
We built a simulation model that allows us to replicate the passenger operations of a 60-mile segment of the NEC between Trenton, New Jersey and New York, Penn Station. We also built a plume model that allows analysts to simulate dispersion of contaminants over a large geographical region, adjusting for wind direction, terrain, and other variables. (Other environmental event scenarios were discussed but are not presented here.) Our econometric model allows time series economic impact estimates of low probability high consequence events associated with a bridge failure for one year and a chlorine exposure event. None of the results are to be taken at face value, yet they clearly illustrate two major vulnerabilities along the NEC that can be addressed with prevention and resilience, respectively.
The hypothetical chlorine events can be prevented by shipping the chlorine in solid form, rather than in liquid form, by closing the rupture as soon as it is noticed, which is enhanced by automatic sensors if they work, and by altering transport routes to bypass large population zones. Even if the event occurs, health effects can be minimized by rapid evacuation, although sheltering in place would likely be recommended by public health authorities. Notably, there have been two incidents with rail cars carrying chlorine in this area during the last few years. Neither resulted in a serious problem, and the last of these was on April 4, 2011 when the authors were working on incidents to simulate.
While this is a low probability event, it most certainly is not implausible, and indeed we could have made it much more severe, which is one of the reasons the chemical industry, including the chlorine industry, has developed its own rail transportation safety plans,(40) and why this particular region of the NEC has merited so much attention from the New Jersey Office of Homeland Security and Preparedness.(41)
Regarding the simulated bridge failure, a total of 41,000 jobs lost in a region with 10 million do not seem like much, only 0.4%, but in an era when the unemployment rate is over 9% and we expect it to be 5% by 2020, which may be an optimistic baseline forecast, these jobs would be noticed. But is this a major loss? For context, New Jersey lost 114,000 jobs from December 2007 through December 2008, which makes this loss measured over almost a decade seem small. Our event, a single bridge failure, is virtually preventable by the owners and operators of the bridge in question. Furthermore, we deliberately picked one of the simplest problems to overcome by shuttling people a short distance. There are other bridge and road failures in this region that would be harder to work around. If this were a terrorist attack, for example, we could anticipate attempts to damage multiple links in the rail system and highways system, which would be extraordinarily difficult to overcome without a substantial investment. In short, in contrast to other rail disruption events we could have tested, this one is relatively modest, albeit painful. Again, however, we reiterate that economic simulation models depend upon assumptions, and in this case these results are assuming the U.S. economy and within it the NJ-NY Metro Region will be growing at a steady rate. For example, the NJ unemployment rate is assumed to be 5% by 2016.
This effort has limitations and offers opportunities to advance science and organizational capacity. The major scientific limitations are in two areas. One is in population at risk. For example, regarding the chlorine event, in order to obtain reliable exposure estimates, it is imperative that we disentangle the daytime population who work in the area from the resident population to avoid double-counting or even triple-counting in the case of those who took the light rail, deboarded at the train station, and worked in a local building. To be more precise about the number of people impacted, we would also need to know how many people were employed in, admitted or, attending the local hospitals, the colleges and universities, and schools in the area. Modeling the human health consequences outside of the red zone necessitates considerably more data and interaction with officials than has been possible to date. We would also need to add equations in the model that allow us to measure feedbacks between these events and property values, sales, loss of taxes, and other relationships. All of this is feasible, but was not available without additional effort. In short, to simulate further consequences and risk management options for the orange and yellow zones was too speculative without better information.
The second point of science regards stigma effects. Prager et al.(42) studied the impact of the July 2005 London underground subway bombings. Estimated passenger journeys decreased by an average of 8.3% for the four months following the terrorist attacks. Passenger trips returned to predicted levels, but the authors suggest that there may have been a smaller effect for nine more months, that is, for over a year. The London events were caused by a terrorist attack and our simulated case was not. But it could have been, and created fear and a stigma effect. Indeed, it certainly would be plausible to create a combination of terrorist events involving chemical plume releases, bridge and station attacks that would leave the region with a more serious problem than the one we used for our illustration.
By far, organizational limitations and opportunities exceed scientific ones. When we developed the three models, we had assumptions about what users would require to operate them. At a minimum, they would need masters-level trained experts in systems engineering, physics/atmospheric chemistry, and econometrics/regional economic modeling on staff. These staff would direct other staff to update the databases. And these experts would need direct access to the managers who would direct the applications and help make them useful and comprehensible for top managers.
After presenting all or portions of this work to groups of from 1 to 200+ people for periods ranging from 15 minutes to two hours, we recognize that our original plan of working closely with a user community with its own staff was optimistic. This specific user community is financially stressed, and it is unrealistic to assume that it will be able to assume much of the responsibility for the work. Specifically, with regard to the economic models, they can envision a consulting arrangement. They do not see how they can dedicate staff to updating this model or any of the others (CGE, versions of input output).(26–34) This message was confirmed by experts in DHS/DOD who had been developing health cost elements for their simulation models and had to discontinue the economic elements because of budget constraints. Ideally, the economic analysis work would be embraced by a multiagency task force that could share the work and responsibility, but we have no evidence that such a task force will emerge.
With regard to the bridge failure scenario, users feel that they can use what we have already provided them, perhaps with a few modest changes, to reconsider their resilience plan, and they understand how similar analyses for other bridges and key structures would be valuable. Their resources, however, for such an effort are limited. The air pollution simulation model and implications it raises are viewed as not the responsibility of a passenger rail system, but rather of the freight rail systems and emergency response groups in government. They would not object to cooperating in an effort to take this model and try out a variety of air pollution events as part of a larger group that deals with response to emergencies in training exercises. But the expertise and responsibility for using the model should not primarily sit with a rail passenger system.
The rail systems model is viewed as a potentially valuable tool for routine planning, as well as for emergency response, and we feel that this approach will be pursued by one or more rail systems. The amount of feedback we received on the rail systems model suggests considerable interest. One user suggested that if they were going to update the data, they would need us to add an interface on how to enter the data. Another pair of potential users have been talking about using this approach to monitor passenger flow within major train stations and then linking that model to the rail systems model. Another potential user showed us the spreadsheet that he uses when there is a failure in the system. He felt that the rail simulation model would allow him to prepare much more detailed plans than currently possible. He showed his immediate supervisor where this model could be placed in the command and control center. A senior manager conceived of using the rail model in concert with the economic model to help assess the advantages and disadvantages of alternative security investments as part of larger capital plans. The most senior manager we spoke with spent twice as much time with us as had been allocated on his schedule, and left with a set of notes and ideas.
These positive experiences demonstrate that using simulation models can engender creative thinking that ranges from new ideas of how to address an existing problem to thinking beyond the current objectives of the organization. The simulations spur management into thinking about consequences and potential implications that follow, including problems that they perhaps would prefer to avoid confronting. It is realistically possible to run numerous analyses that capture the key components of risk analysis and combine the skills of decision makers and researchers. The immediate challenge is to determine the ways of incorporating the models into routine planning so that potential users do not view them as distinct from their normal planning functions. During this decade, we expect to see many more efforts to connect simulation tools and multidisciplinary teams in order to engage in proactive planning exercises on behalf of parties responsible for managing vulnerable systems.
Table III.
Validation Results, Illustrative Times Between Stations, Minutesa
| Train and Direction | Simulation | Real Data | Relative Error |
|---|---|---|---|
| EB Northeast Corridor | 28.28 | 28 | 0.0088 |
| WB Northeast Corridor | 30.55 | 30 | 0.0075 |
| EB North Jersey Coast | 28.50 | 28 | 0.0136 |
| WB North Jersey Coast | 28.34 | 28 | 0.0040 |
| EB Raritan Valley | 17.60 | 17 | 0.0074 |
These five cases are illustrative of the 46.
ACKNOWLEDGMENTS
The authors would like to thank the U.S. Department of Homeland Security’s Science and Technology Directorate for funding the exploration of these issues through the National Transportation Security Centers of Excellence. In particular, the authors appreciate the encouragement of Georgia Harrigan, DHS program officer. We also thank the Construction Engineering Research Laboratory (CERL) of the U.S. Department of Defense for supporting this project, Rail Transportation/Transit Disaster Preparedness and Response Involving Modeling and Characterization of Hazards and Exposures, Project # 10 01 F; Grant #W9132T-10-1-0001 P00002. The opinions, findings, conclusions, and recommendations expressed herein are those of the authors and do not necessarily represent the views of the Department of Homeland Security or CERL.
REFERENCES
- 1.Obama B. Remarks by the President in the State of the Union Address, January 27, 2010. [Accessed April 11, 2011]; Available at: www.whitehouse.gov/the-press-office/remarks-president-state-union-address.html.
- 2.Federal Railroad Administration, U.S. Department of Transportation. Vision for High-Speed Rail in America: High-Speed Rail Strategic Plan. 2009
- 3.US High Speed Rail Association. 21st Century Transportation for America, 2011. [Accessed April 8, 2011]; Available at: www.ushsr.com/hsrnetwork.html.
- 4.Kaplan S, Garrick BJ. On the quantitative definition of risk. Risk Analysis. 1981;1(1):11–27. doi: 10.1111/0272-4332.215153. [DOI] [PubMed] [Google Scholar]
- 5.Greenberg M, Haas C, Cox A, Jr, Lowrie K, McComas K, North W. Ten most important accomplishments in risk analysis, 1980–2010. Risk Analysis. 2012;32(5):771–781. doi: 10.1111/j.1539-6924.2012.01817.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Leung M, Lambert J, Mosenthal A. A risk-based approach to setting priorities in protecting bridges against terrorist attacks. Risk Analysis. 2004;24(4):963–984. doi: 10.1111/j.0272-4332.2004.00500.x. [DOI] [PubMed] [Google Scholar]
- 7.Bier V. Choosing what to protect. Risk Analysis. 2007;27(3):607–620. doi: 10.1111/j.1539-6924.2007.00906.x. [DOI] [PubMed] [Google Scholar]
- 8.Li H, Apostolakis G, Gifun J, VaSchalkwyk W, Leite S, Barber D. Ranking the risks from multiple hazards in a small community. Risk Analysis. 2009;29(3):438–456. doi: 10.1111/j.1539-6924.2008.01164.x. [DOI] [PubMed] [Google Scholar]
- 9.Rose A. Defining and measuring economic resilience to disasters. Disaster Prevention and Management. 2004;13(4):307–314. [Google Scholar]
- 10.Rossoff H, von Winderfeldt D. A risk and economic analysis of dirty bomb attack on the ports of Los Angeles and Long Beach. Risk Analysis. 2007;27(3):533–546. doi: 10.1111/j.1539-6924.2007.00908.x. [DOI] [PubMed] [Google Scholar]
- 11.Cox LA., Jr Improving risk-based decision-making for terrorism applications. Risk Analysis. 2009;29(3):336–341. doi: 10.1111/j.1539-6924.2009.01206.x. [DOI] [PubMed] [Google Scholar]
- 12.Greenberg M, Lowrie K, Mayer H, Altiok T. Risk-based decision support tools: Protecting rail-centered transit corridors from cascading effects. Risk Analysis. 2011;31(12):1849–1858. doi: 10.1111/j.1539-6924.2011.01627.x. [DOI] [PubMed] [Google Scholar]
- 13.Altiok T, Melamed B. Simulation Modeling and Analysis with ARENA. Burlington, MA: Elsevier; 2007. [Google Scholar]
- 14.Rossetti M. Simulation Modeling with ARENA. Hoboken, NJ: Wiley; 2010. [Google Scholar]
- 15.Federal Railroad Administration, Office of Safety. Norfork Southern (NS), Graniteville, South Carolina, January 6, 2005. [Accessed June 20, 2012]; Available at: www.ntsb.gov/investigations/summary/RAR0504.html.
- 16.Sykes R, Cerasoli C, Henn D. The representation of dynamic flow effects in a Lagrangian puff dispersion model. Journal of Hazardous Material. 1999;64:223–247. [Google Scholar]
- 17.Sykes R, Gabruk R. A second-order closure model for the effect of averaging time on turbulent plume dispersion. Journal of Applied Meteorology. 1997;36:165–184. [Google Scholar]
- 18.DTRA. Hazard Prediction and Assessment Capability (HPAC) User Guide Version 4.0.3. San Diego, CA: Prepared for Defense Threat Reduction Agency (DTRA) by Science Applications International Corporation; 2003. [Google Scholar]
- 19.Allwine K, Shinn J, Streit G, Clawson K, Brown M. Overview of urban 2000. Bulletin of the American Meteorological Society. 2002;83(4):521–536. [Google Scholar]
- 20.Chang JC, Hanna SR, et al. Use of Salt Lake City URBAN 2000 field data to evaluate the urban hazard prediction assessment capability (HPAC) dispersion model. Journal of Applied Meteorology. 2005;44(4):485–501. [Google Scholar]
- 21.Warner S, Platt N, Heagy J. Comparisons of transport and dispersion model predictions of the joint urban 2003 field experiment. Journal of Applied Meteorology and Climatology. 2008;47(7):1910–1928. [Google Scholar]
- 22.Urban JT, Warner S, Platt N, Heagy J. Assessment of HPAC urban modelling capabilities using data from the Joint Urban 2003 field experiment. International. Journal of Environment and Pollution. 2011;44(1–4):24–31. [Google Scholar]
- 23.NRC. Standing Operating Procedures for Developing Acute Exposure Guideline Levels for Hazardous Chemicals. Washington, DC: Subcommittee on Acute Exposure Guideline Levels, Committee on Toxicology, Board on Environmental Studies and Toxicology, Commission on Life Sciences, National Research Council; 2001. [Google Scholar]
- 24.NRC. Acute Exposure Guideline Levels for Selected Airborne Chemicals, Vol. 4. Washington, DC: National Academy Press; 2004. [Google Scholar]
- 25.Hauschild V. Current issues hindering update of tg230a and finalization of tg230B—Better defining hazard severity. Deployment Environmental Surveillance Program; 2000. [Google Scholar]
- 26.Greenberg M, Lahr M, Mantell N, Felder F. Understanding the economic costs and benefits of catastrophes and their aftermath: A review and suggestions for the federal government. Risk Analysis. 2007;27(1):83–96. doi: 10.1111/j.1539-6924.2006.00861.x. [DOI] [PubMed] [Google Scholar]
- 27.Haimes Y, Horwowitz B, Lambert J, Santos J, Lian C, Crowther K. Inoperability input–output model for interdependent infrastructure sectors. 1: Theory and methodology. Journal of Infrastructure Systems. 2005;11:67–79. [Google Scholar]
- 28.Haimes Y, Horwowitz B, Lambert J, Santos J, Crowther K, Lian C. A goofball inoperability input–output model for interdependent infrastructure sectors. 1: Case study. Journal of Infrastructure Systems. 2005;11:80–92. [Google Scholar]
- 29.Santos J, Haimes Y. Modeling the demand reduction input-output (I-0) inoperability due to terrorism. Risk Analysis. 2004;24(6):1437–1451. doi: 10.1111/j.0272-4332.2004.00540.x. [DOI] [PubMed] [Google Scholar]
- 30.Conrad K. Traffic, transportation, infrastructure and externalities: A theoretical framework for a CGE analysis. Annals of Regional Science. 1997;31:369–389. [Google Scholar]
- 31.Treyz G. Regional Economic Modeling; A Systematic Approach to Economic Forecasting and Policy Analysis. Boston, MA: Kluwer Academic Publishers; 1993. [Google Scholar]
- 32.Rose A, Liao S-Y. Understanding sources of economic resiliency to natural hazards: Modeling the behavior of lifeline service customers at the sectoral and regional levels in a CGE context. In: van der Veen A, Vetere Arellano AL, Nordik JP, editors. Search for a Common Methodology: Workshop Proceedings. Holland: Delft; 2003. pp. 137–150. [Google Scholar]
- 33.Rose A, Lim D. Business interruption losses from natural hazards: Conceptual and methodological issues in the case of the Northridge earthquake. Environmental Hazards. 2002;4:1–14. [Google Scholar]
- 34.Rose A, Benavides J, Chang S, Szczesniak P, Lim D. The regional economic impact on an earthquake: Direct and indirect effects of electricity lifeline disruptions. Journal of Regional Science. 1997;37(3):437–458. [Google Scholar]
- 35.Sohn J, Kim TJ, Hewings G, Lee JS, Jang S-G. Retrofit priority of transport network links under an earthquake. Journal of Urban Planning & Development. 2003;129(4):195–210. [Google Scholar]
- 36.Munnell A. Policy watch: Infrastructure investment and economic growth. Journal of Economic Perspectives. 1992;6(4):189–198. [Google Scholar]
- 37.Jara-Díaz S. On the relation between users’ benefits and the economic effects of transportation activities. Journal of Regional Science. 1986;26(2):379–391. [Google Scholar]
- 38.Fiscal Policy Institute. World Trade Center jobs in fact take a heavy toll on low-wage workers. [Accessed May 21, 2012];2001 Available at: www.fiscalpolicy.org November 5, 2001. [Google Scholar]
- 39.Greenberg M, Miller KT, Frisch M, Lewis D. Facing an uncertain economic future: Environmental management spending and rural regions surrounding the U.S. DOE’s nuclear weapons facilities. Defence and Peace Economics. 2003;14(1):85–97. [Google Scholar]
- 40.American Chemistry Council, CHEMTREC, the Chlorine Institute, Compressed Gas Association, National Association of Chemical Distributors. [Accessed June 24, 2012];Transportation Security Guidelines for the U.S. Chemical Industry. 2012 Available at: http://cl2.files.cms-plus.com/PDFs/trnsecurguidnce06-02.pdf.
- 41.NEC Master Plan Working Group. The Northeast Corridor Infrastructure Master Plan. [Accessed June 12, 2010];2010 May; Available at: www.Amtrak-NECMasterPlan-FinalReprot_519_2010_va1.pdf. [Google Scholar]
- 42.Prager F, Beeler Asay G, Lee B, von Winterfeldt D. Exploring reductions in London underground passenger journeys following the July 2005 bombings. Risk Analyis. 2011;31(5):773–786. doi: 10.1111/j.1539-6924.2010.01555.x. [DOI] [PubMed] [Google Scholar]