Abstract
Diffusion-weighted imaging (DWI) enables investigation of the brain microstructure by probing natural barriers to diffusion in tissues. In this work, we propose a novel generative model of the DW signal based on considerations of the tissue microstructure that gives rise to the diffusion attenuation. We consider that the DW signal can be described as the sum of a large number of individual homogeneous spin packets, each of them undergoing local 3-D Gaussian diffusion represented by a diffusion tensor. We consider that each voxel contains a number of large scale microstructural environments and describe each of them via a matrix-variate Gamma distribution of spin packets. Our novel model of DIstribution of Anisotropic MicrOstructural eNvironments in DWI (DIAMOND) is derived from first principles. It enables characterization of the extra-cellular space, of each individual white matter fascicle in each voxel and provides a novel measure of the microstructure heterogeneity. We determine the number of fascicles at each voxel with a novel model selection framework based upon the minimization of the generalization error. We evaluate our approach with numerous in-vivo experiments, with cross-testing and with pathological DW-MRI. We show that DIAMOND may provide novel biomarkers that captures the tissue integrity.
1 Introduction
Diffusion-weighted imaging (DWI) enables investigation of the brain microstructure by probing natural barriers to diffusion in tissues. Because the DWI spacial resolution is typically on the order of 6–27mm3, the measured DW signal in each voxel combines the signal arising from a variety of heterogeneous microstructural environments including multiple cell types, sizes, geometries and orientations and extra-cellular space. This is well known to give rise to an overall observed non-monoexponential decay [9,1,7,10]. Multiple models have been proposed to account for the observed non-monoexponential decay. Among them, generative models focus on modeling the biophysical mechanisms underlying the MR signal formation and are of great interest to characterize the white-matter (WM) microstructure. In this context, Assaf et al. [1] proposed in CHARMED to represent the intra-axonal diffusion with a model inspired by the analytic diffusion in impermeable cylinders, which however required b-values up to 10000s/mm2 to distinguish between multiple fascicles. Zhang et al. [10] proposed in NODDI to represent it with a spherical Watson distribution of sticks. The appropriate model for representing each compartment, however, remains an open question.
The solution may lie in considering a more detailed model of the tissue microstructure that gives rise to the diffusion attenuation. Particularly, it is likely that the observed non-monoexponential decay arises from both large scale and small scale intra-voxel heterogeneity (see Fig.1). In [9], Yablonskiy et al. proposed a statistical distribution model of the apparent diffusion coefficient (ADC) that intrinsically reflects the presence of heterogeneous micro-structural environments in each voxel. They assumed that the DW signal in a voxel can be described as a sum of signals from a large number of individual spin packets, each of them undergoing local isotropic Gaussian diffusion described by an ADC D. Originally mono-directional, this model was extended to the multi-directional case by estimation of one ADC per direction. This model, however, does not capture the anisotropic diffusion observed in the brain. It cannot characterize the restricted diffusion such as occurs in dense WM fascicles. A generalization of [9] may be achieved by representing each spin packet with a full diffusion tensor D. This, however, is analytically challenging because it implies the integration of a matrix-variate distribution of probability defined over the set of symmetric positive-definite (SPD) matrices. Basser et al. [2] proposed a normal distribution for symmetric matrices that is however not restricted to SPD matrices.
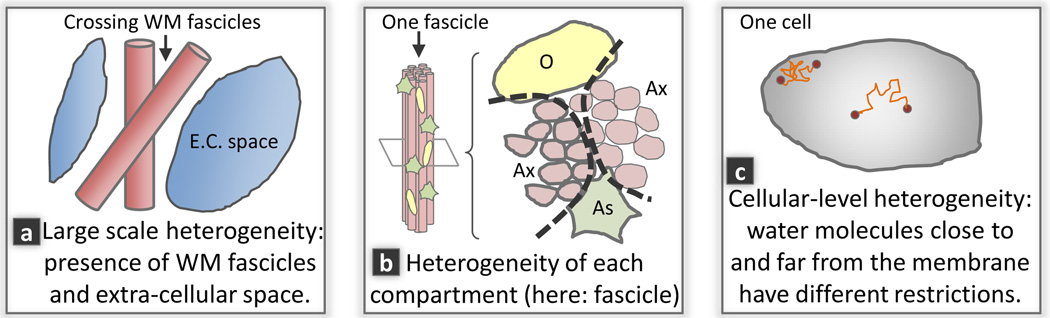
Fig. 1.
Multiple scales of intra-voxel heterogeneity are responsible for the observed non-monoexponential decay (Ax: axons with various degrees of myelination; As: Astrocyte; O: Oligodendrocyte). (a): Large scale heterogeneity includes the mixing of large scale microstructural environments (LSME) such as the mixing of multiple WM fascicles with extra-cellular space. (b): Furthermore, each LSME may contain a complex varying microstructure such as axons with varying radii and degrees of myelination. (c): At an even smaller scale, other biophysical mechanisms such as intracellular heterogeneities and the proximity of cell membranes that locally restricts motion may contribute to the signal decay behavior. For example, Sehy et al. [8] observed a non-monoexponential decay within the intracellular space of a single cell, the frog oocyte.
In contrast, a natural distribution for SPD matrices is the matrix-variate Gamma distribution, which generalizes the Wishart distribution by allowing a non-integer number of degrees of freedom. In [5], a mixture of Wishart distributions with prespecified degree of freedom was used to discretize the manifold of the fascicle orientation distribution in a spherical deconvolution (SD) approach, and was shown to successfuly capture the fascicle orientation. SD, however, relies on the definition of a prespecified convolution kernel that is assumed constant for all the brain. Therefore, variations of the fascicles microstructure (Fig.1b) are conflated with variations of the estimated mixing proportions, and SD cannot provide an indicator of the WM microstructure. Additionally, SD relies on an acquisition with a single non-zero b-value, and water molecules with very different restrictions such as water molecules in the extra-cellular space and in the intra-axonal space cannot be distinguished.
In contrast, a generative model based upon the 3-D generalization of the approach in [9] together with the acquisition of multiple non-zero b-values will enable characterization of both the WM structure and microstructure. However, unlike [5], this requires the identification of the appropriate model complexity, which is a challenging model order selection problem. In the literature, most approaches such as the Bayesian Information Criterion (BIC), the F-Test or the Bayesian Automatic Relevance Determination (ARD) focus on assessing the fitting error of each model while penalizing complex models to avoid overfitting. However, the choice of a penalization strategy and the trade-off between penalization and quality of fit are rather arbitrary and produce highly variable results. In contrast, generative models are predictive models, and a natural measure to identify the appropriate model complexity is the generalization error (GE). It describes how well a model can predict new data not included in the estimation. Typically, a model not complex enough to represent a dataset will have a large GE, and so will a too complex model so that it overfits the data. The GE, however, cannot be computed directly and must be approximated. Leave-one-out cross-validation provides an estimate with low bias but large variance, leading to high root mean squared errors [3]. K-fold cross-validation provides an estimator with lower variance but increased bias. Instead, the .632 bootstrap approach of [3] has been shown to provide low bias and low variance.
In this work, we propose a statistical distribution model of the diffusion in which we model the signal arising from each spin-packet with a 3-D diffusion tensor and the presence of multiple large scale microstructural environments in each voxel with a mixture of peak-shaped matrix-variate Gamma distribution of spin-packets. This has analytical solution and enables us to derive a novel generative model that describes the DIstribution of Anisotropic MicrOstructural eNvironments with DWI (DIAMOND). Our model is derived from first principles and allows for the representation of both unrestricted diffusion and multiple fascicles with heterogeneous orientations, while providing a novel measure of heterogeneity of the microstructure. We determine the number of fascicles at each voxel with a novel model selection framework based upon the minimization of the generalization error estimated with the bootstrap .632 approach [3,6]. We evaluate our approach with numerous in-vivo experiments, with cross-testing and with pathological DW-MRI. Importantly, we show that it may provide a novel biomarker that reflects the WM microstructure integrity.
2 Theory and Methods
A generative model of the diffusion signal
Following the ADC approach of [9], we consider that the measured signal can be described by a sum of signals arising from a large number of individual spin packets within the voxel. In contrast to [9], we consider that each spin packet undergoes homogeneous 3-D Gaussian diffusion represented by a diffusion tensor D, whose contribution for a diffusion gradient gk is : . The fraction of spin packets described by a same D in the voxel is given by a matrix-variate distribution P(D), leading to the signal generation model :
| (1) |
where is the set of 3 × 3 SPD matrices. If a voxel was composed of exactly a single homogeneous microstructural environment (ME) characterized by exactly D0, P(D) could be modeled by a matrix Dirac delta function P(D) = δ(D − D0) and our model is equivalent to DTI. If it were to contain several exactly identifiable ME, a mixture of delta functions could be used. However, it is more realistic to consider that a voxel contains multiple large-scale microstructural environments (LSME) (Fig. 1), each of them having some degree of heterogeneity.
We consider that a voxel contains N LSMEs and we model the composition of each LSME j with a matrix-variate Gamma probability distribution Ppj,Σj(D) of spin packets. Specifically, a random matrix has a matrix-variate Gamma distribution with shape parameters pj > 1 and if it has density:
| (2) |
where Γ3 is the 3-variate gamma function and | · |the matrix determinant. The distribution Ppj,Σj is a peak-shaped distribution. Its expected value is and describes here the average diffusivity of the LMSE j. The shape parameter pj determines the concentration of the distribution, the density (2) becoming more concentrated about as pj increases. This captures the microstructural heterogeneity of each LMSE j. We consider that the LSMEs are in slow exchange by considering where fj ∈ [0, 1] are the volume fractions of occupancy and sum to one, leading to:
| (3) |
The integrals in the right-hand side of (3) are Laplace transforms of Ppj,Σj (D), which have a known analytical expression [4]. This leads to the generative model:
| (4) |
Using the Taylor expansion about u = 0 it follows that: It shows that when pj → ∞ for all j, which corresponds to infinitely narrow Ppj,Σj (D)’s, our model is equivalent to the multi-tensor model. In contrast, finite values of pj captures the heterogeneity of each LMSE. Note that the decay rate decreases as the b-value increases, modeling a non-monoexponential decay.
Model order selection for generative models
We present our novel model order selection approach based on the minimization of the generalization error (GE). The model (4) is a generative model that relates input parameters xk (the diffusion sensitization direction and strength) to output measurements yk (the diffusion attenuation). Denoting by z = {z1, …, zn} with zi = (xi, yi) the set of n training data, by 𝒢z(x) the model whose parameters were estimated with z, and by z0 = (x0, y0) a new hypothetical data point, the GE conditional on the observed data is :
| (5) |
where 𝔼 [․] is the statistical expectation and z0 ~ F indicates that the expectation is taken over the new data point that follows some distribution F. To account for the variability of the observed data points, the unconditional GE can be defined as the expectation of (5) over all . We propose to estimate Eg with the .632 bootstrap approach [3]. It counter-balances the positive bias of the leave-one-out bootstrap estimate by the negative bias of the fitting error estimate , by assessing: . The 0.632 coefficient comes from that, on average, uses data point at each bootstrap iteration, which is approximately equal to 0.632 for large n. We refer to [3] for details of the expressions of and . As in [6], we first consider a model with a single compartment and then progressively increase the model complexity as long as it provides a statistically significant decrease in GE.
Methods
At each voxel, we considered one matrix-variate Gamma distribution with isotropic to model the diffusion of unrestricted water and up to 3 matrix-variate Gamma distributions with tensor to represent up to three fascicles. The .632 bootstrap model order selection was performed with B = 30 bootstrap iterations. Similarly to [7], the model parameters were estimated using a maximum a posteriori approach by considering a diffusion model with gradually increasing complexity, from the ball-and-stick model to the full DIAMOND model.
Evaluation of the benefits of DIAMOND with actual MR measurements is challenging because we cannot rely on any ground truth providing the distribution of MEs in each voxel. First, we performed an experiment to illustrate that our model captures the non-monoexponential decay. In vivo imaging was carried out on a healthy volunteer using a Siemens 3T Trio scanner with a 32 channel head coil and the following parameters : FOV=220mm, 68 slices, matrix=128 × 128, resolution=1.72 × 1.7 × 2mm3. We focused on imaging the body of the corpus callosum (see Fig.2), a region known to contain a single fascicle orientation. We measured the diffusion attenuation in both the parallel and perpendicular directions with respect to the fascicles (Fig.2i), with various b-values from 500 to 5000 by increments of 250. The number of repetition for each b-value was determined to ensure uniform SNR across b-values, resulting in a total of 548 DW images. We also imaged a multi-shell (Fig.2ii) with 95 DW-images (5 b=0, 30 b=1000 and 15 images at each of b=1500, 2000, 2500, 3000). The multi-shell HARDI was utilized to estimate the parameters of our model. We then compared the diffusion decay predicted by DIAMOND to the actual measured diffusion decay.
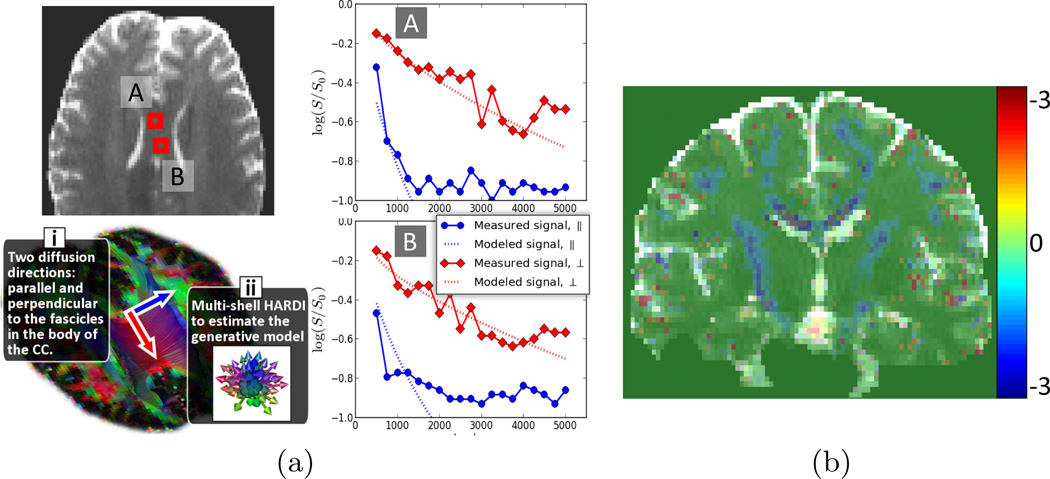
Fig. 2.
(a) Plots of log(Sk/S0). Our model captures the non-monoexponential decay observed in a region of a single fascicle direction. Note that the plotted data points were not used for the model estimation. (b) Cross-testing evaluation: difference between the mean-square prediction error of DIAMOND and MTM (lower is better).
To further characterize DIAMOND, we performed a cross-testing analysis. This procedure consists in repeatedly splitting the set of DW images into a random estimation set and testing set, estimating the parameters with the former and evaluating the performance on the latter. This measures the prediction performance and objectively characterizes how well a model captures a phenomenon. This, however, requires a large number of measurements. We performed a multi-shell acquisition with 395 images (5b = 0 and 15 shells of 26 directions with b ∈ [200, 3000] by increments of 200). We repeated the estimationtesting process 100 times, using at each iteration 70% of the data for estimation and 30% for testing. We computing the mean-square prediction error at each voxel across the iterations. We compared DIAMOND to the multi-tensor model (MTM), which corresponds to using infinitely narrow distributions (pj = ∞).
Finally, a great potential of assessing the distribution of MEs in the brain is the potential derivation of novel bio-markers that reflect the tissues integrity. We imaged a patient with Tuberous Sclerosis Complex (TSC), a genetic disorder characterized by the presence of benign tumors in the brain called cortical tubers. 65 DW-images were acquired with a CUSP65 (CUbe and SPhere) gradient encoding set [7], which achieves multiple b-values and directions with short echo time and high SNR. The data acquisition protocol was approved by the IRB.
3 Results
Fig 2a shows that DIAMOND successfully captures the non-monoexponential decay observed in the body of the corpus callosum. Fig 2b demonstrates that the cross-testing error is qualitatively lower with DIAMOND than with MTM. Quantitatively, a paired t-test on the differences between the testing errors at each voxel shows that DIAMOND is significantly better than MTM (p < 10−8) with a mean error decreased by over 8%. Finally, Fig 3 reports DIAMOND imaging of a TSC patient. It shows decreased concentration parameter pj (i) and increased fraction of unrestricted diffusion (ii) in the region of the tuber.
Fig. 3.
TSC patient with CUSP65 imaging. Particularly, it shows that the orientation of the estimated fascicles (b) and the fractions of occupancy (c) correctly matches the known anatomy, while only 65 DW-images were acquired.
4 Discussion
We proposed a generative model motivated by biophysical considerations of the microstructure that gives rise to the DW signal. Inspired by the approach of [9], we considered that the signal in a voxel is the sum of the signal arising from a large number of homogeneous spin packets within each voxel. In contrast to [9], we considered that each spin packet locally undergoes 3-D Gaussian diffusion described by a diffusion tensor, capturing the 3-D geometrical structure of the local restrictions to water diffusion. We formulated the DIAMOND generative model (4) which describes each large-scale microstructural environment (LSME) in the voxel with a matrix-variate Gamma distribution of spin packets. The concentration of each distribution was estimated, providing a novel measure of the microstructural homogeneity. Interestingly, DIAMOND is equivalent to the multi-tensor model when the distributions are infinitely concentrated. Unlike [5,10], our model does not rely on a convolution kernel with prespecified diffusivity. In contrast to [10], we have considered multiple fascicles per voxel (up to 3). We employed a novel model order selection approach based on the minimization of the generalization error. Using moderate b-values ≤ 3000 s/mm2 (unlike [1]), we showed that both the estimated number of fascicles and fascicle orientations matches the known anatomy, even with a moderate number of DW images (Fig 3b). We showed that DIAMOND captures the non-monoexponential decay (Fig 2a) and better captures the underlying biophysical mechanisms underlying the DW signal formation compared to the MTM (Fig 2b). Interestingly, DIAMOND imaging in a patient with TSC showed that, in the region of the tuber, the estimated fraction of unrestricted diffusion is increased (Fig 3c.ii). This might reflect an increased extra-cellular space, the presence of perivascular spaces, or the presence of giant cells typically observed in TSC brain specimens. Importantly, we observed a reduction in the concentration parameter for the fascicle located in the tuber (Fig 3c.i), indicating an increased anisotropic heterogeneity consistent with the orientation of the fascicle. In contrast, there was no significant heterogeneity consistent with unrestricted diffusion. We speculate that this may reflect heterogeneous myelination or heterogeneous mixture of glial cells as observed in mice models of TSC. In future work we will compare DIAMOND to NODDI and CHARMED with cross-testing, and investigate the possibility of characterizing different types of tubers in TSC. DIAMOND imaging may enable novel investigations in both normal development and in clinical practice.
Acknowledgments
This work was supported in part by NIH grants 1U01NS082320, R01 NS079788-01A1, R01 EB008015, R01 LM010033, R01 EB013248, P30 HD018655, BCH TRP, R42 MH086984, UL1 TR000170 and R21 EB012177. MT was supported by F.R.S-FNRS and B.A.E.F.
References
- 1.Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage. 2005;27(1):48–58. doi: 10.1016/j.neuroimage.2005.03.042. [DOI] [PubMed] [Google Scholar]
- 2.Basser PJ, Pajevic S. A normal distribution for tensor-valued random variables: applications to diffusion tensor MRI. IEEE T. Med Imaging. 2003;22(7):785–794. doi: 10.1109/TMI.2003.815059. [DOI] [PubMed] [Google Scholar]
- 3.Efron B, Tibshirani R. Improvements on cross-validation : The. 632 + bootstrap method. Journal of the American Statistical Association. 1997;92(438):548–560. [Google Scholar]
- 4.Gupta AK, Nagar DK. Matrix Variate Distributions. Boca Raton, Florida: Chapman & Hall/CRC; 2000. [Google Scholar]
- 5.Jian B, Vemuri BC, Ozarslan E, Carney PR, Mareci TH. A novel tensor distribution model for the diffusion-weighted MR signal. Neuroimage. 2007;37(1):164–176. doi: 10.1016/j.neuroimage.2007.03.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Scherrer B, Taquet M, Warfield SK. IPMI. LNCS 7917, Asilomar: USA; 2013. Reliable Selection of the Number of Fascicles in Diffusion Images by Estimation of the Generalization Error; pp. 742–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Scherrer B, Warfield SK. Parametric Representation of Multiple White Matter Fascicles from Cube and Sphere Diffusion MRI. PLoS ONE. 2012;7(11) doi: 10.1371/journal.pone.0048232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sehy JV, Ackerman JJ, Neil JJ. Evidence that both fast and slow water ADC components arise from intracellular space. Magn Reson Med. 2004;48:765770. doi: 10.1002/mrm.10301. [DOI] [PubMed] [Google Scholar]
- 9.Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med. 2003;50(4):664–669. doi: 10.1002/mrm.10578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012;61(4):1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]